A Hierarchical Modeling Approach to Data Analysis and Study Design in a Multi-Site Experimental FMRI Study

Abstract

We propose a hierarchical Bayesian model for analyzing multi-site experimental fMRI studies. Our method takes the hierarchical structure of the data (subjects are nested within sites, and there are multiple observations per subject) into account and allows for modeling between-site variation. Using posterior predictive model checking and model selection based on the deviance information criterion (DIC), we show that our model provides a good fit to the observed data by sharing information across the sites. We also propose a simple approach for evaluating the efficacy of the multi-site experiment by comparing the results to those that would be expected in hypothetical single-site experiments with the same sample size.

1. Introduction

Schizophrenia is a neurocognitive and neuroaffective disease characterized by disordered emotional responsiveness and cognitive dysfunction, deficits in working memory, and reduced frontal and cortical brain volumes in comparison to healthy subjects (APA, 2000; Van Snellenberg, 2009; Glahn, Laird, Ellison-Wright, Thelen, Robinson, Lancaster, Bullmore, & Fox, 2008). Due to the complexity and heterogeneity of symptoms in patients, detailed knowledge of the specific genetic, neurochemical, and neuroanatomical contributions to this disease remains elusive. Understanding the basis of this disease and other cognitive disorders has greatly increased with the use of fMRI (functional magnetic resonance imaging), which can track changes in blood oxygenation in different brain areas over time. This is known as the BOLD (blood-oxygen-level-dependent) signal, and is thought to be correlated with changes in brain activity (DeYoe, Bandettini, Neitz, Miller, & Winans, 1994).

In recent years, there has been a large number of neuroimaging studies performed using fMRI. Statistics play an important role in understanding the resulting data. In her book, Lazar (2008) provides an introduction to fMRI (aimed at statisticians), highlights the important scientific issues in this field, and surveys some common statistical methods. Lindquist (2008) provides a recent survey of the statistical analysis of fMRI data from the initial acquisition of the raw data to its use in locating brain activity. More recently, Woolrich (2012) has reviewed Bayesian inference methods applied to fMRI studies, including haemodynamic modeling, spatial modeling, group analysis, model selection, and brain connectivity analysis. In this paper, we propose a hierarchical Bayesian model for analyzing multi-center fMRI studies.

By utilizing fMRI, several studies have shown that patients diagnosed with schizophrenia display either hypo- or hyper-activation of the dorsolateral prefrontal cortex (DLPFC) during working memory tasks, thus potentially localizing deficits in working memory and other executive processes to the DLPFC (Goghari, Sponheim, & MacDonald, 2010). These results have not been unequivocal, and one primary concern with respect to these studies has been the low number of subjects that are generally involved in single-center fMRI studies (Potkin, Turner, Brown, McCarthy, Greve, Glover, Manoach, Belger, Diaz, Wible, Ford, Mathalon, Gollub, Lauriello, O'Leary, van Erp, Toga, Preda, & Lim, 2009). Since fMRI studies are often limited by the number of subjects that can be recruited at a given site, there has been great interest in performing multi-site studies with the same experimental setup in order to increase the sample size, and thus the statistical power, of a research program (Friedman, Glover, Krenz, & Magnotta, 2006). The challenge in utilizing multiple sites is the introduction of site-specific variability to fMRI results. Such studies need to analytically account for, and ideally minimize, this extra source of variability via study design and statistical analysis of data (Friedman, Stern, Brown, Mathalon, Turner, Glover, Gollub, Lauriello, Lim, Cannon, Greve, Bockholt, Belger, Mueller, Doty, He, Wells, Smyth, Pieper, Kim, Kubicki, Vangel, & Potkin, 2008).

2. Objective

The current study uses multi-center fMRI experimental data collected from the FBIRN (Functional Imaging Biomedical Informatics Research Network) consortium, whose general goal is to make such studies more common by developing optimal experimental and analytic methods that can be utilized by the scientific community (http://www.birncommunity.org/). The specific experiment that we consider examines the differences in DLPFC activation at some regions of interest (ROI) between schizophrenic patients and normal subjects during a working memory task. Our goal is to develop an appropriate statistical model for such studies. We expect that our proposed model provides us with information regarding the most prominent sources of variability in multi-center fMRI experiments. This information could be used to optimize experimental design in future research. Finally, we show how our approach can be used to evaluate the efficacy of the multi-center study by comparing the results of such a study to the expected results of hypothetical single-center studies with an equivalent number of subjects.

To achieve the above objectives, we propose a hierarchical Bayesian model. Our model takes the underlying hierarchical structure (i.e., subjects are nested within sites, and there are multiple observations per subject) of the data into account. This approach provides a simple modular scheme for measuring group, load, gender, hemisphere, age, visit, and handedness effects, which can be easily updated with future experimental observations (Gelman, Carlin, Stern, & Rubin, 2003). The hierarchical Bayesian model also provides information about run, subject, and site variation, which are in turn used to estimate the efficacy of the multi-center study compared to the single-center studies with the same sample size. Using both posterior predictive model checking and model selection based on the deviance information criterion (DIC), we show that the fit of our proposed model to the observed data is substantially better than an alternative model that ignores between-site variation.

3. Experiment

3.1. Sites

The fMRI scanning sites were located in the following institutions: University of California at Irvine (UCI), University of California at Los Angeles (UCLA), University of New Mexico, University of Iowa, University of Minnesota, Duke University/University of North Carolina, Brigham and Women's Hospital, Massachusetts General Hospital (MGH), and Yale University. All sites had obtained approval from their respective Institutional Review Boards for the study. Data analysis was performed at University of California at San Diego (UCSD), Yale, MGH, and UCI.

3.2. Subjects

All subjects recruited for the study were between the ages of 18 and 70, did not have hearing or vision deficiencies, were fluent in English, and were capable of performing the cognitive tasks necessary for the study. Subjects included both males and non-pregnant females, and all subjects were screened for contraindications to MRI. Contraindications included history of major illness, head injury or prolonged unconsciousness, substance (and/or alcohol) abuse, low IQ, or use of migraine treatments. Subjects were recruited for either a healthy comparison group or a schizophrenic/schizoaffective group. Volunteers in the healthy group did not have a first-degree relative with diagnosis of psychotic illness. Volunteers with schizophrenia or schizoaffective disorder had been diagnosed using DSM-IV criteria and had been clinically stable, with no significant changes in psychotropic medications in the past two months, but were excluded if they had significant extrapyramidal symptoms or tardive dyskinesia. Standardized diagnostic evaluations for all subjects were performed as described in Potkin et al. (2009).

3.3. Cognitive Testing

The experiment used the Sternberg Item Recognition Paradigm (SIRP) proposed by Sternberg (1966). This test consists of an encode phase, where subjects memorize a set of target digits. This is followed by a probe phase, where the subjects are presented with single digits, called probes. During this phase, the subjects respond by indicating whether the probe is a target (by pressing with their index finger) or not (by pressing with their middle finger). The SRIP task involved three working memory loads of 1, 3, or 5 target digits, each presented for 6 seconds. For memory loads 1 and 3, asterisks were presented in place of extra digits so that there were still five presented items for each load condition. In the probe phase, the subjects were presented with 14 single digits (probes) for 2.7 seconds each. Only half of the probes were targets. Each run consisted of the three loads presented in a pseudorandom manner, with two memory sets per load. See Potkin et al. (2009) for more detailed discussion of the experiment.

3.4. Scanning and Pre-processing

Imaging protocols were optimized to the site-specific scanners, thus certain sites used spiral acquisitions while others used linear k-space trajectories. As discussed in Potkin et al. (2009), the scanning session consisted of a localizer scan as needed to identify the AC-PC axis; any shimming that a site used (higher order when possible); a 3D T1-weighted scan (FSPGR on GE; MP-RAGE on Siemens scanners, 24 cm FOV, 1.2–1.5 mm slice thickness, 160–170 slices as needed to cover the entire head, sagittal orientation); a T2 scan which set the slice prescription for the remaining EPI scans (FOV 22 cm, 27 slices if possible, 4 mm thickness with a 1 mm gap, 256 × 192 matrix), and the functional scans. The functional scans were T2*-weighted gradient echo EPI sequences, with TR = 2, TE = 30 ms, flip angle 90 deg, acquisition matrix 64 × 64, 22 cm FOV, 27 slices when possible, 4 mm thick with 1 mm gap, oblique axial AC-PC aligned. Six seconds (three acquisitions) of scans were discarded at the beginning of each functional run. Subjects were tested in two different sessions (Visit 1 and Visit 2). Each scan session lasted approximately 1.5 hours. Before the first session there was a brief training session to familiarize the subject with the paradigms in which subjects were required to achieve at least 75 % correct on the SIRP task. The entire procedure was repeated 24 hours to 3 weeks later for the second visit.

Pre-processing was performed at UCSD in collaboration with MGH using FSL (Smith, Jenkinson, Woolrich, Beckmann, Behrens, Johansen-Berg, Bannister, De Luca, Drobnjak, Flitney, Niazy, Saunders, Vickers, Zhang, De Stefano, Brady, & Matthews, 2004), and included motion correction, B0 distortion correction (except for data from scanners that collected spiral images), and slice timing correction. Generalized linear models (GLM) were applied to obtain the activation map. A region of interest (ROI) analysis was used to examine the mean BOLD signal changes in an atlas-based demarcation of the DLPFC. A working version of the data, which consisted of the mean signal change of the activation, denoted as Y, in the left and right hemispheres of the DLPFC was compiled by UCSD for use by FBIRN investigators. The analysis provided in this current paper is based on this dataset. See Potkin et al. (2009) for more detailed description of the data.

3.5. Exploratory Data Analysis

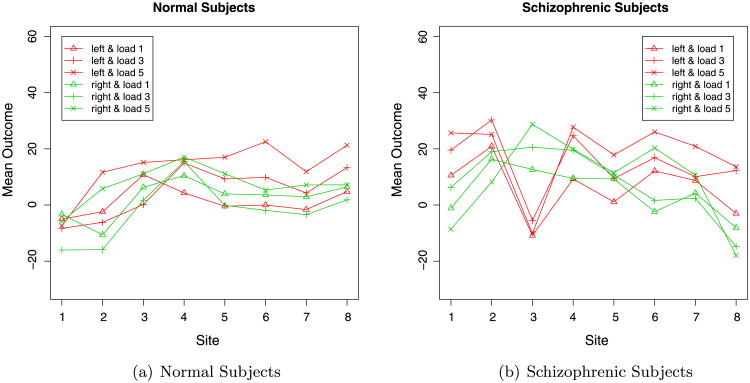
The data include 191 subjects (95 normal and 96 schizophrenic) at eight sites. Figure 1 visualizes the variation of outcomes across sites given group, hemisphere, and load. As is evident in Panels (a) and (b) of Figure 1, there are substantial site differences. In addition, there exists a significant difference between normal subjects and schizophrenic subjects. Moreover, we can see that the left hemisphere (red lines) tends to have higher activation than the right hemisphere (green) across all loads, all sites, and both groups. Substantial load effects are also seen in the two figures. We also notice that Site 3 has a substantially different pattern from other sites.

Figure 1.

Data pattern for normal and schizophrenic subjects. The left panel shows the average response for normal subjects. The right panel shows the average response for schizophrenic subjects. The horizontal axis shows the site number. The vertical axis shows the mean outcome across subjects given site, group, hemisphere, and loads. The site number does not have metric ordering. Connecting points with lines, however, helps to visualize the variation of different outcomes.

Through our exploratory data analysis, we identified an outlier for which the observed measure (Visit 2, Run 3, Load 5 for left hemisphere) was −2,999.00. The typical measurements are between −300 and 300. This was deemed to be a data recording mistake; therefore, we removed the outlier from subsequent data analysis.

4. Methods

4.1. A Hierarchical Model for DLPFC Activation

We propose a hierarchical Bayesian model to examine the difference in DLPFC activation between schizophrenic patients and normal subjects during a working memory task, while accounting for the underlying data structure (i.e., dependencies among repeated measures) and the between-site variation. For hemisphere h, load l, and group g, the observed data (i.e., the average percent signal change of the activation) for the three runs of each visit for subject i at site s are assumed to be normally distributed as follows:

$$Y_{sijk}^{hlg}\sim N({\mu }_{sij}^{hlg},{\sigma }_{\mathit{\text{run}}}^2).$$ (1)

Here, j is the index for visits, and k is the index for runs. It is common for practitioners to average results over runs before analyzing the data. The model we propose, however, allows us to account for variability across runs, which is useful for our specific study design. In this model, ${\sigma }_{\mathit{\text{run}}}^2$ represents run variation. The assumption of a normal distribution seems to be reasonable based upon previous studies (we later discuss a more robust alternative model based upon the Student's t distribution). Further, we assume visit means, ${\mu }_{sij}^{hlg}$, for each subject (given hemisphere, load and group) are normally distributed with a subject-specific mean depending on the overall group effect for a given hemisphere and load, α^hlg, as well as a site effect, ${\gamma }_{si}^{hlg}$,

$${\mu }_{sij}^{hlg}\sim N({\alpha }^{hlg}+{\gamma }_{si}^{hlg},{\sigma }_{\mathit{\text{sub}}}^2),$$

where ${\sigma }_{\mathit{\text{sub}}}^2$ represents subject variance. The group effect is further defined as α^hlg = β₁X_g + β₂X_h + β₃X_l3 + β₄X_l5, where: X_g is the group indicator, with 1 indicating the schizophrenic group and 0 indicating the normal group; β₁ is the expected difference (group effect) between schizophrenic and normal subjects; X_h is a binary indicator for hemisphere, where 1 corresponds to the right hemisphere and 0 corresponds to the left hemisphere; β₂ represents the expected difference (hemisphere effect) between the right hemisphere and the left hemisphere; X_l3 and X_l5 are load indicators where (X_l3 = 0, X_l5 = 0) means Load 1, (X_l3 = 1, X_l5 = 0) indicates Load 3 and (X_l3 = 0, X_l5 = 1) indicates Load 5; and β₃ and β₄ are the expected difference (load effect) between Load 3 and Load 1 and the expected difference between Load 5 and Load 1, respectively. Note that the model for α^hlg could, but does not, include interactions between hemisphere, group and loads. Finally, site effects, ${\gamma }_{si}^{hlg}$, are assumed to be normally distributed with subject-specific site effects, b_si, and within-subject site variance, ${\sigma }_{\mathit{\text{site}}{W}_s}^2$, and then b_si itself is given a normal prior with a site-specific mean, b_s, and across-subject site variance, ${\sigma }_{\mathit{\text{site}}{A}_s}^2$,

$${\gamma }_{si}^{hlg}\sim N(b_{si},{\sigma }_{\mathit{\text{site}}{W}_s}^2),$$ (3)

$$b_{si}\sim N(b_s,{\sigma }_{\mathit{\text{site}}{A}_s}^2).$$ (4)

Note that ${\sigma }_{\mathit{\text{site}}{W}_s}^2$ represents variation of site effects over different measurements within the same subject, and ${\sigma }_{\mathit{\text{site}}{A}_s}^2$ represents variation of site effects across subjects. Furthermore, both ${\sigma }_{\mathit{\text{site}}{W}_s}^2$ and ${\sigma }_{\mathit{\text{site}}{A}_s}^2$ depend on site s.

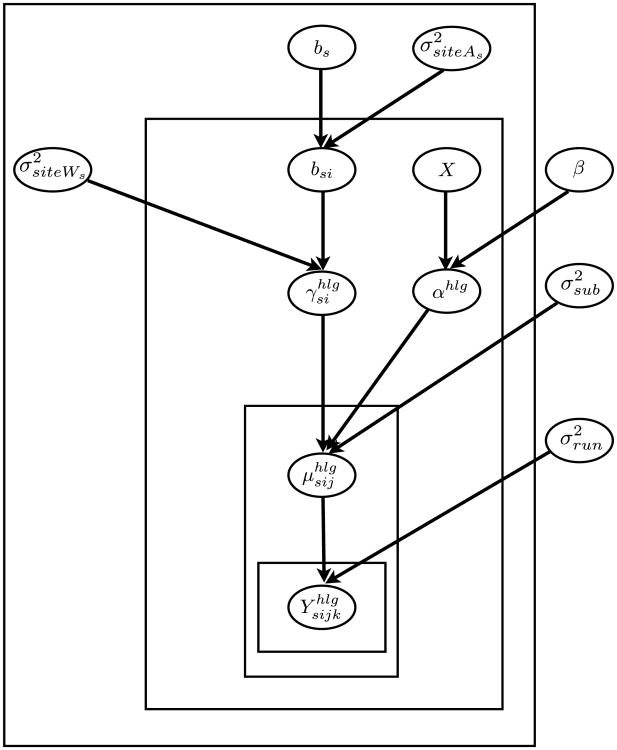
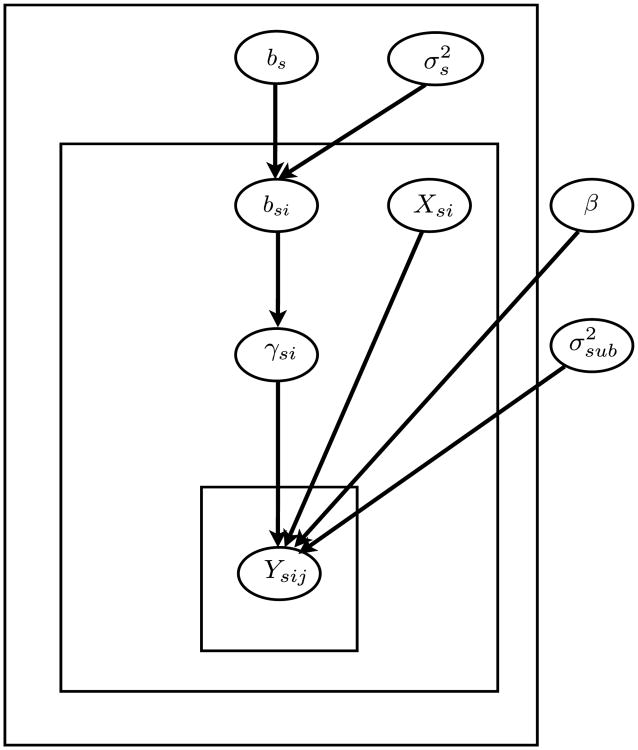
Figure 2 shows a schematic representation of the above hierarchical model. This model provides a framework to capture dependencies among the observations at the lowest level, and among model parameters at higher levels.

Figure 2.

Schematic representation of the hierarchical Bayesian model. Nodes (in ovals) are model parameters and random variables; arrows represent dependencies between nodes. Within each box, nodes are replicated. The only observed nodes are X = (X_g, X_h, X_l3, X_l5) and $y_{sijk}^{hlg}$.

4.2. Model Checking

Our hierarchical Bayesian model takes between-site variation into account while measuring the effects of primary interest (e.g., the group effect). To show why it is important to incorporate between-site variation, we compare our proposed model to an alternative approach that ignores between-site variation and combines all observations from different sites as if they were obtained from a single site. We refer to this model as the complete-pooling model. In contrast, our model allows for different site effects, b_s, for each site while providing partial pooling of site effects towards their overall mean. Here, our model combines information from different sites and hence should improve inference. Such models tend to provide a better fit to the observed data by capturing the overall pattern presented by the data, as well as capturing deviations from the overall pattern in individual clusters (e.g., sites in our data). See Gelman et al. (2003) for an example. Note that another alternative model could be the no-pooling model, where a separate model is fitted to each site. For such models, there is no learning across sites, and the estimates for each site would be obtained based on a relatively small sample. Moreover, in this approach, our findings are specific to each site, such as the group effect, and may not be generalized. Thus, we do not consider the no-pooling model here.

The complete-pooling model can be explained using similar notations as used above for the partial-pooling model. Individual run measurements, $Y_{sijk}^{hlg}$, are assumed to be normally distributed with a visit mean (Equation (1)); and visit means are normally distributed with a subject mean (Equation (2)). Hence, we write the complete-pooling model as follows:

$$\begin{array}{c}{Y}_{sijk}^{hlg}\sim N({\mu }_{sij}^{hlg},{\sigma }_{\mathit{\text{run}}}^2),\\ {\mu }_{sij}^{hlg}\sim N({\alpha }^{hlg},{\sigma }_{\mathit{\text{SubSite}}}^2).\end{array}$$

That is, the subject means depend only on the group, hemisphere, and load effects but not on site effects. Note that the first hierarchical level of the complete-pooling model is the same as our hierarchical model while the second level is different. In this model, ${\sigma }_{\mathit{\text{SubSite}}}^2$ represents a combination of subject variance and site variance; these two sources of variation cannot be estimated separately in this model. An alternative way to look at this specification is that it implicitly assumes ${\sigma }_{\mathit{\text{site}}{W}_s}^2={\sigma }_{\mathit{\text{site}}{A}_s}^2=0$. Note that the complete-pooling model is still a hierarchical model, but it is simpler than our proposed model since it does not distinguish between sites.

One possible approach to comparing models with respect to their goodness-of-fit is posterior predictive model checking (Gelman et al., 2003). To this end, we first fit a model to the observed data, y^obs, and then use the resulting model to replicate (i.e., simulate) many data sets, y^rep. We compare y^rep to y^obs using a test quantity, T, that captures an important aspect (e.g., mean, variance) of the data. In our analysis, we use site-specific means as our test quantity. We use T^rep to denote the values of the test quantity for the replicated data sets, and T^obs to denote the value of the test quantity for the observed data. If the model fits the data well, we expect T^rep to be close to T^obs. Therefore, we use the tail probability of T^obs with respect to the distribution of T^rep, i.e., P (T^obs ≤ T^rep), to measure the goodness-of-fit for a given model. We estimate P (T^obs ≤ T^rep) by finding the proportion of replicated datasets for which T^obs ≤ T^rep. In general, we prefer models for which this estimate is close to 0.5.

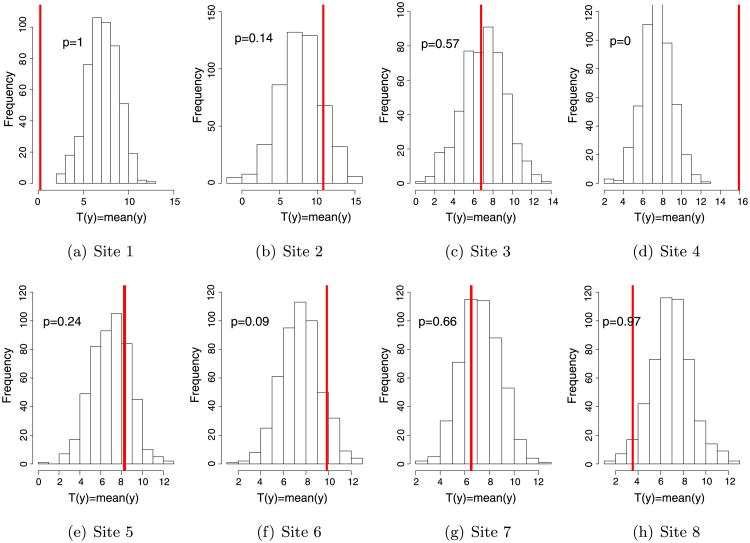
The results for the complete-pooling model are shown in Figure 3. The histograms suggest that a model without site effects is not able to replicate the observed data well. More specifically, the estimate of tail probabilities for Sites 1, 4, 6, 8 are far from 0.5; they are either close to 0 or 1. Table 1 compares the tail probabilities of the partial-pooling model and the complete-pooling model. Clearly, the partial-pooling model provides a better fit to the data by this measure.

Figure 3.

Histogram of posterior distribution of site-specific means simulated from the complete-pooling model. Each panel shows the histogram of posterior distribution of the test quantity (mean) at each site. The vertical red line indicates the observed value of the test quantity at each site. The legend shows the tail probability of the observed value.

Table 1.

Tail probabilities for the partial-pooling model and complete-pooling model. These probabilities should be close to 0.5; values close to 0 or 1 are interpreted as lack of fit. The results suggest that the partial-pooling model proposed in this paper provides a better fit to the data.

Tail probability	Site 1	Site 2	Site 3	Site 4	Site 5	Site 6	Site 7	Site 8
Complete pooling	1.00	0.14	0.57	0.00	0.24	0.09	0.66	0.97
Partial pooling	0.45	0.47	0.45	0.46	0.45	0.45	0.43	0.45

While the above approach provides a simple framework for comparing alternative models, it is often useful to provide a single formal measure of fit. Moreover, the posterior predictive model checking is known to be asymptotically conservative, i.e., favors the null hypothesis (Robins, van der Vaart, & Ventura, 2000). To address this issue, we use a model selection criterion, namely, the Deviance Information Criterion (DIC), to compare the above two models (Spiegelhalter, Best, Carlin, & van der Linde, 2002). For the complete-pooling model, the DIC is 70661. For the partial-pooling model, the DIC is 70023, which is substantially lower than that of the complete-pooling model. Therefore, our conclusion remains as before: the partial-pooling model fits the data better compared to the complete-pooling model.

4.3. Robust Inference Using a t-Distribution Model

Inference under the normal model assumed for $Y_{sijk}^{hlg}$ can be dramatically changed by outliers. To make a more robust inference, we can replace the normal distributions in our hierarchical model by the heavier-tailed Student's t-distribution. To this end, we replace (1) in our hierarchical model by

$$Y_{sijk}^{hlg}\sim t_v({\mu }_{sij}^{hlg},{\sigma }_{\mathit{\text{run}}}^2),$$ (5)

which is equivalent to

$$Y_{sijk}^{hlg}\sim N({\mu }_{sij}^{hlg},V_{sijk}^{hlg}),$$ (6)

$$V_{sijk}^{hlg}\sim \text{Inv}-{\chi }^2(v,{\sigma }_{\mathit{\text{run}}}^2).$$ (7)

The remaining parts of our hierarchical Bayesian model remain as before. For this model, most of the parameters have the same interpretation as our original model, except for ${\sigma }_{\mathit{\text{run}}}^2$, which is the scale parameter in the t -distribution and cannot be directly interpreted as run variance. In addition, this model involves a new parameter, ν, which represents the degrees of freedom. For simplicity, we set ν to a fixed value. Note that as ν goes to infinity, the t model approaches the normal partial-pooling model discussed above. It is also possible to consider the t -distribution at other levels of the hierarchical model, but we do not expect outliers there.

Our results (not shown here) suggest that there is no substantial difference between the normal and the robust t model in terms of posterior predictive model checking. However, with respect to the DIC, the robust t model performs better than the normal model. The DIC for the t model is 67,658, which is substantially lower than 70,023 for the normal model. This was expected because the t distribution has a much heavier tail than the normal distribution. As a result, it can handle outliers better. In the next section, we provide the parameter estimates for both the normal and t models.

5. Results

Statistical inference is performed based on the posterior probability of model parameters given the observed data. For our normal and t models, we use noninformative priors for the effect parameters (e.g., β₁) mainly for computational convenience. More specifically, we assume f (β) ∝ 1, where β = (β₁,β₂,β₃,β₄). While this prior distribution is improper, the posterior distribution is proper. For variance parameters (e.g., ${\sigma }_{\mathit{\text{run}}}^2$), we use the weakly informative prior Inv-χ²(1,10), whose 95 % probability interval is approximately [0,2500]. We chose this prior distribution since we do not expect variances that are larger than 2500. In practice, we could use our domain knowledge to specify more informative priors for model parameters.

We use Markov Chain Monte Carlo (MCMC) methods to simulate samples from the posterior distribution of model parameters. This is described in Appendix A. While our model involves a rather complex hierarchical structure, it does not require intensive computation. Using the R implementation of our model, it takes approximately 20 minutes to obtain 20,000 samples from the posterior distribution of the parameters.

The results in Table 2 suggest that for our hierarchical model, the expected difference between schizophrenic subjects and normal subjects, β₁, is 5.79, which is significant considering the 95 % posterior credible interval [1.3, 10.6]; the expected difference between the right hemisphere and left hemisphere β₂ is −6.02, the expected difference between Load 3 and Load 1, β₃, and the expected difference between Load 5 and Load 1, β₄, are 3.67 and 9.25, respectively. Notice that the effect increases from Load 3 to Load 5. Considering the corresponding 95 % posterior intervals, these effects are considered to be statistically significant.

Table 2.

Posterior expectations and posterior intervals of the group effect, β₁, hemisphere effect, β₂, load effects, β₃ and β₄, based on the normal and t models.

	Normal model		t model
	Posterior expectation	Posterior interval	Posterior expectation	Posterior interval
β1	5.79	(1.32, 10.63)	5.10	(0.78, 9.37)
β2	−6.02	(−8.10, −3.92)	−4.45	(−6.27, −2.27)
β3	3.67	(1.13, 6.14)	3.23	(1.11, 5.37)
β4	9.25	(6.74, 11.75)	9.39	(7.23, 11.60)

While the above estimates change to some extent when we replace the normal distribution in the hierarchical model by the Student's t-distribution for robust inference (Table 2), our overall inference with respect to significance (based on posterior intervals) of group effects, hemisphere effects and load effects remains as before.

Using the normal model, the posterior expectation of run variance ${\sigma }_{\mathit{\text{run}}}^2$ is 1,333, which indicates a large amount of variability from run to run. However, the estimate of subject variance, ${\sigma }_{\mathit{\text{sub}}}^2$, is 80, which indicates a relatively smaller amount of variability across subjects. Variation of site effects within subjects, ${\sigma }_{\mathit{\text{site}}{W}_s}^2$, and across subjects, ${\sigma }_{\mathit{\text{site}}{A}_s}^2$, change substantially from one site to another (Table 3). The estimates in Table 3 confirm our previous findings that Site 3 is quite different from the other sites. The estimated within-subject site variance is extremely large for this site; whereas, its estimated across-subject site variance is relatively small. This is an unusual pattern because it means the site effect for load, hemisphere, and group differs substantially for a single subject. This issue (i.e., high within-subject site variance) is also present but less severe in Site 1.

Table 3.

Estimates (using posterior expectations) of variance of site effects within the same subject, $({\sigma }_{\mathit{\text{site}}{W}_s}^2)$, and across subjects, $({\sigma }_{\mathit{\text{site}}{A}_s}^2)$, based on our hierarchical model with the normality assumption for observed measurements, and the estimated conditional variance of group effects for single-center studies, Var(β₁|Y,Σ̂_s). For our multi-center study, Var(β₁|Y,Σ̂_m) = 6.23. The last column shows the information, e_s = 1 − Var(β₁|Y,Σ̂_m)/Var(β₁|Y,Σ̂_s), gained by the multi-center study compared to hypothetical single-center studies based on the hierarchical Bayesian model.

	${\sigma }_{\mathit{\text{site}}{W}_s}^2$	${\sigma }_{\mathit{\text{site}}{A}_s}^2$	Var(β1|Y,Σ̂s)	es
Site 1	298.5	198.1	6.06	−2.87 %
Site 2	12.7	197.3	5.08	−22.61 %
Site 3	1145.6	44.7	5.88	−6.00 %
Site 4	6.3	215.6	5.47	− 13.85 %
Site 5	8.7	344.0	8.25	24.39 %
Site 6	89.7	114.7	3.63	−71.71 %
Site 7	11.3	411.6	9.68	35.64%
Site 8	64.1	413.2	10.02	37.77 %

6. Quantifying the Efficacy of the Multi-center Study Compared to Single-Center Studies

In this section, we propose a simple method to evaluate the efficacy of the multi-center study using our hierarchical Bayesian model. To this end, we compare our multi-center study to a hypothetical single-center study with the same number of subjects. In reality, however, we do not have the data for such a single-center study since we could not send all the subjects to one center. Fortunately, we can use the probability model we have developed to assess what would be expected in such a scenario. On the one hand, we might expect that a multi-center study would not be as effective as a single-center study with an equivalent number of subjects because of the additional source of variation due to the site effects. On the other hand, we might expect that a multi-center study might be more effective compared to a single-center study that is carried out at a single site with a very large within-site variance. That is, given that there appears to be substantial subject-to-subject variation at one site, the magnitude of that variation can be critically important. As expected, we find that a multi-center study would not be as efficient as a similarly sized single-center study at a site with relatively low site variation, but it could be more efficient if the single-center study has relatively high site variation.

To compare our model to a hypothetical single-center study, it is necessary to choose a measure of efficacy. Since the measurement of interest in this case is the group effect, β₁, we use its posterior variance to compare different study designs; the smaller the variance, the better the precision of our estimate. Let ${\tau }_m^2$ be the variance of the group effect based on a multi-center study, and ${\tau }_s^2$ be the variance of group effect based on a hypothetical single-center study with the same number of subjects at site s. Then,

$$E_s=1-\frac{{\tau }_m^2}{{\tau }_s^2}$$ (8)

measures how much precision gained or lost by the multi-center study design compared to the single-center study design at site s. In our case, s = 1,…, 8.

While it is possible to estimate ${\tau }_m^2$ directly by using the posterior samples from our model, we cannot estimate ${\tau }_s^2$ directly since, in reality, we did not send all subjects to one center.

We can, however, use the parameter estimates (posterior expectations) obtained based on our hierarchical model to calculate the “conditional variance” of β₁ given the observed data, Y, and its corresponding covariance matrix, Σ. Here, Y is the vector of observations $\{Y_{sijk}^{hlg}\}$, and Σ is the covariance matrix that measures dependency between observations. More specifically, we use the posterior expectations of model parameters from our hierarchical Bayesian model to estimate Σ;. We denote this estimate Σ̂. Consequently, we use the following measure of efficacy (based on the conditional variance) to compare the multi-center study to a hypothetical single-center study with the same number of subjects at site s:

$$e_s=1-\frac{Var({\beta }_1|Y,{\widehat{\sum }}_m)}{Var({\beta }_1|Y,{\widehat{\sum }}_s)}.$$ (9)

Here, Σ̂_m is the estimated covariance matrix of Y for the multi-center study, and Σ̂_s is the estimated covariance matrix of Y, assuming that all the subjects are sent to site s. Appendix B shows the derivations of Var(β₁|Y, Σ̂_m) and Var(β₁|Y, Σ̂_s).

Using the above approach, we first estimate the conditional variance of group effects for single-center study, Var(β₁|Y, Σ̂_s), and multi-center study, Var(β₁|Y, Σ̂_m). These estimates are presented in Table 3. Next, we calculate the efficacy of the multi-center study compared to a single-center study for different sites. The last column of Table 3 shows these results for the 8 sites. The results suggest that the multi-center study gains approximately 24.39 % more information compared to the single-center study at Site 5, 35.64 % more information compared to the single-center study at Site 7, and 37.77 % more information compared to the single-center study at Site 8. However, the multi-center study loses approximately 2.87 %, 22.61 %, 6.00 %, 13.85 % and 71.71 % information compared to the single-center studies at sites 1, 2, 3, 4, and 6.

Considering the results provided in Table 3, it becomes clear that the relative efficacy of our multi-center study tends to be mainly determined by across-subject site variation, ${\sigma }_{\mathit{\text{site}}{A}_s}^2$, at site s. For Sites 5, 7, and 8, site variances across subjects are relatively large compared to Sites 1, 2, 3, and 4 (Table 3).

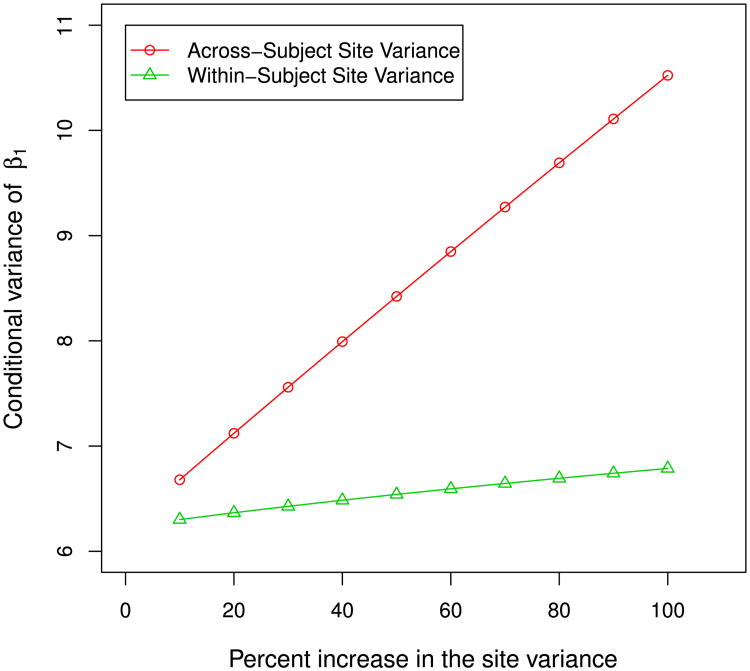
Figure 4 illustrates this finding (i.e., the relative efficacy is mainly dominated by across-subject site variance) using simple simulations. To this end, we gradually increase ${\sigma }_{\mathit{\text{site}}{A}_s}^2$ while keeping all other parameters fixed, and re-calculate the conditional variance of the group effect, β₁. Next, we gradually increase ${\sigma }_{\mathit{\text{site}}{W}_s}^2$ while keeping all other parameters fixed, and recalculate the conditional variance of β₁. The plots in Figure 4 show that the conditional variance of β₁, which was used to measure the overall efficacy of multi-center studies, is mainly influenced by ${\sigma }_{\mathit{\text{site}}{A}_s}^2$. This verifies the results presented in Table 3, where the single-center studies at Sites 5, 7, and 8 are less effective when compared to a multi-center study with the same number of subjects. For these three centers, the across-subject site variances are much larger than the other sites (see Table 3). Furthermore, while Site 3 has an extremely large within-subject site variation, it is still more efficient than the multi-center study because of its relatively small across-subject site variation. Of course, this does not mean that within-subject variance is not important. As we can see in Table 3, Site 1 and Site 2 have similar across-subject site variation while Site 1 has a much larger within-subject site variation. Therefore, it is not surprising that Site 1 is less effective than Site 2 based on their one-to-one comparison with a multi-center study (Table 3).

Figure 4.

Increase in conditional variance of β₁ corresponding to the increase in the across-subject or within-subject site variance. The x axis represents percent increase of either across-subject or within-subject site variance, and the y axis represents the conditional variance of β₁.

Finally, we compare our multi-center study to a hypothetical single-center study whose site variances within and across subjects are the median of the site variances over the 8 different sites. The efficacy measure in this case, denoted as e₀, is −15.81 %. This implies that overall the multi-center study is less efficient than a typical (using the median) single-center study with an equivalent number of subjects.

7. Results for Simulated Data

To examine the performance of our proposed approach in Section 6, we conduct three simulation studies with a simpler experimental structure compared to the real study discussed above. The data are simulated according to the following model:

$$\begin{array}{c}{Y}_{sij}\sim N({\gamma }_{si}+\beta X_{si},{\sigma }_{\mathit{\text{sub}}}^2),\\ {\gamma }_{si}\sim N(b_s,{\sigma }_s^2),\\ b_s\sim N(0,5).\end{array}$$

Here, Y_sij is the observation at the jth visit for the ith subject at site s, X_si is a binary group indicator (i.e., healthy vs. schizophrenic) for that subject, ${\sigma }_{\mathit{\text{sub}}}^2$ is the subject variance, γ_si is the random subject-specific site effect, b_s is the site effect, and ${\sigma }_s^2$ is within-site variance at site s. The schematic representation of this model is shown in Figure 5. Note that this structure resembles that of the real study discussed in this paper, but it does not include hemisphere and load, nor does it incorporate the multiple runs for each visit. This allows us to focus on the multi-center study design issue.

Figure 5.

Schematic representation of the hierarchical Bayesian model used to simulate data. This resembles our hierarchical Bayesian model for real data, but it does not include hemisphere and load, nor does it incorporate the multiple runs for each visit.

For all three simulations, we set β = 5 and ${\sigma }_{\mathit{\text{sub}}}^2=100$. These values are close to what we estimated based on the real data. Further, we assume that there are eight sites, s = 1,…,8, where each site includes 15 healthy subjects and 15 patients. For each subject, we obtain five observations. Therefore, we obtained 150 observations from each site with a total number of 1,200 observations over all eight sites.

In Simulation 1, we assume equal site variance at each site, ${\sigma }_s^2=200$, for s = 1,…, 8. In Simulation 2, we allow site variance change from one site to another by randomly sampling ${\sigma }_s^2$ from Uniform (150, 250). Finally, in Simulation 3, we allow larger variation in ${\sigma }_s^2$ across sites by randomly sampling its values from Uniform(100, 300). For each simulation, we generate 100 datasets according to the above multi-center model.

For each replicated dataset, we record the number of times the multi-center study is more efficient than single-center studies, i.e., e_s > 0. Table 4 shows that on average (over 100 replicated dataset), the multi-center study is more efficient than single-center studies (with equivalent number of subjects) slightly more than 50 % of the time.

Table 4. Results for our three simulation studies.

The first two rows show the percentage of the times our hierarchical model for multiple centers is more efficient (based on e_s and E_s) than single-center studies with the same number of subjects. The last two rows show the results of comparing our hierarchical model to a typical single center (with median values) based on e₀ and E₀. Numbers in parentheses are the corresponding standard errors for the estimates.

	Simulation 1	Simulation 2	Simulation 3
% of es > 0	56.1 (1.1)	54.5 (1.1)	58.5 (1.1)
% of Es > 0	54.8 (3.3)	57.0 (2.9)	58.3 (2.1)
Mean of e0(%)	4.2 (0.6)	3.1 (0.6)	7.2 (0.9)
Mean of E0(%)	−0.6 (2.5)	3.2 (2.8)	7.5 (2.5)

Unlike the real situation discussed in Section 6, we can estimate ${\tau }_s^2$ directly by simulating 1,200 data points (120 healthy subjects and 120 patients with five observations per subject) for site s. That is, we can simulate the scenario where all subjects are sent to a single-center site s. Using these estimates, we can calculate E_s (Equation (8)) directly using the posterior variance of the effect parameter β. We simulate 100 data sets with 1,200 data points for each site to obtain E_s. For each simulated dataset, we first measure the relative efficiency of the multi-center study compared to single-center studies using $E_s=1-\frac{{\tau }_m^2}{{\tau }_s^2}$, where ${\tau }_m^2$ and ${\tau }_s^2$ are estimated by the posterior variances of β for the multi-center study and the single-center study at site s, respectively. For each simulation scenario, the percentage of E_s > 0 are shown in Table 4. The results based on e_s and E_s are quite comparable. Moreover, notice that the overall efficacy of the multi-center study based on E_s improves from Simulation 1 to Simulation 3.

Next, we calculate e₀ to compare the multi-center to a single-center study at a typical site, whose site variance is the median of the site variances over the eight different sites. Table 4 shows the average of e₀ over 100 simulated data sets. Overall, the point estimates indicate that the multi-center study performs slightly better than a typical single-center study. As before, we can calculate E₀ for simulated data by using the direct estimates (as opposed to using the conditional variances) of ${\tau }_m^2$ and ${\tau }_s^2$, where s in this case refers to a typical site (i.e., site variance is the median of the site variances over the eight different sites). As we can see in Table 4, the estimates of E₀ and e₀ are quite comparable for Simulation 2 and Simulation 3. However, for Simulation 1 (equal site variance), using e_s instead of E_s leads to a slightly optimistic evaluation of the efficacy of the multi-center study. (Note that in real situations we cannot calculate E_s directly.) This scenario (i.e., equal site variance) is, of course, quite unlikely in real situations. Notice that the overall efficacy of the multi-center study based on E₀ improves from Simulation 1 to Simulation 3.

8. Discussion

We have proposed a hierarchical Bayesian model for analyzing data from multi-center studies. Using our model, we have found that group effect, hemisphere effect, and load effects are all statistically significant. More specifically, activation of the DLPFC of schizophrenic subjects is significantly higher than that of normal subjects; activation of the DLPFC of right hemisphere is significantly lower than that of left hemisphere; and as load increases, there is a significant increase in the activation of the DLPFC.

Throughout this paper, we used noninformative priors for effect parameters and weakly informative priors for variances. This was mainly for computational convenience. In practice, one might want to choose more informative priors based on previous studies. Our model can be easily extended to accommodate informative priors.

Using posterior predictive checking and DIC, we evaluated how well our model fits the observed data. While we found that our model provides a reasonable fit, it is possible to specify the hierarchical structure differently. For example, we could simplify the model by assuming that the six runs of two visits are exchangeable. Alternatively, we could use a more complex structure, where the distributions of run, visit, and site variation change between different groups (schizophrenic vs. normal). However, we believe that the model proposed in this paper has a reasonable degree of complexity.

In our model, uncertainty is explicitly attributed to run variation, subject variation, site variation within subject, and site variation across subjects. We use our estimates for these different sources of variation to calculate the relative efficacy of the multi-center study compared to hypothetical single-center studies with the same number of subjects.

When comparing a multi-center study to a single-center study with typical values (e.g., median over all centers) of within-subject and across-subject variation, we found that the loss in efficacy is rather small (approximately 16 % in this study). Moreover, we show that multi-center studies could have advantages over single-center studies (with equivalent number of subjects) at sites with large across-subject variation.

For the study discussed in this paper, within-subject variation is very large for Site 3 (1,175.5). To investigate the influence of this site on the overall results, we removed the site from the data, and repeated our analysis. We did not find substantial changes in parameter estimates. Overall, removing Site 3 with large within-subject variation does not have a substantial impact on our analysis (Table 5).

Table 5.

Information gained by the multi-center study without Site 3 compared to single-center studies based on the hierarchical Bayesian model.

	Site 1	Site 2	Site 4	Site 5	Site 6	Site 7	Site 8
es	−5.94 %	−48.74 %	−12.47 %	25.91 %	−69.65 %	36.35 %	40.67 %

Using simulation studies, we can verify our findings based on the real data. Specifically, we show that the multi-center study could be effective in aggregating data across several sites without substantial loss of information. In fact, our simulation studies show that if we allow for higher levels of across-subject variation, multi-center studies can have a better overall performance compared to single-center studies.

While our results suggest that by using proper models the multi-center study can perform reasonably well, more focused investigations are required to identify design choices that can lead to higher efficiency and statistical power for such studies. Also, thorough investigations are needed to identify potential pitfalls for these models; that is, we need to find conditions that could lead to substantial loss of information in multi-center studies.

Our model can be extended to fMRI data on the time series level, which is typically considered in fMRI data analysis. For such data, we need to include parameters that capture time effects along with group effects.

Although the relative efficacy measure we proposed in this paper seems reasonable, it is conceivable that more informative model comparison measures (specifically designed for comparing multi-center and single-center studies) could be proposed. Future research directions could involve finding such measures. Another possible research direction is extending our model to allow for incorporating more information on subjects. For example, we can include clinical measures and demographic variables in our model.

Appendix A

A.1. Gibbs Sampler for the Normal Model

For our hierarchical Bayesian model with normal distribution, we use Markov Chain Monte Carlo (MCMC) to sample from the posterior distribution of model parameters. Given a weakly informative prior $f({\sigma }_{\mathit{\text{run}}}^2)\propto \text{Inv}-{\chi }^2(1,10)$ for ${\sigma }_{\mathit{\text{run}}}^2$, we sample visit mean and run variance as follows:

$$\begin{array}{c}{\mu }_{sij}^{hlg}\sim N(\frac{\frac{{\alpha }^{hlg}+{\gamma }_{si}^{hlg}}{{\sigma }_{\mathit{\text{sub}}}^2}+\frac{3{\overline{Y}}_{sij}^{hlg}}{{\sigma }_{\mathit{\text{run}}}^2}}{\frac{1}{{\sigma }_{\mathit{\text{sub}}}^2}+\frac{3}{{\sigma }_{\mathit{\text{run}}}^2}},\frac{1}{\frac{1}{{\sigma }_{\mathit{\text{sub}}}^2}+\frac{3}{{\sigma }_{\mathit{\text{sub}}}^2}}),\\ {\sigma }_{\mathit{\text{run}}}^2\sim \text{Inv}-{\chi }^2(n+1,\frac{10+\upsilon }{n+1}),\\ \upsilon =\sum _{h,l,g,s,i,j,k}{(Y_{sijk}^{hlg}-{\mu }_{sij}^{hlg})}^2\text{and}n=\sum _{h,l,g,s,i,j,k}1.\end{array}$$

Class mean is determined by group effect, hemisphere effect, and load effects. Let β = (β₁, β₂, β₃, β₄) be coefficients for group effect, hemisphere effect, and load effect; also, let X be the design matrix. Given a weakly informative prior $f({\sigma }_{\mathit{\text{sub}}}^2)\propto \text{Inv}-{\chi }^2(1,10)$ for ${\sigma }_{\mathit{\text{sub}}}^2$ and flat prior f (β) ∝1 for β, we have

$$\begin{array}{c}\beta \sim N({(X^{T}X)}^{-1}{X}^T({\mu }_{sij}^{hlg}-{\gamma }_{si}^{hlg}),{(X^{T}X)}^{-1}{\sigma }_{\mathit{\text{sub}}}^2),\\ {\gamma }_{si}^{hlg}\sim N(\frac{\frac{{\sum }_j({\mathit{\text{mu}}}_{sij}^{hlg}-{\alpha }^{hlg})}{{\sigma }_{\mathit{\text{sub}}}^2}+\frac{b_s}{{\sigma }_{\mathit{\text{site}}{W}_s}^2}}{\frac{2}{{\sigma }_{\mathit{\text{sub}}}^2}+\frac{1}{{\sigma }_{\mathit{\text{site}}{W}_s}^2}},\frac{1}{\frac{2}{{\sigma }_{\mathit{\text{sub}}}^2}+\frac{1}{{\sigma }_{\mathit{\text{site}}{W}_s}^2}}),\\ {\sigma }_{\mathit{\text{sub}}}^2\sim \text{Inv}-{\chi }^2(n+1,\frac{10+\upsilon }{n+1}),\\ \upsilon =\sum _{h,l,g,s,i,j}{({\mu }_{sij}^{hlg}-{\alpha }^{hlg}-{\gamma }_{si}^{hlg})}^2\text{and}n=\sum _{h,l,g,s,i,j}1.\end{array}$$

Given a weakly informative prior $f({\sigma }_{\mathit{\text{site}}{W}_s}^2)\propto \text{Inv}-{\chi }^2(1,10)$ for ${\sigma }_{\mathit{\text{site}}{W}_s}^2$, we sample subject-specific site effects b_si and site variation within subjects ${\sigma }_{\mathit{\text{site}}{W}_s}^2$ as follows:

$$\begin{array}{c}{b}_{si}\sim N(\frac{\frac{6\ast {\overline{\gamma }}_{si}}{{\sigma }_{\mathit{\text{site}}{W}_s}^2}+\frac{b_s}{{\sigma }_{\mathit{\text{visit}}}^2}}{\frac{6}{{\sigma }_{\mathit{\text{visit}}}^2}+\frac{1}{{\sigma }_{\mathit{\text{visit}}}^2}},\frac{1}{\frac{6}{{\sigma }_{\mathit{\text{site}}{W}_s}^2}+\frac{1}{{\sigma }_{\mathit{\text{visit}}}^2}}),\\ {\sigma }_{\mathit{\text{site}}{W}_s}^2\sim \text{Inv}-{\chi }^2(n_{si}+1,\frac{10+{\upsilon }_{si}}{n_{si}+1}),\\ {\upsilon }_{si}=\sum _{h,l,g}{({\gamma }_{si}^{hlg}-b_{si})}^2\text{and}{n}_{si}=\sum _{h,l,g}{1}_{si}.\end{array}$$

Given a weakly informative prior $f({\sigma }_{\mathit{\text{site}}{A}_s}^2)\propto \text{Inv}-{\chi }^2(1,10)$ for ${\sigma }_{\mathit{\text{site}}{A}_s}^2$ and a flat prior f (b_s) ∝ 1 for site mean b_s, we sample site-specific site effects b_s and site variation across subjects ${\sigma }_{\mathit{\text{site}}{A}_s}^2$ as follows:

$$\begin{array}{c}{b}_s\sim N({\overline{b}}_s,\frac{{\sigma }_{\mathit{\text{site}}{A}_s}^2}{n_s}),\\ {\sigma }_{\mathit{\text{site}}{A}_s}^2\sim \text{Inv}-{\chi }^2(n_s+1,\frac{10+{\upsilon }_s}{n_s+1}),\\ {\upsilon }_s=\sum _i{(b_{si}-b_s)}^2\text{and}{n}_s=\sum _i{1}_s.\end{array}$$

A.2. Gibbs Sampler for the t Model

For the hierarchical model with the t -distribution, the Gibbs sampler is similar to what we discussed above, except for the first part of the hierarchy where we introduce latent variable $V_{sijk}^{hlg}$. Given a weakly informative prior $f({\sigma }_{\mathit{\text{run}}}^2)\propto \frac{1}{{\sigma }_{\mathit{\text{run}}}^2}$ for ${\sigma }_{\mathit{\text{run}}}^2,$, we sample ${\mu }_{sij}^{hlg}$ and ${\sigma }_{\mathit{var}}^2$ as follows:

$$\begin{array}{c}{V}_{sijk}^{hlg}\sim \text{Inv}-{\chi }^2(\upsilon +1,\frac{\upsilon {\sigma }_{\mathit{\text{run}}}^2+{(Y_{sijk}^{hlg}-{\mu }_{sij}^{hlg})}^2}{\upsilon +1}),\\ {\mu }_{sij}^{hlg}\sim N(\frac{{\sum }_k\frac{Y_{sijk}^{hlg}}{V_{sijk}^{hlg}}+\frac{{\alpha }^{hlg}+{\gamma }_{si}^{hlg}}{{\sigma }_{\mathit{\text{sub}}}^2}}{{\sum }_k\frac{1}{V_{sijk}^{hlg}}+\frac{1}{{\sigma }_{\mathit{\text{sub}}}^2}},\frac{1}{{\sum }_k\frac{1}{V_{sijk}^{hlg}}+\frac{1}{{\sigma }_{\mathit{\text{sub}}}^2}}),\\ {\sigma }_{\mathit{\text{run}}}^2\sim \mathit{\text{Gamma}}(\frac{N\upsilon }{2},\frac{\upsilon }{2}\sum _{sijkhlg}\frac{1}{V_{sijk}^{hlg}}),N=\sum _{sijkhlg}1.\end{array}$$

Appendix B

Here, we present the steps involved in the derivation of e_s (Equation (9)). To find Σ̂_m we start by rewriting our hierarchical Bayesian model as a multivariate normal model as follows:

$$Y|\beta ,{\widehat{\sum }}_m\sim N(X\beta ,{\widehat{\sum }}_m),$$

where X is the design matrix, and β = (β₁,β₂,β₃,β₄,b₁,…,b₈). The diagonal elements of the matrix are equal to the variance of $Y_{sijk}^{hlg}$,

$$Var(Y_{sijk}^{hlg})={\widehat{\sigma }}_{\mathit{\text{run}}}^2+{\widehat{\sigma }}_{\mathit{\text{sub}}}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{W}_s}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{A}_s}^2.$$

The off-diagonal elements are equal to the covariance of observations. If two observations come from different subjects, the covariance of $Y_{sijk}^{hlg}$ with $Y_{s\prime i\prime j\prime k\prime }^{h\prime l\prime g\prime }$ is 0

$$Cov(Y_{sijk}^{hlg},Y_{s\prime i\prime j\prime k\prime }^{h\prime l\prime g\prime })=0.$$

If two observations belong to the same subject but different hemispheres or loads, then the co-variance of $Y_{sijk}^{hlg}$ with $Y_{sij\prime k\prime }^{h\prime l\prime g}$ is

$$Cov(Y_{sijk}^{hlg},Y_{sij\prime k\prime }^{h\prime l\prime g\prime })={\widehat{\sigma }}_{\mathit{\text{site}}{A}_s}^2.$$

If two observations belong to the same subject and the same hemisphere and load, but different visits, then

$$Cov(Y_{sijk}^{hlg},Y_{sij\prime k\prime }^{hlg})={\widehat{\sigma }}_{\mathit{\text{site}}{W}_s}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{A}_s}^2.$$

Finally, if the two observations belong to the same subject, hemisphere, load, and visit, but different runs, we have

$$Cov(Y_{sijk}^{hlg},Y_{sijk\prime }^{hlg})={\widehat{\sigma }}_{\mathit{\text{sub}}}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{W}_s}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{A}_s}^2.$$

Assuming a flat prior on β and conditional on Σ̂_m, we can derive the posterior distribution of β, which includes the group effect β₁, as follows:

$$\beta |Y,{\widehat{\sum }}_m\sim N({(X^T{\widehat{\sum }}_m^{-1}X)}^{-1}{X}^T{\widehat{\sum }}_m^{-1}Y,{(X^T{\widehat{\sum }}_m^{-1}X)}^{-1}).$$

The conditional variance of β is therefore

$$Var(\beta |Y,{\widehat{\sum }}_m)={(X^T{\widehat{\sum }}_m^{-1}X)}^{-1}.$$

The first element of the above matrix is the conditional variance of the group effect for the multi-center study, Var(β₁|Y,Σ̂_m).

We can use a similar approach to obtain Var(β₁|Y,Σ̂_s) for a single-center study at site s, assuming all subjects are sent to this site only. To this end, we assume

$$Y|\beta \prime ,{\widehat{\sum }}_s\sim N(X\prime \beta \prime ,{\widehat{\sum }}_s)$$

where X′ is the design matrix for the hypothetical single-center study, β′ = (β₁,β₂,β₃,β₄,b_s). Note that in this case, s is fixed and refers to the site to which all subjects are sent.

As before, the diagonal elements of Σ̂_s are equal to the variance of $Y_{sijk}^{hlg},$ similar to the multi-center study, and the off-diagonal elements are equal to the covariance of observations. Note that for a single-center study, we still use a hierarchical model in which there are two visits per subject and three runs per visit given hemisphere and load. Similar to our model for multi-center study, the hierarchical model for a single-center study accounts for within-subject site effects and across-subject site effects. (See Equations (3) and (4).) Therefore, finding the covariance of observations for a single-center study is similar to what we discussed for the multi-center study. The difference is that for a single-center study, s remains fixed for all subjects. Therefore, while the steps to calculate the covariance matrix (discussed below) for a single-center study are similar to those of the multi-center study, the resulting covariance matrices are not the same.

If two observations are obtained from different subjects, their covariance is zero,

$$\text{Cov}(Y_{sijk}^{hlg},Y_{si\prime j\prime k\prime }^{h\prime l\prime g\prime })=0.$$

If two observations belong to the same subject but different hemispheres or loads, then the co-variance of $Y_{sijk}^{hlg}$ with $Y_{sij\prime k\prime }^{h\prime l\prime g\prime }$ is

$$Cov(Y_{sijk}^{hlg},Y_{sij\prime k\prime }^{h\prime l\prime g\prime })={\widehat{\sigma }}_{\mathit{\text{site}}{A}_s}^2.$$

Note that unlike the multi-center study, for a single-center study s is fixed. If two observations belong to the same subject and the same hemisphere and load, but different visits, then

$$Cov(Y_{sijk}^{hlg},Y_{sij\prime k\prime }^{hlg})={\widehat{\sigma }}_{\mathit{\text{site}}{W}_s}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{A}_s}^2.$$

Finally, if the two observations belong to the same subject, hemisphere, load, and visit, but different runs, we have

$$Cov(Y_{sijk}^{hlg},Y_{sijk\prime }^{hlg})={\widehat{\sigma }}_{\mathit{\text{sub}}}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{W}_s}^2+{\widehat{\sigma }}_{\mathit{\text{site}}{A}_s}^2.$$

As mentioned above, both multi-center study and single-center study have similar covariance matrices because they have similar hierarchical structures. For example, we use Equations (3) and (4) for both of them. However, for a single-center study, all subjects have the same within-subject and across-subject site effects since there is only one site; whereas, for the multi-center study, the within-subject and across-subject site effects vary depending on the site from which the observations for the same subject are obtained.

Following the same procedure we discussed for the multi-center study, we can estimate the conditional variance of the group effect Var(β₁|Y,Σ̂_s) for the hypothetical scenario where all subjects are sent to site s.