Abstract
Proton beam radiotherapy unavoidably exposes healthy tissue to stray radiation emanating from the treatment unit and secondary radiation produced within the patient. These exposures provide no known benefit and may increase a patient's risk of developing a radiogenic cancer. The aims of this study were to calculate doses to major organs and tissues and to estimate second cancer risk from stray radiation following craniospinal irradiation (CSI) with proton therapy. This was accomplished using detailed Monte Carlo simulations of a passive-scattering proton treatment unit and a voxelized phantom to represent the patient. Equivalent doses, effective dose and corresponding risk for developing a fatal second cancer were calculated for a 10-year-old boy who received proton therapy. The proton treatment comprised CSI at 30.6 Gy plus a boost of 23.4 Gy to the clinical target volume. The predicted effective dose from stray radiation was 418 mSv, of which 344 mSv was from neutrons originating outside the patient; the remaining 74 mSv was caused by neutrons originating within the patient. This effective dose corresponds to an attributable lifetime risk of a fatal second cancer of 3.4%. The equivalent doses that predominated the effective dose from stray radiation were in the lungs, stomach and colon. These results establish a baseline estimate of the stray radiation dose and corresponding risk for a pediatric patient undergoing proton CSI and support the suitability of passively-scattered proton beams for the treatment of central nervous system tumors in pediatric patients.
1. Introduction
Proton therapy is a promising treatment modality for some central nervous system tumors in pediatric patients. Protons have several depth–dose characteristics, such as a sharp distal fall-off versus depth in tissue, which give proton therapy a theoretical dosimetric advantage over photon radiotherapy in the sparing of nearby tissues and organs (Krejcarek et al 2007). This dosimetric advantage is especially important for children because they are more susceptible to radiation carcinogenesis, which is the radiation late effect of greatest concern. The increased susceptibility is mainly because children generally have longer expected survival times, higher relative biological effectiveness (RBE) for a given type of radiation and endpoint and smaller bodies than adults and, thus, organs that are closer to the proton field. Hence, interest in the potential use of proton therapy for children with cancer is increasing (cf Archambeau et al 1992, Miralbell et al 1997, 2002, Lin et al 2000, Noel et al 2003, Kirsch and Tarbell 2004, St Clair et al 2004, Yuh et al 2004, Lee et al 2005, Lundkvist et al 2005, Mu et al 2005).
Several studies have examined the stray radiation exposures associated with proton therapy (Agosteo et al 1998, Schneider et al 2002, Yan et al 2002, Jiang et al 2005, Polf and Newhauser 2005, Polf et al 2005, Hall 2006, Wroe et al 2007, Zheng et al 2007a, 2007b, 2008), and a few investigations have estimated stray neutron exposures in humanoid phantoms (Fontenot et al 2008, Zacharatou Jarlskog et al 2008, Taddei et al 2008). Miralbell et al (2002) reported a treatment planning study in which the risks of second cancer were compared for proton therapy versus photon therapy following craniospinal irradiation (CSI); the risks from neutron radiation were neglected. Newhauser et al (2009) supplemented the analysis from Miralbell et al to include neutron radiation. Absorbed dose from neutrons is of particular concern because, although absorbed dose is less, RBE of neutrons (including their secondary particles) is generally greater than that of protons, photons and electrons. They predicted stray radiation dose using an adult-sized anthropomorphic phantom. Miralbell et al found that proton therapy carried lower predicted risk of second cancer; Newhauser et al reported that consideration of neutrons increased the risk of second cancer, but proton therapy still carried a lower risk than photon therapy. The results of Miralbell et al and Newhauser et al were based on one patient, a 6-year-old boy, and the dosimetric uncertainties were large and difficult to estimate. Hence, there is a need for additional, independent investigations, particularly with more realistic dose predictions and for patients of other ages.
The aim of this study was to perform a realistic and accurate calculation of the equivalent dose in major organs and tissues and the effective dose from stray radiation for a complete proton CSI treatment. The geometric model comprised a passive-scattering proton therapy treatment unit and a voxelized phantom based on computed tomography (CT) images of a pediatric patient who underwent proton CSI at our institution. The Monte Carlo simulation method was used to calculate absorbed dose from primary (therapeutic) protons, stray neutrons originating in the treatment unit and stray neutrons originating within the patient. The excess risk of second cancer mortality was estimated based on the effective dose from stray radiation.
2. Methods
2.1. Proton treatment technique
A proton radiotherapy plan was created for a 10-year-old male patient with supratentorial primitive neuroectodermal tumor (PNET) who underwent proton CSI using a commercial treatment planning system (TPS) (Eclipse Proton; Varian Medical Systems, Inc., Palo Alto, CA) and whole-body kilovoltage CT images (Newhauser et al 2007a). His stature was representative of a typical 10-year-old boy. As part of the treatment planning process, organ and tissue structures were contoured using the TPS. The plan prescribed 30.6 Gy to the brain and the spinal cord and 23.4 Gy boost dose to the clinical target volume, which was the gross tumor volume in the brain with an additional margin. The patient was treated in the supine position. The plan called for proton fields that included those that were otherwise identical except that the aperture edges were modified slightly to provide feathering of the junctions of the proton fields. For the purposes of this study, the feathering of field junctions was unimportant. Therefore, the feathering was eliminated, and the plan was simplified to six fields: two inferior and superior posterior–anterior spinal fields (IPA and SPA), two right and left posterior oblique cranial fields (RPO and LPO) and two left posterior oblique and left lateral boost fields (LPOB and LLB) to the clinical target volume. Field characteristics are listed in table 1, including proton beam energies at the entrance of the treatment unit and residual water-equivalent ranges at the surface of the patient. The dose distributions were conformed to the target volume of each field using the beam modifiers available in the commercial passive-scattering proton therapy treatment unit (PROBEAT; Hitachi America, Ltd, Tarrytown, NY) in service at The University of Texas M D Anderson Cancer Center (Newhauser et al 2007a), which included a range-modulator wheel (Koehler et al 1975), scattering foils, range shifter, collimator block and range compensator (Wagner 1982). A 6 cm thick collimator block was used to define the proton field for the 180 MeV beams, and a 4 cm collimator was used for the 140 and 160 MeV beams. The snout was set for a large field size (i.e. up to 25 × 25 cm2) for the spinal and cranial fields and for a medium field size (i.e. up to 18 × 18 cm2) for the boost fields. The plan was exported from the TPS for Monte Carlo simulation (see below).
Table 1. Beam specifications of the six fields for proton CSI.
| IPA | SPA | RPO | LPO | LPOB | LLB | |
|---|---|---|---|---|---|---|
| Pre-nozzle proton energy (MeV) | 140 | 140 | 180 | 180 | 160 | 140 |
| Range in patient (cm H2O) | 9.4 | 8.9 | 16.0 | 15.9 | 11.3 | 9.2 |
| SOBP width (cm) | 7 | 7 | 16 | 16 | 7 | 6 |
| Gantry angle (deg) | 180 | 180 | 255 | 105 | 130 | 90 |
| Air gap (cm) | 10 | 10 | 2 | 2 | 2 | 2 |
| Aperture thickness (cm) | 4 | 4 | 6 | 6 | 4 | 4 |
| Collimated field, major axis (cm) | 18.4 | 19.2 | 19.3 | 19.8 | 11.8 | 11.6 |
| Collimated field, minor axis (cm) | 6.8 | 6.6 | 14.3 | 15.0 | 5.5 | 5.4 |
IPA = inferior posterior anterior, SPA = superior posterior anterior, RPO = right posterior oblique, LPO = left posterior oblique, LPOB = left posterior oblique boost, LLB = left lateral boost, SOBP = spread-out Bragg peak.
Nominal air gaps from the treatment plan are presented in table 1. The air gap between the downstream face of the range compensator and the proximal surface of the patient for the cranial and boost fields was 2 cm; the spinal fields had an air gap of 10 cm to allow for additional displacement from the treatment couch. Because the absorbed dose from stray radiation rapidly increases with decreasing air gap (Zheng et al 2007b), an additional simulation was performed where the model was adjusted for an air gap of 2 cm for the spinal fields. The results of this additional simulation may be used to estimate the effective dose from stray radiation if the patient were treated in the prone position.
2.2. Modeling the treatment unit and voxelized phantom
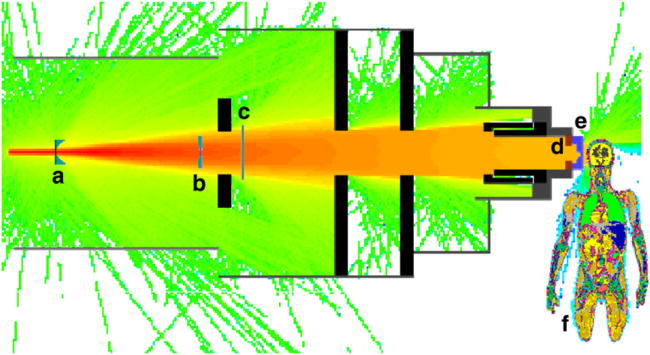
Monte Carlo simulations were performed using the Monte Carlo N-Particle eXtended (MCNPX) code version 2.6b (Pelowitz 2005) with parallel processing on 2.6 GHz, 64 bit processors (AMD Opteron; Advanced Micro Devices, Inc., Sunnyvale, CA). The suitability of the MCNPX code for simulating therapeutic absorbed dose distributions and secondary neutrons associated with proton therapy has been well established (cf Olsher et al 2000, Fontenot et al 2005, 2007, Herault et al 2005, 2007, Koch and Newhauser 2005, Newhauser et al 2005, 2007a, 2007c, Polf and Newhauser 2005, Polf et al 2005, Tayama et al 2006, Zheng et al 2007b, 2008, Koch et al 2008, Titt et al 2008). Figure 1 shows the MCNPX model of the treatment unit used in this work. The model included an elliptical source of protons positioned immediately upstream of the treatment unit (3.29 m from the isocenter) with a lateral Gaussian intensity distribution (horizontal FWHM = 5.4 mm, vertical FWHM = 12.2 mm) that simulated the entrance of the parallel beam into the treatment head. The proton sources were modeled as Gaussian energy distributions with initial mean energies of 140 MeV, 160 MeV and 180 MeV (FWHM = 0.23 MeV, 0.25 MeV and 0.27 MeV, respectively). For simplicity, the treatment plans and simulations were calculated without a treatment couch. Each component of the treatment unit was modeled in detail. The other features of the Monte Carlo model were described elsewhere (Newhauser et al 2007a, Zheng et al 2007b).
Figure 1.
Diagram of the passive-scattering treatment unit and voxelized phantom, oriented for the left-lateral boost field, overlaid on top of a proton flux tally (logarithmic scale). In the beam line from left to right in the diagram are the (a) range-modulator wheel, (b) scattering foils, (c) range shifting plates, (d) block (aperture), (e) range compensator and (f) voxelized phantom. Also shown are the collimators and structural materials composed of stainless steel and brass. The vacuum window and beam monitors (air-filled) are not shown.
The planning CT image of the patient included the entire body except the feet and was the basis of the voxelized phantom. Before the treatment plan was started, the CT images were down sampled into 4 × 4 × 5 mm3 pixels due to constraints on the electronic memory in the TPS and Monte Carlo system. The Hounsfield unit (HU) in each voxel was converted to mass density and material composition using the following approach. The assignment of mass density, ρv, in each voxel, v, was made based on a tri-linear calibration curve similar to that described by Schneider et al (2000) and Newhauser et al (2008). The mass density values from the calibration curve were then discretized into one of 300 density bins in order to conserve memory in the Monte Carlo system. The density bins were of three sizes in order to minimize range errors from discretization effects. Specifically, there were 100 bins for − 1000 ≤ HU < −100, 100 bins for −100 ≤ HU < 100 and 100 bins for 100 ≤ HU < 2500. The material composition chosen for each voxel was assigned based on a nearest-neighbor lookup in a table that listed 48 HU intervals with 48 discrete material compositions (mostly biological materials) (Woodard and White 1986, White et al 1987, 1991). Although a more exact method has been reported that allows for continuously variable material compositions (Van Riper 2005), the number of materials was limited to 48 because of memory constraints in the Monte Carlo system. The HU values used for assignment of mass density and material composition were taken from measurements of the scanner used to image the patient in this study (Newhauser et al 2008). In the MCNPX code, a lattice of over 2 × 106 elements was used to represent the patient. A detailed explanation of this procedure is provided elsewhere (Newhauser et al 2007b).
2.3. Effective dose, equivalent dose and absorbed dose from stray radiation
Following the recommendations of the International Commission on Radiological Protection (ICRP) Publication 92 (2003), the effective dose from stray radiation, E, was calculated as the sum over a specified organ or tissue, T,
| (1) |
where wT is the tissue weighting factor and HT is the equivalent dose in organs and tissues from stray radiation. The wT values were taken from ICRP Publication 60 (1991), which were developed to take into account the differences in the radiosensitivity of various organs and tissues. The values of wT were provided for radiological protection purposes, where the biological effect of an increased risk of attributable fatal cancer was the chief concern. The wT value for the gonads represents a special case because it takes into account the probability of hereditary effects.
HT was calculated as the product of the mean radiation weighting factor, , and the mean absorbed dose for each organ or tissue, DT,
| (2) |
HT values were calculated separately for each component of stray radiation and for each treatment field. The methods used to calculate values for stray radiation are described in section 2.5.
In equation (2), DT was the mass-weighted average value of the absorbed dose. In this work, the organs and tissues were subdivided into volume elements, or ‘voxels’, of fixed size. Therefore, the mass averaging for DT was performed using ρv values and the density-weighted average,
| (3) |
where Dv is the absorbed dose from stray radiation in each voxel in an organ or tissue, T. A voxel was associated with an organ or tissue if all or part of it was within the contoured surface of that organ. The larger the organ, the more voxels it contained; for example, the lungs had 19 600 voxels whereas the thyroid had only 156 voxels. In principle, this inclusive association method meant that the organ dose in equation (3) was averaged over a volume that was slightly larger than the organ. However, this approximation was of little practical consequence because the absorbed dose from stray neutrons decreases gradually with increasing depth in tissue.
DT was calculated for each contoured organ and tissue, including the target volume of each therapeutic field and organs and tissues associated with every tissue weighting factor, except for the skin and remainder organs and tissues. Instead, an average DT for all voxels within the phantom was applied as an approximate absorbed dose to the skin and the remainder organs and tissues for each field.
As described in section 2.2, the patient anatomy was modeled using a lattice, where each anatomical voxel was represented by an element within the lattice. The absorbed dose in a voxel was calculated as the quotient of the energy deposited per volume and the mass density. The energy deposition per volume (MeV cm−3 per source particle) was obtained from an MCNPX type 3 rectangular mesh tally that exactly coincided with the lattice of anatomical voxels. The mass density was obtained using the method described in section 2.2. The mass-averaged absorbed dose from the therapeutic proton beam in the target volume of each field, DT=target, per source particle was calculated according to equation (3). Values of Dv per source particle from a given treatment field were normalized using the DT=target associated with that field, or
| (4) |
so that Dv for stray radiation was calculated in terms of stray radiation mGy per therapeutic Gy. The normalization in equation (4) to therapeutic absorbed dose is convenient, eliminates dependence on the prescribed target dose and is customary in the literature (cf Yan et al 2002). Similarly, E and HT were reported per therapeutic absorbed dose for each field. In addition, E, HT and Dv were also calculated for the prescribed treatment dose of 30.6 Gy for the spinal and cranial fields to the brain and spinal cord and 23.4 Gy for the boost fields to the cranium. E was used to estimate the absolute lifetime risk of attributable second cancer fatality for the prescribed treatment.
2.4. Distinguishing absorbed dose from therapeutic protons, external neutrons and internal neutrons
In this work, stray radiation was defined as the undesirable radiation produced from interactions between the proton beam and the components in the treatment unit or the patient. Secondary neutrons emanating from the treatment unit (or ‘external neutrons’) and within the patient (or ‘internal neutrons’) have been shown to be the primary contributor to absorbed dose from stray radiation (Agosteo et al 1998, Fontenot et al 2008, Zheng et al 2008). E, HT and Dv were calculated separately for both external and internal neutrons. However, because the MCNPX code does not directly differentiate between the absorbed dose from external versus internal radiation, the following method was used to separate the absorbed dose from each of these two components.
To isolate the absorbed dose from external neutrons, Dv,ext, the Monte Carlo system was configured to track neutrons and protons throughout the entire geometry (mode n h; imp:h, n > 0). However, all proton trajectories were terminated immediately upstream of the patient by a proton stopping plane (imp:h = 0), modeled as very thin slab of air. Thus, in simulations with the stopping plane, only external neutrons were incident upon the patient. A type 3 mesh tally (keyword ‘total’) was used to calculate energy deposition in each anatomic voxel of the patient, and Dv,ext was calculated according to the methods described in section 2.3.
Isolating the contribution to absorbed dose from internal neutrons, Dv,int, required a slightly more complex procedure. The additional complexity was necessary because MCNPX tallies did not discriminate between therapeutic (primary) protons and protons that were liberated from inelastic nuclear reactions. First, the absorbed dose from primary protons was calculated by tracking only protons (and not neutrons) throughout the geometry (mode n h; imp:h > 0; imp:n = 0). In this case, secondary neutrons were generated, but their trajectories were immediately terminated at their points of origin. Absorbed dose was calculated in each voxel for primary protons, Dv[p1], using a type 1 mesh tally (keyword ‘pedep’). Second, a simulation was performed in which protons were tracked throughout the model but neutrons were tracked only within the patient (i.e. external neutrons were not allowed to contribute to absorbed dose). This model was identical to the previous one except that the secondary neutrons were tracked within the voxelized anatomy (imp:n > 0 in the phantom). Absorbed dose was calculated in each voxel separately for protons, Dv[p2], and neutrons, Dv[n], using type 1 rectangular mesh tallies (card ‘rmesh’, keyword ‘pedep’). In the MCNPX code, the type 1 mesh tally included energy deposition only from particles that were explicitly specified on the RMESH card (e.g. ‘rmesh21:n pedep’ for neutrons). Thus, the tally excluded the proportion of energy that was deposited by other particles that were being transported, where the list of particles transported was specified on the ‘mode’ card, for example recoil protons (Pelowitz 2005). Therefore, the absorbed dose from recoil protons that originated from interactions with internal neutrons was added to Dv[n] using the methods described by Taddei et al (2008), which was based on the assumption that the ratio of neutron dose to secondary proton dose is constant throughout the body. An average of Dv [p2]/Dv [n] for all voxels outside the treatment field, A, was calculated, including contributions from all treatment fields. This average value was then used to estimate the contribution to absorbed dose from secondary protons for each voxel inside the treatment field, and this contribution was added to the absorbed dose from internal neutrons for that voxel,
| (5) |
Dv,int was calculated in terms of mGy from internal neutrons per therapeutic Gy according to the methods described in section 2.3.
Because of computer memory constraints, photons, alpha particles and other secondary particles were not tracked, and their energy was deposited locally at their points of origin. This was not a limitation of the study because in proton therapy equivalent dose from stray radiation is predominated by neutrons (Agosteo et al 1998, Fontenot et al 2008, Zheng et al 2008).
2.5. Radiation weighting factor
The values of were calculated separately for external and internal neutrons. For external neutrons, the values of were determined for each field following the recommendations specified in ICRP Publication 92 (2003). For external neutrons, was calculated as
| (6) |
where ϕ(En) was the probability density function of the spatially averaged neutron spectral fluence incident upon the voxelized phantom. The energy-dependent expression of the neutron radiation weighting factor was
| (7) |
where En was the neutron energy in MeV. ϕ(En) was tallied in a plane immediately downstream of the treatment unit with lateral dimensions that spanned those of the voxelized phantom in the treatment position. This was performed separately for each treatment field.
The values of for internal neutrons were taken from a study by Newhauser et al (2009) in which organ-specific values were estimated using equations (6) and (7) above, but where the neutron spectral fluence values of the moderated neutrons were tallied within the internal organs of an anthropomorphic phantom receiving craniospinal proton irradiation. They found that values averaged over all organs were 9.75 for the inferior spinal field, 9.42 for the superior spinal field and 7.86 for the cranial field; these values were applied to the values of DT for internal neutrons for the IPA, SPA and the cranial and boost fields, respectively. As shown in section 3.1, the internal neutrons made a relatively small contribution to equivalent dose compared to external neutrons. Furthermore, the variation between organs in radiation weighting factor for internal neutrons was small. Hence, the methods utilized to estimate values were adequate and appropriate for the intents and purposes of this work.
2.6. Attributable lifetime risk of second cancer fatality
The National Council on Radiation Protection and Measurements (NCRP) has recommended a risk coefficient of 8.1% per Sv of effective dose for low-dose-rate, exposure-induced death for males between the ages of 0 and 19 years (1997). This value provides a reasonable estimate of radiation detriment to a general population because it takes into account stochastic effects in various organs as well as hereditary effects. This risk coefficient was used to estimate the excess lifetime risk of second cancer fatality due to stray radiation.
2.7. Uncertainty
To minimize statistical uncertainties in DT, 1 × 109, 5 × 108 and 5 × 108 source particles and their secondary protons and neutrons were tracked for each spinal field, cranial field and boost field simulation, respectively, for a total of 1.2 × 1010 histories. The uncertainties in DT, HT and E were estimated considering only statistical uncertainties and on the assumption that component uncertainties were uncorrelated. Statistical uncertainties in the Dv values were based on the coefficients of variation calculated by the MCNPX code and were reported at the 68% confidence interval. Because the uncertainty in ϕ(En) was less than 1% for neutron energy bins greater than 200 eV and less than 130 MeV, the uncertainty in values was taken as zero. The systematic uncertainties in values of wR(En) and wT were large and difficult to estimate for this patient. However, in the uncertainty analysis, they were assumed to have zero uncertainty. The effects of the uncertainty in wr were discussed in detail by Newhauser et al (2009).
3. Results
3.1. Effective dose from stray radiation
The effective dose from stray radiation, E, for the entire treatment was 418.2 ± 0.7 mSv. This value of E is equivalent to the effective dose associated with approximately 20 whole-body CT scans. The two spinal fields contributed 302.2 ± 0.6 mSv (72%) to E, the two cranial fields contributed 93.5 ± 0.4 mSv (22%) and the boost fields contributed 22.47 ± 0.13 mSv (5%). For the entire set of treatment fields, external neutrons contributed 343.7 ± 0.6 mSv (82%) to E, and internal neutrons contributed 74.4 ± 0.3 mSv (18%). The latter closely approximates the minimum effective dose from stray radiation that may be achieved by enhancements to the treatment unit, for example what might be possible with a spot-scanning treatment unit that emits relatively few neutrons.
Table 2 lists the effective dose from external and internal neutrons for each field. External neutrons were the predominant contributors to E for each field. For external neutrons, the spinal, cranial and boost fields accounted for 69%, 25% and 6% of effective dose, respectively. For the internal neutrons, the spinal, cranial and boost fields accounted for 88%, 11% and 1% of effective dose, respectively.
Table 2.
Contribution to effective dose from stray radiation for a 30.6 Gy CSI and a 23.4 Gy boost from each field and from external and internal neutron stray radiation.
| E (mSv) | |||
|---|---|---|---|
|
|
|||
| Field | External | Internal | Total |
| Spinal (IPA) | 119.2 ± 0.3 | 30.08 ± 0.11 | 149.3 ± 0.4 |
| Spinal (SPA) | 117.3 ± 0.4 | 35.7 ± 0.3 | 152.9 ± 0.5 |
| Cranial (LPO) | 45.1 ± 0.3 | 3.95 ± 0.05 | 49.0 ± 0.3 |
| Cranial (RPO) | 40.4 ± 0.3 | 4.07 ± 0.05 | 44.5 ± 0.3 |
| Boost (LPOB) | 12.23 ± 0.10 | 0.397 ± 0.007 | 12.63 ± 0.10 |
| Boost (LLB) | 9.53 ± 0.09 | 0.313 ± 0.007 | 9.84 ± 0.09 |
| Total | 338.6 ± 0.6 | 78.6 ± 0.3 | 418.2 ± 0.7 |
Abbreviations used are the same as those in table 1.
In the simulations run with an air gap of 2 cm for the spinal fields, E increased by 13% to 473.7 ± 0.7 mSv. This case approximated the effective dose from stray radiation if the patient were treated in the prone position for the posterior–anterior fields, thus eliminating the couch from the path of the therapeutic proton beam.
The product HTwT was the contribution of the equivalent dose from an organ or tissue to effective dose and is an indicator of the risk of stochastic effects. HTwT values are listed in table 3, summed over all fields and multiplied by the prescribed doses of 30.6 Gy for the cranial and spinal fields and 23.4 Gy for the boost fields. As shown, the lungs were the predominant contributors to E, accounting for 86 mSv or 21% of E. The stomach, colon, thyroid and esophagus each contributed between 42 and 61 mSv to E, or between 10% and 14% of E. The liver, breasts, gonads, red bone marrow and remainder each contributed over 20 mSv to E, or 5% of E.
Table 3.
Equivalent dose in organs and tissues from stray radiation, HT, per therapeutic absorbed dose for each field with statistical uncertainties in the total HT listed in terms of percentage error.
| HT (mSv Gy−1) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||
| Organ or tissue | wT | Spinal IPA | Spinal SPA | Cranial LPO | Cranial RPO | Boost LPOB | Boost LLB | ΣHT(mSv) | σ(ΣHT)/ΣHT | ΣHTwT(mSv) |
| Gonads | 0.20 | 1.87 | 0.95 | 0.87 | 0.85 | 0.40 | 0.35 | 122 | 1.70% | 24.3 |
| Red bone marrow | 0.12 | 2.33 | 1.67 | 1.51 | 1.44 | 0.59 | 0.41 | 179 | 0.39% | 21.5 |
| Colon | 0.12 | 7.88 | 2.73 | 1.80 | 1.54 | 0.70 | 0.58 | 391 | 0.26% | 46.9 |
| Lungs | 0.12 | 6.58 | 11.40 | 4.55 | 4.38 | 1.45 | 1.02 | 715 | 0.25% | 85.8 |
| Stomach | 0.12 | 8.31 | 4.92 | 3.06 | 2.12 | 0.89 | 0.82 | 504 | 0.22% | 60.5 |
| Bladder | 0.05 | 3.17 | 1.32 | 0.91 | 0.95 | 0.50 | 0.36 | 176 | 0.67% | 8.8 |
| Breasts | 0.05 | 4.92 | 5.96 | 4.31 | 4.18 | 1.10 | 1.04 | 488 | 1.13% | 24.4 |
| Liver | 0.05 | 8.23 | 5.45 | 2.18 | 3.05 | 0.75 | 0.54 | 514 | 0.12% | 25.7 |
| Esophagus | 0.05 | 5.22 | 14.02 | 7.38 | 6.37 | 2.30 | 1.73 | 846 | 0.48% | 42.3 |
| Thyroid | 0.05 | 2.37 | 13.79 | 10.94 | 9.78 | 3.51 | 2.67 | 884 | 0.54% | 44.2 |
| Skin | 0.01 | 4.39 | 4.20 | 5.29 | 4.71 | 1.88 | 1.38 | 454 | 0.10% | 4.5 |
| Bone surface | 0.01 | 3.43 | 4.27 | 11.63 | 10.06 | 4.13 | 3.16 | 653 | 0.07% | 6.5 |
| Remainder | 0.05 | 4.39 | 4.20 | 5.29 | 4.71 | 1.88 | 1.38 | 454 | 0.10% | 22.7 |
| Clinical target | – | 1.01 | 2.94 | 35.30 | 28.21 | 15.88 | 12.88 | 1429 | 0.19% | – |
| Brain stem | – | 1.38 | 4.77 | 35.10 | 30.56 | 10.01 | 7.54 | 1398 | 0.35% | – |
| Optic chiasm | – | 1.08 | 3.68 | 34.42 | 30.26 | 9.94 | 8.63 | 1353 | 1.00% | – |
| Brain | – | 1.11 | 3.38 | 31.08 | 26.65 | 11.19 | 8.82 | 1255 | 0.05% | – |
| Left cochlea | – | 0.94 | 3.17 | 33.83 | 23.57 | 10.99 | 7.69 | 1223 | 1.20% | – |
| Left optic nerve | – | 1.02 | 3.60 | 31.70 | 24.36 | 8.12 | 7.95 | 1187 | 1.17% | – |
| Right optic nerve | – | 1.03 | 3.64 | 28.07 | 26.98 | 7.01 | 5.76 | 1134 | 1.32% | – |
| Right cochlea | – | 1.03 | 3.53 | 25.55 | 28.92 | 5.17 | 3.87 | 1079 | 1.21% | – |
| Spine | – | 10.91 | 14.81 | 7.19 | 6.39 | 2.31 | 1.47 | 1039 | 0.34% | – |
| Cord | – | 1.81 | 9.96 | 18.56 | 15.67 | 5.10 | 3.73 | 987 | 1.66% | – |
| Pharynx | – | 10.98 | 11.35 | 8.59 | 7.46 | 2.56 | 1.65 | 978 | 0.16% | – |
| Vertebral body | – | 0.99 | 3.29 | 23.49 | 17.75 | 6.26 | 6.26 | 909 | 0.68% | – |
| Left eye | – | 1.61 | 7.93 | 17.18 | 14.44 | 4.83 | 3.73 | 876 | 0.24% | – |
| Right eye | – | 0.97 | 3.33 | 19.82 | 20.15 | 5.18 | 4.15 | 852 | 0.68% | – |
| Oral cavity | – | 0.95 | 3.47 | 21.57 | 15.94 | 5.83 | 5.73 | 845 | 3.40% | – |
| Left lens | – | 0.91 | 3.32 | 17.32 | 18.57 | 4.79 | 3.73 | 778 | 4.02% | – |
| Right lens | – | 6.08 | 9.38 | 4.37 | 3.76 | 1.23 | 1.02 | 624 | 0.16% | – |
| Left kidney | – | 12.34 | 5.37 | 2.26 | 1.70 | 1.02 | 0.62 | 622 | 0.24% | – |
| Heart | – | 12.35 | 4.42 | 1.51 | 2.09 | 0.73 | 0.40 | 581 | 0.26% | – |
| Right kidney | – | 8.17 | 5.59 | 2.22 | 3.09 | 0.77 | 0.55 | 518 | 0.09% | – |
| Small bowel | – | 7.98 | 2.29 | 1.42 | 1.39 | 0.64 | 0.48 | 370 | 0.12% | – |
| Rectum | – | 3.58 | 1.55 | 0.92 | 0.94 | 0.58 | 0.32 | 196 | 0.97% | – |
| Prostate | – | 2.80 | 1.28 | 0.85 | 0.86 | 0.51 | 0.31 | 161 | 1.29% | – |
Abbreviations used are the same as those in table 1.
3.2. Equivalent dose from stray radiation
The values of HT with non-zero values of wT are shown in the upper portion of table 3. Values are listed separately for each treatment field. The results shown are a sum of the contributions from external and internal neutrons. The values, which are the quantity of equivalent dose from stray radiation per absorbed dose of therapeutic radiation, are given in units of millisieverts per gray (mSv Gy−1). For the IPA field, the stomach, liver and colon received the highest equivalent doses, approximately 8 mSv Gy−1 each. For the SPA field, the esophagus, thyroid and lungs received the highest equivalent doses, in the interval of 11 to 14 mSv Gy−1. For the cranial fields, the bone surface and thyroid received the highest equivalent doses, each over 10 mSv Gy−1. The HT values for the boost fields were small compared to those for the spinal and cranial fields, with the thyroid and bone surface receiving the highest equivalent doses because of the reduced field size and, consequently, snout setting. For the organs with non-zero values of wT, HT values ranged between 0.35 and 14.0 mSv Gy−1 for each treatment field. After multiplying the HT values for each treatment field by the prescribed therapeutic absorbed dose for that field and summing over all fields, the thyroid had the largest summed HT value, 884 mSv, and the gonads had the smallest summed HT value, 122 mSv for these organs and tissues.
The HT values for other organs and tissues are listed in the lower portion of table 3. The clinical target volume was the gross tumor volume in the brain with an additional margin. Organs and tissues near the brain had the largest HT values; however, these HT values from stray radiation were small compared to the therapeutic absorbed dose to these organs. Organs and tissues in the lower abdomen and below had the lowest HT values. The contributions from these tissues and organs were aggregated and weighted using the wT value for remainder in the traditional manner (ICRP 1991). The statistical uncertainty in the summed HT for the entire treatment ranged from 0.05% to 4.0% for all organs and from 0.07% to 1.7% for organs with non-zero wT values.
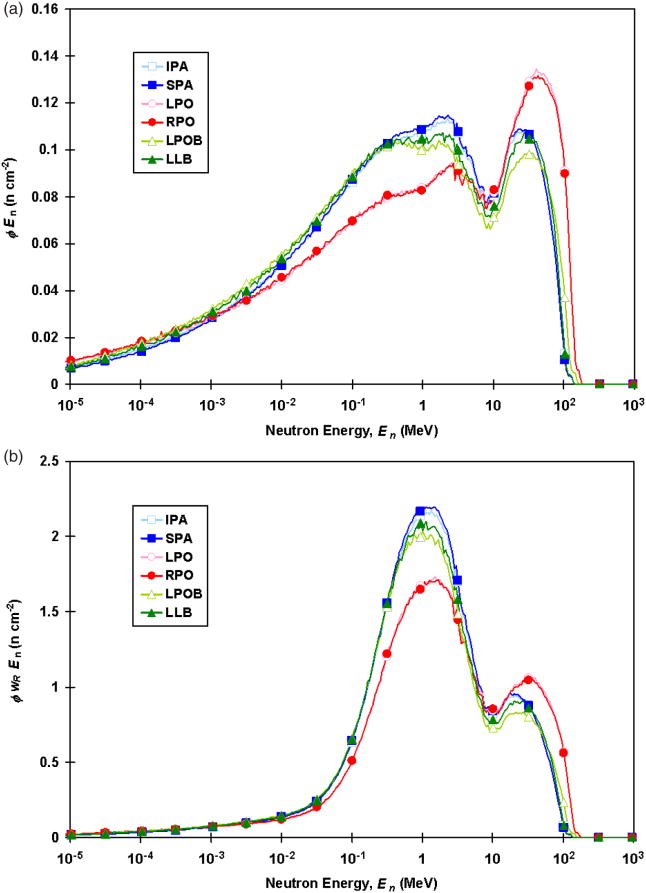
The values associated with each field were determined separately for internal and external neutrons. For external neutrons, values of were calculated from the neutron spectral fluence of external neutrons for each field and were applied to the external neutron absorbed doses. The external neutron spectral fluences, ϕ(En), and those weighted by the analytical expression of wr, ϕ(En)wR(En), are shown in figure 2 for each field. Mean values are listed in table 4. The values for external neutrons calculated in this study (range, 9.1−10.0) were similar to those calculated by Zheng et al (2008) at isocenter for similar beam specifications (range, 9.5−9.8). For internal neutrons, values of were taken from the results of similar fields in a study by Newhauser et al (2009) as described in section 2.5.
Figure 2.
External neutron spectral fluence (a) and external neutron spectral fluence weighted by the analytical expression of the radiation weighting factor (b) for each field. Abbreviations used are the same as those in table 1.
Table 4.
Fluence-weighted average energies, , and mean radiation weighting factors, , for external neutrons, and number of source particles (sp) per therapeutic dose (Gy) in the target volume for each field
| Field |
|
|
sp Gy−1 | ||
|---|---|---|---|---|---|
| Spinal (IPA) | 7.9 | 9.93 | 1.99 × 1012 | ||
| Spinal (SPA) | 7.8 | 10.03 | 2.49 × 1012 | ||
| Cranial (LPO) | 14.1 | 9.17 | 2.41 × 1012 | ||
| Cranial (RPO) | 13.9 | 9.13 | 2.43 × 1012 | ||
| Boost (LPOB) | 8.7 | 9.54 | 1.71 × 1012 | ||
| Boost (LLB) | 8.1 | 9.73 | 1.56 × 1012 |
Abbreviations used are the same as those in table 1.
3.3. Absorbed dose from stray radiation
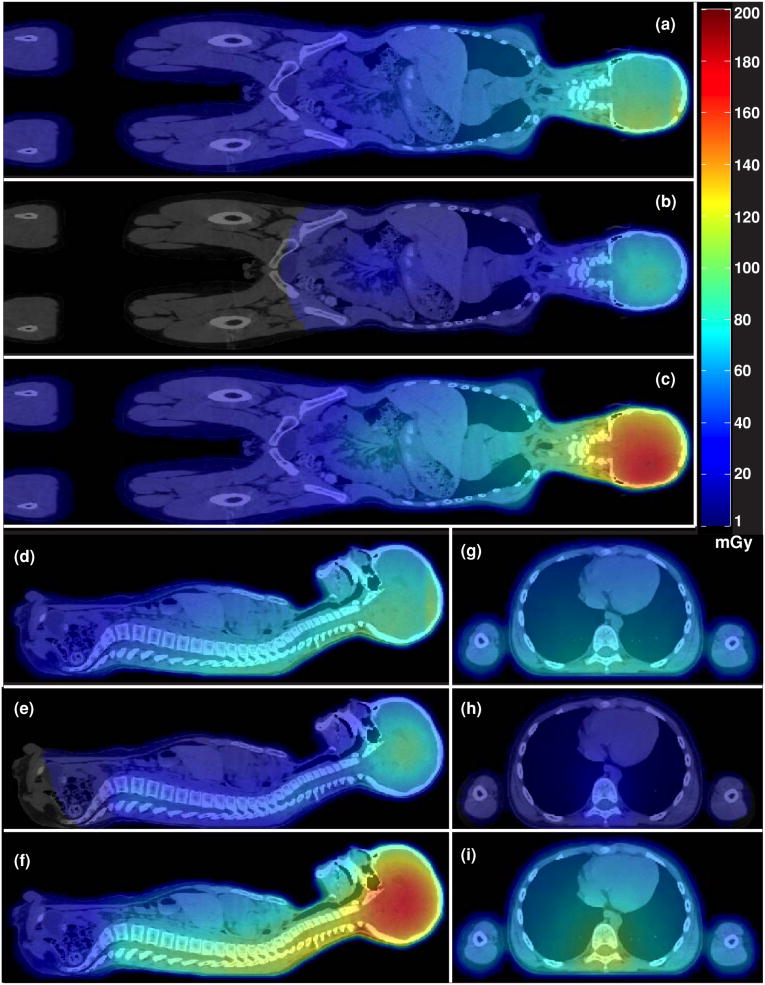
The absorbed dose from stray radiation was calculated in each anatomic voxel. Figure 3 shows the mid-sagittal, mid-coronal and axial planes near the junction of IPA and SPA of the absorbed dose distribution from stray radiation for the entire treatment. This figure thus provides a visual representation of the pervasive dose from stray radiation throughout the body. Because the brain received the highest therapeutic dose, the brain and surrounding organs and tissues received the largest stray radiation dose.
Figure 3.
Absorbed dose for the entire CSI and boost treatment superimposed on the patient's CT images. The coronal plane is shown for external neutrons (a), internal neutrons (b) and all neutrons (c). The mid-sagittal plane is shown for external neutrons (d), internal neutrons (e) and all neutrons (f). The axial plane through the upper spine is shown for external neutrons (g), internal neutrons (h) and all neutrons (i).
Table 4 contains intermediate and final dosimetric quantities that were used to calculate the absorbed dose distributions in the voxelized patient anatomy (see equation (4) in section 2.3). The values of the reciprocal of DT=target, i.e. the number of source particles per absorbed dose from therapeutic protons, are listed. Since the proton fields were roughly similar in energy and size, the number of source particle histories that were required per gray of therapeutic dose to the target volume of each field was also similar (∼2 × 1012).
For the simulations used to determine the absorbed dose from internal neutrons, the mean of the ratio of the type 1 mesh tally for protons, Dv [p2], to that of neutrons, Dv [n], was 2.732 with a standard deviation of 0.5 and a statistical uncertainty of 0.002. This ratio was used to account for the absorbed dose from recoil protons for all fields, as described in section 2.4.
The total computing time for all 20 simulations was 43.9 cpu•years (product of the number of processors used and total elapsed wall clock time, summed over all simulations).
3.4. Attributable lifetime risk of second cancer fatality
Based on the risk coefficient from the NCRP (see section 2.6) and the effective dose calculations from this work (see section 3.1), the corresponding excess attributable lifetime risk of second cancer fatality was estimated at 3.4%.
4. Discussion
Stray radiation doses were calculated for a 10-year-old boy who received craniospinal irradiation with proton beams for the treatment of supratentorial PNET The Monte Carlo calculations were based on a complete proton CSI simulation of a treatment plan and CT images from an actual pediatric patient. The calculated quantities included effective dose from stray radiation, E, and equivalent dose in organs and tissues from stray radiation, HT, and an estimate was made of the corresponding excess attributable lifetime risk of second cancer fatality.
For the entire treatment, E was 418 mSv. The corresponding excess attributable lifetime risk of second cancer fatality from stray radiation for a population of pediatric male patients who receive this treatment was estimated at 3.4%. That is, the risk estimate suggests that approximately 34 out of every 1000 male children treated in this way will die from second cancers that were caused by stray radiation. Although this risk is small in comparison with benefits of the radiotherapy treatment, it is not negligible. The risk coefficients recommended by the NCRP were based on data from a healthy population. The RBE of neutrons for radiogenic second cancer mortality is likely to be higher for a cancer population than for the general public. Thus, the actual risk of second cancer mortality for 10-year-old male patients undergoing proton CSI may be underestimated, which underscores the importance of improving proton beam delivery techniques to reduce the patients' exposures to stray radiation. For example, simply increasing the air gap for the spinal fields may significantly reduce the stray radiation exposure. Moving the snout away from the patient distances the patient from the primary source of external neutrons, i.e. the field-defining collimator, and thus reduces the patient's exposure to external neutrons. In this study, increasing the air gap by a small amount, from 2 cm to 10 cm, reduced E from external neutrons from 399 mSv to 344 mSv, which was a decrease of 14%. A follow-up study is currently under way to explore methods to reduce stray radiation exposures and their risks.
The main clinical implication of this study is that stray radiation emanating from a passive-scattering treatment unit carries a small incremental risk for the development of a fatal radiogenic second cancer. Nonetheless, stray radiation exposures should be reduced as low as is reasonably achievable by utilizing methods suggested in this and previous investigations for passive-scattering treatment units or by utilizing scanned-beam treatment delivery techniques (Hall 2006, Brenner and Hall 2008, Taddei et al 2008, 2009). At present, the role of scanned-beam proton therapy is constrained by a paucity of clinical experience, potential safety issues associated with interplay effects between moving organs and a scanning beam, and an extremely limited availability of scanned treatments worldwide (Pedroni et al 1995, 2004). In fact, at the time of this writing, only one institution in the United States was treating with scanned beams (Anferov et al 2006). Thus, there is a strong impetus for improving the existing proton treatment units that utilize passive-scattering beam spreading.
A second clinical implication of this work is that the predicted incremental risk from passively spreading versus scanning is acceptable in light of the benefits of proton radiotherapy. It is a well established fact that photon craniospinal irradiation provides a substantial benefit to the patient, and it is a key component in the contemporary standard of care, along with surgery and chemotherapy, for medulloblastoma and supratentorial PNET (cf Jereb et al 1982, Timmermann et al 2002, 2006). Miralbell et al (2002) suggested that scanned-beam proton CSI would provide similar tumor control while reducing second cancer risks to approximately 1/15th of those associated with photon therapy. However, that study neglected the risks associated with stray neutron radiation, which some have speculated may cause passive-scattering proton therapy to carry much higher, potentially unacceptable risks (Hall 2006). Importantly, the findings of this work suggest that even passive-scattering proton therapy provides lower second cancer risks than those predicted by Miralbell et al for 6 MV photon IMRT.
Our results were generally consistent with previous investigations. For example, our finding that an increase in air gap reduced the effective dose from external neutrons by 14% is consistent with the findings reported by Zheng et al (2008) and Fontenot et al (2008). Equivalent dose values from the boost fields in this study were only slightly higher than those reported recently by Zacharatou Jarlskog et al (2008), who simulated fields for a passive-scattering treatment unit at a different facility that were roughly similar to our boost fields. In our study, the average equivalent doses for the two boost fields in the thyroid, lungs and stomach were 3.09, 1.23 and 0.855 mSv Gy−1, respectively, whereas the values averaged over all fields from their study were 2.37, 0.781 and 0.193 mSv Gy−1, respectively.
A limitation of the current study was that only protons and neutrons were tracked in the simulations. Other particles were stopped at their origins. In the case of stray photons, this may have caused a slight underestimation in absorbed dose from stray radiation. This is not a serious limitation, however, because the contribution to equivalent dose and effective dose from stray neutrons has been shown to overwhelm the contribution from stray photons (Fontenot et al 2008, Zheng et al 2008).
In conclusion, our Monte Carlo study establishes a baseline estimate of the effective dose from and corresponding risk for a pediatric patient, undergoing proton CSI. These results are unique in their dosimetric accuracy and realism, and they add to the body of evidence supporting the suitability of passively scattered proton beams for the treatment of central nervous system tumors in pediatric patients.
Acknowledgments
The authors are grateful to Dr Uwe Titt for his helpful scientific suggestions and to Lionel Santibañez and Kathryn B Carnes for their assistance in preparing this manuscript. This work was supported in part by Varian Medical Systems, by Northern Illinois University through a subcontract of Department of Defense (award W81XWH-08-1-0205) and by the National Cancer Institute (award 1RO1CA131463-01A1).
References
- Agosteo S, Birattari C, Caravaggio M, Silari M, Tosi G. Secondary neutron and photon dose in proton therapy. Radiother Oncol. 1998;48:293–305. doi: 10.1016/s0167-8140(98)00049-8. [DOI] [PubMed] [Google Scholar]
- Anferov V, Collins J, Friesel DL, Katuin J, Klein SB, Nichiporov D, Wedekind MW. The Indiana university proton therapy system 10th European Particle Accelerator Conf. Edinburgh, UK: EPAC; 2006. pp. 2349–51. [Google Scholar]
- Archambeau JO, Slater JD, Slater JM, Tangeman R. Role for proton beam irradiation in treatment of pediatric CNS malignancies. Int J Radiat Oncol Biol Phys. 1992;22:287–94. doi: 10.1016/0360-3016(92)90045-j. [DOI] [PubMed] [Google Scholar]
- Brenner DJ, Hall EJ. Secondary neutrons in clinical proton radiotherapy: a charged issue. Radiother Oncol. 2008;86:165–70. doi: 10.1016/j.radonc.2007.12.003. [DOI] [PubMed] [Google Scholar]
- Fontenot JD, Newhauser WD, Bloch C, White RA, Titt U, Starkschall G. Determination of output factors for small proton therapy fields. Med Phys. 2007;34:489–98. doi: 10.1118/1.2428406. [DOI] [PubMed] [Google Scholar]
- Fontenot JD, Newhauser WD, Titt U. Design tools for proton therapy nozzles based on the double-scattering foil technique. Radiat Prot Dosim. 2005;116:211–5. doi: 10.1093/rpd/nci229. [DOI] [PubMed] [Google Scholar]
- Fontenot JD, Taddei P, Zheng Y, Mirkovic D, Jordan T, Newhauser WD. Equivalent dose and effective dose from stray radiation during passively scattered proton radiotherapy for prostate cancer. Phys Med Biol. 2008;53:1677–88. doi: 10.1088/0031-9155/53/6/012. [DOI] [PubMed] [Google Scholar]
- Hall EJ. Intensity-modulated radiation therapy, protons, and the risk of second cancers. Int J Radiat Oncol Biol Phys. 2006;65:1–7. doi: 10.1016/j.ijrobp.2006.01.027. [DOI] [PubMed] [Google Scholar]
- Herault J, Iborra N, Serrano B, Chauvel P. Monte Carlo simulation of a protontherapy platform devoted to ocular melanoma. Med Phys. 2005;32:910–9. doi: 10.1118/1.1871392. [DOI] [PubMed] [Google Scholar]
- Herault J, Iborra N, Serrano B, Chauvel P. Spread-out Bragg peak and monitor units calculation with the Monte Carlo code MCNPX. Med Phys. 2007;34:680–8. doi: 10.1118/1.2431473. [DOI] [PubMed] [Google Scholar]
- ICRP. ICRP. Vol. 21. New York: Pergamon; 1991. Recommendations of the international commission on radiological protection: publication 60 Ann. [Google Scholar]
- ICRP. ICRP. Vol. 33. New York: Pergamon; 2003. Relative biological effectiveness (RBE), quality factor (Q), and radiation weighting factor (wR): publication 92 Ann; pp. 1–121. [DOI] [PubMed] [Google Scholar]
- Jereb B, Reid A, Ahuja RK. Patterns of failure in patients with medulloblastoma. Cancer. 1982;50:2941–7. doi: 10.1002/1097-0142(19821215)50:12<2941::aid-cncr2820501239>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Jiang H, Wang B, Xu XG, Suit HD, Paganetti H. Simulation of organ-specific patient effective dose due to secondary neutrons in proton radiation treatment. Phys Med Biol. 2005;50:4337–53. doi: 10.1088/0031-9155/50/18/007. [DOI] [PubMed] [Google Scholar]
- Kirsch DG, Tarbell NJ. New technologies in radiation therapy for pediatric brain tumors: the rationale for proton radiation therapy. Pediatr Blood Cancer. 2004;42:461–4. doi: 10.1002/pbc.10471. [DOI] [PubMed] [Google Scholar]
- Koch N, Newhauser W. Virtual commissioning of a treatment planning system for proton therapy of ocular cancers. Radiat Prot Dosim. 2005;115:159–63. doi: 10.1093/rpd/nci224. [DOI] [PubMed] [Google Scholar]
- Koch N, Newhauser WD, Titt U, Gombos D, Coombes K, Starkschall G. Monte Carlo calculations and measurements of absorbed dose per monitor unit for the treatment of uveal melanoma with proton therapy. Phys Med Biol. 2008;53:1581–94. doi: 10.1088/0031-9155/53/6/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehler AM, Schneider RJ, Sisterson JM. Range modulators for protons and heavy ions. Nucl Instrum Methods. 1975;131:437–40. [Google Scholar]
- Krejcarek SC, Grant PE, Henson JW, Tarbell NJ, Yock TI. Physiologic and radiographic evidence of the distal edge of the proton beam in craniospinal irradiation. Int J Radiat Oncol Biol Phys. 2007;68:646–9. doi: 10.1016/j.ijrobp.2007.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee CT, Bilton SD, Famiglietti RM, Riley BA, Mahajan A, Chang EL, Maor MH, Woo SY, Cox JD, Smith AR. Treatment planning with protons for pediatric retinoblastoma, medulloblastoma, and pelvic sarcoma: how do protons compare with other conformal techniques? Int J Radiat Oncol Biol Phys. 2005;63:362–72. doi: 10.1016/j.ijrobp.2005.01.060. [DOI] [PubMed] [Google Scholar]
- Lin R, Hug EB, Schaefer RA, Miller DW, Slater JM, Slater JD. Conformal proton radiation therapy of the posterior fossa: a study comparing protons with three-dimensional planned photons in limiting dose to auditory structures. Int J Radiat Oncol Biol Phys. 2000;48:1219–26. doi: 10.1016/s0360-3016(00)00741-0. [DOI] [PubMed] [Google Scholar]
- Lundkvist J, Ekman M, Ericsson SR, Jonsson B, Glimelius B. Cost-effectiveness of proton radiation in the treatment of childhood medulloblastoma. Cancer. 2005;103:793–801. doi: 10.1002/cncr.20844. [DOI] [PubMed] [Google Scholar]
- Miralbell R, Lomax A, Bortfeld T, Rouzaud M, Carrie C. Potential role of proton therapy in the treatment of pediatric medulloblastoma/primitive neuroectodermal tumors: reduction of the supratentorial target volume. Int J Radiat Oncol Biol Phys. 1997;38:477–84. doi: 10.1016/s0360-3016(97)00004-7. [DOI] [PubMed] [Google Scholar]
- Miralbell R, Lomax A, Cella L, Schneider U. Potential reduction of the incidence of radiation-induced second cancers by using proton beams in the treatment of pediatric tumors. Int J Radiat Oncol Biol Phys. 2002;54:824–9. doi: 10.1016/s0360-3016(02)02982-6. [DOI] [PubMed] [Google Scholar]
- Mu X, Bjork-Eriksson T, Nill S, Oelfke U, Johansson KA, Gagliardi G, Johansson L, Karlsson M, Zackrisson DB. Does electron and proton therapy reduce the risk of radiation induced cancer after spinal irradiation for childhood medulloblastoma? A comparative treatment planning study. Acta Oncol. 2005;44:554–62. doi: 10.1080/02841860500218819. [DOI] [PubMed] [Google Scholar]
- NCRP. Report Number 126. Bethesda, MD: National Council on Radiation Protection and Measurements; 1997. Uncertainties in fatal cancer risk estimates used in radiation protection. [Google Scholar]
- Newhauser W, et al. A Monte Carlo based dose engine for proton radiotherapy treatment planning. Med Phys. 2007b;34:2406. [Google Scholar]
- Newhauser W, et al. The risk of developing a second cancer after receiving craniospinal proton irradiation. Phys Med Biol. 2009;54:2277–91. doi: 10.1088/0031-9155/54/8/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newhauser W, Fontenot J, Zheng Y, Polf J, Titt U, Koch N, Zhang X, Mohan R. Monte Carlo simulations for configuring and testing an analytical proton dose-calculation algorithm. Phys Med Biol. 2007a;52:4569–84. doi: 10.1088/0031-9155/52/15/014. [DOI] [PubMed] [Google Scholar]
- Newhauser WD, Giebeler A, Langen KM, Mirkovic D, Mohan R. Can megavoltage computed tomography reduce proton range uncertainties in treatment plans for patients with large metal implants? Phys Med Biol. 2008;53:2327–44. doi: 10.1088/0031-9155/53/9/009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newhauser WD, Koch NC, Fontenot JD, Rosenthal SJ, Dan SG, Fitzek MM, Mohan R. Dosimetric impact of tantalum markers used in the treatment of uveal melanoma with proton beam therapy. Phys Med Biol. 2007c;52:3979–90. doi: 10.1088/0031-9155/52/13/021. [DOI] [PubMed] [Google Scholar]
- Newhauser W, Koch N, Hummel S, Ziegler M, Titt U. Monte Carlo simulations of a nozzle for the treatment of ocular tumours with high-energy proton beams. Phys Med Biol. 2005;50:5229–49. doi: 10.1088/0031-9155/50/22/002. [DOI] [PubMed] [Google Scholar]
- Noel G, Habrand JL, Helfre S, Mammar H, Kalifa C, Ferrand R, Beaudre A, Gaboriaud G, Mazeron JJ. Proton beam therapy in the management of central nervous system tumors in childhood: the preliminary experience of the Centre de Protontherapie d′Orsay. Med Pediatr Oncol. 2003;40:309–15. doi: 10.1002/mpo.10283. [DOI] [PubMed] [Google Scholar]
- Olsher RH, Hsu HH, Beverding A, Kleck JH, Casson WH, Vasilik DG, Devine RT. WENDI: an improved neutron rem meter. Health Phys. 2000;79:170–81. doi: 10.1097/00004032-200008000-00010. [DOI] [PubMed] [Google Scholar]
- Pedroni E, et al. The 200-MeV proton therapy project at the Paul Scherrer Institute: conceptual design and practical realization. Med Phys. 1995;22:37–53. doi: 10.1118/1.597522. [DOI] [PubMed] [Google Scholar]
- Pedroni E, et al. The PSI gantry 2: a second generation proton scanning gantry. Z Med Phys. 2004;14:25–34. doi: 10.1078/0939-3889-00194. [DOI] [PubMed] [Google Scholar]
- Pelowitz DB. Report LA-CP-05-0369. Los Alamos, NM: Los Alamos National Laboratory; 2005. MCNPXTM User's Manual, Version 2.5.0. [Google Scholar]
- Polf JC, Newhauser WD. Calculations of neutron dose equivalent exposures from range-modulated proton therapy beams. Phys Med Biol. 2005;50:3859–73. doi: 10.1088/0031-9155/50/16/014. [DOI] [PubMed] [Google Scholar]
- Polf JC, Newhauser WD, Titt U. Patient neutron dose equivalent exposures outside of the proton therapy treatment field. Radiat Prot Dosim. 2005;115:154–8. doi: 10.1093/rpd/nci264. [DOI] [PubMed] [Google Scholar]
- Schneider U, Agosteo S, Pedroni E, Besserer J. Secondary neutron dose during proton therapy using spot scanning. Int J Radiat Oncol Biol Phys. 2002;53:244–51. doi: 10.1016/s0360-3016(01)02826-7. [DOI] [PubMed] [Google Scholar]
- Schneider W, Bortfeld T, Schlegel W. Correlation between CT numbers and tissue parameters needed for Monte Carlo simulations of clinical dose distributions. Phys Med Biol. 2000;45:459–78. doi: 10.1088/0031-9155/45/2/314. [DOI] [PubMed] [Google Scholar]
- St Clair WH, Adams JA, Bues M, Fullerton BC, La Shell S, Kooy HM, Loeffler JS, Tarbell NJ. Advantage of protons compared to conventional X-ray or IMRT in the treatment of a pediatric patient with medulloblastoma. Int J Radiat Oncol Biol Phys. 2004;58:727–34. doi: 10.1016/S0360-3016(03)01574-8. [DOI] [PubMed] [Google Scholar]
- Taddei PJ, Fontenot JD, Zheng Y, Mirkovic D, Lee AK, Titt U, Newhauser WD. Reducing stray radiation dose to patients receiving passively scattered proton radiotherapy for prostate cancer. Phys Med Biol. 2008;53:2131–47. doi: 10.1088/0031-9155/53/8/009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddei PJ, Mirkovic D, Fontenot JD, Giebeler A, Zheng Y, Titt U, Woo S, Newhauser WD. Reducing stray radiation dose for a pediatric patient receiving proton craniospinal irradiation. Nucl Technol. 2009 doi: 10.13182/nt09-a9108. at press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tayama R, Fujita Y, Tadokoro M, Fujimaki H, Sakae T, Terunuma T. Measurement of neutron dose distribution for a passive scattering nozzle at the Proton Medical Research Center (PMRC) Nucl Instrum Methods A. 2006;564:532–6. [Google Scholar]
- Timmermann B, Kortmann RD, Kuhl J, Meisner C, Dieckmann K, Pietsch T, Bamberg M. Role of radiotherapy in the treatment of supratentorial primitive neuroectodermal tumors in childhood: results of the prospective German brain tumor trials HIT 88/89 and 91. J Clin Oncol. 2002;20:842–9. doi: 10.1200/JCO.2002.20.3.842. [DOI] [PubMed] [Google Scholar]
- Timmermann B, Kortmann RD, Kuhl J, Rutkowski S, Meisner C, Pietsch T, Deinlein F, Urban C, Warmuth-Metz M, Bamberg M. Role of radiotherapy in supratentorial primitive neuroectodermal tumor in young children: results of the German HIT-SKK87 and HIT-SKK92 trials. J Clin Oncol. 2006;24:1554–60. doi: 10.1200/JCO.2005.04.8074. [DOI] [PubMed] [Google Scholar]
- Titt U, Zheng Y, Vassiliev ON, Newhauser WD. Monte Carlo investigation of collimator scatter of proton-therapy beams produced using the passive scattering method. Phys Med Biol. 2008;53:487–504. doi: 10.1088/0031-9155/53/2/014. [DOI] [PubMed] [Google Scholar]
- Van Riper KA. A CT and MRI scan to MCNP input conversion program. Radiat Prot Dosim. 2005;115:513–6. doi: 10.1093/rpd/nci184. [DOI] [PubMed] [Google Scholar]
- Wagner MS. Automated range compensation for proton therapy. Med Phys. 1982;9:749–52. doi: 10.1118/1.595123. [DOI] [PubMed] [Google Scholar]
- White DR, Widdowson EM, Woodard HQ, Dickerson JW. The composition of body tissues: II. Fetus to young adult. Br J Radiol. 1991;64:149–59. doi: 10.1259/0007-1285-64-758-149. [DOI] [PubMed] [Google Scholar]
- White DR, Woodard HQ, Hammond SM. Average soft-tissue and bone models for use in radiation dosimetry. Br J Radiol. 1987;60:907–13. doi: 10.1259/0007-1285-60-717-907. [DOI] [PubMed] [Google Scholar]
- Woodard HQ, White DR. The composition of body tissues. Br J Radiol. 1986;59:1209–18. doi: 10.1259/0007-1285-59-708-1209. [DOI] [PubMed] [Google Scholar]
- Wroe A, Rosenfeld A, Schulte R. Out-of-field dose equivalents delivered by proton therapy of prostate cancer. Med Phys. 2007;34:3449–56. doi: 10.1118/1.2759839. [DOI] [PubMed] [Google Scholar]
- Yan X, Titt U, Koehler AM, Newhauser WD. Measurement of neutron dose equivalent to proton therapy patients outside of the proton radiation field. Nucl Instrum Methods B. 2002;476:429–34. [Google Scholar]
- Yuh GE, Loredo LN, Yonemoto LT, Bush DA, Shahnazi K, Preston W, Slater JM, Slater JD. Reducing toxicity from craniospinal irradiation: using proton beams to treat medulloblastoma in young children. Cancer J. 2004;10:386–90. doi: 10.1097/00130404-200411000-00009. [DOI] [PubMed] [Google Scholar]
- Zacharatou Jarlskog C, Lee C, Bolch WE, Xu XG, Paganetti H. Assessment of organ-specific neutron equivalent doses in proton therapy using computational whole-body age-dependent voxel phantoms. Phys Med Biol. 2008;53:693–717. doi: 10.1088/0031-9155/53/3/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Fontenot J, Taddei P, Mirkovic D, Newhauser W. Monte Carlo simulations of neutron spectral fluence, radiation weighting factor and ambient dose equivalent for a passively scattered proton therapy unit. Phys Med Biol. 2008;53:187–201. doi: 10.1088/0031-9155/53/1/013. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Newhauser W, Fontenot J, Koch N, Mohan R. Monte Carlo simulations of stray neutron radiation exposures in proton therapy. J Nucl Mater. 2007a;361:289–97. [Google Scholar]
- Zheng Y, Newhauser W, Fontenot J, Taddei P, Mohan R. Monte Carlo study of neutron dose equivalent during passive scattering proton therapy. Phys Med Biol. 2007b;52:4481–96. doi: 10.1088/0031-9155/52/15/008. [DOI] [PubMed] [Google Scholar]