Propensity Score Estimation in the Presence of Length-biased Sampling: A Nonparametric Adjustment Approach

Abstract

The pervasive use of prevalent cohort studies on disease duration increasingly calls for an appropriate methodology to account for the biases that invariably accompany samples formed by such data. It is well-known, for example, that subjects with shorter lifetime are less likely to be present in such studies. Moreover, certain covariate values could be preferentially selected into the sample, being linked to the long-term survivors. The existing methodology for estimating the propensity score using data collected on prevalent cases requires the correct conditional survival/hazard function given the treatment and covariates. This requirement can be alleviated if the disease under study has stationary incidence, the so-called stationarity assumption. We propose a nonparametric adjustment technique based on a weighted estimating equation for estimating the propensity score which does not require modeling the conditional survival/hazard function when the stationarity assumption holds. The estimator’s large-sample properties are established and its small-sample behavior is studied via simulation. The estimated propensity score is utilized to estimate the survival curves.

1. Introduction

Survival or failure time data typically comprise an initiating event, say onset of a disease, and a terminating event, say death. In an ideal situation, recruited subjects have not experienced the initiating event, the so-called incident cases. These cases are then followed to a terminating event or censoring, say loss to follow-up. In many practical situations, however, recruiting incident cases is infeasible due to logistic or other constraints. In such circumstances, subjects who have experienced the initiating event prior to the start of the study, so-called prevalent cases, are recruited. It is well known that these cases tend to have a longer survival time, and hence form a biased sample from the target population. This bias is termed length bias when the initiating events are generated by a stationary Poisson process (Cox & Lewis, 1966; Zelen & Feinlein, 1969), the so-colled stationarity assumption.

Studies on length-biased sampling can be traced as far back as Wicksell (1925) and his corpuscle problem. The phenomenon was later noticed by Fisher (1934) in his article on methods of ascertainment. Neyman (1955) discussed length-biased sampling further and coined the term incidence-prevalence bias. Cox (1969) studied length-biased sampling in industrial applications, while Zelen & Feinlein (1969) observed the same bias in screening tests for disease prevalence (Asgharian et al., 2002; Asgharian & Wolfson, 2005). More recently, Shen et al. (2009), Qin & Shen (2010) and Ning et al. (2010) have studied the analysis of covariates under biased sampling.

In observational studies, treatment is assigned to the experimental units without randomization. Thus, in each treatment group, the covariate distributions may be imbalanced which may lead to bias in estimating the treatment effect if the covariate imbalance is not properly taken into account (Cochran & Rubin, 1973; Rubin, 1973). The propensity score is a tool that is widely used in causal inference to adjust for this source of bias (Robins et al., 2000; Hernán et al., 2000). Rosenbaum & Rubin (1983) define the propensity score for a binary treatment D as p(D = 1|X) where X is a vector of measured covariates. They show that under some assumptions, treatment is independent of the covariates inside each propensity score stratum (the balancing property of the propensity score).

In cases where the sample is not representative of the population, naive propensity score estimation will not in general have the balancing property. Cheng & Wang (2012) develop a method that consistently estimates the parameters of the propensity score from prevalent survival data. They also present a method that can be used in a special case of length-biased sampling. Their method requires correct specification of the conditional hazard model given the treatment and covariates. We refer to their estimator as CW in the sequel.

Our goal is to develop a method that estimates the propensity score using a weighted logistic regression where weights are estimated nonparametrically. Our estimating equation is designed specifically for length-biased data, i.e., for a disease with stationary incidence. Unlike the method proposed by CW, our method does not require any model specification for the conditional failure time given the exposure and the covariates. We also generalize a nonparametric survival curve estimation method introduced by Huang & Qin (2011) to accommodate confounding as well as length-biased sampling.

2. Length-biased sampling

In this section, we introduce concepts and notations necessary to formulate problems involving length-biased sampling. We adopt the common modeling framework for prevalent cohort studies. We assume that affected individuals in the study population develop the condition of interest (onset) according to some stochastic mechanism at random points in calendar time, and undergo a terminal event (failure) at some subsequent time point that is also determined by a stochastic mechanism. Individuals enter into the study at some census time, and are followed up until the terminal or censoring event.

2.1. Notations

Let T^pop be the time measured from the onset to failure time in the target population with an absolutely continuous distribution F and density f. Also, let D^pop and X^pop be the binary treatment variable and the vector of covariates, respectively. Let T be the same measured time for observed subjects with distribution F_LB. The variables with superscript pop represent the population variables; variables without pop denote the observed truncated variables. It is well known that if the onset times are generated by a stationary Poisson process, then

$$F_{LB}(t)=\frac{{\int }_0^{t}sdF(s)}{{\int }_0^{\infty }sdF(s)}=\frac{1}{\mu }{\int }_0^{t}sdF(s)\text{and}{f}_{LB}(t)=\frac{tf(t)}{\mu },$$ (1)

where f_LB is the density function of F_LB and μ is the mean survival time under F. The observed event time, T, can be written A + R, when A is the time from the onset of the disease to the recruitment time, and R, the residual life time, is the time from recruitment to the event, also called backward and forward recurrence times, respectively. When individuals are also subject to right-censoring, the observed survival time is Y = A + min(R, C), where C is a censoring time measured from the recruitment to the loss to follow-up; for all subjects, both A and min(R, C) are observed. The censoring indicator is denoted by δ (δ = 1 indicating failure). The sample consists of (y_i, a_i, δ_i, d_i, x_i) for n independent subjects. The following diagram illustrates the different random quantities introduced in this Section.

Throughout the paper, we assume that the following assumptions hold:

• A1. The variable (T^pop, D^pop, X^pop) is independent of the calendar time of the onset of the disease.

• A2. The disease has stationary incidence, i.e., the disease incidence occurs at a constant rate.

• A3. The censoring time C is independent of (A, R, D, X).

2.2. Potential outcomes

We use the counterfactual or potential outcome framework to define the causal effect of interest. Potential outcome models are introduced by Neyman (1990) and Rubin (1978) for time independent treatment. We define the counterfactual values (A(d), R(d), Y(d)) corresponding to the backward, forward recurrence times, and observed survival time, respectively, had – possibly contrary to fact – the treatment taken the value d. Also, let T^pop(d) denote the counterfactual response if contrary to the fact that all the individuals would have received the treatment D = d, and let D denote the treatment received. The observed response, T^pop, is defined as DT^pop (1) + (1 − D)T^pop (0).

We make the following identifiability assumptions to link the counterfactual outcome and the observed data (Robins, 1994, 1997):

• A4. Consistency: Potential outcome for a treatment corresponds to the actual outcome if assigned to that treatment.

• A5. No unmeasured confounding: Given the observed covariates X, the counterfactual outcome Y (d) is independent of the assignment of treatment.

• A6. Positivity: Let p_D|X (d|x) be the conditional probability of receiving treatment d given X = x. For each treatment d and for each possible value x, p_D|X (d|x) > 0.

3. Propensity score estimation under length-biased sampling

Assuming a logit model for the propensity score in the target population, we have

$$\pi (\mathbf{x},\alpha )=p(D^{\mathit{\text{pop}}}=1|{\mathbf{X}}^{\mathit{\text{pop}}}=\mathbf{x})=\frac{\text{exp}(\alpha \mathbf{x})}{1+\text{exp}(\alpha \mathbf{x})}.$$ (2)

where α is a p × 1 vector of parameters. The vector of covariates X may include a column of 1s. It can be shown that under assumption A2, we have

$$p_{LB}(D=1|\mathbf{X}=\mathbf{x})=\frac{{\mu }_1(\mathbf{x},\theta )p(D^{\mathit{\text{pop}}}=1|{\mathbf{X}}^{\mathit{\text{pop}}}=\mathbf{x})}{\pi (\mathbf{x},\alpha ){\mu }_1(\mathbf{x},\theta )+(1-\pi (\mathbf{x},\alpha )){\mu }_0(\mathbf{x},\theta )},$$ (3)

where ${\mu }_d(\mathbf{x},\theta )={\int }_0^{\infty }p(T^{\text{pop}}(d)\ge a|\mathbf{X}=\mathbf{x},\theta )da$ for d = 0, 1 is the conditional counterfactual mean failure time if treated at D = d (Bergeron et al. (2008)). Note that under assumptions A5 – 7, p(T^pop(d) ≥ a|, X = x, θ) = p(T^pop ≥ a|D = d, X = x, θ) where θ parametrizes the conditional density of T^pop.

Assuming the proportional hazard model, i.e., λ_T^pop (u|D^pop = d, X^pop = x) = λ₀(u)e^γd+βx, Cheng & Wang (2012) show that the parameter of the propensity score can be consistently estimated using the logistic regression but adjusted for the ‘offset’ term log(α̂(x; Λ̂, γ̂, β̂)) as the intercept where $\mathrm{\alpha ̂}(x;\mathrm{\Lambda ̂},\mathrm{\gamma ̂},\mathrm{\beta ̂})=\frac{{\sum }_{i=1}^n\text{exp}[-\mathrm{\Lambda ̂}(a_i)\text{exp}(\mathrm{\gamma ̂}+\mathrm{\beta ̂}\mathrm{x})}{{\sum }_{i=1}^n\text{exp}[-\mathrm{\Lambda ̂}(a_i)\text{exp}(\mathrm{\beta ̂}\mathrm{x})]}$. The cumulative hazard function Λ is estimated using the Breslow estimator. The consistency of the parameters of the propensity score in the CW method relies on the correct specification of the conditional hazard model given the treatment and covariates.

When the initiating event of the duration variable has stationary incidence, it is possible to devise a robust method for estimating the propensity score that does not require knowledge of the conditional hazard model. See among others Wolfson et al. (2001) and De Uña-álvarez (2004) for examples of such duration variables in medical and labor force studies, respectively.

Let f (t|d, x, θ) be the unbiased conditional density of survival times given the covariates and treatment. Then, under assumptions A1 and A2, the joint density of (A, T) given (D, X) is $f(t|d,\mathbf{x},\theta )/{\int }_0^{\infty }uf(u|d,\mathbf{x},\theta )duI(t>a>0)$ as shown in Asgharian et al. (2006). Assumption A3 is used to show that

$$p(Y\in (t,t+dt),A\in (a,a+da),\delta =1|d,\mathbf{x},\theta )=\frac{f(t|d,\mathbf{x},\theta )S_c(t-a)dtda}{{\mu }_d(\mathbf{x},\theta )},$$

where S_c (․) is the survival function for the residual censoring variable C, respectively. By integrating the above equation over 0 < a < t, we have

$$p(Y\in (t,t+dt),\delta =1|d,\mathbf{x},\theta )=\frac{f(t|d,\mathbf{x},\theta )w(t)dt}{{\mu }_d(\mathbf{x},\theta )},$$ (4)

where $w(t)={\int }_0^t{S}_C(s)ds$ (Shen et al., 2009; Qin & Shen, 2010).

We construct an unbiased estimating equation for estimating the parameters of the propensity score using the weighted logistic regression where weights are estimated nonparametrically. Let F (d|x) be the unbiased conditional distribution of the treatment given the covariates. Then

$$𝔼\left[\delta \frac{(D-\pi (\mathbf{x},\alpha ))}{w(Y)}\right|\mathbf{X}=\mathbf{x}]=𝔼[𝔼\left\{\delta \frac{(d-\pi (\mathbf{x},\alpha ))}{w(Y)}\right|D=d,\mathbf{X}=\mathbf{x}\left\}\right]=\int (d-\pi (\mathbf{x},\alpha ))\int \frac{f(y|\mathbf{x},d,\theta )w(y)}{w(y){\mu }_d(\mathbf{x},\theta )}dy\times \frac{{\mu }_d(\mathbf{x},\theta )dF(d|\mathbf{x})}{\mu (\mathbf{x},\alpha ,\theta )}=\frac{1}{\mu (\mathbf{x},\alpha ,\theta )}\int (d-\pi (\mathbf{x},\alpha ))dF(d|\mathbf{x})=0.$$

The second equality follows from equations (4), and (3). The last equality holds since f (y|x, d) is a proper density and (2). An unbiased estimating equation for α is therefore

$$U(\alpha )=\sum _{i=1}^n{U}_i(\alpha )=\sum _{i=1}^n{\delta }_i{\mathbf{x}}_i^{\top }\frac{(d_i-\pi ({\mathbf{x}}_i,\alpha ))}{ŵ(y_i)}=0,$$ (5)

where $ŵ(y)={\int }_0^y{Ŝ}_C(s)ds$ and Ŝ_C is the Kaplan-Meier estimator of the survivor function of the residual censoring variable C.

The following theorem presents the asymptotic properties of the estimators obtained by (5) in the presence of length-biased sampling when w(․) is replaced by its estimated value.

Theorem 1

Let α̂ be an estimator obtained by (5). Then under conditions C1 – C6 and assumptions A1 – A6, α̂ → α₀ in probability as n → ∞. Moreover,

$$\sqrt{n}(\mathrm{\alpha ̂}-\alpha )\stackrel{d}{\to }𝒩(0,\eta (\alpha )),$$

where η(α) is given in the Appendix.

Proof

See the Appendix.

A consistent plug-in estimator of η(α) is presented in the Appendix.

Note that the censored individuals contribute to this estimating equation through Ŝ_C as well as the uncensored ones. Let $M_{iC}(t)=\mathrm{𝟙}(Y_i-A_i<t,{\delta }_i=0)-{\int }_0^t\mathrm{𝟙}(\text{min}(Y_i-A_i,C_i)>u)d{\mathrm{\Lambda }}_C(u)$, with Λ_C(․) be the cumulative hazard function of the censoring variable. As a part of the proof of Theorem 1, we show that as n → ∞,

$$\frac{1}{n}\sum _{i=1}^n{U}_i(\alpha )=\frac{1}{n}\sum _{i=1}^n[{\delta }_i{\mathbf{x}}_i^{\top }\frac{d_i-\pi ({\mathbf{x}}_i,\alpha )}{w(y_i)}+{\int }_0^s\frac{v(t)d{M}_{iC}(t)}{S_C(t)S_R(t)}]+o_p(n^{-1/2}),s=\text{sup}[t:p(C>t)>0],$$ (6)

where S_R(u) is the survival function of the residual life time and the function v (t) is defined in the Appendix. The second part of the summation in the RHS of (6) is often referred to as the augmentation element (Rotnitzky & Robins, 2005).

4. Survival Curve Estimation

Various methods have been proposed to adjust for length-biased sampling, including: the truncation product-limit estimator (Wang et al., 1986) and the maximum pseudo-partial likelihood estimator (Luo & Tsai, 2009). Here, we generalize the method introduced by Huang & Qin (2011) which incorporates the information in the marginal distribution of the truncation time from disease onset to recruitment time. The bias induced by confounding can be adjusted by creating a pseudo-population using the inverse probability of being in the group that the individuals actually belong to (Nieto & Coresh, 1996; Xie & Liu, 2005; Cole & Hernán, 2004).

Our goal is to estimate the counterfactual survival function S_d(y), where S_d(y) = 𝔼[I(T^pop(d) > t)]. Under assumptions A4–6, the function S_d(y) can be identified using the observed data as follows

$$S_d(t)=𝔼[I(T^{\text{pop}}(d)>t)]=𝔼[\frac{I(D=d)}{p(D=d|\mathbf{X})}I(T^{\text{pop}}>t)].$$

Following Huang & Qin (2011), S_d(t) can be estimated by

$${\mathrm{S̃}}_d(t)=\prod _{u\in [0,t]}[1-d{\mathrm{\Lambda ̂}}_d(u)],$$

where

$$d{\mathrm{\Lambda ̂}}_{id}={\int }_0^t\frac{d{Ñ}_d(t)}{{\mathrm{R̃}}_d(t)}$$

with

$${Ñ}_d(t)=1/n\sum _{i=1}^n\frac{I(d_i=d)}{p(d_i=d|{\mathbf{x}}_i)}{\delta }_{i}I(y_i\le t){\mathrm{R̃}}_d(t)=1/n\sum _{i=1}^n\frac{I(d_i=d)}{p(d_i=d|{\mathbf{x}}_i)}I(y_i\ge t)+{\mathrm{S̃}}_{dA}(t).$$

Also, the product-limit estimator S̃_dA (t) is

$${\mathrm{S̃}}_{dA}(t)=\prod _{u\in [0,t]}[1-\frac{d{\mathrm{Q̃}}_d(u)}{{\mathrm{K̃}}_d(u)}],$$

where

$${\mathrm{Q̃}}_d(u)=1/n\sum _{i=1}^n\frac{I(d_i=d)}{p(d_i=d|{\mathbf{x}}_i)}[I(a_i\le t)+{\delta }_{i}I(y_i-a_i\le t)]{\mathrm{K̃}}_d(t)=1/n\sum _{i=1}^n\frac{I(d_i=d)}{p(d_i=d|{\mathbf{x}}_i)}[I(a_i\ge t)+I(y_i-a_i\ge t)].$$

We utilize our proposed estimating equation (5) to estimate the propensity score and replace p(d_i = d|x_i) with p(d_i = d|x_i,α̂).

5. Simulation Studies

In this Section, we describe a simulation study to examine the performance of the proposed propensity score estimator. Our simulation consists of 500 datasets of sizes 500 and 5000. The censoring variable C is generated from a uniform distribution in the interval (0, τ) where the parameter τ is set such that it results in a desired censoring proportion.

To create length-biased samples, we generate a variable A from a uniform distribution (0, ρ) and ignore those whose generated unbiased failure time is less than A.

We generated the unbiased failure times from the following hazard model h(t|d, x) = 0.2 exp{d − 0.5x₁ + 0.5x₂ + 0.5dx₁ − 0.5dx₂}, where $D~\text{Bernoulli}\left(\frac{\text{exp}\{-0.1+1x_1-1x_2\}}{1+\text{exp}\{-0.1+1x_1-1x_2\}}\right)$ with X₁ and X₂ distributed according to N(0, σ = 0.5). We estimate the parameters of the propensity score using CW and the proposed method and compare the results with the true values. We assume three different censoring proportions 10%, 20% and 30%.

We estimate the parameters of the propensity score using four different estimators: α̂ is the estimator obtained by the proposed method; α̂_w and ${\mathrm{\alpha ̂}}_w^m$ are the estimator obtained by the CW method when the hazard model is correctly and incorrectly specified, respectively, and α̂_Un is obtained by a naive method that does not adjust for the length-biased sampling. In ${\mathrm{\alpha ̂}}_w^m$, we assume that the interaction between the treatment D and the covariate X₂ has been ignored in the fitted hazard model.

Table 1 summarizes the estimated propensity score parameters and their standard errors. Our simulation results confirm that the proposed estimating equation (5) adjusts the length-biased sampling. The standard errors, however, are larger than the one obtained by the CW method, which is the price we pay for relaxing the modeling assumption of the hazard model. As we expected, CW estimator is highly sensitive to model misspecification even when just one of the interaction terms is ignored. Specifically, when the interaction term between the treatment and variable X₂ is omitted in the fitted hazard model, the estimated coefficient corresponding to X₂ in the propensity score model is biased. In general, if variables in the study are correlated, then missing one variable in the hazard model may cause bias in the estimation of other variables in the propensity score model as well.

Table 1.

Simulation: Propensity score parameter estimation. α̂: Estimated parameters using the proposed method. α̂_w: Estimated parameters using the CW method. ${\mathrm{\alpha ̂}}_w^m$: Estimated parameters using the CW method when the hazard model is misspecified. α̂_Un: Estimated parameters when unadjusted for the length-biased sampling. α=(−0.1,1,−1).

Method	Bias	S.D.	Bias	S.D.
10 % Cens.	n = 500		n = 5000
α̂	(0.01,0.04,0.03)	(0.21,0.43,0.45)	(0.00,0.01,0.01)	(0.09,0.18,0.19)
α̂w	(0.08,0.02,0.01)	(0.17,0.28,0.28)	(0.01,0.00,0.01)	(0.06,0.10,0.10)
${\mathrm{\alpha ̂}}_w^m$	(0.03,0.02,0.49)	(0.17,0.29,0.23)	(0.08,0.03,0.48)	(0.06,0.09,0.08)
α̂Un	(0.10,0.50,0.50)	(0.11,0.21,0.22)	(0.10,0.51,0.50)	(0.04,0.07,0.08)
20 % Cens.	n = 500		n = 5000
α̂	(0.01,0.05,0.05)	(0.22,0.42,0.43)	(0.02,0.03,0.03)	(0.09,0.18,0.20)
α̂w	(0.02,0.01,0.01)	(0.17,0.29,0.27)	(0.02,0.01,0.01)	(0.06,0.10,0.10)
${\mathrm{\alpha ̂}}_w^m$	(0.01,0.02,0.47)	(0.16,0.29,0.21)	(0.02,0.05,0.46)	(0.06,0.10,0.08)
α̂Un	(0.11,0.49,0.50)	(0.10,0.22,0.20)	(0.10,0.51,0.50)	(0.04,0.07,0.08)
30 % Cens.	n = 500		n = 5000
α̂	(0.04,0.08,0.09)	(0.22,0.44,0.44)	(0.03,0.06,0.07)	(0.10,0.19,0.20)
α̂w	(0.07,0.00,0.02)	(0.17,0.29,0.29)	(0.08,0.03,0.02)	(0.06,0.10,0.11)
${\mathrm{\alpha ̂}}_w^m$	(0.07,0.02,0.45)	(0.17,0.29,0.21)	(0.03,0.06,0.45)	(0.06,0.10,0.08)
α̂Un	(0.11,0.49,0.50)	(0.10,0.22,0.20)	(0.10,0.51,0.50)	(0.04,0.07,0.08)

5.1. Survival Curve Estimation

Here, we compare our proposed method of estimating the survival curves if treated and untreated with two naive approaches. The naive method (NV1) estimates the propensity score without considering the length-biased sampling and the second naive method (NV2) ignores both the confounding and the length-biased sampling. We generated the unbiased failure times from a Weibull distribution with shape parameter 10 and scale parameter h₂(t|d, x) = 0.2 exp{3d + 2.5x₁ − 2x₂ − 2dx₁ + 1.1dx₂}, where $D~\text{Bernoulli}\left(\frac{\text{exp}\{2x_1-2x_2-2x_1{x}_2\}}{1+\text{exp}\{2x_1-2x_2-2x_1{x}_2\}}\right)$ with X₁ and X₂ are N(2, σ = 0.3). We report the result based on the censoring proportion 30%.

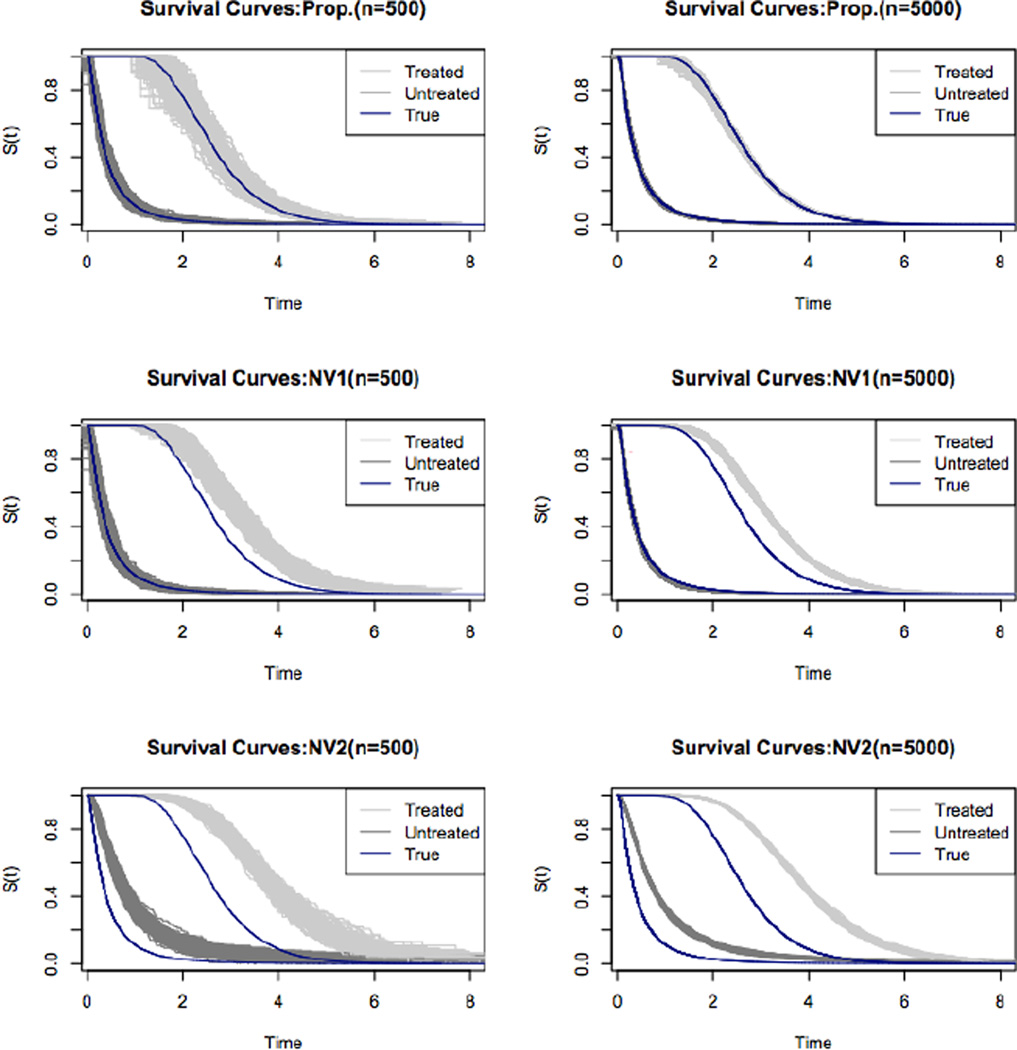
The survival curves for the treated and untreated groups are presented in Figure 1. The light and dark grey shaded areas are the survival curves based on the 500 datasets for treated and untreated individuals, respectively. The dark solid line is the true survival curve. As the plots show, the true survival curve lies entirely in the shaded area provided by our proposed estimator while ignoring either or both of the length-biased sampling and/or confounding result in a biased estimator.

Figure 1.

Simulation: The estimated survival curves using the proposed (Prop.) and two naive estimators. The light and dark shaded areas are the treated and untreated survival curves, respectively. The solid line represents the true curve. NV1 is when the propensity score is naively estimated without considering the length-biased sampling. NV2 is when we ignore both the confounding and the length-biased sampling.

6. Discussion

We present a weighted estimating equation to estimate the parameters of the propensity score from right-censored length-biased samples. In many cases, recruiting prevalent cases is more efficient. However, it is well known that in these cases subjects with longer survival time have a greater chance to be selected. This may affect the distribution of the observed covariates (Bergeron et al., 2008). For example, if treated subjects tend to live longer, then these subjects will be over represented in the observed sample. As such, if the propensity score is fitted without adjusting for this source of bias, it will be skewed to the left. Recently, Cheng & Wang (2012) proposed a method to adjust for the length-biased sampling which requires the correctly specified conditional survival function given the treatment and covariates. This modeling assumption may limit the application of this approach, particularly, when an investigator is interested in estimating the marginal causal effect.

In our proposed method, we estimate the weights nonparametrically. Thus, unlike the existing methods, it does not require any modeling assumptions for the conditional hazard function given the treatment and covariates. Our method produces an unbiased estimator but the standard errors are larger than the method proposed by Cheng & Wang (2012).

Generalizing a nonparametric survival curve estimation method introduced by Huang & Qin (2011), we derive a method for estimating the counterfactual survival curves in the presence of length-biased sampling. The bias induced by confounding is adjusted by creating a pseudo-population using the inverse probability of being in the group to which the individuals actually belong. The treatment assignment probabilities are estimated using the proposed estimating equation.

We confined our attention to the stationary case; the methodology presented in this manuscript can, however, be extended to any other left-truncation cases as long as the left truncation distribution is known (Luo & Tsai, 2009).

Appendix

In this section, we present the assumptions and proofs of the main result. The following conditions are required for establishing Theorem 1:

• C.1 X is a p vector of bounded covariates, not contained in a (p − 1) dimensional hyperplane.

• C.2 sup[t : p(R > t) > 0] ≥ sup[t : p(C > t) > 0]=s and p(δ = 1) > 0.

• C.3 ${\int }_0^s[{({\int }_t^s{S}_C(v)dv)}^2/(S_C^2(t)S_R(t))]d{S}_C(t)<\infty$.

• C.4 det $𝔼\left[{\left\{\delta {\mathbf{X}}^{\top }\frac{D-\pi (\mathrm{X},\alpha )}{w(Y)}\right\}}^{\otimes 2}\right]<\infty$.

• C.5 $\mathrm{\Lambda }=𝔼[\delta {\mathbf{X}}^{\top }\frac{\partial \pi (\mathrm{X},\alpha )}{\partial \alpha }]$ is nonsingular.

• C.6 det $[{\int }_0^s{v}^2(t)/(S_C^2(t)S_R(t))d{S}_C(t)]<\infty$ where $v(t)=𝔼\left[\frac{\delta \mathrm{𝟙}(Y>t){\mathrm{X}}^{\top }[D-\pi (\mathrm{X},\alpha ))]{\int }_t^Y{S}_C(v)dv}{w^2(Y)}\right]$,

C.2 is an identifiability condition (Wang, 1991), C.3–C.6 are required to obtain an estimator with a finite variance.

Proof of Theorem 1. The stochastic process M_C(s) has mean zero,

$$𝔼[M_C(s)]=𝔼[\mathrm{𝟙}(C<Y-A<s)]-{\int }_0^s𝔼[\mathrm{𝟙}(Y-A>u).\mathrm{𝟙}(C>u)]d{\mathrm{\Lambda }}_C(u)={\int }_0^s{S}_C(u){\lambda }_C(u)S_R(u)du-{\int }_0^s{S}_C(u)S_R(u)d{\mathrm{\Lambda }}_C(u)=0.$$

Using the strong consistency of ŵ(y) to w(y) (Pepe & Fleming, 1991), we have

$$\frac{1}{ŵ(Y)}=\frac{1}{w(Y)}[1+\frac{w(Y)-ŵ(Y)}{w(Y)}]+o_p(1).$$

Thus

$$Ũ(\alpha )=\frac{1}{\sqrt{n}}\sum _{i=1}^n{U}_i(\alpha )=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\delta }_i{\mathbf{x}}_i^{\top }\frac{d_i-\pi ({\mathbf{x}}_i,\alpha )}{ŵ(y_i)}=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\delta }_i{\mathbf{x}}_i^{\top }\frac{d_i-\pi ({\mathbf{x}}_i,\alpha )}{w(y_i)}[1+\frac{w(y_i)-ŵ(y_i)}{w(y_i)}]+o_p(1),=\frac{1}{\sqrt{n}}\sum _{i=1}^n[{\delta }_i{\mathbf{X}}_i\frac{D_i-\pi ({\mathbf{X}}_i,\alpha )}{w(Y_i)}+{\int }_0^s\frac{\mathrm{v̂}(t)d{M}_C(t)}{S_C(t)S_R(t)}],$$ (7)

where

$$\mathrm{v̂}(t)=\frac{1}{n}\sum _{i=1}^n[\frac{{\delta }_{i}I(Y_i>t){\mathbf{X}}_i[D_i-\pi ({\mathbf{X}}_i,\alpha ))]{\int }_t^{Y_i}{S}_C(v)dv}{w^2(Y_i)}].$$

The last equality (7) follows from the martingale integral representation $\sqrt{n}(ŵ(Y)-w(Y))$ (Shen et al., 2009; Qin & Shen, 2010).

Using the standard Taylor expansion, we can derive the asymptotic variance of the estimator as follows

$$\eta (\alpha )=\mathrm{\Lambda }\prime {\mathrm{\Sigma }}^{-1}\mathrm{\Lambda },$$

where

$$\begin{array}{cc}\hfill \mathrm{\Sigma }=𝔼[Ũ(\alpha )Ũ(\alpha )]& =𝔼\left[{\left\{\delta {\mathbf{X}}^{\top }\frac{D-\pi (\mathbf{X},\alpha )}{w(Y)}\right\}}^{\otimes 2}{\{1+\frac{w(Y)-ŵ(Y)}{w(Y)}\}}^2\right]\hfill \\ \hfill & =𝔼\left[{\{\delta {\mathbf{X}}^{\top }\frac{D-\pi (\mathbf{X},\alpha )}{w(Y)}+{\int }_0^s\frac{v(t)d{M}_C(t)}{S_C(t)S_R(t)}\}}^{\otimes 2}\right]\hfill \\ \hfill \mathrm{\Lambda }& =𝔼[\frac{\partial U_i(\alpha )}{\partial \alpha }]=𝔼[\frac{\delta }{w(Y)}{\mathbf{X}}^{\top }\frac{\partial \pi (\mathbf{X},\alpha )}{\partial \alpha }]\hfill \end{array}$$

where $v(t)=𝔼\left[\frac{\delta \mathrm{𝟙}(Y>t){\mathrm{X}}^{\top }[D-\pi (\mathrm{X},\alpha ))]{\int }_t^Y{S}_C(v)dv}{w^2(Y)}\right]$ Let ℙ_n be the empirical average. The components of the variance-covariance matrix η(α) can be consistently estimated by

$$\mathrm{\Sigma ̂}={\mathbb{P}}_n\left[{\{\delta {\mathbf{X}}^{\top }\frac{D-\pi (\mathbf{X},\alpha )}{ŵ(Y)}+{\int }_0^s\frac{\mathrm{v̂}(t)d{\mathrm{M̂}}_C(t)}{{Ŝ}_C(t){Ŝ}_R(t)}\}}^{\otimes 2}\right],\mathrm{\Lambda ̂}={\mathbb{P}}_n\left[\frac{\partial U_i(\alpha )}{\partial \alpha }\right]={\mathbb{P}}_n\left[\frac{\delta }{ŵ(Y)}{\mathbf{X}}^{\top }\frac{\partial \pi (\mathbf{X},\alpha )}{\partial \alpha }\right].$$

Also, the stochastic process M_C(s) can be estimated by replacing the Λ_C(․) by its estimate, Λ̂_C(․).