An experimental and theoretical NMR study of NH-benzimidazoles in solution and in the solid state: proton transfer and tautomerism

Abstract

This paper reports the ¹H, ¹³C and ¹⁵N NMR experimental study of five benzimidazoles in solution and in the solid state (¹³C and ¹⁵N CPMAS NMR) as well as the theoretically calculated (GIAO/DFT) chemical shifts. We have assigned unambiguously the "tautomeric positions" (C3a/C7a, C4/C7 and C5/C6) of NH-benzimidazoles that, in some solvents and in the solid state, appear different (blocked tautomerism). In the case of 1H-benzimidazole itself we have measured the prototropic rate in HMPA-d₁₈.

Introduction

Of almost any class of heterocycles it can be said that they have relevant biological and medicinal chemistry properties, because, for instance, over 80% of top small molecule drugs by US retail sales in 2010 contain at least one heterocyclic fragment in their structures [1]. Benzimidazoles besides being the skeleton of many relevant drugs (fungicides, anthelmintics, antiulcerative, antiviral,…) [2–3] are also part of some natural products (the most prominent benzimidazole compound in nature is N-ribosyl-5,6-dimethylbenzimidazole, which serves as an axial ligand for cobalt in vitamin B₁₂) and have interesting ferroelectric properties [4]. Particularly relevant for the present work is their proton conducting abilities, based of the 1,3-N–H···N hydrogen bonds, not only in benzimidazole polymers but in molecular compounds [5–6].

Degenerated tautomerism (autotrope) [7–8] simultaneously simplifies and complicates the NMR spectra of molecules in solution to the point that the assignment of some signals that become magnetically equivalent (isochronous) [9–10] by fast proton exchange has been much neglected. With the advent of solid-state NMR spectroscopy and the suppression of prototropic tautomerism, the assignment problem arises anew. In recent years, the use of very pure NMR solvents, particularly DMSO-d₆, and highfield instruments has lead to obtain solution spectra where the prototropy has been considerably slowed down.

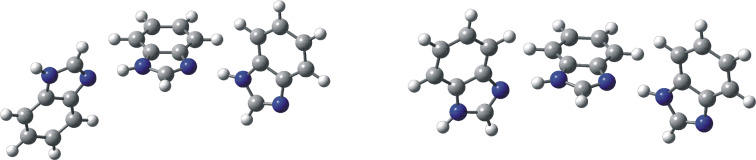
We present in this paper a study of four N-unsubstituted 1H-benzimidazoles (Figure 1) including 2-methyl-1H-benzimidazole (2) that shows in the solid state ferroelectric switching in two dimensions due to its pseudo-tetragonal crystal symmetry [4], and 2-benzyl-1H-benzimidazole (4) a vessel-dilating and spasm-reducing agent known as dibazol or bendazole [3], where the tautomerism has been blocked resulting in the concomitant problem of assignment of some signals. We have selected 1-methyl-1H-benzimidazole (5) as the simplest benzimidazole without tautomerism.

Figure 1.

The five studied compounds.

The use of theoretically calculated chemical shifts has been decisive to solve this problem. We have used from 2001 [at the 6-31+G(d) level] [11] and then, from 2007, at the 6-311++G(d,p) level [12], a statistical approach that consists in comparing GIAO calculated absolute shieldings (σ, ppm) with experimental chemical shifts (δ) determined either in solution or in the solid state:

δ¹H = 31.0 – 0.97 σ¹H [13]

δ¹³C = 175.7 – 0.963 σ¹³C [12]

δ¹⁵N = –154.0 – 0.874 σ¹⁵N [12]

These equations give excellent results except for atoms (generally, carbon) linked to halogen atoms (I > Br > Cl >> F) [11,14] where relativistic corrections are necessary [15].

Results and Discussion

The experimental data are all original although averaged values of all nuclei have been reported for the three NH-benzimidazoles 1, 2 and 4 [16–21]; besides ¹³C and ¹⁵N NMR chemical shifts of 5 have been published [22–23].

Three kinds of calculations have been done: isolated molecules (gas phase), continuous model solvated molecules in DMSO, and hydrogen-bonded trimers for 1, to simulate the crystal [24]. The central benzimidazole is N–H···N hydrogen bonded to two other benzimidazoles like in the crystal chain (catemer). Two trimers, A and B, that differ in the conformation of the first benzimidazole were calculated for this compound, but the differences in energy are very small, less than 0.1 kJ·mol⁻¹ (Figure 2).

Figure 2.

Trimers A (left) and B (right) of 1.

First, we will discuss the six carbon atoms of the benzene ring of benzimidazole (3a, 4, 5, 6, 7, 7a) and then the remaining atoms (N1, C2, N3 and those of the substituent). In NH-benzimidazoles, when prototropic tautomerism occurs (Figure 3), the signals of the benzimidazole carbons in groups of two coalesce in an average signal (the same happens with the N atoms but the chemical shifts are so different that there are no problems of assignment). Actually, this was a very common occurrence, but in the series of compounds of Table 1, only for benzimidazole itself and for 3, average signals were observed in DMSO-d₆, a solvent known to slow down the prototropic exchanges. For these two compounds, we recorded the spectra in HMPA-d₁₈, which is better for this purpose [25] observing the signals of compounds where the prototropic exchange is blocked.

Figure 3.

The tautomerism of 1H-benzimidazole.

Table 1.

Calculated and experimental ¹H and ¹³C chemical shifts of the benzene part.

Compound	1H calcd gas	1H calcd DMSO	1H exp. HMPA-d18 273 K	13C calcd gas	13C calcd DMSO	13C exp. HMPA-d18 273 K	13C exp. CPMAS
1
4	7.81	7.79	7.54	121.67	119.58	118.7	119.4
5	7.20	7.34	7.11	121.68	121.79	120.1	123.0
6	7.24	7.41	7.11	122.88	123.04	121.2	123.8
7	7.32	7.67	7.42	108.23	110.99	110.9	112.9
3a	–	–	–	144.67	144.22	143.4	143.1
7a	–	–	–	132.70	133.54	133.7	136.4
1 tri A
4	7.89	7.93	7.54	119.85	118.28	118.7	119.4
5	7.26	7.39	7.11	122.10	121.91	120.1	123.0
6	7.28	7.39	7.11	122.93	122.73	121.2	123.8
7	7.49	7.77	7.42	110.00	111.88	110.9	112.9
3a	–	–	–	143.85	143.62	143.4	143.1
7a	–	–	–	134.13	134.76	133.7	136.4
1 tri B
4	7.91	7.90	7.54	119.99	118.42	118.7	119.4
5	7.28	7.38	7.11	122.02	121.87	120.1	123.0
6	7.26	7.39	7.11	122.72	122.68	121.2	123.8
7	7.48	7.75	7.42	110.18	112.00	110.9	112.9
3a	–	–	–	143.84	143.35	143.4	143.1
7a	–	–	–	134.04	134.62	133.7	136.4
Compound	1H calcd gas average	1H calcd DMSO average	1H exp. DMSO-d6 average	13C calcd gas average	13C calcd DMSO average	13C exp. DMSO-d6 average	13C exp. CPMAS
1
4/7	7.695	7.825	7.58	115.08	115.21	115.3
5/6	7.27	7.385	7.17	122.37	122.28	121.7
3a/7a			–	138.94	138.98	138.4
NH			12.44
2
4	7.70	7.68	7.47	120.78	118.54	117.8	117.4
5	7.11	7.23	7.11	121.22	121.09	120.7	121.7
6	7.06	7.21	7.10	121.91	121.86	121.2	121.7
7	7.21	7.54	7.40	107.79	110.32	110.5	111.6
3a	–	–	–	145.08	144.60	143.5	142.9
7a	–	–	–	135.53	136.25	134.3	134.7
NH			12.14
3	1H calcd gas	1H calcd DMSO	1H exp. HMPA-d18 273 K	13C calcd gas	13C calcd DMSO	13C exp. HMPA-d18 273 K	13C exp. CPMAS
4	7.87	7.88	7.72	122.65	120.89	120.8	114.7 118.0
5	7.43	7.59	7.37	124.08	124.84	123.2	120.3 122.1
6	7.37	7.57	7.42	125.89	126.68	125.1	128.1 130.7
7	7.31	7.67	7.58	109.07	112.00	112.9	108.2 109.3
3a	–	–	–	144.54	143.87	142.9
7a	–	–	–	132.27	133.24	135.1
NH			15.05
4	1H calcd gas	1H calcd DMSO	1H exp. DMSO-d6	13C calcd gas	13C calcd DMSO	13C exp. DMSO-d6	13C exp. CPMAS
4	7.74	7.70	7.52	120.46	118.51	118.3	120.2
5	7.27	7.38	7.10	121.91	122.22	120.9	123.0
6	7.12	7.28	7.11	122.64	122.79	121.6	124.8
7	6.95	7.32	7.40	107.24	109.79	110.9	113.5
3a	–	–	–	144.14	143.43	143.4	143.0
7a	–	–	–	134.27	135.43	134.3	135.2
NH			12.28
5	1H calcd gas	1H calcd DMSO	1H exp. DMSO-d6	13C calcd gas	13C calcd DMSO	13C exp. DMSO-d6	13C exp. CPMAS
4	7.80	7.77	7.64a	121.81	119.62	119.2	119.1
5	7.23	7.36	7.19a	121.55	121.73	121.3	121.2
6	7.20	7.36	7.25a	122.32	122.53	122.1	123.2
7	7.24	7.59	7.54a	106.50	109.36	110.1	110.7
3a	–	–	–	146.49	145.60	143.3	143.4
7a	–	–	–	135.58	136.21	134.5	134.7

^{a 3}J₄₅ = 7.89, ⁴J₄₆ = 1.26, ⁵J₄₇ = 0.78, ³J₅₆ = 7.14, ⁴J₅₇ = 1.30, ³J₆₇ = 7.99 Hz.

The assignment of the signals of Table 1, Table 2 and Table 3 was straightforward following these steps: i) A NOESY experiment identifies H7 (7.54 ppm) of 5 by its proximity to the N-methyl group; ii) the analysis of the ABCD system of the protons H4, H5, H6 and H7, identifies the remaining protons; iii) a series of 2D experiments assign the CH carbons (HMQC) as well as the quaternary carbons C3a and C7a (HMBC).

Table 2.

Calculated and experimental ¹³C chemical shifts of the imidazole and substituent parts.

Compound	1H calcd gas	1H calcd DMSO	1H exp. HMPA-d18	13C calcd gas	13C calcd DMSO	13C exp. HMPA-d18	13C exp. CPMAS
1
2	7.64	7.95	8.21	136.78	140.77	141.6	143.1
1 tri A
2	8.01	8.32	8.21	139.05	141.86	141.6	143.1
1 tri B
2	7.95	8.24	8.21	138.24	141.16	141.6	143.1
Compound	1H calcd gas	1H calcd DMSO	1H exp. DMSO-d6	13C calcd gas	13C calcd DMSO	13C exp. DMSO-d6	13C exp. CPMAS
1
2			8.20			141.9
2
2	–	–	–	146.54	151.70	151.2	153.6
Me	2.41	2.50	2.47	14.37	14.42	14.6	12.6
						13C exp HMPA-d18
3a,b
2	–	–	–	138.96	139.54	140.8 2JCF = 39.1	135.2 137.8
CF3	–	–	–	123.53	123.96	120.0 1JCF = 270.1	116.0
4
2	–	–	–	151.48	155.02	153.5	157.1
CH2	4.18	4.22	35.0	38.73	38.42	35.0	36.0
Cipso	–	–	–	139.73	139.83	137.7	136.2
Cortho	7.30	7.54	7.30	129.32	129.28	128.5	~127
Cmeta	7.38	7.49	7.33	128.76	129.44	128.8	~127
Cpara	7.34	7.38	7.22	126.76	127.15	126.5	124.3
5
2	7.41	7.74	8.16c	140.83	144.14	144.5	144.6
NMe	3.62	3.80	3.82c	29.78	30.69	30.6	29.7

^aIn HMPA-d₁₈ 273 K; ^{b 19}F calc.: −63.35 (gas), −63.84 (DMSO); ¹⁹F exp.: −62.8 (HMPA-d₁₈); −61.2 (CPMAS). ^{c 4}J_HMe = 0.42 Hz.

Table 3.

Calculated and experimental ¹⁵N chemical shifts of the imidazole part.

Compound	15N calcd gas	15N calcd DMSO	15N exp. HMPA-d18	15N exp. CPMAS
1
N1	−247.63	−240.09	−228.4	−221.8
N3	−125.53	−140.75	−134.0	−143.9
1 tri A
N1	−227.89	−222.08	−228.4	−221.8
N3	−142.23	−149.24	−134.0	−143.9
1 tri B
N1	−227.80	−221.92	−228.4	−221.8
N3	−142.21	−149.18	−134.0	−143.9
Compound	15N calcd gas average	15N calcd DMSO average	15N exp. DMSO-d6 average	15N exp. CPMAS
1
N1/N3	−186.58	−190.42	a
2
N1	−246.87	−240.39	−230.3	−219.5, −224.2
N3	−127.73	−142.15	−137.9	−146.9
			15N exp HMPA-d18
3b
N1	−247.40	−241.51	−230.4	−225.9
N3	−120.36	−132.07	a	−142.8
4
N1	−245.40	−241.11	−230.8	−221.8
N3	−130.39	−141.51	−136.6	−147.2
5
N1	−241.25	−232.11	−235.6	−233.4
N3	−128.38	−143.76	−136.4	−135.4

^aNot observed; ^bIn HMPA-d₁₈ 273 K.

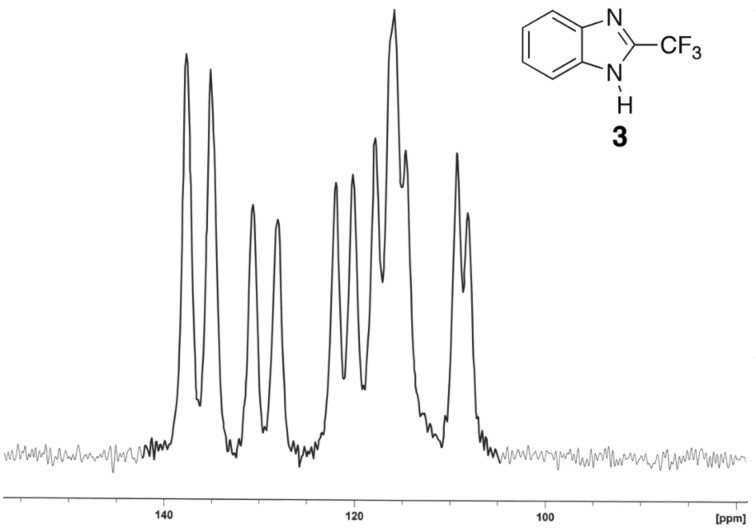
In the case of 3 all signals are considerably split in the solid state (Figure 4).

Figure 4.

The ¹³C CPMAS NMR spectrum of 3.

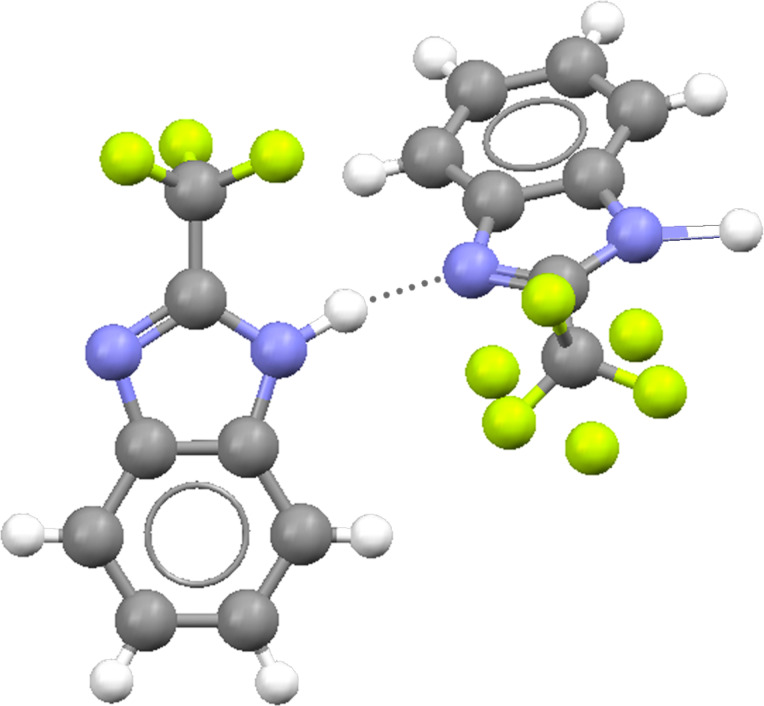
The X-ray structure of compound 3 is known and reported in the Cambridge Structural Database (refcode: ZAQRIU01) [4,26]. There are two independent molecules and in one of them, the CF₃ is disordered (Figure 5). The most probable explanation of the splittings of Figure 4 is the existence of two independent molecules, a fact that is well documented in the literature [27–30].

Figure 5.

The two independent molecules of 3 drawn with the Mercury program [26].

We have collected in Table 4 the different equations obtained from the data of Table 1, Table 2 and Table 3.

Table 4.

Linear regression equations, intercepts in ppm. If not specified, both trimers yield the same results.

Eq.	No	Intercept	Slope	R2	Atom	Exp.	Calcd
1	26	(3.2 ± 0.7)	(0.55 ± 0.10)	0.563	1H	solution	gas phase
2	26	(1.2 ± 0.6)	(0.81 ± 0.08)	0.797	1H	solution	DMSO
3	59	−(0.2 ± 1.3)	(1.00 ± 0.01)	0.993	13C	solution	gas phase
4	59	−(0.7 ± 0.7)	(1.000 ± 0.001)	0.998	13C	solution	DMSO
5	59	−(0.7 ± 2.0)	(1.01 ± 0.02)	0.987	13C	CPMAS	gas phase
6	59	−(0.8 ± 1.2)	(1.01 ± 0.01)	0.993	13C	CPMAS	DMSO
7a	58	−(0.2 ± 1.3)	(1.00 ± 0.01)	0.994	13C	solution	gas phase
8a	58	−(0.7 ± 0.7)	(1.000 ± 0.005)	0.998	13C	solution	DMSO
9a	53	−(0.6 ± 1.9)	(1.01 ± 0.02)	0.989	13C	CPMAS	gas phase
10a	53	−(1.1 ± 1.3)	(1.01 ± 0.01)	0.995	13C	CPMAS	DMSO
11	6	(6.6 ± 7.2)	(0.95 ± 0.06)	0.986	13C	CPMAS	monomerb
12	6	(5.2 ± 3.3)	(0.96 ± 0.03)	0.997	13C	CPMAS	trimer Ab
13	6	(3.7 ± 3.4)	(0.98 ± 0.03)	0.997	13C	CPMAS	trimer Bb
14	14	−(22.3 ± 7.3)	(0.86 ± 0.04)	0.978	15N	solution	gas
15	14	(10.5 ± 9.1)	(1.02 ± 0.05)	0.976	15N	solution	DMSO
16	14	−(51.0 ± 7.1)	(0.72 ± 0.04)	0.970	15N	CPMAS	gas
17	14	−(23.5 ± 7.5)	(0.86 ± 0.04)	0.976	15N	CPMAS	DMSO
18	10	−(1.4 ± 6.6)	(0.96 ± 0.03)	0.991	15N	solution	monomerb
19	10	(6.6 ± 10.4)	(1.00 ± 0.05)	0.979	15N	solution	trimerb
20	10	−(29.8 ± 5.3)	(0.82 ± 0.03)	0.991	15N	CPMAS	monomerb
21	10	−(23.8 ± 7.5)	(0.85 ± 0.04)	0.984	15N	CPMAS	trimerb

^aThe ¹³C signal of the CF₃ group has been removed. ^bDMSO calculations.

i) The ¹H chemical shifts are much more consistent with calculations for DMSO as solvent than with those of isolated molecules (gas phase). For 26 points, the R² coefficient increases from 0.56 (eq. 1) to 0.80 (eq. 2). The use of the monomer or the central part of the trimer has no influence. The worse point is H7 of 4 that appears at 7.40 ppm and fitted with eq. 2 has a value of 7.14 ppm. The origin of this discrepancy is that the theoretical conformation corresponding to the X-ray structure is not stable and reverts to the minimum one, which has the benzyl group rotated.

ii) The ¹³C chemical shifts (eqs. 3–13) are very well reproduced by the calculations: high R² values, small intercepts (in several cases, not significant) and slopes close to 1. Systematically, the worse point was the carbon atom of the CF₃ substituent (halogen substituents produce effects that are not well reproduced by our calculations that not include relativistic corrections) [15], removing it does not significantly modify the regression values (compare eqs. 3–6 with eqs. 7–10). CPMAS values agree better with calculations including DMSO solvent effect (compare eqs. 9 and 10) and also better with trimer B (in turn, slightly better than with trimer A, compare intercept and slopes of eqs. 12 and 13) than with the monomer (eq. 11).

iii) Concerning ¹⁵N NMR (eqs. 14–21), the R² values are lower than with ¹³C NMR. Both for solution and for CPMAS, the gas phase and DMSO calculations are comparable in terms of R² (eqs. 14–17), however, the values of the slopes (the closer to 1, the better) and intercepts (the closer to 0, the better), clearly favored the DMSO calculations. Surprisingly, the monomer appears preferable to the trimer (eqs. 18,19 and 20,21) which is understandable for the solution but not for the solid state. More complex approaches, such as periodic calculations [31], are necessary.

Influence of the substituent at position 2 on the tautomerization rate

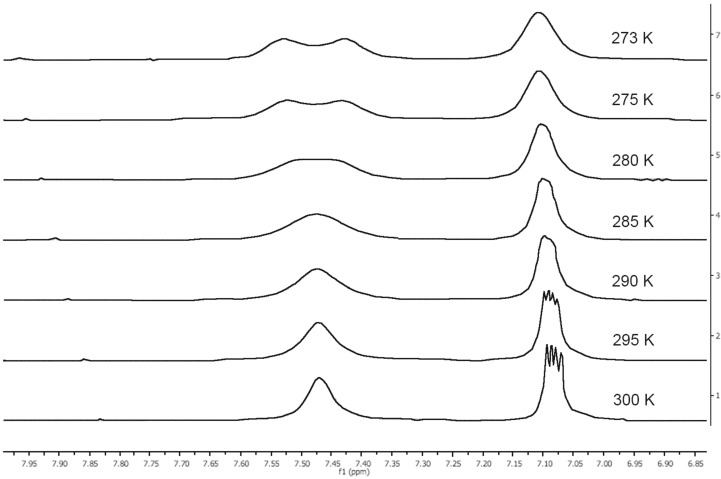
We have observed a different behavior for the four NH-benzimidazoles: 1 and 3 yielded average signals in DMSO-d₆ and only in HMPA-d₁₈ the prototropic exchange was slow, on the other hand 2 and 4 behaved as if the tautomerism was blocked in DMSO-d₆. In the case of 1 a dynamic NMR (DNMR) study in HMPA-d₁₈ was performed (Figure 6).

Figure 6.

The evolution of the spectrum of 1 with temperature in HMPA-d₁₈.

The relevant data are: T_C = 277.5 K and Δν = 0.12 ppm = 48 Hz; from them and using the Eyring equation [ΔG^‡_TC = 19.12 × T_C × (10.32 + log T_C/k_C)] [32], we obtained: k_C = 67.88 s⁻¹ and ΔG^‡_277.5 = 58.0 kJ·mol⁻¹. This barrier is similar to that of pyrazole in the same solvent (58.6 kJ·mol⁻¹ at 289 K) [33].

The effect of the substituent at position 2 on the rate (roughly, CF₃ and H, fast; CH₂C₆H₅ and CH₃, slow) is probably the consequence of steric and electronic effects; many years ago, we showed that intramolecular hydrogen bonds also affect the rate [34]. The calculated electrostatic potential minima associated to the lone pair of the N3 follow the tautomerization rate ranking of the molecules (−0.085 au, CF₃, −0.103, H, −0.104, CH₂C₆H₅ and −0.105, CH₃).

Conclusion

The data reported here for NH-benzimidazoles when the prototropy is blocked should be useful to determine the tautomeric composition when there are substituents at positions 4(7) or 5(6), for instance, in the case of omeprazole, a 5(6)-methoxy-1H-benzimidazole derivative [35–36]. Besides, solid state results as well as GIAO calculations provide new data to characterize this important family of compounds. Finally, by means of DNMR experiments it was possible to determine the barrier to proton transfer of benzimidazole itself in HMPA-d₁₈, thus providing a missing value in heterocyclic tautomerism of azoles and benzazoles [33].

Experimental

Four of the compounds reported in this paper are commercial (Sigma-Aldrich): 1, 2, 3 and 5. We reported the synthesis of the fifth one, 4, in [37].

NMR spectroscopy

Solution NMR spectra were recorded on a Bruker DRX 400 (9.4 Tesla, 400.13 MHz for ¹H, 100.62 MHz for ¹³C and 40.54 MHz for ¹⁵N) spectrometer with a 5 mm inverse-detection H-X probe equipped with a z-gradient coil, at 300 K. Chemical shifts (δ) are given from internal solvent, DMSO-d₆ 2.49 for ¹H and 39.5 for ¹³C. Typical parameters for ¹H NMR spectra were spectral width 4800 Hz and pulse width 8.3 μs at an attenuation level of 0 dB. Typical parameters for ¹³C NMR spectra were spectral width 21 kHz, pulse width 12.5 μs at an attenuation level of −6 dB and relaxation delay 2s, WALTZ-16 was used for broadband proton decoupling; the FIDS were multiplied by an exponential weighting (lb = 1Hz) before Fourier transformation.

Inverse proton detected heteronuclear shift correlation spectra, (¹H,¹³C) gs-HMQC and (¹H,¹³C) gs-HMBC, were acquired and processed using standard Bruker NMR software and in nonphase-sensitive mode. Gradient selection was achieved through a 5% sine truncated shaped pulse gradient of 1 ms.

Selected parameters for (¹H,¹³C) gs-HMQC and (¹H,¹³C) gs-HMBC spectra were spectral width 4800 Hz for ¹H and 20.5 kHz for ¹³C, 1024 × 256 data set, number of scans 2 (gs-HMQC) or 4 (gs-HMBC) and relaxation delay 1s. The FIDs were processed using zero filling in the F₁ domain and a sine-bell window function in both dimensions was applied prior to Fourier transformation. In the gs-HMQC experiments, GARP modulation of ¹³C was used for decoupling.

Selected parameters for (¹H,¹⁵N) gs-HMQC and (¹H,¹⁵N) gs-HMBC spectra were spectral width 3500 Hz for ¹H and 12.5 kHz for ¹⁵N, 1024 × 256 data set, number of scans 4, relaxation delay 1s, 37–60 ms delay for evolution of the ¹⁵N,¹H long-range coupling. The FIDs were processed using zero filling in the F₁ domain and a sine-bell window function in both dimensions was applied prior to Fourier transformation.

For ¹⁹F NMR (379.50 MHz) a 5 mm QNP direct-detection probehead equipped with a z-gradient coil, at 300 K was required.

Chemical shifts (δ) are given from internal solvent, DMSO-d₆ 2.49 and HMPA-d₁₈ 2.57 for ¹H; 39.5 and 35.8 for ¹³C, and for ¹⁵N and ¹⁹F NMR, nitromethane (0.00) and one drop of CFCl₃ in CDCl₃ (0.00) were used as external references

Typical parameters for ¹H NMR were: spectral width 4800 Hz and pulse width 10.25 μs at an attenuation level of −3.0 dB. For ¹³C NMR: spectral width 21 kHz, pulse width 8.75 μs at an attenuation level of −3 dB and relaxation delay 2 s, WALTZ-16 was used for broadband proton decoupling; the FIDS were multiplied by an exponential weighting (lb = 1Hz) before Fourier transformation. For ¹⁹F NMR: spectral width 55 kHz, pulse width 13.57 μs at an attenuation level of −6 dB and relaxation delay 1s.

Variable temperature: A Bruker BVT3000 temperature unit was used to control the temperature of the cooling gas stream and an exchanger to achive low temperatures. To avoid problems at low temperatures caused by air moisture, pure nitrogen was used as bearing, driving and cooling gas. When not stated explicitly, the temperature was 293 K.

We have always used a 1.4 M solution of the compounds either in DMSO-d₆ or in HMPA-d₁₈; this corresponds, in the case of 1, to 10 mg in 0.6 mL. To avoid water contamination, a new sealed ampoule was open for each experiment.

Solid state ¹³C (100.73 MHz) and ¹⁵N (40.60 MHz) CPMAS NMR spectra were obtained on a Bruker WB 400 spectrometer at 300 K using a 4 mm DVT probehead. Samples were carefully packed in 4 mm diameter cylindrical zirconia rotors with Kel-F end-caps. Operating conditions involved 2.9 µs 90° ¹H pulses and decoupling field strength of 86.2 kHz by TPPM sequence. ¹³C spectra were originally referenced to a glycine sample and then the chemical shifts were recalculated to the Me₄Si [for the carbonyl atom δ (glycine) = 176.1] and ¹⁵N spectra to ¹⁵NH₄Cl and then converted to nitromethane scale using the relationship: δ ¹⁵N(nitromethane) = δ^{1 5}N(ammonium chloride) − 338.1.

Typical acquisition parameters for ¹³C CPMAS were: spectral width, 40 kHz; recycle delay, 5–60 s; acquisition time, 30 ms; contact time, 2–4 ms; and spin rate, 12 kHz. In order to distinguish protonated and non-protonated carbon atoms, the NQS (Non-Quaternary Suppression) experiment by conventional cross-polarization was recorded; before the acquisition the decoupler is switched off for a very short time of 25 μs [38–40]. For ¹⁵N CPMAS were: spectral width, 40 kHz; recycle delay, 5–60 s; acquisition time, 35 ms; contact time, 7–9 ms; and spin rate, 6 kHz.

Solid state ¹⁹F (376.94 MHz) NMR spectra were obtained on a Bruker WB 400 spectrometer using a MAS DVT BL2.5 X/F/H probe. Samples were carefully packed in 2.5 mm diameter cylindrical zirconia rotors with Kel-F end-caps.

Typical acquisition parameters ¹⁹F{¹H} MAS were: spectral width, 75 kHz; recycle delay, 10 s; pulse width, 2.5 μs and proton decoupling field strength of 100 kHz by SPINAL-64 sequence; recycle delay, 10 s; acquisition time, 25 ms; 128 scans; and spin rate, 25 kHz. The ¹⁹F spectra was referenced to ammonium trifluoroacetate sample and then the chemical shifts were recalculated to the CFCl₃ [δ (CF₃CO₂NH₄⁺) = −72.0].

Computational details

Using the Gaussian 09 facilities [41], GIAO [42–43]/B3LYP [44–46]/6-311++G(d,p) [47–48] calculations were carried out; DMSO effects were calculated using the PCM continuum model [49] also with the Gaussian 09 series of programs.

Supporting Information

File 1

Optimized geometry of the systems, and chemical shifts in gas phase and PCM/DMSO environment.

Dedicated to our friend Professor Viktor Milata from the Slovak University of Technology, Bratislava, Slovak Republic.