Testing for ontological errors in probabilistic forecasting models of natural systems

Significance

Science is rooted in the concept that a model can be tested against observations and rejected when necessary. However, the problem of model testing becomes formidable when we consider the probabilistic forecasting of natural systems. We show that testability is facilitated by the definition of an experimental concept, external to the model, that identifies collections of data, observed and not yet observed, that are judged to be exchangeable and can thus be associated with well-defined frequencies. We clarify several conceptual issues regarding the testing of probabilistic forecasting models, including the ambiguity of the aleatory/epistemic dichotomy, the quantification of uncertainties as degrees of belief, the interplay between Bayesian and frequentist methods, and the scientific pathway for capturing predictability.

Abstract

Probabilistic forecasting models describe the aleatory variability of natural systems as well as our epistemic uncertainty about how the systems work. Testing a model against observations exposes ontological errors in the representation of a system and its uncertainties. We clarify several conceptual issues regarding the testing of probabilistic forecasting models for ontological errors: the ambiguity of the aleatory/epistemic dichotomy, the quantification of uncertainties as degrees of belief, the interplay between Bayesian and frequentist methods, and the scientific pathway for capturing predictability. We show that testability of the ontological null hypothesis derives from an experimental concept, external to the model, that identifies collections of data, observed and not yet observed, that are judged to be exchangeable when conditioned on a set of explanatory variables. These conditional exchangeability judgments specify observations with well-defined frequencies. Any model predicting these behaviors can thus be tested for ontological error by frequentist methods; e.g., using P values. In the forecasting problem, prior predictive model checking, rather than posterior predictive checking, is desirable because it provides more severe tests. We illustrate experimental concepts using examples from probabilistic seismic hazard analysis. Severe testing of a model under an appropriate set of experimental concepts is the key to model validation, in which we seek to know whether a model replicates the data-generating process well enough to be sufficiently reliable for some useful purpose, such as long-term seismic forecasting. Pessimistic views of system predictability fail to recognize the power of this methodology in separating predictable behaviors from those that are not.

Science is rooted in the concept that a model can be tested against observations and rejected when necessary (1). However, the problem of model testing becomes formidable when we consider natural systems. Owing to their scale, complexity, and openness to interactions within a larger environment, most natural systems cannot be replicated in the laboratory, and direct observations of their inner workings are always inadequate. These difficulties raise serious questions about the meaning and feasibility of “model verification” and “model validation” (2), and have led to the pessimistic view that “the outcome of natural processes in general cannot be accurately predicted by mathematical models” (3).

Uncertainties in the formal representation of natural systems imply that the forecasting of emergent phenomena such as natural hazards must be based on probabilistic rather than deterministic modeling. The ontological framework for most probabilistic forecasting models comprises two types of uncertainty: an aleatory variability that describes the randomness of the system, and an epistemic uncertainty that characterizes our lack of knowledge about the system. According to this distinction, which stems from the classical dichotomy of objective/subjective probability (4), epistemic uncertainty can be reduced by increasing relevant knowledge, whereas the aleatory variability is intrinsic to the system representation and is therefore irreducible within that representation (5, 6).

The testing of a forecasting model is itself a statistical enterprise that evaluates how well a model agrees with some collection of observations (e.g., 7, 8). One can compare competing forecasts within a Bayesian framework and use new data to reduce the epistemic uncertainty. However, the scientific method requires the possibility of rejecting a model without recourse to specific alternatives (9, 10). The statistical gauntlet of model evaluation should therefore include pure significance testing (11). Model rejection exposes “unknown unknowns”; i.e., ontological errors in the representation of the system and its uncertainties. Here we use “ontological” to label errors in a model’s quantification of aleatory variability and epistemic uncertainty (see SI Text, Glossary). [Other authors have phrased the problem in different terms; e.g., Musson’s (12) “unmanaged uncertainties.” In the social sciences, “ontological” is sometimes used interchangeably with “aleatory” (13).]

The purpose of this paper is to clarify the conceptual issues associated with the testing of probabilistic forecasting models for ontological errors in the presence of aleatory variability and epistemic uncertainty. Some relate to long-standing debates in statistical philosophy, in which Bayesians (14) spar with frequentists (15), and others propose methodological accommodations that draw from the strengths of both schools (10, 16). Statistical “unificationists” of the latter stripe advocate the importance of model checking using Bayesian (calibrated) P values (16, 17, 18, 19) as well as graphical summaries and other tools of exploratory data analysis (20). Bayesian modeling checking has been criticized by purists on both sides (21, 22), but one version, prior predictive checking, provides us with an appropriate framework for the testing of forecasting models for ontological errors.

Among the concerns to be addressed is the use of expert opinion to characterize epistemic uncertainty, a common practice when dealing with extreme events, such as large earthquakes, volcanic eruptions, and climate change. Frequentists discount the quantification of uncertainties in terms of degrees of belief as “fatally subjective—unscientific” (23), and they oppose “letting scientists’ subjective beliefs overshadow the information provided by data” (21). Bayesians, on the other hand, argue that probability is intrinsically subjective: all probabilities are degrees of belief that cannot be measured. Jaynes’s (24) view is representative: “any probability assignment is necessarily ‘subjective’ in the sense it describes only a state of knowledge, and not anything that could be measured in a physical experiment.” Immeasurability suggests untestability: How can models of probabilities that are not measureable be rejected?

Our plan is to expose the conceptual issues associated with the uncertainty hierarchy in the mathematical framework of a particular forecasting problem—probabilistic seismic hazard analysis (PSHA)—and resolve them in a way that generalizes the testing for ontological errors to other types of probabilistic forecasting models. A glossary of uncommon terms used in this paper is given in SI Text, Glossary.

Probabilistic Seismic Hazard Analysis

Earthquakes proceed as cascades in which the primary effects of faulting and ground shaking may induce secondary effects, such as landslides, liquefactions, and tsunamis. Seismic hazard is a probabilistic forecast of how intense these natural effects will be at a specified site on earth’s surface during a future interval of time. Because earthquake damage is primarily caused by shaking, quantifying the hazard due to ground motions is the main goal of PSHA. Various intensity measures can be used to describe the shaking experienced during an earthquake; common choices are peak ground acceleration and peak ground velocity. PSHA estimates the exceedance probability of an intensity measure X; i.e., the probability that the shaking will be larger than some intensity value x at a particular geographic site over the time interval of interest, usually beginning now and stretching over several decades or more (5, 25, 26). It is often assumed that earthquake occurrence is a Poisson process with rates constant in time, in which case the hazard model is said to be time independent.

A plot of the exceedance probability F(x) = P(X > x) for a particular site is called the hazard curve. Using hazard curves, engineers can estimate the likelihood that buildings and other structures will be damaged by earthquakes during their expected lifetimes, and they can apply performance-based design and seismic retrofitting to reduce structural fragility to levels appropriate for life safety and operational requirements. A seismic hazard map is a plot of the exceedance probability F at a fixed intensity x as a function of site position (27, 28) or, somewhat more commonly, x at fixed F (29–31). Official seismic hazard maps are now produced by many countries, and are used to specify seismic performance criteria in the design and retrofitting of buildings, lifelines, and other infrastructure, as well as to guide disaster preparedness measures and set earthquake insurance rates. These applications often fold PSHA into probabilistic risk analysis based on further specifications of loss models and utility measures (32, 33). Here we focus on assessing the reliability of PSHA as a forecasting tool rather than its role in risk analysis and decision theory.

The reliability of PSHA has been repeatedly questioned. In the last few years, disastrous earthquakes in Sumatra, Italy, Haiti, Japan, and New Zealand have reinvigorated this debate (34–39). Many practical deficiencies have been noted, not the least of which is the paucity of data for retrospective calibration and prospective testing of PSHA models, owing to the short span of observations relative to the forecasting time scale (40, 41). However, some authors have raised the more fundamental question of whether PSHA is misguided because it cannot capture the aleatory variability of large-magnitude earthquakes produced by complex fault systems (35, 38, 42). Moreover, the pervasive role of subjective probabilities in specifying the epistemic uncertainty in PSHA has made this methodology a target for criticism by scientists who adhere to the frequentist view of probabilities. A particular objection is that degrees of belief cannot be empirically tested and, therefore, that PSHA models are not scientific (43–45).

We explore these issues in the PSHA framework developed by earthquake engineers in the 1970s and 1980s and refined in the 1990s by the Senior Seismic Hazard Analysis Committee (SSHAC) of the US Nuclear Regulatory Commission (5). For a particular PSHA model H_m, the intrinsic or aleatory variability of the ground motion X is described by the hazard curve F_m(x) = P(X > x | H_m). The epistemic uncertainty is characterized by an ensemble {H_m: m ∈ M} of alternative hazard models consistent with our present knowledge. A probability π_m is assigned to F_m(x) that measures its plausibility, based on present knowledge, relative to other hazard curves drawn from the ensemble.

Ideally, the model ensemble {H_m} could be constructed and the model probabilities assigned according to how well the candidates explain prior data. Various objective methods have been developed for this purpose: resampling, adaptive boosting, Bayesian information criteria, etc. (46, 47). However, the high-intensity, low-probability region of the hazard space F ⊗ x most relevant to many risk decisions is dominated by large, infrequent earthquakes. The data for these extreme events are usually too limited to discriminate among alternative assumptions and fix key parameters. Therefore, in common practice, the model ensemble {H_m} is organized as branches of a logic tree, and the branch weights {π_m}, which may depend on the hazard level x, are assigned according to expert opinion (5, 48, 49).

If the logic tree spans a hypothetically mutually exclusive and completely exhaustive (MECE) set of possibilities (50), π_m can be interpreted as the probability that F_m(x) is the “true” hazard value $\widehat{F}\left(x\right)$, and operations involving the plausibility measure {π_m} must obey Kolmogorov’s axioms of probability; e.g.,

$${\displaystyle \sum _{m\mathrm{\in }M}{\pi }_m=1}.$$ [1]

In PSHA practice, logic trees are usually constructed to sample the possibilities, rather than exhaust them, in which case the MECE assumption is inappropriate. One can then reinterpret π_m as the probability that F_m(x) is the “best” among a set of available models (12, 47, 51) or “the one that should be used” (52). This utilitarian approach increases the subjective content of {F_m(x), π_m}, as well as the possibilities for ontological error. We will call {F_m(x), π_m} the experts’ distribution to recognize this subjectivity, regardless of whether {H_m} comes from a logic tree or is constructed in a different way.

For conceptual simplicity, we will assume the discrete experts’ distribution {F_m(x), π_m} samples a continuous probability distribution with density function p(ϕ), where ϕ = F(x₀) at a fixed hazard value x₀. We denote this relationship by {ϕ_m} ∼ p(ϕ) and call p the extended experts’ distribution. Various data-analysis methods have been established to move from a discrete sample to a continuous distribution, although the process also compounds the potential for ontological error. Given the extended experts’ distribution, the expected hazard at fixed x₀ is

$$\overline{\varphi }=\underset{0}{\overset{1}{{\displaystyle \int }}}\varphi \hspace{0.17em}p\left(\varphi \right)d\varphi .$$ [2]

This central value measures the aleatory variability of the hazard, conditional on the model, and the dispersion of p about $\overline{\varphi }$ describes the epistemic uncertainty in its estimation.

Epistemic uncertainty is thus described by imposing a subjective probability on the target behavior of H_m, which is an objective exceedance probability, ϕ_m. This procedure is well established in PSHA practice (5, 53), but it encounters frequentist discomfort with degrees of belief and Bayesian resistance to attaching measures of precision to probabilities. [In Bayesian semantics, the frequency parameters of aleatory variability are usually labeled as “chances” rather than as probabilities. According to Lindley (14), “the distinction becomes useful when you wish to consider your probability of a chance, whereas probability on a probability is, in the philosophy, unsound.” Jaynes (24) also rejects the identification of frequencies with probabilities.] Although these concerns do not matter much in the routine application of risk analysis, where only the mean hazard is considered (32, 54, 55), they must be addressed within the conceptual framework of model testing.

In our framework, testability derives from a null hypothesis, here called the “ontological hypothesis,” which states that data-generating hazard curve $\widehat{\varphi }$ (the “true” hazard) is a sample from the extended experts’ distribution, $\widehat{\varphi }\sim p\left(\varphi \right)$. If an observational test rejects this null hypothesis, then we can claim to have found an ontological error.

Testing PSHA Models

One straightforward test of a PSHA model is to collect data on the exceedance frequency of a specified shaking intensity, x₀, during N equivalent trials, each lasting 1 y. If ϕ_m = F_m(x₀) is the 1-y exceedance probability for a particular hazard model H_m, and the data are judged to be unbiased and exchangeable under the experimental conditions—i.e., to have a joint probability distribution invariant with respect to permutations in the data ordering (56–58)—then the likelihood of observing k or more exceedances for each member of the experts’ ensemble is given by the tail of a binomial distribution:

$$P\left(k|{\varphi }_m\right)={\displaystyle \sum _{n=k}^N\left(\begin{array}{c}N\\ n\end{array}\right){\varphi }_m^n{\left(1-{\varphi }_m\right)}^{N\mathrm{-}n}}.$$ [3]

Under the extended experts’ distribution, the unconditional probability is the expectation,

$$P\left(k\right)={\displaystyle \underset{0}{\overset{1}{\int }}P\left(k|\varphi \right)p\left(\varphi \right)d\varphi }.$$ [4]

For notational simplicity, we suppress the dependence of P on N.

There have been only a few published attempts to test PSHA models against ground motion observations (59–62). To our knowledge, all have assumed a test distribution $P\left(k|\overline{\varphi }\right)$ that has been computed from [3] using the mean exceedance probability rather than from the unconditional distribution [4]. This reflects the view shared by many hazard practitioners that the mean hazard is the only hazard needed for decision making (54, 55, 63, 64).

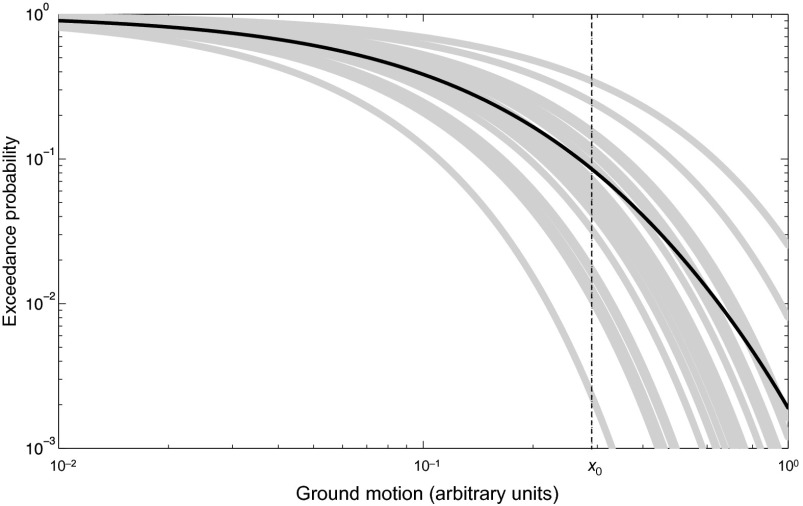
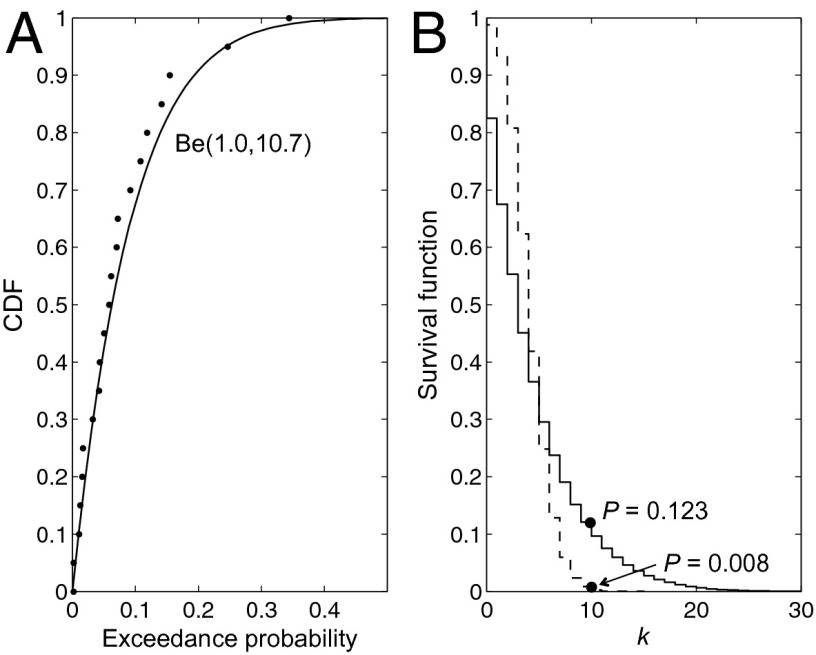
However, a test based on $P\left(k|\overline{\varphi }\right)$ is often overly stringent, as can be seen from a simple example. We consider a PSHA model that comprises an experts’ ensemble of 20 equally weighted hazard curves, each an exponential function, $F_m\left(x\right)=\exp \left(\mathrm{-}{\lambda }_{m}x\right)$ (Fig. 1). The values sampled at x₀ (arbitrarily chosen to be 0.29) give a mean exceedance probability of $\overline{\varphi }=0.085$ and can be represented by a beta distribution Be(α, β) with parameters α = 1.0 and β = 10.7 (Fig. 2A). Suppose this ground motion threshold is exceeded k = 10 times in n = 50 y; then the P value conditioned on the mean hazard is $P\left(k|\overline{\varphi }\right)=0.008$, whereas the unconditional value is P(k) = 0.123 (Fig. 2B). Thus, although this observational test rejects $\widehat{\varphi }=\overline{\varphi }$ at a fairly high (99%) confidence level, it cannot reject the ontological hypothesis $\widehat{\varphi }\mathrm{\sim }p\left(\varphi \right)$, even at a low (90%) level.

Fig. 1.

A simple PSHA model used in our testing examples. Gray lines show the experts’ ensemble of 20 exponential hazard curves {F_m(x): m = 1, …, 20}. Black line is the corresponding mean hazard curve $\overline{F}\left(x\right)$. The distribution of values sampled at x₀ (dashed line) is given in Fig. 2.

Fig. 2.

Results from test 1. (A) Discrete points are the cumulative distribution function (CDF) of the experts’ ensemble {F_m(x₀): x₀ = 0.29, m = 1, …, 20} from Fig. 1. When assigned equal weights (π_m = 1/20), this ensemble can be represented by an extended experts’ distribution Be(1.0, 10.7), shown by the solid line. (B) Dashed line is the survival function (1 – CDF) of k or more exceedances in n = 50 trials conditioned on the mean hazard; solid line is the survival function of the unconditional exceedances, computed from Eq. 4. For the observation k = 10, the P value of the former is 0.008 and that of the latter is 0.123.

Finding an ontological error may not directly indicate what is wrong with the model. The ontological error might indicate that the parameters of the model were badly estimated, or that the basic structure of the model is far from reality. In our example test, a small P value could imply that either the beta distribution of ϕ, which characterizes the epistemic uncertainty, or the exponential distribution of F_m(x), which characterizes the aleatory variability, is wrong (or that both are). A small P value might also indicate that the data-generating process is evolving with time, so the data used for testing do not have the same distribution as the data used to calibrate the model.

Bayesian updating under the ontological hypothesis can improve the parameter estimates and thereby sharpen the extended experts’ distribution, but it cannot discover ontological errors, such as the inadequacy of the exponential distribution or a time dependence of the parameter λ not included in the time-independent model. To do that we must subject our “model of the world,” given here by p(ϕ), to a testing regime guided by an experimental concept that appropriately conditions nature’s aleatory variability.

Primacy of the Experimental Concept in Ontological Testing

The experimental concept in our PSHA example is very simple. We collect a set of yearly data {x_n: n = 1, 2, …, N} and construct a binary sequence {e_n: n = 1, 2, …, N} by assigning e_n = 1 if x_n exceeds a threshold value x₀ and e_n = 0 if it does not. We observe that the sequence sums to k. We judge that the joint probability distribution of {e_n} is unchanged by any permutation of the indices; the yearly data are thus exchangeable and the sequence is Bernoulli. In the earthquake forecasting problem, we further assert, through a leap of faith, that future years are exchangeable with past years; i.e., the data sequence is exchangeable in Draper et al.’s (57) second sense. The predictive power of the time-independent PSHA model hangs on this assertion.

In general terms, the experimental concept specifies collections of data, observed and not yet observed, that are judged to be exchangeable when conditioned on a set of explanatory variables. Exchangeable events can be modeled as identical and independently distributed random variables with a well-defined frequency of occurrence (65, 66). This event frequency or chance—the limiting value of k/N in our example—represents the aleatory variability of the data-generating process (5, 6). Theoretical considerations and a finite amount of data can only constrain this probability within some epistemic uncertainty, quantified by the extended expert’s distribution.

Exchangeability thus distinguishes the aleatory variability, given by P(k | ϕ), from the epistemic uncertainty, given by p(ϕ). In our PSHA example, the exchangeability judgment links Eqs. 3 and 4 to de Finetti’s (65) representation of a Bernoulli process conditioned on p(ϕ) and thus connects the testing experiment to the frequentist concept of repeatability.

The primacy of the experimental concept can be illustrated by extending our PSHA example. The test in Fig. 2 (test 1) derives from an experimental concept based on a single exchangeability judgment. Now consider a second experimental concept (test 2) that distinguishes exceedance events in years when some observable index A is zero from those in years when A is unity. The data-generating process provides two sequences, {e_n⁽⁰⁾: n = 1, 2, …, N₀} when A = 0 and {e_n ⁽¹⁾: n = 1, 2, …, N₁} when A = 1. Both are judged to be Bernoulli, and they are observed to sum to k₀ and k₁ respectively. If A correlates with the frequency and/or magnitude variations in the earthquake rupture process, e.g., if the occurrence of large earthquakes and consequent ground shaking stronger than x₀ are more likely when A = 1, then the expected frequency of k₁/N₁ might be greater than that of k₀/N₀.

As this example makes clear, it is not the aleatory variability intrinsic to the model that matters in testing, but rather the aleatory variability defined by the exchangeability judgments of the experimental concept. In other words, aleatory variability is an observable behavior of the data-generating process—nature itself—conditioned by the experimental concept to have well-defined frequencies. A model predicting this behavior can thus be tested for ontological error by frequentist (error statistical) methods.

Suppose that, in a 50-y PSHA experiment, there are N₀ = 35 y when A = 0 and N₁ = 15 y with A = 1. Further suppose that no exceedances of the ground motion threshold are observed in the former set (k₀ = 0), and 10 are recorded in the latter (k₁ = 10). Test 1 applied to these datasets returns an identical result (k = 10), so the model passes with a prior predictive P value of 0.123, as shown in Fig. 2. However, in test 2, the A = 1 observation is much less likely under the ontological hypothesis (P₁ = 0.0006) than the A = 0 observation (P₀ = 0.231), and the P value for the combined result is quite small, 0.0012 (Fig. 3). Therefore, the model can be rejected by test 2 with high confidence.

Fig. 3.

Results from test 2. In a 50-y PSHA experiment, no ground motion exceedances are observed in the 35 y when A = 0 (Left), which gives P₀ = 0.231, and 10 exceedances are observed in the 15 y with A = 1 (Right), which gives P₁ = 0.0006. The P value for the combined result is 0.0012.

From this experiment, we infer that the data-generating process $\widehat{F}$ is probably A dependent and therefore time dependent (all years are not exchangeable). Hence, we might seek an alternative model that captures this type of time dependence in its aleatory variability, and we might reelicit expert opinion to characterize the epistemic uncertainty in its (two or more) aleatory frequencies.

In ontological testing, Box’s famous generalization that “all models are wrong, but some are useful” (67) can be restated as “all models are wrong, but some are acceptable under particular experimental concepts.” Qualifying a model under an appropriate set of experimental concepts is the key to model validation, in which we decide if a model replicates the data-generating process well enough to be sufficiently reliable for some useful purpose, such as long-term seismic forecasting. In our example, a model that passes test 1 may be adequate for time-independent forecasting, but, by failing test 2, it should be rejected as a viable time-dependent forecast.

Discussion

For frequentists, a probability is the limiting frequency of a random event or the long-term propensity to produce such a limiting frequency (9, 68); for Bayesians, it is a subjective degree of belief that a random event will occur (14). Advocates on both sides have argued that degrees of belief cannot be measured and, by implication, cannot be rejected (9, 24, 69). In the words of one author (70), “the degree of belief probability is not a property of the event (experiment) but rather of the observer. There exists no uniquely true probability, only one’s true belief.” Within the subjectivist Bayesian framework, one’s true belief can be informed, but not rejected, by experiment.

For us, the use of subjective probability such as expert opinion poses no problems for ontological testability as long as the experimental concept defines sets of exchangeable data with long-run frequencies determined by the data-generating process. These frequencies, which characterize the aleatory variability, have epistemic uncertainty described by the experts’ distribution. Expert opinion is thus regarded as a measurement system that produces a model that can be tested.

To illustrate this point with an example far from PSHA, we recall an experiment reported by Sir Francis Galton in 1907. During a tour of the English countryside, he recorded 787 guesses of the weight of an ox made by a farming crowd and found that the average was correct to a single pound (71). The experts’ distribution he tabulated passes the appropriate Student’s t test (retrospectively, of course, because this test was not invented until 1908).

We note one difference between farmers and PSHA experts. The experts’ distribution measures the epistemic uncertainty at a particular epoch, which may be larger or smaller depending on how the experts are able to sample the appropriate information space. In Galton’s experiment, a farmer looks individually at the ox, reaching his estimate more or less independently of his colleagues. As more farmers participate, they add new data, and the epistemic uncertainty is reduced by averaging their guesses. At a particular epoch, adding more PSHA experts will better determine, but usually not reduce, the epistemic uncertainty, because they rarely make independent observations but work instead from a common body of knowledge, which may be very limited. This and other issues related to the elicitation of expert opinion, such as how individuals should be calibrated and how a consensus should be drawn from groups, have been extensively studied (5, 72, 73).

The ontological tests considered here are conditional on the experimental concept, which may be weak or even wrong. An experimental concept will be incorrect when one or more of its exchangeability judgments violate reality. The constituent assumptions can often be tested independently of the model; e.g., through correlation analysis and other types of data checks (57, 74, 75). In our example, if the frequency estimator k/N increases in the long run (e.g., if the proportion N₁/N₀ increases), then the event set is not likely to be exchangeable, and the experimental concept of test 1 needs to be rethought to allow for this secular time dependence.

Through exchangeability judgments, the experimental concept ensures that aleatory variables have well-defined frequencies, which is just what we need to set up a regime for testing the ontological hypothesis. Bayesian model checking provides us with several options for pure significance testing. The ontological hypothesis can be evaluated using

• i)the prior predictive P value, computed directly from Eq. 4 (17);
• ii)the posterior predictive P value, computed after the experts’ distribution has been updated according to Bayes; e.g., ${\pi \prime }_m\mathrm{\propto }{\varphi }_m^k{\left(1\mathrm{-}{\varphi }_m\right)}^{N\mathrm{-}k}{\pi }_m$ (18, 76); or
• iii)a partial posterior predictive P value, computed for a data subset after the experts’ distribution has been updated using a complementary (calibration) data subset (77).

An ontological error is discovered when the new data are shown to be inconsistent with p(ϕ) or its updated version p′(ϕ); e.g., when a small P value is obtained from the experiment.

Among these options, the posterior predictive checks (ii) and (iii) are most often used by Bayesian objectivists because their priors are often improper and uninformative (20, 77). Moreover, in many types of statistical modeling, the goal is to assess the model’s ability to fit the data a posteriori, not its ability to predict the data a priori. According to Gelman (78), for example, “All models are wrong, and the purpose of model checking (as we see it) is not to reject a model but rather to understand the ways in which it does not fit the data. From a Bayesian point of view, the posterior distribution is what is being used to summarize inferences, so this is what we want to check.” In particular, the power of the test, or more generally its severity (9), is not very important. “If a certain posterior predictive check has zero or low power, this is not a problem for us: it simply represents a dimension of the data that is automatically or virtually automatically fit by the model” (75).

In forecasting, however, we are most interested in a model’s predictive capability; therefore, severe tests based on the prior predictive check (i) are always desirable. This testing regime is entirely prospective; the models are independent of the data used in the test (the testing is blind), and there are no nuisance parameters. The extended experts’ distribution p(ϕ) is subjective, informative, and always proper. “Using the data twice” is not an issue, as it is with the posterior predictive check (ii) (16). If based on the same data, prior predictive tests are always more severe than posterior predictive tests. Continual prospective testing now guides the validation of forecasting models in civil protection and other operational applications (79–82).

When the experimental concept is weak, lots of models, even poor predictors, can pass the test. An experimental concept provides a severe test, in Mayo’s (9) sense, if it has a high probability of detecting an ontological error of the type that matters to the model’s forecasting application. Severe tests require informative ensembles of exchangeable observations (although we must admit that these are often lacking in long-term PSHA). In practice, batteries of experimental concepts must be used to specify the aleatory variability of the data-generating process and organize severe testing gauntlets relevant to the problem at hand.

When the problem is forecasting, the most crucial features of an experimental concept are the assertions that past and future events are exchangeable. Scientists make these leaps of faith not blindly, but through careful consideration of the physical principles that govern the system behaviors they seek to predict. Therefore, the experimental concepts used to test models, as much as the models themselves, are the mechanism for encoding our physical understanding into the iterative process of system modeling. Validating our predictions through ontological testing is the primary means by which we establish our understanding of how the world works, and thus an essential aspect of the scientific method (1). It seems to us that the more pessimistic views of system predictability (2, 3) fail to recognize the power of this methodology in separating behaviors that are predictable from those that are not.

This power can be appreciated by considering cases where the exchangeability of past and future events is dubious. A notorious example is the prediction of financial markets. Exchangeability judgments are problematic in these experiments, because the markets learn so rapidly from past experience (83, 84). Without exchangeability, no experimental concept is available to discipline the system variability. Processes governed by physical laws are less contingent and more predictable than these agent-based systems; for example, exchangeability judgments can be guided by the characteristic scales of physical processes, leading to well-configured experimental concepts.

The points made in this paper are basic and without mathematical novelty. In terms of the interplay between Bayesian and frequentist methods, our view aligns well with the statistical unificationists (10, 85). However, it differs in the importance we place on the experimental concept in structuring the uncertainty hierarchy—aleatory, epistemic, ontological—and our emphasis on testing for ontological errors as a key step in the iterative process of forecast validation.

As with many conceptual discussions of statistical methodology, the proof is in the pudding. Does the particular methodology advocated here help to clarify any persistent misunderstandings that have hampered practitioners? We think so, particularly in regard to the widespread confusion about how to separate aleatory variability from epistemic uncertainty. Consider two examples:

• •In a review of the SSHAC methodology requested by the US Nuclear Regulatory Commission, a panel of the National Research Council asserted that “the value of an epistemic/aleatory separation to the ultimate user of a PSHA is doubtful… The panel concludes that, unless one accepts that all uncertainty is fundamentally epistemic, the classification of PSHA uncertainty as aleatory or epistemic is ambiguous.” (54). Here the confusion stems from SSHAC’s (5) epistemic/aleatory classification scheme, which is entirely model-based and thus ambiguous.
• •In his discussion of “how to cheat at coin and die tossing,” Jaynes (24) describes the ambiguity of randomness in terms of how the tossing is done; e.g., how high a coin is tossed. “The writer has never thought of a biased coin ‘as if it had a physical probability’ because, being a professional physicist, I know that it does not have a physical probability.” His confusion arises because he associates the aleatory frequency with the physical process, which is ambiguous unless we fix the experimental concept.

Both the model-based and physics-based ambiguity in setting up the aleatory/epistemic dichotomy can be removed by specifying an experimental concept. By testing the ontological hypothesis under appropriate experimental concepts, we can answer the important question of whether a model’s predictions conform to our conditional view of nature’s true variability.