A whole-genome simulator capable of modeling high-order epistasis for complex disease

Abstract

Genome-wide association studies (GWAS) have been successful in finding numerous new risk variants for complex diseases, but the results almost exclusively rely on single-marker scans. Methods that can analyze joint effects of many variants in GWAS data are still being developed and trialed. To evaluate the performance of such methods it is essential to have a GWAS data simulator that can rapidly simulate a large number of samples, and capture key features of real GWAS data such as linkage disequilibrium (LD) among single-nucleotide polymorphisms (SNPs) and joint effects of multiple loci (multilocus epistasis). In the current study, we combine techniques for specifying high-order epistasis among risk SNPs with an existing program GWAsimulator[Li and Li 2008] to achieve rapid whole-genome simulation with accurate modeling of complex interactions. We considered various approaches to specifying interaction models including: departure from product of marginal effects for pair-wise interactions, product terms in logistic regression models for low-order interactions, and penetrance tables conforming to marginal effect constraints for high-order interactions or prescribing known biological interactions. Methods for conversion among different model specifications are developed using penetrance table as the fundamental characterization of disease models. The new program, called simGWA, is capable to efficiently generate large samples of GWAS data with high precision. We show that data simulated by simGWA are faithful to template LD structures, and conform to pre-specified diseases models with (or without) interactions.

Introduction

In the past few years, waves of genome-wide association studies (GWAS) have identified numerous genetic risk factors of complex diseases[Hindorff, et al.; Manolio 2013; O'Seaghdha and Fox 2011; Willer and Mohlke 2012]. Although published GWAS analyses rely almost exclusively on single-marker scans, the importance of joint effects of multiple risk variants is increasingly recognized by both methodologists and practitioners of the field[Aschard, et al. 2012; Cordell 2009; Kirino, et al. 2013; Lucas, et al. 2012; Ma, et al. 2012; MacLellan, et al. 2012; Pandey, et al. 2012]. Many statistical methods have been attempted for analyzing such joint effects, from multiple regression models, to haplotype-based tests, and to tests for interactions of multiple loci (within a genomic region or across the whole genome)[Gao, et al. 2013; Gyenesei, et al. 2012; Hahn, et al. 2003; Jin, et al. 2010; Oh, et al. 2012; Wan, et al. 2010; Wu, et al. 2010; Yang, et al. 2012; Yang, et al. 2011; Yang and Gu 2013]. To facilitate development of new statistical methods and better understand high-order gene-gene interactions (epistasis), it is essential to have a GWAS data simulator that not only can simulate huge amounts of genotype data with realistic genome-wide LD structure in reasonable computational time, but also can correctly model complex interactions among many risk loci.

A rapid whole-genome simulator called GWAsimulator[Li and Li 2008] does a great job in simulating marginal effects using “retrospective sampling” [Durrant, et al. 2004] (first sampling genotypes at risk loci conditional on disease status, then generating haplotypes by a moving-window algorithm). The algorithm simply copies and binds small pieces of haplotypes templates from real-world populations, making it possible to generate very large data sets in reasonable time, and at the same time, making it capable of simulating realistic LD structure by using real-population haplotype templates such as those from the HapMap project[Gibbs, et al. 2003]. However, the algorithm lacks a way to correctly handle multilocus interactions, which restricts its utility in studying complex diseases models with complex interactions.

A general way to specify higher order effects of multiple SNPs is to use a penetrance table. The penetrance at the risk locus is the conditional probability that an individual with a given genotype is affected by the disease of interest. A penetrance table consists of penetrance values for all possible combinations of multilocus risk genotypes, which, in conjunction with the genotype frequencies, fully characterizes the joint distribution of disease status and genotypes at the risk loci. We had previously developed a novel method[Yang and Gu 2008] for generating complex penetrance tables involving high order interactions for any given set of marginal effects of risk loci and risk alleles frequencies.

In the present study, we combine improved interaction model specification with GWAsimulator’s retrospective sampling to achieve rapid whole-genome simulation of GWAS data with accurate modeling of complex interactions. The resulting new algorithm is implemented in an R package called simGWA, which allows convenient and accurate specification of high-order effects using various approaches, including (A) departure from product of marginal effects for pair-wise interactions, (B) logistic regression models for low-order interactions, (C) penetrance tables conforming to given marginal constraints for high-order interactions, and (D) special penetrance tables prescribing known biological interactions. Penetrance table is used as the canonical characterization of complex disease models and to simulate genotypes at the disease loci. We will first introduce how penetrance tables are used in the simulation. Then, we describe GWAsimulator’s disease modeling and its limitation in specifying interactions, followed by description of our approaches to generate correct penetrance tables for complex disease models. Finally we give an overview of the implementation of simGWA and the evaluation of its performance.

Methods

Flexible choice of disease models can be achieved by using penetrance tables to specify how combinations of risk SNPs affect the disease status.

Assume that the disease prevalence is K, and it involves m disease loci. At locus i (i = 1,2,…,m), g_i (=0, 1 or 2) is the risk allele count and p_i is the risk allele frequency. For a multilocus genotype combination G = (g₁,g₂,…,g_m), denote the penetrance by f (G) = Pr(affected | G), which is the probability of being affected conditional on genotype G. Then, for a case subject, the probability that it has genotype G₀ is

$$\text{Pr}(G_0|\text{affected})=\frac{\text{Pr}(\text{affected}|G_0)\times \text{Pr}(G_0)}{\sum _{G=\{g_1,\dots ,g_m\}}\text{Pr}(\text{affected}|G)\times \text{Pr}(G)}=\frac{f(G_0)\text{Pr}(G_0)}{\sum _{G=\{g_1,\dots ,g_m\}}f(G)\times \text{Pr}(G)}$$ (1)

For a control subject,

$$\text{Pr}(G_0|\text{unaffected})=\frac{\text{Pr}(\text{unaffected}|G_0)\times \text{Pr}(G_0)}{\sum _{G=\{g_1,\dots ,g_m\}}\text{Pr}(\text{unaffected}|G)\times \text{Pr}(G)}=\frac{(1-f(G_0))\text{Pr}(G_0)}{\sum _{G=\{g_1,\dots ,g_m\}}(1-f(G))\text{Pr}(G)}$$ (2)

The denominators in the above formulae are summed over all possible genotypes comprising the m disease loci. Under assumptions of Hardy-Weinberg equilibrium and that all disease loci are unlinked, the probability of a genotype G is calculated as

$$\text{Pr}(G)=\prod _{i=1}^m\text{Pr}(g_i)=\prod _{i=1}^m[1+I(g_i=1)]p_i^{g_i}{(1-p_i)}^{2-g_i}$$ (3)

Thus, given the full penetrance table f (·) and allele frequencies p_i of all risk loci, it is straightforward to determine the distribution of genotypes in cases and controls using equations (1) and (2).

These equations form the basis for “retrospective sampling” (sampling genotypes or haplotypes of subjects conditional on the disease status) used by GWAsimulator[Li and Li 2008]. It is more efficient than a “prospective” approach, where multisite joint disease genotypes are randomly generated, but only accepted at a probability equal to the penetrance of that genotype combination[Peng and Amos 2010; Pinelli, et al. 2012].

After determining genotypes at the disease loci from retrospective sampling, genotypes at neighboring positions on the same chromosome are simulated one-by-one using a moving-window algorithm[Durrant, et al. 2004]. Simply speaking, for each partially simulated haplotype, the algorithm first finds haplotypes that match the already simulated haplotype in a small window among the haplotype templates. In these matched template haplotypes, the alleles at the next un-simulated position are counted and used to get the probability to simulate the allele at this position. This process is then repeated again to get the next allele on the template, until the whole chromosome is simulated.

Using templates ensures that the simulated chromosomes bear LD structures similar to the population of interest. Such templates may be generated from existing GWAS data, or easily retrieved from the HapMap[Gibbs, et al. 2003] website, where phased data are provided for Caucasians (CEU data set), Africans (YRI data set) and East Asians (CHB+JPT). Naturally, the accuracy and resolution of the simulated LD structures depend on the sample sizes and data quality of the original template-generating samples.

Model specification used by GWAsimulator

GWAsimulator assumes that the penetrances link to the genotypes through a logistic function. Specifically, assuming there are m risk SNPs, when there are no interactions, the logit function of penetrances is

$$\text{logit}(f(G))=\text{logit}(\text{Pr}(\text{affected}|g_1,\dots g_m))=\alpha +{\beta }_{11}{I}_{\{g_1=1\}}+{\beta }_{12}{I}_{\{g_1=2\}}+\cdots +{\beta }_{m1}{I}_{\{g_m=1\}}+{\beta }_{m2}{I}_{\{g_m=2\}}$$ (4)

and when pair-wise interactions exist between some SNP pairs, it is

$$\text{logit}(f(G))=\text{logit}(\text{Pr}(\text{affected}|g_1,\dots g_m))=\alpha +\sum _{i=1}^m[{\beta }_{i1}{I}_{\{g_i=1\}}+{\beta }_{i2}{I}_{\{g_i=2\}}]+\sum _{k,l}[{\gamma }_{kl,11}{I}_{\{g_k=1,g_l=1\}}+{\gamma }_{kl,12}{I}_{\{g_k=1,g_l=2\}}+{\gamma }_{kl,21}{I}_{\{g_k=2,g_l=1\}}+{\gamma }_{kl,22}{I}_{\{g_k=2,g_l=2\}}]$$ (5)

where logit(x) = x / (1−x); α is the constant coefficient; β_i1 and β_i2 are the coefficients for the effects of having 1 copy of targeted allele and 2 copies of the allele at the i th risk SNP, respectively; g_i is the number of copies of the targeted allele at SNP i, and I_{gi=n} is an indicator function of whether the copies of the allele is n; γ_kl,11, γ_kl,12, γ_kl,21, and γ_kl,21 are coefficients for the interaction between SNP k and SNP l, associated to 4 genotype combinations of the two SNPs. If the coefficients are known, penetrances for every possible genotype combination could be determined from the logistic models and then used for data generation.

For easier interpretation, the coefficients α, β and γ are not directly used by the GWAsimulator program as the input parameters. Instead, they are calculated within the program from user-specified relative risks (RR). When there is no interaction, a pair of genotypic relative risks specify the marginal genotypic effects at SNP i, r_i1 = f (g_i = 1) / f (g_i = 0) and r_i2 = f (g_i = 2) / f (g_i = 0), where f (·) is the penetrance function. When pair-wise interactions exist, in addition to the RRs at each locus, departure of relative risks for genotype combinations from the product of corresponding marginal relative risks is also specified. For interaction between SNP k and SNP l, departure from product of marginal relative risks is defined as

$$d_{kl,uv}=\frac{f(g_k=u,g_l=v)/f(g_k=0,g_l=0)}{r_{ku}{r}_{lv}}.$$

If there is no interaction, the SNP effects are independent. Thus, instead of using formula (4), coefficients β could be estimated one by one using a set of single-locus models

$$\text{logit}(f(g_i))=\text{logit}(\text{Pr}(\text{affected}|g_i))={\alpha }_i+{\beta }_{i1}{I}_{\{g_i=1\}}+{\beta }_{i2}{I}_{\{g_i=2\}}$$ (6)

In case when there are pair-wise interactions, similar simplification could also be used if a pair of interacting SNPs could be taken as an independent group of factors from other SNPs. In this case, we have

$$\text{logit}(\text{Pr}(\text{affected}|g_k,g_l))={\alpha }_{kl}+{\beta }_{k1}{I}_{\{g_k=1\}}+{\beta }_{k2}{I}_{\{g_k=2\}}+{\beta }_{l1}{I}_{\{g_l=1\}}+{\beta }_{l2}{I}_{\{g_l=2\}}+{\gamma }_{kl,11}{I}_{\{g_k=1,g_l=1\}}+{\gamma }_{kl,12}{I}_{\{g_k=1,g_l=2\}}+{\gamma }_{kl,21}{I}_{\{g_k=2,g_l=1\}}+{\gamma }_{kl,22}{I}_{\{g_k=2,g_l=2\}}$$ (7)

In GWAsimulator, β coefficients are calculated from (6), regardless of whether interactions are involved. After that, γ coefficients for interaction terms are obtained from the two-locus model (7) with the same β coefficients obtained previously. This simple 2-step estimation is not always appropriate. If there are interaction effects, the estimation of γ from (6) ignoring the interaction terms might not be correct. Besides this, equation (7) does not always hold true, either. A simple example is that when a risk SNP is involved in interactions with multiple SNPs, it is not possible to single out this SNP with a single interacting SNP to estimate the pair-wise interaction coefficients.

A general modeling approach using Penetrance tables in simGWA

In the present work, we provide and evaluate methods to correctly specify multilocus disease models with or without epistatic effects, and with either pairwise or high-order interactions. Since penetrance tables are a more general and flexible way to precisely characterize complex joint effects of multiple risk loci, methods for conversion among different model specification methods are developed using penetrance table as the primary characterization of disease models. All methods described below are implemented in an R package called simGWA that produces the correct multilocus penetrance table, and then simulates disease loci genotypes and applies retrospective sampling by a modified GWAsimulator engine to rapidly generate genome-wide marker genotype data (see Figure 1).

Figure 1.

Schematic representation of four approaches for specifying disease models and methods for converting them to penetrance tables used by simGWA. The models used in GWAsimulator are shown in the dashed oval, in which, marginal relative risks and departure from product of marginal RR (A1) are required from users to estimate logistic model coefficients (B), and then the penetrance table is created internally in GWAsimulator. We identified problem in estimation of logistic model coefficients from model (A1) to (B). In simGWA package, we first convert departure from product of marginal RR (A1) to departure from product of joint RR (A2), and then estimate logistic coefficients and penetrances by numerical calculations. Other ways to generate penetrance tables in simGWA include: (B) calculating penetrances directly from logistic model given coefficients values for low-order interactions; (C) using package simP to get joint penetrances for high-order interactions; (D) using other user specified penetrance table structures, such as heterogeneous model and threshold model (see methods). In methods A1, A2 and C (shown in solid oval), the marginal relative risks are constrained to model the marginal effects at the disease loci.

(1) Correctly modeling pair-wise interactions using relative risks

Our first method addresses the misspecification problem of GWAsimulator when interaction exists, by correctly calculates the logistic model coefficients from given values of relative risks (RR). Because direct estimation requires solving high-dimensional nonlinear functions that can quickly become intractable, we developed an iterative approach to circumvent the problem. First, the departure from product of marginal RRs is converted to departure from the product of 2 “boundary” joint RRs involving reference genotypes at individual disease locus (see definition of d'_kl,uv below). Then, values of the latter are used in iterative numerical computation to obtain the logistic model coefficients and the full penetrance table. This procedure is Option 1 shown in Figure 1 as path from (A1) to (A2) and then to (B).

Marginal RR and joint RR

Marginal RR is commonly used when describing the effects of individual SNPs. However, when it comes to interactions, joint RR (the risk ratio of a joint genotype (g_k = u, g_l = v) to the reference (g_k = 0, g_l = 0) : RR_kl,uv = (g_k = u, g_l = v) / (g_k = 0, g_l = 0)) gives a better characterization of the relative risks comparing genotype combinations.

For two disease loci k and l, the departure from product of marginal relative risk of having genotype with u copies of disease allele at k and v copies at l is defined as the ratio of the joint RR to the product of the 2 marginal RRs:

$$d_{kl,uv}=\frac{R{R}_{kl,uv}}{r_{ku}{r}_{lv}}=\frac{f(g_k=u,g_l=v)/f(g_k=0,g_l=0)}{\{f(g_k=u)/f(g_k=0)\}\{f(g_l=v)/f(g_l=0)\}}$$

while the departure from product of 2 “boundary” joint RR is defined as

$${d^{\text{'}}}_{kl,uv}=\frac{R{R}_{kl,uv}}{R{R}_{kl,u0}·R{R}_{kl,0v}}=\frac{f(g_k=u,g_l=v)/f(g_k=0,g_l=0)}{\{f(g_k=u,g_l=0)/f(g_k=0,g_l=0)\}\{f(g_k=0,g_l=v)/f(g_k=0,g_l=0)\}}.$$

For a given set of values of d_kl,uv, the values of d'_kl,uv can be determined by solving a system of linear equations.

Numerical algorithm to estimate coefficients and penetrance table

Assuming logistic model in formula (5), the coefficients need to estimate are α, β_i1 and α_i2 (1≤ i ≤ m), and for all interacting SNP pairs between SNPs k and l, γ_kl,11, γ_kl,12, γ_kl,21 and γ_kl,22. The estimation is achieved by iterative calculating the coefficients and constructing the penetrance table. At each iteration, we first construct the full penetrance table from the current set of coefficients. From the full penetrance table, the joint RR and marginal RR values are calculated and compared with those specified originally in the model. The difference between the current RR values to those from the model specifications is used to update the logistic model coefficients accordingly to reduce the difference. After many iterations, the full penetrance table conforms well to all joint RR and marginal RR constraints with neglectable bias.

We start by letting α⁽⁰⁾ = log(K / (1−K)) and all SNP coefficients ${\beta }_{iu}^{(0)}$ and ${\gamma }_{kl,uv}^{(0)}$ equal to 0. The penetrance for each genotype is then a constant, Pr(affected | g₁,…g_m) = K.

Suppose at iteration s, the previously estimated coefficients are α^(s−1), ${\beta }_{iu}^{(s-1)}(1\le i\le m,u\in \{1,2\}),{\gamma }_{kl,uv}^{(s-1)}$ (k,l are interacting SNPs, u,v)∈{1,2}), and the penetrance table calculated from the coefficients is f^(s−1). The following steps are taken to update their values in the iteration.

• Step 1: for each 1≤i≤m, update β_iu and penetrance table f. From the full penetrance table f^(s−1), the marginal penetrances at locus i are calculated by weighed average of all penetrances involving a certain genotype at this locus, and the weight is the corresponding multilocus genotype frequency. Denote the derived marginal penetrances as $f_{i0}^{(s-1)}{f}_{i1}^{(s-1)}$, and $f_{i2}^{(s-1)}$ for the 3 genotypes at SNP i. Then update ${\beta }_{iu}^{(s)}={\beta }_{iu}^{(s-1)}+\text{log}(\frac{r_{iu}}{f_{iu}^{(s-1)}/f_{i0}^{(s-1)}})$, and update the penetrance table based on the new set of coefficients. Denote the final penetrance table after updating ${\beta }_{iu}^{(s)}$ for all SNPs as f^(s,1)

• Step 2: update the value of a. After step 1, the disease prevalence might not equal to K. From penetrance table f^(s,1), calculate the current disease prevalence K^(s,1), then a is updated to α^(s,2) = α^(s−1) + log(K / K^(s,1)). Accordingly, the new penetrance table from the coefficients is now f^(s,2).

• Step 3: for each pair of interacting SNPs K and l, update the values of γ_kl,uv(u,v = 1,2). In this step we estimate departure from joint relative risks from f^(s,2). Estimations are d'_kl,uv^(s,2). Then the updated γ values are γ_kl,uv^(s) = γ_kl,uv^(s−1) + log(d'_kl,uv / d'_kl,uv^(s,2)). Denote the penetrance table after updating for all γ_kl,uv as f^(s,3)

• Step 4: update the value of a as in step 2. After this updating, the logistic model coefficients are now α^(s), β_iu^(s), γ_kl,uv^(s) and the penetrance table calculated from them is f^(s).

• Step 5: check the maximum change of values to all coefficients in step 1–4 against a pre-set tolerance threshold (default value of 10⁻¹⁰ is used for results shown below). Iterations of step 1–4 are repeated until the maximum change is below tolerance or a maximum number of iterations is reached.

(2) Effectively modeling higher-order interactions

High-order interactions can be modeled in simGWA either by logistic models (this is Option 2 marked in Figure 1 as (B)) or by sampling penetrance tables generated using the previously developed simP R package[Yang and Gu 2008] (this is Option 3 marked in Figure 1 as (C)).

For the logistic model approach (Option 2), a formula similar to equation (4) is used to determine the penetrances of multi-locus genotypes, with additional higher-order product terms for interactions among multiple risk SNPs. Users need to specify all coefficients in the model. The simGWA package automatically calculates the penetrance table when interactions are limited between pairs of SNPs. Going beyond pair-wise interactions, the users have to calculate and specify each penetrance values. Although the calculation is straightforward, we discourage the use of this approach when modeling higher than pairwise interactions because the biologically interpretation of the higher-order product terms becomes less clear. Instead, we recommend directly assign multilocus penetrances conforming to assigned marginal effects. This can be done by simP[Yang and Gu 2008] (Option 3), a previously developed R package that can perform two very useful functions: First, it can generate unlimited number of random penetrance tables that satisfy a given set of marginal relative risk constraints. Second, for any given penetrance table, it quickly evaluates the effects of single SNPs, collective effects of interactions, and the fraction of disease variation explained by the corresponding genetic model. This information could aid selecting interesting interaction models for data simulation. For example, using simP, we were able to generate hundreds of genetic models with null marginal effects for all risk SNPs, but their joint effects account for a substantial amount of disease variability.

(3) Special penetrance tables prescribing known biological models

Some well-known interaction models can be directly specified using penetrance tables (this is Option 4 marked in Figure 1 as (D)). Below are two such examples.

1. Heterozygous model. Occurrence of any risk genotype from different loci causes the disease. In Table 1, occurrence of AA genotype or any B allele causes the disease (penetrance is 1).

2. Threshold model. Disease phenotype manifests (penetrance is 1) when the total number of risk alleles/genotypes reaches a threshold.

Table 1.

Penetrance table of a heterozygous model with two SNPs. Occurrence of risk genotype AA or allele B results in a penetrance of 1.

	bb	bB	BB
aa	0	1	1
aA	0	1	1
AA	1	1	1

Evaluation of simGWA performances

To evaluate the performances of simGWA, we applied the simulator over a range of genetic models of multilocus interactions and used HapMap phased data for Caucasians (CEU) as template. The simulated GWAS datasets include a total of 676,565 SNPs on the Affymetrix Genome-Wide Human SNP Array 6.0 to mimic the real genotyping platform.

The GWAS data were simulated for a binary trait with 5 risk SNPs. They locate on 5 randomly selected chromosomes. Among the five SNPs, SNP1, SNP3 and SNP4 have no marginal effect at all; SNP2 has a multiplicative effect, and the relative risks of genotypes with one and two copies of risk alleles (compared with that of no copy) are 1.5 and 2.25, respectively; SNP5 has a dominant effect, and the relative risk of both risk genotypes is 2. Namely, r₁₁ = r₁₂ = 1; r₂₁ = 1.5, r₂₂ = 2.25; r₃₁ = r₃₂ = 1; r₄₁ = r₄₂ = 1; r₅₁ = r₅₂ = 2.

Assuming the marginal effects described above, two types of models were considered in terms of SNP-SNP interactions: one with no interaction at all, and the other with pairwise interactions between 2 SNP pairs (SNP1 interacting with SNP2, SNP3 with SNP4). In the latter, the effect sizes of the pairwise interactions, as measured by departure from product of marginal RRs, are d_12,11 = 0.2, d_12,12 = 1, d_12,21 = 2, d_12,22 = 3, d_34,11 = 0.5, d_34,12 = 2, d_34,21 = 2, d_34,22 = 1.6. For each model, we generated data sets containing 676,565 SNPs for 2000 cases and 2000 controls using simGWA, by: (1) converting the marginal RR model to joint RR model; (2) numerically calculating logistic model coefficients and generating the penetrance table; (3) generating genetic data. To compare performance, we also generated datasets using GWAsimulator and the same parameters for disease models with or without pairwise interactions. Under each of the 2 models, 1,000 replication datasets were generated by simGWA and GWAsimulator, respectively.

Results

Comparable performance in terms of Local LD structure & computational time

Both programs took about 52 minutes to simulate genotypes of 676,565 SNPs for 4000 subjects with a single thread on a Linux machine with 2 CPUs of Intel Xeon 5430 Quad Core 2.66 GHz and 32 GB of memory.

For both simGWA and GWAsimulator, genome-wide LD structures in the simulated data were comparable to those in the real population of HapMap CEU. A typical example is given in Figure 2, which confirms that local LD structures by HaploView [Barrett, et al. 2005] were faithfully maintained in both datasets generated by the two simulators.

Figure 2. Comparison of LD structures.

An example of LD structures in simulated samples in a region of 150 SNPs flanking a disease locus compared to that in the HapMap CEU template (top panel). The bottom 2 panels show results using the GWAsimulator (middle) and simGWA(Bottom). Each data set has 60 individuals. Pink vertical bar shows the position of a risk SNP. The LD structure were plot using Haploview.

Agreement between simGWA and the GWAsimulator when there is no interaction

The two simulators handle parameters for disease models differently. However, we may compare effect sizes of each risk SNP estimated based on the simulated penetrance tables. Table 2 summarizes the comparisons when interactions exist or not, expressed in terms of genetic information loss (the reduction in explained heritability) if an individual SNP was ignored. When there is absolutely no interaction (“pure marginal effect” model), marginal effect size of individual risk SNPs were almost identical by both simulators.

Table 2.

Characteristics of the simulated disease models.

		Information loss by ignoring a SNP
		h2	SNP1	SNP2	SNP3	SNP4	SNP5
	simGWA	0.04	0.00	0.27	0.00	0.00	0.74
Pure marginal effect	GWAsimulator	0.04	0.00	0.26	0.00	0.00	0.75
	simGWA	0.19	0.54	0.60	0.26	0.26	0.20
Interaction model	GWAsimulator	0.08	0.31	0.32	0.20	0.20	0.39

Models were built using simGWA and the GWAsimulator when there was no interaction or there were 2 interacting SNP pairs (SNP1 and SNP2, SNP3 and SNP4). Of the 5 SNPs, 3 do not have any marginal effect (SNP1, SNP3, SNP4). The 3rd column in the table shows the proportion of disease variation that is explainable by the joint effect of all 5 SNPs (heritability of disease). The next few columns summarize the genetic information loss by ignoring any of the 5 SNPs

For every pair of datasets generated by the two simulators, difference in genotype distributions was tested by χ²; at each risk SNP, in cases and in controls separately. There were 5000 tests comparing the genotypes at 5 risk SNPs in 1,000 cases datasets, and another 5000 tests in 1,000 controls datasets. The smallest p-value from the 10000 tests was 0.070. This confirms that the distributions of risk genotypes were not different in datasets generated by the 2 simulators. Further tests were carried out comparing distributions of all two-locus combined genotypes; the similarity still holds.

simGWA correctly simulates pair-wise interactions

When there were interactions, simGWA correctly calculated all interaction terms in the penetrance table, which could differ substantially from those used by GWAsimulator even though the disease model is specified in the same manner. This is clearly seen in the bottom half of Table 2: there were differences both in the total heritabilities calculated by the two methods, and in the effect sizes of the risk SNPs (measured as the decrease in explained disease variation when a risk SNP was ignored). The differences were due to overly simplified specification of the logistic model coefficients in GWAsimulator for SNPs involved in interactions, as demonstrated in Table 3. If two SNPs have no marginal effect nor any interaction between them, their combined effects should be null, such as in the case of SNP1 and SNP3, or SNP1 and SNP4.

Table 3.

Summary of interaction effects when there are interactions in the models.

		SNP1*2	SNP3*4	SNP1*3	SNP1*4
Joint effects of SNP pairs	simGWA	0.55	0.22	0.00	0.00
	GWAsimulator	0.35	0.25	0.13	0.13
Interactions effects of SNP pairs	simGWA	0.49	0.22	0.00	0.00
	GWAsimulator	0.23	0.10	0.00	0.00

Models were built using simGWA and the GWAsimulator when there were 2 pairs of SNPs with pair-wise interactions (SNP1 and SNP2, SNP3 and SNP4). For the two SNP pairs that really interact (SNP1*2, SNP3*4), and two other SNP pairs that entails no interactions (SNP1*3, SNP1*4), the interaction effects in the penetrance tables are summarized. “Information in SNP pairs” shows the proportion of variance in the total heritability that is explainable by only considering the SNP pair (joint effect). The last two rows of the tables show the variance explainable by the pair-wise interaction of the two SNPs.

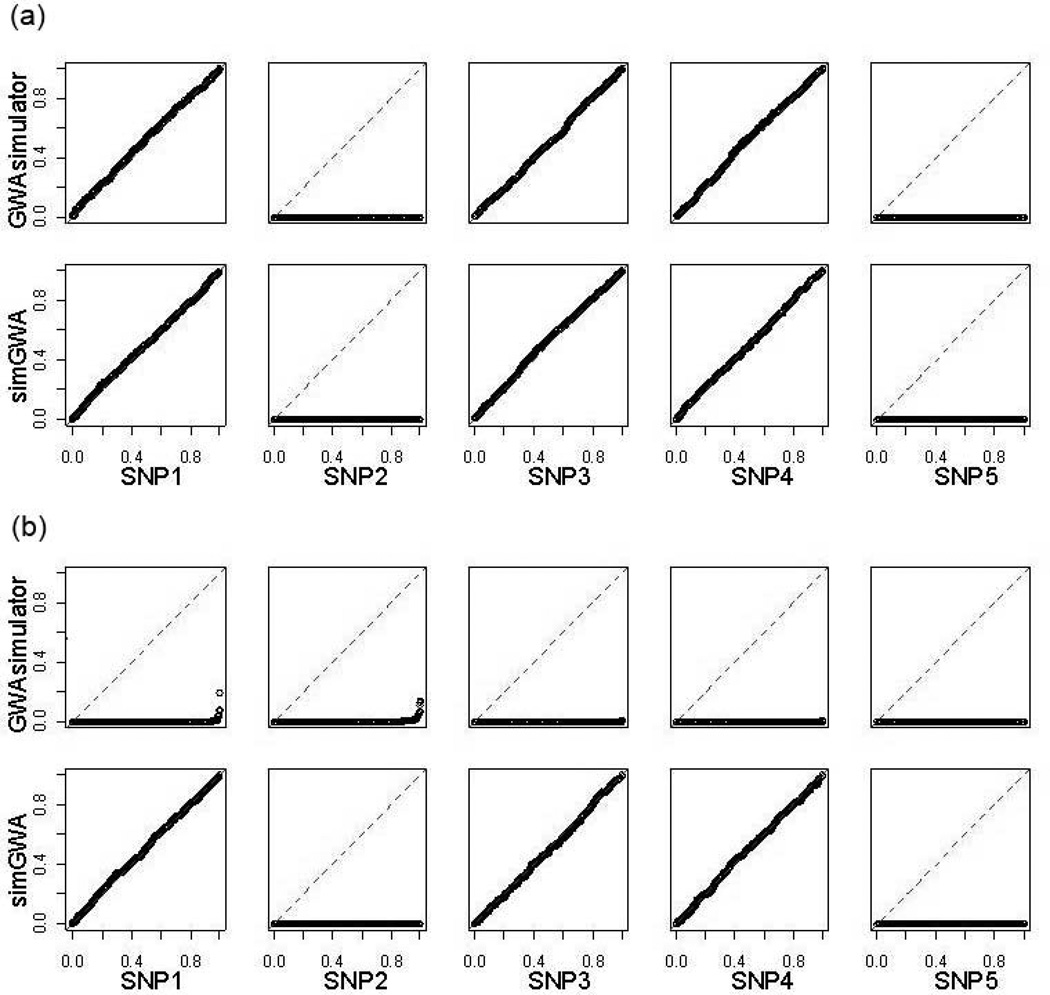
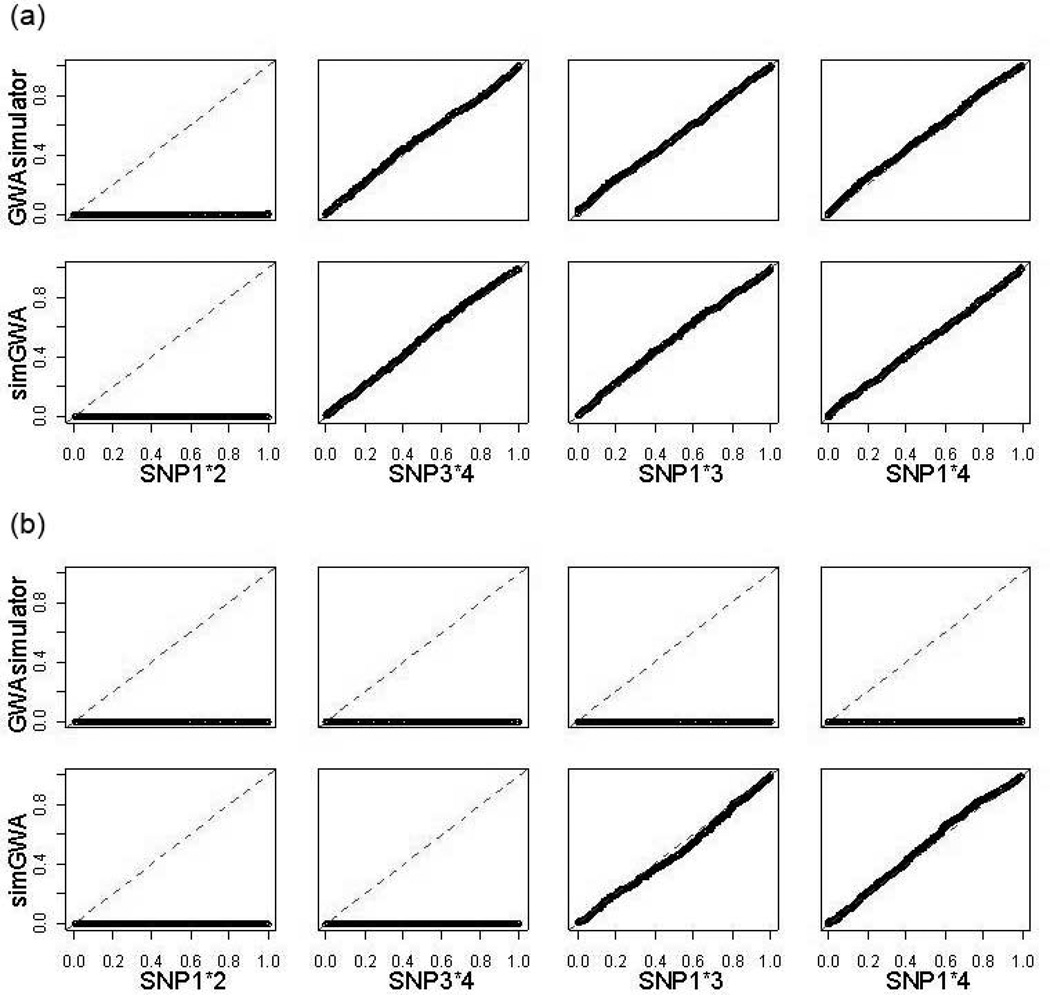
However, as shown in Table 3, while the penetrance table calculated by simGWA resulted in a correct value of 0 for the combined effects of 2 such pairs of SNPs, substantial nonzero values (0.13 for both pairs) were assigned by GWAsimulator. This is supported by association test results on the simulated datasets. Single-SNP association test p values should approximately follow the uniform distribution when the SNP has no marginal effect. As seen in Figure 3, under models of no interaction, distributions of single-SNP tests for SNP1, SNP3, and SNP4 in both simGWA- and GWAsimulator-generated datasets follow perfectly the uniform distribution (Panel A); however, under interaction models, the distributions in GWAsimulator-generated datasets completely diverged from the uniform (Panel B) even though these SNPs had no marginal effects. Similar observations were made for interaction tests and displayed in Figure 4. Again, under pure marginal effect models, p values of pairwise interaction tests for SNP1-SNP3 and SNP1-SNP4 correctly follow the uniform distribution in both simGWA- and GWAsimulator-generated datasets. But when there were interactions, the distributions in GWAsimulator-generated datasets completely diverged from the uniform (Panel B) even though no interaction effects were simulated for these SNP pairs.

Figure 3. QQ plots compare p-value distributions for χ² test for the risk SNPs.

Each plot compares the distributions of χ² test p values (x-axis) on 1000 simulated data sets against the uniform distribution (y-axis). Close to the diagonal line means the p values are approximately uniform. If there is any signal, the plot lies below the diagonal. The two panels are: (A) Model without interactions; (B) Interaction model.

Figure 4. QQ plots compare p-value distributions for interaction test for the risk SNP pairs.

Each plot compares the distributions of interaction test p values (x-axis) on 1000 simulated data sets against the uniform distribution (y-axis). Close to the diagonal line means the p values are approximately uniform. If there is any signal, the plot lies below the diagonal. The two panels are: (A) Model without interactions; (B) Interaction model.

Discussion

We presented a novel method for correctly specifying SNP interaction effects and an improved GWAS data simulator using this method called simGWA. Penetrance table is used as the fundamental characterization of disease models, and commonly-used means for interaction model specification (deviation from product of relative risks or logistic model coefficients) are converted to use correct penetrance tables. Arbitrary logistic models or a general-purpose penetrance generator (simP) were used to generate penetrance tables for high-order interactions. Genotype simulation in simGWA is built on the highly efficient GWAsimulator[Li and Li 2008]. Before GWAsimulator, many used the coalescent model[Donnelly and Tavare 1995; Hudson 2002] of population genetics or forward time simulation[Peng and Amos 2010; Pinelli, et al. 2012] to reconstruct the evolutionary history. Although the approach works well for sampling a theoretical population that follows the Wright–Fisher model[Hudson 2002], the simulators are generally not as efficient for GWAS data simulation. Moreover, GWAsimulator adopts an empirical approach and the “retrospective sampling” based on real-population templates, and works excellently when there are no interactions. simGWA fully takes advantage of its efficient simulation engine and by employing new methods to correctly specify SNP interaction effects. This resulted in a useful tool for rapid generation of GWAS data under complex interaction models for studying complex disease.

Existing methods such as GENS[Amato, et al. 2010] and GENS2[Pinelli, et al. 2012] also used multi-locus penetrance tables to model gene-environment interactions. These methods were limited to GxE interactions involving at most 2 disease loci and a single environment factor. It would be interesting to see if the methods can be combined with that of simGWA to simulate GxE interactions involving more environment variables and higher-order penetrance tables.

Although the present work is focused on simulating GWAS data for binary traits, it is possible to extend simGWA to simulate GWAS data for quantitative traits for studies using population-based sampling. However, correct modeling of higher-order interactions for sampling based on quantitative trait values will not be straightforward and deserves further investigation.

We note that simGWA has some limitations similar to GWAsimulator. For example, flaws in the template phase data (e.g., ascertainment bias) would be passed to the generated data. Also, long-range LDs are not considered; and it allows only one disease locus on each chromosome. These flaws may be remediable in many situations. For example, if there is need to simulate multiple disease loci on the same chromosome in different LD blocks, one can simulate that chromosome in multiple chunks each harboring a risk SNP, with possibly slight loss of LD information at the ends connecting the chunks.

In summary, simGWA provides a rapid GWAS data simulator that is able to mimic realistic LD and correctly model complex interactions among risk SNPs. As more and more efforts are put to in-depth analysis of GWAS data to find “missing heritability”, many sophisticated analytical methods are in development and we anticipate that simGWA will provide a useful tool for method evaluation.