Bootstrap for the case-cohort design

Summary

The case-cohort design facilitates economical investigation of risk factors in a large survival study, with covariate data collected only from the cases and a simple random subset of the full cohort. Methods that accommodate the design have been developed for various semiparametric models, but most inference procedures are based on asymptotic distribution theory. Such inference can be cumbersome to derive and implement, and does not permit confidence band construction. While bootstrap is an obvious alternative, how to resample is unclear because of complications from the two-stage sampling design. We establish an equivalent sampling scheme, and propose a novel and versatile nonparametric bootstrap for robust inference with an appealingly simple single-stage resampling. Theoretical justification and numerical assessment are provided for a number of procedures under the proportional hazards model.

1. Introduction

In clinical or epidemiologic investigation of infrequent disease endpoints, cohort studies require a large sample size, but full-cohort covariate data collection can be costly. Case-cohort sampling (Prentice, 1986) offers an economical alternative, to collect covariates only from the cases and a simple random subcohort. A number of statistical methods have been developed for the proportional hazards model under such sampling. Prentice (1986) and Self & Prentice (1988) proposed a pseudolikelihood approach. Kalbfleisch & Lawless (1988) and Chen & Lo (1999) suggested methods to take better advantage of the data so as to improve estimation efficiency. Borgan et al. (2000), Kulich & Lin (2004), and Nan (2004) studied a variant of the design where some covariates or surrogate measures are available for the full cohort. Other semiparametric models have also been investigated, including the additive hazards model (Kulich & Lin, 2000), linear transformation models (Chen, 2001; Kong et al., 2004; Lu & Tsiatis, 2006; Chen & Zucker, 2009), and the accelerated failure time model (Nan et al., 2006; Kong & Cai, 2009).

Statistical challenges with the case-cohort design lie in the two-stage sampling. After the first stage resulting in the full study cohort, the second stage selects a subcohort by simple random sampling without replacement. As a result, interval estimation based on asymptotic distribution theory, which is routinely adopted and specific to each point estimation procedure, is often cumbersome to derive and implement. Although the jackknife approach of Barlow (1994) to variance estimation in the proportional hazards model may deal with some of these issues, neither approach permits confidence band construction for an infinite-dimensional quantity, e.g., a covariate-specific survival function for prediction. While a bootstrap method would be advantageous in these regards, how to resample is not obvious since the covariates are not available for the full cohort. The only existing bootstrap method is due to Wacholder et al. (1989), which has been adopted for the proportional hazards model and accelerated failure time model (Kong & Cai, 2009). However, the method fixes the case numbers in the subcohort and full cohort. Theoretical justification is lacking and it may not always perform well.

We propose a novel nonparametric bootstrap that involves only a single-stage resampling, after establishing an equivalent sampling scheme for the case-cohort design. Three existing point estimation methods under the proportional hazards model will set the stage and illustrate our proposal.

2. Point estimation methods under the proportional hazards model

Write the survival time as T and the censoring time as C. As a result of censoring, they are observed only through follow-up time X = T ∧ C and censoring indicator Δ = I(T ≤C), where ∧ is the minimization operator and I(·) is the indicator function. Denote the covariate vector by Z; we confine our attention to time-independent covariates. The proportional hazards model (Cox, 1972) postulates

$$d{\mathrm{\Lambda }}_z(t)=e^{{\beta }_0^{\mathrm{T}}z}d{\mathrm{\Lambda }}_0(t),T⫫C\mid Z,$$ (1)

where Λ_z is the cumulative hazard function of T given Z = z, Λ₀ is an unspecified baseline cumulative hazard function, β₀ is an unknown regression coefficient, and ⫫ denotes statistical independence. Under cohort sampling, the data consist of (X_i, Δ_i, Z_i), i = 1, …, n, as n independent replicates of (X, Δ, Z). Define counting process N_i(t) = Δ_iI(X_i ≤ t) and at-risk process Y_i(t) = I(X_i ≥ t). Further, introduce empirical processes

$$\begin{array}{l}A(t)=\frac{1}{n}\sum _{i\in \mathcal{F}}{N}_i(t),B(t)=\frac{1}{n}\sum _{i\in \mathcal{F}}{Z}_i{N}_i(t),\\ U(t,\beta )=\frac{1}{n}\sum _{i\in \mathcal{F}}{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},V(t,\beta )=\frac{1}{n}\sum _{i\in \mathcal{F}}{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i},\end{array}$$

where 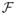≡ {1, …, n} is the index set. The maximum partial likelihood estimator (Cox, 1972, 1975), β̂, is the solution of

$$\mathrm{\Psi }(\beta )=B(\infty )-{\int }_0^{\infty }\frac{V(s,\beta )}{U(s,\beta )}dA(s).$$

The Breslow (1972) estimator of Λ₀(t) is Λ̂(t; β̂), with

$$\widehat{\mathrm{\Lambda }}(t;\beta )={\int }_0^t\frac{dA(s)}{U(s,\beta )}$$

These functional representations are due to Huang & Wang (2000).

However, under the case-cohort design, the covariates are ascertained only for the cases, for whom Δ_i = 1, and a simple random subcohort 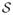⊂ 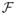of size m. Thus, U(t, β) and V(t, β) in Ψ(β) and Λ̂(t; β) are no longer available; they are the full-cohort empirical estimates of E{Y (t)e^βTZ} and E{Y(t)Ze^βTZ}, respectively. Different replacements are made in the following three case-cohort estimation procedures, giving rise to

$${\mathrm{\Psi }}_k(\beta )=B(\infty )-{\int }_0^{\infty }\frac{V_k(s,\beta )}{U_k(s,\beta )}dA(s),{\widehat{\mathrm{\Lambda }}}_k(t;\beta )={\int }_0^t\frac{dA(s)}{U_k(s,\beta )},$$ (2)

and subsequently estimator {β̂_k, Λ̂_k(t; β̂_k)}, for k = 1, 2, 3. Self & Prentice (1988) adopted the subcohort counterparts,

$$U_1(t,\beta )=\frac{1}{m}\sum _{i\in \mathcal{S}}{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},V_1(t,\beta )=\frac{1}{m}\sum _{i\in \mathcal{S}}{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}.$$

Chen & Lo (1999) showed that one can make better use of the case-cohort data. Both E{Y (s)e^βTZ} and E{Y(s)Ze^βTZ} are weighted averages of case- and control-specific quantities, e.g., E{Y(s)e^βTZ} = E(Δ)E{Y(s)e^βTZ | Δ = 1} + {1 − E(Δ)}E{Y (s)e^βTZ| Δ = 0}, and estimating the case-specific quantities may utilize the full cohort instead of the subcohort. By taking m₁/m as an estimate of E(Δ) with m₁ = 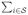Δ_i, their first method adopts

$$\begin{array}{l}{U}_2(t,\beta )=\frac{m_1}{m}\frac{1}{n_1}\sum _{i\in {\mathcal{F}}^1}{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{1}{m}\sum _{i\in {\mathcal{S}}^0}{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},\\ V_2(t,\beta )=\frac{m_1}{m}\frac{1}{n_1}\sum _{i\in {\mathcal{F}}^1}{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{1}{m}\sum _{i\in {\mathcal{S}}^0}{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i},\end{array}$$

where n₁ = Δ_i, 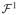= {i ∈ 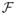: Δ_i = 1}, and 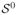= {i ∈ 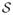: Δ_i = 0}. If n₁/n instead is used as an estimate of E(Δ), their second method has

$$\begin{array}{l}{U}_3(t,\beta )=\frac{1}{n}\sum _{i\in {\mathcal{F}}^1}{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{n-n_1}{n}\frac{1}{m-m_1}\sum _{i\in {\mathcal{S}}^0}{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},\\ V_3(t,\beta )=\frac{1}{n}\sum _{i\in {\mathcal{F}}^1}{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{n-n_1}{n}\frac{1}{m-m_1}\sum _{i\in {\mathcal{S}}^0}{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}.\end{array}$$

Rescaled estimating functions nΨ₁(β) and nΨ₂(β), and therefore β̂₁ and β̂₂, do not require the full cohort size, n. As pointed out in Prentice (1986), the case-cohort design does not necessarily require a full cohort roster and thus n need not be known; see also Chen & Lo (1999, Remark 2). However, β̂₃ and the three estimators of the baseline cumulative hazard function require that the full cohort be well-defined and n known.

These regression coefficient estimators, as commonly adopted, have been well studied, and their asymptotics-based inference procedures have been developed (Self & Prentice, 1988; Chen & Lo, 1999). However, inference for the baseline cumulative hazard function or a covariate-specific survival function is only available in a pointwise fashion for the method of Self & Prentice (1988). A nonparametric bootstrap is desirable to permit simple and automatic inference, for these as well as other procedures.

3. Equivalent sampling scheme and the proposed bootstrap

Efron’s (1979) bootstrap would mimic the two-stage sampling to resample the full cohort as a pseudo-population, but the full cohort is not fully observed and possibly not even well-defined. Therefore, the procedure is not applicable, as recognized by Wacholder et al. (1989). In the sample survey literature, Gross (1980), Bickel & Freedman (1984), Chao & Lo (1985), and Sitter (1992a,b) developed methods to construct a pseudo-population for simple random sampling without replacement. Although these methods can be adapted, the resulting bootstraps may not be ideal, for several reasons. First, the resampling is complex, especially when n/m is not an integer. Second, cases outside the subcohort are not utilized. Third, this approach does not apply when the full cohort size n is unknown. Finally, a resample may contain only censored observations. Cohort sampling might suffer this complication as well (e.g., Kosorok, 2008) but it can be particularly acute with typical case-cohort studies, where the endpoint is infrequent and the subcohort has limited size.

Appealing to finite population sampling theory seems natural to deal with simple random sampling without replacement; this tactic is also commonly taken for asymptotic studies (e.g., Chen & Lo, 1999; Kulich & Lin, 2000; Kong et al., 2004). However, the full cohort is a random sample, not a finite population of interest. We rather pursue a direct approach by establishing an equivalent sampling scheme.

Proposition 1

The joint distribution of a set of random variables that are independent and identically distributed is invariant to reordering by a random permutation.

Since simple random sampling can be implemented via permutation, the subcohort in the case-cohort design consists of independent and identically distributed random variables, and so does its complement. Furthermore, the two sets are independent of each other. This fact does not contradict the well-known dependence structure from simple random sampling, which is conditional on the full cohort. Write the complement of 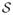as 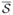= 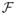\ 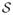. Then, {(X_i, Δ_i, Z_i) : i ∈ 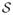} are m independent replicates of (X, Δ, Z), and {(X_iΔ_i, Δ_i, Z_iΔ_i) : i ∈ 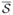} are n – m independent replicates of (XΔ, Δ, ZΔ). This results in an equivalent single-stage parallel sampling scheme.

This sampling equivalence first facilitates a model-free asymptotic study for the three estimation methods introduced in § 2.

Proposition 2

Re-define β₀ as the solution of

$$E\{ZN(\tau )\}-{\int }_0^{\tau }\frac{E\{Y(s)Z{e}^{{\beta }^{\mathrm{T}}Z}\}}{E\{Y(s)e^{{\beta }^{\mathrm{T}}Z}\}}dE\{N(s)\}=0$$ (3)

and subsequently

$${\mathrm{\Lambda }}_0(t)={\int }_0^t\frac{dE\{N(s)\}}{E\{Y(s)e^{{\beta }_0^{\mathrm{T}}Z}\}},t\in [0,\tau ],$$

where τ = sup{t : pr(X > t) > 0}. Suppose that the subcohort fraction m/n converges to a constant ρ ∈ (0, 1) as both m and n – m approach ∞, and that the conditions in the Appendix hold. Then, for each k = 1, 2, 3, β̂_k is consistent for β₀ and Λ̂_k(t, β̂_k) is consistent for Λ₀(t) uniformly in t ∈ [0, τ]. In addition, n^1/2{β̂_k − β₀, Λ̂_k(·; β̂_k) − Λ₀(·)} converges weakly to a Gaussian process.

Remark 1

This result is slightly more general than those of Self & Prentice (1988) and Chen & Lo (1999) as obtained under the proportional hazards model (1). The model (1) implies the above definitions of β₀ and Λ₀(·), but not vice versa.

More importantly, our proposal of parallel bootstrapping 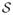and 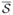naturally follows. We adapt the multiplier or weighted bootstrap, which assigns a nonnegative random weight to each individual and thus averts the complication of a resample without uncensored observations (cf. Kosorok, 2008). These independent and identically distributed weights, ξ_i for i ∈ 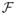, are independent of the data and have unit mean and unit variance; the standard exponential distribution was used in all our numerical studies reported later. However, a typical multiplier bootstrap as applied to a single sample standardizes the weights by their average such that the sum is fixed to the sample size (e.g., Kosorok et al., 2004; Kosorok, 2008), leading to the Bayesian bootstrap of Rubin (1981) if the standard exponential distribution is chosen for ξ_i. In contrast, we do not carry out the standardization and consequently our bootstrap resamples have random sizes m* and n*– m* for 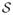and 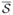, respectively, where m*= 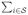ξ_i and n* = ξ_i. While superfluous in the single-sample case, this modification is critical in the case-cohort design particularly when the full cohort size n is unknown and thus 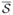is not well defined. In this circumstance, our bootstrap remains applicable provided that the point estimator is defined.

We now detail the proposed bootstrap for the three estimation methods. Define the bootstrap counterparts,

$$\begin{array}{l}{m}_1^{\ast }=\sum _{i\in \mathcal{S}}{\xi }_i{\mathrm{\Delta }}_i,n_1^{\ast }=\sum _{i\in \mathcal{F}}{\xi }_i{\mathrm{\Delta }}_i,\\ A^{\ast }(t)=\frac{1}{n^{\ast }}\sum _{i\in \mathcal{F}}{\xi }_i{N}_i(t),B^{\ast }(t)=\frac{1}{n^{\ast }}\sum _{i\in \mathcal{F}}{\xi }_i{Z}_i{N}_i(t),\\ U_1^{\ast }(t,\beta )=\frac{1}{m^{\ast }}\sum _{i\in \mathcal{S}}{\xi }_i{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},V_1^{\ast }(t,\beta )=\frac{1}{m^{\ast }}\sum _{i\in \mathcal{S}}{\xi }_i{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i},\\ U_2^{\ast }(t,\beta )=\frac{m_1^{\ast }}{m^{\ast }}\frac{1}{n_1^{\ast }}\sum _{i\in {\mathcal{F}}^1}{\xi }_i{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{1}{m^{\ast }}\sum _{i\in {\mathcal{S}}^0}{\xi }_i{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},\\ V_2^{\ast }(t,\beta )=\frac{m_1^{\ast }}{m^{\ast }}\frac{1}{n_1^{\ast }}\sum _{i\in {\mathcal{F}}^1}{\xi }_i{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{1}{m^{\ast }}\sum _{i\in {\mathcal{S}}^0}{\xi }_i{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i},\\ U_3^{\ast }(t,\beta )=\frac{1}{n^{\ast }}\sum _{i\in {\mathcal{F}}^1}{\xi }_i{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{n^{\ast }-n_1^{\ast }}{n^{\ast }}\frac{1}{m^{\ast }-m_1^{\ast }}\sum _{i\in {\mathcal{S}}^0}{\xi }_i{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},\\ V_3^{\ast }(t,\beta )=\frac{1}{n^{\ast }}\sum _{i\in {\mathcal{F}}^1}{\xi }_i{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}+\frac{n^{\ast }-n_1^{\ast }}{n^{\ast }}\frac{1}{m^{\ast }-m_1^{\ast }}\sum _{i\in {\mathcal{S}}^0}{\xi }_i{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}.\end{array}$$

The bootstrap estimator { ${\widehat{\beta }}_k^{\ast },{\widehat{\mathrm{\Lambda }}}_k^{\ast }(t;{\widehat{\beta }}_k^{\ast })$} results from

$${\mathrm{\Psi }}_k^{\ast }(\beta )=B^{\ast }(\infty )-{\int }_0^{\infty }\frac{V_k^{\ast }(s,\beta )}{U_k^{\ast }(s,\beta )}{dA}^{\ast }(s),{\widehat{\mathrm{\Lambda }}}_k^{\ast }(t;\beta )={\int }_0^t\frac{{dA}^{\ast }(s)}{U_k^{\ast }(s,\beta )},k=1,2,3.$$ (4)

Just like β̂₁ and β̂₂, their bootstrap counterparts ${\widehat{\beta }}_1^{\ast }$ and ${\widehat{\beta }}_2^{\ast }$ do not require the knowledge of the full cohort size n.

Theorem 1

Adopt the definitions and conditions in Proposition 2. Suppose that the nonnegative random variable ξ₁ of unit mean and unit variance satisfies ${\int }_0^{\infty }\text{pr}{({\xi }_1>x)}^{1/2}dx<\infty$. Conditionally on the data, $n^{1/2}\{{\widehat{\beta }}_k^{\ast }-{\widehat{\beta }}_k,{\widehat{\mathrm{\Lambda }}}_k^{\ast }(·,{\widehat{\beta }}_k^{\ast })-{\widehat{\mathrm{\Lambda }}}_k(·,{\widehat{\beta }}_k)\}$ has the same asymptotic distribution as n^1/2{β̂_k − β₀, Λ̂_k(·, β̂_k) − Λ₀(·)} for each k = 1, 2, 3.

The proposed bootstrap gives rise to robust inference, similar to Barlow (1994) but different from model-based inference of Self & Prentice (1988) and Chen & Lo (1999). The distribution of { ${\widehat{\beta }}_k^{\ast }-{\widehat{\beta }}_k,{\widehat{\mathrm{\Lambda }}}_k^{\ast }(·,{\widehat{\beta }}_k^{\ast })-{\widehat{\mathrm{\Lambda }}}_k(·,{\widehat{\beta }}_k)$} can be simulated to approximate that of {β̂_k − β₀, Λ̂_k(·, β̂_k) − Λ₀(·)}. The implementation requires trivial coding beyond the point estimators.

Remark 2

Case-cohort sampling specializes to cohort sampling when n = m. In this case, our proposal reduces to the multiplier bootstrap, which is different from the model-based resampling method of Lin et al. (1994) for the proportional hazards model. Recently, Cheng & Huang (2010) developed general theory for the bootstrap in semiparametric models under cohort sampling. They considered the proportional hazards model as an example, but focused only on the regression coefficients.

4. Numerical studies

We simulated under a proportional hazards model with a constant baseline hazard and two covariates. The two covariates were independent, each with a uniform distribution between −1 and 1; their coefficients were both unity. The censoring time depended linearly on the first covariate, having a uniform distribution between 0 and 1.5. The full cohort size was 1000. As a realistic scenario, the baseline hazard was set to 12.5, resulting in approximately 90% censoring, and the subcohort size was set to 200. For a more comprehensive assessment, two additional scenarios were studied as well. One reduced the subcohort size to 100, while the other changed the baseline hazard to 1 for a censoring rate of approximately 50%. With these three scenarios, the expected sizes of combined cases and subcohort were 280, 190, and 600, including 100, 100, and 500 expected cases, respectively.

To compare with the proposed bootstrap, we also evaluated asymptotics-based inference for the regression coefficients β₁ and β₂ as in Chen & Lo (1999, Remark 5) and the bootstrap of Wacholder et al. (1989); asymptotics-based pointwise inference for the baseline cumulative hazard function Λ₀(·) would require tedious derivation and was not examined. For both bootstrap methods, we computed standard errors, Wald-type and percentile confidence intervals for β₁, β₂, α₁ = log Λ₀(0.5), and α₂ = log Λ₀(1). Moreover, a confidence band for the baseline survival function S₀(·) over time [0, 1.25] was constructed, by transformation from the equal-precision band for log Λ₀(·); an equal-precision band has boundaries parallel to those of the corresponding pointwise Wald-type confidence intervals. The calculation was based on 1000 bootstrap resamples, but our numerical experiments indicated that a much smaller bootstrap size, say, 200, would typically suffice for standard errors and Wald-type confidence intervals (cf. Efron & Tibshirani, 1993, § 6.4).

Table 1 reports the results from 2000 replications. The proposed bootstrap performed well overall, more so with a larger subcohort; the performance for β₁ and β₂ was largely comparable to that of the asymptotics-based inference procedures. The standard errors all tracked the standard deviations closely. The Wald-type and percentile confidence intervals had coverage probabilities reasonably close to the nominal level, but the latter slightly outperformed the former for α₁ and α₂. The confidence bands for S₀(·) also had good coverage probabilities. In comparison, the bootstrap of Wacholder et al. was less satisfactory except for β₁ and β₂ in the circumstance of 90% censoring. At 50% censoring, the second method of Chen & Lo was noticeably more efficient than their first method for β₁ estimation. However, the bootstrap of Wacholder et al. showed little difference in the standard errors. In addition, the confidence intervals for α₁ and α₂ often under-covered whereas the confidence bands for S₀(·) tended to over-cover.

Table 1.

Case-cohort simulations to compare the proposed bootstrap (Prop.) with asymptotics-based inference (Asymp.) and the bootstrap of Wacholder et al. (WGPB)

	Self & Prentice					Chen & Lo: 1st					Chen & Lo: 2nd
	β1	β2	α1	α2	S0	β1	β2	α1	α2	S0	β1	β2	α1	α2	S0
censoring rate: 90%, subcohort size: 200
B	29	31	−43	−29		22	29	−40	−26		19	27	−40	−25
SD	353	279	208	207		339	269	205	203		332	268	204	201
SE, Asymp.	350	266				338	257				334	256
WC, Asymp.	94.7	94.1				94.7	94.0				94.8	94.2
SE, WGPB	366	282	192	185		347	266	185	176		346	266	184	176
WC, WGPB	95.9	96.0	93.4	92.1		95.3	95.0	92.5	91.2		95.7	95.1	92.5	91.6
PC, WGPB	94.9	94.8	90.2	89.8	99.5	94.0	94.2	89.7	89.1	99.6	94.7	94.2	90.0	89.0	99.5
SE, Prop.	365	277	219	215		345	261	212	207		338	258	210	205
WC, Prop.	95.8	95.8	97.0	96.8		95.1	95.0	96.0	96.0		95.3	94.5	95.9	96.0
PC, Prop.	94.1	93.7	94.6	94.5	96.3	94.4	93.7	94.4	94.2	95.8	94.7	93.6	94.4	94.3	96.3
censoring rate: 90%, subcohort size: 100
B	73	60	−50	−41		52	46	−42	−32		53	47	−42	−33
SD	457	361	233	236		420	328	221	222		409	327	220	219
SE, Asymp.	436	344				403	319				390	313
WC, Asymp.	93.8	94.2				93.7	92.9				93.8	93.6
SE, WGPB	509	410	259	255		417	338	208	202		415	337	208	201
WC, WGPB	96.9	97.8	96.0	95.2		94.4	95.3	93.8	92.5		94.5	95.3	93.7	93.1
PC, WGPB	94.5	95.1	92.0	92.0	99.7	93.2	93.8	91.0	90.3	99.5	93.6	93.7	90.5	90.7	99.7
SE, Prop.	464	364	252	252		413	325	230	229		397	318	228	224
WC, Prop.	96.4	97.2	97.2	97.2		94.8	95.0	95.7	96.5		93.7	93.8	95.6	96.3
PC, Prop.	93.2	93.3	93.7	94.5	96.1	93.2	93.5	94.0	94.0	95.8	93.1	93.2	94.2	94.5	95.7
censoring rate: 50%, subcohort size: 200
B	33	28	−4	13		0	7	−1	8		−1	6	−1	7
SD	224	205	90	125		151	137	77	104		128	134	76	100
SE, Asymp.	216	193				149	129				127	126
WC, Asymp.	94.2	93.9				94.8	93.8				94.8	92.8
SE, WGPB	206	199	79	115		122	126	65	87		122	125	65	88
WC, WGPB	92.8	94.4	91.9	93.0		87.9	92.8	90.3	89.7		93.5	92.8	90.8	91.2
PC, WGPB	98.9	98.8	95.2	95.8	99.7	87.9	92.8	90.2	88.8	99.4	93.5	93.3	90.5	90.5	99.2
SE, Prop.	219	195	89	126		148	127	76	101		126	123	75	96
WC, Prop.	95.0	94.0	95.2	95.8		94.5	93.5	94.7	94.5		94.2	92.1	94.5	94.7
PC, Prop.	93.2	92.5	94.5	93.8	96.8	94.8	93.2	94.7	94.3	94.6	94.2	92.1	94.5	94.0	94.7

B: Empirical bias (×1000); SD: Empirical standard deviation (×1000); SE: Average standard error (×1000); WC: Empirical coverage (%) of 95% Wald-type confidence interval; PC: Empirical coverage (%) of 95% percentile confidence interval or confidence band.

Empty cells indicate either unavailable or inapplicable results.

Typical case-cohort studies involve infrequent disease endpoints, and have a fairly large full cohort and a moderate-sized subcohort, say, in thousands and hundreds, respectively. The preceding simulations and our other numerical experience suggest that the proposed bootstrap is generally reliable in such circumstances. Furthermore, the bootstrap also performs well with more frequent disease endpoints.

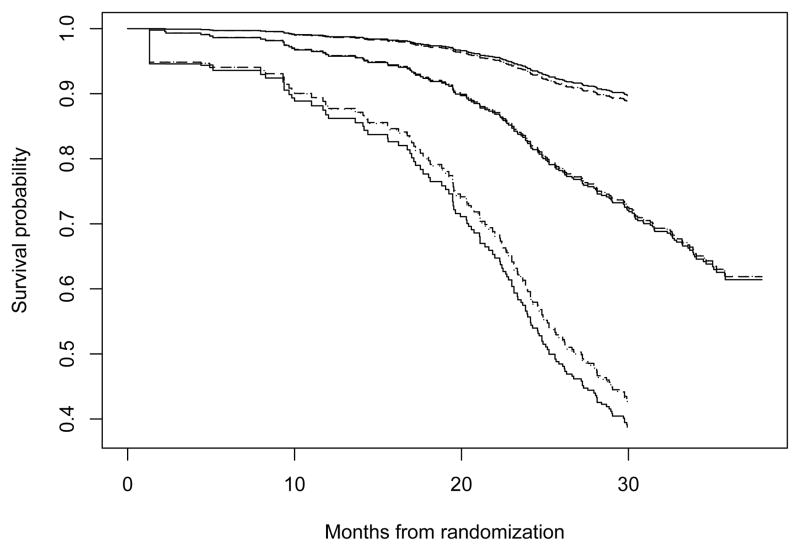
As an illustration, we analyzed data from the ACTG 175 trial conducted by the AIDS Clinical Trials Group (Hammer et al., 1996). The study evaluated four treatments, zidovudine, zidovudine plus didanosine, zidovudine plus zalcitabine, and didanosine, in HIV-1 infected adults whose screening CD4 counts were between 200 and 500 per cubic millimeter. A total of 2467 participants were randomized, and the mean follow-up was 29 months with 154 deaths observed. We considered a survival model with two continuous covariates, age and log(CD4), and five binary ones, treatment indicators, hemophilia, and presence of symptomatic HIV infection. All these baseline covariates were measured in the dataset, and the full cohort was sampled to emulate the case-cohort design. We began with fitting the proportional hazards model to the full cohort, and subsequently drew 100 subcohorts of size 240 and averaged the case-cohort point estimates and standard errors. The results are summarized in Table 2, where the bootstrap size of 1000 was used. The case-cohort estimates were, on average, all close to those from the full-cohort analysis, but more variable. The two methods of Chen & Lo had estimates comparable to each other and more efficient than those of Self & Prentice. Consistent with the earlier simulation results, the standard errors from our bootstrap were very similar to the asymptotics-based ones for all three case-cohort methods. We also estimated the survival function for an individual with given covariates and constructed a 95% confidence band by the proposed bootstrap, using the same approach as in the earlier simulations for the baseline survival function. Figure 1 shows the averaged survival functions and averaged confidence bands over the 100 simulated subcohorts, for the three case-cohort methods. The confidence bands for the two Chen & Lo methods were barely distinguishable, and tighter than that for Self & Prentice.

Table 2.

Analysis results of the ACTG 175 study

	ZDV+ddI	ZDV+ddC	ddI	age	hemophilia	symptom	log(CD4)
	Full cohort analysis
estimate	−0.627	−0.391	−0.685	0.039	0.586	0.788	−1.673
SE, Asymp.	0.226	0.209	0.230	0.009	0.273	0.175	0.248
	Case-cohort analyses
Self & Prentice	−0.699	−0.404	−0.758	0.044	0.740	0.828	−1.841
SE, Asymp.	0.361	0.359	0.361	0.015	0.517	0.310	0.436
SE, Prop.	0.374	0.362	0.377	0.017	0.497	0.320	0.473
Chen & Lo: 1st	−0.692	−0.419	−0.751	0.042	0.678	0.810	−1.811
SE, Asymp.	0.343	0.329	0.345	0.014	0.416	0.279	0.402
SE, Prop.	0.348	0.330	0.350	0.014	0.420	0.285	0.421
Chen & Lo: 2nd	−0.693	−0.419	−0.752	0.043	0.682	0.811	−1.813
SE, Asymp.	0.338	0.324	0.339	0.013	0.409	0.274	0.395
SE, Prop.	0.348	0.330	0.351	0.014	0.416	0.285	0.421

ZDV: zidovudine, ddI: didanosine, ddC: zalcitabine, symptom: presence of symptomatic HIV infection.

SE: standard error. Asympt.: asymptotics-based, Prop.: based on the proposed bootstrap.

Case-cohort estimates and standard errors are averages over 100 simulated subcohorts.

Fig. 1.

Estimated survival functions and 95% confidence bands over [0, 30] months, as averages over 100 simulated subcohorts, for a 35-year-old individual in the zidovudine arm with symptomatic HIV infection, hemophilia, and baseline CD4 count of 200. The solid, dotted, and dashed lines correspond to the Self & Prentice, the first of Chen & Lo, and the second of Chen & Lo methods, respectively.

5. Discussion

Despite using simple random sampling without replacement in the second stage, the case-cohort design gives rise to an independent data structure. This result facilitates statistical developments using standard tools such as empirical process theory. In the literature, Bernoulli sampling has been suggested in place of simple random sampling, partly to have an independent and identically distributed sample so as to exploit standard theory (e.g., Kulich & Lin, 2000, 2004; Nan et al., 2006). It is now clear that this alteration may be unnecessary for the purpose.

The three procedures in § 2 are among a large collection of case-cohort estimation methods for the proportional hazards model. Often, one method does not dominate another in both feasibility and efficiency. For example, the first method of Chen & Lo is more efficient than Self & Prentice when estimating the regression coefficients. However, with time-dependent covariates, the former requires each case outside the subcohort to have its whole covariate history available. In contrast, the latter only needs the covariate at the failure time, which is more realistic particularly with prospective sampling. Another reason for the co-existence of many methods is to accommodate sampling variations, e.g., stratified sampling (Borgan et al., 2000). A general and automatic tool for inference, such as the proposed bootstrap, is thus particularly attractive.

We have focused on the proportional hazards model because of its popularity. The proposed bootstrap should apply to other models with justifications similar to Theorem 1. Under the framework of our modularized proof as given, essentially it suffices to establish that a new estimator is a well-behaved and sufficiently smooth functional of empirical processes. This is clearly the case for the estimators of Kulich & Lin (2000) under the additive hazards model. However, those of Lu & Tsiatis (2006) under linear transformation models and Nan et al. (2006) and Kong & Cai (2009) under the accelerated failure time model may challenge the proof. With the former, an explicit profile estimating function for the finite-dimensional parameter may not exist. In the accelerated failure time model case, the estimating functions are not smooth. Nevertheless, existing techniques may be adopted or adapted to address these complications.

Appendix

Proofs of Proposition 2 and Theorem 1

We impose the following fairly standard regularity conditions:

Condition A1

The upper support point τ of X is finite. Further, pr(T > τ) > 0 and pr(C = τ) > 0.

Condition A2

The covariate Z is bounded.

Condition A3

The matrix

$$D={\int }_0^{\tau }\left(\frac{E\{Y(s)Z^{\otimes 2}{e}^{{\beta }_0^{\mathrm{T}}Z}\}}{E\{Y(s)e^{{\beta }_0^{\mathrm{T}}Z}\}}-{\left[\frac{E\{Y(s)Z{e}^{{\beta }_0^{\mathrm{T}}Z}\}}{E\{Y(s)e^{{\beta }_0^{\mathrm{T}}Z}\}}\right]}^{\otimes 2}\right)dE\{N(s)\}$$

is nonsingular, where υ^⊗2 ≡ υυ^T for vector υ.

Condition A1 is adopted to avoid lengthy technical tail treatment.

By Proposition 1, the distribution of {β̂_k, Λ̂_k (·, β̂_k), ${\widehat{\beta }}_k^{\ast },{\widehat{\mathrm{\Lambda }}}_k^{\ast }(·,{\widehat{\beta }}_k^{\ast })$} is the same under either case-cohort or single-stage parallel sampling, for any k = 1, 2, 3. Thus, it suffices to prove Proposition 2 and Theorem 1 under the latter sampling scheme, as we do below. We only present the proofs for the case of k = 2, the first method of Chen & Lo (1999). Those for the other two methods are similar and thus omitted.

Proof of Proposition 2

We express Ψ₂(β) and Λ̂₂(t; β) as functionals of empirical processes, and exploit empirical process theory. Such an approach was taken by Huang & Wang (2000) and Kosorok (2008, § 4.2.1) under cohort sampling, and becomes feasible and effective for the case-cohort design under its equivalent single-stage parallel sampling scheme. The empirical processes are defined for either the sub-cohort 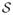or its complement 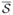. Specifically, the four processes in Ψ₂(β) and Λ̂₂(t; β) as given by (2) can be written as

$$\begin{array}{l}A(t)=\frac{m}{n}\frac{1}{m}\sum _{i\in \mathcal{S}}{N}_i(t)+\left(1-\frac{m}{n}\right)\frac{1}{n-m}\sum _{i\in \overline{\mathcal{S}}}{N}_i(t),\\ B(t)=\frac{m}{n}\frac{1}{m}\sum _{i\in \mathcal{S}}{Z}_i{N}_i(t)+\left(1-\frac{m}{n}\right)\frac{1}{n-m}\sum _{i\in \overline{\mathcal{S}}}{Z}_i{N}_i(t),\\ U_2(t,\beta )=\left(\frac{1}{m}\sum _{i\in \mathcal{S}}{\mathrm{\Delta }}_i\right)\frac{\frac{m}{n}\frac{1}{m}{\sum }_{i\in \mathcal{S}}{\mathrm{\Delta }}_i{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i}+(1-\frac{m}{n})\frac{1}{n-m}{\sum }_{i\in \overline{\mathcal{S}}}{\mathrm{\Delta }}_i{Y}_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i}}{\frac{m}{n}\frac{1}{m}{\sum }_{i\in \mathcal{S}}{\mathrm{\Delta }}_i+(1-\frac{m}{n})\frac{1}{n-m}{\sum }_{i\in \overline{\mathcal{S}}}{\mathrm{\Delta }}_i}+\frac{1}{m}\sum _{i\in \mathcal{S}}(1-{\mathrm{\Delta }}_i)Y_i(t)e^{{\beta }^{\mathrm{T}}{Z}_i},\\ V_2(t,\beta )=\left(\frac{1}{m}\sum _{i\in \mathcal{S}}{\mathrm{\Delta }}_i\right)\frac{\frac{m}{n}\frac{1}{m}{\sum }_{i\in \mathcal{S}}{\mathrm{\Delta }}_i{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}+(1-\frac{m}{n})\frac{1}{n-m}{\sum }_{i\in \overline{\mathcal{S}}}{\mathrm{\Delta }}_i{Y}_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}}{\frac{m}{n}\frac{1}{m}{\sum }_{i\in \mathcal{S}}{\mathrm{\Delta }}_i+(1-\frac{m}{n})\frac{1}{n-m}{\sum }_{i\in \overline{\mathcal{S}}}{\mathrm{\Delta }}_i}+\frac{1}{m}\sum _{i\in \mathcal{S}}(1-{\mathrm{\Delta }}_i)Y_i(t)Z_i{e}^{{\beta }^{\mathrm{T}}{Z}_i}.\end{array}$$

Condition A1 effectively limits the time scale to finite interval [0, τ]. Let 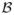be an arbitrary compact neighborhood of β₀. Under Condition A2, the classes of functions associated with these empirical processes, {N(t) : t ∈ [0, τ]}, {ZN(t) : t ∈ [0, τ]}, {Δ}, {ΔY(t)e^βTZ : t ∈ [0, τ], β ∈ 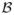}, {(1 − Δ)Y(t)e^βTZ : t ∈ [0, τ], β ∈ 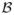}, {ΔY(t)Ze^βTZ : t ∈ [0, τ], β ∈ 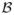}, and {(1 − Δ)Y(t)Ze^βTZ : t ∈ [0, τ], β ∈ 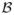}, are all Donsker; see, e.g., Kosorok (2008, § 4.2.1).

Since Donsker implies Glivenko–Cantelli, the empirical processes in A(t), B(t), U₂(t, β), and V₂(t, β), converge in probability to their respective limits, uniformly in t ∈ [0, τ] and β ∈ 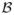if applicable. By Condition A1, the limit of U₂(t, β) is bounded away from 0 for t ∈ [0, τ] and β ∈ 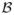. One can then show that uniformly Ψ₂(β) converges in probability to the left-hand side of (3), which is a monotone function and admits a unique solution β₀ by Condition A3. Therefore, β̂₂ converges in probability to β₀. The same technique can be used to prove the uniform convergence of Λ̂₂(t; β). This, coupled with the consistency of β̂₂, establishes that Λ̂₂(t; β̂₂) converges in probability to Λ₀(t) uniformly in t ∈ [0, τ].

By Taylor expansion,

$$0={\mathrm{\Psi }}_2({\widehat{\beta }}_2)={\mathrm{\Psi }}_2({\beta }_0)+{\mathrm{\Psi }}_2^{\prime }({\beta }_0)({\widehat{\beta }}_2-{\beta }_0)+o_p({\widehat{\beta }}_2-{\beta }_0)$$

since ${\mathrm{\Psi }}_2^{″}(\beta )$ is bounded by Condition A2. Using similar techniques as before, one can show that ${\mathrm{\Psi }}_2^{\prime }({\beta }_0)$ converges in probability to −D, which is nonsingular by Condition A3. Therefore,

$${\widehat{\beta }}_2-{\beta }_0=D^{-1}{\mathrm{\Psi }}_2({\beta }_0)\{1+o_p(1)\}.$$

Similarly,

$$\begin{array}{l}{\widehat{\mathrm{\Lambda }}}_2(t;{\widehat{\beta }}_2)-{\mathrm{\Lambda }}_0(t)={\widehat{\mathrm{\Lambda }}}_2(t;{\beta }_0)-{\mathrm{\Lambda }}_0(t)+J(t)({\widehat{\beta }}_2-{\beta }_0)+o_p({\widehat{\beta }}_2-{\beta }_0)\\ ={\widehat{\mathrm{\Lambda }}}_2(t;{\beta }_0)-{\mathrm{\Lambda }}_0(t)+J(t)D^{-1}{\mathrm{\Psi }}_2({\beta }_0)\{1+o_p(1)\},\end{array}$$

where J(t) is the limit of ∂Λ̂₂(t; β)/∂β|_β=β0. Thus, asymptotically {β̂₂ − β₀, Λ̂₂(t; β̂₂) − Λ₀(t)} is a linear function of {Ψ₂(β₀), Λ̂₂(t; β₀) − Λ₀(t)}.

Given the asymptotic linearity, it remains to establish the asymptotic normality of {Ψ₂(β₀), Λ̂₂(·; β₀) − Λ₀(·)}. Observe that A(·), B(·), U₂(·, β₀), and V₂(·, β₀) are asymptotically equivalent when the term m/n in these expressions is replaced by its limit ρ. For example,

$$A(t)=\rho \frac{1}{m}\sum _{i\in \mathcal{S}}{N}_i(t)+(1-\rho )\frac{1}{n-m}\sum _{i\in \overline{\mathcal{S}}}{N}_i(t)+\left(\frac{m}{n}-\rho \right)\left\{\frac{1}{m}\sum _{i\in \mathcal{S}}{N}_i(t)-\frac{1}{n-m}\sum _{i\in \overline{\mathcal{S}}}{N}_i(t)\right\},$$

where the last term is o_p(n^−1/2). The asymptotic normality of {A(·), B(·), U₂(·, β₀), V₂(·, β₀)} then follows from the properties of Donsker classes and the functional delta method. Using Gill (1989, Lemma 3) and the chain rule, one can show that Ψ₂(β₀) and Λ̂₂(·; β₀) are compactly differentiable functionals of {A(·), B(·), U₂(·, β₀), V₂(·, β₀)}. Finally, the functional delta method leads to the asymptotic normality of {Ψ₂(β₀), Λ̂₂(·; β₀) − Λ₀(·)}.

Proof of Theorem 1

In parallel with A(t), B(t), U₂(t, β₀), and V₂(t, β₀), their counterparts A*(t), B*(t), $U_2^{\ast }(t,{\beta }_0)$, and $V_2^{\ast }(t,{\beta }_0)$ in (4) involve bootstrapped empirical processes and bootstrapped subcohort fraction m*/n*. By Kosorok (2008, Corollary 10.14), these bootstrapped empirical processes converge in probability to their respective limits, uniformly in t ∈ [0, τ] and β ∈ 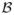if applicable. By the law of large numbers and the continuous mapping theorem, m*/n* converges in probability to ρ. Then, the same argument as in the consistency proof of Proposition 2 establishes the consistency of ${\widehat{\beta }}_2^{\ast }$ for β₀ and ${\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\widehat{\beta }}_2^{\ast })$ for Λ₀(t) uniformly in t ∈ [0, τ].

Similar to the proof of Proposition 2, we further obtain

$$\begin{array}{l}{\widehat{\beta }}_2^{\ast }-{\beta }_0=D^{-1}{\mathrm{\Psi }}_2^{\ast }({\beta }_0)\{1+o_p(1)\},\\ {\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\widehat{\beta }}_2^{\ast })-{\mathrm{\Lambda }}_0(t)={\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\beta }_0)-{\mathrm{\Lambda }}_0(t)+J(t)D^{-1}{\mathrm{\Psi }}_2^{\ast }({\beta }_0)\{1+o_p(1)\}.\end{array}$$

By Kosorok (2008, Theorem 2.6), the bootstrapped empirical processes in A*(t), B*(t), $U_2^{\ast }(t,{\beta }_0)$, and $V_2^{\ast }(t,{\beta }_0)$ minus their expectations are all O_p(n^−1/2). So is ${\mathrm{\Psi }}_2^{\ast }({\beta }_0)$. Then, coupled with the asymptotic linearity result on β̂₂ and Λ̂₂(t; β̂₂), we obtain

$$\begin{array}{l}{\widehat{\beta }}_2^{\ast }-{\widehat{\beta }}_2=D^{-1}\{{\mathrm{\Psi }}_2^{\ast }({\beta }_0)-{\mathrm{\Psi }}_2({\beta }_0)\}+o_p(n^{-1/2}),\\ {\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\widehat{\beta }}_2^{\ast })-{\widehat{\mathrm{\Lambda }}}_2(t;{\widehat{\beta }}_2)={\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\beta }_0)-{\widehat{\mathrm{\Lambda }}}_2(t;{\beta }_0)+J(t)D^{-1}\{{\mathrm{\Psi }}_2^{\ast }({\beta }_0)-{\mathrm{\Psi }}_2({\beta }_0)\}+o_p(n^{-1/2}).\end{array}$$

Thus, asymptotically { ${\widehat{\beta }}_2^{\ast }-{\widehat{\beta }}_2,{\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\widehat{\beta }}_2^{\ast })-{\widehat{\mathrm{\Lambda }}}_2(t;{\widehat{\beta }}_2)$} is the same linear function in terms of { ${\mathrm{\Psi }}_2^{\ast }({\beta }_0)-{\mathrm{\Psi }}_2({\beta }_0),{\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\beta }_0)-{\widehat{\mathrm{\Lambda }}}_2(t;{\beta }_0)$}, as {β̂₂ − β₀, Λ̂₂(t; β̂₂) − Λ₀(t)} in terms of {Ψ₂(β₀), Λ̂₂(t; β₀) − Λ₀(t)}.

It remains to show that $n^{1/2}\{{\mathrm{\Psi }}_2^{\ast }({\beta }_0)-{\mathrm{\Psi }}_2({\beta }_0),{\widehat{\mathrm{\Lambda }}}_2^{\ast }(t;{\beta }_0)-{\widehat{\mathrm{\Lambda }}}_2(t;{\beta }_0)\}$, conditionally on the data, has the same asymptotic distribution as n^1/2{Ψ₂(β₀), Λ̂₂(t; β₀) − Λ₀(t)}. This can be obtained by using a conditional multiplier central limit theorem (Kosorok, 2008, Theorem 2.6) along with the functional delta method and chain rule, as argued in the asymptotic normality proof of Proposition 2.