The perceptual effects of learning object categories that predict perceptual goals

Abstract

In classic category learning studies, subjects typically learn to assign items to one of two categories, with no further distinction between how items on each side of the category boundary should be treated. In real life, however, we often learn categories that dictate further processing goals, for instance with objects in only one category requiring further individuation. Using methods from category learning and perceptual expertise, we studied the perceptual consequences of experience with objects in tasks that rely on attention to different dimensions in different parts of the space. In two experiments, subjects first learned to categorize complex objects from a single morphspace into two categories based on one morph dimension, and then learned to perform a different task, either naming or a local feature judgment, for each of the two categories. A same-different discrimination test before and after each training measured sensitivity to feature dimensions of the space. After initial categorization, sensitivity increased along the category-diagnostic dimension. After task association, sensitivity increased more for the category that was named, especially along the non-diagnostic dimension. The results demonstrate that local attentional weights, associated with individual exemplars as a function of task requirements, can have lasting effects on perceptual representations.

The visual world is complex, with objects comprised of many visual features that we can selectively attend to, depending on current goals. The mushroom enthusiast on a walk in the woods might choose to disregard anything that does not fall in the mushroom category, temporarily attending to perceptual information found in mushrooms and not other categories. As she develops expertise, she would probably want to learn to identify individual species, a feat that would be supported by a host of changes in perceptual strategies and of neural responses in visual areas when looking at mushrooms. She may also learn to distinguish edible from non-edible mushrooms, which would be greatly facilitated if a perceptual dimension existed that predicted edibility. But if she learns more about cooking with wild mushrooms, she may also learn about other dimensions that may speak to the freshness of the mushroom, dimensions that may not be relevant to identify species or categorize them as edible or not, but that would only be relevant for edible mushrooms. Our goals with objects, often multifaceted, influence how we perceive them.

Psychologists have long been interested in the interplay between categorization and perception and how they support these sorts of complex behaviors. Studies that investigate the behavioral and neural mechanisms of these experience-driven abilities come from two broad literatures (Palmeri & Gauthier, 2004). On the one hand, work in the field of categorization has led to models that make simplifying assumptions about object representations but offer detailed accounts of the mechanisms used to make decisions about objects (e.g., Nosofsky, 1986; Ashby, 1992). Many experiments in category learning are relatively short, on the order of one experimental session, which is sufficient to show how observers attend to different stimulus dimensions depending on the categorization task they are engaged in. On the other hand, research in the field of object recognition, including the area of perceptual expertise, places less emphasis on decisions: instead, models have focused on describing the format of object representations (e.g., Biederman, 1987; Edelman, 1997; Riesenhuber & Poggio, 1999). While brief learning studies with novel objects have been conducted, for instance to test sensitivity of the representations to various manipulations (e.g., viewpoint, Bülthoff, Edelman, & Tarr, 1995; Tarr, Williams, Hayward, & Gauthier, 1998), more extensive training studies have also investigated more permanent changes that occur with the acquisition of expertise in a domain (e.g., Gauthier, Tarr, Anderson, Skudlarski, & Gore, 1999; Wong, Palmeri, & Gauthier, 2009a; Wong, Palmeri, Rogers, Gore, & Gauthier, 2009b).

Over the last twenty years, research in these two fields has contributed to our understanding of how experience with objects affects our long-term perception of them. A general trend is for phenomena to first be investigated during training itself, with subsequent studies asking whether mechanisms that are engaged by task demands have long-term effects for perception. The present study extends this research tradition to expand our understanding of how learning to categorize and identify objects influences our perception. To place our work in context, we highlight how some phenomena originally obtained during category learning were later shown to have long-term effects outside of category learning. We then proceed to discuss one effect that has been obtained during category learning, and why we believe studying its long-term influence on perception may be important.

Exemplar models of categorization include mechanisms for changing representations according to the demands of the current tasks. Assuming that objects are points in a multidimensional space defined by different visual feature dimensions, learning to categorize an object exaggerates the importance of particular features that are diagnostic of category membership, while minimizing the importance of other features that are not diagnostic for category learning (Kruschke, 1992; Nosofsky, 1986; Nosofsky & Palmeri, 1997). For instance, if objects that vary in size and color are categorized into large vs. small objects, then size is diagnostic of category membership while color is not. During categorization, the similarity of objects along the diagnostic dimension is typically found to decrease, while it may increase or at least be unaffected for the non-diagnostic dimension. These changes are implemented as shifts in the attentional weights assigned to different dimensions (Nosofsky, 1986). While such a mechanism was originally conceived of as operating online to account for current task demands, later work demonstrated that attentional “stretching” of a dimension that is diagnostic during categorization can have lasting effects for perception outside of categorization judgments. Goldstone (1994) elegantly demonstrated that after categorizing greyscale squares according to their size (or alternatively, their brightness), perceptual discrimination judgments for pairs of these squares (when categorization was now entirely irrelevant) were facilitated for the dimension that was diagnostic during earlier categorization. While perceptual learning typically follows practice discriminating along the relevant discrimination (Fine & Jacobs, 2002), in this case perceptual improvements follow attention shifts to a dimension that was useful in the previous categorization task. This phenomenon was termed acquired distinctiveness.

Building on these early results, later work considerably extended the reach of the idea that learning to categorize depends on selective attention to relevant dimensions by showing that it also applied to more complex stimuli and especially, more complex dimensions. Goldstone and Steyvers (2001) created a space of faces using two randomly selected pairs of bald men and morphing each pair to create an arbitrary dimension. These two dimensions were then combined in an orthogonal fashion to create a matrix of faces that can be categorized along one or the other axis. The experiments demonstrated that subjects could learn to categorize along these novel dimensions, suggesting that selective attention did not require existing knowledge of dimensions, nor dimensions to be particularly simple or verbalizable, to operate during category learning. Subsequent work using morphspaces of cars extended these findings by showing that stretching of complex morphspaces during category learning causes perceptual stretching during a discrimination task (Folstein, Gauthier, & Palmeri, 2012a; Folstein, Palmeri, & Gauthier, 2012b), and in one case the influence on perception was observed for several days after category learning (Folstein, Newton, Van Gulick, & Palmeri, 2012c).

These demonstrations that selective attention during category learning can have effects outside of categorization, for a relatively long time after the categorization experience, increase the relevance of these effects for understanding how long-term object representations are created. Another line of research addressing how experience influences object representations includes studies that manipulate not the dimension along which subjects categorize objects, but the task that they perform (Nishimura & Maurer, 2008; Scott, Tanaka, Sheinberg, & Curran, 2006; Tanaka, Curran, & Sheinberg, 2005; Wong et al., 2009a; Wong et al., 2009b; Wong, Folstein, & Gauthier, 2011; 2012). These studies have generally used between-subjects comparisons to study the effect of associating different tasks with the same objects. The results have suggested that qualitative aspects of perception (as well as of neural representations) are not fully determined by the visual appearance of the objects. For instance, Wong and colleagues (Wong et al., 2009a; 2009b) used a between-subjects design to study the effects of learning novel visual objects called Ziggerins in two different ways. One group learned to individuate Ziggerins, labeling each one with a unique name, while another group learned to categorize Ziggerins into one of six basic-level families that differed in their part structure. Those who learned to individuate Ziggerins improved at subordinate-level categorization and showed increased holistic processing, which is a hallmark of face processing and expertise (Richler, Palmeri & Gauthier, 2012; Bukach, Phillips, & Gauthier, 2010), while those who learned to categorize Ziggerins at the basic-level only improved at basic-level categorization and showed no holistic processing (these effects were accompanied by differential changes in the visual system, Wong et al., 2009b). These considerations raise the question of whether categorization and task associations are sufficient to explain the sort of specialization we might see in the visual system for various object categories. Do the representations in different domains of objects such as faces (Kanwisher, McDermott, & Chun, 1997), scenes (Epstein & Kanwisher, 1998), tools (Mahon, Schwarzbach, & Caramazza, 2010), letters (James, James, Jobard, Wong, & Gauthier, 2005), numbers (Shum et al., 2013), and musical notation (Wong & Gauthier, 2010) get differentiated due to associations between these categories and the tasks we generally perform with them? Whereas animals and tools are very dissimilar, there are domains like letters, numbers, and musical notation that contain exemplars that are much less distinctive across categories. For instance, letters and numbers are perceived as more similar to one another by Canadian mail sorters who see them co-occurring more frequently (Polk & Farah, 1995). Thus, it is possible to think of a single space (alphanumeric characters) that could be divided by a category boundary (into letters and numbers), and each category could then be associated with different tasks.

In the current work, we wanted to create a paradigm that would allow us to begin to study the long-term perceptual effects when subjects learn to process objects that are visually similar in different ways. In the category learning studies we reviewed above, dimensional modulation was the same on both sides of the category boundary, as would be expected since the categories were not dissociated in any other way then having received different labels. In other words, after categorizing according to brightness, discrimination of squares that differ in brightness is facilitated, but there is no sense in which bright and dark squares are treated qualitatively differently. In such situations, and the models designed to explain them, changes in attentional weights apply to an entire dimension and equally on both sides of the category boundary (Kruschke, 1992; Love, Medin, & Gureckis, 2004; Nosofsky, 1986). But there is another line of work which argues that categorization may sometimes require attentional weights that are associated with specific exemplars rather than with entire dimensions, affording learning of more complex categories with exception items, and providing more flexibility to adapt to context (Aha & Goldstone, 1992; Blair, Watson, Walshe, & Maj, 2009; Sakamoto, Matsuka, & Love, 2004; Yang & Lewandowsky, 2004). As we described above, the mushroom enthusiast may pay attention to some aspects of the mushrooms that are diagnostic for freshness, but only if the mushroom is edible (because freshness is not relevant to non-edible mushrooms). Aha & Goldstone (1992) created a stimulus space in which different dimensions were relevant for categorization in different parts of the space. Categorization of transfer exemplars in this space was used to demonstrate that different dimensions were stretched in different parts of the stimulus space. Several models of categorization can account for these sorts of contextual effects using stimulus-specific attentional weights (Aha & Goldstone, 1992; Kruschke, 2001; Love & Jones, 2006; Rodrigues & Murre, 2007).

Just as prior demonstrations of selective attention during category learning were extended by demonstrating that the effects have long-term influences on perception, we wish to study the long-term perceptual effects of a learning situation where subjects first learn to divide a space of objects according to a category boundary (as in other category learning tasks with complex and novel dimensions), and then learn to perform different tasks with objects on either side of the category boundary. This second aspect of our training protocol is essentially a within-subject version of between-subjects manipulations performed in several expertise studies (e.g., the Ziggerin work described above). It adds the interesting complication that objects that are visually quite similar are learned in the context of tasks that, in a between-subjects design, have been used to simulate what are often considered qualitatively different kinds of object recognition (i.e., processes that tend to be associated with face-like vs. non-face like processing).

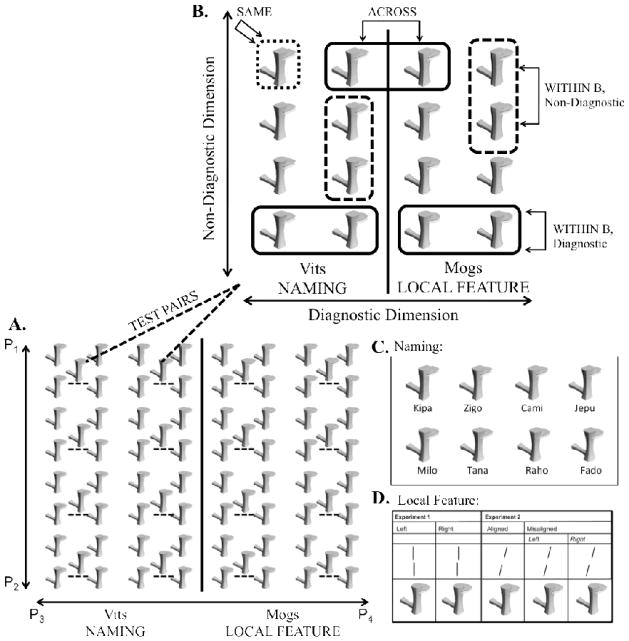
Experiments designed to look at contextual effects have investigated categorization performance itself during learning, without measuring its effects on a different discrimination task, in a task for which the learned categories are no longer relevant. Stimulus-specific attentional mechanisms may eventually help explain how objects that are highly similar (such as numbers, letters and, musical notations) can come to be processed in different ways, regardless of current task instructions. But for this mechanism to be able to account for such category specialization, we first need to test whether stimulus–specific weighing of different dimensions can have lasting implications for perception outside of categorization behavior. To do so, in a novel training paradigm, we taught subjects to perform different tasks on either side of a category boundary. On one side, the objects should be individuated, and on the other side they should be categorized on the basis of a binary local feature (See Figure 1). Following such task learning, we assessed perceptual discrimination of transfer objects positioned throughout the trained space, specifically comparing discrimination along the diagnostic and non-diagnostic dimensions.

Figure 1.

A. Morphspace of novel objects, Ziggerin-morphs, created from four parent Ziggerins (P₁–P₄, see Figure 2) along two morph lines. The morphspace can be divided into two categories, creating a diagnostic feature dimension and non-diagnostic dimension; category boundary and category-task assignment were counterbalanced between subjects. Ziggerin-morphs not underlined with a dotted line (8×8 set) were used for the training tasks. Ziggerin-morphs underlined with a dotted line (4×4 set) within the training set were used in the discrimination test. B. Ziggerin-morphs used for the discrimination task. Same and different pairs were used. Different pairs were within and across the category boundary and in both the diagnostic and non-diagnostic direction. C. Examples of the eight Ziggerin-morphs from the Vit category that were learned as individuals with unique names. D. The Vernier lines used as the local feature judgment task for the Mog category. In Experiment 1, lines were judged as top line left or right, and in Experiments 2 lines were judged as aligned or misaligned (regardless of whether misaligned left or right).

We should clarify at the outset that when we manipulate the task, we also manipulate the stimulus dimensions that are relevant. Schneider & Logan (in press) define a task as “a representation of the instructions required to achieve accurate performance of an activity”, which is, essentially, the subject’s perspective in an experiment like ours. As experimenters, we have knowledge of the stimulus manipulations and ideal strategy that subjects do not have. There are demonstrations in category learning of variation among individuals in the specific rules and exceptions they may store (e.g., Nosofsky et al., 1994), and other evidence that simply presenting response mappings as “tasks” can have important consequences over and above learning specific response mappings (Dreisbach, Goschke, & Haider, 2006, 2007; Dreisbach & Haider, 2008). In the present work we are not implying that the specifics of how the tasks are presented are critical - for instance, we using naming in the identification task, but there is recent work suggesting naming is not necessary for effects of identification (Bukach et al., 2012). However, to reflect the fact that what subjects experienced is learning to perform different tasks with objects in two similar categories, we refer to our manipulation as a task manipulation, but it would not be wrong to think of these tasks as essentially defined by the dimensions that are useful to carry them out.

To preview our analyses, we will seek evidence of three different phenomena. First, we will assess whether learning the primary category boundary that divides the space in two halves leads to acquired distinctiveness, operationalized as better discriminability for pairs of objects that vary along the dimension diagnostic for category learning (i.e., diagnostic pairs), relative to pairs of objects that vary along the non-diagnostic dimension (non-diagnostic pairs) (Goldstone, 1994). We expect to replicate this classical finding but it should be noted that there are only a handful of demonstrations of acquired distinctiveness with complex stimuli in a multidimensional space (Folstein et al, 2012a; 2012b; Goldstone & Steyvers, 2001; Gureckis & Goldstone, 2008; Livingston and Andrews, 2005)¹. However, as would be the case for similar results in prior studies with simple or complex dimensions, acquired distinctiveness could be attributed to attention being selectively directed toward the entire dimension. Therefore we considered two other effects that can speak to more local changes in similarity space.

In particular, in a second analysis, we will investigate whether changes in discriminability depend on the side of the space as a function of having learned different tasks on each side of the space. We expect more improvement in discriminability with training on the individuation side, especially for the “non-diagnostic” dimension, which is only relevant for individuation. These results could not be accounted for by stretching of global dimensions, because they would be local to one part of the space only. Thus, differential discriminability within this space as a function of task associations would suggest that stimulus-specific attentional weights (Aha & Goldstone, 1992; Kruschke, 2001; Love & Jones, 2006; Rodrigues & Murre, 2007) have long-lasting effects in perceptual discrimination.

Finally, we will also assess evidence of acquisition of categorical perception. Categorical perception is defined as better discriminability for objects in different categories relative to those within category, when physical distance is equal (Harnad, 1987). Practically speaking, categorical perception is a local stretching of the space for exemplars near a category boundary. Using category learning of brightness vs. size, Goldstone (1994) found evidence for increased discriminability across the category boundary (learned categorical perception) above and beyond evidence of stretching of the entire relevant dimension. Others have found evidence of learned categorical perception with simple shapes or more complex shapes that varied in local features, and with color patches (Livingston, Andrews, & Harnad, 1998; Özgen & Davies, 2002). However in prior work using category learning with complex objects morphed along different dimensions, no evidence for categorical perception was obtained (Freedman, Riesenhuber, Poggio, & Miller, 2003; Gillebert, Op de Beeck, Panis, & Wagemans, 2009; Jiang et al., 2007; Folstein et al., 2012a). Here, because we used morphed stimuli we expected no categorical perception after the initial category learning phase of our training, which resembles the procedure in these studies. However we asked whether learning different tasks on the two sides of the space might differentiate the categories further, such that categorical perception might emerge. On the other hand, to the extent that categorical perception depends on learned equivalence (or compression) of stimuli on each side of a category boundary (Livingston et al., 1998), teaching subjects to individuate objects on one side of the space in the second phase of our training paradigm may work against categorical perception.

Experiment 1

Subjects first learned to categorize objects into two categories, then learned a different task, individuation vs. local feature judgment, for each category. We measured discriminability along different dimensions of the shape space for pairs of objects within and across categories at three time points, before training, after category learning and after task association.

Methods

Subjects

Subjects were recruited from the Vanderbilt University and Nashville, TN community; they gave informed consent and received monetary compensation for their participation. The study was approved by the local IRB. Thirty-two subjects (12 male) aged 21–32 (mean = 24.84, SD = 3.47) completed all 10 sessions of the study. This sample size was chosen on the basis of a pilot study in which 24 subjects were trained for 5 sessions in a simpler version of the training paradigm used here (details and data available upon request). The interaction between day (Day 5 vs. Day 1) and task assignment (individuation task vs. local task as in Experiment 1) had an effect size of η_p²=.036. Since in Experiment 1 we increased training to 10 days and added an explicit category learning phase before the task association training, we assumed that the effect size would be at least 50% larger than in the pilot. Given this, our sample size of 32 will yield power of .9 to obtain an effect of this size at an alpha of .05. All subjects reported normal or corrected to normal visual acuity.

Stimuli and equipment

The experiment was conducted on Apple Mac Minis (OSX 10.6.5, 2Ghz Intel core 2 duo) using 20-inch CRT monitors (1,024×768 pixel screen resolution) with MATLAB R2009b (Mathworks, Natick, MA, USA) and the Psychtoolbox (http://psychtoolbox.org/; Brainard, 1997). Subjects were allowed to sit a comfortable distance from the monitor (approximately 40cm).

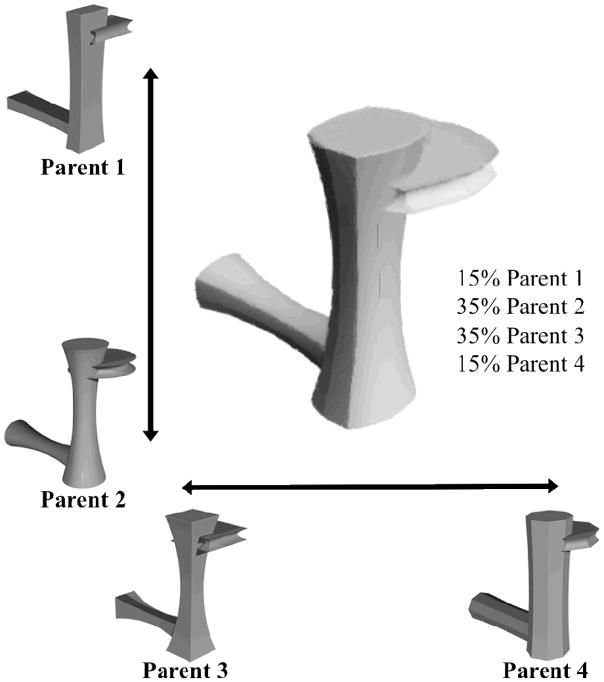
The stimuli were geometric, realistically-shaded novel objects, Ziggerin-morphs, created by morphing (using Norrkross MorphX software, Martin Wennerberg) 4 parent objects that shared a common configuration of parts, selected from a set used by Wong and colleagues (2009a) (Figure 2). Thus, objects varied within the morphspace along two dimensions, each defined by the changes in shape and shading along the morph line from one parent object to the other for each pair of parent objects. Objects were 148–150 pixels wide and 154–162 pixels in height and subtended approximately 6×6 degrees of visual angle. An 8×8 set of objects, evenly spaced in the morphspace, was used in training (Figure 1A). All 64 training objects were used for category learning. For task-association training, a subset of 16 objects on each side of the space was used. On the side of the space assigned to individuation for a given subject, 8 of the 16 objects were given individual names (Figure 1C), and the other 8 objects were used as “no-name” foils. On the side of the space assigned to the local feature judgment for a given subject, all 16 objects were used in the same manner in the local feature task (Figure 1D). A separate 4×4 set of 16 objects (Figure 1B), evenly interspersed among the training objects, was used for the discrimination tests.

Figure 2.

Four parent Ziggerins (P₁–P₄ in Figure 1A) used to create the Ziggerin-morphs. Changes between Parents 1 and 2 make up one dimension of the morphspace and changes between Parents 3 and 4 make up the other dimension. To create each Ziggerin-morph for the training and testing sets two intermediate morphs, one from each parent pair (e.g. 20% Parent 1, 80% Parent 2 and 40% Parent 3, 60% Parent 4), are morphed together to populate the space. Vernier lines are added after morphing. In the center is an example Ziggerin-morph from the training set with the local feature misaligned to the left.

Each Ziggerin-morph also had two lines on its main body (in the same location for all objects) that were used for the local feature task (Vernier discrimination judging in which direction two lines are misaligned). These were two black vertical lines that were each 1 pixel wide, 20 pixels long, and had opacity of 30%. The two lines were separated by 2 pixels from left to right, a small misalignment since this is a perceptual learning task, and by 14 pixels from the bottom of the top line to the top of the bottom line. Two versions of the local feature were created for each object in the space, top line left and top line right, which were used with equal frequency in all parts of the experiment, such that the local feature was not diagnostic of either category membership or individual object identity (Figure 1D).

Procedure

The experiment consisted of 10 sessions, with two sessions never more than 7 days apart (mean = 1.57, SD = 0.92) and sessions completed in a period of 12–21 days (mean = 15.34, SD = 2.90) – see Table 1. There were two between-subjects counterbalancing factors, the dimension assigned for the category boundary in the morphspace, and the category-task assignments to each side of the space, which resulted in four counterbalanced groups. All examples given here illustrate a vertical category boundary in which the left-hand category, Vits, was named and the right-hand category, Mogs, was associated with the local feature task (Figure 1A).

Table 1.

Tasks and number of trials for each session of Experiment 1.

Session	Task(s)	Number of trials
Day 1	Discrimination test 1	1,120
	Category learning	1,024
Day 2	Category learning	1,536
Day 3	Category learning	1,024
	Discrimination test 2	1,120
Day 4	Name learning part 1	840
	Local feature learning 1	960
Day 5	Name learning part 2	1,200
	Local feature learning 2	960
Day 6	Alternating blocks of naming and LF	1,080 Name/960 LF
Day 7	Mixed trials with task instruction	480
	Mixed trials with no task instruction	480
Day 8	Mixed trials with no task instruction	960
Day 9	Mixed trials with no task instruction	960
Day 10	Mixed trials with no task instruction	960
	Discrimination test 3	1,120

Discrimination test

The discrimination test was administered on Days 1 (before training), 3 (after category learning), and 10 (after task association). The objects and trials were identical in all sessions, although the trial order was randomized each time.

Each discrimination trial began with a 500msec fixation cross followed by the first object presented for 1000msec, a 500msec inter-stimulus interval blank screen, and then the second object, which remained on the screen until a response was made. The subject had to indicate if the two objects were the same (‘S’ key) or different (‘L’ key). The first object appeared in the center of the screen and the second object appeared in an offset location (10–30 pixels in one of 8 directions). Subjects were asked to respond as quickly as they could while still being accurate.

For each discrimination test, subjects completed 20 blocks of 56 unique trials. Sixteen trials in each block were same trials, using all 16 test objects (Figure 1B). The 40 different trials showed 40 distinct pairs of objects that varied in distance and direction in the object space. Twenty of these trials showed objects varying along the diagnostic dimension and 20 along the non-diagnostic dimension, with 12 critical trials for each dimension. For the diagnostic critical trials, the objects either fell within the same category (4 trials on each side) or crossed the category boundary (4 trials). For the non-diagnostic critical trials, all 12 pairs fell within a given category, 6 trials on each side.

Category learning

On Days 1– 3, subjects learned to categorize objects according to a boundary that divided the space in half (counterbalanced across subjects).

Each trial began with a 500msec fixation cross and then a single object was presented in the center of the screen until the subject indicated if the object was a Vit (‘V’ key) or a Mog (‘M’ key). Initially, they had to simply guess the object’s category. Subjects received feedback on all trials while the object was still on screen (e.g. “Correct. That is a Mog”). Each block consisted of 128 trials with each of the 64 training objects shown twice; 8 blocks on Days 1 and 3, and 12 blocks on Day 2.

Task association, name learning

Subjects learned to name 4 objects from the named category (e.g., Vits in our example) on Day 4 and 8 names on Day 5. The names were novel four-letter words (Zigo, Kipa, Cami, Jepu, Milo, Tana, Raho, Fado). The order in which objects were learned and object-name pairings were randomly chosen for each subject. Each time subjects learned new objects (introduced in groups of 2), each object was presented together with its name (e.g. “This is Raho”) 6 times. In naming blocks, each trial began with a 500msec fixation cross then a single object was shown on the screen until the subject made a response. Subjects responded with the first letter of the object’s name (e.g. ‘R’ key for Raho). Twenty-four foil objects that did not have names were also included (20% of trials) and subjects had to press the ‘N’ key for “No Name” on these trials. After incorrect trials, subjects received feedback with the object and its name shown.

Task association, local feature learning

On Days 4 and 5, after completing the name learning task, subjects learned to do the local feature task with objects from the other category (e.g., Mogs in our example). The local feature task was a simple Vernier line judgment, in which subjects had to judge if the top line was to the left or right of the bottom line (Figure 1D). Each trial began with a 500msec fixation cross then a single object was presented in the center of the screen until the subject made a response (‘Q’ key for top line left and ‘P’ key for top line right right). After incorrect trials, subjects received feedback with the object and the correct response shown. Half of the trials were top line right and half were top line left. On Days 4 and 5, subjects completed 10 blocks of 96 trials (16 local feature objects × 6).

Task association, alternating blocks

On Day 6, subjects completed 20 alternating blocks of naming and the local feature task. At the beginning of each block the task was presented for 1sec. Each trial began with a 500msec fixation cross and then a single object was presented in the center of the screen until the subject made a response (‘Q’ or ‘P’ in local feature blocks, letter corresponding to first letter of a name or ‘N’ in naming blocks). There were 10 naming blocks of 108 trials each (8 named objects × 12, plus 12 foil trials) and 10 local feature blocks of 96 trials each (16 local feature objects × 6). Feedback was given on incorrect trials.

Task association, mixed trials

The goal of the training is to encourage subjects to associate objects with different tasks, rather than with instructions. To promote such associations, on Days 7–10, subjects completed mixed trials that included objects from both categories randomly intermixed. Without explicit task instructions, subjects had to perform the category-appropriate task, naming or local feature, for each object. Each trial began with a 500msec fixation cross and then a single object appeared on the screen until the subject made a response (‘Q’ or ‘P’ for aligned or misaligned local feature or the first letter of the object’s name or ‘N’ for “no name”). “No Name” foil objects occurred on 20% of naming trials, or 10% of total trials. Subjects received feedback on incorrect trials. For example, if the object was a named object and was “Jepu” but the subject pressed ‘Q’ for “aligned” thinking it was a local feature object, the feedback would say, “That object is a Vit and is supposed to be named. That is Jepu.”

Eight objects were used from each side of the space, such that the objects associated with each task were from mirrored locations. On Days 7–10 subjects completed 10 blocks of 96 trials (48 trials per task, 8 objects × 6). The words “naming” or “local feature” were included on each trial for the first 5 blocks on Day 7 to help subjects learn the task.

Results

Due to computer problems, data from a few category learning sessions were lost (~4.24% of the all category learning trials for 5/32 subjects): critically, although data were not saved, subjects completed these trials. In addition, one subject experienced only 8 out of 20 blocks in the Day 1 discrimination test. Analyses were conducted including all available data for all subjects to preserve counterbalancing of the design.

Training results

Subjects successfully learned to categorize objects, name them, perform the local feature task, and later to perform the category-appropriate task for an object (See supplemental materials for detailed analyses of the training results; Table S1).

Discrimination test results

Mean discriminability (d′; Green & Swets, 1966) was calculated for pairs within the space on the object discrimination tests on Day 1 (before any training), Day 3 (after category learning), and Day 10 (after category-task association training) (Figure 3). Trials with extreme reaction times (less than 100msec or greater than 5000msec) were removed from the analysis (.4% of the trials). We also searched for extreme values in mean d′ by subject for each session defined as individual session d′ scores that were more than the 25^th or 75^th percentile plus 3 times the 75-25 percentile range. These criteria identified 3 extreme values, which were winsorized (Wilcox, 2005) to the next highest (or lowest) value in the data set.

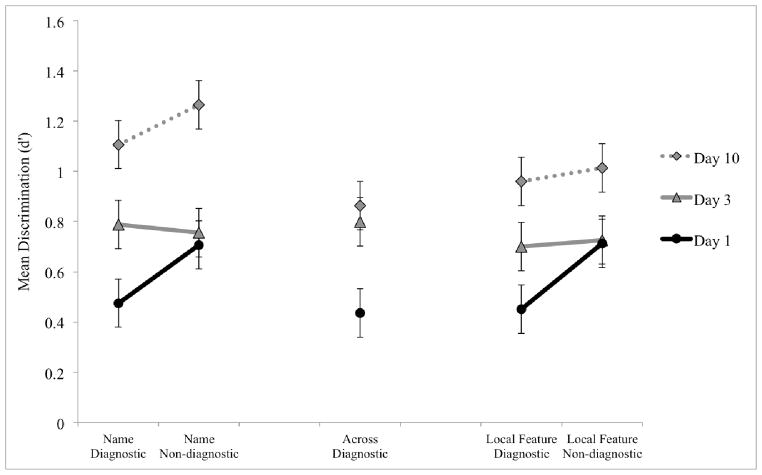
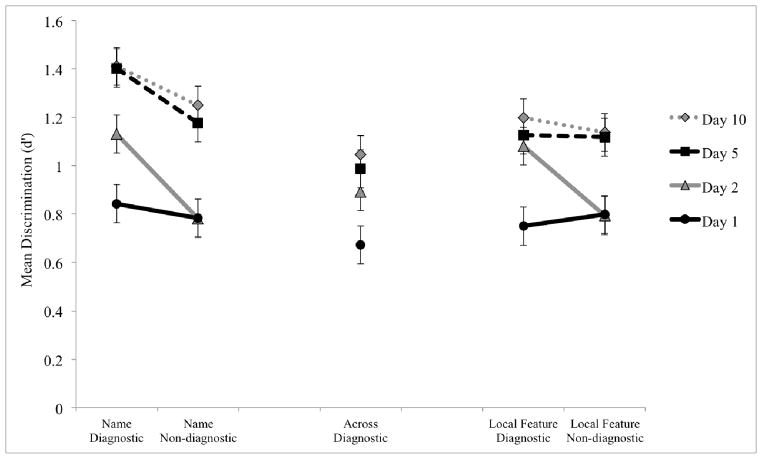
Figure 3.

Discrimination test results in Experiment 1 on Days 1, 3 and 10, for each location and direction of object pair in the space: named category, across category, and local feature category in the diagnostic and non-diagnostic directions. Error bars are 95% confidence intervals of the within subjects effects.

We analyzed discrimination trials by their diagnosticity (category diagnostic or non-diagnostic) and their location, either across the category boundary or within either the naming category or the local feature category. This allowed us to test for global stretching and shrinking of feature sensitivity along dimensions of the space but also to see if there were more local changes in discriminability in just one part of the object space. Only pairs of test objects that were adjacent in the space (24 out of 40 total different pairs) were included in this analysis so that we could compare performance for across versus within category pairs².

Diagnosticity effect due to category learning

In a first analysis, we compared discriminability for diagnostic and non-diagnostic pairs on Day 3 (following category learning) to Day 1. Across-category diagnostic pairs were not included in this analysis because task (or rather “future task assignment”) was included as a factor to assess for any baseline difference that would need to be taken into account on Day 10, but the diagnosticity effect was essentially unchanged when all diagnostic trials were compared to all non-diagnostic trials. Performance on Day 1 was better for pairs that were later non-diagnostic than diagnostic. This is likely a spurious result since the design was fully counterbalanced and no secondary tasks had been learned by Day 3.

From Day 1 to Day 3, performance improved along the diagnostic dimension on both sides of the space, while performance on the non-diagnostic dimension did not change. This was supported by a 2×2×2 ANOVA on discriminability with day (Day 1, Day 3), diagnosticity (diagnostic, non-diagnostic) and task (name, local feature) as within-subjects factors. We found an effect of day (F_1,31=5.85, MSE=1.560, p=.022, η_p²=.15) and a nearly significant interaction of diagnosticity and day (F_1,31=3.78, MSE=1.003, p=.061, η_p²=.10) demonstrating the greater change in the diagnostic compared to the non-diagnostic direction between Days 1 and 3. Post-hoc Tukey LSD tests (p<.05) showed a significant change from Day 1 to Day 3 on the diagnostic dimension but not for the non-diagnostic dimension. There were no significant effects of or interactions with task, which was expected given that subjects had not yet learned the category-specific tasks.

These results replicate stretching of a dimension diagnostic for learned categories, relative to a non-diagnostic dimension (Folstein et al., 2012a; Goldstone, 1994; Goldstone & Styvers, 2001) and extend this finding from familiar categories such as faces and cars to a space of novel objects.

Differences on the two sides of the space following task association

In a second analysis, we measured the influence of having learned different tasks on discrimination performance. Because both the diagnostic and non-diagnostic dimensions are relevant to naming but neither is relevant to the local feature task (after categorization), we might expect superior learning on the Naming side. We initially compared performance on Day 10, after task association training, to that on Day 3, after category learning. Across-category diagnostic pairs were again not included because task was included as a factor, but the effect in performance between sessions is essentially unchanged when all diagnostic trials were compared to all non-diagnostic trials.

We conducted a 2×2×2 ANOVA on discriminability with within-subjects factors of day (Day 3, Day 10), diagnosticity (diagnostic, non-diagnostic) and task (name, local feature). This ANOVA revealed a main effect of day (F_1,31=36.37, MSE=7.545, p=.0001, η_p²=.54) and a significant interaction between day and task (F_1,31=4.54, MSE=0.318, p=.041, η_p²=.13). Post-hoc Tukey LSD tests (p<.05) revealed a significant improvement from Day 3 to Day 10 on both sides of the space (for both tasks). These changes did not interact with diagnosticity (F_1,31=1.18, MSE=.106, p=.287, η_p²=.04).

We also performed the same analysis comparing Day 10 to Day 1, to take into account the spurious dimensional differences on Day 1 that could contribute to final performance on Day 10. Again, we found a significant main effect of day (F_1,31=78.33, MSE=15.966, p=.0001, η_p²=.72) and a significant interaction between day and task (F_1,31=6.68, MSE=.578, p=.015, η_p²=.18). These changes were not influenced by diagnosticity, and the 3-way interaction between day, task, and diagnosticity was not significant (F_1,31=1.17, MSE=0.106, p=.287, η_p²=.04).

When Day 10 is contrasted to Day 3, discriminability improved along both dimensions, which makes sense since both are used for the naming task and thus are relevant at this stage. These changes are greater on the naming side of the space but extend to the local feature side of the space as well, even though the non-diagnostic dimension and the diagnostic dimension within the category are not relevant for the local feature task. When we consider the omnibus ANOVA with all three discrimination test time points, there is a significant interaction between day and task (F_2,62=3.76, MSE=.311, p=.029, η_p²=.11). This effect is the result of increased discriminability on Day 3, and while there is change along both dimensions on Day 10, there is also more change along the non-diagnostic dimension on the Naming side.

These results suggest both local and general learning effects within the space. On the one hand, performance improved more for pairs on the Naming than the Local Feature side. On the other hand, performance – even for the non-diagnostic dimension – also improved on the Local Feature side. Given there was no learning on the non-diagnostic dimension on Day 3, this is likely due to the relevance of this dimension in the Naming task, generalizing to the other side of the space. However, the learning does not appear to be general to all parts of the space, based on the results for the diagnostic-across pairs, which did not improve between Day 3 and Day 10, as discussed in the next section.

Categorical perception

We evaluated whether categorical perception was observed at any point during the experiment by comparing performance on across versus within category diagnostic pairs on both sides of the space (we report the contrast across vs. within, collapsed across sides, because in no case was the difference between the two sides significant). In no case did we find evidence for categorical perception. If anything, whenever the difference was significant, the change in performance was larger for within category pairs (see Table 2). As can be appreciated from Figure 4, no significant learning occurred on across pairs after category learning. By Day 10, discriminability shows the opposite of a categorical perception effect in that performance is better for within category vs. across category pairs.

Table 2.

Mean d′ for discrimination performance in Experiment 1 on Days 3 and 10 and the difference between Days for diagnostic objects pairs across the category boundary (Across) and object pairs within a category, collapsed across task (Within). F-value, p-value, and effect size are for a main effect of location in the space, either across or within category.

Day	Across	Within	F-value	p-value	Effect size (ηp2)
Day 3	0.799	0.745	0.30	0.585	0.01
Day 10	0.864	1.033	3.12	0.088	0.09
Day 3 – Day 1	0.364	0.281	0.56	0.461	0.02
Day 10 – Day 3	0.064	0.288	9.81	0.004	0.24
Day 10 – Day 1	0.428	0.569	1.73	0.198	0.05

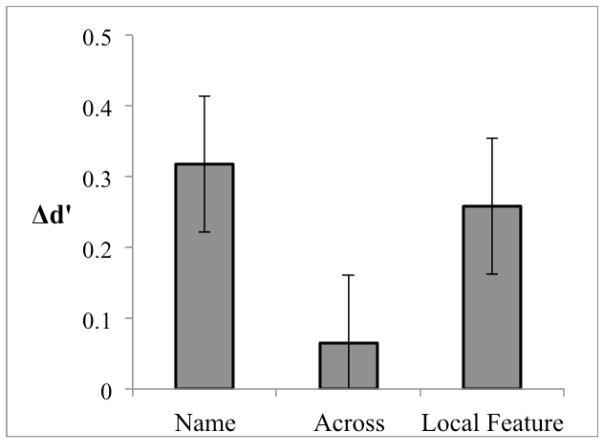
Figure 4.

Change in d′ in Experiment 1 between Day 3 (post-category learning) and Day 10 (post-task association training) in the diagnostic direction only: within the name category, across the category boundary, and within the local feature category. Error bars are 95% confidence intervals.

To test whether this effect may be due to subjects somehow learning less in the center than on the outside of the space, we considered performance and learning for pairs that differed on the non-diagnostic dimension, comparing those pairs that were either near or far from the category boundary (Table 3). If the reverse categorical perception effect for the diagnostic pairs was associated with the specific objects in these pairs, we would expect that when the same objects are part of the non-diagnostic trials, performance for far pairs would also be worse than for the near pairs. This was not found in any of the contrasts. In other words, after Day 3, while objects compared in an across pair evidenced learning when they are compared to other objects in the same category, the same objects do not evidence any learning when they are compared to objects from a different category. Therefore, it seems that what drove the reverse categorical perception effect is a local improvement in discriminability for the diagnostic dimension on each side of the space.

Table 3.

Mean d′ for discrimination performance in Experiment 1 on Days 3 and 10 and the difference between Days for non-diagnostic objects pairs Far and Near to the category boundary. F-value, p-value, and effect size are for a main effect of location in the space, either far or near from the boundary.

Day	Far	Near	F-value	p-value	Effect size (ηp2)
Day 3	0.636	0.733	0.08	0.785	0.003
Day 10	1.011	0.989	0.05	0.821	0.002
Day 3 – Day 1	0.020	0.060	0.53	0.473	0.02
Day 10 – Day 3	0.375	0.256	0.001	0.970	0.00005
Day 10 – Day 1	0.395	0.316	0.87	0.359	0.03

Discussion

In Experiment 1, we asked how distinct task associations for objects on each side of a category boundary might alter discriminability along complex feature dimensions. First, we replicated the diagnosticity effect obtained following category learning (Folstein et al., 2012a; Goldstone, 1994; Goldstone & Styvers, 2001). The experience of categorizing these objects produced stretching along the dimension orthogonal to the category boundary, leading to improvements on perceptual judgments.

Second, we observed an influence of learning different tasks on discriminability, in different parts of the same similarity space. After task association, subjects showed increased discriminability along both dimensions on both sides of the space, but this change was greater on the Naming side. On the one hand, perceptual improvements on the local feature side suggest an effect of practice with the tasks, which results in global stretching of the entire diagnostic and non-diagnostic dimensions. Note that neither of these dimensions is relevant to the local feature task, and only the diagnostic dimension is relevant to the categorization requirements of the training (i.e., to know which task needs to be performed, subjects must decide which side the objects falls in). Therefore, this improvement on the local feature side of the space, especially for the non-diagnostic dimension, appears to reflect generalization from learning about the non-diagnostic dimension on the Naming side, a global effect of training on the similarity space. On the other hand, the fact that more learning took place on the Naming side suggests a local effect of learning, with more stretching in the part of the space where these dimensions were relevant to individuation. A local stretching over and above a more global stretching is similar to what was reported by Goldstone (1994), except in that case the local effect occurred at the category boundary (and was deemed evidence for categorical perception).

Third, we therefore explored whether local stretching occurred at the category boundary. Learning different tasks on each side of the space resulted in a reversed categorical perception effect, such that objects within a category became even easier to discriminate than those between categories. Local effects at the category boundary have been observed as local expansion of the representations near the boundary (relative to baseline) in some studies (Goldstone, 1994) and in other cases as a compression of the representations on either sides of the category boundary, leaving representations unchanged (relative to baseline) near the category boundary (Livingston et al., 1998). We would not expect compression to occur, at least not on the Naming side of the space, since while subjects learned these objects are part of a category, they were not to ignore the differences between them. As far as we know, the perceptual learning that resulted from task associations is the first example of expansion on both sides of the category boundary while leaving the representations at the boundary unchanged. This occurred despite the fact that exemplars near the boundary were seen during this training phase just as much as exemplars far from the boundary.

Note that in Experiment 1, it is impossible to know whether changes in discrimination were due to performing different tasks on different exemplars vs. having to actually associate the tasks with these exemplars. This is because in the initial phase of training in Experiment 1, task instructions were provided on each training trial such that subjects were not required to know the task to perform for an object, whereas in the later phase of training, subjects were shown an object without instructions and had to perform the correct task. This limitation was addressed in Experiment 2.

Experiment 2

Experiment 2 uses the same general design as Experiment 1, with the addition of another discrimination test on Day 5 before the start of the mixed trials learning phase, the first point at which subjects are expected to know which task to perform for a given object without instructions.

In this Experiment, we mainly sought to replicate and extend our finding of local changes in perceptual learning due to task associations. We also began to address which aspect of the training was necessary for the asymmetry in discrimination improvement. Experiment 2 therefore includes an additional discrimination test after the first phase of training, but before subjects are required to learn the task associations, to reveal how much perceptual learning if any can be attributed to the initial phase of training where the two tasks were done separately (first all of the naming trials then all of the local feature trials) such that task instruction is explicitly provided. To further distinguish the two phases of training in Experiment 2, speed was emphasized during the second training phase by shortening stimulus presentation times and adding response deadlines. These changes should encourage subjects to learn the object-task mappings that need not be learned (although they could be) in phase 1 because trials are blocked by task.

Methods

Subjects

Subjects were recruited from the Vanderbilt University and Nashville, TN community; they gave informed consent and received monetary compensation for their participation. The study was approved by the local IRB. Thirty-six subjects (19 male) aged 18–39 (mean = 22.83, SD = 5.54) completed all 10 sessions of the study. Data are reported here for 32 subjects (15 male, mean age = 22.53, SD = 5.71); four subjects were excluded for exceedingly poor accuracy during training (accuracy of zero for more than 3 blocks in the mixed trials on Days 7, 8 or 9). Three more subjects began the study but did not complete all of the sessions. All subjects reported normal or corrected to normal visual acuity.

Stimuli and equipment

The set-up and equipment was the same as Experiment 1 with the exception of the monitors; Experiment 2 used 21.5-inch LCD monitors (1920×1080 resolution). Ziggerin-morph stimuli were the same as in Experiment 1 and shown about 25% larger on the screen than in Experiment 1 in hopes of making them a bit easier to individuate. In Experiment 2, the Vernier lines were tilted and subjects had to judge if the two lines were aligned or misaligned. This was done to reduce the facilitation from using the distance of the edge of the object for the local feature task. Misaligned lines were separated by 2 pixels from left to right and by 24 pixels from the bottom of the top line to the top of the bottom line. Both lines were tilted +10 degrees to the right of vertical. We hoped that tilting the lines would increase the difficulty of the local feature task, to better equate the naming and local feature tasks in Experiment 2.

Procedure

The experiment consisted of 10 sessions (see Table 4), with two sessions never more than 4 days apart (mean = 1.97, SD = 1.37), and subjects completed all sessions within a period of 12–21 days (mean = 17.72, SD = 3.67).

Table 4.

Tasks and number of trials for each session of Experiment 2.

Session	Task(s)	Number of trials
Day 1	Discrimination test 1	784
	Category learning	1,536
Day 2	Category review	256
	Discrimination test 2	784
Day 3	Name learning part 1	1,000
	Local feature learning 1	960
Day 4	Name learning part 2	1,200
	Local feature learning 2	960
Day 5	Name review	120
	Local feature review	128
	Discrimination test 3	784
Day 6	Mixed trials with task instruction	400
	Mixed trials with no task instruction	800
Day 7	Mixed trials speeded, 3 sec response	1,200
Day 8	Mixed trials speeded, 2 sec response	1,200
Day 9	Mixed trials speeded, 1.5 sec response	1,200
Day 10	Mixed trials speeded review	240
	Discrimination test 4	784

Discrimination test

The dependent measure was identical to that in Experiment 1 and was administered four times, on Days 1 (before training), 2 (after category learning), 5 (after task learning alone), and 10 (after mixed trials). See Table 4 for number of trials in this and all other tasks.

Category learning

The category learning procedure was the same as in Experiment 1, but it was shorter and only administered on Day 1 with a short review on Day 2.

Task association, name learning

The names and name learning procedure were the same as Experiment 1. The percentage of “No Name” foil trials was 20% for all training blocks.

Task association, local feature learning

The local feature learning procedure was the same as that used in Experiment 1 but used an aligned/misaligned judgment (instead of left/right).

Task association, mixed trials

On Days 6–10, subjects completed blocks of mixed trials with objects from both categories in the same block using the same procedure as Experiment 1. However, we further manipulated stimulus presentation time and response deadline: On Day 6, as subjects learned the mixed task the object remained on the screen until a response was made and there was no time limit for a response. On Days 7–10, the stimulus was presented on the screen for only 1.5sec and subjects had a limited response window that began with the stimulus onset of 3sec on Day 7, and which decreased to 2sec on Day 8 and 1.5sec on Days 9 and 10. If subjects did not make a response within the given window they received feedback to go faster and were advanced to the next trial.

Results

Due to computer problems, two subjects did not complete a small portion of the training; one subject missed 11% of the Day 4 name learning trials and another 11% of the Day 3 local feature learning trials. Also, one subject completed only 11 out of 14 blocks of the Day 5 discrimination test. Data that were collected for these subjects for the trials they completed was included in the analyses since they missed such a small part of the training and to preserve counterbalancing.

Training results

Subjects successfully learned to categorize objects, name them, perform the local feature task and later to perform the category-appropriate task for an object (see Supplemental materials for detailed results; Table S2).

Discrimination test results

Figure 5 shows the mean discriminability (d′) on the object discrimination test on Day 1 (before any training), Day 2 (after category learning), Day 5 (after task learning), and Day 10 (after mixed trials training). Trials with extreme reaction times (less than 100msec or greater than 5000msec) were removed from the analysis (less than 1% of the trials).

Figure 5.

Discrimination test results in Experiment 2 on Days 1 (pre-training), 2 (post-category learning), 5 (post-task learning), and 10 (post mixed trials) shown by location and direction of object pair in the space: named category, across category, and local feature category in the diagnostic and non-diagnostic directions. Error bars are 95% confidence intervals.

Diagnosticity effects due to category learning

Between Day 1 and Day 2, discriminability improved along the diagnostic dimension on both sides of the space, with no change along the non-diagnostic dimension. This is seen in 2×2×2 ANOVA of discrimination performance (d′) with day (Day 1, Day 2), diagnosticity (diagnostic, non-diagnostic) and task (name, local feature) as within-subject factors. There was a significant effect of day (F_1,31=5.96, MSE=1.494, p=.021, η_p²=.16) as well as an interaction between day and diagnosticity (F_1,31=9.42, MSE=1.569, p=.004, η_p²=.23) demonstrating greater change in sensitivity in the diagnostic compared to the non-diagnostic direction between Days 1 and 2. At this point, as expected, there was no significant effect of task (F_1,31=.21, MSE=.054, p=.647, η_p²=.01).

Differences on the two sides of the space following task association

In Experiment 2, we introduced an additional discrimination test at the end of Day 5, after tasks were practiced separately in different blocks for each category, but before mixed trials required subjects to know the task associated with each exemplar.

We first compared performance on Day 5 to that on Day 2, to look at the perceptual learning following blocked task practice. As can be seen in Figure 5, similar to Experiment 1, there was an increase in sensitivity along both dimensions, on both sides of the space, but there was a greater increase on the Naming side. We conducted a 2×2×2 ANOVA on discrimination performance (d′) with within-subjects factors of day (Day 2, Day 5), diagnosticity (diagnostic, non-diagnostic) and task (name, local feature). We found a main effect of day (F_1,31=8.996, MSE=4.309, p=.005, η_p²=.225) and a significant interaction between day and task (F_1,31=4.835, MSE=.355, p=.036, η_p²=.135). As in Experiment 1, the interaction between day and diagnosticity was not significant, although the effect size for the interaction is larger than in Experiment 1(F_1,31=3.514, MSE=.646, p=.070, η_p²=.102).

Second, we compared discrimination performance after Day 10 following mixed trials, relative to Day 5. As seen in Figure 5, despite 4 additional days of practice there was very little change between Day 5 and Day 10. This is supported by a 2×2×2 ANOVA on discrimination performance (d′) with within-subjects factors of day (Day 5, Day 10), diagnosticity (diagnostic, non-diagnostic) and task (name, local feature) in which we found a main effect of task (F_1,31=4.646, MSE=1.749, p=.039, η_p²=.130) resulting from better overall discrimination on the Naming side compared to the Local Feature side, but no significant effects of day or diagnosticity (p>.25). Thus, it appears that the changes in discriminability in Experiment 1 at the end of the entire training protocol did not require 10 days, nor did they require practice in mixed trials. It should be noted that this lack of perceptual learning after Day 5 was observed even though learning on the training tasks was still evidenced in faster reaction times (Table S2).

Categorical perception

We assessed if categorical perception was observed at any point during the experiment by comparing performance on across vs. within category diagnostic pairs on both sides of the space (we report the contrast across vs. within for both tasks together because in no case was the difference between the two sides significant).

Across all comparisons of time points, we found no evidence for categorical perception (see Table 5). As in Experiment 1, when the difference between across and within pairs was significant, performance, or change in performance, was greater for within pairs than across pairs.

Table 5.

Mean d′ for discrimination performance in Experiment 2 on Days 2, 5, and 10 and the difference between Days for diagnostic objects pairs across the category boundary (Across) and within a category, collapsed across task (Within). F-value, p-value, and effect size are for a main effect of location in the space, either across or within category.

Day	Across	Within	F-value	p-value	Effect size (ηp2)
Day 2	0.893	1.106	3.08	0.089	0.09
Day 5	0.986	1.265	6.26	0.018	0.17
Day 10	1.045	1.304	4.41	0.044	0.12
Day 2 – Day 1	0.220	0.309	1.44	0.240	0.04
Day 5 – Day 2	0.094	0.159	0.67	0.419	0.02
Day 5 – Day 1	0.313	0.468	3.13	0.087	0.09
Day 10 – Day 5	0.059	0.040	0.08	0.782	0.003
Day 10 – Day 2	0.152	0.199	0.26	0.613	0.008
Day 10 – Day 1	0.372	0.508	1.83	0.186	0.06

To test whether this reverse categorical perception for diagnostic pairs was due to objects on the outside of the space being easier than those in the inside, we considered performance for pairs that varied on the non-diagnostic dimension, comparing those that were near the category boundary to those that were far from the category boundary (Table 6). For these non-diagnostic pairs, performance was comparable for far and near pairs in all comparisons, clarifying that the reverse categorical perception effect was specific to the diagnostic dimension. Learning after Day 2 was only found for comparisons of objects within a category, and not objects across two categories, providing further evidence of local within-category learning.

Table 6.

Mean d′ for discrimination performance in Experiment 2 on Days 2, 5, and 10 and the difference between Days for non-diagnostic objects pairs Far and Near to the category boundary. F-value, p-value, and effect size are for a main effect of location in the space, either far or near from the boundary.

Day	Far	Near	F-value	p-value	Effect size (ηp2)
Day 2	0.740	0.825	2.83	0.103	0.08
Day 5	1.075	1.197	2.57	0.119	0.08
Day 10	0.180	1.216	0.37	0.546	0.01
Day 2 – Day 1	0.005	−0.032	0.24	0.630	0.01
Day 5 – Day 2	0.372	0.335	0.24	0.629	0.01
Day 5 – Day 1	0.340	0.341	0.00004	0.995	0.00
Day 10 – Day 5	0.105	0.019	1.14	0.294	0.04
Day 10 – Day 2	0.440	0.391	0.52	0.476	0.02
Day 10 – Day 1	0.445	0.360	1.08	0.307	0.03

Discussion

Overall, the results of Experiment 2 replicate the effects we observed in Experiment 1 and demonstrate that sensitivity to features of complex objects changes with experience categorizing objects, but also following task associations in different parts of the space. We again observed evidence of acquired distinctiveness as a result of the initial category learning, improvements in discrimination both globally and locally in the similarity space following task association, and reversed categorical perception with greater improvement in discrimination of pairs within than across categories.

By adding another discrimination test after task learning but before mixed trials, we found that the changes associated with practicing different tasks with each object category could be observed after 3 days of blocked practice, and did not increase with further training that required subjects to associate a task directly with these objects. It is possible that strong associations between exemplars and tasks are created automatically even during blocked practice, we simply cannot tell in the current design.

General Discussion

Our primary goal was to study the changes in perceptual discrimination in a similarity space following the association of visually similar objects to different tasks. Prior work had shown that the same objects associated with different tasks through learning could be processed differently by different subjects (Wong et al., 2009a; Wong et al., 2009b). However those results, just like the global acquired distinctiveness obtained here and in other studies as a function of category learning, could be explained by attentional weights selectively applied to an entire dimension. Here, we were specifically interested in more local effects in the similarity space, which some models of categorization explain using attentional weights associated with each exemplar (Aha & Goldstone, 1992; Kruschke, 2001; Love & Jones, 2006; Rodrigues & Murre, 2007). Such local effects have in the past been obtained during category learning (Aha & Goldstone, 1992; Blair et al., 2009; Sakamoto et al., 2004; Yang & Lewandowsky, 2004) but here we demonstrate local expansion of similarity space during perceptual judgments. As such, we suggest that models with stimulus specific attentional weights, which can account for local effects, are not only important to explain category learning, but they are also important for perceptual learning.

First, we replicated the diagnosticity effect due to category learning that has been obtained previously in morphspaces of faces and cars (Folstein et al., 2012a; Goldstone, 1994; Goldstone & Styvers, 2001). Following category learning we observed an increase in sensitivity specific to the diagnostic dimension. This result was seen in Experiment 1 after 3 category learning sessions (3,584 total trials), and also in Experiment 2 where the category learning was significantly shorter (just one session and a short review, 1,792 total trials). This stretching specific to the diagnostic dimension is a robust effect of learning a category boundary within an object feature space that applies as well to novel objects as familiar ones and that develops relatively rapidly.

Second, the changes we observed following task associations suggested both global and local changes to feature sensitivity in the space. In both Experiments 1 and 2, we saw changes in discrimination for both the diagnostic and non-diagnostic directions in all parts of the space, but these changes also differed in their magnitude on each side of the space depending on task. In both experiments, we observed a significant day x task interaction revealing greater improvement on the Naming side of the space. At the same time, we did not find evidence for a significant 3-way interaction of day x task x diagnosticity, although the effect size was larger in Experiment 2 than Experiment 1. It is possible that a study with a larger sample size and/or an improved training protocol can yield such an interaction, which would provide even stronger evidence that objects can be processed differently on each side of the space.

Lastly, we observed what we called, for lack of a better term, reverse categorical perception in both experiments. Essentially, no further expansion of the similarity space took place once objects were no longer explicitly categorized, even though 1) there was considerable pressure to “categorize” objects to perform different tasks during mixed trials practice and 2) there was ample evidence of perceptual learning due to task practice, even learning that involved comparisons of the near boundary exemplars to the more distant ones. Prior work using the same category learning procedure in a space of morphed cars found either no evidence of categorical perception (Folstein et al., 2012b) or a small advantage for across pairs relative to within pairs regardless of diagnosticity (Folstein et al., 2012a). Consistent with this, we only observed reverse categorical perception following task associations.

These results illustrate what we believe may be the earliest stages of category differentiation, whereby a homogenous stimulus space can be parsed into qualitatively different categories that recruit different processing strategies and perhaps even different neural substrates in the brain. While our paradigm is unlikely to capture exactly how real-world categories may emerge due to differential experience with objects that may be visually similar (e.g., letters and numbers, or same vs. other race faces), it serves as a first approximation of this process in the laboratory. In the real world, an object category and its associated task may be learned less sequentially, but separating these two stages of category creation in our design allowed us to separate their effects on perceptual learning. Despite our best efforts to encourage automatic associations of different tasks with objects, subjects may have employed a two-step process in the final stages of training, first categorizing an object as a Vit or a Mog, and then performing the appropriate task. This may not match what happens with real-world object categories, at least not categories of expertise that can engage a specialized process extremely fast (Curby & Gauthier, 2009; Richler, Mack, Gauthier, & Palmeri, 2009). Our discrimination measure in Experiment 2 did not reveal any change in discriminability following mixed trial training, but future work, perhaps with objects that are more easily discriminated, could be more sensitive. More experience with these object categories may be required to achieve the sort of expertise observed in real-world domains, but such expertise may also depend on categories being further differentiated in semantic space through associations with non-perceptual information (for instance, letters are associated with phonological representations, while musical notation can be associated with multimodal information depending on the specific musical training).

Conclusions

We developed a paradigm fit to study how object categories associated with different tasks can be learned in a continuous similarity space. Our work bridges between traditions in category learning and perceptual expertise, to suggest that an important way to extend models of categorization is to consider that many category boundaries result in different perceptual goals on either side of the boundary. Experience performing a specific task with objects in a category can change the psychological space such that later perceptual decisions with these objects are affected. We observed evidence for local changes in similarity across the psychological space in addition to the global changes typically obtained following category learning, suggesting that perceptual learning in a subpart of a similarity space relies on stimulus-specific attentional weights (Love & Jones 2006; Kruschke, 2001).