Stress Transmission within the Cell

Abstract

An outstanding problem in cell biology is how cells sense mechanical forces and how those forces affect cellular functions. During past decades, it has become evident that the deformable cytoskeleton (CSK), an intracellular network of various filamentous biopolymers, provides a physical basis for transducing mechanical signals into biochemical responses. To understand how mechanical forces regulate cellular functions, it is necessary to first understand how the CSK develops mechanical stresses in response to applied forces, and how those stresses are propagated through the CSK where various signaling molecules are immobilized. New experimental techniques have been developed to quantify cytoskeletal mechanics, which together with new computational approaches have given rise to new theories and models for describing mechanics of living cells. In this article, we discuss current understanding of cell biomechanics by focusing on the biophysical mechanisms that are responsible for the development and transmission of mechanical stresses in the cell and their effect on cellular functions. We compare and contrast various theories and models of cytoskeletal mechanics, emphasizing common mechanisms that those theories are built upon, while not ignoring irreconcilable differences. We highlight most recent advances in the understanding of mechanotransduction in the cytoplasm of living cells and the central role of the cytoskeletal prestress in propagating mechanical forces along the cytoskeletal filaments to activate cytoplasmic enzymes. It is anticipated that advances in cell mechanics will help developing novel therapeutics to treat pulmonary diseases like asthma, pulmonary fibrosis, and chronic obstructive pulmonary disease.

Introduction

The lungs are dynamic organs that are continuously subjected to mechanical forces throughout development and adult life. These forces play a key role in development, growth, function and dysfunction of lungs and their effects are exerted on the cell level (cf. ¹⁸²). Lung tissue is constantly under tensile stress that is a result of the distension of the lung by the transpulmonary pressure. Tensed pulmonary parenchyma, vasculature, and the airway tree are the scaffolding upon which pulmonary cells adhere, contract, migrate, secrete, differentiate, and proliferate. When exposed to mechanical loads, cells respond both mechanically and chemically. Their mechanical response is characterized by deformation of the cellular force-bearing structure that, in turn, gives rise to mechanical stresses that tend to resist deformation. Their chemical response is characterized by a cascade of biochemical signals that are triggered and regulated by mechanical stresses and that ultimately lead to a host of biological responses. For example, secretion of pulmonary surfactant is mediated by mechanical stretching of epithelial type II cells which adhere to tensed alveolar septal tissue (cf. ^4,207). While septal stretching plays a key role in surfactant secretion, excessive stretching may compromise permeability of the alveolar epithelial cell barrier that results in lung injury and edema. Such injury, termed volutrauma, may be caused by high inflating pressure during mechanical ventilation of patients suffering from acute respiratory distress syndrome (ARDS; ^51,52) and other conditions of lungs having low-functional residual capacity due to a disease. Pulmonary fibroblasts are main producers of extracellular matrix (ECM) constituents (e.g., collagens). Transforming growth factor beta (TGF-β), which is the main cytokine that stimulates fibroblasts to produce ECM, is upregulated by mechanical stretch (77). Tensile forces also regulate the connective tissue growth factor that is able to stimulate ECM protein release through a TGF-β-independent pathway (162). Airway smooth muscle stretch that occurs during deep inspirations provides a potent dilating effect that accounts for the limited degree of narrowing in the healthy airway during maximal bronchial provocation (59,60).

On the other hand, mechanical stresses generated within cells by their contractile machinery also influence lung function. Stresses generated by the cells are taken by the ECM. Active smooth muscle contraction is opposed not only by distending stress conferred on the adventitia and other cells by surrounding parenchyma, but also by stresses associated with compression, buckling, and folding of the airway epithelium and submucosa. This, in turn, has important implications on severity of airway obstruction (59), as well as on an increase in parenchymal tissue resistance and stiffness in asthma (109).

In circulating cells, mechanical stresses also play a key biological role. Neutrophils are often larger than the diameter of the capillary vessel through which they must pass. This transit is influenced by deformability of both the neutrophil and the pulmonary capillary wall. The pressure drop across the capillary segment is the stress that acts on and initiates deformation of the stopped neutrophil. This is critical for both neutrophil transit through the pulmonary vasculature and in the changes that occur during inflammation. Circulating mediators activate neutrophils and reduce their deformability. This results in prolongation of transit times, sequestration, and adhesion to endothelial cells, as well as to injury to the barrier that leads to ARDS.

Mechanical forces applied to the cells are transmitted over receptors that mediate cell-ECM (integrins) and cell-cell (cadherins) adhesions. These receptors are physically connected to the intracellular molecular network known as the cytoskeleton (CSK; ^152,196). Cells resist applied forces by developing mechanical stresses in the CSK as they undergo shape distortion. A measure of this resistance is stiffness that is defined as the ratio of the stress to the strain associated with the deformation. The cells also transmit applied forces through the CSK over long distances and over defined directions (91,134). This channeled long-distance force transmission is specific to networks of fibers (e.g., the cytoskeletal lattice, collagen gel in vitro) and not to materials such as rubber, metals, or clay. It enables mechanical forces to reach signaling molecules that are physically immobilized in the CSK and thus trigger a cascade of biochemical activities that are essential for biological functions of the cell.

The CSK is not a passive structure. All living cells generate active mechanical stress within the CSK via their actinmyosin contractile apparatus even before application of external forces. This active stress is termed prestress (198,202). Modulations of the prestress by increased or decreased contractile activity enable cells to regulate and tune their shape stability (99,197). Cell shape stability, in turn, is known to play important roles in cell adhesion, spreading, growth, differentiation and apoptosis (30, 167), and cell mechanical properties (cf. ^{172, 198, 202}) via cytoskeletal remodeling (cf. ^{18, 76}). Prestress-dependent cytoskeletal remodeling is also fundamental for cell crawling, invasion, wound healing via the mechanisms of force transmission through the CSK (91), and the resultant mechanotransduction.

Studies of mechanobiology of living cells have encompassed two fundamental interlocked questions. One is the question of mechanics—namely by what mechanisms does the cell develop and transmit mechanical stresses in response to externally applied forces? The other is the question of mechanotransduction—namely how such mechanical stresses are processed into biochemical responses? In this article, we discuss the current understanding of these problems by emphasizing the underlying biophysical mechanisms. The article is organized into five major sections. Following the introductory section, we describe mechanisms by which cells develop mechanical stresses to resist deformation due to externally applied loads. In the third section, we describe how stresses are transmitted through the CSK over long distances. In the fourth section, we describe mechanochemical control of molecular assembly and remodeling of the CSK. We conclude the article by addressing future challenges in cellular mechanics and mechanobiology.

Development of Mechanical Stress in Cells

We begin by posing a fundamental question of cellular mechanics: by what means do cells develop mechanical stresses that resist cell deformation? The answer to this question is essential for understanding many cellular integrated functions including migration, growth, mitosis, apoptosis and mechanotransduction. To address this question, two engineering approaches have been employed: a continuum mechanics description and a discrete mechanics description.

The continuum approach assumes that the stress-bearing structure of the cell is a mechanical continuum that fills the space defined by cell boundaries. It begins with consideration of infinitesimally small element of the continuum, referred to as a “point particle,” but having no direct relationship with physical particles (e.g., atoms, molecules, etc.) or with stress-bearing elements of the cell (e.g., filaments, stress fibers, etc.). The contributions of physical stress-bearing elements to the local mechanical properties at the microscale are replaced by an average within the point particle. The microscale mechanics of point particles is governed by field equations that describe the basic laws of mechanics (e.g., balances of mass, linear momentum, angular momentum, energy, etc.). These equations together with equations that describe mechanical properties of the point particle (i.e., constitutive equations) are then integrated, subject to conditions prescribed at the boundary of the cell.

The discrete approach begins with considerations of discrete finite-size stress-bearing elements of the cell (e.g., cytoskeletal filaments and fibers). The number of these elements is large but finite; they form a discrete network which does not fill the space within the cell body and which is defined by its mash size. At this stage, stresses and strains cannot be defined as continuous variables. Instead, attention is turned to forces and displacements at each node of the network where the structural elements are connected. The mechanics of each element is governed by balance of forces and moments at every node by kinematic compatibility conditions (i.e., connected elements must move together) and by conditions prescribed at the boundary of the network. This results in a large number of discrete forces and discrete displacements throughout the network. Calculating all these forces and displacements, except in very simple structures, is a hopeless task. Instead, applying a coarse-graining average to this discrete forces and displacements transforms them into continuous stress and strain fields. This, in turn, enables the usage of the powerful mathematical framework of continuum mechanics.

In the sections that follow, we describe how the above approaches come into play in cellular mechanics. We begin by describing major stress-bearing components of the CSK.

Molecules of the cytoskeleton

The CSK is the major stress-bearing structure of the cell. Its mechanical properties arise from the complex network of biopolymers that comprise the cytoskeletal lattice, which undergoes continuous remodeling and is driven by molecular motors that convert chemical energy of adenosine triphosphate (ATP) into mechanical forces. Actin microfilaments, microtubules, and intermediate filaments are major biopolymers of the CSK, as well as a number of actin binding and cross-linking proteins (cf. ²). In general, those filamentous biopolymers are much less flexible than synthetic polymers, yet they can still exhibit significant conformational changes driven by thermal Brownian fluctuations. In polymer physics, a measure of filament flexibility is given by the persistence length (L_p), which defines a length scale over which a filament remains unbent in a thermal bath. Roughly, L_p is the minimum length at which the filament ends become uncorrelated due to Brownian motion. It can be shown that L_p = B/k_bT where B is the bending (flexural) rigidity of the filament, and k_bT is the energy of thermal fluctuations; k_b is the Boltzmann constant and T is the absolute temperature (50,64,72). If the filament's contour length (L_c, i.e., the length of fully extended filament) L_c ⪢ L_p, then the filament is flexible and does not resist bending, whereas filament's resistance to extension and compression is determined by its conformational entropy and is described as entropic elasticity. As a result of conformational changes, these filaments exhibit strain-hardening (or stiffening) behavior during stretching. If L_c ⪡ L_p, then the filament behaves as a straight elastic rod that resists tension, compression, and bending due to straining of chemical bonds and is described as enthalpic elasticity. If L_c ~ L_p, the filament is semi-flexible and its resistance to tension, compression, and bending includes both entropic and enthalpic contributions (29). For small deformations, filament's resistance to extension/compression can be quantified by the Young's modulus of elasticity (E).

Filamentous actin (F-actin) is a polymer composed of actin monomers. Its L_p is on the order of 10¹ μm, diameter 5 to 10 nm, Young's modulus of elasticity is very high, E ~ 10³ MPa, (e.g., comparable to that of nylon and collagen fibrils), and B ~ 10⁻¹ pN.μm² (72), Table 1. In response to stretching of isolated actin filaments (L_c = 1–15 μm), their tension-strain curve exhibits initial strain-hardening at low tensions (0–50 pN) and low strains (0.4–0.6%), which is indicative of filament's conformational changes. The curve becomes linear at intermediate to high tensions (50–230 pN), which is indicative of the enthalpic elasticity (127). The physiological contour length of F-actin is L_c ≤ 1 μm, whereas the distance between actin cross-links within the CSK is on the order of 10² nm. Those lengths are at least an order of magnitude smaller than L_p, which explains why within the CSK actin filaments appear straight and unbent (161,184). This, in turn, suggests that in living cells the contribution of actin filaments to the mechanical stresses may be primarily through enthalpic elasticity.

Table 1.

Mechanical Properties of Actin Microfilaments, Microtubules, Intermediate Filaments, and Actin Stress Fibers Obtained from in vitro Measurements

Filament Type	D (nm)	Lp (μm)	E (MPa)	Emax (MPa)	Fmax (nN)	εmax (%)	B (pN·μm2)
Actin microfilaments	5–10	10–20	2600	*	0.4	0.9	0.073
Microtubules	25/12	5000	1700	*	*	*	22–44
Intermediate filaments	10	1	6.4	80	14	220	0.003
Stress fibers	200–1000	*	1.45	100	380	275	≥100

D is filament diameter; L_p is persistence length; E is elastic modulus, F_max is tensile force at which the filament breaks; E_max is elastic modulus corresponding to F_max; ε_max is strain corresponding to F_max; B is bending rigidity;

^*no data available.

Data for microtubules include inner/outer diameters. Modified from reference 171 with permission from Stamenović.

Cytoskeletal actin filaments are often cross-linked with myosin motor proteins that are capable of generating tensile force in the actin filaments through the ATP-driven process of cross-bridge cycling. As a result of this action, the CSK becomes prestressed. Cytoskeletal actin filaments are also found grouped together with myosin and other actin-binding proteins to form bundles known as actin stress fibers which have much larger diameter (0.2–1 μm), much lower elastic modulus (E ~ 1 MPa) and much higher bending rigidity (B ≥ 10² pN.μm²) than individual actin filaments. During stretching, stress fibers exhibit a strain-hardening behavior over a wide range of strains (41), Table 1.

Microtubules are polymers of α- and β-tubulin dimers organized as hollow tubes (25-μm outer diameter and 12-μm inner diameter). They have nearly the same elastic modulus as actin filaments (E ~ 10³ MPa), but a much greater L_p ~ 10³ μm and B ~ 10¹ pN.μm² (72), Table 1. Since their physiological L_c ⪡ L_p, one would expect microtubules to appear straight on the whole cell level. Immunofluorescent images of CSK-based microtubules show, however, that they appear bent and wavy (12, 99, 198), suggesting that some type of internal mechanical force must act on microtubules. Conceivably the wavy shapes of CSK-based microtubules indicate their buckling as they oppose compression exerted by contractile forces of the actin network.

Intermediate filaments are family of proteins (e.g., vimentin, desmin, keratin, lamin, etc.)~10-nm diameter, which are much more flexible (L_p ~ 10⁰ μm, B~10⁻³ pN.μm²) and much more extensible (E ~10⁰ to 10¹ MPa) than either actin filaments or microtubules (64), Table 1. Their physiological L_c = 10 to 20 μm is much greater than their L_p, which explains their wavy appearance in cells (99). This suggests that intermediate filaments may contribute to mechanical stresses of the CSK through the conformational entropy changes (64). This entropic nature of intermediate filament elasticity is also reflected through their strain-hardening behavior (105). However, in living cells the contribution of the entropic elasticity of intermediate filaments to the whole cell elasticity appears to be minor. Only when cells become highly strained and intermediate filaments become fully extended, taut and stiffened, their contributions to the overall elastic response of the cell becomes significant, presumably through the enthalpic mechanisms (199,200).

Cells contain a large numbers of proteins that crosslink the filaments, control their lengths, generate mechanical forces, and provide elasticity and mechanical connectivity to the cytoskeletal lattice and other cellular structures. We briefly describe several of those proteins that are important for biomechanics of the cell. We have already mentioned the role of myosin cross-bridges in contractile force generation which is essential for prestressing the CSK. Filamin-A cross links actin filaments into networks and participates in the anchoring of cell membrane proteins for the actin CSK. Titin (connectin) is important for contraction of striated muscles. Spectrin links actin to intermediate filaments and also provides mechanical stability of the cell membrane and underlying supporting cortical CSK in erythrocytes (193). All these proteins are highly flexible (filamin-A L_p = 20 nm; titin L_p = 10 nm; and spectrin L_p = 7.5 nm) and their elasticity may contribute to the elastic response of the whole cell. Talin, vinculin, paxilin, α-actinin, and zyxin are backbone proteins of focal adhesion (FA) plaques that link actin stress fibers to FA integrins. Many of these proteins are also present in stress fibers. Plectin mediates interaction between intermediate filaments, microtubules and actin filaments (185). Microtubule actin cross-linking factor (MACF1) links F-actin to microtubules (31,126).

In summary, knowledge of biophysical properties of cytoskeletal polymers is necessary for understanding their mechanical roles and contributions to the cytoskeletal mechanical responses. However, it is not sufficient to predict those responses. For example, there is a several orders of magnitude difference between the elastic modulus of individual actin filaments, and microtubules (~10⁹ Pa) on one hand, and the apparent elastic modulus (stiffness) of the cytoskeletal network of living cells (~10² to 10⁴ Pa) on the other hand (1,7,8,44,55–58,168,178,198,202). Thus, to bridge the gap between elasticity of individual filaments and the elasticity of the whole CSK, one can envision constructing a network that incorporates both the elastic properties of the individual proteins and their geometrical arrangements and structural organization following basic features of cytoskeletal architecture.

Bridging the gap between molecules and cytoskeletal lattice mechanics

Cellular solid networks

A simple way to reconcile a huge disparity between the filament elastic modulus E and the whole CSK elastic modulus (G) is to scale E with the relative density (volume fraction, Φ) of filaments within the CSK using the cellular solid network model. Cellular solids are discrete networks comprising interconnected elastic rod elements that stretch, bend, and twist in response to an applied load. Assuming that stresses and strains in discrete elements can be described from equations of continuum mechanics (this is known as the affine assumption), it can be shown that the if the main mode of deformation of individual elements is stretching, then G ~ EΦ, whereas if the main mode of element deformation is bending and/or twisting, then G ~ EΦ² (71, 203). (Note that this is not thermally driven bending, rather it is mechanically driven by externally applied forces.) Taking into account the short physiological length of cytoskeletal F-actin, that is, L_c ⪡ L_p, its very high resistance to stretching (E ~ 10⁹ Pa) and low resistance to bending (B~10⁻¹ pN·μm²), Satcher and Dewey (160), proposed a cellular solid model of the actin CSK where filament bending is the main mode of deformation. For cytoskeletal actin Φ ~ 10⁻³, and therefore the model predicts the cytoskeletal stiffness of G ~10³ Pa (160, 161, 173). A similar prediction would be obtained for CSK-based microtubules whose E and Φ are similar to that of cytoskeletal F-actin (173), although their bending rigidity is much higher (B ~10¹ pN·μm²). In the case of actin stress fibers, however, stretching rather than bending should be the main mode of deformation since they have much lower resistance to stretching (E ~ 10⁶ Pa) and much higher resistance to bending (B ≥ 10² pN·μm²) than either microfilaments or microtubules. Thus in a cellular solid network made up of stress fibers, the main mode of deformation would be tension and hence G ~ EΦ. Assuming that the relative density of stress fibers is similar to that of actin filaments, Φ ~ 10⁻³, we predict that G ~ 10³ Pa. Based on the above quantitative predictions, it follows that the stiffnesses of major stress-bearing networks of the CSK are within the same order of magnitude, G ~10³ Pa, which is consistent with values measured in living cells.

In summary, the cellular solid model shows how different modes of deformation of individual cytoskeletal filaments, their elasticity, and their relative density in the cytoskeletal network can contribute to the overall elasticity of the CSK. The model can predict cytoskeletal elastic modulus that is quantitatively consistent with data obtained from living cells. However, the cellular solid model does not account for the strain-hardening behavior of cells nor does it take into account the contribution of cytoskeletal prestress to the mechanical responses of the cell. Moreover, it is a macroscopic model that does not naturally incorporate the contributions of thermal and nonthermal dynamics of the CSK, as well as the contributions of cross-link mechanics on the mechanical response of the cell and therefore, it is not a complete model of cytoskeletal mechanics.

Polymer networks

One strategy in studies of cytoskeletal mechanics is to use actin polymer networks reconstituted in vitro as a minimal model of the CSK. This approach avoids the complexity of measurements in living cells and instead focuses on few mechanisms that are believed to be key determinants of cytoskeletal mechanics. Purified actin forms long filaments of L_c = 10 to 20 μm which when in solution form entangled networks. Since this L_c is close to filament's L_p, it follows that stiffness of entangled F-actin networks primarily originates from both entropic and enthalpic elasticity of F-actin. Rheological measurements of stiffness of entangled actin networks (69,87,105,209) have yielded values far lower than measured stiffness of living cells. Since in living cells L_c of F-actin does not exceed 1 μm, making it very difficult for the filaments to entangle, it is highly unlikely that the cytoskeletal actin is organized as an entangled network. Addition of cross-linking actin-binding proteins to reconstituted F-actin networks has produced higher network stiffness (68,106,108,195,208) than in entangled networks, but still orders of magnitude are lower than that found in living cells. This higher stiffness of the cross-linked networks than of the entangled networks may reflect the contribution of elasticity of cross-linkers, as well as an increase in the enthalpic contributions of actin filaments since cross-linking effectively reduces filament's L_c.

Theoretical studies of entangled and cross-linked actin networks produced predictions of their equilibrium elastic modulus (G). By considering only the conformational changes of F-actin, MacKintosh et al. (130) obtained that for an entangled network $G~L_p^{1.4}{k}_{b}T∕{\xi }^{4.4}$ and for a densely cross-linked network $G~L_p^2{k}_{b}T∕{\xi }^5$, where ξ is the average spacing between filaments. For L_p = 15 μm, T = 310 K, and ξ = 0.3 μm (68,69), the predicted value for the entangled network is G ~ 10⁻² kPa and for the densely cross-linked network G ~ 10⁻¹ kPa, consistent with experimental data from in vitro studies.

To address the discrepancies between the cytoskeletal and in vitro actin mechanics, Gardel and co-workers (66, 67) attempted to mimic the cytoskeletal actin network using in vitro actin networks formed at physiological concentrations, where actin filaments were shortened by gelsolin to L_c of 1 to 2 μm, which is close to their physiological length, and cross-linked with the physiologically relevant filamin-A. Because of high flexibility of filamin-A, cross-links are highly compliant, and have little effect on the linear mechanical response (i.e., constant G) of the network for low-applied stresses (<1 Pa). However, under large-applied stress (>1 Pa), a dramatic nonlinearities and a strain-hardening effect were observed, much greater than in the case of rigidly cross-linked networks (68). By measuring incremental stiffness superimposed to the states of large shear prestress, a linear stiffness versus shear prestress relationship was obtained (66), Figure 1, which is similar to the stiffness versus contractile prestress relationship observed in living cells (198,202). Importantly, the values of the stiffness obtained at high prestress are quantitatively consistent with the values from intact cells at an approximately same stress level.

Figure 1.

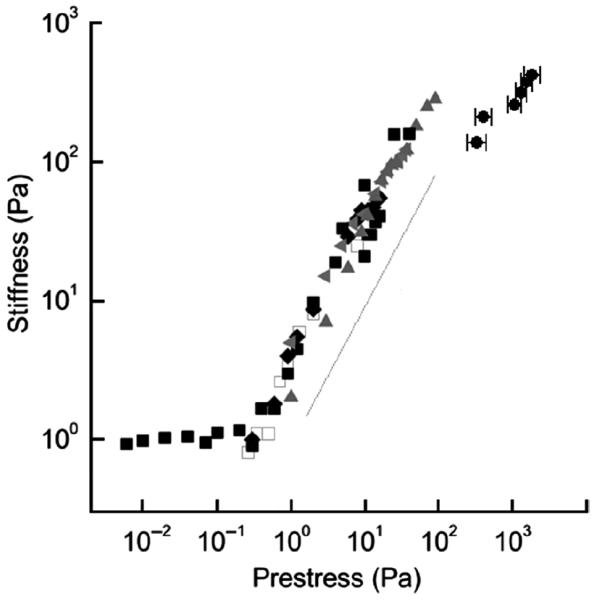
Stiffness of actin networks cross-linked with filamin-A increases with increasing shear prestress. Measurements were carried out using a stress-controlled parallel plate rheometer in gels with different actin concentration (c_A) and different molar ratios of filamin-A (R): c_A = 36 μM, R = 1/100 (open squares); c_A = 48 μM, R = 1/100 (solid squares); c_A = 74 μM, R = 1/100 (diamonds); c_A = 36 μM, R = 1/50 (left-pointing triangles); c_A = 53 μM, R = 1/50 (upward-pointing triangles). For comparison, data from measurements in living airway smooth muscle cells (202) are included (solid circles near the top right corner). Modified from reference 66 with permission from Gardel et al.

Studies of Gardel and co-workers (66) have shown that flexibility and nonlinear elasticity of filamin-A cross-linker are critical for the consistency of the filamin-actin model's ability to replicate cellular data. On the other hand, mechanical measurements in cells deficient in filamin-A showed that their strain-hardening behavior is similar to control cells (36,110), suggesting that filamin-A may not have such a central role in living cells as it does in the in vitro model. It is also unclear how externally applied shear prestress translates to steady tension on the filamin-actin networks in comparison to the cytoskeletal prestress generated by the cell's contractile motors. In that regard, cross-linked actin networks activated by myosin may be a more realistic description of the CSK.

It has been shown that in entangled actin networks with dispersed myosin molecular motors, activation of myosin motors by ATP causes enhanced filament sliding that leads to more fluidized mechanical properties (95, 128). However, in actin networks cross-linked by extremely strong, irreversible cross-links (biotin-avidin), molecular motor activity leads to strain-hardening behavior (141), consistent with the cellular behavior, but quantitatively the stiffness (~10² Pa) is at the lower bound of the range of measured cellular stiffness (cf. ⁷).

Another type of an in vitro model of the CSK is dendritic (branching) networks. These networks can mimic the branching actin structures in lamellipodia of motile cells (184), which are exposed to compressive loads during lamellipodia protrusion as the leading edge pushes against the cell membrane. Chaudhuri and colleagues (29) measured the response to compression of actin dendritic networks formed in vitro. They found that following an initial strain-hardening regime, the networks exhibited a reversible softening regime at higher loads. This stiffening-softening response is characterized by stiffnesses (~1 to 5 kPa) that are higher than the stiffness measured in cross-linked actin networks, suggesting that there may be a difference in the mechanisms by which dendritic and cross-linking networks resist deformation. Chaudhuri et al. (29) explained the observed softening behavior as a consequence of elastic buckling of individual actin filaments under compression that avoids catastrophic fracture of the network. The observation of both stiffening and softening suggests a complex interplay between entropic and enthalpic elasticity in determining the mechanical properties of actin networks.

In summary, studies of mechanics of reconstituted actin networks revealed the importance of cross-linker flexibility, filament length, and the relative contributions of entropic vs. enthalpic elasticity of F-actin in cytoskeletal mechanics. The ability of actin-filamin networks to replicate cellular mechanical properties indicates their potential as a synthetic model of the CSK.

Control of cytoskeletal shape by prestress

Critical to cell shape stabilization is the fact that the CSK carries pre-existing tensile stress (prestress), even before application of an external force. Owing to mechanical interconnectedness of the cytoskeletal lattice, the prestress is transmitted to all of the structural elements of the cell. Results from mechanical measurements on various types of cultured adherent cells indicate that changes in cytoskeletal prestress are paralleled by changes in cell stiffness, regardless of the means by which the prestress is modulated or the types of experimental techniques that are utilized (21, 44, 55, 56, 58, 94, 132, 135, 153, 158, 159, 168, 178, 191, 197, 198, 202). Prestress in the actin cortical membrane has been studied as early as 1930s (34). However, its importance for cellular mechanics has begun to be fully understood and appreciated much later, following the arrival of the cellular tensegrity model in the early 1980s (103,104). Here we describe mechanisms by which prestressed cytoskeletal lattice resists shape distortion with a special focus on the cellular tensegrity model.

Cytoskeleton as a prestressed reticulated structure

Stress-bearing elements of prestressed reticulated structures carry tensile forces before application of an external load. This initial state of tension defines the prestress as a sum of all tensile forces transmitted across an arbitrary trans-sectional surface per unit surface area (cf. ^62,173,175). In the absence of the prestress, the intrinsic resistance to shape distortion is lacking in these structures because freedom of motion of their structural elements is not fully constrained. In the presence of a prestress, however, their taut structural elements move relative to each other until they attain a configuration which provides equilibrium between external forces and those carried by the structural elements. The larger the initial tensile forces carried by those elements, that is, the larger the prestress, the smaller the deformation those structures would undergo at a given applied force before they attain a new equilibrium configuration. Consequently, the greater the prestress, the greater the stiffness of the structure. This implies that the structure secures resistance to distortion from the prestress and that the prestress confers the shape stability to the structure as expressed by its stiffness. This stiffening with increasing level of prestress is characterized by an approximately linear relationship between the stiffness and the prestress (62,173,175,180). This also implies that the stiffness of structure is on the same order of magnitude as the prestress. Importantly, the manner in which the prestress is generated and balanced does not qualitatively affect this relationship; neither do elastic properties of individual structural components bear significant effect (175, 196). This linear relationship between the stiffness and the prestress is therefore an a priori prediction of prestressed structures.

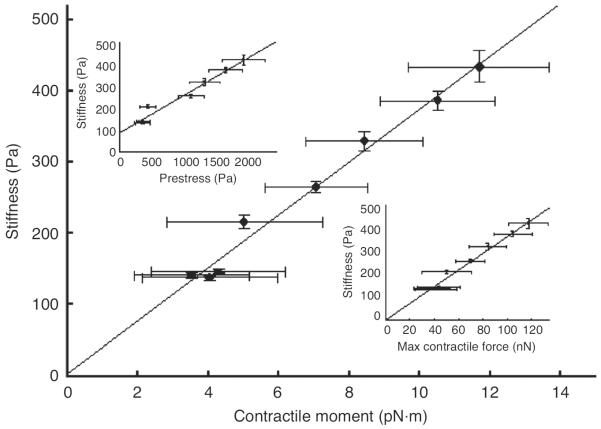
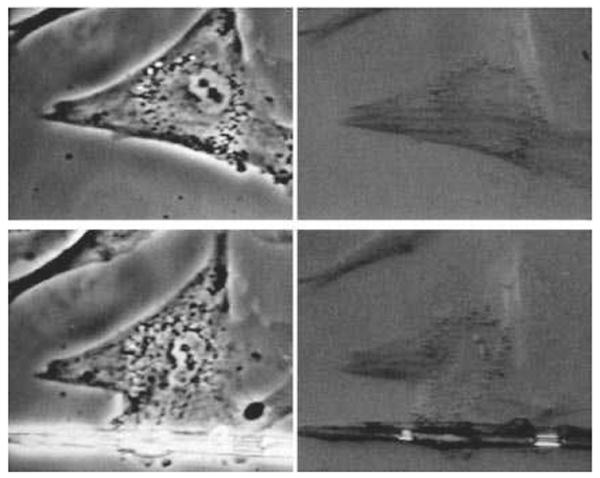
To test this prediction, we measured independently cell stiffness and various metrics of cell contractile prestress in living airway smooth muscle cells whose contractility was modulated by graded doses of contractile (histamine) and relaxant (isoproterenol) agonists (179, 198, 202). Cell stiffness was measured by the magnetic twisting cytometry (MTC) technique, which applies mechanical force to the CSK by magnetic twisting of integrin-bound ferromagnetic beads (196). The contractile prestress was determined by the traction microscopy technique (19, 189), which measures traction at the cell-substrate interface that arises in response to cell contraction (Figs. 2A and 2B). The data indicate a strong linear association between cell stiffness and the prestress (Fig. 3), which is consistent with the a priori prediction of prestressed models of the CSK.

Figure 2.

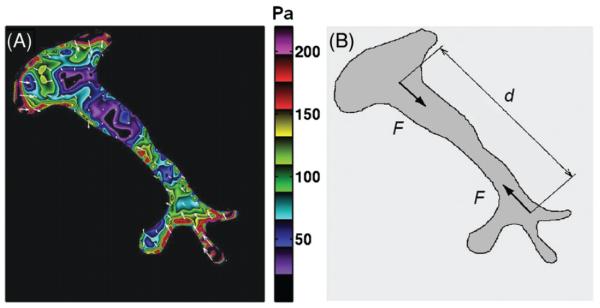
(A) Traction filed distribution measured by traction force micrscopy (19) in a living human airway smooth muscle cell treated with 10 μM histamine; white arrows indicate directions of local tractions and the color code indicates the magnitude of traction in Pa. Reproduced from reference 189 with permission from Tolić-Nørrelykke. (B) The traction filed from (A) can be replaced by a pair of forces (dipole) of magnitude F and at distance d. The strength of the dipole or the net contractile moment is given as the product F·d.

Figure 3.

Stiffness of airway smooth muscle cells increases proportionally with various metrics of cell contractile stress. The relationship between the stiffness and the net contractile moment is shown. Top inset: relationship between the stiffness and the cytoskeletal prestress. Because the traction must balance the contractile prestress, the prestress is computed from a force balance at a section of the cell perpendicular to its long axis, where the prestress is given as the net force normalized by the cell cross-sectional area. Bottom inset: relationship between stiffness and the maximum contractile force of the CSK. The stiffness is measured by the magnetic twisting cytometry technique (132). Reproduced from reference 202 with permission from Wang.

In addition to stimulating contractile force generation by causing an increase in the number of myosin cross-bridges attached to actin filaments, contractile agonists also induce polymerization of cytoskeletal F-actin. Both effects are known to cause an increase in cell stiffness (61, 137, 186). Thus, the observed stiffening behavior in response to the histamine treatments shown in Figure 3 may be nothing more than the effect of cytoskeletal remodeling and/or myosin cross-bridge recruitment. On the other hand, increasing the cytoskeletal prestress by rapid equibiaxial cell stretching, which has a little effect on myosin cross-bridge recruitment and on actin polymerization, also produces cell stiffening (153,158,159,191). Even when actin-myosin cross-linking is inhibited by DB-cAMP (dibytryl adenosine 3′ ,5′ -cyclic monophosphate), cells still exhibit stiffening in response to stretching (159). While the contribution of cytoskeletal remodeling to cell stiffening cannot be ruled out, the fact that stiffening persists, regardless of how the prestress is modulated, strongly suggests that the cell stiffness may be determined primarily by the prestress.

It is important to emphasize distinctions between the linear dependence of the stiffness on the prestress as predicted by the prestressed reticulated model of the CSK and a similar relationship obtained from measurements on the cross-linked actin-filamin networks (66; Fig. 1). First, in the prestressed CSK model this relationship is mainly due to geometrical reorganization of the cytoskeletal lattice in response to an applied external load. This prediction would not change substantially if the cytoskeletal components are linearly elastic or nonlinearly elastic. In the actin-filamin networks, however, the stiffening is mainly due to the nonlinear elasticity of the filamin-A cross-linker; for if filamin-A were linearly elastic, the network stiffness would remain constant at all levels of the prestress. Second, in the prestressed CSK model the prestress is essential for stabilizing the shape and resisting shearing loads; in the absence of prestress, there is no resistance to shearing (i.e., structural stiffness would be zero). On the other hand, the actin-filamin networks have a finite stiffness even before application of prestress (Fig. 1) and therefore, the prestress is not essential for their stabilization. Consequently, when a shear prestress is applied to the actin-filamin network it does not destabilize it but rather produces a stiffening effect. On the other hand, if the absence of prestress leaves internal freedom of motion of structural elements unconstrained, any shear stress would destabilize such a structure. Thus, there is a fundamental difference in the mechanisms by which prestressed models of the CSK and the actin-filamin networks resist shape distortion. In a physiological condition, under normal mechanical loading of the cell, both mechanisms might be at work.

A secondary, but not less important question is how the cytoskeletal prestress is balanced. One possibility is that the prestress is balanced in its entirety by adhesive tethers to the ECM, for example, like a spider's web (38). Another possibility is that at least part of the prestress is balanced by internal compression elements that exists within the CSK and by swelling pressure of the cytosol (cf. ⁹⁹). The main difference between these two descriptions is that in the former the force balance at each internal node of the network includes only tensile forces, and in the latter it also includes compressive forces. Despite this distinction, both descriptions share the same central mechanisms by which the cytoskeletal lattice opposes changes in shape due to externally applied load, namely the prestress.

A special class of prestressed networks where tension in elastic line elements is balanced by compression of internal struts is tensegrity architecture. Ingber proposed tensegrity as a building principle of biological design that governs the CSK (97–99,103,104). During past decades, the cellular tensegrity model has gained a considerable interest in cell biology because it can account for a number of behaviors observed in living cells.

Cellular tensegrity model

Tensegrity or tensional integrity is a structural-relationship principle that describes reticulated structures whose structural stability is maintained through the interaction of a continuous network of tensed (prestressed) elements (cables) and isolated compression elements (struts) that counterbalance tension (65, 154), Figure 4. At each nodal point, compression of a single strut balances tension of several cables. If the structure is anchored to the substrate, then at each anchoring node compression in the strut and/or anchoring force balance tension in the cables. In the absence of prestress (i.e., cables become slack), the structure becomes unstable since rigidity and/or connectedness of its structural elements are insufficient to fully constrain their freedom to move and deform. Consequently, tensegrity structures do not have intrinsically stable shape (like, e.g., rocks, bricks or rubber), and thus they require the prestress for shape stabilization. An example of a tensegrity structure is a pop tent where tension (i.e., prestress) in the fabric is counterbalanced by compression in the poles and by anchoring forces of the ground pegs. Maintaining this tension is critical for stabilization; otherwise the tent would collapse since neither the fabric possesses structural rigidity nor the poles possess structural connectedness that could provide stability to the tent.

Figure 4.

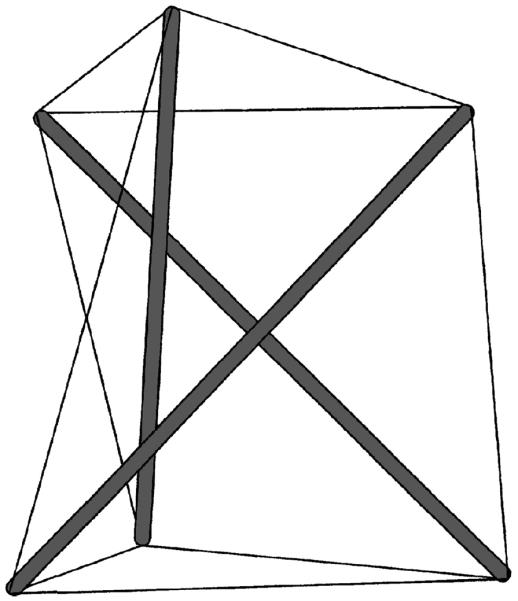
A simple tensegrity structure comprising three compression-supporting struts (thick gray bars) interconnected with nine pre-tensed cables (thin black lines). At each node, compression of a single bar balances tension of three cables.

The pivotal idea of the Ingber's cellular tensegrity model is that cytoskeletal prestress is maintained through a complementary force balance between contractile microfilaments that actively generate tensional forces and other intracellular and extracellular molecular structures that oppose and balance these forces (97–104). Cytoskeletal contractile stress is transmitted to the ECM via integrin focal adhesion plaques (49, 80). Traction forces that arise at the extracellular adhesions are largely responsible for opposing cytoskeletal contractile forces (6, 19, 43, 73, 198, 202). However, contractile forces are also opposed by cytoskeletal microtubules (12,81,92,177,198) that can buckle in that process, but carry high levels of compressive forces (~10² pN) per microtubule when laterally supported by intermediate filaments (14, 177) or by viscous cytoplasm (12). A protein that connects F-actin with microtubules is MACF1 (31, 126). Experimental data from various studies confirm that cells utilize this type of force balance to self-organize and to stabilize their CSK (48, 92, 111, 151, 177, 197, 198). Altering this force balance either internally by modulating the contractile stress, or externally by applying mechanical forces to the ECM and the cell, leads to redistribution of tension and compression in the load-bearing components of the CSK and linked structures that can, in turn, alter shape stability of the whole CSK and change biochemical activities at the nanometer scale (176). (Mechanochemical control of molecular assembly of the CSK via the complementary force balance is described below in section “Mechanotransduction.”)

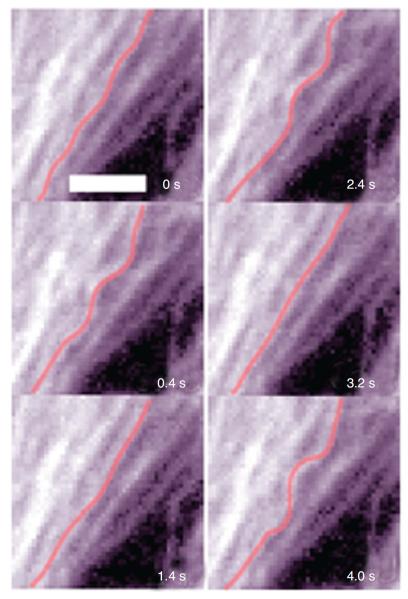
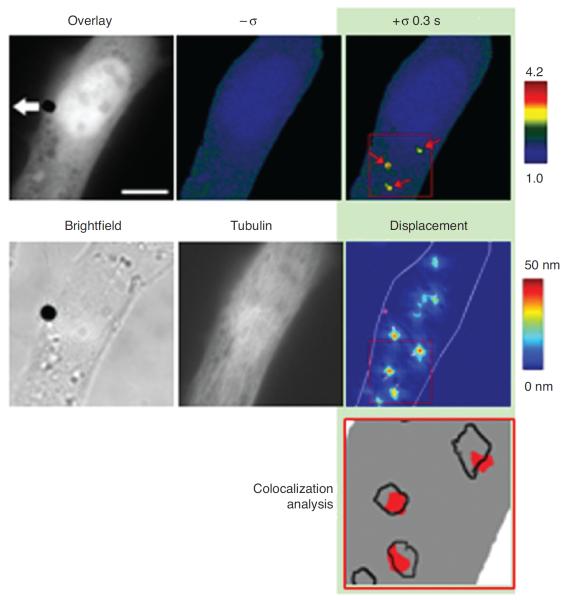
Microtubules and ECM adhesions traction forces have been put forward as candidates for balancing the prestress in the cellular tensegrity model. Microscopic visualization of green fluorescent protein-labeled microtubules of living cells shows that microtubules buckle as they oppose contraction of the actin network (12, 198, 204), Figure 5. It was not known, however, whether compression forces that cause this buckling could balance a substantial fraction of the contractile prestress. If they do, then disruption of microtubules should cause a significant shift of forces from the CSK to the ECM, causing a substantial increase in traction, providing contractile forces remain unaltered. To investigate this possibility, we used the traction cytometry technique to measure changes in the traction map caused by disruption of microtubules (177). We found that in highly stimulated and spread human airway smooth muscle cells, the traction increases on an average by 13% following disruption of microtubules by colchicine. We also calculated the elastic energy stored in the flexible substrate as a work done by traction forces on deformation of the substrate (19). We obtained that this energy increases following disruption of microtubules (177). By depicting cytoskeletal microtubules as slender elastic struts supported laterally by soft intermediate filament network and using the post-equilibrium buckling theory (188), we found that the energy associated with buckling of microtubules is quantitatively consistent with the increase in substrate energy following microtubule disruption (177). In a subsequent study, Hu et al. (92) showed that contribution of microtubules to balancing the contractile prestress increases as cell spreading decreases; as the cell projected area in contact with ECM decreases from 1800 to 500 μm², the percent change in traction following disruption of microtubules increases from a few percent to 80%. Taken together, these results suggest that microtubules could balance a substantial fraction of the prestress, depending on the extent of cell spreading (92, 170). Since in vivo cells seldom exhibit highly spread forms, their contribution to stress distribution in the CSK can be very significant.

Figure 5.

Microtubules visualized over time in a beating cardiac muscle cell expressing green fluorescent protein-tubulin. Whenever the cell contracts, the microtubule (highlighted in red) buckles indicating that it resists contraction of the cytoskeletal actin network. Scale bar = 3 μm. Reproduced from reference 12 with permission form Brang-wynne et al.

While the cellular tensegrity model has been successful in describing various behaviors of cells, there are prominent critics who question the basic premises of the model. We address some of those critiques below and also try to clarify contentious issues and confusions.

The word tensegrity has come to mean different things to different investigators. In the structural mechanics literature, clear distinction between tensegrity structures and other prestressed structures is made based on the presence of internal compression-supporting struts in the former and their absence in the latter (cf. ¹⁹⁴). In the mathematical literature, tensegrity is formulated based on the principle of elastic stability, that is, all prestressed structures assume equilibrium configuration that minimizes their potential energy. Insofar as this principle holds, all prestressed structures, regardless of the manner by which the prestress is balanced, are tensegrity structures (cf. ³⁵). In his studies, Ingber tends to use a broader notion of tensegrity, close to the energetic formulation (cf. ^{99, 102}), whereas Heidemann and colleagues tend to use the more restrictive notion of tensegrity that is based on the structural formulation (82, 102). This unsettled difference in the usage of the term “tensegrity” became source of contention and confusion. The fundamental difference between the structural form and energetic form of tensegrity is how the prestress is balanced. The former requires that the substantial portion of the prestress is balanced by internal compression-supporting elements, whereas the latter does not require them. Semantic and substantive issues aside, both are prestressed structures and both utilize prestress to resist shape distortion.

Critics of the cellular tensegrity model tend to question the importance of microtubules as compression-supporting elements of the CSK. Their critiques are partly based on the circumstantial evidence that the observed wavy shape of cytoskeletal microtubules results from fluid flow in the surrounding cytosol and therefore microtubules do not support compression (82).

Experimental findings which show that in living cells microtubules carry a substantial compressive load as they resist actin contraction (12, 15, 92, 177, 198) rule out such an interpretation. While these findings do not prove the cellular tensegrity hypothesis, they are consistent with one of its main premises—existence of tension-compression synergy within the CSK.

Another critiques are based on the fact that the CSK is a non-elastic and dynamic remodeling network, exposed to dynamic external loads and internal thermal and non-thermal fluctuations, whereas tensegrities are static elastic structures. It has been shown that in response to transient uniform substrate stretching (a brief stretch-unstretch maneuver), adhering airway smooth muscle cells initially soften (“fluidize”) and then solidify subsequently (115, 190). The greater the prestress before the cells are subjected to transient stretching, the greater the extent of this fluidization. These observations ostensibly conflict with the idea that an increase in mechanical distension of cells leads to build up of cytoskeletal prestress, which in turn leads to cell stiffening through tensegrity mechanisms. Fluidization is consistent with the behavior of soft glasses that are dynamic, metastable, nonequilibrium materials (see the next section for details; ¹⁹⁰), quite opposite from static, self-equilibrated, stable tensegrities. Another possibility is that transient stretching produces structural disorder within the CSK such that the complementary force balance between molecular components is temporarily lost, which leads to a loss of structural stability and to softening. It is known that steady loading of a physiological magnitude generally leads to stiffening (strain-hardening) rather than softening of a living cell (32, 36, 37, 96, 110, 122, 196, 197), suggesting that the softening during a transient stretching of the whole cell might originate from decoupling cytoskeletal filaments from their cross-linking proteins. Over longer timescale, however, the structural organization of the CSK and force balance is regained through structural remodeling, which leads to the observed solidifying of the CSK through restoration of prestress (190).

In summary, the cellular tensegrity model has articulated the role of cytoskeletal prestress that has become invaluable to the cellular mechanics field. The model also revealed the mechanical role of microtubules as compression-supporting elements of the CSK. On the other hand, tensegrities (and other prestressed reticulated models of the CSK) are macroscopic, static elastic structures that do not naturally incorporate effects of dynamic fluctuations of cytoskeletal biopolymers, nor do they include cross-linker and contractile motor mechanics. In order for tensegrity to become a complete model of the CSK, it has to account for the dynamic nature of the CSK. Whether such undertaking is feasible and realizable remains to be seen.

Cytoskeletal prestress as a determinant of cell rheological behaviors

The problem of cell dynamic resistance to deformation is treated in detail in the chapter entitled “Material Properties of the Cytoskeleton.” However, for completeness, we discuss this problem in this section emphasizing the role of the cytoskeletal prestress.

Living cells display viscoelastic behavior, which is characterized by time- and frequency-dependent material responses. Unlike elastic materials that attain equilibrium instantaneously following the application of an external loading, in viscoelastic materials this process is delayed and impeded by internal viscous stresses. The response of viscoelastic materials to a sinusoidal oscillatory loading is described by the dynamic modulus (G*), which is defined as the stress-to-strain ratio under oscillatory conditions. Mathematically, it is a complex quantity whose real part is indicative of the elastic response and is referred to as the elastic (storage) modulus (G₁), while the imaginary part is indicative of the viscous response and is referred to as the viscous (loss) modulus (G₂), that is, G* = G₁ + iG₂, where $1=\sqrt{-1}$ is the imaginary unit. The magnitude (|G*|) of G* equals the ratio of the stress amplitude to the strain amplitude and can be obtained as $\mid G{\mid }^{\ast }=\sqrt{G_1^2+G_2^2}$. Because of the dampening effect of viscous forces, there is a phase lag (φ) between stress and strain, which can be obtained as tanφ = G₂/G₁, where 0 ≤ φ ≤ π/2. In the limit when φ = 0, stress and strain are in phase, G* = G₁, and the material response is purely elastic, and when φ = π/2, stress and strain are out of phase, G* = iG₂, and the material response is purely viscous. When 0 < φ < π/2, stress and strain are out of phase and the material response is viscoelastic.

In response to sinusoidal forces, cells continuously deform such that their dynamic modulus G* scales with frequency (f) of the imposed loading according to a weak power law, G* ~ f^α, where α is a constant, over a wide range of frequencies (10⁻² to 10³ Hz; cf. ^88,89), Figure 6. The power-law behavior implies that macroscopic deformation of the cell is governed by processes that are not tied to any specific frequency scale, that is, that cell's rheological behaviors are not tied to any particular internal time scale or any distinct molecular rate process (55, 56, 125). Consequently, the power-law behavior cannot be described by simple spring-dashpot models with a discrete number of time constants (e.g., Maxwell model, Voigt model, and a standard linear solid model), although models composed of a large number of discrete units with distributed time constants can simulate it (cf. ⁷). Instead, this behavior is usually described by an empirical law known as structural (hysteretic) damping (cf. ^55,56,125). Mathematically, structural damping can be described by the following equation

$$G^{\ast }=A{f}^{\alpha }\cos (\alpha \pi ∕2)+iA{f}^{\alpha }\sin (\alpha \pi ∕2),$$ (1)

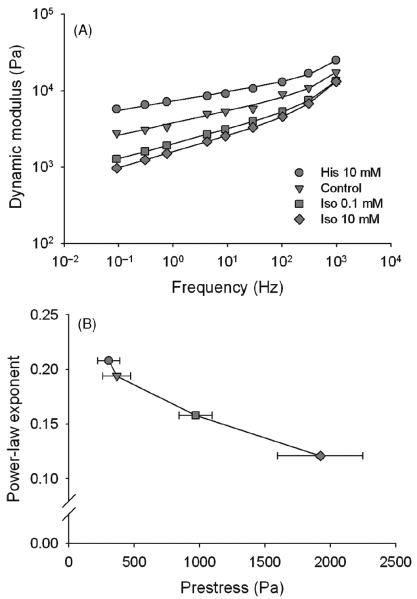
where A is a constant. The first term on the right-hand side of Eq. 1 equals G₁ and the second term equals G₂. It follows from Eq. 1 that |G*| = Af^α and that φ = απ/2 and hence, φ is independent of frequency. In living cells, observed values of scaling exponent α range from 0.05 to 0.35, depending on the cell type, the experimental technique and the cytoskeletal prestress. Exponent α can be viewed as an index of transition between Hookean elastic solid (α = 0) and Newtonian viscous fluid (α = 1) behaviors, whereas for 0 < α < 1, the cell behavior can be characterized as viscoelastic (55, 56, 125, 179). The power-law behavior of cells persists over a wide range of experimental conditions, including modulations of the cytoskeletal prestress, regardless whether cells are probed locally or on the whole cell level (1, 7,44,46,55–57,89,121,125,148,158,168,178,179,191,210). When the cytoskeletal prestress increases/decreases, G* also increases/decreases (Fig. 6A), while α decreases/increases (44,55,56,125,158,168,179,191; Fig. 6B). Since α is an index of transition between elastic solid and viscous fluid behaviors, it follows that this transition is controlled by the cytoskeletal prestress. Thus, these findings revealed an intriguing role of the prestress: although it maintains structural stability of the cell under applied mechanical loads, it may also regulate rheological properties of the cell that are essential for other cell functions.

Figure 6.

(A) Magnitude of the dynamic modulus of cultured airway smooth muscle cells increases with increasing frequency of loading according to a weak power law. Measurements were carried out using the oscillatory magnetic twisting cytometry technique (55) under control conditions and following treatments with a bronchoconstriction histamine (His) and bronchodilator isoproterenol (Iso). Data are means, SE do not exceed 5% and are not shown; solid lines are best fits. (B) The power-law exponent decreases with increasing contractile prestress. Data are means ± SE obtained from the slopes of the power-law relationships in (A); data for the prestress are means ± SE obtained from measurements in Figure 3 (top inset). Modified from reference 179 with permission from Stamenović et al.

During recent years, soft glass rheology (SGR) has gained a great interest in cell biology since it can account for the power-law as well as other dynamic behaviors observed in living cells (3,18,44,55,56,76,125,190). It is a semi-empirical theory derived from soft matter physics (169). Because soft glasses include a diverse type of materials, including foams, emulsions, slurries, pastes and colloids, their common mechanical behavior must not be determined by specific molecular mechanisms and organization, but rather it reflects generic system properties at some higher level of structural organization. These generic features include that the ultrastucture of soft glasses is discrete, disordered, crowded, metastable, and away from thermodynamic equilibrium. Due to the crowdedness, structural elements (whatever they may be) are trapped by interactions with neighboring elements (e.g., cross-links, hydrophilic interactions, charge effects, or steric constraints). To escape these traps, thermal Brownian fluctuations alone are not sufficient. Instead, structural elements are envisioned as being agitated and jostled by their mutual interactions with neighboring elements. Physical origins of these nonthermal agitations are largely unknown. However, their influence can be represented by an empirical, nondimensional parameter referred to as an effective noise temperature (x). When x = 1, particles cannot escape from their energy traps and on the macroscale material behavior is perfectly elastic; this state is known as the glass-transition. When x > 1, particles can escape from the traps and the microstructure is becoming disordered; as a result, the material can flow like a fluid. Under applied mechanical stress, soft glasses undergo structural rearrangements during which structural elements cross over nonthermal energy barriers. On the macroscale, this results in a very slow, power-law deformation. According to the SGR theory, x is directly related to the power-law exponent α as x = α + 1 (169). Since experiments show that α is controlled by the cytoskeletal prestress, it follows that the cytoskeletal dynamics is also controlled by the prestress; that is, that an increase/decrease in the prestress causes the level of the effective noise temperature to decrease/increase.

In addition to the power-law rheology, soft glassy materials are characterized by aging, rejuvenation, and fluidization, all of which have been observed in living cells (18,115,190). Because of crowding, particles can become trapped by their surrounding neighbors. With time, however, the system will jump from one metastable state to another, and slowly evolve into configurations that are more and more stable. This is known as aging and on macroscale it is characterized by increasing stiffness (18). This process can be reversed by applying a sufficiently large oscillatory shear stress that can provide an additional energy that can overcome energy barriers and drive structural rearrangements. As a consequence, the stiffness returns to its earlier value. This is known as rejuvenation (18). In response to transient substrate stretching, cells exhibit rapid softening followed by a slow regaining of stiffness. This process is known as fluidization and can be explained by similar mechanisms as aging and rejuvenation (115,190). Importantly, all these soft glassy behaviors of living cells are dependent on the level of cell contractility and thereby on the level of the cytoskeletal prestress.

The observations that showed that glassy-like activities of cells are closely associated with changes of cell contractility lead to an interpretation that the nonthermal fluctuations of the cytoskeletal microstructure may be ATP-related (3,76,121,190). Gunst and Fredberg (76) have shown that integrated molecular transitions that occur within the contractile cycle of the airway smooth muscle can be interpreted in the context of SGR, suggesting that the CSK of airway smooth muscle cells may behave as a glassy material whose mechanical function is driven by an effective noise temperature. While it is plausible that nonthermal fluctuations in cells may be ATP-driven, it is noteworthy that actin gels cross-linked in vitro with filamin-A, also exhibit a weak power-law behavior over the same timescale as living cells, with the power-law exponent exhibiting the same dependence on the prestress as in living cells (67). This behavior of inert gels is certainly not ATP-driven, suggesting that the dependence of the power-law exponent on the prestress that is observed in both living cells and in inert actin gels may be a generic property of prestressed actin structures rather than a specific ATP-dependent activity.

There are other theories that can explain the power-law rheology of cells. The transition between the fluid and solid behavior has been often framed in the context of sol-gel transition (181,187,206). Gels near a critical gelation point exhibit power-law phenomena (cf. ¹²⁰) similar to soft glasses near glass transition (169). In that regard, it is important to point out that both gel transition and glass transition are believed to arise from the same mechanisms, namely kinetic arrest due to crowding of clusters (164). The power-law behavior of cells could also result from folding, unfolding and conformational changes of cytoskeletal proteins (16,123). All these theories, however, do not account for the effect of the prestress on the power-law behavior.

Two new models were recently proposed with the aim of linking the power-law rheology to the prestress. Both models focus on the dynamics of individual semiflexible polymers under tension. A key premise in those models is that mechanical tension carried by semiflexible polymers of a prestressed cytoskeletal lattice influences their molecular dynamics and thereby affects the rheology of the whole CSK. Both studies used the wormlike chain (WLC), which is as a minimal model of a semiflexible polymer (50), as a basis of their modeling and in both models the WLC dynamics is thermally driven. In one of the models (131,157), an enthalpic effect leads to nonlinear elasticity of bonds, causing a strain-hardening behavior where the stiffness of the chains rises and a power-law-like time-dependent deformation (creep) flattens as increasing tension is applied. This model represents a potential link between the concept of prestress from tensegrity and polymer dynamics (172). The second model, which is called the glassy WLC model (116, 117, 163), is based on the premise that biopolymers are themselves sticky and will interact as they slide past each other to relax applied tension. This increased friction slows the relaxation modes in comparison to those of the ordinary WLC model and readily leads to cell-like behaviors. Conceptually, this model is similar to the active cross-linked gel model (88).

When elastic cables in a tensegrity model are replaced by viscoelastic Voigt elements (i.e., a spring and a dashpot in parallel), it can account for the observed dependence of the cellular dynamic modulus on the prestress (23, 24, 183). During deformation, Voigt cables undergo geometrical rearrangements that cause a redistribution of their viscoelastic time constants such that a qualitatively new viscoelastic behavior of the structure as a whole emerges. Since geometrical rearrangements in tensegrities are governed by the prestress, the time constant redistribution becomes prestress dependent, which explains why the dynamic modulus changes with the prestress. Viscoelastic tensegrity do not naturally account for the power-law behavior since they are composed of a discrete number of structural elements, which implies a discrete number of viscoelastic time constants, whereas power-law rheology implies a continuous spectrum of time constants. Given the hierarchical nature of living tensegrity systems that have structural elements of various size scales (99), these elements may naturally display a large range of time scales that could contribute to the power-law behavior.

Measurements of the oscillatory response or airway-smooth muscle cells over an extended range of frequencies (10⁻³-10³ Hz), which includes physiological frequencies, revealed the existence of two distinct power-law regimes separated by a plateau region from 10⁻¹ to 10⁰ Hz (178). Similar behavior was also reported for other cell types, under different loading conditions (46,114,148,178). Two power-law regimes separated by a plateau region over a well-defined frequency range imply that rheological processes are not frequency scale invariant. While theoretically SGR allows the possibility that at very low frequencies a power-law regime changes to another regime (169), its current mathematical formulation (Eq. 1) allows only a single power-law regime (55, 56, 125). Mechanisms that lead to the multiple power-law behavior of cells remain largely unknown. A theoretical model of myosin-activated entangled actin networks can predict a similar behavior (128) but, as pointed out earlier, entangled actin networks are not adequate model of cytoskeletal mechanics. Chowdhury et al. (33) proposed a model based on nonequilibrium to equilibrium transition of noncovalent protein-protein interactions as a possible mechanism for explaining the multiple power-law behavior of cells, but the model does not account for the plateau region that separates the power-law regimes.

In summary, the weak power-law, aging, rejuvenation, and fluidization behaviors that are observed in living cells are signatures of soft glass dynamics. These phenomena are also closely associated with the cytoskeletal prestress—a behavior that cannot be explained by the current SGR model. Cross-linked actin networks, on the other hand, can replicate the basic power-law and prestress-dependent behaviors of living cells, suggesting that the mechanisms that they embody may be essential for understanding dynamic behaviors of the CSK.

Computational analysis of cytoskeletal mechanics

Kim et al. (112, 113) proposed a comprehensive computational model of the CSK that encompasses key characteristics of polymer networks, cellular solids, and prestressed structures. The modeling begins with a uniform distribution of actin monomers with cross-linking proteins dispersed randomly, which are then allowed to polymerize until almost all of the monomers are incorporated into filaments (113). Two types of cross-linkers were considered, ones that form actin bundles (i.e., stress fibers) and other ones that form orthogonal actin networks. Motion of the monomers, filaments, and cross-linkers followed Brownian dynamics, and bonding occurred according to a first order irreversible process. Following polymerization, a coarse graining procedure is applied to obtain macroscopic field properties. The authors studied the relative contributions of thermal fluctuations of the network, of bending and tensile stiffnesses of actin filaments and linking proteins, as well as the contributions of prestress on the network mechanical responses.

The analysis revealed three distinct regimes of the network behavior, each dominated by different mechanisms by which the network develops stress to resist deformation. At low prestress, bending of actin filaments and of cross-linkers play the most important role; at intermediate prestress, bending of cross-linkers affects the mechanical response the most; at high prestress, stretching of actin filaments and cross-linkers becomes dominant. In the last case, only a small fraction of actin filaments connected via highly stretched cross-linkers supports a majority of the load. Notably, entropic effects due to thermal fluctuations appear to be important only at relatively low prestress and when the average cross-linking distance is comparable to or is greater than filament's L_p, suggesting that in the CSK entropic elasticity has a minor contribution to the overall elastic response. The model predicts an approximately linearly increasing stiffness versus prestress relationship, consistent with the observations in living cells Modulations of bending and stretching stiffnesses of F-actin and cross-linkers by an order of magnitude did not alter this relationship, which is consistent with the tensegrity model. The dynamic stiffness of model follows the power-law rheology, which also exhibits the dependence on the prestress similar to living cells.

Onck et al. (146) obtained similar results using a simpler, two-dimensional network comprising linearly elastic semiflexible polymers. They found that the network exhibited stiffening that is caused by nonaffine network rearrangements rather than by the stiffening of individual network's constituents. During deformation, the filaments rotate in the direction of straining, which induces a transition from a filament bending-dominated to a filament stretching-dominated response.

In summary, the computational model provides insights into the microscopic origin of the cytoskeletal responses to mechanical deformations. The model shows that those responses may be attributable to different mechanisms, depending on the amount of the prestress. The proposed computational framework can be further developed to study phenomena associated with unbinding of the cross-linker, such as stress relaxation, network reorganization, plastic deformation by shear, as well as the effects of active force generation on the model's mechanical responses.

Non-cytoskeletal structures and mechanisms

A prevailing view in the cellular mechanics community has been that the cytoplasm can be modeled as a single phase (viscous, viscoelastic, or elastic) and that the CSK is a major force bearing structure of the cell. In reality, the cytoplasm is composed of the cytosol (liquid) and the CSK (solid) phases. Those phases do not necessarily move together when cells migrate, divide, or bleb rendering the cytoplasm as a biphasic medium whose behavior can be explained in terms of poroelasticity (138). In addition to the cytoplasm, other cellular structures, including lipid membranes and the nucleus, also are exposed to mechanical forces and participate in bearing mechanical stresses. While the relative contribution of cellular lipid membranes to the overall stress-bearing capacity of the cell is relatively minor in comparison to the contribution of the CSK, their deformability and mechanical stresses that they carry play important biological roles (cf. ^{107, 136}). The nucleus, however, participates in the overall force balance in the cell more prominently and can impact mechanical functions of the cell (22,25,39,40,75). The nucleus is also a cellular mechanosensor whose shape, structure, and mechanical properties are closely associated with gene expression and transcriptional regulation (40). Here we provide basic descriptions of cytoplasmic poroelasticity and of mechanics of cellular lipid membranes and their impact on cellular functions. A detailed description of the mechanics of the nucleus can be found in the chapter entitled “Mechanics of the Nucleus.”

Poroelasticity of the cytoplasm

The presence of a freely moving cytosol in a porous CSK may modify the cytoskeletal mechanical response. Two mechanisms play a key role in this interaction: (i) an increase of fluid pore pressure induces a dilation of the CSK, and (ii) contraction of the CSK causes a rise in pore pressure if the fluid is prevented from escaping the pore network. If excess pore pressure induced by contraction of the CSK is allowed to dissipate through diffusive fluid mass transport, further time-dependent deformation of the CSK progressively takes place. Pore pressure can be greater in one part of the cell than in another and would not equilibrate instantaneously. This would affect stress distribution in the cell and also cause alterations in cell shape and mechanical properties (i.e., a higher pressure would result in higher cytoskeletal stiffness). A simplest model that can describe these phenomena is a poroelastic model where the solid phase is viewed as being elastic and the liquid phase as being viscous (9).

The cytosol is composed of water and a variety of proteins and organelles. The timescale (t_r) for pressure relaxation in a poroelastic body is given as t_r ~ L²/D, where L is body length and D is diffusion constant. D is a product of the bulk modulus that characterizes the resistance of the solid phase to volume change, and the hydraulic permeability that characterizes the ease with which the fluid flows through pores; permeability is proportional to the square of the pore size and inversely proportional to the fluid viscosity. The pore size needed to create significant poroelastic effects over timescale of 1–1000 s, which is associated with a variety of cellular mechanical events (e.g., cell crawling), is estimated to be 30 to 60 nm (28,138). This is smaller than the pore size of the cytoskeletal lattice (85). However, the cytosol also contains ribosome chains and other objects that tend to “clog” cytoskeletal pores and thus effectively reduce cytoskeletal pore size, thereby creating the condition where the poroelastic effects become significant (138). Several theoretical models of cytoplasmic poroelasticity have been proposed (42, 84). For example, Herant and colleagues (84) have shown that a biphasic poroelastic model of the neutrophil can simulate passive aspiration of a neutrophil into a micropipette, active extension of a pseudopodium by a neutrophil exposed to a local stimulus, and crawling of a neutrophil inside a micropipette toward a chemoattractant against a varying counterpressure. Experimental studies have revealed that under external osmotic swelling, water crosses cell membrane faster than it moves within HeLa cells (28). Those data also show that two parts of the cytoplasm, ~5 μm apart, could be strongly out of hydrodynamic equilibrium at time scale of tens of seconds, consistent with the hypothesis of a poroelastic cytoplasm. Perfusion of one side of blebbing human melanoma cell with a contractile force inhibitor blocked blebbing on the drug-perfused side, whereas it continued on the medium-perfused side (27). This, in turn, suggests that the pressure that drives blebbing is generated and used locally and is not equilibrated across the cell, which is again consistent with poroelasticity. Taken together, these studies indicate that cytoplasmic poroelasticity may be needed for a complete understanding of stress transmission within the cell. While the poroelastic hypothesis does not rule out the primary role of the CSK in the stress transmission in the cell and in determining cell shape, a broader approach that also includes hydrodynamic forces, transport and ionic physiology may be needed for a more complete picture of cellular mechanics. Testing this hypothesis is not an easy task and it would require novel research approaches and a joint effort of CSK and ion physiology communities (138).

Lipid membranes

The lipid bilayer is a 5-nm thick membrane made of two layers of lipid molecules. These membranes engulf cells (plasma membrane) and cell organelles (nucleus, mitochondria, endoplasmatic reticulum, Golgi apparatus, etc.), separating them from their outside environments. Types of lipids in each of the two layers are different, thus creating a transmembrane asymmetry that affects mechanical responses of the membrane during bending and stretching.

Mechanical measurements on living cells have shown that permeabilization of the plasma membrane by a detergent saponin has a minor effect on the cell stiffness and viscosity when compared with membrane intact cells (197). These findings suggest that the plasma membrane has a minor role as a stress-bearing component of the cell. On the other hand, mechanical measurements on isolated lipid bilayer membranes have shown that they can provide significant elastic resistance to imposed deformation. The elastic resistance to stretching of the membrane area is the highest, on the order of 10¹–10² MPa (5, 54, 78), suggesting that any deformation of the whole cell that causes changes in the surface area of the cell (e.g., lamellipodia protrusions, phagocytosis) could be energetically very costly, and that the membrane rather than the CSK should be the dominant stress-bearing component of the cell. However, the plasma membrane has an excessive surface area, which is wrinkled, pleated, and folded such that deformations that cause changes in cell surface area do not lead to the bilayer stretching (79). On the other hand, some organelle membranes do not have large excessive surface and deformation of such organelles may be elastically resisted by the membrane. For example, the membrane engulfing the endoplasmatic reticulum is pulled into tube-like invaginations by molecular motors that run along microtubules (205). The resistance of the membrane to this action can be large enough to stall the motors, stop the tube elongation and even lead to elastic recoil of the tube. Changes in the lipid composition of the bilayer can alter the stress bearing capacity of the membrane and thus impact the rate and direction of extension of the tube (cf. ¹⁰⁷). For example, an increase in the cholesterol content in the bilayer leads to an increase in its expansion stiffness (145).

Because the lipids and transmembrane proteins of the bilayer can freely flow past each other, the bilayer does not provide elastic resistance to shear deformation (i.e., zero shear modulus). This, in turn, limits how forces can be applied to the membrane surface. For example, various motor proteins have specific binding sites for lipids on the inner leaflet of the bilayer. Without a shear modulus, the lipid part of the membrane to which the motor is anchored will passively flow, as the motor walks slowly along its actin or microtubule tracks, with no relative motion of the CSK. If, however, the motor moved rapidly, a significant viscous resistance in the bilayer may develop which may cause deformation of the CSK (cf. ¹⁰⁷).

Since the resistance to bending of the lipid membrane is significantly lower than the resistance to stretching, the membrane spontaneously curves because of the transmembrane asymmetry. This inability of the lipid bilayer to maintain a planar shape seems to be essential for the biological function of membranes and for their ability to undergo various shape transformations such as vesicle budding or fusion. Thus, local accumulation of lipids in specialized domains, which determines membrane resistance to bending, has important mechanical and biological consequences (cf. ¹⁰⁷).

Some of membrane proteins form channels through which ions can flow. The opening and closing of these channels (gating) can be triggered by mechanical signals. For example, stretching of the membrane due to osmotic swelling, bending of the membrane due to lipid composition changes in one of the leaflets, or tilting of the channel by externally applied force to the channel, but not to the membrane, may all cause conformational changes in the channel proteins that would result in opening of the channel (cf. ^{107, 136}). Activation of stretch-sensitive ion channels can result in changes in intracellular ion concentration that, in turn, has different downstream effects, including activation of signaling pathways that may lead to changes in gene transcription.

In summary, it is clear that the lipid bilayer is not simply an inert thin barrier that separates the cell and organelles from their external environment. The lipid composition of bilayers, which governs bilayer structural and material properties, can have a profound effect on a number of processes important to the normal functioning of cells. Bilayer deformation is a common factor involved in all of these processes (136).

Section summary

The overwhelming body of evidence has shown that the cytoskeletal prestress plays a central role in cellular mechanics. It provides shape stability to the cell by maintaining structural stiffness of the CSK and regulates cell's rheological behaviors. The strain-hardening behavior of cells appears to have two origins, one is kinematic due to realignment of cytoskeletal filaments in the direction of applied loading, as described by the tensegrity model and by nonaffine network models, and the other is elasticity of actin filaments and cross-linkers, as described by the cross-linked actin network models. Bending of cytoskeletal filaments appears to be important for stress buildup only at low prestress, when the filaments are not taut and where Brownian dynamics and associated conformational entropy of cytoskeletal filaments also have important contribution to cytoskeletal elasticity.

Considering the central role of the prestress in cellular mechanics, it is noteworthy to point out similarities with lung parenchymal mechanics (62). Like the CSK, the lung parenchyma is also prestressed. The distending transpulmonary pressure is transmitted through the parenchymal tissue and distends all intrapulmonary structures. Like in the CSK, the prestress confers in a direct proportion to its magnitude the parenchymal shear modulus, which is critical for shape stability of organ, region, vessel, airway and alveolus (see chapter “The Lung Parenchyma” for details). This similarity between the role of the prestress in cellular and parenchymal mechanics suggests that it may form the basis of function at different scale levels. For example, as the cytoskeletal prestress increases, cells stiffen and their elastic response becomes increasingly nonlinear. This nonlinearity, on the other hand, may play essential role in mechanotransduction of surfactant secretion. It has been observed that variable stretching of epithelial type II cells enhances their surfactant secretion (4). Any nonlinearity along the mechanotransduction pathways could result in such an amplification effect through the phenomenon known as the stochastic resonance (4).

Long-Distance Force Transfer

External forces that are transferred across integrins in focal adhesions and channeled through the CSK can alter signaling activities deep inside the cell (98, 100). For example, pulling on integrins with micropipettes in living endothelial cells results in immediate alignment of nuclear border and of nucleoli inside the nuclei in the direction along the applied force (134), Figure 7, and also induces displacement of mitochondria up to 20 μm away from the point of disturbance (198). Another evidence for the long-distance force transfer is provided from intracellular stress tomography measurements (90, 91, 201). This technique enables instant observation of deformation within the CSK in response to applied forces via integrin receptors with a displacement resolution of ~5 nm (93). Measurements on airway smooth muscle cells reveal islands of displacements at distances greater than 20 μm from the point of force application, Figure 8A. When the contractile force generation was inhibited by caldesmon and cytoskeletal prestress diminished, the displacements were localized only around point of force application, Figure 8B. When the prestress was restored, the displacement islands distal from the point of force application reappeared, Figure 8C (91). When the prestress was either increased by histamine or lowered by DBcAMP, displacements of the intranuclear nucleoli significantly increased or decreased, respectively (90). When the actin CSK was disrupted by cytochalasin D, the displacement islands disappeared (91). Together, these findings suggest that the prestress and connectedness of the cytoskeletal network are essential for transfer of mechanical signals through the cytoplasm over long distances.

Figure 7.

Phase contrast (left) and corresponding birefringence microscopic images (right) of the CSK before (top) and after (bottom) forces are applied to integrins. The data show immediate molecular realignment in the cytoskeleton following force application. The appearance of nucleoli in distorted cells indicates molecular realignment in these regions. Reproduced from reference 134 with permission from Maniotis et al.

Figure 8.

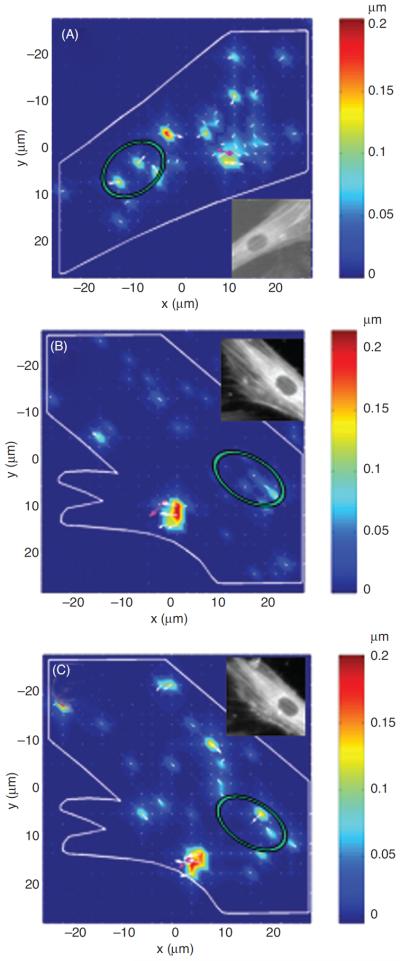
Actin cytoskeleton displacement patterns measured by intracellular stress tomography (91) are modulated by prestress. An external displacement is applied to the human airway smooth muscle cell locally via a magnetic bead (position indicated by the pink dot) attached to an integrin receptor on the cell's apical surface, and islands of intracellular displacements are observed distal from the point of force application. Control yellow fluorescent protein-actin cell (A). Cell infected with a low level of green fluorescent protein-caldesmon before (B) and after (C) treatment with calcium ionophore A-23187 (52 g/ml for 10 min), an inhibitor of caldesmon. The pink arrow represents the direction and the magnitude of the bead lateral displacement. Insets in A, B, and C are fluorescent images of the corresponding cells, showing patterns of stress fibers. Green ellipses represent the nuclei of the cells. Reproduced from reference 91 with permission from Hu et al.

The long-distance force transmission mediated by intermediate filaments was also observed in response to fluidflow-induced shear stress applied to the apical surface of endothelial cells (83). On the other hand, in a single study, Heidemann and colleagues (82) failed to observe long-distance force transmission in fibroblasts. They used a micropipettes coated with ECM protein laminin to apply various mechanical forces to cell surface. They observed only local deformations. However, the authors did not report that laminin-coated pipettes formed FA complexes at the point of application, which are critical for force transmission between integrins and the internal CSK (135,196).

Laurent and co-workers (122) attempted to reconcile the inconsistency between the results of the Heidemann's group and the results that reported long-distance force transmission. Using the MTC technique to measure mechanical properties of alveolar epithelial cells, Laurent and colleagues found that that the submembranous “cortical” CSK, which is mainly composed of actin, is less stiff and more responsive to external forces than the “deep” subcortical CSK, which also includes intermediate filaments and microtubules. Based on these findings, those authors concluded that “mechanical deformation is transmitted globally throughout the network, whereas the cell surface is able to `sense' very local deformation forces.”

Ingber hypothesized that the channeled long-distance force transmission in cells is a consequence of the discrete nature of the cytoskeletal tensegrity architecture. His hypothesis was based on the observations that in a simple physical tensegrity model (composed of 6 struts and 24 cables) a force applied at a joint was transmitted to distal joints via tensed cable elements (97). However, in most known discrete structures the distance of force transmission depends on their mash size; the smaller the mash size, the shorter the distance of force transmission. The simple tensegrity model used by Ingber had the size on the same order of magnitude as its mash size. Since the complex cytoskeletal lattice has the mash size on the order of 10² nm, it cannot explain the observed force transmission over distances greater than 20 μm by simply being discrete. Some other structural features of the CSK need to be considered.

Force transmission mediated by stress fibers

A possible explanation for long-distance force transfer in cells is offered by Wang and Suo (201). They hypothesized that the ability of cells to propagate forces over long distances originates from inhomogeneity of the CSK, where tensed and stiff actin stress fibers are embedded in the surrounding compliant network. If the fiber tensile prestress is much greater than the elastic modulus of the surrounding network, then the fiber moves like a violin string when subjected to a transverse force. Similarly, if the elastic modulus of the fiber is much larger than that of the surrounding network, the force propagates longitudinally along the fiber, that is, the fiber acts as force guide, while the attenuating diffusive transmission through the surrounding soft network is small. This is similar to the force transmission in a spider web, where mechanical disturbances are transmitted along the radial, tensed, and stiffened threads that are surrounded by slack and compliant lateral threads. Experimental data show that the prestress in actin stress fibers is ~10² to 10³ kPa and that their elastic stiffness is ~10³ to 10⁴ kPa (41), both of which are much greater than stiffness of the surrounding soft network, ~10⁻¹to 10¹ kPa (cf. ⁷). Thus, it follows from the above model that stress fibers may guide longitudinal and transverse force propagation through the cell, while the attenuating effect of the surrounding soft CSK is minor. The model also predicts that loss of prestress in the fiber would cause attenuation of force propagation, consistent with the experimental observations that blocking contractile force generation inhibits long-distance force transfer in living cells (90,91).

While the model may be reasonable for describing long-distance force transmission in two-dimensional cell cultures on stiff substrates, where stress fibers are prominent, this may not be the case in three-dimensional cultures which often lack stress fibers (63, 74). For cells in three-dimensional cultures some other stiff structures within the cell body, such as microtubules or intermediate filament bundles, may be needed for long-distance force transmission. Although three-dimensional ECM represents a realistic environment for many cell types, in some cell types (e.g., vascular endothelial cells or pulmonary epithelial cells) their in vivo environment is effectively two-dimensional and thus, the stress-fiber model may be a good representation in those cells.

Channeling of force transmission by the contractile apparatus “zippering” action

Chandran and colleagues (26) also considered force propagation along stress fibers. However, in their model the channeled force transmission does not stem from material inhomogeneity of the CSK. Rather it is provided by the lateral action of contractile forces that facilitate unidirectional stress propagation, while preventing lateral, dispersive stress propagation through the CSK. The model is based on the qualitative observation of “zipper-like” actin-myosin interaction. This means that an immobilized myosin filament is able to bind actin filaments from different directions and “zipper” those filaments in the direction parallel to the myosin filament. As a result of this action, actin filaments would bend and the force of the myosin power-stroke that would be transmitted along a bent actin filament to the rest of the cytoskeletal network. Because of the bent shape of the actin filament, the force would have a parallel and a perpendicular (lateral) component relative to the myosin filament. This is different from previous actinmyosin models that consider only the parallel component of the contractile force. The authors hypothesized that the lateral component of the contractile force would prevent stresses to propagate in the lateral direction, which in turn, prevents dispersion and attenuation of the propagating stress. Using a simple coarse-graining implementation, the authors showed that their model with the zipper-like actin-myosin interaction can simulate bend-like long-distance stress propagation within an elastic cytoskeletal continuum.

Isostatic model of the cytoskeleton

In his approach to long-distance force propagation, Blumenfeld (11) considered a structural property known as isostaticity as framework for describing this phenomenon. The author pointed out that the long-distance force transmission cannot be explained using the framework of classical (Saint-Venant's) theory of elasticity that a priori predicts dispersive stress transmission and therefore attenuation over short distances. Instead, he proposed an isostatic model of the CSK that naturally predicts channeled long-distance force transmission. Because of potentially high relevance of this model for cellular mechanics, it is useful to provide a basic description of isostaticity.

In the classical elasticity, equations that describe local balance of linear and angular momentum (i.e., equilibrium equations) are not sufficient to determine stress in the body since there are fewer equations than the unknown components of stress tensor. Therefore, additional equations are needed. These include the Saint-Venant strain compatibility equations (i.e., adjacent parts of the body must strain together) and the constitutive stress-strain equations (Hooke's Law) that describe elastic properties of the body. Because of the mathematical form of the compatibility equations and the constitutive equations, the resulting stress field differential equation is elliptic, which a priory predicts dispersive stress propagation and attenuation over short distances (11). In isostatic networks, however, because of their specific structural organization, one can determine forces in each structural member only from equilibrium equations and structural properties of the network, without invoking constitutive equations (10). In that way, one can obtain the stress field differential equation that is hyperbolic and which predicts long-distance stress propagation.

To determine forces in each member of a network for a given external loading and given boundary conditions, the number of unknown forces in the network must match the number of equilibrium equations. Structures where all member forces can be determined from static equilibrium are called statically determined (e.g., simple triangle truss) and they belong to the class of isostatic structures. If the number of structural members is greater than the number of equilibrium equations, the structure is statically undetermined and additional conditions are required. Generally, such structures are not isostatic. If the number of structural members is smaller than the number of equilibrium equations, then the structure is unstable and would require additional constrains to be stabilized and to become isostatic.

Blumenfeld (11) described several scenarios for isostaticity of the CSK. One scenario is when all nodes of the cytoskeletal network can support torques. This would be the case where all cytoskeletal filaments can carry bending moments, which is analogous to the cellular solid model (160). This situation may occur when forces applied to the cell are too small such that filaments do not buckle, collapse and become slack. Another scenario is when some nodes can and some cannot support torques. In the case of the latter, all filaments at the node must carry tensile forces (e.g., actin filaments and intermediate filaments) except one filament that may carry compressive forces (e.g., microtubules and stress fibers). In the limit where none of the nodes can support torques, the structure becomes tensegrity. Blumenfeld (11) also pointed out that the CSK could be partly isostatic, that is, some parts of the CSK are isostatic and some are not. He speculated that through cytoskeletal remodeling, cells may favor partial isostaticity as an efficient strategy to selectively propagate mechanical signals through some parts of the cytoplasm and to block propagation through other parts.

The isostatic model can be also used to explain the observed sensitivity of the long-distance force transfer to the cytoskeletal prestress. According to Blumenfeld (11), modulations of the prestress can have one of three effects on the isostatic cytoskeletal network: (i) no filament tighten or slacken; (ii) loose filaments tighten; and (iii) taut filaments slacken. In the first case, the CSK will remain isostatic and there will be little effect on force transmission. In the second case, for example during increased contractile activities or due to substrate stretching, the tightening of the filaments adds force-bearing elements to the CSK and thus it becomes statically undetermined and loses its isostaticity. Consequently, force transmission will become dispersive and attenuated over short distances. In the third case, for example when the contractile force generation is inhibited, the slackening of the filaments reduces the number of force-bearing elements in the CSK and it becomes unstable and also loses its isostaticity. Consequently, force-transmission along the slacken elements will not be possible and force channels will disintegrate. This is consistent with the experimental observation of disrupted long-distance force transmission in caldesmon-treated airway smooth muscle cells (91). This also explains why the prestress is necessary for long-distance force transmission.

In summary, the isostaticity theory provides a new framework for studying long-distance force transmission in cells. Since isostatic networks do not require structurally defined pathways, such as stress fibers, for force transmission, they can explain how cells transmit forces in a three-dimensional ECM (63, 74) and in cells adhering to two-dimensional soft substrates where stress fibers are much less pronounced than on rigid substrates (53). On the other hand, the concept of isostaticity depends critically on the distribution of tensile and compressive/bending supporting filaments in the CSK. Whether such distribution is at least approximately satisfied in living cells awaits experimental verification.

Section summary

Experimental studies have shown that mechanical forces are propagated through the cytoplasm and into the nucleus along preferential cytoskeletal pathways. This force transmission is much faster than diffusive biochemical responses, suggesting that this phenomenon is primarily mediated by biophysical factors. It has been also shown that connectedness of the cytoskeletal network and the cytoskeletal prestress are essential for force propagation. Several theoretical models have been advanced to explain this phenomenon. While those models differ conceptually, all of them require the prestress as a crucial component that enables force propagation. None of the models have been rigorously tested yet.

Mechanotransduction

Studies of mechanotransduction have been focused on mechanosensitive molecules and cellular components; integrins, cadherins, myosin motors, stretch-activated ion channels, growth factor receptors, cytoskeletal biopolymers and a host of other molecules and structures have been shown to contribute to mechanotransduction. However, little is known how all these molecules and structures function within the mechanical milieu of the CSK. Many of these signaling molecules are immobilized on the CSK, on the nuclear lattice and on the ECM. Owing to mechanical interconnectedness of those structures and the ability of the CSK to transfer forces over long distances, mechanical stresses can induce distortions of signaling molecules and thereby alter their biochemistry at multiple sites simultaneously and produce a concerted response (cf. ^{99, 100}). As a result, structure and function are seamlessly integrated in living cells.

One important question that might be asked is: is there any fundamental difference between mechanotransduction- and soluble factor (e.g., a growth factor)-induced signal transduction? If there is no difference, one might replace mechanical cues or factors with soluble factors. Otherwise, mechanical cues might be indispensable for the fundamental functions of living cells.

To address this question, Na and co-workers (142–144) combined fluorescence resonance energy transfer (FRET) technology with the MTC technique and compared intracellular Src kinase activation by either an epidermal growth factor (EGF) or by a local mechanical loading with the MTC device (Fig. 9). They found that mechanical activation of Src by stresses applied via integrins is at least 40-fold faster than that by EGF. More importantly, in contrast to EGF-induced diffusive Src activation, stress-induced Src activation is only localized to some specific sites on the endosomal membrane, where the strong activation sites are always colocalized with local large microtubule deformation (142). These findings suggest that mechanotransduction appears to be unique in activation of cytoplasmic enzymes.

Figure 9.

Rapid, long-range strong Src activation sites in the cytoplasm colocalize with sites of large microtubule displacements. The cell was cotransfected with CFP-YFP Src reporter and mCherrytubulin. A step function stress σ (17.5 Pa) was first applied for 3 s via an RGD-coated bead, and FRET changes were recorded. Then the microtubule deformation map was acquired when an oscillatory stress was applied for ~30 s (0.3 Hz; peak stress = 24.5 Pa, equivalent to a constant stress of 17.5 Pa; reference 91). In this representative cell, strong Src activation sites coincide with large deformation sites (>15 nm) of microtubules in the same cell at the same focal plane (~1 μm above cell base). The overlay image is the YFP Src reporter image superimposed with the bead. Pink circles indicate bead center position; white arrows represent microtubule deformation direction. Red arrows point to strong Src activation sites. In the colocalization analysis panel, red represents strong Src activation, and black lines represent large microtubule displacements. Three other different cells showed similar results. Of strong Src activation sites, ~80% (15 of 19) were colocalized with sites of microtubule deformation >15 nm. Scale bar = 10 μm. Reproduced from reference 143 with permission from Na et al.

To test further if mechanotransduction via integrins follows the same activation cascades as the soluble growth factors, this group of investigators compared activation of Rac, another important enzyme in cell spreading and migration, by a local stress and by platelet-derived growth factor (PDGF; ¹⁵⁰). It has been shown that PDGF-induced Rac activation is downstream from Src (147). Surprisingly, Poh et al. (150) found that Rac can be directly activated by a local stress to the integrins, independent of the presence or activity of Src, since Src knockout or inhibition had no effects on stress-induced Rac activation. These data suggest that mechanotransduction via integrins might be fundamentally different from soluble factor-induced signal transduction. Taken together, these findings underscore the indispensable role of mechanical forces in vital cell functions and biological responses.

Mechanotransduction is a broad topic that exceeds scope of this article. For more detailed description of this phenomenon we direct readers to the article “Mechanotransduction” in Comprehensive Physiology. Here we describe how micromechanical properties of the CSK combined with thermodynamics of polymerization and depolymerization of molecular aggregates can be used to explain assembly and remodeling of the CSK and FAs (176).

Mechanochemical control of molecular assembly

The CSK is a dynamic structure that undergoes continual turnover and sustained self-assembly of individual molecular components over periods of seconds to minutes (118,124,140,181). Yet the cell is able to maintain the structural integrity of the cytoskeletal lattice and carry out robust mechanical behaviors over hours to days (12,118). Thus, understanding how molecules assemble into dynamic cytoskeletal structures, maintain structural integrity and shape stability to the cell, and at the same time alter the rate and pattern of their assembly in response to mechanical and chemical cues, is one of the most fundamental challenges in cellular biophysics (176).

Thermodynamics shows that when tensile forces are applied to filamentous biopolymers of the CSK or to the molecular cluster of the FA plaque, the chemical potential (i.e., the change in the free energy due to a change in the number of molecules in the system) of those molecular aggregates decreases relative to the molecular reservoir of free, non-assembled monomers (20, 86, 98, 166). Since a decrease in potential is favored physically, lowering the chemical potential through this mechanical means will drive biopolymer assembly. In contrast, when tensile forces are relaxed or compressive forces are applied, polymer self-assembly is disfavored, and depolymerization is promoted. The difference in the chemical potential (Δμ) of an aggregate or polymer relative to the molecular reservoir in response to a tensile or a compressive force (F) can be described by the following equation (cf. ^86,166)

$$\Delta \mu =\Delta {\mu }_0-F{\ell }_0-\frac{F^2}{2k}{\ell }_0,$$ (2)

where Δμ₀ is the difference in the potential in the absence of force, ℓ₀ is the average length of a monomer before force application, and k is tensile stiffness (i.e., spring constant) of the polymer/aggregate. The last term in Eq. 2 represents the elastic potential of the polymer per monomer (for simplicity, it is assumed that the polymer behaves as a linear elastic material). The molecular exchange between the cytoplasm (reservoir of free monomers) and polymers depends on the sign of Δμ; if Δμ < 0, free monomers would tend to join the polymer (i.e., polymer assembly) and if Δμ > 0, polymer would lose monomers (i.e., polymer disassembly). According to Eq. 2, tensile forces (F > 0) cause Δμ to decrease, whereas compressive forces (F < 0) causes Δμ to increase, but in both cases the elastic potential decreases Δμ. This contribution of the elastic potential may be negligible in the case of actin filaments that have relatively high tensile stiffness, but it may be important in the case of the FA adhesion plaque whose stiffness is much lower than that of F-actin (8,148).

The complementary force balance at the FA level (Fig. 10), where tensile force of actin stress fibers (F_SF) is opposed by the joint action of traction force (τ) at ECM adhesions and compression force of microtubules (F_MT), is given as

$$F_{SF}=\tau +F_{MT}.$$ (3)

Figure 10.

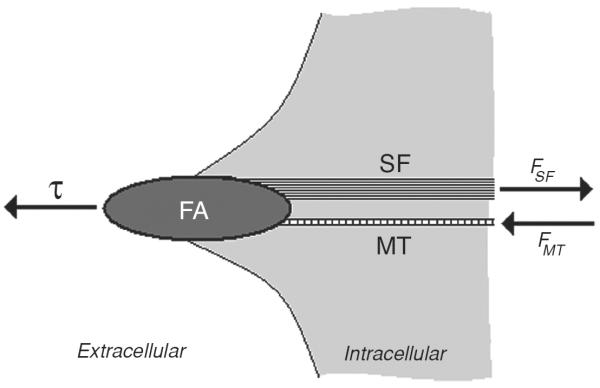
Schematic representation of the complementary force balance at the focal adhesion (FA) level. Tension (F_SF) in the actin stress fiber (SF) is balanced by traction force (τ) at the FA attachment to the substrate and compression force (F_MT) of the cytoskeletal microtubule (MT).

By combining mechanically induced change in the chemical potential (Eq. 2) with the complementary force balance at the FA level (Eq. 3), one can predict assembly of various molecular structures in response to changes in F_SF. If F_SF would increase because of myosin motor activity, then F_MT and τ would also increase (Eq. 3). Consequently, the chemical potential of actin filaments and FAs would decrease (Eq. 2) causing their assemble (6,17,70,91,124,155), whereas the chemical potential of microtubules would increase (Eq. 2) and they would disassemble, as observed in living cells (156). If, on the other hand, τ is increased by straining the ECM, F_SF would increase while F_MT would diminish (Eq. 3). Consequently, according to Eq. 2, FAs and microtubules would grow, and this is again what is seen in cells (6,13,111,204,212).

It was discovered that by straining the ECM (which results in increasing τ) increases cytoskeletal prestress (i.e., increasing F_SF) by activating the small GTPase Rho, which stimulates Rho-associated kinase (ROCK) to enhance myosin light chain phosphorylation, while promoting actin polymerization through another effector, mDia (156). Because of the complementary force balance (Eq. 3), F_MT diminishes when microtubules are disassembled, while the enhanced τ acting on FA integrins feeds back to activate Rho-dependent contractility, thereby amplifying this response. The complementary force balance also influences assembly of the proteins that form the backbone of the FA. For example, decreasing cytoskeletal prestress alters the binding kinetics of the FA protein zyxin by increasing its unbinding constant (K_off), whereas vinculin in the same FAs does not change its kinetics (124).

Cell-cell contacts mediated by cadherins enable load transfer between adjacent cells (152) and shift part of cytoskeletal tension from integrin-containing FAs to cadherin-based cell-cell contacts, such that when FAs disassemble, cell-cell junctions strengthen and grow. These changes in molecular self-assembly within cell junctional complexes that could be mediated via force transfer between FAs, cytoskeletal filaments, and cell-cell contacts are of great physiological importance because they regulate vascular permeability in vitro and in vivo (133).

Mechanical stress also influences the actin polymerization that drives formation of protrusive lamellipodia and filopodia that extend from the leading edge of cells and mediate cell migration (101, 176). The proximal ends of lamellipodia and filopodia are linked to regions of the actin CSK, or to underlying FAs at the cell base that anchor them to the substrate. Filopodia and lamellipodia push against the tensed plasma membrane and against proximal linkages to the tensed actomyosin filament networks at the leading edge. The basal anchoring points of filopodia and lamellipodia act like flexible hinges and thus, these structures wave up and down as the cell moves forward. This up-and-down motion may be caused by the joint contractile activity of the CSK and by thermal fluctuations of actin filaments in the lamellipodia rear, where the actin network appears disassembled and actin filament lengths close to their L_p (184). When the tip of the exploring filopodium gets in contact with the ECM, a new FA assembles that anchors the filopodium to the substrate and stabilizes it, opening thereby a new venue of force transmission between the cell and the ECM. This, in turn changes local force balance and alters stress distribution within the CSK. Changes in this force balance due to elevation of cytoskeletal contractile forces or external mechanical signals control cell migration (129,139,149,165).

The observed transfer of mechanical forces from FA integrins to the nuclear envelope and the sub nuclear organelle nucleoli (90, 134) raises the possibility that assembly and function of intranuclear structures, such as chromatin protein complexes and nuclear matrix scaffolds involved in gene transcription, RNA processing, DNA replication, and other nuclear functions, could potentially be regulated directly by mechanical stresses channeled from the cell surface over the CSK (98, 103, 119). Although direct mechanical effects on gene transcription have not been demonstrated, it is known that the nucleus must physically expand before DNA replication can proceed (211).

Section summary

Cells maintain their structure and function through continuous molecular assembly and disassembly. Stress-stabilized CSK may provide a conduit for preferential force channeling across the cell so that mechanical loads applied at the macroscale can result in conformational changes at the nanoscale. In this manner, the prestressed CSK may facilitate mechanotransduction. Due to existence of the complementary force balance between microfilaments, microtubules, FAs as well as other load-bearing cellular components, mechanical forces can be shifted back and forth between load-bearing elements and thereby alter their remodeling. This mechanical balance has important physiological relevance for cells, tissues, and organs (176). One simple example is how transferring of forces from microtubules to the ECM via FAs decompresses microtubules and therefore promotes their polymerization and nerve growth. It has been observed that nerves will extend new processes in whatever direction external tension is applied to their ECM adhesions (45,81). Another example is the observation that microtubules buckle when heart cells contract and they straighten up when the cells relax (12; Fig. 5). An abnormal increase in microtubule assembly in heart cells increases their resistance to contraction and leads to heart failure in animals (192).

Conclusion

In this article we discussed mechanism by which cells resist shape distortion, propagate mechanical signals through the cytoplasm and transduce them into biochemical responses. We compared and contrasted various theories and models of cytoskeletal mechanics and emphasized common mechanism as well as their conceptual and sometimes irreconcilable differences. Despite differences in approaches and in conceptual descriptions, majority of studies have shown that cytoskeletal prestress has a central role in cellular mechanics and that the controlling physics is at the level of integrative cytoskeletal lattice properties. It has become evident that the prestress is essential for defining the most fundamental properties of the cytoskeletal phenotype: the ability to deform, contract, transfer forces, and remodel, which are critical for higher physiological functions of the cell, including migration, secretion, mitosis, apoptosis, and mechanotransduction. Prestressed models of the CSK, most prominent of which is the tensegrity model, have been instrumental in explaining the importance of the prestress and structural properties of the CSK in resisting deformation, shape stabilization, and stress propagation. However, these deterministic models may not be well suited to describe the dynamic responses of the cell. On the other hand, rheological measurements on cross-linked actin networks reconstituted in vitro have been successful in replicating cellular mechanical behaviors, including the effects of the prestress on cell deformability and the power-law rheology, indicating that those networks may have captured the governing mechanisms of cytoskeletal mechanics. While those mechanisms have not yet been fully understood, the actin networks can include the effects of cross-linking mechanics, thermal and nonthermal dynamics of cytoskeletal molecules and contractile force generation, which are important for mechanical functioning of the CSK and which have been absent from the prestressed models of the CSK.

Future studies should investigate the feasibility of other types of models of the CSK, including hierarchical and multimodular structures composed of large number of simple units as well as cytoplasmic poroelasticity. With increasing model complexity, it may become possible to obtain a unifying, physically based structure-function model of cytoskeletal mechanics amenable to computational and structural analysis which would become a useful tool to cell biologists, physiologists, and other life science investigators for studying and understanding cellular functions. This focus on the mechanical aspect of cellular function does not preclude the importance of numerous chemically mediated mechanisms that are known to influence cytoskeletal mechanical responses. Rather, it elucidates a higher level of organization in which biochemical events function and may be regulated.

The complementary force balance, which is in the core of the cellular tensegrity model, has been instrumental in describing in qualitative terms mechanochemical control of assembly and disassembly of various cellular structures and molecular clusters. However, a comprehensive theory that can describe mechanotransduction in a predictable and quantitative manner is still lacking. To understand this problem, it is important to know how cells transmit and balance mechanical forces. For example, intracellular mechanical signaling pathways need to be elucidated and compared with known signaling pathway for growth factor. Furthermore, it remains to be seen whether mechanical stress can directly activate proteins and genes inside the nucleus or it needs facilitation from soluble molecules in the cytoplasm. Thus, as eloquently summarized by a group of leading cellular biomechanics investigators (47), one of major challenges in future research in cellular biomechanics is to connect basic principles of mechanics (conservation of mass, momentum, and energy) with basic principles of biology so as to unify mechanics with cell biology, development, and molecular biology. Once this connection will be made, it may be possible to predict quantitatively and from first principles various integrated cellular functions including migration, division, differentiation, and mechanotransduction. Biology could thus become a predictive and mechanistic science that “could be used not only to make informed decisions but also to improve health by creating new effective drugs, therapies and inexpensive replacement tissues.”