The risk of developing a second cancer after receiving craniospinal proton irradiation

Abstract

The purpose of this work was to compare the risk of developing a second cancer after craniospinal irradiation using photon versus proton radiotherapy by means of simulation studies designed to account for the effects of neutron exposures. Craniospinal irradiation of a male phantom was calculated for passively-scattered and scanned-beam proton treatment units. Organ doses were estimated from treatment plans; for the proton treatments, the amount of stray radiation was calculated separately using the Monte Carlo method. The organ doses were converted to risk of cancer incidence using a standard formalism developed for radiation protection purposes. The total lifetime risk of second cancer due exclusively to stray radiation was 1.5% for the passively scattered treatment versus 0.8% for the scanned proton beam treatment. Taking into account the therapeutic and stray radiation fields, the risk of second cancer from intensity-modulated radiation therapy and conventional radiotherapy photon treatments were 7 and 12 times higher than the risk associated with scanned-beam proton therapy, respectively, and 6 and 11 times higher than with passively scattered proton therapy, respectively. Simulations revealed that both passively scattered and scanned-beam proton therapies confer significantly lower risks of second cancers than 6MV conventional and intensity-modulated photon therapies.

1. Introduction

Recent advances in cancer detection and treatment have led to large improvements in survival. The 10 year survival rates in the United States are approximately 59% for adults and 75% in children (Ries et al 2006). Many believe that survival rates and quality of life can be further improved by using more targeted treatments such as proton radiotherapy (Steinberg et al 1990, McAllister et al 1997, Miralbell et al 2002, Suit 2003, Taylor 2003, Lee et al 2005, Yock et al 2005). If rates of long-term survival are increased, then so is the importance of minimizing consequential treatment-related late effects that may appear years or even decades after the treatment (see figure 1 in Preston et al (2002) and Sigurdson et al (2005)). In particular, survivors of childhood cancer face the prospect of developing second cancers later in life, with potentially devastating physical and psychological consequences. It has long been known that radiation increases the risk of second cancers and that children are at greater risk than adults. Consequently, much effort has been expended to develop strategies that reduce exposures to healthy tissues, including the use of intensity-modulated photon radiotherapy (IMRT) and proton therapy.

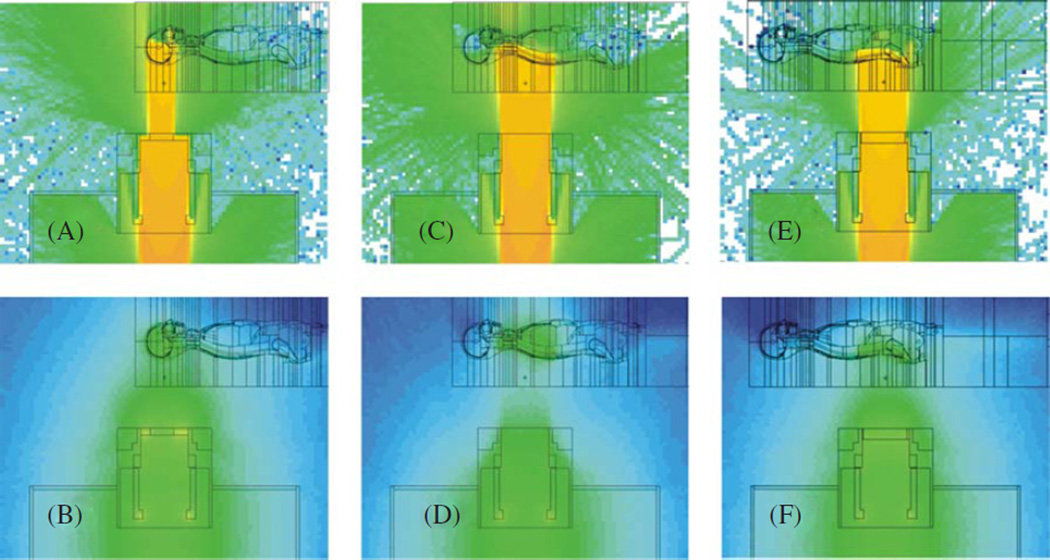
Figure 1.

Monte Carlo simulation of particle fluences for the three craniospinal treatment fields. The upper plots represent the logarithm of the proton fluence, including primary protons and secondary protons generated via (n, xp) reactions in the treatment unit and in the phantom. The corresponding lower plots represent the logarithm of neutron fluence, including neutrons generated internally and externally to the phantom. Note that the fluence in each plot was scaled to maximize the visibility of the shape of the distributions, not their magnitude. (A), (B) Cranial field. (C), (D) Superior spinal field. (E), (F) Inferior spinal field.

(This figure is in colour only in the electronic version)

Proton therapy is a scarce but rapidly emerging treatment modality (Sisterson 2005). In the United States, five major proton therapy centers are presently in operation, and at least six more are expected to commence treating cancer patients, including children, in the next 5 years. Much of the rationale for using proton therapy is based on theoretical considerations, such as treatment planning studies, and on a limited number of patient outcome studies. Skeptics argue that the proliferation of proton therapy should be contingent on the availability of demonstrable benefit, e.g. from multi-institution randomized clinical trials comparing survival rates after proton versus photon therapies. Proponents, however, argue that waiting for clinical trial data would only confirm the obvious while slowing the pace of progress. As a practical matter, it appears that many new proton therapy centers will begin treating patients before the results of clinical trials are available. In the interim, we must rely on theoretical predictions of expected benefits and detriments, and these predictions should be as accurate and complete as reasonably achievable.

Perhaps the most difficult detriment to predict is the risk of developing radiogenic second cancer. This risk is common to all forms of radiotherapy, and the risks are usually overwhelmed by the benefit of surviving the original cancer. In a recent study on pediatric cancer treatments, Miralbell et al (2002) calculated that the risk of developing a second cancer after craniospinal irradiation is substantially lower with proton therapy. Specifically, they reported that the second cancer risk associated with scanned-beam protons was 8 times less than with IMRT and 15 times less than with conventional radiotherapy. However, that study did not take into account the cancer risks associated with stray neutron exposures, which are inherent with proton therapy. Hall (2006) has cautioned that the neutron exposures may be a predominant consideration in deciding whether proton therapy is appropriate, particularly when contemplating the use of passively scattered beams to treat children.

The aim of this work was to compare the risk of developing a second cancer after craniospinal radiation using 6 MV conventional photon therapy, 6 MV intensity-modulated photon therapy and proton radiotherapy taking into account neutron exposures from the latter. In addition, we sought to compare the neutron exposures resulting from the two most common proton beam spreading techniques, passive scattering and magnetic scanning. To accomplish these goals, we combined dosimetric data from Monte Carlo simulations with cancer risk coefficients from the literature.

2. Methods and materials

We investigated how whole-body stray neutron exposures influence the projected risk that a patient receiving craniospinal proton irradiation will develop a second cancer. Stray radiation doses were calculated using Monte Carlo simulations of a proton therapy treatment unit with a detailed anthropomorphic phantom. Doses from the primary beam were taken from the literature. The doses from primary and stray radiation were combined in order to estimate the total attributable risk of the development of a fatal or non-fatal second cancer.

2.1. Calculation of absorbed dose, radiation weighting factor, equivalent dose and effective dose

In patients receiving proton therapy, the in-field (primary) dose is predominated by primary protons and the out-of-field dose is predominated by neutrons (Agosteo et al 1998, Yan et al 2002, Fontenot et al 2008, Taddei et al 2008). For organs that are partially inside the treatment field, the relative contribution of protons and neutrons depends mainly on the fraction of the organ inside the treatment field. In this work, we report new calculations of the out-of-field doses of stray radiation and then combine these with previously reported in-field doses, in order to estimate the risk of second cancer from both in-field and out-of-field radiation.

Neutron radiation exposures were calculated with the Monte Carlo Proton Radiotherapy Treatment Planning (MCPRTP) code (Newhauser et al 2007a). The MCPRTP system uses the Monte Carlo N-particle eXtended code (MCNPX 2002(b), Hendricks et al 2006) as a radiation dose calculation engine and a commercial proton treatment planning system (Eclipse; Varian Medical Systems, Palo Alto, CA) for all other treatment-planning tasks. The Monte Carlo simulations included realistic models for ion energy loss and energy straggling, multiple Coulomb scattering and elastic and non-elastic nuclear reactions. The MCPRTP system was described in detail elsewhere (Newhauser et al 2007a, 2008). A pediatric medulloblastoma treatment was examined because children are more susceptible to radiogenic cancers than adults, the expected survival time is long (for example, Stavrou et al (2001) reported 52% survival at 10 yr), and the relatively large neutron exposures expected from the deeply penetrating cranial fields and elongated spinal fields (Zheng et al 2007a). The medulloblastoma treatment was simulated based on a simplified version of standard craniospinal proton irradiation (St Clair et al 2004). In our study, the treatment technique comprised four fields, including inferior and superior spinal fields delivered in the posterior–anterior (PA) direction, and symmetric right and left cranial fields delivered in the posterior–oblique direction (denoted as RPO and LPO). The prescribed absorbed dose (D) to the entire target volume was 36 Gy, which was consistent with the prescribed dose in the study by Miralbell et al (2002). There were, however, two noteworthy differences in our method relative to theirs: patient size and organs size of the target volume. Miralbell et al considered a 3 yr old boy whose treatment included only the spinal axis. In our study, the stray radiation exposures to this boy were estimated from calculations for an adult male where the treatment included irradiation of both the spinal axis and cranium. The impact of these differences is discussed later. The water-equivalent range, water-equivalent spread-out Bragg peak (SOBP) width and field sizes for the treatment fields used in the dose calculations were as follows: cranial field (12 cm range, 12 cm SOBP width and 208 cm² area), superior spinal field (8 cm range, 8 cm SOBP width and 150 cm² area), inferior spinal field (8 cm range, 8 cm SOBP width and 144 cm² area). Lastly, a complete craniospinal irradiation usually includes a boost field to the posterior fossa. The boost field was excluded for simplicity in this study; its proportion of the stray radiation exposure was small (Taddei et al 2009).

The stray radiation exposures associated with proton CSI was assessed with Monte Carlo simulations that included the treatment unit and a stylized male phantom, as shown in figure 1. A stylized phantom was selected because of it allows greater reduced simulations times compared to a comparable voxelized phantom. We used the Computerized Anatomical Man (CAM) phantom, which is an anatomically realistic male phantom that was developed by Billings and Yucker (Billings and Yucker 1973) for dose assessments in manned spaceflight, comprises 2531 discretely defined geometric cells. The CAM model was converted for use with MCNPX in a previous work (Fontenot et al 2008). CAM was also enhanced to utilize more detailed and accurate information on the elemental compositions and mass density of various tissues and organs. Specifically, we assigned six materials (organ tissue, skeletal muscle, compact bone, bone marrow, skeletal bone and air) and six mass densities based on data taken from Woodard and White (1986). Another enhancement was the addition of strategically placed 2 cm diameter spherical receptors in various tissues and organs (e.g. bladder, rectum, colon, lungs, stomach, liver, esophagus and thyroid). These spherical tallies provided a relatively simple and computationally efficient means to simultaneously tally the absorbed dose and neutron spectral fluence in a wide variety of locations throughout the body. Equivalent dose to the remaining organs at risk (bone marrow, skin, bone surface and remainder) was taken as the average equivalent dose over all explicitly defined organs. The properties of the treatment fields, e.g. range, modulation width and field size, were selected to provide a realistic and representative dose distribution in the phantom. For simplicity, the RPO and LPO cranial fields were replaced with a single posterior field. The proton fields incident on the phantom were used only to generate the stray radiation exposures; the doses from the therapeutic proton radiation were taken from Miralbell et al (2002). The accuracy of three-dimensional Monte Carlo dose predictions in heterogeneous phantoms was verified previously (Titt et al 2008). Heterogeneity corrections, which are still common in photon therapy dose calculations, were not applied since both the methods from Mirallbell et al for predicting therapeutic dose and our methods for predicting stray radiation dose included explicit modeling of the heterogeneities in the patient or phantom.

We simulated neutron exposures for the double scattering nozzle used at our institution as well as for an idealized scanning nozzle (Newhauser et al 2008). The nozzles and radiation transport were simulated using the MCNPX code, which was previously benchmarked for proton therapy applications (Fontenot et al 2005, Koch and Newhauser 2005, Newhauser et al 2005, Polf and Newhauser 2005, Polf et al 2005, Tayama et al 2006, Herault et al 2007, Newhauser et al 2007a, 2007b, Zheng et al 2007a). The Monte Carlo code simulated the entire trajectories of individual particles, beginning with protons entering the nozzle. The particle trajectories were tracked through various beam shaping and collimating components, nozzle shielding and the patient or phantom. Our double scattering nozzle (Hitachi Ltd; Probeat, Tarrytown, NY) was previously described in detail (Newhauser et al 2007a, Zheng et al 2007a). We simulated the treatment with a scanning nozzle just as we would a double scattering treatment except that all neutrons emanating from the treatment unit (external neutrons) were artificially terminated. Thus, only neutrons generated inside the patient (internal neutrons) were present. This method ensured a fair comparison of the proton nozzles by holding constant the absorbed dose distributions from primary proton beam. Comparing the proportion of exposure from internal versus external neutrons is also important for evaluating the shielding of a proton therapy treatment head (Fontenot et al 2008, Taddei et al 2008), particularly when static or dynamic collimators are used (Bues et al 2005).

To evaluate the exposures to a patient, we included an anthropomorphic phantom in the simulation following the methods described by Fontenot et al (2008) and references therein. Figure 1 shows the nozzle, phantom and particle fluences from individual proton treatment fields. To facilitate comparison with results from the literature, we calculated a figure of merit defined as the quotient of the effective dose, E, and the therapeutic absorbed dose, D, at the isocenter. E is the weighted sum of equivalent doses to individual tissues (H_T), where we followed methods developed for radiation protection purposes (ICRP 1990, 2003). We also calculated the radiation weighting factor (w_R) for neutrons based on the Monte Carlo simulations of the neutron spectral fluences. For the reader’s convenience, this calculation approach is reviewed below.

The effective dose is given by

$$E=\sum _{\mathrm{T}}{H}_{\mathrm{T}}·w_{\mathrm{T}},$$ (1)

where the equivalent dose, H_T, for each organ or tissue T is given by

$$H_{\mathrm{T}}=\sum _{\mathrm{R}}{w}_{\mathrm{R}}·D_{\mathrm{T}}.$$ (2)

In evaluating equation (1), we used tissue weighting factors, denoted by w_T, from ICRP Publication 60 (1990) (see table 1). There the mean absorbed dose to an organ or tissue (D_T) is given by a mass-weighted average over the entire organ, or

$$D_{\mathrm{T}}=\frac{1}{m}{\int }_{m_{\mathrm{T}}}D\mathrm{d}m.$$ (3)

However, in this work, we estimated D_T from one or more subvolumes located within the organ or tissue. For example, the mean dose to lung was taken as the average dose in two spherical subvolumes (4.2 cm³ each) of lung tissue, one each in the central regions of the right and left lungs. The use of subvolumes was used for simplicity and computational efficiency. The radiation weighting factor in equation (2) is a function of neutron energy, E_n, and may be calculated using a variety of empirical expressions, such as the most recent recommendation from ICRP Publication 92 (2003), which was used in this work and is given by

$$w_{\mathrm{R}}=2.5[2-{\mathrm{e}}^{-4E_{\mathrm{n}}}+6{\mathrm{e}}^{-\text{ln}{(E_{\mathrm{n}})}^2/4}+{\mathrm{e}}^{-\text{ln}{(E_{\mathrm{n}}/30)}^2/2}].$$ (4)

The radiation weighting factor was designed to be conservative when applied to the general population. However, the neutron radiation weighting factor for pediatric cancer patients may be higher, although the available estimates are highly uncertain (NRC 2006). Therefore, to test the impact of uncertainty in w_R in our projected cancer risks, described below, we compared results after multiplying the neutron radiation weighting factor in equation (4) by scaling factors of 1, 2.5, 5, 20 and 35. Varying the scaling factor values allowed us to gauge the sensitivity of our results to a possible systematic underestimation of the neutron radiation weighting factors. While the choice of individual scaling factor values was somewhat arbitrary, the interval of values was selected to bracket the range of plausible w_R values.

Table 1.

Coefficient of lifetime risk of fatal second cancer (M_T), tissue weighting factor (w_T) and lethality fraction (L_T) from ICRP Publication 60 (1990).

Tumor site	MT(%/Sv)	wT	LT
Gonads	0.10	0.2	0.70
Bone marrow (red)	0.50	0.12	0.99
Colon	0.85	0.12	0.55
Lung	0.85	0.12	0.95
Stomach	1.10	0.12	0.90
Bladder	0.30	0.05	0.50
Breast	0.20	0.05	0.50
Liver	0.15	0.05	0.95
Esophagus	0.30	0.05	0.95
Thyroid	0.08	0.05	0.10
Skin	0.02	0.01	0.002
Bone surface	0.05	0.01	0.70
Remainder	0.50	0.05	0.71

2.2. Calculating the risk of developing a radiogenic second cancer

The risk of developing a second cancer was calculated for each organ or tissue using

$$R_{\mathrm{T}}=H_{\mathrm{T}}·M_{\mathrm{T}}/L_{\mathrm{T}},$$ (5)

where R_T is the absolute lifetime risk of secondary cancer, H_T is the equivalent dose from equation (2), M_T is the coefficient of lifetime risk of fatal cancer per unit of radiation exposure, and L_T is the organ-specific lethality factor. The lethality factors convert the result from risk of fatal cancer to risk of cancer that is fatal or non-fatal. The values of M_T and L_T were taken from ICRP Publication 60 (1990) and are listed in table 1. These values were selected for consistency with the methods of Miralbell et al (2002) and because they are widely accepted.

The total lifetime risk to the patient for the development of a second cancer was calculated as

$$R=\sum _{\mathrm{T}}{R}_{\mathrm{T}}$$ (6)

and the yearly risk as

$$R_y=R/t_{\mathrm{L}},$$ (7)

where the remaining lifetime t_L is the life expectancy minus the age at treatment (in this case, 76 − 3 = 73 yr).

To estimate R for a particular treatment modality, we combined the risks from the primary beams, using data from Miralbell et al (2002), with risks from the stray radiation using data from this work. Thus, we were able to explicitly partition the sources of risk in equation (6), yielding

$$R=\sum _{\mathrm{T}}(R_{\mathrm{T},\text{primary}}+R_{\mathrm{T},\text{stray}}).$$ (8)

To compare treatment modalities with one another, we calculated the relative risk according to

$$R_{\text{rel}}=R/R_0,$$ (9)

where R₀ was the value from equation (8) for the scanned-beam proton treatment.

3. Results

The absorbed dose from stray radiation, radiation weighting factor and equivalent dose from stray radiation are listed in table 2 for the major organs and tissues. These values were simulated using the passively scattered proton therapy beam delivery method and include only contributions from stray radiation, i.e. they do not include the in-field contribution from the primary beam. The corresponding values for an idealized scanned-beam delivery are listed in table 3. The equivalent dose for the complete three-field treatments varied from 2.5 mSv (to the gonads from the scanned-beam treatment) to approximately 443 mSv (to the esophagus and thyroid from the passively scattered treatment). The values of equivalent dose generally decreased with distance from the therapeutic field and were on average two times higher from passive beams than from scanned beams. The radiation weighting factor for neutrons, which was calculated inside various organs, was on average slightly larger and more variable for the scanned treatment (mean w_R = 9.0, interval of 5.9–10.9) than for passively scattered treatment (mean w_R = 8.0, interval of 6.7–9.2). The difference in w_R values from passively scattered treatments relative to the corresponding values from scanned-beam treatments was due to changes in the shape of the neutron spectra due to external neutrons. The effective dose from stray radiation was 187 mSv (E/D = 5.2 mSv Gy⁻¹) for the passive proton treatment versus 89 mSv (E/D = 2.5 mSv Gy⁻¹) for the scanned-beam treatment. The lifetime risk of second cancer due to stray radiation was 1.5% for the passively scattered treatment versus 0.7% for the scanned-beam treatment. For stray radiation from the passively scattered treatment, the largest proportions of the lifetime risk were assumed by the skin (51% of total risk), thyroid (10%), colon (8%), lung (8%) and stomach (8%). Together these organs were associated with 85% of the risk of second cancer associated with all tissues and organs exposed to stray radiation. Risks posed by the scanned proton treatments were quite similar, with the skin (47%), thyroid (17%), stomach (9%), esophagus (7%) and lung (6%) together assuming 86% of the total risk of a second cancer from stray radiation. Skin predominated the risk of second cancer from stray radiation because the value of M_T/L_T in equation (5) for skin is larger (by factors of 10–350) than for all other organs and tissues in table 1.

Table 2.

Predicted exposures of stray radiation from craniospinal irradiation using passively scattered proton beams, including absorbed dose of stray radiation per therapeutic absorbed dose (D_T/D), radiation weighting factor (w_R) for neutrons, equivalent dose from stray radiation per therapeutic absorbed dose (H_T/D_T), lifetime risk of fatal or non-fatal second cancer (R_T) from stray radiation corresponding to the entire three-field, 36 Gy treatment and the corresponding percentage of risk in all tissues and organs (R_T/R). The values of absorbed dose and radiation weighting factor values are listed separately for the cranial, superior spinal and inferior spinal treatment fields. These data were simulated for a commercially available treatment unit at The University of Texas M D Anderson Cancer Center (Newhauser et al 2007a).

	DT/D (Gy/Gy)			wR(Sv/Gy)			HT/D (Sv/Gy)			RT (%)	RT/R (%)
Organ	Cranial	Sup spine	Inf spine	Cranial	Sup spline	Inf spine	Cranial	Sup spine	Inf spine
Gonads	2.30 × 10−5	3.71 × 10−5	5.97 × 10−5	6.7	6.7	7.2	1.54 × 10−4	2.49 × 10−4	4.30 × 10−4	0.00	0.1
Bone marrow (red)	1.06 × 10−4	2.76 × 10−4	2.27 × 10−4	7.8	7.9	8.1	8.27 × 10−4	2.18 × 10−3	1.84 × 10−3	0.09	2.6
Colon	7.06 × 10−5	9.36 × 10−5	3.72 × 10−4	7.8	8.1	9.2	5.51 × 10−4	7.58 × 10−4	3.42 × 10−3	0.26	7.8
Lung	1.45 × 10−4	5.80 × 10−4	2.40 × 10−4	8.0	8.5	8.1	1.16 × 10−3	4.93 × 10−3	1.94 × 10−3	0.26	7.6
Stomach	8.94 × 10−5	1.86 × 10−4	4.04 × 10−4	8.0	8.3	9.1	7.15 × 10−4	1.54 × 10−3	3.68 × 10−3	0.26	7.7
Bladder	3.52 × 10−5	4.45 × 10−5	1.05 × 10−4	7.2	7.2	7.8	2.53 × 10−4	3.20 × 10−4	8.19 × 10−4	0.03	0.9
Breast	1.56 × 10−4	3.07 × 10−4	2.44 × 10−4	8.1	8.4	8.3	1.26 × 10−3	2.58 × 10−3	2.03 × 10−3	0.08	2.5
Liver	8.82 × 10−5	1.55 × 10−4	4.04 × 10−4	8.0	8.2	9.1	7.06 × 10−4	1.27 × 10−3	3.68 × 10−3	0.03	0.9
Esophagus	2.00 × 10−4	1.08 × 10−3	1.20 × 10−4	7.9	9.1	7.5	1.58 × 10−3	9.83 × 10−3	9.00 × 10−4	0.14	4.1
Thyroid	2.00 × 10−4	1.08 × 10−3	1.20 × 10−4	7.9	9.1	7.5	1.58 × 10−3	9.83 × 10−3	9.00 × 10−4	0.35	10.4
Skin	1.06 × 10−4	2.76 × 10−4	2.27 × 10−4	7.8	7.9	8.1	8.27 × 10−4	2.18 × 10−3	1.84 × 10−3	1.74	51.4
Bone surface	1.06 × 10−4	2.76 × 10−4	2.27 × 10−4	7.8	7.9	8.1	8.27 × 10−4	2.18 × 10−3	1.84 × 10−3	0.01	0.4
Remainder	1.06 × 10−4	2.76 × 10−4	2.27 × 10−4	7.8	7.9	8.1	8.27 × 10−4	2.18 × 10−3	1.84 × 10−3	0.12	3.6

Table 3.

Predicted exposures of stray radiation from a craniospinal irradiation using scanned proton beams, including absorbed dose of stray radiation per therapeutic absorbed dose (D_T/D), radiation weighting factor (w_R) for neutrons, equivalent dose of stray radiation per therapeutic absorbed dose (H_T/D_T), lifetime risk of fatal or non-fatal second cancer (R_T) from stray radiation corresponding to the entire three-field, 36 Gy treatment, and the corresponding percentage of risk in all tissues and organs (R_T/R). The values of absorbed dose and radiation weighting factor values are listed separately for the cranial, superior spinal and inferior spinal treatment fields. The dosimetric data were simulated for an idealized scanned-beam proton therapy unit from which no leakage radiation emanated, i.e. only stray radiation generated internally to the patient was considered.

	DT/D (Gy/Gy)			wR(Sv/Gy)			HT/D (Sv/Gy]			RT (%)	RT/R (%)
Organ	Cranial	Sup spine	Inf spine	Cranial	Sup spine	Inf spine	Cranial	Sup spine	Inf spine
Gonads	7.12 × 10−7	1.94 × 10−6	6.14 × 10−6	5.9	7.3	8.4	4.18 × 10−6	1.41 × 10−5	5.16 × 10−5	0.0004	0.02
Bone marrow (red)	1.66 × 10−5	1.26 × 10−4	7.66 × 10−5	7.6	9.1	9.5	1.26 × 10−4	1.15 × 10−3	7.28 × 10−4	0.04	2.3
Colon	1.65 × 10−6	5.12 × 10−6	1.19 × 10−4	7.1	9.3	10.9	1.18 × 10−5	4.79 × 10−5	1.30 × 10−3	0.08	4.9
Lung	3.43 × 10−5	2.16 × 10−4	4.79 × 10−5	8.5	10.4	10.1	2.92 × 10−4	2.25 × 10−3	4.84 × 10−4	0.10	6.3
Stomach	5.38 × 10−1	6.69 × 10−5	2.23 × 10−4	8.1	10.2	10.7	4.34 × 10−5	6.81 × 10−4	2.4 × 10−3	0.14	8.8
Bladder	5.46 × 10−7	1.97 × 10−6	2.15 × 10−5	7.1	7.8	9.5	3.90 × 10−6	1.53 × 10−5	2.05 × 10−4	0.00	0.3
Breast	1.01 × 10−5	1.53 × 10−4	8.97 × 10−5	8.6	9.6	9.4	8.68 × 10−5	1.47 × 10−3	8.46 × 10−4	0.03	2.2
Liver	3.57 × 10−6	5.96 × 10−5	5.96 × 10−4	7.9	10.3	10.8	2.82 × 10−5	6.14 × 10−4	2.12 × 10−3	0.02	1.0
Esophagus	5.22 × 10−5	7.73 × 10−4	3.37 × 10−5	9.3	10.5	9.4	4.88 × 10−4	8.16 × 10−3	3.16 10−4	0.11	6.8
Thyroid	5.22 × 10−5	7.73 × 10−4	3.37 × 10−5	9.3	10.5	9.4	4.88 × 10−4	8.16 × 10−3	3.16 × 10−4	0.27	17.3
Skin	1.66 × 10−5	1.26 × 10−4	7.66 × 10−5	7.6	9.1	9.5	1.26 × 10−4	1.15 × 10−3	7.28 × 10−4	0.72	46.3
Bone Surface	1.66 × 10−5	1.26 × 10−4	7.66 × 10−5	7.6	9.1	9.5	1.26 × 10−4	1.15 × 10−3	7.28 10−4	0.01	0.3
Remainder	1.66 × 10−5	1.26 × 10−4	7.66 × 10−5	7.6	9.1	9.5	1.26 × 10−4	1.15 × 10−3	7.28 × 10−4	0.05	3.3

Next we describe the results of risk calculations that include both therapeutic and stray radiation. Acomparison of the yearly cancer risks is summarized in table 4 for treatments using conventional photon therapy (CRT), intensity-modulated photon therapy (IMRT), passively scattered proton therapy (PSPT) and magnetically scanned intensity-modulated proton therapy (IMPT). The proportions of risk associated with primary and secondary radiation are listed separately, along with their sum (total risk). Using the radiation weighting factors listed in tables 2 and 3 and calculating the relative risk with equation (9), we found that the risk of second cancer associated with IMRT and CRT were, respectively, factors of 7 and 12 higher than with IMPT. The relative risk from passively scattered proton therapy was only a factor of 1.2 larger than that from IMPT; that is, the risk following IMRT and CRT were factors of 6 and 11, respectively, larger than following PSPT. The yearly risks from IMPT and PSPT were both extremely small, at 0.060% and 0.070%, respectively. The risks associated with both IMPT and PSPT were predominated by primary (in-field) radiation associated with the therapeutic proton beams and not by stray neutron radiation. As noted previously by Miralbell et al (2002), these small yearly risks can lead to substantial lifetime risks for young patients with good prognoses for survival of their first cancer. For example, the risk projections for the 3 year old boy (i.e. our reanalysis of data from Miralbell et al that additionally took into account neutrons) revealed the lifetime risk of second cancer incidence was approximately 4.4% following IMPT, 5.1% following PSPT, 31% following IMRT and 55% following CRT. To place the risks associated with proton therapy in context, they are much larger than the risk of anesthesia-related (2.2 deaths per 10 000 procedures, or 0.02% incidence (Lagasse 2002)) and slightly larger than lifetime occupational risks faced by healthy workers in various ‘safe’ industries, e.g. trade, government, agriculture (0.2–1.8% lifetime incidence of fatal accident, assuming a 40 year working career (NCRP 1993)).

Table 4.

Comparison of organ doses and risks of second cancer from various treatment modalities, including conventional photon therapy (CRT), intensity-modulated photon therapy (IMRT), passively scattered proton therapy (PSPT) and magnetically scanned proton therapy (IMPT). The values for CRT, IMRT and the primary component of IMPT were taken from Miralbell et al (2002). The stray radiation contributions to PSPT and IMPT treatments were simulated using a Monte Carlo model. The primary contribution for PSPT was approximated as the primary value for IMPT. The values in the bottom row represent the relative risk of second cancer incidence, where each value was normalized to the result for IMPT.

	Risk associated with primary radiation			Risk associated with secondary radiation		Risk associated with primary and secondary radiation
Tumor site	CRT	IMRT	IMPT	PSPT	IMPT	PSPT	IMPT
Annual risk of second cancer, Ry, (%/yr)
Stomach and esophagus	0.15	0.11	0.0	0.0055	0.0033	0.005	0.003
Colon	0.15	0.07	0.0	0.0036	0.0010	0.004	0.001
Breast	0.0	0.0	0.0	0.0012	0.0005	0.001	0.000
Lung	0.07	0.07	0.01	0.0035	0.0013	0.014	0.011
Thyroid	0.18	0.06	0.0	0.0049	0.0037	0.005	0.004
Bone and connective tissue	0.03	0.02	0.01	0.0002	0.0001	0.010	0.010
Leukemia	0.07	0.05	0.03	0.0012	0.0005	0.031	0.030
All	0.75	0.43	0.05	0.0200	0.0105	0.070	0.060
Lifetime risk of second cancer, R, in percent
All	54.8	31.4	3.7	1.5	0.76	5.1	4.4
Ratio of lifetime risk of second cancer from various irradiation to that from IMPT, Rrel
All	12.4	7.1	0.8	0.3	0.2	1.2	1.0

It is possible that the radiation weighting factors listed in tables 2 and 3, which were developed for radiation protection of healthy individuals, were underestimated by equation (4) when applied to a cancer patient. Similarly, the risk coefficients, tissue weighting factors and lethality factors in table 1 may introduce a bias when applied to survivors of childhood cancer. For example, young children who survive a first cancer may be more susceptible to developing some second malignancies, such as cancer of the female breast (NRC 2006). To test the sensitivity of our findings to systematic errors in this regard, we varied the w_R value for neutrons and recalculated the R and R_rel values. When the w_R values were increased by a factor of 2.5, the risk from stray neutrons and from primary radiation were approximately in equal proportion for PSPT. Similarly, equipoise for IMPT was observed when the w_R values were increased by a factor of 5. However, even with these increases, the proton treatments still had lower risks of second cancer incidence than either IMRT or CRT. On increasing w_R by a factor of 20, the second cancer risks associated with PSPT rose to approximately equal those of IMRT. On increasing w_R by a factor of 35, the risk from PSPT rose to approximately equal that of CRT.

4. Discussion

We used Monte Carlo simulations of stray neutron exposures to organs throughout the body to estimate the risk of developing a second cancer in a patient receiving craniospinal proton irradiation. In addition, we took into account exposures associated with the primary radiation beam (i.e. the therapeutic field) from a previous investigation. Our results confirm that proton therapy offers substantially lower second cancer risks than 6 MV photon radiotherapies, even when the risk associated with neutrons is taken into account.

Our findings are qualitatively and quantitatively similar to those of Miralbell et al (2002) and Mu et al (2005). Those studies suggested that proton therapy offered lower risk for the development of second cancer, although Mirabell et al did not account for the contribution of neutron radiation. Mu et al estimated neutron effective dose at 47 mSv for a 23.4 Gy treatment with IMPT only, and these were based on values from the literature. Our estimates of effective dose from neutrons were 89 mSv for IMPT and 187 mSv for PSPT, which was due in part to our larger (36 Gy) treatment dose. Our risk analysis, which did take neutrons into account, revealed that the second cancer risks associated with the passively scattered and scanned proton treatments were predominated by contributions from the primary beams; the neutron exposures comprise a much smaller proportion of the total risk. For example, we estimated that the second cancer risk from IMRT was 7.1 times larger than from IMPT, which is not substantially different from the factor of 8.6 reported by Miralbell et al (2002).

One of the major clinical implications of this work is that the cancer risks associated with proton therapy are predominated by primary proton radiation, not stray neutron radiation. In particular, our results shed some light on the troublingly large uncertainties in the assumed neutron radiation weighting factor. Hall (2006) recently cautioned that pediatric patients receiving passively scattered proton therapy might be at excessive risk of developing second cancers if the true neutron weighting factor has been substantially underestimated (in this study, we calculated typical w_R values of approximately 8). Our analysis suggests, however, that proton therapy has a lower associated risk of second cancer when compared with IMRT or CRT. This finding holds if w_R ≤ 50 for the neutron exposures, which contains the interval of plausible values.

The interval of ‘plausible’ neutron radiation weighting factors is itself somewhat controversial, and because of its central importance to this investigation, some discussion is warranted. The Biological Effects of Ionizing Radiation (BEIR) committee of the National Research Council recently reviewed experimental data on the relative biological effectiveness (RBE) of neutrons for the induction of cancer (NRC 2006). This quantity is closely related to the radiation weighting factor for neutrons in equation (4). For the induction of solid tumors they concluded that, for the purpose of risk estimation, the relevant RBE data from rodent experiments were in the interval of 20–50, whereas lower neutron RBE values were relevant for leukemia. In their analysis of atomic bomb survivors, the BEIR committee adopted a much lower, constant value of w_R = 10 and stated that they rejected a suggestion that ‘a weighting factor of roughly 30 for the neutron-absorbed dose might be a better choice than 10’ (NRC 2006). However, the exact choice remains controversial and the importance of this fact cannot be overstated. For example, Kellerer et al (2006) recently analyzed the data for atomic bomb survivors and deduced that the 95% confidence interval of neutron RBE values was 25–400. They emphasized that ‘the inferences are at present tentative’ and that their analysis ‘included no separate category for neutron dose’. Because the true RBE values for neutrons will not be known with certainty anytime soon, we adopted the recommendation of the BEIR committee, which is consistent with the preponderance of evidence in the literature, namely, that the true value of the neutron RBE for carcinogenesis is 50 or less, with uncertainties that are large and difficult to estimate. Even with such large uncertainties in the neutron weighting factor, it is still possible to make meaningful comparisons of the second cancer risks from proton therapy versus photon therapy.

To demonstrate this, consider the following example. We mathematically solved for the value of w_R that yielded equal risks for IMRT and PSPT. This solution yielded w_R = 152, or approximately 19 times higher than the value we used. Similarly, the mathematical solution of equal risks for IMRT and IMPT yielded w_R = 333, or approximately 37 times higher than the value we used. These w_R values are well beyond the interval of plausible values. Thus, based on the calculations of the pediatric treatment considered here, one may reasonably conclude that proton therapy offers a lower risk of second cancer regardless of the value used for the neutron weighting factor or its uncertainty; the same conclusion holds for all plausible values of w_R.

That being said, we wish to underscore the important role of other, smaller but not negligible sources of uncertainty in risk projections for proton therapy patients. For example, the neutron-absorbed dose values are dependent on many variables, including the beam range, field size, air gap and distance from the treatment unit (Zheng et al 2007a, 2007b, 2008). Recent studies have also shown that the dosimetric results depend to some extent on the method of calculation (Fontenot et al 2008, Zheng et al 2008).

While this study had several features that might be viewed as limitations, we are confident of our conclusions. First, the phantom used for neutron dose calculations was selected for computational efficiency; it was substantially larger than the 3 year old patient for which the primary radiation exposures were calculated. However, this was not a serious limitation because the out-of-field neutron-absorbed dose and radiation weighting factor generally did not vary strongly with depth or position within the phantom. Furthermore, the use of an adult phantom necessitated larger proton beam ranges, SOBP widths and field sizes than would have been required for the patient, which would result in an overestimation of the equivalent dose from neutrons (Zheng et al 2007a, 2007b, 2008). Because each of these factors tended to increase the neutron exposures, the true risks associated with the proton treatments may be somewhat lower than our estimates. Lower neutron-related risks would not change the major findings of this work; rather, they would reinforce them.

Finally, Hall (2007) recently posed the following important question. ‘Does it make any sense to spend over $100 million on a proton facility, with the aim to reduce doses to normal tissues, and then to bathe the patient with a total body dose of neutrons, the RBE of which is poorly known, when the technology to avoid it is available and already in use elsewhere?’ In the same article, Hall opined that ‘protons are a major step forward for radiotherapy, but neutrons are bad news and must be minimized by the use of spot scanning techniques’. While we agree that proton therapy represents a major advance, we differ with Hall’s other key statements and inferences. First, low-cost proton therapy systems (<$15 million US) are on the horizon, and in our view, even the high-capacity $100 million facilities represent an excellent value when one considers the achievable savings in total cost to society through reductions in treatment-related morbidity and mortality. For example, Lundkvist et al (2005) reported a cost/benefit analysis in which they found that proton therapy for childhood medulloblastoma provided lower total cost and better outcomes than conventional radiation therapy. Second, our results revealed that proton therapies carry lower risks of second cancer, even with large and poorly known values of neutron RBE for carcinogenesis, as discussed above. Third, in the case we examined, using spot scanning instead of passive scattering reduced the second cancer risk by only about 20%, after taking into account the contributions to risk from the therapeutic beam and stray radiation. This reduction would come at a cost; there are potentially serious yet poorly understood risks associated with the dosimetric hot and cold spots caused by the interplay of beam and organ motion (Grozinger et al 2006). In fact, given that fewer than 300 patients have been treated with scanned proton beams (Timmermann et al 2007) versus more than 40 000 (Sisterson 2005) with scattered proton beams, many of the recently claimed benefits from scanned-beam treatments seem overly optimistic and premature.

Given the complexities and uncertainties associated with second-cancer risk assessments, additional studies are needed to test whether the same conclusions will hold for patients of other ages and anatomical statures. At present, the available literature on stray radiation exposures for proton therapy is still extremely limited compared with that for photon therapy. For these reasons, we caution against drawing sweeping conclusions about proton radiotherapy until more information becomes available. In our laboratory, additional studies are now under way to address some of these issues, with an emphasis on improving the accuracy of absorbed doses from the primary and stray radiation fields.