Characterization of Size, Anisotropy, and Density Heterogeneity of Nanoparticles by Sedimentation Velocity

Abstract

A critical problem in materials science is the accurate characterization of the size dependent properties of colloidal inorganic nanocrystals. Due to the intrinsic polydispersity present during synthesis, dispersions of such materials exhibit simultaneous heterogeneity in density ρ, molar mass M, and particle diameter d. The density increments ∂ρ/∂d and ∂ρ/∂M of these nanoparticles, if known, can then provide important information about crystal growth and particle size distributions. For most classes of nanocrystals, a mixture of surfactants is added during synthesis to control their shape, size, and optical properties. However, it remains a challenge to accurately determine the amount of passivating ligand bound to the particle surface post synthesis. The presence of the ligand shell hampers an accurate determination of the nanocrystal diameter. Using CdSe and PbS semiconductor nanocrystals, and the ultrastable silver nanoparticle (M₄Ag₄₄(p-MBA)₃₀), as model systems, we describe a Custom Grid method implemented in UltraScan-III for the characterization of nanoparticles and macromolecules using sedimentation velocity analytical ultracentrifugation. We show that multiple parametrizations are possible, and that the Custom Grid method can be generalized to provide high resolution composition information for mixtures of solutes that are heterogeneous in two out of three parameters. For such cases, our method can simultaneously resolve arbitrary two-dimensional distributions of hydrodynamic parameters when a third property can be held constant. For example, this method extracts partial specific volume and molar mass from sedimentation velocity data for cases where the anisotropy can be held constant, or provides anisotropy and partial specific volume if the molar mass is known.

Ligand-stabilized nanoparticles and quantum dots (QDs) have become important materials in a wide variety of applications including nanomedicine,¹ sensing,² and optoelectronics.³ Because key elements of these applications are tailored around the nanoscale properties of the particles’ inorganic core and organic ligand shell, there is a pressing need for methods that can reliably quantify the heterogeneities within the particle’s two components. Although transmission electron microscopy (TEM) has become a routine tool to determine the shape and size of the inorganic core in high-resolution detail, any organic materials bound on the nanocrystal surface are usually impossible to discern, due to their low atomic contrast. Yet, in many instances, it is the hydrodynamic radius and overall core and shell properties that are of interest. For instance, in applications related to drug delivery and biomarkers, the efficacy and toxicity of the nanoparticles are both size and surface property dependent.^1,4 In QD-based photovoltaics⁵ and transistors,⁶ it is becoming increasingly clear that progress in device performance is contingent upon the judicious engineering of the ligand shell, which plays a pivotal role in the transport properties,⁷ surface passivation,⁸ and self-assembly⁷ of QD solids. Hence, it is essential to be able to measure parameters related to overall hybrid particle (inorganic core and organic ligand shell) properties as they influence solubility, electronic properties, assembly and reactivity.

Analytical ultracentrifugation (AUC) is a solution-based fractionation technique that allows the hydrodynamic and thermodynamic characterization of colloids, where all components in a dispersion can be detected and measured. It is based on first-principle transport models and does not require any standards. It is the only technique so far proven to be sensitive to minute changes in the density and size of both the core and shell components of nanoparticles, all the while providing robust statistics that give a complete picture of a sample in question.⁹⁻¹⁸ For these reasons, AUC is the premier technique for the characterization of nanoparticles in the solution environment.

In AUC, large centrifugal force fields (up to 250000g) are used to sediment macromolecules or nanoparticles in an appropriate buffer solution. The particles will sediment by forming a moving boundary, which creates a concentration gradient that also induces diffusion flux. Both sedimentation and diffusion transport are measured over time by observing changes in the concentration profile during the experiment. This transport process separates particles according to their hydrodynamic properties, which include mass, friction, and density. These properties determine the sedimentation and diffusion coefficients for each particle. The analysis of the data is then tasked with identifying individual sedimentation and diffusion coefficients of any particles with distinct hydrodynamic properties. Traditional sedimentation analysis approaches parametrize the sedimentation and diffusion coefficients of the sedimenting particles in terms of the frictional ratio and molar mass, while a constant partial specific volume for all particles is assumed.¹⁹⁻²⁴ For proteins and other biopolymers, this is often a good assumption, and small errors resulting from slight deviations in the partial specific volume, most often due to solvation, have negligible effects on the obtained sedimentation coefficient, and somewhat larger discrepancies in the molar mass transformations are typically tolerated. On the other hand, such a parametrization may lead to significant error when studying nanoparticles, which frequently have a constant frictional ratio (i.e., a fixed anisotropy or shape), and a broad range of partial specific volumes due their variable core–shell structure. But in some cases, a constant anisotropy can be established by inspecting the particles by TEM, or where X-ray crystallography structures are available, the molar mass is known, and the anisotropy can be estimated with programs like UltraScan-SOMO.^25,26

In this work, we present a new generalized analysis approach and software implementation ideally suited for nanoparticles, quantum dots, and macromolecular systems for which some parameters like anisotropy, density, or mass are known a priori, and can be used as a constraint in the fit of the sedimentation velocity (SV) experimental data to obtain the unknown hydrodynamic parameters. When mixtures of particles are expected, it is important that the constrained parameter stays constant during the experiment for all species in the mixture. This approach is termed the Custom Grid method, and is implemented in UltraScan-III,²⁷ a well-known, freely available software package for the analysis of sedimentation experiments that models the data with linear combinations of finite element solutions^28,29 of the Lamm equation.³⁰ This method employs a parametrization of the sedimentation coefficient s and diffusion coefficient D that relies on constraints in either molar mass M, frictional ratio φ, or partial specific volume ν̅. When the anisotropy is known, φ can be held fixed to obtain both ν̅ and M. When ν̅ is known, φ and M can be obtained. In all cases, the sedimentation and diffusion coefficients can be obtained. By performing a search over a two-dimensional grid of possible parameter values, mixtures with heterogeneity in either of the two fitted parameters can then be resolved. An arbitrary parametrization of the sedimentation and diffusion space can be obtained using the following six relationships:

1

2

3

4

5

6

where V is the volume of a solvated particle (eq 1), N refers to Avogadro’s number, r₀ is the radius of the minimal sphere with frictional coefficient f₀ (eq 2). f₀ can be obtained from the Stokes–Einstein relationship (eq 3), which defines the frictional coefficient for a spherical particle in a solvent with viscosity η and radius r₀. The frictional ratio is a measure of the particle’s anisotropy, and is given by f/f₀ (eq 4). The frictional ratio relates the frictional coefficient of any anisotropic particle to the frictional coefficient of a sphere which has the same volume as the particle. R is the ideal gas constant, and T is the temperature in Kelvin.

To resolve heterogeneities in the two parameters in question, the Custom Grid approach discretizes the unknown parameters into a two-dimensional grid. For example, if M is used as a constant constraint, the grid can be built over ν̅ and φ, whereas when φ is used as a constant constraint, the grid can be built over ν̅ and M. We demonstrate the utility and validity of the presented method by analyzing SV data using the Custom Grid approach from a series of CdSe and PbS QDs of varying sizes, and the ultrastable silver nanoparticle M₄Ag₄₄(p-MBA)₃₀.³¹⁻³³ Notably, we were able to directly measure the density, size and molar mass distributions of the hybrid ligand-stabilized nanocrystals, and the anisotropy and partial specific volume of the silver nanoparticle with high statistical significance because AUC experiments measure many more particles than are available, for example, in electron microscopy experiments. We show that this approach can be used for both heterogeneous as well as monodisperse solutions. The analysis presented in this work, along with its user-friendly software implementation, paves the way toward the adoption of SV as a standard characterization tool for nanoparticle and QD researchers.

Data Analysis

The change in concentration C along the radius r and over time t of a sedimenting and diffusing particle in the analytical ultracentrifuge is described by the Lamm equation L (eq 7),³⁰ with boundary conditions m (meniscus) and b (bottom of the AUC cell):

7

The solution of this equation requires knowledge of the sedimentation coefficient s, diffusion coefficient D, and the angular velocity, ω. Given these parameters, a complete solution can be found using the adaptive space-time finite element method (ASTFEM^28,29). In the fitting approach, a grid of s and D parameter pairs is constructed such that all sedimenting particles are represented by one of the grid points. Each grid point represents a complete finite element solution, and the final solution encompassing the total concentration C_T of all solutes is given by the linear combination (eq 8):

8

where L is the Lamm equation solution for grid point i, j, and x_i,j represents the concentration of particle i, j. If the particle is not present, its concentration will be set to zero by the fitting algorithm. A non-negatively constrained least-squares fitting algorithm³⁴ is used to determine the partial concentration of all species described by the grid points, and to filter out nonexisting species in a series of refinement steps that are performed by the two-dimensional spectrum analysis (2DSA, see section SI-1, Supporting Information).³⁵ Because the construction of the initial grid domain is left up to the user, it is important that the parametrization of the grid reflects molecular properties that are meaningful to the investigator. In the case of the CdSe and PbS samples, the anisotropy is known to be globular from TEM, and the parameters of interest are either the s or M for the first grid dimension, and the density or ν̅ in the second dimension. In the case of the silver nanoparticles, M is known from the crystal structure and instead φ and the density are of interest. To achieve the appropriate parametrization, we assume a constant anisotropy for the CdSe and PbS QDs, discretize s with the desired resolution, and reparameterize the diffusion coefficient using eq 9, which we obtain from substituting eqs 1–5 into eq 6:

9

Here, ρ is the density of the solvent and all other parameters are as described earlier. For the silver nanoparticle analysis, we discretize ν̅ in eqs 1 and 5, φ in eq 4, and substitute f from eq 4 into eqs 5 and 6 to obtain our grid. The final model for the QD analysis is represented by a modification of eq 8, where D is expressed as a function of s and ν̅ at constant frictional ratio φ, as shown in eq 10, and for the silver nanoparticle analysis, the final model expresses both s and D as a function of a grid over ν̅ and φ at constant molar mass M (eq 11):

10

11

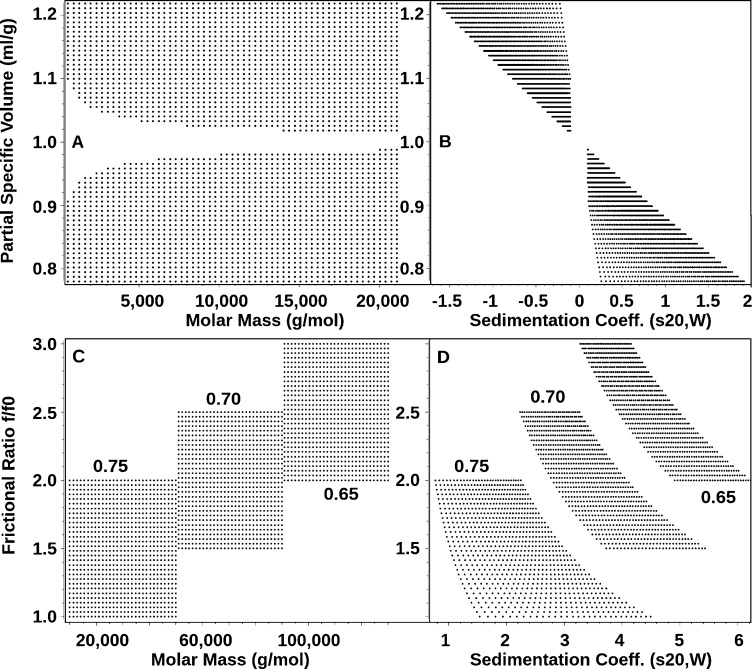
The approach presented here is general and can also be applied to biological macromolecules and synthetic polymers. It permits multiple parametrization options, allowing for the creation of other custom grids that can incorporate constraints available from a variety of experimental sources (mass spectrometry, X-ray crystallography, NMR, electron microscopy, densitometry, and others). Using eqs 1–6, transformations of the variable grid parameters to any nonconstant parameter of interest are possible. For this purpose, UltraScan provides a convenient module (see Figure S-1, Supporting Information) to create and display arbitrary custom grids that can be fitted with the 2DSA method, either on a local computer or on a remote supercomputer, and allows the user to combine multiple subgrids for selected regions of the parameter domain into a global supergrid. If the subgrids represent individual species with different partial specific volumes, as may be encountered when a mixture composed of polymers with dissimilar chemical composition (DNA, proteins, carbohydrates, complexes, etc.) is analyzed, each subgrid can be constructed with a separate partial specific volume (see Figure 1C,D). Such a grid requires prior knowledge about the approximate position where each species sediments. This can be obtained by measuring each component individually before placing it into a mixture. All grids are simulated in standard parameter space (adjusted to water at 20 °C), as are the results. Corrections for temperature, solvent density, and viscosity are made transparently in UltraScan using user-supplied buffer conditions and experimentally derived temperature values. For grids based on absolute molar mass, correct values for either ν̅ or φ, as well as buffer density and viscosity are required to allow UltraScan to automatically map the custom grid to the corresponding s–D pairs. It is also possible to simulate floating particles with densities lower than the solvent density, but the software will automatically exclude solutes with sedimentation coefficients ranging from −0.2 to +0.2 s from the selected parameter range (Figure 1A,B). In such a case, the particle will neither sediment nor float, even at the highest speeds possible in currently available instruments. For highly heterogeneous mixtures, it is possible to define logarithmically spaced grids to provide a better resolution for a wide coverage in molar mass, or to create multimodal grids. Several grid examples are shown in Figure 1, which illustrates these options.

Figure 1.

Visualization of Custom Grid custom grid examples. Shown are comparisons between molar mass (A, C) and sedimentation coefficient (B, D) views of selected custom grid representations for experimental systems containing continuous partial specific volume changes (A+B) and grid regions with discrete partial specific volumes (the partial specific volume, with units mL/g, used for the grid definition is indicated for each corresponding grid region). The example shown in panels A and B permits fitting of both sedimenting and floating particles, with nonsedimenting species excluded from the grid where s-values are between −0.2 and +0.2 s. Note the exponential grid spacing when regular molecular weight grids are translated to sedimentation coefficients. Both examples show grids linear in the molecular weight dimension, but the UltraScan software also permits the definition of grids that are linear in the sedimentation coefficient parameter.

Experimental Methods

Analytical Ultracentrifugation

CdSe QD samples were measured in their native solvent, 1-octadecene at 20 °C with density and viscosity of 0.789 g/mL and 4.32 cP, respectively. PbS samples were run in octane containing 5% oleic acid at 20 °C with density and viscosity of 0.7054 g/mL and 0.611 cP, respectively. For CdSe samples, SV experiments were performed at 50 000 rpm for 10.61 Å, 25 000 rpm for 17.05 Å, and 18 000 rpm for 20.15 Å CdSe QDs. Data were obtained by collecting the intensity between 300 and 700 nm at radial lengths between 5.98 and 7.2 cm. Radial intensity data were extracted at 484 nm for 10.61 and 17.05 Å QDs and at 529 nm for 20.15 Å QDs. In all cases, wavelengths were chosen where the intensity of the xenon light source is high while the optical density of the sample is between 0.2 and 0.8. For PbS samples, experiments were performed at 8000 rpm with 424 nm detection. The silver nanoparticle (M₄Ag₄₄(p-MBA)₃₀) was dissolved by placing a few microliters of slurry in 50 mM NaOH and vortexing for 5 min until well dissolved. A dilution of 0.6 absorbance units at 425 nm was measured at 30 000 rpm. Between 100 and 200 scans were collected for all experiments in intensity mode (see Figures S-2–S-7, Supporting Information, for experimental and fitted SV data, and residuals). Between 0.4 and 0.45 mL were loaded for each sample. Further details about AUC equipment and the details of the QD synthesis are listed in section SI-2 (Supporting Information).

Results and Discussion

Numerous studies have used AUC to study hybrid inorganic–organic colloidal systems.^16,17,36,37 Typically, in order to access the particle size information such as the molar mass and the hydrodynamic diameter using AUC, the average density of the particle must be known and this is usually problematic for systems containing both inorganic and organic components. In addition, the level of solvation is unknown, as is its effect on the anisotropy of the particle. For QDs, the majority of the aforementioned studies generally assumed a certain particle density by estimating the organic ligand shell thickness. There are, however, reports that employed the use of complementary techniques such as thermogravimetric analysis and total organic carbon analysis to directly measure the number of polymers bound to the particle surface.³⁸ Alternatively, techniques such as dynamic light scattering (DLS), fluorescence correlation spectroscopy (FCS), and asymmetric flow field flow fractionation (AFFFF) can also be utilized to independently measure the diffusion coefficient and the hydrodynamic particle size.³⁹

For the quantum dots, three sizes of CdSe and two sizes of PbS particles ranging between 10.61 Å and 20.15 Å were analyzed. The final particles consist of an inorganic core and an organic ligand shell. As illustrated in Figure 2, the difference between the total particle radius, R_total and the radius of the core, R_core, reflects the thickness of the compact shell containing organic surfactants and solvent molecules. The shell thickness and its total mass can provide information about the ligand packing density on the particle surface as well as the ligand conformation. CdSe and PbS core sizes can be determined using the band edge calibration methods,^40,41 where the absorption maxima at the first exciton bands yield the particle diameter (see Figure S-8, Supporting Information). Direct inspection of TEM data suggests spherical shape (φ = 1) and verifies homogeneity in anisotropy for PbS and CdSe for all particles in the mixture (see Figure S-9, Supporting Information).

Figure 2.

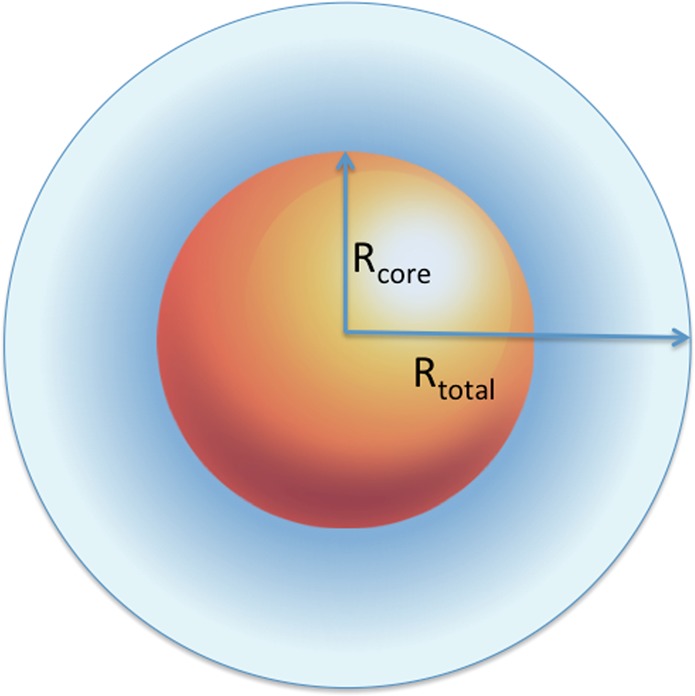
Schematic representation of the inorganic CdSe and PbS core with their organic ligand shells. R_total indicates the radius of the solvated QD–ligand core–shell.

For the silver nanoparticle, an X-ray crystallography-derived structure is available.³¹ From this crystal structure, a one-bead-per-atom bead model with atomic van der Waals radii was constructed and used to estimate both the anisotropy and the volume of the unsolvated particle. This estimate is performed with the Zeno method⁴² implemented in UltraScan-SOMO^25,26 (see section SI-1, Supporting Information, for an explanation of the method). The hydrodynamic radius, the translational diffusion coefficient, and the frictional ratio of the unhydrated particle can be directly computed using the Stokes–Einstein relation (eq 3), and using the same equation, and the computed volume, the frictional coefficient of the minimal sphere can be calculated. Together, the two frictional coefficients provide φ (eq 4). From the computed volume and the known mass of the particle, ν̅ of the unhydrated particle can be computed. We note that in our calculation, the volume contributions from the hydrogens were not included, because they were not available in the crystal structure, with only a negligible error expected.

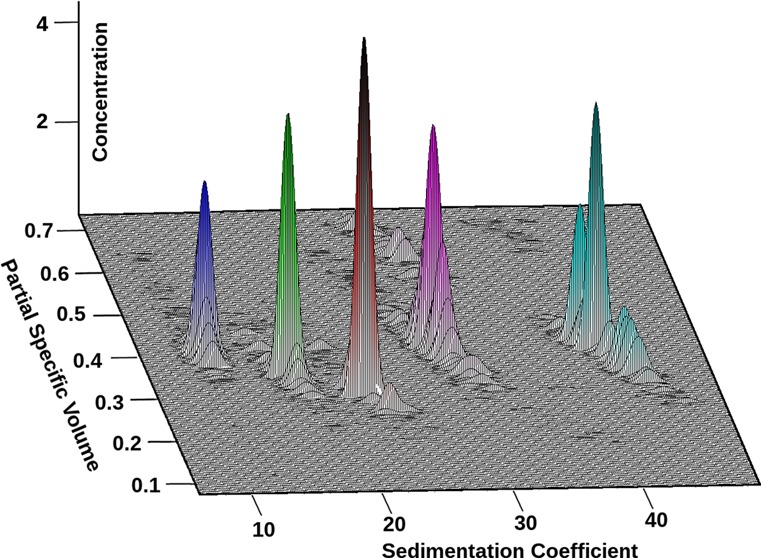
Results obtained from the Custom Grid–Monte Carlo analyses of the CdSe and PbS samples are listed in Table 1; results for the silver nanoparticle analysis are shown in Table 2. Experimental data, finite element fits, and residuals are shown in Figures S-2–S-7 (Supporting Information). Diffusion-corrected van Holde–Weischet integral sedimentation coefficient distributions and combined pseudo-three-dimensional plots demonstrating the particle ν̅, s, and the relative solute concentrations of the five QD particles are shown in Figure 3.

Table 1. Results obtained from the Custom Grid–Monte Carlo Analysis Using SV Data for CdSe and PbS QDs of Radii between 10.61 and 20.15 Å^a.

sample	Rcore (Å)	Mt (g/mol, ×104)	s20,w (s, ×10–13)	D20,w (cm2/s, ×10–7)	ν̅ (mL/g)	ρp (g/mL)	Rtotal (Å)
CdSe 10.61	10.61	3.61 (2.96, 4.25)	10.9 (10.2, 11.6)	12.1 (10.8, 13.4)	0.39 (0.33, 0.45)	2.57	17.7
PbS 12.60	12.60	5.68 (4.68, 6.69)	16.6 (14.5, 18.8)	10.8 (9.24, 12.5)	0.34 (0.26, 0.43)	2.91	19.7
PbS 15.00	15.00	7.13 (4.64, 9.62)	21.8 (18.3, 25.3)	10.6 (7.85, 13.4)	0.30 (0.16, 0.43)	3.39	20.2
CdSe 17.05	17.05	16.1 (12.5, 19.7)	28.8 (26.0, 31.5)	7.29 (6.18, 8.41)	0.40 (0.31, 0.49)	2.49	29.4
CdSe 20.15	20.15	26.0 (19.5, 32.5)	41.3 (37.1, 45.6)	6.32 (5.06, 7.58)	0.38 (0.27, 0.49)	2.61	33.9

^aR_core is the particle core radius obtained from TEM/absorption spectroscopy; M_total is the total molar mass of ligand stabilized QDs; s_20,w is the standardized sedimentation coefficient, D_20,w is the diffusion coefficient, ν̅ is the partial specific volume, R_total is the total particle radius including the organic ligand shell, and ρ_p is the particle density. Values in parentheses refer to the 95% confidence interval determined in the Monte Carlo analysis.

Table 2. Results Obtained from the Custom Grid–Monte Carlo Analysis Using Velocity Data for M₄Ag₄₄(p-MBA)₃₀ Compared to the Zeno Prediction Based on the X-ray Crystallographic Structure Published in Ref (31)^a.

analysis	ν̅ (mL/g)	φ	M (fixed)	s20,w (×10−13 s)	D20,w (×10−6 cm2/s)	Rh (Å)
Custom Grid	0.27 (0.21, 0.32)	1.46 (1.23, 1.70)	9621.8 g/mol	4.19 (3.91, 4.46)	1.45 (1.31, 1.59)	14.0 (12.7, 15.5)
Zeno	0.239	1.245		5.33	1.85	12.1

^aValues in parentheses reflect the 95% confidence intervals from the Monte Carlo analysis. The values predicted by Zeno do not consider bound waters, which explains the discrepancies in ν̅, φ, and R_h.

Figure 3.

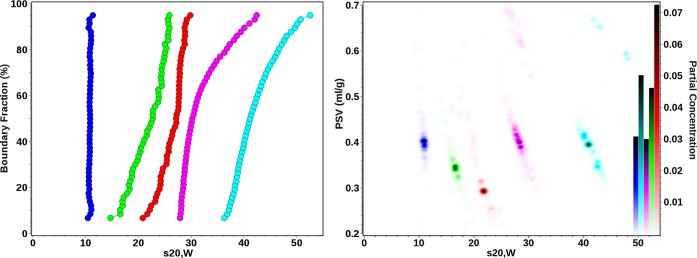
Combined van Holde–Weischet²¹ (left) and pseudo-three-dimensional plots (right) of CdSe and PbS QDs demonstrating their partial specific volume (PSV) distributions with respect to their sedimentation speeds (standardized to water at 20 °C) and their partial concentrations, which is given by the color scale in the right y-axis. Blue, CdSe 10.61; green, PbS 12.60; red, PbS 15.00; magenta, CdSe 17.05; cyan, CdSe 20.15, also compare Table 1.

From these data, an inverse correlation between ν̅ and s is apparent for all particle size distributions. Particle sedimentation velocities are proportional to the particle mass and size, but their size is inversely proportional to their diffusion coefficients. Furthermore, particle diffusion and sedimentation speeds are also affected by their densities. The average bulk density of the stabilizing ligand mixture is approximately 0.87 g/mL, whereas those of the PbS and CdSe particle cores are 7.60 and 5.19 g/mL, respectively. Consequently, the overall density of smaller nanocrystals is less than that of larger nanocrystals, because the lower density ligand occupies a higher volume fraction of the smaller nanocrystals. This relationship is evident when the trend for ν̅ as a function of R_total is examined. As judged by the integral distributions of the solute populations shown in Figure 3 (right panel), the density and sedimentation coefficients of the majority of the solutes are fairly monodisperse. However, some heterogeneity is apparent in some of the samples (Figure 3, left panel). Relationships between particle sedimentation and diffusion speeds, mass and density of CdSe and PbS with respect to particle core size are illustrated in Figure S-10 (Supporting Information) using the results from Table 1. As expected, the sedimentation speed, the particle molar mass, the total particle volume, and the hydrodynamic size all have a positive relationship with QD core size. Within the particle size distribution of a solute, the heterogeneity in density can be observed. For CdSe, the average particle density was found to vary between 2.5 g/mL for 10.61 Å particles and 2.9 g/mL for 20.15 Å particles. As expected, the density rises with increasing particle size as the core volume fraction rises. For PbS QDs, the change in particle density for the two studied sizes is much greater than that observed for CdSe. The average overall density of 12.6 Å PbS QDs is 2.91 g/mL and 3.38 g/mL for 15.0 Å PbS QDs. The difference can be explained by the combination of the high core density, 7.6 g/mL for PbS compared to 5.19 g/mL for CdSe, and the lower amount of bound surfactants. CdSe QDs have oleylamine and trioctylphosphine ligands bound to both Cd and Se sites, whereas for PbS, each oleic acid molecule is bound to two Pb sites, while S surfaces are uncapped. Taken together, these results illustrate the ability of the Custom Grid method to resolve heterogeneity in both s and density when φ can be fixed.

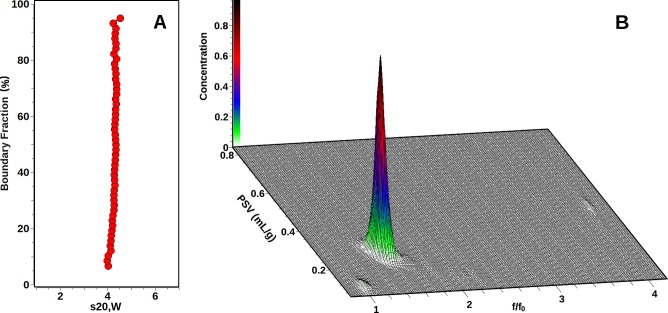
The sedimentation results for M₄Ag₄₄(p-MBA)₃₀ are summarized in Table 2. An integral van Holde–Weischet distribution plot results in a vertical line, clearly showing a single species (see Figure 4A). The observed s-value is consistent with a monomer of the silver nanoparticle, and therefore the molar mass can be constrained using the known molar mass available from the crystal structure.³¹ As a consequence, both frictional ratio and partial specific volume can be fitted in a custom grid. This result is shown in Figure 4B. Again, a single major peak is apparent, reflecting the monomeric structure of M₄Ag₄₄(p-MBA)₃₀. The observed results clearly demonstrate the effects of hydration or solvation on a nanoparticle, and in conjunction with molecular modeling using the Zeno algorithm from the UltraScan-SOMO suite, permit estimates of the level of hydration present under these conditions. The results available from the Zeno simulation reflect only the unhydrated particle, without any contributions from bound sodium ions or water molecules. The difference in ν̅ therefore reflects the hydration contribution. As expected, the ν̅ of the particle increases once hydration is considered, since the density of water is significantly less than the bulk density of the nanoparticle. Likewise, the hydrodynamic radius R_h is increased for the hydrated particle, allowing a first approximation to estimate the thickness of the hydration shell (0.6 Å). Clearly, water is not uniformly bound to the surface of the nanoparticle. Instead, any water and cation binding most likely occurs near the hydrophilic carboxyl moieties located at the exterior of the molecule, at the end of each benzoate residue. Likewise, the increase in frictional ratio observed in the experiment compared to the Zeno simulation for the anhydrous particle is likely caused by the binding of water molecules at the ends of the benzoate residues, replacing the overall globular shape of the anhydrous particle with more extended spike-like shapes. The biggest difference is seen in the reduction of the sedimentation coefficient, which is caused by both an increase in ν̅, and an increase in the frictional ratio. Together, these results illustrate the important effects of hydration on the nanoparticle properties.

Figure 4.

M₄Ag₄₄(p-MBA)₃₀ SV results. (A) integral van Holde – Weischet distribution showing a nearly vertical slope, indicating homogeneity of the sample. (B) Three-dimensional view of the Custom Grid–Monte Carlo analysis with a fixed molar mass constraint reflecting the single species observed in panel A and a variable frictional ratio (x-axis) and variable partial specific volume (y-axis). Two apparent contaminants with insignificant partial concentrations are also found at f/f₀ values of approximately one and four. The color gradient reflects the partial concentration of each species.

Like any other method, the Custom Grid approach is subject to limitations that must be understood. To apply the Custom Grid approach, which at its base, is a two-dimensional evaluation method, one of the three properties affecting hydrodynamic transport (frictional ratio, molar mass, and partial specific volume) must be known a priori and remain constant for all particles included in the evaluation. Like any other sedimentation experiment, the quality of the result depends on the signal strength of both sedimentation and diffusion of the solutes under investigation. For example, if molecules are sedimenting too fast, diffusion information may be limited, which will degrade the results.

Conclusions

The Custom Grid function in UltraScan-III provides a high resolution method to characterize heterogeneity in two out of three hydrodynamic parameters: molar mass, partial specific volume, and anisotropy. In the case of hybrid nanoparticle systems such as inorganic CdSe or PbS cores with an organic stabilizer ligand shell, anisotropies can be determined with an independent method like TEM, and the heterogeneity in size and density can be simultaneously determined using SV experiments. From the results, detailed information about the size and density of the organic ligand shell can be obtained. As shown in the case of M₄Ag₄₄(p-MBA)₃₀, where molar masses are available from atomic structures or mass spectrometry, effects of hydration on solvated nanoparticles can be determined, and hydration shells can be quantified. The custom grid function in UltraScan-III permits a full hydrodynamic characterization of nanoparticles by exploiting information from other experiments as a constraint in the fitting function. This provides access to their density, hydrodynamic size, partial specific volume, anisotropy, hydration, and molar mass. It was found that organic ligand stabilized CdSe QDs of core–shell sizes between 10.61 and 20.15 Å have an average density between 2.51 and 2.95 g/mL, whereas those for 12.60 and 15.00 Å PbS QDs are 2.91 and 3.38 g/mL, respectively. The hydrated silver nanoparticle M₄Ag₄₄(p-MBA)₃₀ was shown to have a partial specific volume of 0.27 mL/g, and an anisotropy factor of 1.46. We have shown that AUC provides statistically meaningful measurements of the hydrodynamic size and diffusion coefficient of nanocrystals and also enables direct insight into the nature of the ligand shell surrounding the inorganic core. The method presented here is suitable for characterizing mixtures that present heterogeneities in any of these parameters, as long as one of the parameters can be constrained to a single value that is true for all particles in the mixture.

Supporting Information Available

Theoretical details, experimental details, screenshot of the UltraScan-III Custom Grid Editor, data for PbS, CdSe, and M₄Ag₄₄(p-MBA)₃₀, absorption spectra of CdSe and PbS samples, representative TEM images of PbS and CdSe QDs, and a plot illustrating the relationship of particle diffusion coefficient and sedimentation coefficient versus QD core size and particle overall density and a plot illustrating the relationship of total molecular mass versus QD core size. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States