Parameter Choice Matters: Validating Probe Parameters for Use in Mixed-Solvent Simulations

Abstract

Probe mapping is a common approach for identifying potential binding sites in structure-based drug design; however, it typically relies on energy minimizations of probes in the gas phase and a static protein structure. The mixed-solvent molecular dynamics (MixMD) approach was recently developed to account for full protein flexibility and solvation effects in hot-spot mapping. Our first study used only acetonitrile as a probe, and here, we have augmented the set of functional group probes through careful testing and parameter validation. A diverse range of probes are needed in order to map complex binding interactions. A small variation in probe parameters can adversely effect mixed-solvent behavior, which we highlight with isopropanol. We tested 11 solvents to identify six with appropriate behavior in TIP3P water to use as organic probes in the MixMD method. In addition to acetonitrile and isopropanol, we have identified acetone, N-methylacetamide, imidazole, and pyrimidine. These probe solvents will enable MixMD studies to recover hydrogen-bonding sites, hydrophobic pockets, protein–protein interactions, and aromatic hotspots. Also, we show that ternary-solvent systems can be incorporated within a single simulation. Importantly, these binary and ternary solvents do not require artificial repulsion terms like other methods. Within merely 5 ns, layered solvent boxes become evenly mixed for soluble probes. We used radial distribution functions to evaluate solvent behavior, determine adequate mixing, and confirm the absence of phase separation. We recommend that radial distribution functions should be used to assess adequate sampling in all mixed-solvent techniques rather than the current practice of examining the solvent ratios at the edges of the solvent box.

Introduction

Computational probe mapping is frequently applied in structure-based drug design (SBDD) to identify potential binding pockets along a protein surface (i.e., hot spots).¹⁻⁴ However, mapping is usually limited by the implementation of gas-phase minimizations, wherein protein flexibility and solvent competition are ignored. This leads to a rugged potential surface and many local energy minima, where druggable sites are indistinguishable from irrelevant minima. Furthermore, predictions based on a static receptor structure often neglect important binding-site features, such as the presence of transient cavities⁵ or bridging water molecules.⁶ As a result, appropriately modeling the binding potential continues to be a challenge for SBDD.

Several computational and experimental models have emerged that address the limitations of traditional solvent mapping. The multiple protein structure (MPS) method addressed the issue of protein flexibility by creating pharmacophore models from consensus mapping of conformational ensembles with solvent probes.⁷⁻¹⁰ While this technique has demonstrated success in mapping the binding sites of pharmaceutically relevant targets,^8,11,12 it cannot account for desolvation penalties or water-bridging contacts, which may be essential to accurate prediction. The multiple solvent crystal structure (MSCS)^13,14 technique uses X-ray crystallography to determine receptor structures in the presence of competing water and organic solvent. This paved the way for fragment-based methods by providing the first experimental identification of preferred sites for probe binding. MSCS results have demonstrated high potential for use in drug development and have inspired several new computational approaches.

Simultaneous protein flexibility and solvent mapping was first implemented in 2009 when molecular dynamics (MD) simulations were used as a tool to map hot spots.¹⁵ Seco et al. performed MD simulations with seven proteins that were solvated by a 20% volume/volume (v/v) solution of water and isopropanol (IPA). Although their method sought to detect binding sites and predict druggability, it did not address aromatic hotspots and was unable to reproduce some of the experimental binding sites. Yang and Wang have conducted similar studies that included phenol with the alcohol/water mix to address aromatic interactions.^16,17 Another MD-based approach, site identification by ligand competitive saturation (SILCS), was implemented with a ternary-solvent box composed of 1 M benzene (BNZ), 1 M propane, and water to locate hot spots and to reproduce experimental binding sites.^18,19 The authors introduced a dummy atom with a virtual repulsion term for both BNZ and propane in order to solubilize the hydrophobic solvents and prevent probe–probe aggregation. However, this repulsive term may alter proper mapping. Their fragment maps for BNZ along the trypsin surface found abundant local minima that were mapped equally or better than the valid binding site.¹⁹ In addition, Guvench and MacKerell noted that the repulsive term may also prevent the mapping of secondary binding sites due to the unnatural physical interactions that are enforced between the hydrophobic probes.¹⁵ The most recent technique was developed by Bakan et al.,²⁰ which uses mixtures of water with multiple probes simultaneously (IPA, acetamide, acetic acid, isopropylamine). Although each of these MD-based techniques have shown some success in identifying binding sites, they were limited in their ability to selectively map hot spots without the use of either a weighting or artificial repulsion term. Many spurious minima were also identified.

Over the past few years, we have worked to develop mixed-solvent molecular dynamics (MixMD) using AMBER, with an aim of solvent mapping across a wide range of targets.^21,22 Instead of simply showing that probes could occupy regions of known binding sites, we sought to establish a stronger foundation that would allow for application of our method to target systems without requiring a priori knowledge of the binding sites. Our initial study with MixMD used a 50% w/w solvent box composed of acetonitrile (ACN) and water, and the results showed that MixMD reproduced binding sites from MSCS studies with excellent convergence to the true hot spots and no spurious minima.^21,22

We were interested in extending the probe set for MixMD to fully enable identification of hydrogen-bonding sites, hydrophobic contacts, protein–protein interactions, and aromatic pockets. Here, we show what happens when poor parameters are used in mapping a protein. We then use MD simulations of water-probe boxes to examine which remain evenly mixed. It is important to identify additional functional sites, particularly aromatic sites, for MixMD to be most useful for SBDD. We explain our choice of using OPLS parameters²³ for IPA in MixMD.²¹ We also identify additional probe solvents that expand the ability of MixMD to locate important interaction profiles in protein–ligand binding: acetone (ACE), N-methylacetamide (NMA), imidazole (IMI), and pyrimidine (1P3). We highlight the importance of developing a solid foundation for mapping with MD, particularly as it relates to the validation of parameters through detailed evaluation of metrics for probe–probe dispersion.

Methods

Probe Parameters

Solvent probes were selected to represent specific interaction types for use in MixMD (Table 1). Parameters for ACE,²⁴ ACN,²⁵ and NMA²⁶ were obtained from studies of liquid solvent with AMBER. AMBER parameters have not been specifically developed for IPA or aromatic heterocycles. Therefore, we explored the suitability of OPLS parameters, which were developed to work with TIP3P water²⁷ and to reproduce the empirical data for pure liquids.²⁸ The adaptation of nonbonded parameters from OPLS for use in AMBER simply required the conversion of σ to r_min, where 2^1/6 × σ/2 = r_min. This is necessary because BOSS²⁹ and AMBER³⁰ use different combining rules for van der Waals (vdw) parameters. A comprehensive list of the parameters used in our MixMD simulations is given in Table S1 and Figure S1 of the Supporting Information.

Table 1. List of Solvent Probes Included in Development of MixMD Functional Group Types and Their Interaction Profile.

solvent	mapping role
isopropanol (IPA)	hydrogen bond donor/acceptor, small hydrophobic
acetonitrile (ACN)	polar, amphipathic
acetone (ACE)	polar, hydrogen bond acceptor only
N-methylacetamide (NMA)	protein backbone
imidazole (IMI)	5-membered polar aromatic
pyridine (PYR)	6-membered aromatic (more soluble)
pyridazine (1P2)	6-membered aromatic (more soluble)
pyrimidine (1P3)	6-membered aromatic (more soluble)
pyrazine (1P4)	6-membered aromatic (more soluble)
benzene (BEN)	6-membered aromatic (less soluble)
phenol (IPH)	6-membered aromatic (less soluble)

MD Simulations

Pure solvent boxes of no fewer than 200 probe molecules were built using the tleap module in AMBERTOOLS. MD simulations were performed in AMBER10³¹ through the sander module with SHAKE³² and a 1 fs time step.²⁷ Each solvent box was subjected to 1000 steps of steepest descent followed by 49,000 cycles of conjugate gradient minimization and then heated over 20 ps from 10 to 300 K at constant volume. Two nanoseconds of equilibration were followed by a 5 ns simulation at constant pressure with the temperature held at 300 K by a weak-coupling algorithm.³³ The Berendsen coupling method was chosen because it was used in the original publication of AMBER parameters for the solvent molecules used in this study. Particle mesh Ewald³⁴ was implemented with a vdw cutoff of 8 Å. The behavior of the pure-probe boxes was used to confirm proper behavior in our setup. Detailed results are in Table S2 and the text of the Supporting Information. The final boxes of organic solvent were also used in the setup of the mixed boxes.

Mixed-solvent boxes were created in tleap by solvating a single probe molecule with a layer of TIP3P water²⁷ and then a layer of the equilibrated box of pure, organic solvent. The size of the outer box of probes is adjusted to achieve the desired solvent ratio. At least 2500 water molecules and the equivalent mass of probe molecules necessary to achieve a 50% w/w solution were used in order to ensure that realistic solvent behavior would be observed (Table S3, Supporting Information). Each layered mixed-solvent box underwent the same procedure for minimization, heating, equilibration, and production simulation as described for the pure-solvent boxes above.

It should be noted that Berendsen’s coupling method³³ can sometimes be problematic for simulations of mixtures because differential heating can occur for different components of the system.³⁵ Our use of the method with the small boxes could be considered a worst-case scenario, where probes may (or may not) have a small bias to aggregate. Any mixture of water and probe solvent that displays homogeneous behavior under these circumstances is likely to be robust to a wide range of applications. In our examination of thermolysin with IPA+water, we chose the Andersen coupling method to be consistent with our other published applications of MixMD.^21,22 There is no bias from the temperature coupling that can cause the differences seen in the two parameter choices for IPA when used in MixMD of thermolysin.

We characterized the distribution of probe density by computing atom–atom radial distribution functions (RDFs) with the radial command in ptraj. The final 1 ns of production time was used to calculate the RDF with a bin size of 0.1 Å. When the solvent probes are fully solubilized into water, they are well dispersed throughout the solvent box, and the RDF converges toward unity at the vdw cutoff. When phase separation occurs in simulations of mixed solvent, too many probes and too little water occupy the local microenvironment around each probe. This makes the local environment too dense with organic probes, and the RDF will not converge to unity within the vdw cutoff. Accordingly, we used these RDF descriptions of mixed vs aggregated solvent systems to evaluate the structure of each mixed-solvent box.

The carbon–carbon (r_CC), carbon–oxygen (r_CO), carbon–nitrogen (r_CN), nitrogen–nitrogen (r_NN), nitrogen–oxygen (r_NO), and oxygen–oxygen (r_OO) distributions were assessed between probe–probe, water–water, and probe–water as was relevant for each probe molecule. For brevity, only representative RDFs are shown for each case below. Cumulative density distributions of r_OO for water–water distances in mixed solvent were also examined to determine the number density of water within the volume sphere. For the case of a 50% w/w mixed-solvent box, equitable distribution of solvent probes and water within the system will give a cumulative plot for r_OO of water–water distances that differs from the r_OO of pure water. The distribution of water molecules relative to one another is less than in pure solvent because obviously the presence of a miscible probe reduces the number of water molecules that can occupy the local microenvironment around each water.

Results and Discussion

Earlier papers—ours included—have used the behavior at the edges of the simulation box to prove even mixing of probes and water. The reasoning was that the box edges are far from the protein, outside the vdw cutoff, and should have minimal bias in the ratio of probe to water. If the edges of the box had the same ratio as the setup solvent box, then there was even mixing. However, taking a step back to these basic simulations of solvent boxes provided a better means of measuring mixing: the use of a RDF. RDFs of the solvents relative to one another can be calculated for simulations of proteins, and we recommend they be used in all mixed-solvent simulations to judge whether the behavior of the probes and waters are reasonable.

The RDF, or pair correlation function g(r), can be used to describe the structure of the solvent based on atom/molecule pairs in a system. The function g(r) enables a precise description of how likely a probe molecule will have another probe present at a separation distance of r. This function may be simplified for a liquid system in a solvent box, where g(r) is proportional to the observed number density (ρ_o) divided by the expected number density (ρ_e). The value ρ_o is the total number of atoms at a given distance, and ρ_e is the number expected at that same distance if the solvent were uniformly distributed. If the probe solvent and water are evenly mixed, the RDF will converge to 1.0 at long ranges. If it converges to a larger number, this indicates phase separation (further discussion below). The values of g(r) at 8 Å are given for the mixed water–solvent boxes in Table 2.

Table 2. Proper Mixing of 50/50 Solvent Boxes, Including the Pair Correlation Function g(r) at a Distance of 8 Å.

probe	mixed, g(r)	probe	mixed, g(r)
isopropanol (IPAOPLS)	yes, 1.06	imidazole (IMI)a	yes, 1.06
isopropanol (IPASeco)	no, 1.51	pyridine (PYR)a	no, 1.63
acetonitrile (ACN)b	yes, 1.02	pyridazine (1P2)a	no, 1.30
acetone (ACE)a	yes, 1.12	pyrimidine (1P3)a	yes, 1.01
acetone (ACE)b	yes, 1.03	pyrazine (1P4)a	no, 1.57
N-methylacetamide (NMA)a	yes, 1.10	benzene (BNZ)a	no, 1.79
N-methylacetamide (NMA)b	yes, 1.01	phenol (IPH)a	no, 1.48

^aOPLS parameters.

^bAMBER parameters.

Previously, MixMD was validated with ACN as a probe, which specifies hot spots for amphipathic nitrogen-containing ligands.²¹ We applied AMBER parameters for ACN from Grabuleda et al.,²⁵ and they accurately reproduce experimental data from MSCS. For completeness, we ran simulations of ACN+H₂O boxes to confirm that the RDF demonstrated appropriate convergence to unity (Figure S2, Supporting Information).

Importance of Realistic Parameters: The Case of Isopropanol

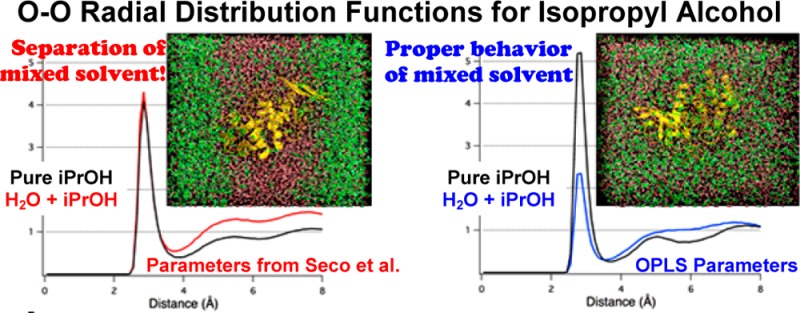
In trying to reproduce simulations of thermolysin in IPA+H₂O published by Seco et al.,¹⁵ we found that the IPA phase-separated from water (Figure 1A). It is unclear whether the authors observed this same behavior, and they do not note which temperature-coupling method was used. They noted “partial phase separation” in the paper, and they rescaled the reference values for probe density to account for the solvent behavior. However, the bulk phase separation we observed signifies the implementation of inadequate parameters for liquid IPA, which were derived from the AMBER parameter files for threonine with charges assigned after RESP calculations (IPA_Seco).

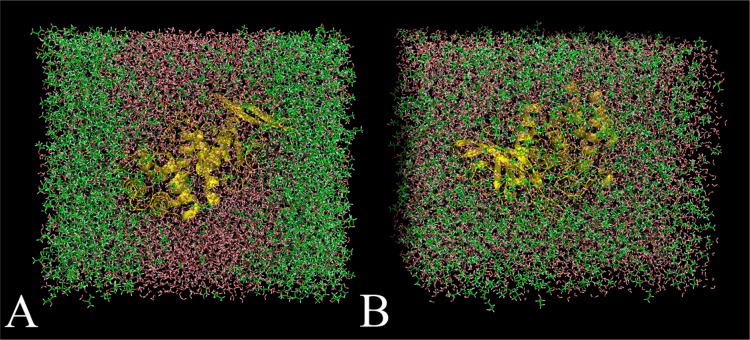
Figure 1.

Snapshots of MixMD simulations of thermolysin in IPA+H₂O executed using the protocol outlined in Seco et al.¹⁵ (A) Fully flexible simulations of thermolysin were performed with a mixed box of 50% w/w IPA_Seco+H₂O. Five independent runs were calculated, and every simulation resulted in the solvent layers separating between 4 and 5 ns and remaining separated when simulations were extended to 10 ns. This solvent behavior was unrealistic because IPA and water are completely miscible. (B) The same simulation using IPA_OPLS²³ resulted in solvent remaining well distributed for the entire equilibration and 10 ns of production in all five independent simulations.

We turned to the work of Jorgensen et al. for alcohol parameters because they were developed to specifically reproduce a variety of pure-solvent behaviors and interactions with TIP3P water.²⁸ For small boxes without protein, we compared our simulations of IPA_OPLS+H₂O to experiments by Langdon and Keyes that determined the density for IPA+H₂O systems at different temperatures.³⁶ We found that our mixed box of IPA_OPLS+H₂O reproduced the experimental density at 308 K (0.830g/mL) to within 0.06%. Our ability to replicate this fundamental data confirmed the use of good parameters for our IPA+H₂O systems. Indeed, MixMD simulations of thermolysin resulted in proper mixing using the IPA parameters from Jorgensen et al. (IPA_OPLS, Figure 1B).

The RDFs for the IPA probes (r_OO and r_CC) and water (r_OO) in mixed-solvent boxes further justified the use of OPLS parameters. Figure 2 compares the O–O RDF for both mixed-solvent and pure-solvent boxes of IPA. The r_OO for (IPA-IPA)_OPLS converged to unity with an appropriately shorter peak than that of pure liquid alcohol. However, the r_OO for (IPA-IPA)_Seco remained well above 1.0 at 8 Å and featured a large peak for the first solvent shell, the same as seen in the simulation of a pure IPA box. All simulations with IPA_Seco feature RDFs that indicate aggregation of the solvent molecules. For this first example, the count data behind the RDFs will be discussed in detail to further explain our interpretation, which is supported by viewing the boxes.

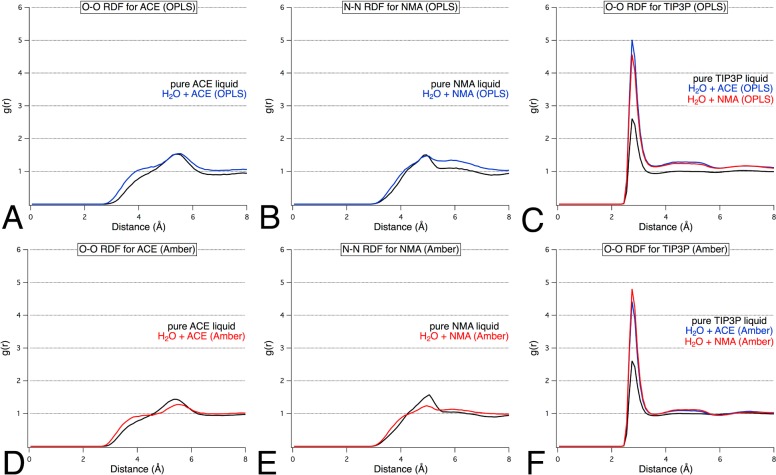
Figure 2.

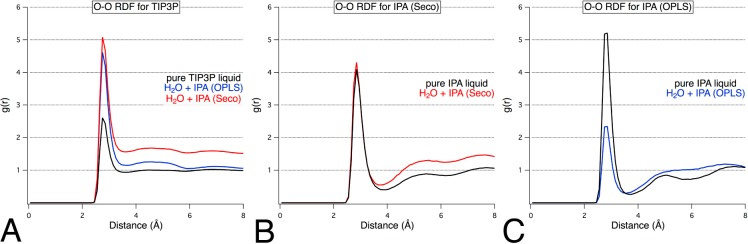
O–O radial distribution functions for (A) water–water and (B,C) probe–probe in a mixed-solvent environment with IPA. The impact of different parameters for IPA is demonstrated by the poor convergence to unity for O–O in simulations of 50% w/w IPA_Seco (B) when compared to the appropriate convergence obtained for the same mixed solvent with IPA_OPLS parameters (C).

IPA and the great majority of organic solvents chosen for this study are miscible with water (Table 3). The definition of miscibility is that the two solutions are homogeneously distributed at all ratios of the two solvents. It might be reasonable to find some bias or local structure in the first and second solvent shells, but bulk separation should not be seen at long ranges. This has critical correspondence with one of the basic underlying assumptions of RDFs. RDFs are founded on a uniform distribution of solvent to describe ρ_e (solvent count/box volume); any deviations from uniformity (1.0) reflects the local structure of the solvent.

Table 3. List of Probes for MixMD and Experimental Observations from Two Different Sources.

solvent	MSDS	CRC handbook
acetone (ACE)	soluble	miscible
acetonitrile (ACN)	soluble	miscible
benzene (BNZ)	no data	slightly soluble
imidazole (IMI)	soluble at about 50g/L	very soluble
isopropanol (IPA)	soluble	miscible
N-methylacetamide (NMA)	soluble	no data
phenol (PHO)	no data	soluble
pyrazine (1P4)	no data	soluble
pyridazine (1P2)	no data	miscible
pyridine (PYR)	soluble	miscible
pyrimidine (1P3)	no data	miscible

In all the RDFs in Figure 2, water has its maximum g(r) at 2.75 Å, and the IPA maxima are at 2.85 Å. For pure water at 2.75 Å, the maximum g(r) is 2.6, and the cumulative count of water is 1.4 molecules (Table 4). If we define the first solvent shell between 2.45 and 3.15 Å, it contains 3.9 neighboring water molecules. When simulated in a mixture with IPA_OPLS, there are 1.1 waters within 2.75 Å and 2.9 waters within 3.15 Å (Table 4). Of course, both counts are reduced because some of the interactions are occasionally fulfilled by IPA. This is also incorporated into ρ_e, where the larger box volume reduces the expected density. It is that reduced expectation (actually 0.244 at 2.75 Å) that results in a g(r)of 4.6. This is higher than the g(r) maximum from the pure water simulation, but it does not reflect more interactions with water molecules. Within a 7.95 Å radius sphere, the observed and expected counts are nearly equal and g(r) approaches 1.0, showing that the molecules have a uniform distribution over larger scales.

Table 4. Detailed Values Behind the RDFs in Figure 2^a.

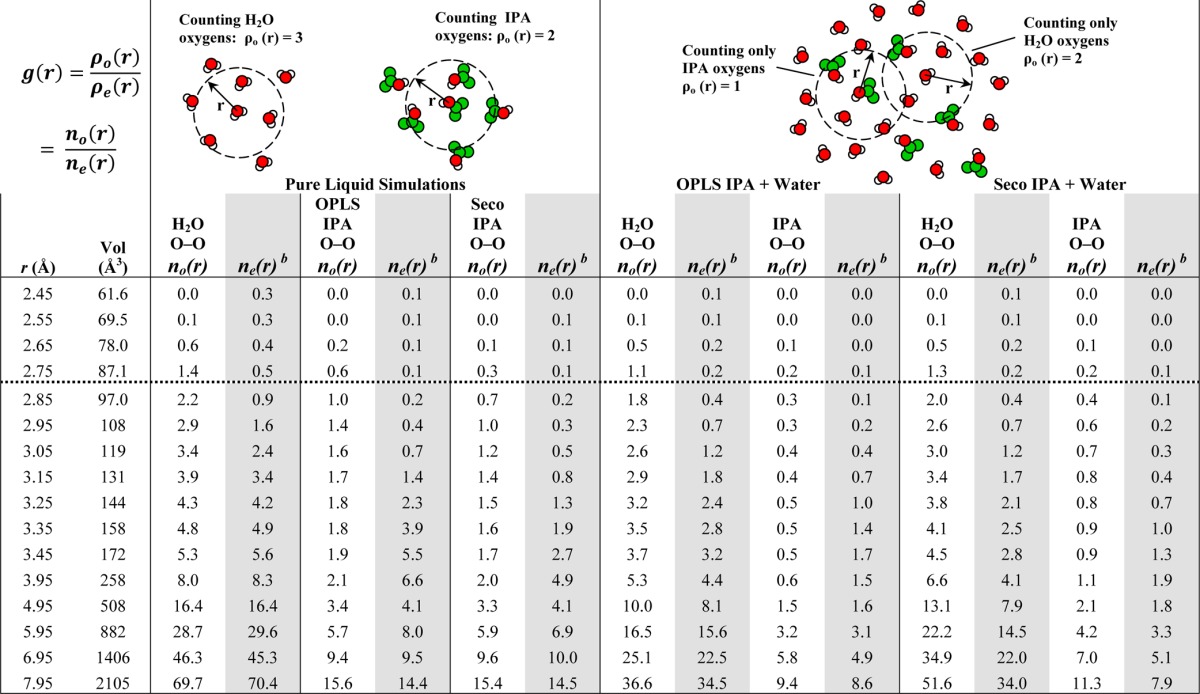
^aBoth ρ_o and ρ_e depend on the volume of the simulation box; this drops out and makes each g(r) = n_o(r)/n_e(r). The values in this table have been rounded; the g(r) in the figures are the exact values. Dashed horizontal line indicates the maxima in g(r).

^bValues for n_e(r) are based on the volume of the count sphere, the number of solvent in the whole box, and size of the whole box during the simulation.

For the mixture of water and IPA_Seco, a dramatically different picture emerges. Within a 7.95 Å radius sphere, the expected count of water was 34.0, but the observed count was 51.6 water molecules (Table 4). Clearly, there are too many waters close to one another! Furthermore, g(r) asymptotically approaches 1.5 at 7.95 Å. Phase separation (as in Figure 1A) is best quantified by high g(r) at long r, but even the local changes reflected the phenomenon. Within 2.75 and 3.15 Å, there are 1.3 and 3.4 waters (Table 4), respectively, which is much closer to the values shown in the pure-water boxes. The mixed box equilibrated to a slightly larger volume (1% change), which is reflected in the slight differences in the expected counts between IPA_Seco+water and IPA_OPLS+water. However, the 1% change does not explain the maximum g(r) of 5.1, which is based on the increase in number of water molecules.

The same patterns are seen in the RDFs of the IPA oxygens (Table 4). Pure IPA simulations show appropriate behavior for both sets of parameters (black lines in Figure 2BC, Table S2 and text in Supporting Information). Though the RDFs may imply IPA_OPLS has slightly tighter solvent shells, they both sum to the same number of IPA molecules in the first solvent shell (2.1 for IPA_OPLS and 2.0 for IPA_Seco). For mixed simulations, both IPA_Seco and IPA_OPLS show lower counts than pure-solvent boxes at their g(r) maxima (2.85 Å) and within their solvent shells (3.95 Å). However, g(r) of IPA_Seco unmistakably approaches 1.4 at 7.95 Å.

Additional Probes for Hydrogen-Bonding and Protein–Protein Interactions

Influenced by the discrepancies in solvent behavior observed for IPA_Seco and IPA_OPLS, we carefully examined the behavior of existing parameters for additional solvent probes to determine their applicability in MixMD. The inclusion of various probe types, including complicated molecular fragments, would facilitate the development of accurate pharmacophores for druggable hot spots, ligand binding sites, and protein–protein interactions. The selection of additional probes for expanding the functional groups represented in MixMD was based on existing MSCS data and common interaction types found in protein–ligand systems. IPA maps both hydrogen bond-accepting and -donating locations, but additional hydrogen-bonding probes are needed to develop robust pharmacophore maps of binding sites. ACE and NMA were selected because each molecule represents a different hydrogen-bonding profile. ACE locates where the protein donates hydrogen bonds, and NMA represents protein–protein or peptide binding.

Specific parameters for ACE and NMA had been developed for use with AMBER^24,26 and OPLS.^28,37 Simulations of ACE+H₂O and NMA+H₂O were performed using each parameter set to assess their suitability. The g(r) was calculated for probe–probe, probe–water, and water–water interactions within the binary-solvent boxes. Analysis of the resulting RDF plots indicated that in each case all g(r) converged to unity near 8 Å. We found that both the AMBER and OPLS parameters for liquid ACE and NMA demonstrated correct behavior according to RDF plots and visual inspection (Figure 3). The O–O RDF for water from the mixed-solvent simulations also illustrate that solvent mixing has occurred. Analysis of the cumulative plots for the r_OO of water in solution with ACE or NMA showed that the number density of water within the local volume sphere was half the number density observed in pure water simulations, which is the expected result for a well-distributed system of 50% w/w probe and water. Visual analysis of the trajectory snapshots served to corroborate the occurrence of proper solvent mixing. However, the RDF’s deviation from unity at 8 Å was slightly higher for the OPLS descriptions of ACE and NMA (Table 2). For this reason, we would recommend that the AMBER parameters be used for ACE and NMA in our MixMD method, especially when the AMBER parameters are also used to describe the protein.

Figure 3.

(A,D) O–O and (B,E) N–N radial distribution functions for probe–probe and O–O RDFs for water–water (C,F) in a mixed-solvent environment with ACE and NMA. The impact of optimized parameters from AMBER versus general solvent parameters from OPLS is shown in the slightly better convergence to unity for simulations using AMBER parameters (D–F) compared to OPLS (A–C) parameters.

Search for an Aromatic Probe

In particular, we wanted to find parameters for soluble heterocycles that could map aromatic hot spots without requiring an artificial repulsive term. No other MD approach for probe mapping has successfully integrated aromatic probes without an artificial interaction term. Futhermore, we were particularly interested in developing probes that matched common heterocycles used in modern pharmaceuticals. As a result, our initial investigation into an appropriate aromatic probe led to IMI.

A highly polar diazole, IMI, is miscible with water and is present as a functional group in a wide range of biologically active molecules, including mercaptopurine (anticancer), ketoconazole (antifungal), and moxonidine (antihypertensive). IMI parameters were derived from Jorgensen and McDonald,³⁸ and then simulations of pure IMI and IMI+H₂O were conducted to assess the potential of IMI as a probe for MixMD. The proper convergence of the RDF plots to 1.0 showed that IMI was properly solubilized and well distributed within the binary-solvent system (Figure 4). Our pure-solvent RDFs were consistent with the results of Jorgensen and co-workers^38,39 and further validated our parameter choice and the accuracy of our protocol. Also, visualization of simulation snapshots confirmed that the IMI probe was well dispersed in the aqueous solution.

Figure 4.

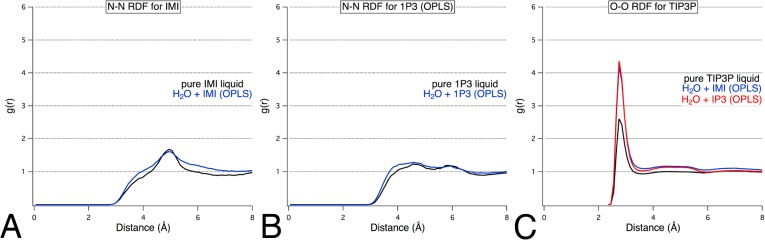
N–N radial distribution functions for (A,B) probe–probe and (C) water–water in a mixed-solvent environment with (A) IMI and (B) 1P3. Appropriate convergence was obtained for both probe types.

Many other nitrogen-containing heterocycles were examined. OPLS parameters for PYR, 1P2, 1P3, and 1P4 were each simulated in a binary water–probe solution. Visualization of the simulations of PYR+H₂O, 1P2+H₂O, and 1P4+H₂O clearly showed that they underwent phase separation. This was proved by RDFs that converged to values well above 1.0 at 8 Å (Figure 5). However, 1P3+H₂O yielded a well-dispersed system with well-behaved RDF plots (Figure 4).

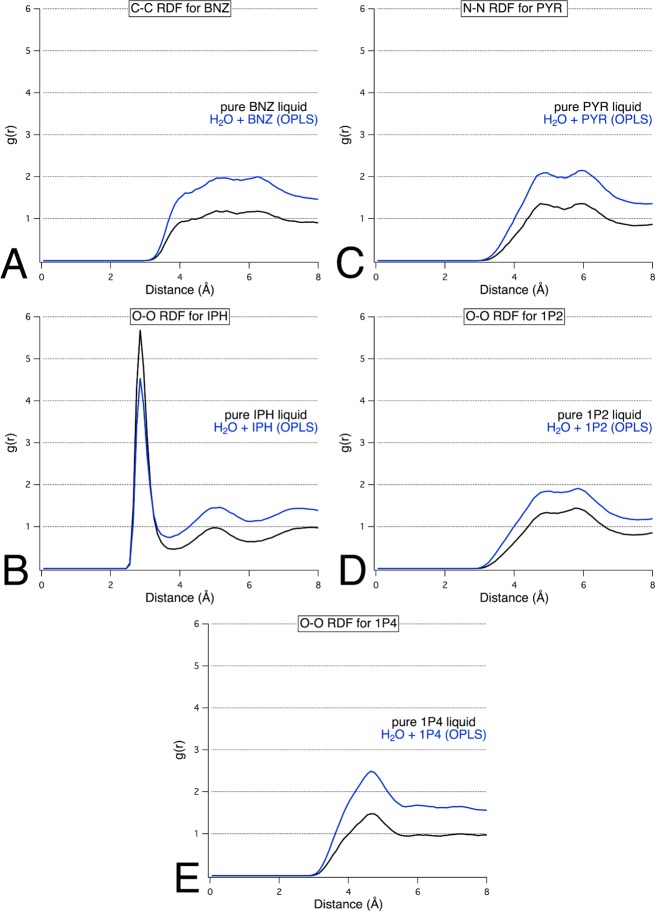
Figure 5.

Probe–probe radial distribution functions for mixed solvent environments composed of (A) BNZ+H₂O, (B) PYR+H₂O, (C) IPH+H₂O, (D) 1P2+H₂O, and (E) 1P4+H₂O clearly showed phase separation, with g(r) values well above 1.0 at 8 Å.

We also examined two nonpolar aromatic probes, BNZ and IPH, simply to confirm that they are not appropriate probes when an artificial repulsive term is not used. Comparison of the resultant RDF plots to the reference RDF plot of pure water showed that the g(r) values for BNZ+H₂O and IPH+H₂O do not converge to unity within 8 Å (Figure 5). In fact, the g(r) for BNZ+H₂O indicated convergence to a value of 2. The simulations with IPH as a probe molecule showed a converged g(r) of approximately 1.45 at 8 Å. Visualization of snapshots from these simulations showed significant aggregation of the probe molecules, verifying that these probes are not be soluble enough for use with MixMD without inclusion of a repulsive term.

Because BNZ is one of the solvent probes used in SILCS, we were able to compare the RDF results for our MixMD simulations of BNZ+H₂O to the published results from SILCS mapping studies.¹⁸ The BNZ probe used in SILCS was parametrized based on the CHARMM force field and contained a repulsive term to correct for probe–probe aggregation. Although a nonbonded cutoff of 8 Å with a 5–8 Å switching term was applied in SILCS, the probe–probe distance for BNZ converged to 1.0 at ∼13 Å (solvent box size was 72 Å × 58 Å × 43 Å). In comparison, the soluble aromatic probes applied in MixMD converged at approximately 6–7 Å. The first solvent shell of BNZ in SILCS was observed at 9 Å, while we observed the first peak at 4–5 Å. The presence of the second hydrophobic probe (propane) in SILCS simulations may have influenced these differences in RDF. However, the use of a repulsive term to prevent probe–probe aggregation does not correspond with the experimental properties of BNZ, suggesting that SILCS simulations with high concentrations of BNZ may yield incorrect results.

To determine whether BNZ and IPH would disperse more readily in the presence of an “intermediary” probe, ternary mixed-solvent boxes were constructed to contain 1 M aromatic probe and 1 M IPA in water. We hypothesized that the introduction of the IPA molecule would enhance available interactions and aid in the dispersion of the aromatic probes into water. However, this was not observed in simulations of the ternary-solvent boxes. At 5 ns of production time, the BNZ molecules were predominantly clustered along one side of the solvent box, while the IPA molecules were dispersed throughout the water. An additional 20 ns of production time did not change the observed aggregation (Figure 6). Ternary-solvent simulations with IPH indicated a similar result; after 5 ns of production time, IPH was separated with some dispersion toward the interior. Elongating the run time out to 25 ns showed no significant improvement (Figure 6).

Figure 6.

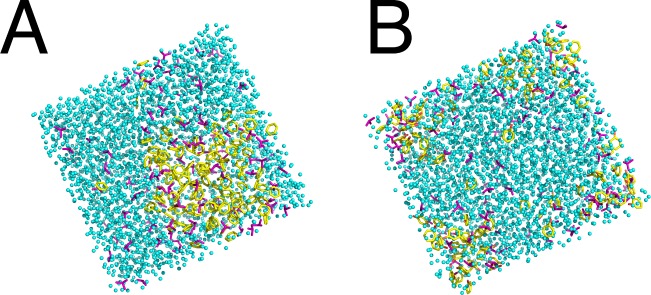
Representative snapshots of MD trajectory for solvent boxes of 1 M aromatic probe (yellow) and 1 M IPA (purple) in water (cyan) for (a) BNZ+IPA+H₂O at 25 ns and (b) IPH+IPA+H₂O at 25 ns.

Solubility

Although all of the probes selected for use in our validation study had experimental data establishing their solubility in water, not all of these probes were soluble in simulation (Table 3). The solvation conditions applied in a MixMD simulation included high probe concentrations, which may have affected probe solubility. To determine whether the outcomes we observed were justified based on experimental data, we considered their miscibility. The terms soluble and miscible are frequently used interchangeably; however, they are two distinct properties. Solubility is dependent upon temperature and pressure and refers to the ability of a solute (solid, liquid, or gas) to dissolve into a solvent (solid, liquid, or gas), thereby forming a homogeneous mixture. Miscibility refers to the ability of two liquids to form a homogeneous solution, independent of proportion.

All probes that have been experimentally categorized as miscible were well dispersed in our computational simulations, with two exceptions (Table 3). Pyridine is a weak base with a nontrivial concentration of protonated pyridinium ions (pK_a of 5.3) following solubilization into water. This effect was not simulated in our studies, and we suggest that the charged species may be responsible for solubilizing the uncharged pyridine molecules into water. A similar explanation may also be extended to pyridazine.

Ternary-Solvent System: Toward Full Pharmacophore Modeling using MixMD

One advantage of using SILCS as a tool for solvent mapping has been that the ternary-solvent box can enable the development of a complete pharmacophore model from a single MD run because the three probe types identify aromatic, hydrophobic, and hydrogen-bonding sites.^18,19 Using three of the probes with parameter sets we have validated for MixMD, we constructed a ternary system with IMI (aromatic probe), IPA (hydrophobic and hydrogen-bonding probe), and water at a concentration of 33% w/w by probe. Visualization of the trajectory data indicated appropriate solvent mixing, and our RDF results showed that both organic probes were fully dispersed into solution (Figure 7). Total run time required a comparable amount of simulation time to a binary MixMD simulation; the total cost was an additional 4 or 8 h of production time on an 8-core CPU as compared to a binary IPA+H₂O or IMI+H₂O simulation, respectively.

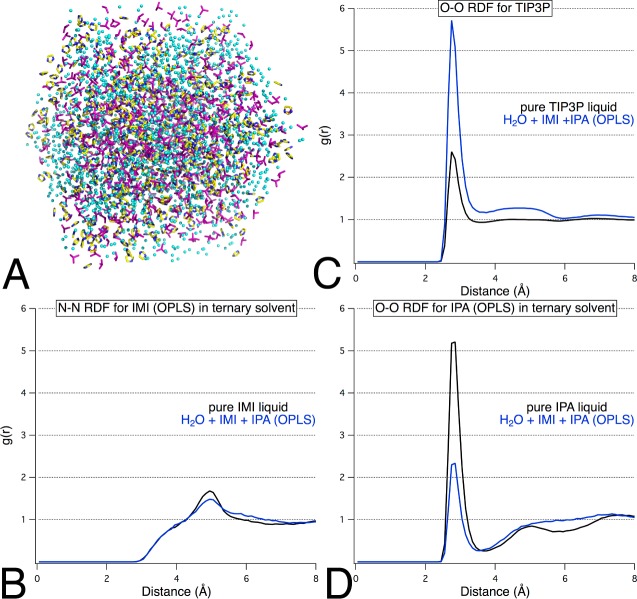
Figure 7.

(A) Final snapshot from the production simulation of a mixed-solvent box containing IMI+IPA+H₂O illustrates that the probes are well mixed within the system. (B–D) Probe–probe and water–water radial distribution functions for IMI and IPA establish convergence to unity within the trisolvent environment.

We suggest that the use of this ternary MixMD model may offer several advantages over the SILCS approach. We have shown that MixMD can be used to identify maximally occupied sites without recovering additional spurious minima, which is a feature that was not consistently seen in the SILCS studies.¹⁹ In addition, instead of requiring water to act as a hydrogen-bonding probe, in MixMD, the druggable hydrogen-bonding sites can be identified in competition with water using IPA as the probe. This is important for ascertaining whether a drug-like molecule that contains a similar function group could displace water molecules at the proposed hydrogen-bonding site. A further advantage of using MixMD is the array of available probes, which can be tailored to an investigator’s mapping needs. For example, either IMI or 1P3 could be used in the ternary box to locate aromatic hotspots that are specific to the size of the ring. The ternary mixture of 33% w/w ACE+ACN+H₂O was also simulated, and the results depicted a well-distributed solvent system for use in hot spot mapping with MixMD (Figure S3, Supporting Information).

Conclusion

We have examined solvent parameters for neat liquid from the literature for use in hot spot mapping through MixMD. Our work highlights the importance of parameter validation and analysis of simulation data when performing computational solvent mapping in order to obtain appropriate behavior. Influenced by the poor results obtained using a standard set of parameters used in the field for liquid isopropanol in water, we identified a set of functional group probes with specific parameters available for liquid simulation. We pursued validation of these parameters for neat and mixed-solvent simulations and identified six probes for use with TIP3P in MixMD: acetonitrile, acetone, imidazole, isopropanol, N-methylacetamide, and pyrimidine. Of course, these probes should be used with more proteins beyond thermolysin (Figure 1) to prove their applicability. We have previously applied OPLS IPA parameters to also examine elastase, HEWL, HEWL, p53 core, and RNase A.²² Furthermore, we are currently using all of these probes to map 10 additional protein systems, but these are separate studies in their own right.

The extent of ideal dispersion is most easily quantified by using the cumulative RDF of r_OO for water. Although published results for pyridine and pyridazine indicated that they are miscible with water, these two probes were observed to separate from the aqueous phase during our simulations, rendering them unsuitable for solvent mapping in our context. We hypothesized that this disparity between experiment and computation was caused by the presence of the corresponding ionized species, which were not simulated. In order to avoid unphysical mapping or reduced accuracy, our simulations did not employ the use of an artificial repulsion or weighted density term. We have successfully expanded the range of probes that can be incorporated into MixMD studies to allow for the mapping of druggable sites, including hydrogen-bonding regions, aromatic pockets, and protein–protein interfaces. With the proposed ternary-solvent systems, a full pharmacophore model could be created from the simulation of a single protein+probes+water system, which would greatly reduce the computational costs of MixMD studies. This is a clear advantage of the SILCS method that we would like to incorporate. Ultimately, investigators could “mix and match” the probes used in MixMD to identify hotspots with a greater degree of specificity.

Supporting Information Available

Full description of the structures and parameters of all probe solvents, results of the pure-solvent simulations, listing of the exact number of water and probe solvents for each mixed-box simulation, and RDFs for ACN+H₂O and ACE+ACN+H₂O simulations. This material is available free of charge via the Internet at http://pubs.acs.org..

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States