Sparse dictionary learning of resting state fMRI networks

Abstract

Research in resting state fMRI (rsfMRI) has revealed the presence of stable, anti-correlated functional subnetworks in the brain. Task-positive networks are active during a cognitive process and are anti-correlated with task-negative networks, which are active during rest. In this paper, based on the assumption that the structure of the resting state functional brain connectivity is sparse, we utilize sparse dictionary modeling to identify distinct functional sub-networks. We propose two ways of formulating the sparse functional network learning problem that characterize the underlying functional connectivity from different perspectives. Our results show that the whole-brain functional connectivity can be concisely represented with highly modular, overlapping task-positive/negative pairs of sub-networks.

I. Introduction

An active area of research in resting-state fMRI is identification of sub-networks based on functional co-activation. Independent Component Analysis (ICA) has over time become the primary technique for model-free analysis of fMRI data. ICA assumes that the fMRI data can be explained by a mixture of independent sources, and finds components that are either spatially or temporally independent [1]. An alternate approach that can be used to analyze whole-brain connectivity is graph-cut based clustering methods [2]. However, both approaches are unable to reveal sub-networks that partly share common neuro-anatomical structures. In fact, it has been argued that sparsity of components is necessary for effective performance of the ICA algorithm [3]. Recent work by Lee et al [4] exploit the sparsity property in order to decompose the temporal series into components. Clustering methods usually aim to find the optimal parcellation of functionally connected regions, and by definition, cannot find overlapping groupings.

Seed-based analyses in resting state fMRI have shown that the brain is organized into functionally modular subnetworks, which are replicable across subjects. In this paper, we introduce a data-driven sparse dictionary learning method with the aim of finding functional sub-networks that repeatedly occur across a subset of the subjects. Sparse representations do not require these resulting components, or ”atoms” to be independent, or non-overlapping. We apply the dictionary learning method to two types of network representations - one using node weights, and the other using edge weights. Results obtained from a large dataset of normative controls show that both representations lead to convergent yet complementary results.

II. Materials

BOLD fMRI was acquired with a Siemens 3 Tesla system using a whole-brain, gradient-echo echo planar sequence with the following parameters: TR/TE = 3000/32 ms, flip = 90 deg, FOV = 192×192 mm, matrix = 64×64, slice thickness =3mm, voxel resolution = 3×3×3 mm, number of timepoints = 120. A gradient-echo T1-weighted image (MPRAGE) image was acquired to aid spatial normalization to standard atlas space. We analyzed resting-state fMRI data of 421 normal participants, aged 8-21 years old (mean 15.9 years, stdev 3.3 years).

Functional images were slice-time corrected, motion corrected, spatially smoothed (6mm FWHM, isotropic), grand-mean scaled using intensity normalization and temporally filtered to retain frequencies 0.01-0.1 Hz. Several sources of confounding variance, including six motion parameters, mean white matter time-course, mean CSF timecourse, and mean whole-brain time-course were regressed out. The residual time course for each subject was co-registered with the anatomical image and transformed to standard MNI anatomical space.

We used 160 regions of interest (ROIs) recently described by Dosenbach et al. [5], which were derived from a metaanalysis of a large sample of task-based fMRI studies. Each ROI was a non-overlapping 10mm diameter sphere, and was categorized as belonging to one of six networks: default-mode, cingulo-opercular, fronto-parietal, sensorimotor, occipital, or cerebellar. The mean time-series at each ROI were extracted from the registered fMRI image. The average correlation between any two regions was computed using the Pearson correlation coefficient. This resulted in one correlation matrix of size r × r per subject.

III. Methods

Let C_i ∈ ℝ^r×r denote a correlation matrix, for i ∈ {1, 2, …, M}, where r is the number of ROIs and M is the number of subjects.

A. Sparse dictionary learning on pair-wise correlations

A matrix of correlations C can be interpreted as a network where an edge between two vertices i and j has weight C_ij. In this formulation, we define an observation to be the set of all edge weights of a subject. Thus there are as many observations as there are subjects. This is identical to vectorizing each correlation matrix C_i, leading to an edge weight vector e_i = vec(C_i) ∈ ℝ^r(r−1)/2 for every subject. Note that we account for the symmetric form and discard the upper triangular part of C_i. Edge weight vectors of all subjects are concatenated to form the data matrix Y^e = [e₁, e₂, …, e_M] of size N × M, where N = r(r − 1)/2. (Note that superscript e stands for edge-weights). We would like to find representative networks that capture the variation in the edge weights across subjects. The task of identifying the dictionary and the respective representation can be modeled as the sparse dictionary learning problem that attempts to find a dictionary, D^e of atoms (columns of D^e) that best represent the given data Y^e with few components. Formally, we have

$$\begin{array}{cc}\underset{{\mathrm{D}}^e,{\mathrm{X}}^e}{\text{minimize}}& {\Vert {\mathbf{Y}}^e-{\mathbf{D}}^e{\mathbf{X}}^e\Vert }_F^2\\ \text{subject to}& {\Vert {\mathrm{x}}_i\Vert }_0\le L,i=1,\dots ,\mathit{\text{mT}}.\end{array}$$ (1)

Here, Y^e ∈ ℝ^r×rM, D^e ∈ ℝ^r×K, X^e ∈ ℝ^K×rM.

The desired set of atoms best represents the data in a maximally sparse linear decomposition.

B. Sparse dictionary learning of ”one-vs-all” correlations

The j-th column in the symmetric matrix C_i represents correlations between the j-th ROI and all other ROIs. In this formulation, we can represent each ROI in the network by a vector of weights, i.e, by the column corresponding to the ROI in the C_i matrix. Assuming that the resting-state functional networks are modular, we can expect that the columns corresponding to ROIs that belong to the same functional sub-network to be similar. In particular, we expect that any two ROIs belonging to the same functional subnetwork will exhibit strong positive correlations with all other ROIs within the same sub-network. By considering the M × r columns from the M correlation matrices calculated for all subjects, we, therefore, would like to find dictionary of representative vectors whose sparse linear combinations explain all available ”one ROI vs. all other ROIs” correlations.

We achieve this by assuming the columns of C_i to be individual data points and by employing sparse dictionary learning in the space of the respective ”one ROI vs. all other ROIs” correlation vectors. Specifically, the column vectors from all correlation matrices are collected in a data matrix, which amounts to concatenating all the connectivity matrices to form a r×rM matrix Yⁿ = [C₁, C₂, …, C_M], where the observations are the columns of the data matrix Yⁿ(superscript n stands for node-weights). We assume the space of the column-vectors is sparse, i.e, each column-vector can be expressed as a linear combination of a small number of basis vectors, or ”atoms” drawn from a dictionary. Using the formulation similar to Equation. 1, we find a basis of atoms that can be used to generate the ”one-vs-all” correlation vector of any ROI of any subject. Thus, we find a dictionary Dⁿ such that ${\Vert {\mathbf{Y}}^n-{\mathbf{D}}^n{\mathbf{X}}^n\Vert }_F^2$ is minimized, and the coefficients, or the columns of matrix Xⁿ are L-sparse.

C. K - Singular Value Decomposition (K-SVD)

An efficient algorithm called K-SVD for estimating sparse dictionaries has been proposed in [6] to solve the optimization problem in Equation 1. Given the size of the dictionary K, and the sparsity level L, we use the K-SVD algorithm to identify the two dictionaries D^e and Dⁿ, and the respective sets of sparse coefficients X^e and Xⁿ. For a given atom, the row in X^e (or in Xⁿ) indicates the prevalence of the corresponding atom. Computing the row norms of the X^e and Xⁿ allows us to rank the atoms in each of the two representations with respect to their importance for decomposition. In the subsequent section, we will provide a detailed analysis of the highest-rank atoms in the two methods.

Model selection: Choice of K and L

In order to understand the effect of model selection on the resulting dictionary, the above algorithm was run for varying values of dictionary size K and sparsity level L. The resulting dictionaries were compared using the Hausdorff distance metric, as follows.

Consider the formulation with edge-weights: we consider two dictionaries ${\mathbf{D}}_1^e=[{\mathbf{d}}_{11},{\mathbf{d}}_{12},\dots ,{\mathbf{d}}_{1K}]$ and ${\mathbf{D}}_2^e=[{\mathbf{d}}_{21},{\mathbf{d}}_{22},\dots ,{\mathbf{d}}_{2K}]$ to be close if any atom d_1i in ${\mathbf{D}}_1^e$ is close to some atom d_2j in ${\mathbf{D}}_2^e$, and vice-versa. This is quantified using the Hausdorff distance $H({\mathbf{D}}_1^e,{\mathbf{D}}_2^e)$.

$$d({\mathbf{D}}_1^e,{\mathbf{D}}_2^e)=\underset{{\mathbf{d}}_{1i}\in {\mathbf{D}}_1}{max}\underset{{\mathbf{d}}_{2j}\in {\mathbf{D}}_2}{min}{\Vert {\mathbf{d}}_{1i}-{\mathbf{d}}_{2j}\Vert }_2$$ (2)

$$d({\mathbf{D}}_2^e,{\mathbf{D}}_1^e)=\underset{{\mathbf{d}}_{2j}\in {\mathbf{D}}_2}{max}\underset{{\mathbf{d}}_{1i}\in {\mathbf{D}}_1}{min}{\Vert {\mathbf{d}}_{1i}-{\mathbf{d}}_{2j}\Vert }_2$$ (3)

$$H({\mathbf{D}}_1^e,{\mathbf{D}}_2^e)=max\left\{\mathbf{d}({\mathbf{D}}_1^e,{\mathbf{D}}_2^e),d({\mathbf{D}}_2^e,{\mathbf{D}}_1^e)\right\}$$ (4)

This measure is used to compute two sets of values:

1. $\Delta {\mathbf{D}}_L(K,L)=H({\mathbf{D}}_{K,L}^e,{\mathbf{D}}_{K,L+1}^e)$ which quantifies the variation due to L,

2. $\Delta {\mathbf{D}}_K(K,L)=H({\mathbf{D}}_{K,L}^e,{\mathbf{D}}_{K+1,L}^e)$, which quantifies the variation due to K.

The best parameters, K* and L* is chosen to be the pair for which both distances are low. This ensures that the atoms are stable, i.e, we obtain a similar decomposition even if K* and L* are perturbed. To facilitate comparison between the two formulations, the same values of K* and L* were chosen for the node weight formulation as well.

IV. Results and Discussion

Figure 1 shows the Hausdorff distance between dictionaries as K and L are varied (separately), for the K-SVD on edge weights. For a fixed K and an incrementally varying sparsity level L, atoms are fairly stable for moderate to high values of L (Figure 1a). However variation in K alone shows the opposite effect; atoms are stable for low values of L (Figure 1b). The highlighted area in both figures indicates the values of K and L for which the variation in the dictionary is minimal. Based on these properties K* = 12 and L* = 3 were chosen to be the best parameters for the K-SVD algorithm. The decomposition was run with these parameters for both formulations, followed by the identification of two rank-one atoms, one for each formulation.

Figure 1. Model selection: Choice of dictionary size K and sparsity L for the edge-weight formulation.

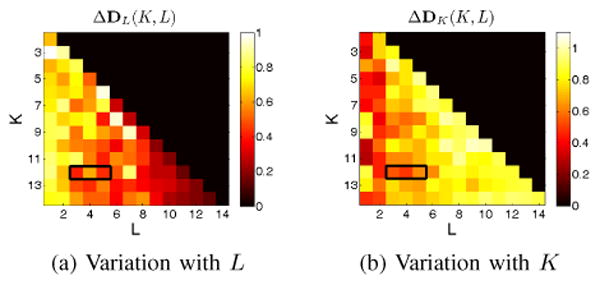
(a) Variation with L

(b) Variation with K

Visualization of atoms

Pair-wise correlations

For the formulation with pair-wise correlations, an atom is a vector of edge-weights, where each edge denotes the strength of correlation between two ROIs. This can be visualized as a graph using the Kamada-Kawai spring embedding algorithm [7]. The spring embedding algorithm finds a two-dimensional layout representation of the graph, such that ROIs that are spatially close in the resulting layout have strong functional connections as represented in the atom.

For display purposes only, in order to make the resulting network more legible, the elements of the highest ranked atom with values < 0.405 of the maximum were set to zero. This threshold was selected such that no more than 4% of ROIs lose all their connections to other ROIs. This results in the network shown in Figure 2a. Positive correlations are shown as black edges, negative correlations as red. Thicker edges denote stronger correlations. The nodes are color-coded with respect to the neural networks identified in task-based studies (please note that this label information was not used in our K-SVD optimization).

Figure 2. Visualization of the highest ranked atom from both formulations.

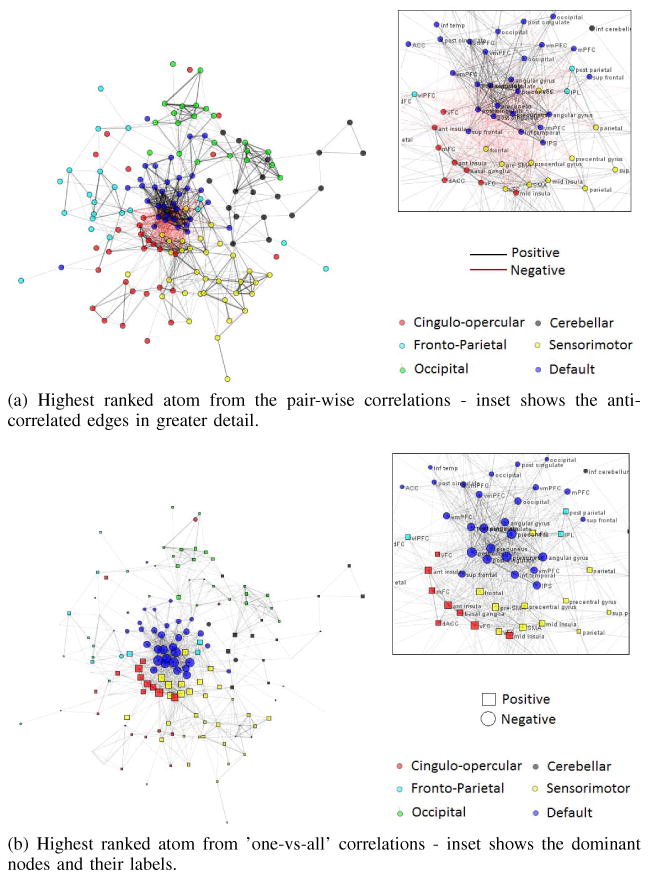
(a) Highest ranked atom from the pair-wise correlations - inset shows the anti-correlated edges in greater detail.

(b) Highest ranked atom from ’one-vs-all’ correlations - inset shows the dominant nodes and their labels.

Observe that this atom is made up of highly modular sub-networks. The six Dosenbach networks are clearly separated. This atom also reveals anti-correlated nature of one of the pairs - the default-mode (task-negative) and the sensorimotor/cingulo-opercular (task-positive) subnetworks. The inset in Figure 2a shows the negative edges in greater detail. The supplementary motor area, ventral and mid frontal cortex, middle and anterior insula make up the task-positive network, while the precuneus, posterior cingulate cortex and the ventro-medial prefrontal cortex are present in the task-negative network.

”One vs. all” correlations

In the decomposition obtained from the one-vs-all case, an atom is a vector of node-weights. This is reflected in the network by the size of the nodes in Figure 2b. The sizes of the nodes are proportional to the absolute values of the respective atom elements, while the shape of the nodes reflects the sign of the elements in the atom. Since we do not obtain any information about the edges using this formulation, we use the same layout from Figure 2a to visualize this atom and facilitate comparison between the two.

Strikingly, the same network pair was highlighted in this formulation as well - the default-mode network and the cingulo-opercular/sensorimotor network. The specificity of the two networks is remarkable: most prominent elements of the atom represented correlations with ROIs predominantly from the task-negative default mode network and from the task-positive sensorimotor and cingulo-opercular networks. Also note that the atom itself is sparse since the node weights of all other nodes are significantly smaller. It needs to be emphasized that the sign of the elements in the atom is ambiguous, as the sparse decomposition remains intact if the signs of all atom elements and the respective coefficient in the linear representation of the data are reversed at the same time. At the same time, the difference in the signs of any two atoms elements is indicative of anti-correlation between the respective ROIs.

Taken together, this suggests that the sparse-learning method captured the anti-correlated nature of two of the most important large-scale cortical networks. Furthermore, other atoms obtained in either of these decompositions reflected anti-correlation in a different pair of sub-networks(not shown here).

V. Conclusion

In summary, the results of our study suggest that functional networks in the human brain can be characterized by a small number of pairs of highly specialized anti-correlated functional networks. Sparse dictionary learning is able to effectively identify these pairs, while retaining the overlapping nature of the networks. Importantly, different representation of the connectivity information allows the sparse learning approach to reveal different aspects of the data. While in this study we focused on resting state functional co-activation of healthy brain, the same sparse analysis can be applied in other functional neuroimaging studies.