A Model of the Medial Superior Olive Explains Spatiotemporal Features of Local Field Potentials

Abstract

Local field potentials are important indicators of in vivo neural activity. Sustained, phase-locked, sound-evoked extracellular fields in the mammalian auditory brainstem, known as the auditory neurophonic, reflect the activity of neurons in the medial superior olive (MSO). We develop a biophysically based model of the neurophonic that accounts for features of in vivo extracellular recordings in the cat auditory brainstem. By making plausible idealizations regarding the spatial symmetry of MSO neurons and the temporal synchrony of their afferent inputs, we reduce the challenging problem of computing extracellular potentials in a 3D volume conductor to a one-dimensional problem. We find that postsynaptic currents in bipolar MSO neuron models generate extracellular voltage responses that strikingly resemble in vivo recordings. Simulations reproduce distinctive spatiotemporal features of the in vivo neurophonic response to monaural pure tones: large oscillations (hundreds of microvolts to millivolts), broad spatial reach (millimeter scale), and a dipole-like spatial profile. We also explain how somatic inhibition and the relative timing of bilateral excitation may shape the spatial profile of the neurophonic. We observe in simulations, and find supporting evidence in in vivo data, that coincident excitatory inputs on both dendrites lead to a drastically reduced spatial reach of the neurophonic. This outcome surprises because coincident inputs are thought to evoke maximal firing rates in MSO neurons, and it reconciles previously puzzling evoked potential results in humans and animals. The success of our model, which has no axon or spike-generating sodium currents, suggests that MSO spikes do not contribute appreciably to the neurophonic.

Introduction

Local field potentials reflect the activity of local subpopulations of neurons. Unfortunately, interpretation of these potentials is rarely straightforward (Pesaran, 2009). Models that quantitatively relate neural activity to extracellular potentials have a long history (Lorente de Nò, 1947; Rall, 1962; Rall and Shepherd, 1968), but applying these models to in vivo experimental data requires knowledge of the physiology, circuit structure, and morphology of local populations of neurons (Fernández-Ruiz et al., 2013; Reimann et al., 2013).

The medial superior olive (MSO) in the mammalian auditory brainstem is a candidate brain region for developing and applying computational models to study extracellular potentials. The extracellular potentials measured in vivo in this region, referred to as the auditory neurophonic (Weinberger et al., 1970), are large (hundreds of microvolts to millivolts) and have prominent oscillations that follow the frequency of acoustic pure tone stimuli up to several kilohertz (Tsuchitani and Boudreau, 1964; Boudreau 1965; Mc Laughlin et al., 2010). They have a stereotyped “dipole-like” spatial profile in response to monaural stimulation (Galambos et al., 1959; Biedenbach and Freeman, 1964; Clark and Dunlop, 1968; Caird et al., 1985; Mc Laughlin et al., 2010). Recording single-unit activity in the MSO in vivo is notoriously difficult (spikes are small and obscured by the large neurophonic), so the neurophonic provides another window on activity in this structure.

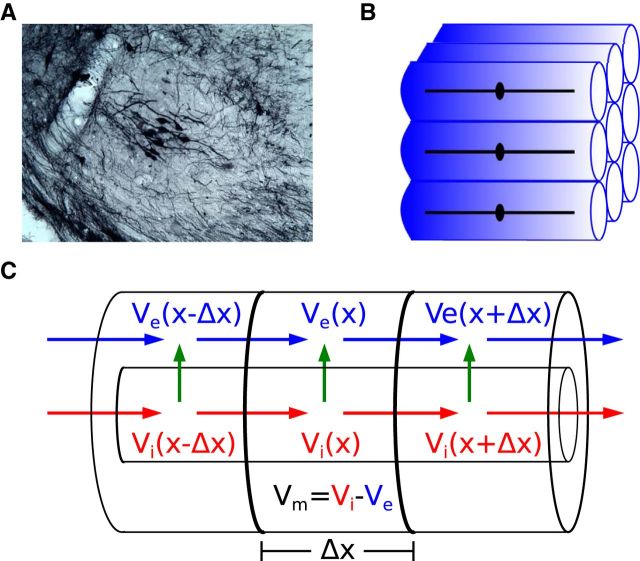
Early investigators proposed that postsynaptic currents in MSO neurons are the dominant generators of the neurophonic (Galambos et al., 1959; Biedenbach and Freeman, 1964). Their conceptual theory goes as follows. Principal cells in the MSO are typically bipolar: two dendrites extending oppositely away from the soma with each dendrite receiving afferent excitatory inputs from one ear (Stotler, 1953; Smith, 1995; Rautenberg et al., 2009) (Figure 1A). Consequently, monaural auditory input should generate synaptic current into one dendrite (current sink) and a compensatory efflux of current from the soma and opposite dendrite (current source) (Figure 1B). A local population of MSO neurons receiving similar monaural inputs should resemble, therefore, a collection of sink/source pairs and generate a dipole field along the “dendritic” (mediolateral) axis of the MSO (Figure 1C).

Figure 1.

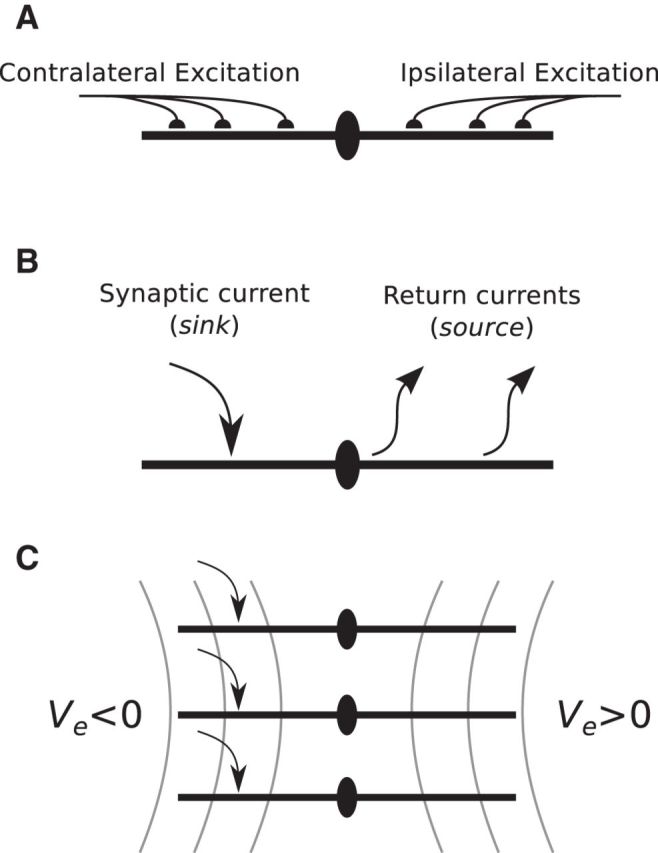
The dipole theory of the neurophonic. A, Schematic of excitatory inputs to principal cells of the MSO. Excitatory inputs largely target the dendrites, and inputs from the two ears are segregated on opposite dendrites. B, The arrangement of excitatory inputs and bipolar morphology suggest that monaural inputs to MSO neurons will act as a current dipole: excitatory currents are sinks and compensatory outward currents are sources. C, An idealized representation of a local subpopulation of MSO neurons. The gray lines indicate isopotential V_e field lines of the dipole-like field that would be generated by a local subpopulation receiving monolateral excitatory input and satisfying the symmetry and synchrony assumptions described in the text.

We develop an idealized model of the neurophonic that adds quantitative and biophysical detail to this conceptual “dipole theory.” Our approach allows us to relate the cell-level dynamics of MSO neurons to the population-level neurophonic response. We argue, based on the arrangement of MSO neurons, their bipolar morphology, and strong phase locking of their afferent inputs, that we can describe the spatial profile of the neurophonic in a one-dimensional spatial domain. We then make semiquantitative comparisons between in vivo data and simulations.

Our model reproduces distinctive features of the in vivo neurophonic response to monaural inputs: large amplitude and high-frequency oscillations, broad spatial reach, and dipole-like spatial profile. Moreover, we explain how cell-level mechanisms (synaptic time scales, bipolar morphology, voltage-gated membrane currents, somatic inhibition) shape the population-level neurophonic. In sum, we demonstrate that biophysically based modeling, combined with reasoned simplifications, can approximate in vivo field potentials and assist in their interpretation.

Materials and Methods

One-dimensional model of the neurophonic

We develop a one-dimensional model of extracellular potentials generated by a local subpopulation of MSO neurons. We first describe the assumptions of symmetry and synchrony that we make to simplify the problem.

Spatial symmetry.

Principal cells of the MSO have a predominantly bipolar morphology and are arranged in an orderly pattern (Stotler, 1953) (Figure 2A). On the basis of this anatomical observation, we make the following idealizations: all MSO neurons in a local subpopulation have identical morphology (soma with two dendrites), the somata of neighboring cells are aligned on a 2D plane, and contralateral and ipsilateral dendrites extend in opposite directions orthogonal to the plane of cell bodies. We illustrate this idealized MSO subpopulation in Figure 2B.

Figure 2.

Model of the neurophonic based on symmetry and synchrony assumptions. A, Small population of MSO neurons after injection of a retrograde tracer (BDA) in the inferior colliculus (gerbil, courtesy of Dr. T. Franken). The section is coronal: lateral is to the left, medial to the right, dorsal is up, ventral is down. The bipolar morphology, with dendrites extending medially and laterally, and the stacking of cell bodies along a dorsoventral axis, are clearly visible. B, An idealized subpopulation of MSO neurons with identical bipolar dendrites and symmetric spatial arrangement. We assume synaptic inputs to all cells are identical, so it suffices to compute V_m in one representative neuron and the V_e field in a surrounding “virtual cylinder” of extracellular space. C, V_m of representative neuron and V_e in the virtual cylinder are computed using the compartmental method. In each Δx segment, the intracellular and extracellular voltages, V_i and V_e, are dynamically coupled via transmembrane currents (green arrow), which themselves are functions of the membrane potential (V_m = V_i − V_e). Blue and red arrows indicate extracellular and intracellular currents, respectively.

The spatial arrangement of MSO neurons in vivo is not perfectly symmetric, and MSO dendrites are not uniformly bipolar. Nonetheless, our model represents a plausible idealization. A recent anatomical study in gerbils reported a significant process of development in the first postnatal weeks during which time MSO cell bodies become increasingly aligned and dendritic arbors undergo extensive pruning (Rautenberg et al., 2009). Our assumption of spatial symmetry recalls the seminal work of Rall and Shepherd (1968). They modeled extracellular fields in the olfactory bulb and approximated the arrangement of mitral and granule cells with unbranched dendritic cable models extending radially with spherical symmetry. Our idealized subpopulation of MSO neurons has longitudinal symmetry along the “dendritic” (mediolateral) axis.

Temporal synchrony.

Excitatory inputs to the MSO in cats are strongly phase locked to pure tone stimuli (Blackburn and Sachs, 1989, Joris et al., 1994a; Winter and Palmer, 1990). Indeed, specializations in the stage of the auditory pathway between sensory neurons in the cochlea and MSO neurons (i.e., bushy cells in the cochlear nucleus) can enhance phase locking and temporal precision of inputs to the MSO (Joris et al., 1994a,b), so that, at frequencies <700 Hz, these inputs can be a nearly perfectly periodic spike train with very little jitter. With increasing frequency, phase-locking increasingly loses its “picket-fence” character, although it can still be enhanced at frequencies of ∼1 kHz (Joris et al., 1994b). To idealize this temporal precision, we require that synaptic inputs arrive periodically at a frequency determined by the stimulus. In other words, the simulated excitatory inputs have no temporal jitter.

We make one additional idealization: we say that synaptic inputs to all neurons in the model arrive in synchrony with one another. Thus, every cycle of pure tone stimulus generates identical inputs to all neurons in the local subpopulation, and these inputs arrive perfectly locked to the same phase of the stimulus waveform. This idealization neglects sources of timing differences in the synaptic inputs to neighboring neurons, such as the effects of synaptic jitter, cochlear delays, and (possible) gradients of tuning to interaural time differences in the MSO. On a local level, it is plausible that nearby neurons receive similar inputs because there is an orderly tonotopic organization of the MSO (Guinan et al., 1972; Karino et al., 2011). Also, reports suggest that intrinsic properties covary with position along the tonotopic axis (Baumann et al., 2013) or are homogeneous across a large extent of the nucleus (Scott et al., 2007). We know of no evidence to suggest more than modest variability in intrinsic properties at a local level. Furthermore, the great variety of ITD sensitivity and tuning curves seen (e.g., in responses to broadband noise) (Yin and Chan, 1990) is drastically reduced with tonal stimuli as used and simulated here. Tonal ITD curves of different neurons are quasi-sinusoidal and can be simply scaled to overlay each other, which is much less the case for responses to broadband stimuli (e.g., noise) due to effects of cochlear filtering.

Current flow confined to virtual cylinders.

The idealized subpopulation of MSO neurons is shown in Figure 2B. We have marked a thin layer of extracellular space surrounding each neuron with a blue shaded region. We call this a “virtual cylinder.” A consequence of the assumptions discussed above (spatial symmetry and temporal synchrony of synaptic and membrane currents) is that there can be no difference in the membrane potentials of two nearby neurons and no difference in the extracellular potentials across the boundary of adjacent virtual cylinders. In the absence of any voltage gradient across these boundaries, all extracellular current must flow within the confined volume (essentially one-dimensional) that surrounds each neuron and extends beyond the distal ends of the dendrites. Moreover, because all neurons and virtual cylinders in the local population are assumed to be identical, it suffices to compute the intracellular and extracellular potentials associated with a single neuron. The activity in and around any one neuron represents the entire subpopulation.

The model architecture provides an estimated upper bound for the amplitude of extracellular potentials. Disruption of spatial symmetry or temporal synchrony would allow current to exit the virtual cylinder and thereby reduce the extracellular potentials generated by the combined activity of neurons in the local subpopulation. The seemingly restrictive assumptions of symmetry and synchrony are formally necessary to justify the reduction of the volume conductor to a one-dimensional virtual cylinder, but in effect we are only requiring that the spatial gradient of the extracellular voltage has one dominant direction (along the dendritic axis). Such an assumption is frequently invoked in current source density analyses of local field potentials (Nicholson and Freeman, 1975; Mitzdorf 1985), including in the auditory brain stem (Mc Laughlin et al., 2010). In a neural population with modest spatial heterogeneity and modest temporal jitter, the virtual cylinder construct can still be plausible. Contributions of any individual neuron to V_e are relatively small; thus, all neurons in a local subpopulation will experience a similar extracellular “bath” that is the aggregate, population-level V_e.

Compartmental method coupling MSO neuron model to extracellular space

Under the symmetry and synchrony conditions, we can describe activity of a local subpopulation of MSO neurons by a single “representative” neuron surrounded by a confined extracellular layer. We model this representative MSO neuron using a biophysically based model developed for gerbil MSO (Mathews et al., 2010). The neuron model has two identical dendrites (150 μm length, 3.5 μm diameter) and a central cylindrical soma (20 μm length, 20 μm diameter).

In typical simulations of spatially extended neurons, one computes the membrane potential V_m using the compartmental method under the assumption that the extracellular potential V_e is so small that it can be ignored (Segev and Burke, 1998; Rall, 2011). One assumes V_e = 0 and, as a consequence, V_m = V_i where V_i is the intracellular potential referenced to some ground electrode. To model the neurophonic, the extracellular potential must be non-zero and nonuniform so we modify the typical compartmental method. We discretize both the intracellular and extracellular domains into compartments of length Δx and then compute the dynamically coupled intracellular, transmembrane, and extracellular potentials. We used 23 compartments in the spatial discretization (Δx = 15 μm in dendrites, Δx = 6.67 μm in soma) (Mathews et al., 2010). The following model development closely follows Rall's treatment of a passive “axon in oil” (Rall, 2011).

Figure 2C illustrates this modified compartmental method. For simplicity of notation, we omit subscripts and let x denote the center of the k^th compartment. Conservation of current (Kirchoff's law) requires current balance relations between intracellular (axial) current (I_i; units milliamperes) and transmembrane current in the intracellular compartment as follows:

In this notation, the transmembrane current is current per unit length (i_m, units milliamperes per centimeter). By convention, outward membrane current (i.e., transfer of positively charged ions from intracellular to extracellular space) is positive. The term I_i(x − Δx/2, t) is the intracellular current flow from compartment k − 1 to k. A similar current balance relation holds in each extracellular compartment between extracellular current (I_e, units milliamperes) and the transmembrane current as follows:

Current flow between adjacent compartments within the MSO neuron and along the extracellular virtual cylinder are governed by Ohm's law as follows:

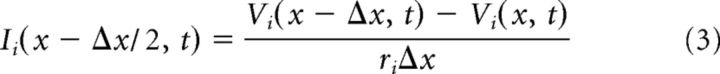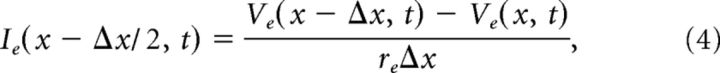where r_i and r_e are the intracellular and extracellular resistances per unit length (units ohms per centimeter). At the interface of the soma and dendrites, the denominator is actually a sum of two terms of the form rΔx/2, to account for the fact that r_i, r_e, and the compartment length Δx have different values in soma and dendrite compartments. We omit this here to maintain the clarity of our presentation.

Following the model of Mathews et al. (2010), we use R_i = 200 Ωcm for the core resistivity of the neuron. We then set r_i = R_i/A_i(x) where A_i(x) is the cross-sectional area of the intracellular compartment. The extracellular resistance r_e has not, to our knowledge, been measured in the auditory brainstem. We set the extracellular resistivity to be 300 Ωcm, a value in line with previous modeling studies of cortical local field potentials (Holt and Koch, 1999; Lindén et al., 2011). We then set r_e = R_e/A_e(x) where A_e(x) is the cross-sectional area of the extracellular compartment (an annulus surrounding the neuron). We suspect that resistivity in the auditory brainstem may be higher than in cortex because of dense packing of myelinated fibers, but in the absence of measured values we use this relatively conservative value. Larger values of R_e would increase the amplitude of the simulated neurophonic.

We estimated the extracellular cross-sectional area A_e(x) from a recent anatomical study of gerbil MSO. Rautenberg et al. (2009) reported that cell bodies of mature MSO neurons have an average diameter of 13 μm and have a packing density of ∼7 cells per 100 μm. From these measurements, we reasoned that the virtual cylinder radius is ∼10% larger than the soma radius. The soma radius in the Mathews et al. (2010) model is 10 μm, so we set the radius of the virtual cylinder to be 11 μm. We explore the effect of varying this parameter value in Figure 7.

Figure 7.

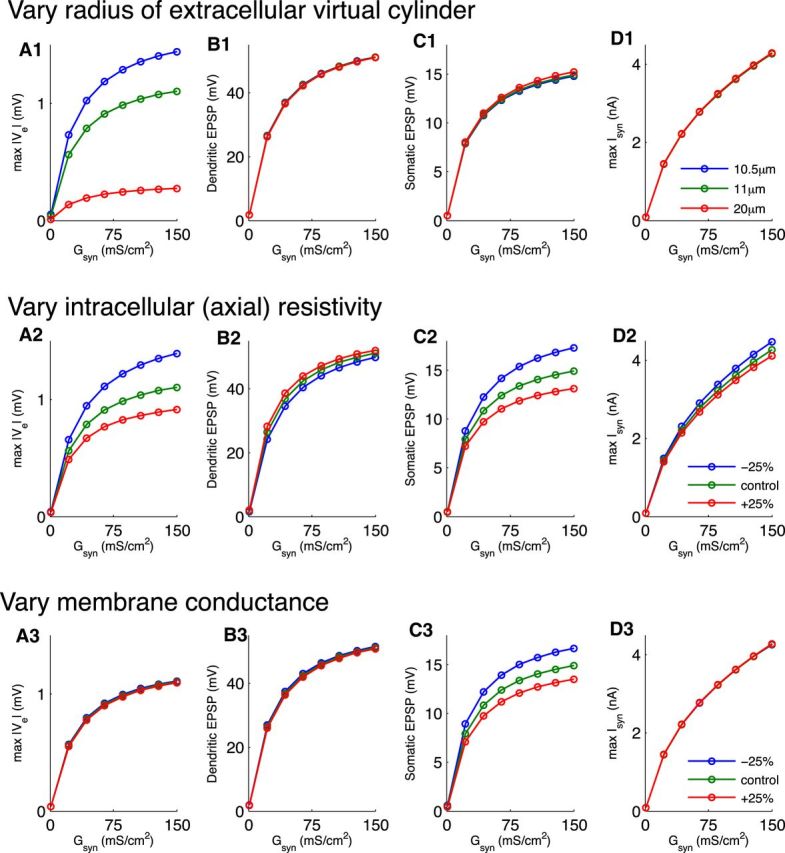
Effect of peak synaptic conductance and virtual cylinder radius on amplitude of the simulated neurophonic. Abscissa in all panels is value of G_syn parameter in Equation 14. A, Maximum amplitude of V_e in response to a single monolateral excitatory synaptic event. B, Maximum amplitude of EPSP measured in the dendrite that received synaptic input. C, Maximum amplitude of EPSP measured in the soma of the neuron model. D, Maximum amplitude of excitatory synaptic current. Excitatory current (an inward current) is considered negative by convention, but here we plot its amplitude as a positive value. Colored lines indicate the radius of the virtual cylinder. In all panels, maxima are computed over all spatial locations. Simulation results presented in other figures use G_syn = 10 mS/cm² and virtual cylinder radius 11 μm, unless noted otherwise.

We combine the Equations 1–4 to get two equations relating transmembrane current to intracellular and extracellular voltage as follows:

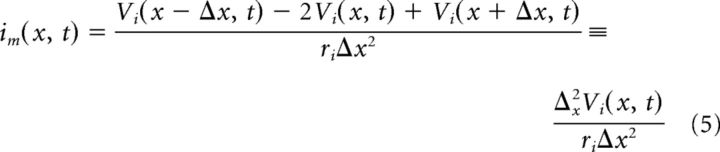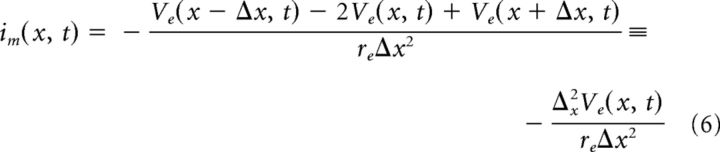Intracellular and extracellular voltages are coupled via the transmembrane current. We let I_m denote the transmembrane current density (I_m = 1000 i_m/σ, units microamperes per centimeter squared, σ is the compartment circumference). It is the sum of capacitative, leak, ionic, and synaptic currents, all of which depend on the transmembrane potential as follows:

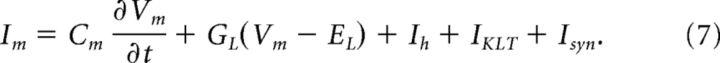C_m is the membrane capacitance (0.9 μF/cm²), G_L is the leak conductance (0.3 mS/cm²), and E_L is the reversal potential of the leak current (−60 mV). I_h is hyperpolarization-activated cation current that is active at rest and modeled as a passive leak current with reversal potential of −43 mV, ∼20 mV above the resting membrane potential. Its maximal conductance is 0.86 mS/cm² in the soma and 0.18 mS/cm² in the dendrites; this is the “step-gradient” model of Mathews et al. (2010). I_KLT is the low-threshold K⁺ current. This current is modeled with a dynamic and voltage-gated conductance I_KLT = G_KLTm⁴h(V_m − E_KLT). The peak conductance G_KLT is 17 mS/cm² in the soma and 3.6 mS/cm² in the dendrites; the reversal potential E_KLT is −106 mV. The gating variables m and h evolve according to equations of the form du/dt = [u_∞ (V_m) − u]/τ_u(V_m) where u = m or h and the following:

I_KLT and I_h are active at resting membrane potentials. For further details regarding these ion currents and their parameter values, see Mathews et al. (2010). We do not include an initial segment, axon, or spike-generating sodium currents in the model. We expect spikes and back-propagating action potentials to make negligible contributions to the neurophonic because of reports that sodium channels are substantially inactivated in the soma near the resting potential (Scott et al., 2010) and MSO spikes are small in vivo (Franken et al., 2013; van der Heijden et al., 2013). We describe our model of synaptic current I_syn below (see Eq. 14).

The membrane current density I_m is related to both V_i and V_e (Eqs. 5 and 6). Thus, the above equations yield an augmented compartmental method that is a system of coupled equations (two per spatial location) for the unknown variables V_i(x,t) and V_e(x,t) as follows:

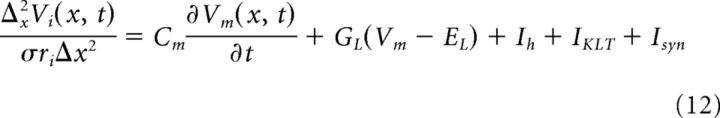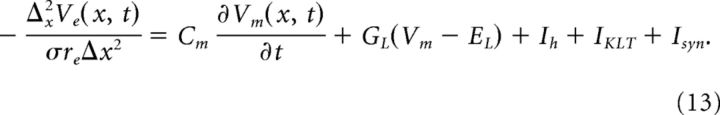These equations are coupled in space by adjacent compartments and across the membrane through the relationship V_m = V_i − V_e. They form a system of differential algebraic equations. One could implement a simple numerical scheme to evolve the solution in time. Suppose V_i and V_e are known at time t, then one could compute V_m(t + Δt) from Equation 12 (e.g., using a forward Euler integration step) and then update V_e by solving Equation 13 as a linear algebraic system. Instead, we use a more accurate and efficient method that treats the differential algebraic system simultaneously. We use the Suite of Nonlinear and Differential/Algebraic Equation Solvers (SUNDIALS) and its interface to MATLAB (sundialsTB) (Hindmarsh et al., 2005). This solver uses a variable order, variable coefficient backward differentiation with an adaptive time step. We required absolute and relative error tolerances of 10⁻⁶ and extracted the solution at 1 μs time steps. Simulation code is available on the ModelDB website (accession #152112). In practice, these equations must be modified slightly at the boundaries of the soma and dendrites to account for the fact that a number of parameters (compartment area and length, KLT, and h peak conductances) are different in soma and dendrite compartments. For clarity of presentation and notation, we have not shown these modifications explicitly in the above equations.

There are two sets of boundary conditions we must specify. In the intracellular domain, we apply a “sealed end” (zero axial current) boundary condition at the ends of the dendrites. In the extracellular domain, we impose a “mixed” condition that requires all current flowing past the ends of the dendrites to go to a distant electrical ground along a (one-dimensional) resistive pathway. This extracellular boundary condition forces V_e to approach 0 mV (at ground) linearly. The extracellular boundary condition introduces two additional parameters: the distance from the distal edge of a dendrite to the electrical ground (d_g) and the resistivity of this pathway (r_g). We set d_g = 1 mm and r_g = r_e (identical to the extracellular resistivity surrounding the neuron).

Simulated synaptic inputs

We model excitatory synaptic current as an α function conductance multiplied by a driving force as follows:

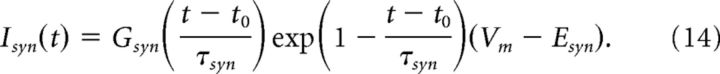G_syn is the peak conductance per area, τ_syn is the time constant describing the rise and decay of the conductance, t₀ is the onset time of the synaptic event, and E_syn is the reversal potential. The peak conductance is a critical parameter that determines the amplitude of the simulated neurophonic and excitatory postsynaptic potentials in the membrane voltage. We typically set G_syn = 10 mS/cm² to generate a simulated neurophonic that is of similar amplitude to in vivo data we present below. We illustrate the effect of varying this parameter in Figure 7. Unless otherwise stated, we set E_syn = 0 mV and τ_syn = 0.2 ms for excitatory inputs based on in vitro data for gerbil MSO (Jercog et al., 2010; Fischl et al., 2012). Excitatory synaptic inputs are located on the dendrites of MSO cells (Couchman et al., 2012). In our initial investigations (data not shown), we found that varying the location of dendritic synapses had only modest effects on the simulated neurophonic. For instance, V_e responses to inputs localized at one site on a dendrite appear nearly identical to V_e responses to inputs distributed along the entire dendrite (data not shown). We therefore fix a single dendritic synaptic site (per side) 145 μm from the center of the soma.

In some simulations, we also include inhibition (see Figs. 12 and 13). Inhibition in gerbil MSO targets the soma (Couchman et al., 2012), so we simulate inhibition by adding a synapse site in soma of the neuron model. The temporal relationship between excitation and inhibition in vivo is unknown, but following recent in vitro work in gerbil MSO, we let inhibition precede excitation by 0.35 ms (Roberts et al., 2013). We modeled the dynamics of inhibitory current using a double exponential function (0.4 ms rise time, 2 ms decay time) and a reversal potential of −90 mV (Magnusson et al., 2005). We set the peak inhibitory conductance to 4 mS/cm² in one compartment of the soma so that excitatory and inhibitory conductances were approximately balanced (for excitatory G_syn = 10 mS/cm² in one dendrite compartment), as found in vitro (Couchman et al., 2012).

Figure 12.

Response of the model to 1 kHz monolateral excitatory inputs with somatic inhibition. Inhibitory events precede excitatory events by 0.35 ms. Peak synaptic conductance is 10 mS/cm² for excitation and 4 mS/cm² for inhibition. A, Spatiotemporal profile of membrane potential. The ordinate represents the mediolateral or dendritic distance in micrometers, with 0 representing the soma. The abscissa is the time axis; it begins at 4 ms to show only the ongoing response. The black icon at left represents the dimensions of the neuron model. The resting membrane potential is −60 mV. B, Spatiotemporal profile of the simulated neurophonic; note the change in scale on the ordinate from A. The dashed black line at t = 6.3 ms indicates the time at which the spatial cross-sections in Figure 13 are taken. C, Spatiotemporal profile of the simulated neurophonic with mean value removed from every spatial location. This mimics the 10 Hz high pass filter imposed by data acquisition system in experiments of Mc Laughlin et al. (2010). D, Difference of simulated neurophonic responses with and without inhibition (i.e., the difference between Figs. 12C and 4C).

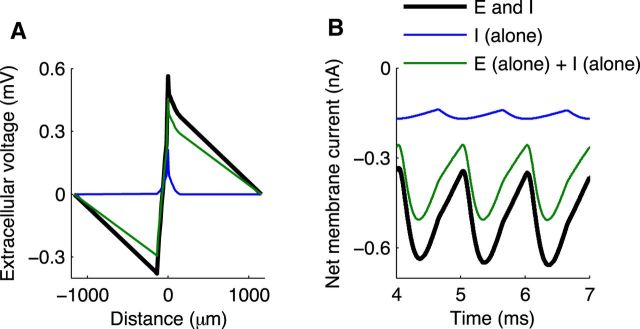
Figure 13.

Contribution of inhibition to V_e field and membrane current. A, Spatial profile of V_e field at t = 6.3 ms (cross-section indicated by black line in Fig. 12B). Inhibition alone produces local increase in V_e (blue). Interplay of inhibition and excitation (black) increases V_e field more than the linear sum of inhibition alone and excitation alone (green). B, Membrane current in the near dendrite (side receiving excitatory input). Interplay of inhibition and excitation generates a larger sink (more negative membrane current) in the near dendrite (black) than the linear sum of membrane currents produced in the near dendrite by excitation alone and inhibition alone (green). Parameters are the same as in Figure 12.

To approximate the temporal pattern of synaptic conductances to MSO neurons for pure tone stimuli, we let the onset times define a train of repeating synaptic events. Recall that this pattern of activation is a consequence of our idealization that all synaptic inputs are identical and in synchrony with one another (see Materials and Methods). This idealization neglects temporal jitter and imperfect entrainment of synaptic events. To emulate a 1000 Hz monaural tone, for instance, we stimulate the model MSO neuron with a 1000 Hz train of excitatory synaptic inputs that arrive on one dendrite.

The binaural stimuli used in experiments were binaural beats: pure tones presented to both ears with a 1 Hz interaural frequency difference. To emulate these stimuli, we stimulate the neuron model with trains of excitatory synaptic events arriving on both dendrites at slightly mismatched frequencies (1 Hz difference).

In vivo recordings

We compare our simulation results with in vivo recordings of the neurophonic response to monaural tones and binaural beat stimuli. Responses to monaural tones were reported by Mc Laughlin et al. (2010), and detailed experimental methods can be found therein. Responses to binaural beats are published here for the first time. In brief, extracellular voltages were measured in anesthetized adults cats of either sex (0.2 mg/kg acepromazine and 20 mg/kg ketamine i.m., followed by pentobarbital i.v. for maintenance) using a five-channel microelectrode (quartz/platinum-tungsten, TREC, 2–4 MΩ). The approach of the electrode was selected to target the low-frequency region of the MSO. The electrode was advanced in 100 μm steps along the dendritic (mediolateral) axis. Acoustic stimuli were monaural pure tones (100–2500 Hz, 2 s duration, 70 dB sound pressure level) and binaural beats (ipsilateral tone frequency 1 Hz greater than contralateral tone frequency). We present data from a single recording electrode and a single MSO penetration (animal S0733D, electrode #2). There is considerable variability within and across recording sessions, but dipole-like patterns of the neurophonic are a common finding (Mc Laughlin et al., 2010; and see figures therein for visualizations of additional monaural datasets).

A technical detail that complicates the interpretation of the experimental data is that the signal acquisition system was not DC-coupled: all recordings were filtered (10 Hz to 10 kHz) by the TREC headstages. The 10 Hz lower cutoff removes the “DC” component of the signal; the amplitude of oscillations of the neurophonic is preserved but not the absolute voltage. In some figures of modeling results, we approximate this 10 Hz high-pass filter by removing the mean value of the simulated extracellular voltage independently at each spatial location.

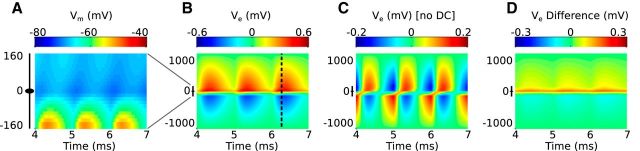
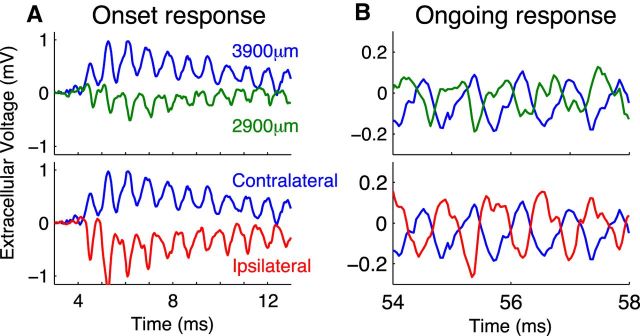
Figure 3 shows example neurophonic responses to a 1200 Hz monaural tone. We distinguish between the onset response (up to ∼25 ms after stimulus onset) and the later ongoing response. Short excerpts from the onset and ongoing responses are shown in Figure 3A and Figure 3B, respectively. In the top row, we show responses recorded to contralateral stimulation measured at two penetration depths: 2900 and 3900 μm (1 mm separation). In the bottom row, we show the same response to the contralateral stimulus at 3900 μm, but now compare it with the response to ipsilateral stimulation. Both onset and ongoing responses show prominent oscillations that match the frequency of the pure tone stimulus. The onset response also includes a slowly changing shift in the DC-level around which the extracellular voltage oscillates. This slow-wave potential (Tsuchitani and Boudreau, 1964) is visible as a positive shift of the extracellular voltage for the contralateral response at 3900 μm (blue), a negative shift for the contralateral response at 2900 μm (green), and a negative shift for the ipsilateral response at 3900 μm (red). We do not model this slow-wave potential and will restrict our comparisons between model simulations and data to the ongoing neurophonic (Fig. 3B). Because of the 10 Hz high pass filter, the ongoing response oscillates around a mean near 0 mV.

Figure 3.

In vivo neurophonic response to 1200 Hz monaural tone. Top row, Response to contralateral stimuli recorded at two depths in the brainstem. Each trace is a brief portion of a longer recording; these data are not averaged. Larger depth (blue) indicates more dorsolateral recording position. Bottom row, Comparison of responses to contralateral (blue) and ipsilateral (red) tones at 3900 μm recording depth. A, Onset responses include a slow-wave potential. B, Ongoing responses oscillate around 0 mV because of 10 Hz high pass filter in the data acquisition system. Oscillations in the neurophonic match the stimulus frequency (1200 Hz).

The data in Figure 3 show five distinctive features of the neurophonic that we seek to produce in the model. First, as we just pointed out, the responses exhibit prominent oscillations that follow the frequency of the pure tone stimulus (1200 Hz in this case). Second, the neurophonic has a broad spatial extent (millimeter scale), as evidenced by the prominent oscillations measured 1 mm apart (green and blue). Third, these oscillations are large, typically hundreds of microvolts. In the example traces in Figure 3B, the peak-to-trough amplitude is ∼0.3 mV. Fourth, the polarity of the neurophonic response reverses when the ear of stimulation is changed. In Figure 3A, the initial response to contralateral stimulation is a positive deflection of the extracellular voltage (blue), whereas the initial response to the ipsilateral stimulation is a negative deflection (red). Fifth, the polarity of the extracellular voltage reverses as one moves along the dendritic axis of the MSO. In the top panels, the recording positions are separated by 1 mm and are on opposite sides of the MSO. This polarity reversal with recording position appears as a nearly half-cycle phase shift in the ongoing oscillation (Fig. 3B, blue and green). Mc Laughlin et al. (2010) analyzed the phase shifts in detail.

Results

Monolateral excitation: spatial profile of neurophonic resembles dipole field

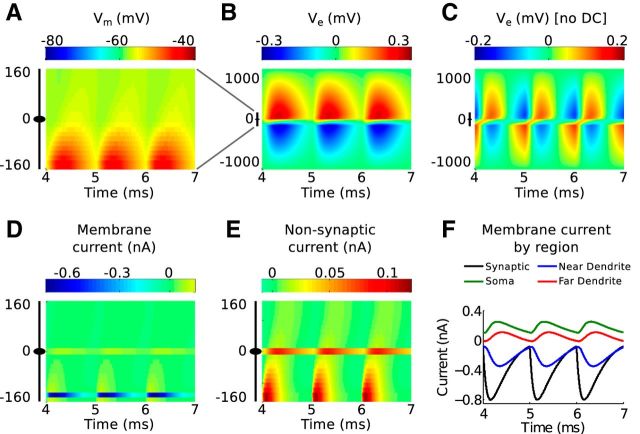
We first show that the model produces a dipole-like neurophonic in response to monolateral excitatory input that replicates the distinctive features of in vivo data. Figure 4 shows spatiotemporal profiles of simulated responses to a 1 kHz train of periodic excitatory inputs arriving on one dendrite (“near dendrite,” negative value on the vertical axis) over a time span of 3 ms. Figure 4A shows the membrane potential of the model MSO cell. Each synaptic event in this simulation (G_syn = 10 mS/cm²) drives a ∼15 mV EPSP in the near dendrite. These EPSPs attenuate as they travel through the neuron; they are ∼5 mV in the soma and 3 mV in the opposite dendrite (“far dendrite”). EPSP propagation is not instantaneous; the peaks of the somatic EPSPs occur 0.3 ms after the peaks of the corresponding dendritic EPSPs. As we will see, this finite propagation time of EPSPs differs from the instantaneous spread of extracellular voltage along the neuron.

Figure 4.

Response of the model to 1 kHz monolateral excitatory inputs. A, Spatiotemporal profile of membrane potential. The ordinate represents the mediolateral or dendritic distance in micrometers, with 0 representing the soma. The abscissa is the time axis; it begins at 4 ms to show only the ongoing response (after transient effects caused by the initial resting state of the neuron model have disappeared). The black icon at left represents the dimensions of the neuron model. The resting membrane potential is −60 mV. B, Spatiotemporal profile of the simulated neurophonic; note the change in scale on the ordinate from A. C, Spatiotemporal profile of the simulated neurophonic with mean value removed from every spatial location. This mimics the 10 Hz high pass filter imposed by data acquisition system in experiments of Mc Laughlin et al. (2010). D, Spatiotemporal profile of membrane current. E, Spatiotemporal profile of membrane current excluding synaptic current. Note the difference in color scale in D and E. F, Synaptic current (black) and sum of membrane currents in the three regions of the neuron model (colors): near dendrite (side with synaptic input), soma, and far dendrite (side opposite to synaptic input).

Figure 4B shows the spatiotemporal profile of extracellular voltage V_e generated in response to the same sequence of monolateral excitatory inputs (but note the change in the vertical axis and color scale). This is the simulated neurophonic. Each synaptic event generates a negative deflection in V_e near the site of the synaptic input that attenuates to zero at the distant electric ground (at −1000 μm). Simultaneously, a positive deflection in V_e appears on the opposite side of the model MSO neuron. This deflection also attenuates to zero at the distant electric ground (at 1000 μm). The black icon just left of the vertical axis origin marks the location of the MSO neuron; in this region, the polarity of the extracellular voltage changes abruptly.

As we discussed in Materials and Methods, it is necessary to remove the mean value (at each spatial position) of the simulated neurophonic to compare model results with our experimental data. Figure 4C shows the result of applying this operation to the simulated neurophonic. There is now a temporally alternating dipole pattern in the spatiotemporal profile. Similar to the example “ongoing” data in Figure 3B (top), the oscillations on opposite sides of the MSO neuron are out of phase with one another. The synaptic inputs we use in these simulations are modest (∼15 mV EPSP amplitude in the dendrites), but they suffice to produce ∼0.3 mV peak-to-trough oscillations in V_e. This amplitude is consistent with the example data shown in Figure 3. We explore the relationship between EPSP size, V_e amplitude, and key parameter values further in Figure 7.

Mc Laughlin et al. (2010) noted, with regard to their in vivo data, that it is impossible to infer from these “filtered” patterns whether a single sink/source pair generates the neurophonic or whether it is due to two out-of-phase sink/source pairs (as would be generated by dendritic excitation and somatic inhibition, for example). In the model, the interpretation is clear because we have access to the “unfiltered” results in Figure 4B. A single sink/source pair (excitation in one dendrite and return currents distributed throughout the neuron) generates a dipole-like spatial distribution of V_e.

In Figure 4 (bottom row), we dissect the membrane currents that generate the simulated neurophonic. By convention, we say that excitatory current is an inward current, and we represent this as a negative value. We refer to inward currents as sinks. The large sink associated with synaptic current is apparent on the near dendrite (negative value on vertical axis) in Figure 4D. Conservation of current requires the rest of the cell to generate compensatory outward currents that return the synaptic current to the extracellular space. We refer to these compensatory outward (positive) currents as sources. They appear as small, positive values distributed across the neuron.

The source currents are difficult to discern on the color map in Figure 4D, so we excluded the synaptic current and plotted the remaining membrane currents on a new color scale (Fig. 4E). The nonsynaptic currents are largest in the dendritic regions close to the synaptic inputs (near dendrite) and in the soma. The nonsynaptic currents on the near dendrite represent local current loops that form immediately after the onset of each synaptic event to return current to the extracellular space. The soma acts as a prominent secondary source because it has a much larger diameter than the dendritic compartments (20 μm compared with 3.5 μm) and greater density of low-threshold potassium conductance. Small outward currents are also generated in the far dendrite.

What emerges from these results is a dynamic and spatially distributed pattern of current sinks and sources in MSO neurons. They are not simply a spatially stationary sink/source pair. Nonetheless, these currents combine to generate the symmetric appearing dipole-like neurophonic in Figure 4B.

In Figure 4F, we summarize the spatiotemporal dynamics of membrane currents by computing the sum of membrane currents within three regions of the cell: near dendrite (same side as synaptic input), soma, and far dendrite (opposite side from synaptic input). The difference between the membrane current in the near dendrite (blue) and the synaptic current (black) indicates that there is substantial outward current in the near dendrite (as shown in Fig. 4D), but the net current for the near dendrite is sink-like. The soma (green) and far dendrite (red) act as current sources because they return current to the extracellular space and do not receive strong inward currents. By construction of the model (conservation of current), the total membrane current summed across the entire neuron is zero at all times. The reversal from sink (near dendrite) to source (soma and far dendrite) as one moves axially along the neuron reflects the notion that MSO neurons act as current dipoles. Indeed, similar spatial patterns of sink and source currents have been obtained with current source density analysis (Mc Laughlin et al., 2010).

To summarize these simulations, we have observed the distinctive features of the neurophonic that we introduced previously and highlighted in Figure 3. The simulated neurophonic response exhibits prominent oscillations (hundreds of microvolts in amplitude, kilohertz scale frequency, millimeter scale spatial reach). Moreover, the simulated neurophonic exhibits the distinctive spatial profile of a dipole field. Synaptic current on one dendrite acts as a current sink to produce a region of negative V_e near the synaptic input site. Postsynaptic return currents distributed across the neuron act as a current source and generate a region of positive V_e on the opposite side of the MSO. We note that symmetry in the model guarantees that the polarity of the field would reverse if the synaptic input entered on the upper dendrite (positive depths) instead of the lower dendrite.

Monaural inputs: comparison of simulated and in vivo neurophonic

To compare directly the spatiotemporal dynamics of the simulated and in vivo neurophonic responses to monolateral/monaural inputs, we “cycle-averaged” the experimental data. As in Mc Laughlin et al. (2010), at each recording depth we averaged all instances of the extracellular voltage recorded at the same phase of the pure tone stimulus. By repeating this averaging for all phases in a single cycle of the pure tone stimulus, we isolated the stimulus-driven oscillations in the neurophonic.

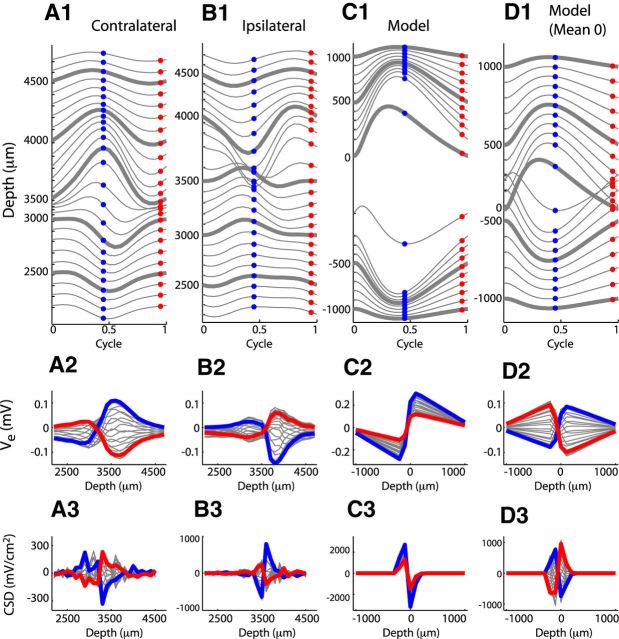
We plot cycle-averaged neurophonic responses to 1200 Hz monaural pure tones in Figure 5A1, B1. Each line in the top panels is the trajectory of one cycle of the cycle-averaged neurophonic response. These data were collected at 100 μm increments as an electrode was advanced through the brainstem (see Materials and Methods). Each line represents a different recording depth; we have spaced the V_e trajectories from adjacent recording sites by 0.04 mV to improve the clarity of the figure.

Figure 5.

Comparison of neurophonic response to 1200 Hz monaural pure tones (contralateral and ipsilateral) and monolateral input trains (model). Data are from the same recording sessions as those in Figure 3. Top row, Cycle-averaged neurophonic responses plotted over one cycle at each recording depth. The vertical position of each trace is determined by its mean value and by a 0.04 mV offset between adjacent traces for clarity of presentation. Bottom row, Spatial profile of cycle-averaged neurophonic responses. The blue and red dots in the top panels form the blue and red spatial profiles in the bottom panels. A, In vivo neurophonic response to contralateral tone. B, In vivo neurophonic response to ipsilateral tone. C, Simulated neurophonic response for excitation on dendrite at negative depth. One cycle of the ongoing response (after transient effects caused by the initial resting state of the neuron model have disappeared). D, Same as in C with mean value removed at each spatial location to mimic the effect of the 10 Hz high pass filter imposed by the data acquisition system in experiments.

In Figure 5A2, B2, we show spatial profiles of these cycle-averaged data. To orient the viewer, we marked the cycle-averaged trajectories in Figure 5A1, B1 with blue and red dots at two phases in the cycle and colored their corresponding spatial profiles in Figure 5A2, B2.

The dipole-like nature of the neurophonic is apparent in the spatial profiles (bottom panels) as a sudden polarity reversal along the x-axis. This transition occurs near 3000 μm recording location for the contralateral tone (Fig. 5A2) and 3500 μm for the ipsilateral tone (Fig. 5B2). These polarity reversals are also evident in the cycle-averaged trajectories in the top panels. In Figure 5A1, large negative deflections of the extracellular voltage at depths <3000 μm become large positive deflections at larger depths. The reverse trend is visible in the cycle-averaged responses to ipsilateral tones shown in Figure 5B1; the transition here is at a depth of ∼3500 μm. The spatial profiles in the bottom panel also exhibit the millimeter-scale spatial reach of the neurophonic.

In Figure 5C1, we show simulation results for a 1200 Hz train of monolateral synaptic inputs. Our simulations do not include noise or synaptic variability, so a single cycle of the simulated response is identical to a cycle-averaged response. The vertical axis in Figure 5C1 and the horizontal axis in Figure 5C2 show the spatial extent of the model. The soma is located at the origin (0 μm depth, by definition). The depth axis takes negative and positive values because the dendrites extend away from the soma in opposite directions. The excitatory synaptic inputs and the associated current sinks were located on one dendrite at a depth of −145 μm. This configuration simulates the contralateral in vivo data in Figure 5A. We simulate ipsilateral responses by moving the synaptic inputs to the opposite dendrite (positive depth). Simulation results in this case are identical (by symmetry) after reflection about the 0 μm spatial location (data not shown).

The model displays the expected dipole-like pattern of extracellular voltage. V_e is negative on the side of the neuron receiving synaptic inputs and transitions sharply to positive values near the soma (depth of 0 μm). The spatial profile (Fig. 5C2) highlights the millimeter-scale spatial reach of the simulated neurophonic that is achieved by setting the distant electric ground to be 1 mm from the ends of the MSO neuron.

To present our simulation results in a manner comparable to the in vivo data, we removed the mean value of V_e at each spatial location. This mimicked the 10 Hz high pass filtering of the data (see Materials and Methods). Simulation results with the DC component removed are shown in Figure 5D. The most apparent effect of this “DC removal” is that the simulated extracellular voltage now appears to be comprised of two out-of-phase positive–negative going oscillations: one at negative depths and one at positive depths. This spatial pattern is also present in the in vivo data (Fig. 5A,B). In the model, this pattern is not indicative of any secondary current sinks/sources contributing to the neurophonic. Instead, it is simply an artifact of the high pass filtering operation that removes the time-averaged mean of V_e at each recording location.

Extracellular field potentials are frequently studied with current source density (CSD) analysis (Mitzdorf 1985), including in auditory brain stem (Mc Laughlin et al., 2010). We therefore compared a CSD analysis of the cycle-averaged recordings to the simulated V_e responses (Fig. 5, bottom row). As in Mc Laughlin et al. (2010), we perform a one-dimensional CSD analysis of the in vivo data along the direction of the electrode track by taking a second spatial derivative using a finite difference approximation. In principle, the second spatial derivative of V_e should yield the spatial distribution of membrane currents (see Eq. 6). But, in our CSD analysis, we have sampled the simulated V_e on a relatively coarse grid (100 μm increments) to match the experimental procedure in Mc Laughlin et al. (2010). This leads to a difference between the result of the CSD analysis and the distribution of membrane currents. The CSD analysis of the simulated neurophonic in Figure 5C3 suggests a symmetric sink/source pair, whereas the simulated membrane currents (shown in Fig. 4D) consist of a localized current sink (the synapse) and small-amplitude current sources distributed across the cell.

In the in vivo neurophonic responses, we observe two prominent peaks in the spatial profile of the CSD (Fig. 5A3,B3) that are antiphasic (compare blue and red lines). This pattern is characteristic of neurophonic responses as explored in greater detail by Mc Laughlin et al. (2010). Upon removing the DC level at each spatial location to mimic the in vivo recordings, we find that the simulated CSD qualitatively reproduces this spatial profile (Fig. 5D3).

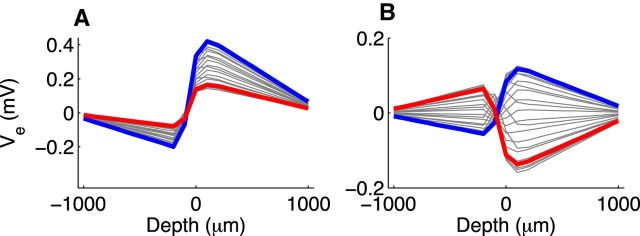
Our model, as is, does not replicate all features of the cycle-averaged in vivo data. For instance, the in vivo spatial profiles are asymmetric. At larger depths in this recording (more dorsolateral positions in the MSO), peak-to-trough amplitudes of the neurophonic tend to be larger for both ipsilateral and contralateral tones. One way to incorporate this asymmetry into the model is to assume that the current pathways to electric ground are not identical. When we made the extracellular resistance at positive depths half the value of the resistance at negative depths, the model produced similarly asymmetric spatial profiles (Fig. 6). Such an asymmetry in extracellular resistance could occur if dendrites are less tightly packed on one side of the MSO than the other. Asymmetries in the intracellular domain (e.g., differences in the lengths of ipsilateral and contralateral MSO dendrites or their conductance profiles) could also shape the spatial distribution of V_e.

Figure 6.

Spatial profile of simulated neurophonic response to 1200 Hz monaural pure tones using asymmetric extracellular resistivity. For these simulations only, extracellular resistivity between the end of the far dendrite (positive depth) and electric ground is half the value as the resistivity between the near dendrite (negative depth) and electric ground. A, Simulated neurophonic response for excitation on dendrite at negative depth. One cycle of the ongoing response (after transient effects caused by the initial resting state of the neuron model have disappeared). B, Same as in A with mean value removed at each spatial location. A is same format as Figure 5C2 and B is same format as Figure 5D2.

Another discrepancy evident in Figure 5 is that the polarity reversal in the model occurs over a narrower region (along the depth axis) than in the in vivo data. In the depth profiles (Fig. 5D2), the zero-crossings of the spatial profiles occur at nearly a single point for all times during the stimulus cycle. In contrast, the zero-crossings in the experimental profiles are more dispersed (Fig. 5A2; and, to a lesser degree, in Fig. 5B2). The location of the zero-crossing in the model is determined by the spatial distribution of current (i.e., the location of synaptic inputs, the morphology of the cell, and the profile of membrane conductance in the cell). A model that simulates the neurophonic as the combined activity of a spatially distributed population of MSO neurons with temporally jittered synaptic inputs would therefore produce a more dispersed region of zero-crossings. As a basic demonstration of this principle, Mc Laughlin et al. (2010) used a phenomenological “model, a collection of current dipoles, to show” that this aspect of the data may be the result of variability in the location and relative phases of the current sinks that generate the neurophonic. Our model requires complete temporal synchrony and spatial symmetry of the synaptic inputs, so we could not include this variability in the current framework.

In summary, despite some differences between the in vivo and simulated neurophonic, the computational model generates V_e responses that are consistent with the classical description of the neurophonic as a dipole field (Galambos et al., 1959) and that replicate important features of in vivo data. The spatiotemporal profile of the simulated neurophonic is a consequence of conservation of current and the spatial segregation of excitatory synapses on dendrites of bipolar MSO neurons. The sink associated with dendritic excitation (Fig. 4D) creates negative deflections of V_e. The compensatory current source, which is distributed across the neuron (as shown in Fig. 4E,F), creates the region of positive extracellular voltages.

Amplitude of neurophonic: effect of synaptic strength, packing density, and electrotonic length

For the comparison simulations of Figure 5, we reproduced features of the neurophonic using one set of parameter values (peak synaptic conductance 10 mS/cm² and extracellular radius 11 μm). Exact values are not available from available physiological data, so we investigated the range of V_e amplitudes that the model can produce when we vary these parameters.

We simulated neurophonic responses to a single monolateral excitatory input as we varied G_syn and the extracellular radius (Fig. 7, top row). Increasing G_syn increases the amount of current injected to the dendrite (Fig. 7D1). This stronger sink increases the maximum V_e amplitude (Fig. 7A1) as well as the maximum dendritic and somatic EPSPs (Fig. 7B1,C1). For our “control” extracellular radius of 11 μm (green) and these synaptic strengths, the maximum V_e amplitude covers a range of 1 mV, the maximum EPSPs cover a range of ∼50 mV in the dendrite and ∼15 mV in the soma, and the maximum synaptic currents cover a range of ∼4 nA. Amplitudes of physiologically realistic synaptic currents and EPSPs in cat MSO neurons are not known, but Couchman et al. (2012) reported that the average excitatory current per afferent fiber measured in gerbil MSO in vitro is 2.6 nA with 2–4 inputs necessary to evoke an action potential. The parameter values we use, therefore, are physiologically reasonable. With these reasonable parameter values, the model can produce the range of V_e amplitudes typically seen in vivo.

The simulated neurophonic amplitude also depends on the extracellular resistance. This depends, in turn, on the extracellular radius (see Materials and Methods). We repeated these simulations for two additional values of the radius of the extracellular virtual cylinder (10.5 and 20 μm), corresponding to a virtual cylinder with radius 5% or 100% larger than the soma.

A smaller radius of the extracellular virtual cylinder, which corresponds to denser packing of MSO neurons, generates substantially larger maximal V_e (blue). When the virtual cylinder radius was decreased to 10.5 μm, the amplitude of V_e reached 3 mV for the largest synaptic inputs tested. Expanding the radius of the virtual cylinder corresponds to less dense packing of MSO cells. This decreases the maximum amplitude of V_e (red). For a radius of 20 μm, the simulated neurophonic is smaller, and the maximum V_e amplitudes reaches at most a few hundred microvolts for large synaptic inputs.

These simulations indicate that postsynaptic currents in MSO can plausibly generate a neurophonic response in the hundreds of microvolts to millivolts scale, consistent with in vivo data. We note, however, that the amplitude of the simulated neurophonic responses represents an upper bound for a given parameter set. If the assumptions of perfect spatial symmetry of MSO neurons and temporal synchrony of synaptic inputs are significantly violated, we expect that the V_e amplitude would be reduced.

We next tested the effects of varying intracellular parameters that control the electrotonic length of the MSO neuron model. In Figure 7, row 2, we decreased (blue) and increased (red) the intracellular (axial) resistivity by 25% away from its “control” value of 200 Ωcm. In row 3, we similarly manipulated the total membrane conductance of the cell above and below its control value. In both cases, increasing the parameter value (red) increases the electrotonic length of the neuron: increased axial resistivity and membrane conductance lead to greater attenuation of EPSPs as they propagate to the soma (compare EPSP sizes in soma in Figure 7C). This is expected from the classical theory of passive cables that tells us that electrotonic length, and therefore EPSP attenuation, increases with the square root of axial resistivity and membrane conductance (Rall, 2011).

Parameters controlling the electrotonic length of the neuron model can also affect the distribution of membrane currents (i.e., sinks and sources) and thereby change the neurophonic. In particular, we observe that decreasing the intracellular resistivity increases V_e (Fig. 7A2, blue line). In contrast, the total membrane conductance appears to have little effect on V_e amplitude for these simulated synaptic inputs (Fig. 7A3).

High-frequency oscillations: necessity of fast synaptic kinetics

We have shown neurophonic responses that exhibit prominent, high-frequency oscillations (Fig. 3). Mc Laughlin et al. (2010) measured a neurophonic response at frequencies as high as 2500 Hz. Boudreau (1965) reported detectable oscillations in the neurophonic response for frequencies up to 4 kHz. These frequencies are well above the rhythms typically observed in local field potentials. Can postsynaptic currents in MSO neurons generate these high-frequency V_e oscillations? As we explain below, we found that fast synaptic kinetics are necessary for the model to generate high-frequency oscillations.

For each recording and simulation, we measured the maximum (over all recording sites) of the peak-to-trough difference of the cycle-averaged neurophonic. In this study, we only made comparisons between the model and data for pure tone frequencies >1000 Hz. At lower frequencies, the spatial profile of the neurophonic response measured in vivo does not always exhibit clear dipole-like features (Mc Laughlin et al., 2010). The reason for this is unclear and is a topic of ongoing investigation.

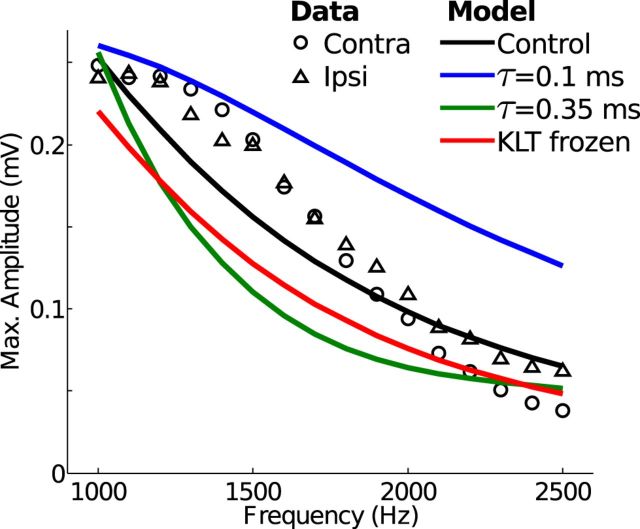
The maximum amplitude of recorded neurophonic responses to monaural pure tone stimuli (symbols in Fig. 8) is highest near 1000 Hz and decreases for higher stimulus frequencies. At 2500 Hz, the highest stimulus frequency used in these recordings, there is still a measurable oscillation. Simulated neurophonic responses using physiologically plausible parameter values show a similar trend (black line). The maximum amplitude decreases from ∼0.25 mV at 1 kHz to ∼0.05 mV at 2500 Hz.

Figure 8.

Maximum amplitude of oscillations in the neurophonic response to monaural pure tones (data) and monolateral trains of excitation (model). Maximum amplitude of oscillations is calculated as the maximum (over all recording depths) of the peak-to-trough change in voltage in one cycle of the cycle-averaged neurophonic response. In vivo neurophonic responses to contralateral (circles) and ipsilateral (triangles) tones compared with simulated neurophonic responses. In the “control” case of the model (black line), synaptic inputs have τ_syn = 0.2 ms and peak conductance G_syn = 10 mS/cm². Fast synaptic kinetics (blue) have τ_syn = 0.1 ms. Slow synaptic kinetics (green) have τ_syn = 0.35 ms, and peak conductance is tripled to maintain the amplitude of the response at 1 kHz. Red line indicates simulated neurophonic response when the low-threshold K⁺ conductance is “frozen” at its value for resting membrane potential.

Generating V_e oscillations in response to high stimulus frequencies is not trivial. The simulated neurophonic likely overstates the amplitude of high-frequency oscillations because we assumed complete temporal synchrony of synaptic inputs. Jitter of synaptic events would decrease the amplitude of oscillations in the neurophonic response, and this jitter (or loss of phase locking) increases relative to the stimulus period at higher frequencies (Joris et al., 1994a,b). Even with the assumption of perfect phase locking of synaptic inputs, we still found that the exceptionally fast synaptic kinetics found in MSO were necessary for the model to generate in vivo-like high-frequency oscillations. Fast synaptic kinetics (small τ_syn in Eq. 14) prevent temporal summation of the synaptic “sink” currents and thus maintain the amplitude of oscillations for high-frequency inputs. If, for example, we decrease the synaptic time constant from 0.2 ms to 0.1 ms (faster synaptic kinetics, blue), the model produces oscillations that exceed the in vivo amplitudes at all frequencies tested.

In contrast, slower synaptic kinetics (τ_syn = 0.35 ms, green) led to temporal summation of the synaptic sink currents; thus, oscillations in the simulated neurophonic attenuate at high frequencies. To maintain ∼0.25 mV amplitude oscillations in response to 1 kHz input trains (i.e., to match the in vivo amplitude at this stimulus frequency) for these slower synaptic events, we needed to increase the synaptic strength to G_syn = 30 mS/cm² (threefold increase). Despite this larger maximum synaptic conductance, the slower synaptic kinetics cause the amplitude of oscillations in the simulated neurophonic to decay substantially when we increase stimulus frequency >1 kHz. We tested slower synaptic time constants (results not shown) and found that if τ_syn was >0.4 ms, the simulated neurophonic response could not exceed ∼0.1 mV for 1 kHz inputs, even with additional increases of the peak synaptic conductance.

Fast synaptic kinetics appear to be necessary, therefore, for the simulated neurophonic to sustain oscillations in response to high stimulus frequencies. We wondered whether other specializations of MSO neurons contribute to this distinctive feature of the neurophonic. In addition to exceptionally fast synaptic kinetics, MSO neurons are remarkable for having low input resistance and fast membrane time constant (Scott et al., 2010). These properties are due, in part, to the presence of low threshold potassium (KLT) currents that are active for membrane potentials near rest (Svirskis et al., 2004). To investigate how the voltage-dependent dynamics of the KLT conductance contribute to simulated neurophonic responses, we froze the KLT conductance at the model's resting membrane potential.

When the KLT conductance is frozen, the model's resting membrane time constant is preserved, but the ability of the KLT current to rapidly repolarize the cell after an excitatory event is impaired (Day et al., 2008; Meng et al., 2012). We found that freezing the KLT dynamics slightly reduces the maximum amplitude of oscillations of the simulated neurophonic responses for all stimulus frequencies tested (compare red and black lines).

Freezing KLT leads to increased temporal summation of successive EPSPs and, consequently, sustained depolarization of the membrane potential in response to high-frequency synaptic inputs. This sustained depolarization decreases the driving force associated with each synaptic conductance because the membrane potential remains closer to the synaptic reversal potential. In response to 1500 Hz input trains, for instance, V_m at the synapse location depolarizes an additional ∼10 mV when KLT is frozen, thereby reducing the peak synaptic current by ∼20% compared with simulations with dynamic KLT. Freezing KLT decreases the total amount of synaptic “sink” current generated by each synaptic event and, as a consequence, decreases V_e amplitude at all frequencies tested. For larger synaptic inputs, the relative differences between dynamic and frozen KLT are larger.

Bilateral excitation: spatial profile of neurophonic depends on relative timing of synaptic events

The presumed generator of the neurophonic, the MSO, is an early stage of binaural processing that is exquisitely sensitive to interaural time differences (Goldberg and Brown, 1969; Yin and Chan, 1990). It is of considerable interest, therefore, to characterize the neurophonic for binaural, as opposed to monaural, stimuli. As we explain below, we find that the spatial profile of the simulated neurophonic changes depending on relative timing of synaptic events arriving on opposite dendrites.

In Figure 9, we show the spatiotemporal profile of the simulated membrane potential and neurophonic response to a bilateral 1 kHz train of excitatory inputs. We varied the time delay between onsets of the two synaptic inputs: 0.5 ms time difference (out-of-phase inputs, row A) and 0 ms (coincident inputs, row B). The left column shows the spatiotemporal pattern of membrane potential evoked by these input trains. Each synaptic event triggers an EPSP that spreads along the neuron. The greatest depolarization of the soma occurs when the two events are coincident. Maximum V_m in the soma is −54.4 mV in Figure 9A1 and −52.5 mV in Figure 9B1.

Figure 9.

Response of the model to 1 kHz bilateral excitatory inputs. Row A, Excitatory inputs arrive out of phase on the two dendrites (0.5 ms time difference). Row B, Excitatory inputs arrive in phase on the two dendrites (coincident inputs). A1, B1, Spatiotemporal profile of membrane potential. The ordinate represents the mediolateral or dendritic distance in micrometers, with 0 representing the soma. The abscissa is the time axis; it begins at 4 ms to show only the ongoing response. The black icon at left represents the dimensions of the neuron model. A2, B2, Spatiotemporal profile of the simulated neurophonic; note the change in scale on the ordinate from left column. A3, B3, Spatiotemporal profile of the simulated neurophonic with mean value removed from every spatial location. This mimics the 10 Hz high pass filter imposed by data acquisition system in experiments of Mc Laughlin et al. (2010).

The second column shows the simulated neurophonic for these two synaptic configurations. Figure 9A2 shows V_e in response to inputs that arrive out of phase on opposite dendrites (0.5 ms time difference). The V_e response can be understood as a sequence of dipole-like events. Each synaptic event generates a distribution of current sinks and sources that produces a dipole-like pattern in extracellular voltage similar to what was observed in previous (monolateral) simulations. The locus of the current sink (and the region of negative V_e) switches from one side of the neuron to the other as the site of excitatory synaptic current alternates between the two dendrites. There is some interaction between consecutive synaptic events: inputs to either dendrite generate positive V_e near the soma; thus, there is a sustained region of positive V_e near the soma. When the simulated results are “filtered” by removing the mean at each spatial location (Fig. 9A3), this central region of positive V_e disappears and the mean-zero V_e profile appears as two out-of-phase positive-negative going oscillations.

When the time difference between synaptic events is eliminated (row B), the simulated neurophonic does not exhibit these dipole features. In this case of coincident bilateral synaptic inputs, V_e is zero beyond the distal ends of the dendrites (Fig. 9B2). The simulated neurophonic for this synaptic configuration consists of spatially focused regions (near the neuron model) of positive V_e. The excitatory inputs create two current sinks located on opposite dendrites and a compensatory current source around the soma and proximal regions of the dendrites. For this configuration of synaptic inputs, the contribution of the current source dominates and only positive extracellular voltages are observed. Figure 9B3 shows the same neurophonic response after the filtering. The spatial profile remains localized near the neuron model, but an oscillation appears because of the requirement that the mean (over time) at each spatial location is zero.

The extracellular potential is zero beyond the distal ends of the model dendrites because of the symmetric arrangement of identical synaptic inputs and the assumption of a one-dimensional current path to ground. There can be no current flow along the one-dimensional path to ground (and, equivalently, no gradient in the extracellular voltage) unless there is some additional current sink/source present in the extracellular space. In a model including a 3D volume conductor, one would still expect substantial narrowing of the V_e spatial profile. The V_e response produced by the two dendritic sinks would have opposite polarity and would (nearly) cancel one another in the region of extracellular space extending beyond the ends of the dendrites.

These observations have a striking implication: we expect the spatial profile of the neurophonic to depend on the relative timing of bilateral synaptic excitation. In particular, the neurophonic response to out-of-phase inputs should be dipole-like and the response to coincident bilateral excitation should be narrow (not dipole-like). This is a nonintuitive finding: coincidence of inputs is generally thought to result in the highest output rate of MSO neurons. We are suggesting, therefore, that maximal MSO spike rates are associated with neurophonic responses with minimal spatial spread.

Binaural inputs: comparison of simulated and in vivo neurophonic

A binaural beat consists of two pure tones played to opposite ears with a slight frequency difference (Wernick and Starr, 1968; Kuwada et al., 1979; Mc Laughlin et al., 2010). Over the course of the beat period, these stimuli sample all possible interaural phase differences. The binaural beat stimulus, therefore, produces bilateral excitatory inputs to MSO neurons with time differences that depend on the phase of the binaural beat. We cannot, however, infer the relative timing of synaptic inputs directly from the interaural phase relation of the binaural beat stimulus because transmission times from the cochlea to the MSO may differ for inputs from the two ears.

We observed in Figure 9 that the spatial profile of the simulated neurophonic depends on the relative timing of bilateral synaptic inputs. On the basis of this insight obtained from our simulations, we expected to find interaural phases of the binaural beat for which the in vivo neurophonic response resembles a dipole-like field and other interaural phases for which the response is more spatially focused. We expected that these instances should be separated in time by half the beat period: out-of-phase synaptic inputs should generate dipole-like spatial distributions of V_e and coincident synaptic inputs should generate non-zero V_e in a spatially focused region. Indeed, we found such instances in the in vivo recordings, thereby validating our prediction.

In Figure 10, we show in vivo (Figure 10A–C) and simulated (Figure 10D,E) neurophonic responses to a binaural beat stimulus. The simulated results have been filtered to remove the mean at each spatial location. The binaural beat consisted of a 1200 Hz pure tone presented to the contralateral ear and a 1201 Hz pure tone to the ipsilateral ear. The 1 Hz interaural frequency difference produces a beat with a 1 s beat period. In Figure 10A–C, we show cycle-averaged responses presented in the format of Figure 5. As before, each line in the top row represents a different recording depth. Here, we have spaced adjacent V_e trajectories by 0.08 mV. Because of the 1 Hz frequency mismatch between the two tones, we could not cycle-average over the entire stimulus duration. Instead, we performed cycle-averaging (relative to the 1200 Hz frequency) over short time windows (50 ms) at different times within the binaural beat stimulus to sample the neurophonic locked to the carrier frequencies at the two ears for different interaural phase relationships.

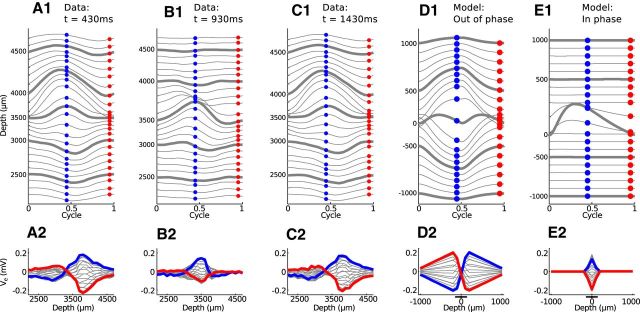
Figure 10.

Comparison of neurophonic response to 1200/1201 Hz binaural beat (A–C) and bilateral input trains (D,E). Top row, Cycle-averaged neurophonic responses plotted over one cycle at each recording depth. The vertical position of each trace is determined by its mean value and by a 0.08 mV offset between adjacent traces for clarity of presentation. Bottom row, Spatial profile of cycle-averaged neurophonic responses. The blue and red dots in the top panels form the blue and red spatial profiles in the bottom panels. Cycle-averaging was performed over a 50 ms time window. A, In vivo neurophonic response at t = 430 ms after stimulus onset. B, In vivo neurophonic response at t = 930 ms (half of the beat cycle after A). C, In vivo neurophonic response at t = 1.43 s (one beat cycle after A). D, Simulated neurophonic response for out-of-phase bilateral excitation. E, Simulated neurophonic response for in-phase bilateral excitation. Simulation results have been “filtered” by removing the mean (over time) at each spatial location to mimic the 10 Hz high pass filter of the in vivo data. A, C, Experimental data resemble simulations in D. B, Experimental data resemble simulations in E.

As discussed above, we expected the spatial profile of the neurophonic to change over the course of the beat period. We first found a temporal interval where the spatial profile resembled a dipole-like field. This is shown Figure 10A and is 430 ms after stimulus onset. The neurophonic response recorded 1 s later (one cycle later in the beat) is shown in Figure 10C. The responses in Figure 10A, C are nearly identical because the interaural phase of the binaural beat stimulus is the same at these two instants. The inputs to the two ears are nearly out of phase at these times (0.43 interaural phase difference). This does not, however, necessarily imply that inputs to MSO neurons also arrive out of phase because transmission delays along the auditory pathway may alter their relative timing.

These neurophonic responses resemble the dipole-like patterns observed in response to monaural stimulation, both in the cycle-averaged trajectories (top panels) and in the spatial profiles (bottom panels) (compare withFig. 5A). From our simulations of bilateral inputs, we infer that these responses come at a time during the binaural beat when synaptic inputs on opposite dendrites arrive out of phase with one another (Fig. 9A3). We simulated this synaptic configuration, bilateral excitation with a half-cycle phase difference (∼0.417 ms time difference), and display the resulting V_e response in Figure 10D. The simulated neurophonic exhibits a dipole-like pattern that is qualitatively similar to the in vivo neurophonic (Fig. 10A,C).

The similarity between the spatial profiles of the in vivo and simulated V_e suggest that synaptic inputs are arriving out of phase at the instants we selected in Figure 10A, C. If this is the case, then we expected on the basis of our simulation results that the neurophonic in an intermediate time window would represent the response to coincident synaptic inputs. In other words, we expected to observe a more spatially focused V_e response 930 ms after stimulus onset (half the beat period after Fig. 10A and half the beat period before Fig. 10C).

Figure 10B confirms this prediction. The spatial profile of the in vivo neurophonic (Fig. 10B2) does not resemble a dipole-like pattern. Instead, the dominant feature is an oscillation centered near the 3500 μm recording depth. Simulation results for coincident inputs show a similar spatially narrow oscillation (Fig. 10E). The model underestimates the spread of the neurophonic (V_e is 0 mV beyond the ends of the dendrites of the neuron model) but produces a spatiotemporal profile that is similarly characterized by a central oscillation.

The time at which the in vivo neurophonic response appears spatially localized (Fig. 10B) is 930 ms after the onset of the binaural beat. This corresponds to an interaural time difference of ∼58 μs (contralateral leading). If our interpretation is correct, then this is also the time when synaptic inputs to the local population of MSO neurons generating the neurophonic are coincident. Coincident inputs drive maximum firing rates in MSO neurons, so 58 μs (contralateral leading) would be the predicted best delay of the local population of neurons generating the neurophonic. We cannot verify this prediction without recordings that isolate single-unit activity, but we note that this best delay is well within the range of values observed in MSO neurons of the cat (Yin and Chan, 1990).

Do binaural responses resemble the sum of monaural responses?

Our computational model consists of a soma, two dendrites, passive membrane currents, and voltage-gated subthreshold currents (I_h and I_KLT). It does not include spike-generating sodium currents, nor does it include an axon and initial segment. A consequence of this simplification is that the model does not generate spikes in response to coincident bilateral inputs. Indeed, as we will see in Figure 11, there is little difference between the spatiotemporal pattern of V_e produced by the model in response to bilateral inputs and sum of responses to the same inputs presented monolaterally. To verify that this is not an unreasonable simplification, we also compared the in vivo neurophonic response to binaural stimuli to the sum of responses to the corresponding sounds presented separately to the two ears.

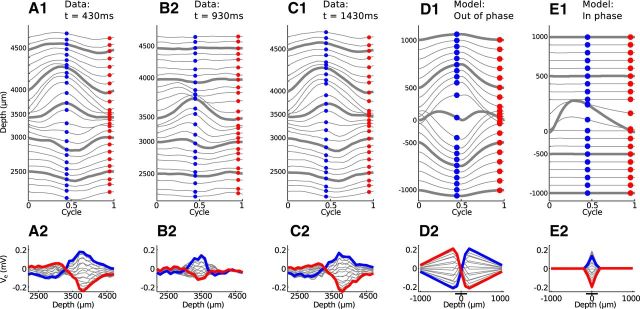
Figure 11.

Comparison of summed monaural neurophonic responses. Figure format is the same as in Figure 10. A–C, In vivo data are sum of response to 1200 Hz contralateral tone and 1201 Hz tone in ipsilateral ear. D, E, Simulations are sum of monolateral responses to 1200 and 1201 Hz input trains. Similarity between these figures and Figure 10 shows neurophonic responses to binaural stimuli resemble the sum of responses to corresponding monaural stimuli.

To visualize this comparison, we repeated the simulations and analysis from the previous section, by taking the sum of responses to 1200 Hz and 1201 Hz pure tones presented monaurally in experiments and monolaterally in the simulations. Figure 11 shows the resulting temporal and spatial profiles of the summed neurophonic responses (format identical to Fig. 10). For these example data (Fig. 11A–C) and simulations (Fig. 11D,E), the sum of responses to monaural stimuli is nearly indistinguishable from the responses to binaural stimuli in Figure 10. The in vivo neurophonic responses share the “linear” property of the model. Spiking activity in MSO neurons is typically nonlinear: spike counts evoked by binaural inputs at favorable interaural delays are larger than the sum of spike counts evoked by monaural inputs (Yin and Chan 1990, van der Heijden et al., 2013). Because the binaural neurophonic recordings presented here do not differ substantially from the sum of monaural responses, there are no obvious indications that MSO spiking activity contributes to the cycle-averaged in vivo neurophonic responses.

Contributions of inhibition to the neurophonic

Up to this point, we have shown that the spatial arrangement, dynamics, and timing of excitatory inputs can explain spatiotemporal features of neurophonic responses recorded in vivo. MSO neurons also receive inhibitory inputs (targeted to the soma), so we explored their contributions to the neurophonic. Simulated responses to 1 kHz trains of monolateral excitation and somatic inhibition show that inhibition hyperpolarizes the neuron model's membrane potential (Fig. 12A) and leaves the dipole-like spatial profile of V_e intact (Fig. 12B). Inhibition is slow relative to the 1 kHz stimulus frequency. Consequently, the contributions of inhibition to the V_e response can be difficult to detect when the DC component of V_e is removed to mimic the low pass filtering in our neurophonic recordings (Fig. 12C). Indeed, the DC-removed simulation results, including inhibition (Fig. 12C), are nearly identical to simulations without inhibition (compare withFig. 4C).

The contributions of inhibition to the simulated neurophonic are subtle, but they can be substantial (when DC is not removed). In Figure 12D, we show the difference between V_e evoked by monolateral excitation and somatic inhibition and V_e evoked by excitation alone (i.e., the difference between Figs. 12B and 4B). Inhibition increases V_e near the soma by ∼0.3 mV (approximately doubling the amplitude) in these simulations. In addition, the amplitude of the neurophonic increases by ∼25% in the regions of extracellular space beyond the ends of the neuron model's dendrites (more positive V_e in the upper half of the figure and more negative V_e in the lower half).

V_e increases near the soma because inhibition is an outward current (source). Indeed, if somatic inhibition were the only input to the cell, then V_e would be positive near the soma and zero beyond the ends of the neuron model's dendrites (Fig. 13A, blue). Somatic inhibition creates a symmetric distribution of membrane current (source in the soma, sinks in the dendrites). As we discussed with regard to coincident bilateral inputs, symmetric distributions of membrane current generate V_e profiles that do not extend beyond the ends of the neuron model. This localized contribution of inhibition to the V_e response cannot, therefore, account for the increased spatial reach of V_e.

In fact, excitation and inhibition interact so that the neurophonic response to excitation and inhibition is not simply the linear sum of the responses to excitation alone and inhibition alone (Fig. 13A, compare green and black). Inhibition makes a local contribution to the spatial distribution of V_e as an outward current in the soma, and it also acts indirectly to increase the amount of excitatory synaptic current entering the dendrite. Inhibition targets the soma, but its hyperpolarizing effect on membrane potential spreads into the dendrites (Fig. 12A). Near the site of the excitatory synapse, this hyperpolarizing effect increases the driving force for excitation (membrane potential is further from the reversal potential for excitation). Figure 13B shows the net membrane current in the near dendrite for excitatory and inhibitory inputs (black) compared with the net membrane currents combined from simulations with excitation alone and inhibition alone (green). Inhibitory synaptic currents do not enter the near dendrite directly, but the interplay of excitation and inhibition increases the net inward membrane current. This strengthens the effective sink in the near dendrite and increases the spatial spread of V_e.

Discussion

Summary of main findings

An essential challenge in neuroscience is to understand the coordinated activity of neural populations and circuits in vivo. Local field potentials provide windows into neural activity, but how can meaningful conclusions be drawn from these data? Our approach balances mechanistic detail with reasoned abstraction. We argued that the spatial arrangement of MSO neurons, their bipolar morphology, and the timing of synaptic inputs are sufficiently regular to justify an idealization. We envisioned a local subpopulation of MSO neurons with spatial symmetry and temporally synchronized synaptic inputs. Based on these assumptions, we formulated a one-dimensional description that coupled intracellular and extracellular domains of a “representative” MSO neuron.

The model reproduces the spatiotemporal patterns of recorded neurophonic responses. The simulated V_e has dipole-like characteristics similar to in vivo neurophonic responses to monaural stimuli (Fig. 5) and provides important insights (e.g., that in-phase binaural inputs generate spatially contracted V_e profiles) (Fig. 10). We expect that these spatiotemporal features would be present in more detailed descriptions without perfect symmetry and synchrony.

Several notable observations emerge. First, the coordinated activity of bipolar neurons can produce a V_e response with millimeter-scale spatial reach even though the neurons are only hundreds of micrometers across. Second, coincident bilateral inputs evoke narrow V_e spatial profiles even though these inputs are expected to evoke maximal MSO firing (Fig. 9). We observed such spatial contraction in the in vivo data (Fig. 10). Third, fast synaptic kinetics are essential for the neurophonic to exhibit prominent oscillations in response to high-frequency stimuli (Fig. 8). Fourth, inhibition increases V_e near the soma and its spatial reach (Figs. 12 and 13). We predict that, if inhibition were blocked (as in Brand et al., 2002), the neurophonic response would decrease even though spiking activity should increase.

MSO neurons as generators of the neurophonic

Early investigators hypothesized that postsynaptic currents in MSO neurons are the likely generators of the neurophonic (Galambos et al., 1959; Biedenbach and Freeman, 1964; Moushegian et al., 1964; Tsuchitani and Boudreau, 1964; Clark and Dunlop, 1968). They observed “dipole-like” spatial profiles of extracellular voltage in response to monaural tones and clicks. They reasoned that synaptic inputs to one dendrite of a bipolar MSO neuron would generate these spatial profiles of extracellular voltage. Mc Laughlin et al. (2010) provided empirical support for this classical, conceptual theory by using current source density analysis to ascertain the spatial distribution of putative generators of the neurophonic.

Our results bolster this consensus understanding of the neurophonic. Although we did not seek to “fit” simulation results to particular data traces, our findings are quantitative insofar as we used a biophysically based MSO model (Mathews et al., 2010) and made reasonable estimations of neural and extracellular parameters. For the parameter values used, the simulations provide an upper bound estimate of the neurophonic. Deviations from the assumptions of spatial symmetry of MSO neurons and temporal synchrony of synaptic inputs and membrane currents would reduce the amplitude of the simulated V_e.

Our model, a simplified, one-dimensional description, renders tractable a complicated 3D problem. Inevitably, this approach leaves out biophysical details that, although of apparently little consequence in accounting for the qualitative and semiquantitative features we have described, may be important for answering some questions. For example, we use deterministic synaptic inputs that are identical on both dendrites and periodic. The model, therefore, is not meant to reproduce any of the observed variability and fluctuations in the experimentally recorded neurophonic (visible in Fig. 3) or possible differences in contralateral and ipsilateral synaptic inputs (Jercog et al., 2010).

Simulated and cycle-averaged responses to binaural stimuli appear to match the sum of responses to monaural stimuli (compare Figs. 10 and 11). There is little evidence in our analysis, therefore, that MSO spikes and back-propagating action potentials (both absent from the model) and other nonlinear mechanisms (such as voltage-gated potassium currents) alter this apparently linear property of the neurophonic. This observation parallels recent work in the barn owl. Kuokkanen et al. (2010) concluded that postsynaptic spikes in the nucleus analogous to the MSO do not contribute appreciably to the neurophonic.

Available MSO physiological data support the negligible contribution of spikes to V_e: action potential back-propagation in MSO neurons is weak in vitro (Scott et al., 2007), and somatic sodium channels are substantially inactivated near the resting potential (Svirskis et al., 2004; Scott et al., 2010). Previous studies of the neurophonic in cat (Caird et al., 1985) and barn owl (Sullivan and Konishi 1986; Kuokkanen et al., 2013), as well as juxtacellular recordings in gerbil MSO (van der Heijden et al., 2013), also found that responses to binaural stimuli resemble the sum of responses to corresponding monaural stimuli, but note that Wernick and Starr (1968) reported some differences. Axons, spike-generating currents, and other biophysical details could be included in future studies. See, for instance, work on cortical field potentials using morphologically detailed neuron models (Lindén et al., 2011; Fernández-Ruiz et al., 2013; Reimann et al., 2013).

Signatures of MSO biophysics in the neurophonic

Our biophysically based model enabled us to establish connections between cell-level dynamics of MSO neurons and population-level V_e. These insights are particularly valuable for the MSO because single unit in vivo electrophysiology is notoriously difficult in this nucleus, in part because the neurophonic masks spiking activity. Juxtacellular and intracellular whole-cell in vivo data have only recently been reported (Franken et al., 2013; van der Heijden et al., 2013). In the absence of a large corpus of intracellular or even extracellular data, debates continue regarding the distribution of interaural delays (McAlpine and Grothe, 2003; Joris and Yin, 2007) and the kinetics and timing of inhibition (Brand et al., 2002; Grothe, 2003; Zhou et al., 2005; Pecka et al., 2008; Roberts et al., 2013) and excitation (Jercog et al., 2010; Roberts et al., 2013). Systematic theory-based analyses of the neurophonic, a more accessible in vivo data source, may offer new perspectives on these puzzles and provide a bridge between in vivo data obtained in larger species (cat, dog, monkey) and small-headed rodents (gerbil, guinea pig, chinchilla).

Features of the neurophonic can impose stringent requirements on the generators of these fields. For instance, how can neurophonic responses follow pure tone stimuli at frequencies of several kilohertz (Boudreau 1965; Mc Laughlin et al., 2010), much higher than observed in cortical local field potentials? We showed that remarkably fast excitatory synapses, as exist in the MSO (Golding and Oertel, 2012), are necessary (Fig. 8). Submillisecond synaptic time scales also exist in the brainstem of barn owls where intracellular and extracellular voltages oscillate at high frequencies (several kilohertz) (Funabiki et al., 2011; Ashida et al., 2013).

We also found signatures in the simulated neurophonic of inhibition and the voltage-gated KLT. These currents increase the simulated neurophonic's amplitude (Figs. 8 and 12). Inhibition is a source current that increases V_e locally near the soma, and it enhances excitatory (sink) currents by hyperpolarizing the neuron model's membrane potential. KLT helps to rapidly repolarize the membrane potential between synaptic events and thus maintains the driving force of the excitatory (sink) current. Pharmacological manipulations of these currents could provide additional evidence of how they shape the neurophonic.

Wider relevance

Our idealized approach cannot be applied universally because symmetry and synchrony are not ubiquitous. Nonetheless, some brain regions can be identified that possess their own characteristic spatial symmetry (olfactory bulb: Rall and Shepherd, 1968; cerebellum: Nicholson and Llinas, 1971). Rall and Shepherd's (1968) foundational use of symmetry and synchrony motivated our modeling approach. Their achievement, predicting the existence of dendro-dendritic synapses in the olfactory bulb, argues convincingly that idealized models can provide deep insights into the origins and interpretation of extracellular signals.

The avian auditory brainstem also exhibits a prominent, sound-evoked neurophonic as in cat (Sullivan and Konishi, 1986; Wagner et al., 2009). Neurons in the nucleus laminaris, the avian analog of the MSO, are bipolar and spatially ordered in chickens (Smith and Rubel, 1979). But in most regions of the barn owl nucleus laminaris, neurons have short dendrites with no orderly spatial arrangement (Carr and Boudreau, 1993). Interestingly, despite basic similarities in the barn owl and mammalian neurophonics, the underlying neural generators are thought to be different. Kuokkanen et al. (2010, 2013) argue that the excitatory afferent terminals onto the nucleus laminaris are the dominant generators of the neurophonic in barn owl. Comparative studies of the neurophonic across species and brain regions could prove a fruitful avenue of future research.

Field potentials are a means to bridge human electrophysiology and animal single-unit physiology. There is an ongoing controversy regarding the neuroanatomical origin of binaural components in brainstem potentials measured at the scalp in humans or animals. The response to binaural stimulation is invariably smaller than the sum of the responses to either ear, and its generators are generally thought to be in the lateral superior olive (Goksoy et al., 2005; Riedel and Kollmeier, 2006), where cells are inhibited from one ear and excited from the other. However, lesion studies in the cat have indicated the MSO as a more likely source than the lateral superior olive (Sontheimer et al., 1985; Melcher, 1996). Our results suggest that these seemingly conflicting results can be reconciled by considering the spatial contraction of V_e evoked by coincident stimulation of the MSO, which may explain smaller potentials recorded, at a distant location, binaurally than summed monaurally.