Voxel-based clustered imaging by multiparameter diffusion tensor images for glioma grading

Abstract

Gliomas are the most common intra-axial primary brain tumour; therefore, predicting glioma grade would influence therapeutic strategies. Although several methods based on single or multiple parameters from diagnostic images exist, a definitive method for pre-operatively determining glioma grade remains unknown. We aimed to develop an unsupervised method using multiple parameters from pre-operative diffusion tensor images for obtaining a clustered image that could enable visual grading of gliomas. Fourteen patients with low-grade gliomas and 19 with high-grade gliomas underwent diffusion tensor imaging and three-dimensional T1-weighted magnetic resonance imaging before tumour resection. Seven features including diffusion-weighted imaging, fractional anisotropy, first eigenvalue, second eigenvalue, third eigenvalue, mean diffusivity and raw T2 signal with no diffusion weighting, were extracted as multiple parameters from diffusion tensor imaging. We developed a two-level clustering approach for a self-organizing map followed by the K-means algorithm to enable unsupervised clustering of a large number of input vectors with the seven features for the whole brain. The vectors were grouped by the self-organizing map as protoclusters, which were classified into the smaller number of clusters by K-means to make a voxel-based diffusion tensor-based clustered image. Furthermore, we also determined if the diffusion tensor-based clustered image was really helpful for predicting pre-operative glioma grade in a supervised manner. The ratio of each class in the diffusion tensor-based clustered images was calculated from the regions of interest manually traced on the diffusion tensor imaging space, and the common logarithmic ratio scales were calculated. We then applied support vector machine as a classifier for distinguishing between low- and high-grade gliomas. Consequently, the sensitivity, specificity, accuracy and area under the curve of receiver operating characteristic curves from the 16-class diffusion tensor-based clustered images that showed the best performance for differentiating high- and low-grade gliomas were 0.848, 0.745, 0.804 and 0.912, respectively. Furthermore, the log-ratio value of each class of the 16-class diffusion tensor-based clustered images was compared between low- and high-grade gliomas, and the log-ratio values of classes 14, 15 and 16 in the high-grade gliomas were significantly higher than those in the low-grade gliomas (p < 0.005, p < 0.001 and p < 0.001, respectively). These classes comprised different patterns of the seven diffusion tensor imaging-based parameters. The results suggest that the multiple diffusion tensor imaging-based parameters from the voxel-based diffusion tensor-based clustered images can help differentiate between low- and high-grade gliomas.

Highlights

• •We have developed a novel unsupervised method for voxel-based clustered imaging.
• •Each class ratio in clustered images differentiated high from low-grade gliomas.
• •The 16-class clustered images showed the best performance for the differentiation.
• •Each class comprised different patterns of the seven diffusion tensor-based features.
• •Multiple parameters from diffusion tensor images are useful for glioma grading.

1. Introduction

Gliomas are the most common primary neoplasms of the central nervous system (CNS), and are classified according to a grading system, commonly that of the World Health Organization (WHO), on the basis of their histological appearance. Tumour grading is an important factor that influences the choice of therapy, such as adjuvant radiation and chemotherapy (Louis et al., 2007b).

Patients with low-grade gliomas (LGGs) (WHO grade II) may live for a long time, and the 5-year survival rate is 42%–92% (Sanai and Berger, 2008). In contrast, patients with high-grade gliomas (HGGs) (WHO grades III and IV) have a worst prognosis of brain tumours (Law et al., 2006); particularly, glioblastoma (WHO grade IV) develops rapidly (Ohgaki and Kleihues, 2007), and the 5-year survival rate is only 2% (McLendon and Halperin, 2003). Therefore, patients with HGGs need to be treated as soon as possible and more aggressively with chemotherapy and radiation. Thus, it is important to accurately classify gliomas into low or high grades to provide the best treatment for patients.

Magnetic resonance imaging (MRI) is essential for non-invasively diagnosing the existence, extent and characteristics of brain tumours. Different MRI sequences are used for evaluation and include T1-weighted image (T1WI), contrast-enhanced T1-weighted image (T1WIce), T2-weighted image (T2WI), diffusion-weighted imaging (DWI) and fluid-attenuated inversion-recovery (FLAIR) sequences. The images can provide much information about tumours, such as tumour morphology, the presence of enhancement, intra-tumoural haemorrhage or peri-tumoural oedema and can be helpful to predict tumour grade. The presence of contrast enhancement is often regarded as a sign of malignancy. Watanabe et al. reported that enhancement was present in 11 of 12 HGGs in their study, and histological examination revealed that areas of enhancement were related to neovascularity in tumour tissue or tumour cell infiltration (Watanabe et al., 1992). However, it was also reported that 9% of malignant gliomas lacked enhancement and 48% of LGGs were enhanced (Scott et al., 2002). These studies suggested that T1WIce was less useful than expected for prediction of glioma grade. Furthermore, gadolinium-based contrast agents, which are typically used in MRI, can cause side effects. Acute reactions after injection of gadolinium may cause flushing and nausea as minor reactions and hypotension and bronchospasm as intermediate reactions. In addition to these side effects, severe reactions are all symptoms of minor and intermediate reactions and sometimes cause cardiac arrest (Thomsen, 2003). Thus, T1WIce cannot be used for definitive pre-operative glioma grading because of insufficient information or side effects.

Some previous studies have used other MRI sequences without contrast agents, including diffusion tensor imaging (DTI), for glioma grading. Diffusion is sensitive to water movement, particularly along axonal fibres. DTI provides useful information about diffusion measurements and enables calculation of several parameters from DTI. Because tumour cells of gliomas mainly invade along white matter tracts (Scherer, 1938), we believe that DTI is a potentially useful sequence because of its sensitivity to white matter abnormalities (Filippi et al., 2001). Fractional anisotropy (FA) and apparent diffusion coefficient (ADC) calculated from DTI are more sensitive indicators of the integrity of white matter and tumour infiltration than are T1WI or T2WI (Price et al., 2003). Thus, DTI parameters can have an important role in the assessment of tumours. It has been reported that compared with white matter, HGGs show a mixture of hyper- and iso-intensities in DWI (Tien et al., 1994; Stadnik et al., 2001). One study found that lower ADC values corresponded to increased cellularity and HGGs (Kao et al., 2013). However, another study found no significant difference in ADC values between LGGs and HGGs (Lam et al., 2002). The FA values of LGGs were significantly lower than those of HGGs (Inoue et al., 2005; Kao et al., 2013), whereas another study showed low FA ratios in the tumour centres of both LGGs and HGGs (Goebell et al., 2006). These previous studies suggest that glioma grading with a single parameter of MRI remains controversial.

Recently, a pattern recognition method using multiple parameters has been applied to predict tumour grading. In a study, support vector machine (SVM), which is a widely used supervised machine-learning method because of its remarkable performance of classification, was applied and involved 161 features extracted from manually defined regions of interest (ROIs) on T1WI, T1WIce, T2WI, FLAIR and perfusion MRI using a contrast agent, and a combination of multiple features that differentiated HGGs and LGGs with an accuracy of 87.8%, sensitivity of 84.6% and specificity of 95.5% was reported (Zacharaki et al., 2009). Another study used a self-organizing map (SOM) based on a competitive learning algorithm, which is a type of neural network unsupervised learning, with seven features extracted from wavelet-filtered ADC, ADC, FLAIR and T2WI for each voxel (Vijayakumar et al., 2007). SOM was labelled for seven tissue classes, including low- and high-grade tumours, in a supervised manner using 700 voxel-based training pattern vectors. Although the sample size was small (four patients with low- and six with high-grade tumours), the method differentiated low-grade tumour from other tissues, with a sensitivity of 88% and a specificity of 98%, and high-grade tumour from other tissues, with a sensitivity of 87% and a specificity of 93%. Although pattern recognition methods with multiple parameters and a supervised manner can be useful for prediction of tumour grading, they have some problems in clinical applications. In voxel-based labelling, because it is impossible to examine the pathology of each voxel, supervised voxel-based labelling can be inaccurate and cause rater bias. Furthermore, complicated features make it difficult to determine the most sensitive parameter for characterizing grading. Therefore, a pattern recognition method with multiple uncomplicated parameters without supervised information can be helpful to predict glioma grade. Furthermore, SOM is well-known to its visualization and would help to lead to a novel classification.

This study aimed to develop a new method using multiple DTI-based parameters for voxel-based clustered images in an unsupervised manner that can be used to visually grade gliomas. We also determined if the method is really helpful for pre-operative prediction of glioma grade in a supervised manner.

2. Materials and methods

2.1. Subjects

We retrospectively reviewed 111 patients who were aged 6–87 years and had newly diagnosed and histologically confirmed diffusely infiltrative gliomas, defined according to the WHO classification (Louis et al., 2007a), between March 2010 and June 2013 in Kyoto University Hospital. We classified grade II as LGG (n = 36) and grades III and IV gliomas as HGG (n = 75) in this study. Patients with LGGs had 22 diffuse astrocytomas, eight oligodendrogliomas, four oligoastrocytomas and two mixed oligoastrocytoma. Patients with HGGs had 17 anaplastic astrocytomas, three anaplastic oligoastrocytomas, two anaplastic oligodendrogliomas and 53 glioblastomas. Among these patients, 51 underwent DTI and magnetization-prepared rapid gradient-echo (MP-RAGE). We excluded 13 patients who had undergone previous tumour resections or exposures to radiotherapy or chemotherapy prior to DTI acquisition. We also excluded three patients whose tumours were located around the temporal basal regions that were severely influenced by distortions of DTI (Mangin et al., 2002) and one patient because of appreciable motion artefacts in MP-RAGE. We excluded one patient <12 years of age because FA values in the frontal white matter are significantly lower in children aged 8–12 years than in adults because of less myelination in children (Klingberg et al., 1999). Consequently, 33 patients (22 men, 11 women) were enrolled in the study. Thirty-two patients had undergone tumour resections, and one had only undergone a biopsy. Twenty-one tumours were located in the frontal region, seven in temporal, two in parietal, one in occipital and two in frontoparietal (Table 1). This study was approved by the Ethics Committee of the Kyoto University Graduate School of Medicine (C 570), and written informed consent was obtained from all patients.

Table 1.

Summary of patient data.

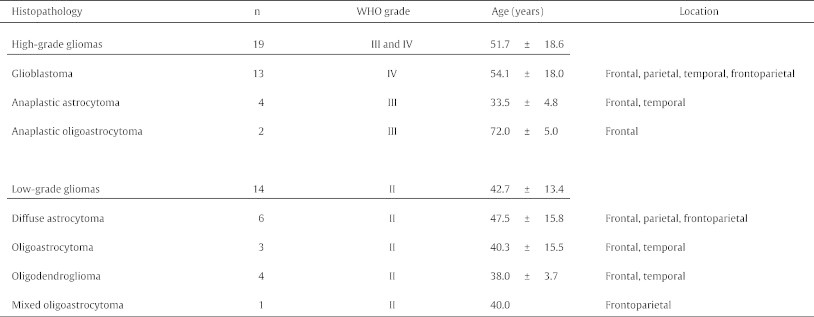
Age (years) is given as means ± standard deviation.

2.2. MRI data acquisition and pre-processing

MRI images were scanned on a 3 Tesla Trio (Siemens, Erlangen, Germany) equipped with an eight-channel phased-array head coil.

DWI in an axial orientation used the following parameters: repetition time = 10,500 ms; echo time = 96 ms; flip angle = 90°; field of view = 192 × 192 mm; slices = 70; and voxel size = 2 × 2 × 2 mm. Diffusion weighting was isotropically distributed along 81 directions by using a b-value of 1500 s/mm² (Jones et al., 1999). Nine volumes with no diffusion weighting (b = 0 s/mm²) were also acquired at points throughout acquisition. A set of diffusion-weighted data was acquired during a scanning time of approximately 18 min.

MP-RAGE using the following parameters was used to acquire three-dimensional T1-weighted anatomical images: repetition time = 2000 ms; echo time = 4.38 ms; flip angle = 8°; field of view = 176 × 192 mm; slices = 160; and voxel size = 1 × 1 × 1 mm. A dual-gradient field map in an axial orientation was also obtained by using the following parameters: repetition time = 511 ms; echo time 1/echo time 2 = 5.19/7.65 ms; flip angle = 60°; field of view = 192 × 192 mm; slices = 46; and voxel size = 3 × 3 × 3 mm.

DTI data were analysed using FSL [FMRIB Software Library v5.0.2.2, http://www.fmrib.ox.ac.uk/fsl (Smith et al., 2004)]. The data were corrected for eddy currents and head motion using affine registration to the first b = 0 reference volume. The data were also corrected for geometric distortions occurring in an echo planar image (EPI) (Jezzard and Balaban, 1995) by FUGUE, which is a part of the FSL tool for EPI correction of distortions caused by static magnetic field inhomogeneities (Jenkinson et al., 2012). Field inhomogeneities were measured by using a field-map image, and EPI was unwarped according to field-map data. Seven features, including DWI, FA, first eigenvalue (L1), second eigenvalue (L2), third eigenvalue (L3), mean diffusivity (MD) and raw T2 signal with no diffusion weighting (S0), were extracted from DTIs using the FMRIB's diffusion toolbox (FDT) program (Smith et al., 2004). The diffusivities derived from DTI measurements were separated into components parallel (L1) and perpendicular (L2 and L3) to the white matter tract. These components are referred to as MD, (L1 + L2 + L3)/3. FA, which assigns values between 0 and 1, represents how strongly water diffuses in the direction of the principal eigenvector (Holodny et al., 2001).

2.3. Feature extraction for clustering

The overview of the processing pipeline in the study is depicted in Fig. 1. The summary is as follows:

• 1Feature extraction from DTI.
• 2Clustering using SOM followed by K-means (KM).
• 3Visualization of whole brain images by diffusion tensor-based clustering images (DTcIs).
• 4Classification using DTcIs by SVM.

Fig. 1.

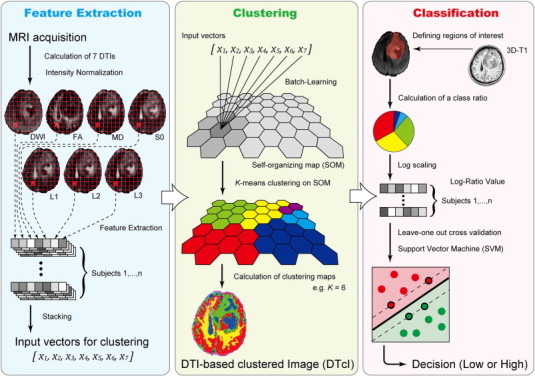
Simplified graphical overview of the processing pipeline.

Features for unsupervised clustering were extracted from voxels on the seven intensity-normalized diffusion tensor images sampled at every 64 (4 × 4 × 4) voxels within the binary mask image obtained by FSL's Brain Extraction Tool (BET). The number of extracted features was 3552 ± 315 (mean ± SD) for each subject. The features of all subjects were then stacked and used for input vectors defined as T = {b_m,1 ≤ m ≤ n}, where b_m is the mth vector and n is the number of vectors (117,232 in the study). The individual input vector (b_m) is defined as b_m = [x₁,x₂,x₃,x₄,x₅,x₆,x₇], where x₁,…,x₇ are components of the input vector. The components of each input vector (b_m) were extracted from DWI, ADC, MD, S0, L1, L2 and L3 images in the study.

2.4. Unsupervised clustering

The extracted feature vectors were used for calculating voxel-based clustered images. We applied the two-level clustering approach of SOM (Kohonen, 1995) and the KM algorithm (MacQueen, 1967) for unsupervised clustering (Fig. 1). First, a large number of input vectors were clustered into a much larger than the expected number of clusters, defined as ‘protoclusters’, by SOM. Then, the protoclusters were classified into the expected number of clusters, defined as ‘clusters’, by KM. The KM algorithm is a popular partition algorithm for clustering. Similar two-level clustering approaches have been reported (Chuang et al., 1999; Vesanto and Alhoniemi, 2000; Thomassey and Happiette, 2007) and applied in the fields of medicine (Wang et al., 2002) and others (Beccali et al., 2004; Lu et al., 2006). The two-level clustering approach has the following two important benefits compared with the KM algorithm, which is one of the most famous and effective unsupervised clustering approaches: One is noise reduction. It is known that the KM algorithm is very sensitive to outliers (Velmurugan and Santhanam, 2010). Because protoclusters are local averages of the input vectors and outliers can be filtered out, they are more robust to outliers than are the original vectors. The other is the reduction of the computational cost. Furthermore, the two-dimensional arrangement of the larger protoclusters by SOM can be easily visualized, thus, providing useful information about the features (Jin et al., 2004).

2.4.1. Unsupervised clustering: SOM

SOM is based on a competitive learning algorithm, which is a type of neural network unsupervised learning. It typically comprises hexagonal and two-dimensional grids of map units (also called neurons) defined as H = {w_i; 1 ≤ i ≤ K × L}. Here, K and L are the numbers of columns and rows, respectively, w_i represents the weight vectors assigned to the ith unit of the SOM architecture, defined as w_i = [v₁,…,v_d], where d is the dimension of the weight and v₁,…,v_d are components of the weight vector. The dimension of the weight vector was seven in this study.

A major problem in the standard sequential SOM algorithm is that the results differ according to the input order. Therefore, the batch-learning algorithm for the SOM (batch-learning self-organizing map; BLSOM) (Kohonen, 1995) was used in the study. The results by BLSOM are consistent because its learning does not depend on the input order. Other advantages of BLSOM compared with the standard sequential SOM are that no learning rate has to be specified by the user of the algorithm and convergence of the input vectors is faster towards their final values (Brugger et al., 2008). The following algorithm was used for BLSOM:

• 1Initialize the weight vectors w_i(0) of all map units.
• 2Calculate the Voronoi sets V_i(t) = {b | d(b_j, w_i(t)) < d(b_j, w_k(t))∀_k≠i} and the sums $s_i\left(t\right)=\sum _{j=1}^{\left|V_i\left(t\right)\right|}{b}_j$.
• 3Update the weight vectors according to $w_i\left(t+1\right)=\sum _j{h}_{ij}\left(t\right)s_j\left(t\right)/\sum _j\left|V_i\left(t\right)\right|h_{ij}\left(t\right)$.
• 4Repeat steps 2 and 3 until a predefined number of steps τ.

Here, w_i(t) is a weight vector in the tth step and h_ij(t) is the neighbourhood function defined by h_ij(t) = exp(−r_i − r_j²/2σ²(t)), where r_i and r_j are the ith and jth units of the SOM architecture, respectively, r_i − r_j denotes the Euclidean distance between r_i and r_j, and σ(t) is the neighbourhood radius defined by σ(t) = σ_final + (σ_initial − σ_final)(1 − t/τ), where σ_initial and σ_final are the neighbourhood radii in the initial and final steps, respectively. In the study, the initial weight vectors w_i(0) in step 1 were defined on the basis of principal component analysis of the input vectors b_m by $w_i\left(0\right)=\overline{b}+10s_1\left\{\left(k-K/2\right)/K\right\}{a}_1+10s_2\left\{\left(l-L/2\right)/L\right\}{a}_2$, where $\overline{b}$ is the average vector of b_m, a₁ and a₂ are the eigenvectors of the first and second principal components and s₁ and s₂ are the standard deviations of the first and second principal components. k and l are the kth column and lth row in the ith unit of the SOM architecture, respectively. The parameters for BLSOM used in the study were defined as K = 20, L = 20, σ_initial = 3.0, σ_final = 2.0 and τ = 100 based on the previous studies. Vijayakumar et al. used SOM for segmentation of brain tumour on MRI with pre-defined parameters of K = 20, L = 20 (Vijayakumar et al., 2007). Furthermore, Vesanto and Alhoniemi who reported two-level clustering suggested that the number of protoclusters N was determined as N = k_max², where k_max was an estimated maximum number of clusters (Vesanto and Alhoniemi, 2000). Because we predefined k = 20 from the viewpoint of a pathological estimation, the number of protoclusters was 400 according to the formula. According to the previous report and formula, we think the 20 × 20 matrix may be acceptable. Chavez-Alvarez et al. reported that the neighbourhood function was Gaussian with an initial radius (σ_initial) of 3.0 when K = 20 and L = 20 in their study (Chavez-Alvarez et al., 2014). To determine a final radius (σ_final), we tested BLSOM with a set of parameters (0.01, 0.05, 0.1, 0.25, 0.5, 1, 2, 3) according to the previous study (Ehsani and Quiel, 2008). Lower final radius than 2.0 could cause stepping-stone like clusters by the KM++ with k = 20, which was the maximum number in the study, partly because of overfitting. Therefore, we finally applied σ_final = 2.0, which did not cause any stepping-stone like clusters. As to τ, the number of total iterations of SOM, some previous neuroimaging studies applied 100 iterations for SOM and suggested that 100 iterations were sufficient to establish convergence of SOM, and, therefore we followed them (Peltier et al., 2003; Liao et al., 2008). We have implemented BLSOM software (in-house developed products) developed in C++.

One of the greatest advantages of SOM is the powerful visualization (Vesanto and Alhoniemi, 2000), which enables SOM to be suited for data understanding or survey. There are two common methods to visualize the results of SOM, U-Matrix and Component Planes. Especially, the Component Planes can show the information of each parameter in each map unit and associations between clusters and variables (Alhoniemi et al., 1999). We used the Component Planes to visualize the relation between variables of each DTI-based parameter clearly. Using the Component Planes, SOM may allow us to evaluate the classification options different from a fixed diagnosis (Wang et al., 2002).

2.6. Unsupervised clustering: KM clustering

The KM algorithm is a classic statistical clustering method (MacQueen, 1967) computed in an off-line mode and does not perform competitive learning as does SOM. Its objective, for K clusters, is to iteratively minimize the within-class inertia by assigning the feature vectors to the nearest cluster centre and update its value. The number of clusters has to be determined prior to calculation.

The algorithm of the standard KM is as follows:

• 1Start by initializing C that will contain K cluster centres $c_k\in {ℝ}^d$ such that 1 ≤ K ≤ N. The set C = {c₁,c₂,…,c_k} will be initialized with the vectors x_j randomly chosen from the data set $X\subset {ℝ}^i$.
• 2Assign each vector x_j from the data set to the nearest centre c_k using the Euclidean distance metric, d(x_j,c_k) = x_j − c_k.
• 3Update the new cluster centres c_k with the average value of its members by $c_k=\left(1/C_k\right)\sum _{x_j\in C_k}{x}_j$, where C_k represents the number of elements in the respective cluster.
• 4Repeat steps 2 and 3 if any partition was modified since last iteration.

Although the procedure will always terminate, the standard KM might converge to a local minimum because it uses vectors chosen at random from the data set to initialize the clusters. Therefore, we used a modified version of KM, called the K-means++ (KM++) algorithm (Arthur and Vassilvitskii, 2007), that chooses centres at random from the data points but weighs the data points according to their squared distance from the closest centre already chosen. The KM++ algorithm shows drastic improvement in both speed and accuracy compared with the classic algorithm. The KM++ algorithm is defined as follows:

• 1aTake one centre c₁, chosen uniformly at random from X.
• 1bTake a new centre c_i, choosing x ∈ X with probability $D{\left(x\right)}^2/\sum _{x\in X}D{\left(x\right)}^2$
• 1cRepeat step 1b until we have taken K centres altogether.

• 2–4. Proceed as with the standard KM algorithm.

In addition to KM++, we repeated KM++ trials and selected the best cluster among different clusters from multiple KM++ trials by the silhouette index (Rousseeuw, 1987). It calculates the silhouette index for each datum, average silhouette index for each cluster and overall average silhouette index for the total data set. Using the method, each cluster could be represented by so-called silhouette, which is based on the comparison of its tightness and separation. The average silhouette index can be applied for evaluation of clustering validity. The overall average silhouette index (SI) is defined by $SI=\left(1/K\right)\sum _{j=1}^K{S}_j$, where S_j is a silhouette local coefficient defined by $S_j=\left(1/n_j\right)\sum _{i=1}^{n_j}{s}_i$, where s_i is a silhouette index for the i-th object defined by s_i = (b_i − a_i)/max(b_i,a_i), where a_i is the mean distance between object i and objects of the same class j and b_i is the minimum mean distance between object i and objects in class closest to class j. In the study, 1000 KM++ trials were performed in each K. We have little prior knowledge about the number of K, and it can differ according to what users want to know (e.g. tumour detection, tumour grading or outcome prediction) using the clustered images. In the present study, we empirically chose the numbers of K = 4, 6, 8, 10, 12, 16, 20 according to the number of estimated segmentations in the abnormal brain with a glioma. We implemented these algorithms in the in-house SOM software, which enabled the use of BLSOM followed by KM++.

2.7. Diffusion tensor-based clustered image (DTcI)

After unsupervised clustering by BLSOM followed by KM++, 400 protoclusters (weighted vectors) with K-class label information were generated. Label information of the nearest protocluster using the Euclidean distance metric was assigned to each voxel on the seven intensity-normalized diffusion tensor images within the binary mask image from FSL's BET. Finally, voxel-based images with K-class label information were obtained. We called them DTcIs (Fig. 1). Using the unsupervised clustering method, DTcIs can be easily obtained without any initial segmentation.

2.8. Classification using DTcI: definition of ROI

Gliomas generally show unclear and irregular boundaries with discontinuities and variety. ROIs were manually traced by two of the authors in the DTI space according to abnormalities on MP-RAGE, without any knowledge of the clinical or pathological data. It should be noted that ROIs were defined on the basis of abnormal signal intensities in MP-RAGE, which could include tumour as well as oedema, necrosis and cystic parts. For simplicity, we defined ROIs per four axial slices from the top slice of the abnormal regions and counted the total number of voxels in each patient. If the number of voxels was <400, we redefined ROIs per two axial slices to increase the number of total voxels. Finally, the number of voxels in each ROI ranged from 326 to 9316. We only used these ROIs for feature extraction for SVM as mentioned in the next subsection.

2.9. Classification using DTcI: feature extraction for tumour grading

The ratio of each class in DTcIs was calculated from ROIs in each subject. Then, the common logarithmic value of the ratio was calculated by log₁₀(p + 10⁻²), where p is a ratio of each class (%) and used for input features to SVM. The features were defined as log-ratio values according to $\text{U}=\left\{x_i\in {ℝ}^K,1\le i\le N\right\}$, where N is the number of subjects (Fig. 1).

2.9.1. Classification using DTcI: SVM

SVM (Vapnik, 1998) is a widely used method because of its remarkable classification performance and the simplicity of its theory and implementation. Accordingly, we chose a linear kernel SVM as a classifier to distinguish between LGGs and HGGs. The hyperparameter (C) of the linear kernel SVM was optimized by using a two-step grid-search technique with five-fold cross-validation according to the recommendation described in a practical guide to SVM classification (Hsu et al., 2003; Ota et al., 2014). First, the best value of C_coarse was found by a coarse grid-search on log₂C = −5, −3, …, 15. Then, the best value of C_fine was obtained by a fine grid-search on log₂C = C_coarse − 2, C_coarse − 1.75, …, C_coarse + 1.75, C_coarse + 2. The best C_fine was used to generate the final classifier for each training set.

A LOOCV strategy was used to assess the classification performance because the strategy is widely used in machine learning and allows using most of the data for training (Dosenbach et al., 2010). During LOOCV, each subject is designated as a test subject in turn, while the remaining subjects are used to train the SVM classifier. The decision function derived from the training subjects is then used to classify or calculate a decision value about the test subject. After all LOOCV repeats, the accuracy, sensitivity and specificity for all folds are averaged together to generate the final accuracy, sensitivity and specificity estimate. We also evaluated decision values (Chang and Lin, 2011) for receiver operating characteristic (ROC) curves and area under the curve (AUC). Furthermore, we repeated the LOOCV strategy 100 times to calculate confidence intervals (CIs) of these estimates.

We used C++ and the LIBSVM library (Chang and Lin, 2011; software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm) to implement a linear kernel SVM with a two-step grid-search technique and a LOOCV strategy.

2.10. Statistical analysis

To determine if the classification performances were significantly different according to the number of K in the KM++ method (K = 4, 6, 8, 10, 12, 16, 20), we repeated the LOOCV strategy 100 times. AUCs in different K were then analysed by one-way ANOVA followed by Tukey's multiple comparison tests. Differences were considered significant for p < 0.05.

Then, to evaluate the behaviour of the classifier in the K-class that revealed the best classification performance, we used the pROC library for R to generate ROC curves with 95% CIs computed with 2000 stratified bootstrap replicates (Robin et al., 2011).

Wilcoxon–Mann–Whitney tests with exact p-values and CIs calculated by a permutation test were used to compare the log-ratio values of each class in the K class that revealed the best classification performance between the LGG and HGG groups (Hothorn et al., 2006). Because of the multiple comparisons in K classes, a Bonferroni correction for multiple comparisons was applied, and differences between the groups were considered to be significant at a level of p < 0.05/K.

The ratios of normalized intensities on the seven diffusion tensor images of each class in the K class that revealed the best classification performance were analysed with the bootstrapped 95% CIs. The statistical software package R version 3.0.2 (The R Foundation for Statistical Computing, http://www.r-project.org/) was used to perform all statistical analyses.

3. Results

3.1. Unsupervised clustering

Fig. 2 illustrates the Component Planes in seven DTI-based variables by the SOM analysis. Visual inspection of the SOM patterns demonstrated that the Component Planes of DWI and FA were obviously different from the others. Although general patterns of MD, S0, L1, L2 and L3 Component Planes seemed similar, the details among them differed. In the case of K = 16 (Fig. 2), for example, FA values in class number 13, DWI values in class number 15 and MD, S0, L1, L2 and L3 values in class number 4 were highest among all classes. SOM also showed that the DWI component of class numbers 1, 2, 9, 12 and 13 had variations from low to high values, and that the FA component of class numbers 9, 10, 12 and 14 had variations from low to high values. Class numbers 12, 13 and 16 in the L1 Component Plane were higher than those of the MD, S0, L2 and L3 Component Planes. Class numbers 2, 6, 7 and 8 in the MD, L1, L2 and L3 Component Planes were higher than those in the S0 Component Plane. Class number 9 in the MD and L1 Component Planes was higher than that in the S0, L2 and L3 Component Planes.

Fig. 2.

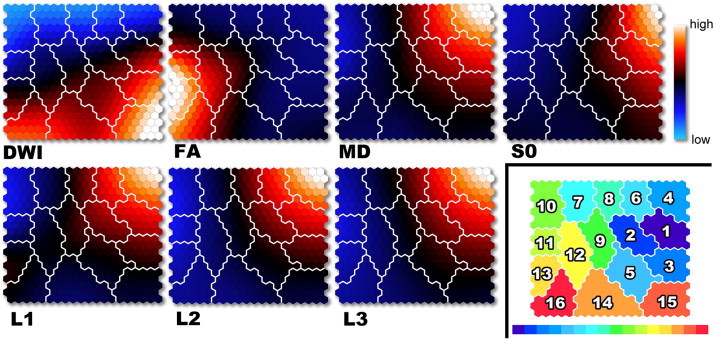
Visualization of seven DTI-based variables on Component Planes with SOM. Each node (protocluster) is colorized from blue to red according to the intensities in each diffusion tensor image. The white lines between nodes denote inter-class borderlines obtained by KM++ with K = 16 on SOM. SOM component planes can help to interpret detailed intensity profiles or patterns in each diffusion tensor image (lower right). The 16-class cluster map on the 20 × 20 SOM. Each class number corresponds to intensity on DTI-based clustered images. DWI = diffusion-weighted imaging; FA = fractional anisotropy; L1 = first eigenvalue; L2 = second eigenvalue; L3 = third eigenvalue; MD = mean diffusivity; S0 = raw T2 signal without diffusion weighting.

Representative cases of LGGs and HGGs are shown in Fig. 3. Although the boundaries of LGGs could be clearly recognized, it was much difficult to recognize the boundaries of HGGs. Furthermore, DTcIs revealed few warm coloured classes, such as class numbers 14, 15 and 16 in LGGs, whereas there were more warm coloured classes in HGGs than in LGGs. Thus, the clear differentiations between LGGs and HGGs on DTcIs could be visually recognized.

Fig. 3.

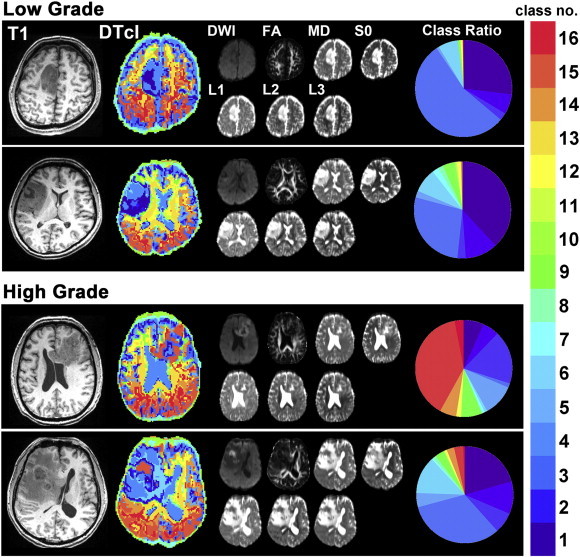
The representative cases of low- (upper) and high- (lower) grade gliomas, including the 16-class DTcIs that showed the highest classification performance. The T1-weighted images, DTcIs, seven diffusion tensor images and the ratios in each class number are shown for each patient. DWI = diffusion-weighted imaging; FA = fractional anisotropy; L1 = first eigenvalue; L2 = second eigenvalue; L3 = third eigenvalue; MD = mean diffusivity; S0 = raw T2 signal without diffusion weighting. Each colour on DTcIs and circular charts correspond to each class number, shown in the colour bar.

3.2. SVM classification using DTcI

The performances of LOOCV using DTcI and SVM are shown in Fig. 4. The differences in AUCs were significant among the classes [F(6, 693) = 246.1, p < 10⁻¹⁶⁸, ${\eta }_p^2=0.68].$ Tukey's post-hoc tests showed that AUC was significantly higher for the 16-class DTcIs than for others (p < 0.001). The tests also showed that AUCs were significantly higher for the 12- and 20-class DTcIs than for the 4-, 6-, 8- and 10-class DTcIs (p < 0.001). There were no significant differences in AUCs between the 12-class and 20-class DTcIs. The tests also showed that AUC was significantly lower for the 4-class DTcIs than for the others (p < 0.001). AUC of the 16-class DTcIs was the highest among classes (0.912; 95% CI = 0.903–0.922) (Fig. 5). The sensitivity, specificity and accuracy of the 16-class DTcIs were 0.848 (95% CI = 0.845–0.852), 0.745 (95% CI = 0.733–0.757) and 0.804 (95% CI = 0.800–0.809), respectively. In contrast, AUC of the 4-class DTcIs was the lowest (0.729; 95% CI = 0.718–0.739). There were no significant group differences in AUCs between in the 6-, 8- and 10-class DTcIs (0.856, 0.844 and 0.850, respectively).

Fig. 4.

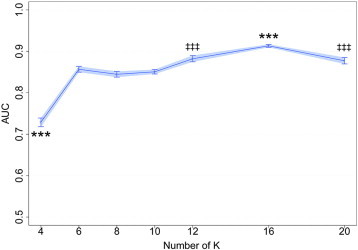
Plots of AUC versus the number of K in the KM++ method. Values are means and error bars, and light blue shades represent 95% CIs. ***p < 0.001 (versus all the rest). ‡‡‡p < 0.001 (versus K = 4,6,8,10,16), one-way ANOVA followed by Tukey's multiple comparison tests. The 16-class diffusion tensor-based clustered images significantly showed the highest AUC (0.912; 95% CIs = 0.903–0.922).

Fig. 5.

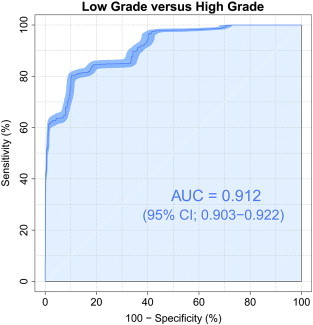
ROC curves (dark blue line), with AUC and 95% CIs shown in blue shades surrounding the dark blue line, for differentiating high-grade from low-grade gliomas by using the 16-class diffusion tensor-based clustered images.

3.3. Differences in log-ratio values

The log-ratio values of each class of the 16-class DTcIs that had the highest classification performance were compared between LGGs and HGGs (Fig. 6). The values of class numbers 14, 15 and 16 were significantly higher in HGGs than in LGGs (p < 0.005, r = 0.52; p < 0.001, r = 0.60; p < 0.001, r = 0.73; respectively). The values of class numbers 12 and 13 also revealed higher trends in HGGs (p < 0.01, r = 0.48; p < 0.01, r = 0.50; respectively).

Fig. 6.

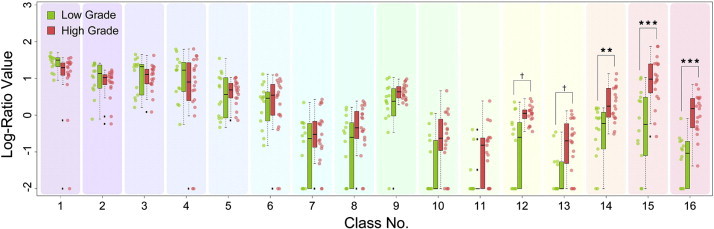
Strip chart and box plots showing median, interquartile range, inner fence and outliers (○) for log-ratio values of each class by 16-class diffusion tensor-based clustered images in patients with low- (green) and high- (red) grade gliomas. ***p < 0.001, **p < 0.005, †p < 0.01 by exact Wilcoxon–Mann–Whitney rank sum tests.

3.4. Ratio of DTI-based parameters

The ratios of normalized intensities of the seven diffusion tensor images for each class number in the 16-class DTcIs that revealed the highest classification performance are shown in Fig. 7.

Fig. 7.

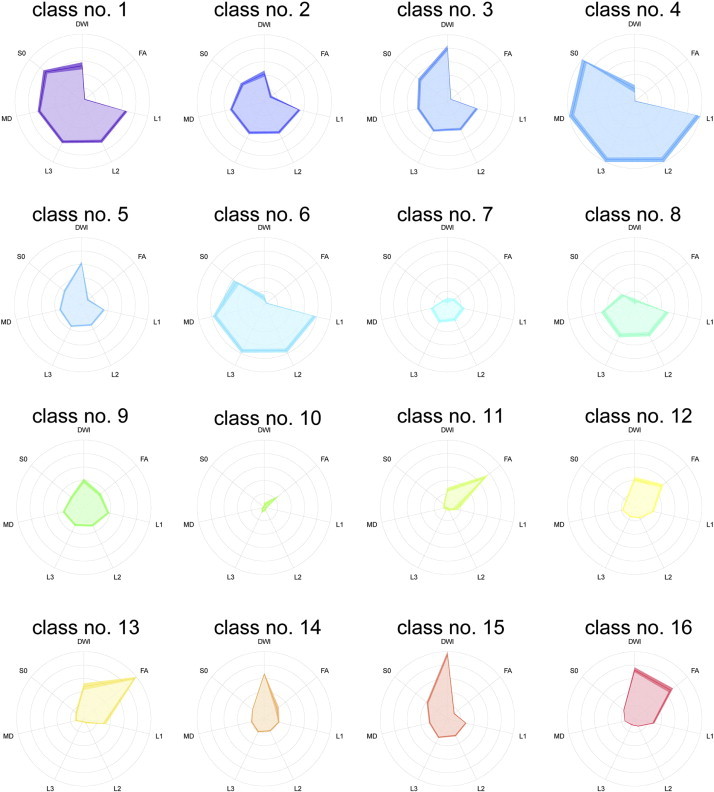
Radar charts of seven DTI-based variables in each class by 16-class diffusion tensor-based clustered images. Shades surrounding dark-coloured lines represent bootstrapped 95% CIs. DWI = diffusion-weighted imaging; FA = fractional anisotropy; L1 = first eigenvalue; L2 = second eigenvalue; L3 = third eigenvalue; MD = mean diffusivity; S0 = raw T2 signal without diffusion weighting.

As mentioned above, the ratios of class numbers 14, 15 and 16 were significantly higher in HGGs than in LGGs. The chart patterns of class numbers 14 and 15 seemed similar and comprised high DWI values and low FA values. Class number 15 had the highest DWI values among all. In FA, class number 14 had higher values than class number 15. The variables of class number 16 comprised high FA and DWI values and were different from those of class numbers 14 and 15. All three classes included low values in MD, S0, L1, L2 and L3. Although the variables of class numbers 3 and 5 included high DWI values and low values for other features, there were no significant differences in the log-ratio values between LGGs and HGGs (p = 0.28, r = –0.19; p = 0.84, r = 0.03; respectively).

The indices of class numbers 12 and 13 also revealed higher trends in HGGs. The chart patterns of class numbers 12 and 13 were very different from those of class numbers 14, 15 and 16. The highest FA values were seen in class number 13. The variables of class numbers 12 and 13 included low DWI values. Low values in MD, S0, L1, L2 and L3 were seen in class numbers 12, 13, 14, 15 and 16.

4. Discussion

4.1. Study overview

In this study, we investigated a two-step procedure for predicting glioma grade. In the first step, the unsupervised clustering method with SOM followed by KM++ was used to obtain voxel-based DTcIs with multiple DTI-based parameters. DTcIs enabled visual grading of gliomas. In the second step, the validity of DTcIs for glioma grading was assessed in a supervised manner using SVM. The 16-class DTcIs revealed the highest classification performance for predicting the glioma grade. The sensitivity, specificity, accuracy and AUC of the 16-class DTcIs for differentiating HGGs and LGGs were 0.848, 0.745, 0.804 and 0.912, respectively. The classifier in the 16-class DTcIs showed that the ratios of class numbers 14, 15 and 16 were significantly higher and those of class numbers 12 and 13 showed higher trends in HGGs than in LGGs. Thus, these results indicate that our clustering method of seven parameters can be useful for determining glioma grade visually, despite not using a complicated combination of a high number of features from many modalities.

4.1.1. Clustering method

The two-level clustering approach was used in our study since it has the following two important benefits: noise reduction and computational cost. Because of the character of KM++ mentioned in the Materials and methods section, outliers extracted from DTI parameters can make its clustering accuracy worse. When BLSOM is applied prior to KM++, outliers can be filtered out and the clustering accuracy will be better. The AUC only with the KM++ algorithm without BLSOM was 0.646 with K = 16 and remarkably worse than that with the two-level clustering approach. Another important benefit is the reduction of the computational cost. In our study, the KM++ was repeated 1000 times to obtain more stable results. The computational time of the two-level clustering approach for 1000 KM++ trials was 210 s (204 s for BLSOM and 6 s for 1000 KM++ trials) for 117,232 input vectors in the study. On the other hand, the computational time only for the 1 KM++ trial without BLSOM was 305 s and around 85 hours for 1000 KM++ trials. For these facts, the two-level approach can be effective especially for clustering of a larger data set.

Deciding optimal parameters for SOM is not easy as previous studies mentioned in their studies. Although we applied most of the parameters according to previous studies　(Vesanto and Alhoniemi, 2000; Vijayakumar et al., 2007; Ehsani and Quiel, 2008; Chavez-Alvarez et al., 2014) in the study, it remains unclear, as mentioned in the Materials and methods section, whether these parameters for SOM lead to the best performance or not. The parameters might be verified by undertaking a prospective, randomized controlled study.

Our segmentation method does not need any initial segmentation for defining tumour lesions because features were extracted from the whole brain. Indeed, the DTcIs can segment the brain as some parts of normal and abnormal areas unintentionally, but the method does not need any initial segmentation for defining tumour lesions and it is an important advantage of unsupervised clustering methods. When defining tumour lesions as an initial segmentation, it is needed to draw regions of interest intentionally or decide automatically which voxel is tumour, oedema, necrosis or normal tissue with a supervised clustering method. However, it is impossible to decide the correct boundary between normal and abnormal pathology on MRI. The voxel out of the boundary may include tumour cells considered from the infiltrative nature of glioma, which may influence grading of gliomas. We think that clustering for images of gliomas without an initial segmentation is an indispensable advantage and our method can satisfy this point.

4.2. Number of classes in DTcIs

The 16-class DTcIs had the best classification performance between HGGs and LGGs in this study. It is assumed that brain tumour images can be segmented at least into four classes (white matter, grey matter, CSF and abnormality) (Rajini and Bhavani, 2012). Within abnormalities, they can be consisted of tumour cells (high/low), gliosis, oedema, necrosis, haemorrhage, and the mixed structure of some of them. Therefore, when we consider the combination of those, several kinds of classes may be reasonable. Furthermore, we found the same cluster in grey matter and in tumours. Class numbers 14–16 that had significantly higher HGG values were seen in grey matter and showed low MD values, which corresponded to increased cellularity (Lam et al., 2002; Kao et al., 2013). This finding may indicate high cellularity within tumour areas. However, it is difficult to say on the basis of our results which class would fit to what tissue. Pathological studies of each class in DTcIs by biopsy or resection could clarify the relationship.

4.3. Multiple parameters in DTI

We selected L1, L2 and L3, that are the basis of DTI-related parameters, in order to compare previous pathological studies using those parameters. We also selected DWI, FA, ADC and S0 that are familiar to neurosurgeons in order to compare previous studies that used one of those parameters as a single parameter for glioma grading. In the previous study, Griffith et al. researched the pathologies of MD [(L1 + L2 + L3)/3], L1 and radial diffusivity [(L2 + L3)/2] and compared each parameter. Although MD was calculated from L1, L2 and L3, they have different information at least from the viewpoint of pathology (Griffith et al., 2012). We therefore think that each parameter has an important role clinically and pathologically and selected these parameters in the study. Some previous studies used one parameter, especially ADC, for tumour grading. Although one study suggested that HGGs with lower ADC values corresponded to increased cellularity (Kao et al., 2013), another reported that there was no significant difference in ADC values between LGGs and HGGs (Lam et al., 2002). These studies suggest that differentiating glioma grade on the basis of only one parameter is difficult. In our study, we used seven DTI-based parameters, including DWI, FA, MD, S0, L1, L2 and L3, and the results suggested that the DTI-based multiple parameters were useful for predicting glioma grade. However, it remains unclear which parameters have the most influence on clustering tumours. We identified unique DWI and FA Component Planes that can be predictive of malignancy. A previous study revealed no significant differences in DWI between LGGs and HGGs and indicated that predicting tumour grade only by using DWI had a limitation (Kono et al., 2001). Class numbers 14, 15 and 16 that were significantly higher in HGGs showed similar DWI values but different patterns of values in other DTI-based parameters. In addition to the results, we also calculated the AUC if using the combination of only DWI and FA, only DWI and only FA. However, the AUC of two parameters of DWI and FA was 0.642, 0.645, and 0.637, respectively and they all were much lower than the AUC of seven parameters. The additional analyses also support the idea that combined multiple parameters could be useful for predicting the grade of gliomas. Conversely, although FA values of HGGs were higher than LGGs in a previous study (Kao et al., 2013), class numbers 14 and 15 showed low FA values. Although general patterns of MD, S0, L1, L2 and L3 Component Planes in SOM seemed similar, their subtle differences revealed by multi-variate pattern analysis may be important for predicting grade. In fact, a pathological study using MRI reported that higher astrocytosis correlated with higher ADC and L1 (Griffith et al., 2012). Most cases of reactive astrocytosis can be identified from the infiltrating edge of an astrocytoma (Ironside, 1994), and it may be difficult to distinguish diffuse astrocytoma from astrocytosis (Camelo-Piragua et al., 2011). Axonal damage and cellular infiltration led to a reduction of L1 (Boretius et al., 2012), and radial diffusivity [(L2 + L3)/2] has been proposed as a marker of demyelination (Klawiter et al., 2011). Furthermore, loss of oligodendrocytes correlated with L2 and L3 but not L1 (Griffith et al., 2012). Although we extracted seven parameters from DTI, it remains unclear which combination of the parameters is the best or if additional parameters can increase the accuracy for glioma grading. Several features other than the seven parameters, for example, eigenvectors, might provide better results if included. Further studies are needed to assess which combination of parameters is best for glioma grading.

One of the limitations in our study was the influence of distortions on voxel-based clustering. Original DWIs for DTI were acquired by using EPI to reduce acquisition time and artefacts related to physiological motion. Unfortunately, this fast acquisition scheme is highly sensitive to eddy currents induced by the large diffusion gradients and to another distortion induced by susceptibility artefacts (Mangin et al., 2002). A prominent source of artefacts for EPI is the effect of inhomogeneities close to tissue–air and tissue–bone interfaces, such as those around the frontal sinus and petrous bone (Jezzard and Clare, 1999). To reduce artefacts by eddy currents, the data were corrected by using the FDT program (Smith et al., 2004). Furthermore, the FUGUE program was used to reduce susceptibility artefacts for EPI that depend on the subject's head geometry. Only DTI-based parameters were used for glioma grading in our study, although conventional MRI sequences, such as T1WI, T1WIce and T2WI, were scanned. The reason is that these conventional images are spatially different from DTI because of distortions. The differences require more accurate image registration between them for calculating voxel-based images. Multiple parameters of DTI-based parameters as well as conventional MRI parameters combined with an accurate registration algorithm may generate voxel-based clustered images that predict the grade of gliomas more accurately.

4.4. Ratio of DTI-based parameters in LGG and HGG

The ratios of class numbers 14, 15 and 16 were significantly higher in HGGs than in LGGs. Class numbers 14, 15 and 16 seemed similar with regard to high DWI values. There was no significant difference between LGGs and HGGs in a past study (Kono et al., 2001), suggesting that grading tumours only by DWI is controversial. In our study, class numbers 3 and 5, which were not different between LGGs and HGGs, also had high DWI values. These results support the controversy regarding DWI and suggest that glioma grading only by DWI may be difficult.

Class numbers 14 and 15 had low FA values. In contrast, class number 16 had high FA values. Some researchers have reported that changes in FA in gliomas may indicate tumour cell infiltration (Schluter et al., 2005; Kallenberg et al., 2013). A reduction in FA seemed to be the common denominator among structural abnormalities (Wieshmann et al., 1999). Lower FA values were seen in LGGs in one study (Inoue et al., 2005), whereas another study showed no significant differences between LGGs and HGGs (Goebell et al., 2006). In our study, both increases and decreases in FA were seen in tumours. Particularly, class numbers 13 and 16 showed that high FA values were also included in HGGs.

Class numbers 14–16, which had significantly higher values in HGGs, seemed to have low MD values. However, most classes (numbers 2, 3, 5, 7, 8, 9, 10, 11, 12 and 13) with low MD values were not different between HGGs and LGGs. These results suggest that it is difficult to predict glioma grade only by using one parameter, such as DWI, FA or MD as discussed in many previous studies.

4.5. Glioma grading

The current gold standard for determining glioma grade is histopathological assessment. However, the limitations of histopathological assessment because of the heterogeneity of gliomas are well known. First, there is a possibility of sampling error. Because only a few small pieces of tissue are assessed and we tend to examine T1-enhancing lesions, the most malignant tissue may not be obtained. Sampling errors may occur especially for biopsy only (Law et al., 2006). Even if we resect most tumours, a thorough investigation is not always made in the resected tumour, and this is a histopathological limitation at present. Several studies have been conducted to evaluate more accurate selection of targets by using positron emission tomography (PET) images with ¹⁸F-labelled fluorodeoxyglucose and ¹¹C-labelled methionine to reduce sampling errors (Levivier et al., 1995; Pirotte et al., 2004). However, the radiotracer injection in PET is invasive because of radiation exposure. By using DTcIs, we can non-invasively predict the grade of gliomas with accuracy and may perform regional grading of glioma, which is useful for targeting biopsy. Gliomas are heterogeneous tumours. If we can preoperatively predict the regional grading of a tumour, we can know which region must be resected, including peri-tumoural oedematous lesions. Second, some LGGs develop into HGGs, and ≥10% of gliomas dedifferentiate into more malignant grades (Law et al., 2006). We cannot know when tumour grade progresses. By using regional grading based on DTcIs, we can clarify when LGGs progress into HGGs during follow-up and provide an appropriate adjuvant treatment at the optimum time. The potential benefit of the proposed method in the present study could be emphasized by undertaking a prospective, randomized controlled study.

5. Conclusion

This study applied a two-level clustering approach, which consisted of SOM followed by the KM++ algorithm, for unsupervised clustering of a large number of input vectors with multiple features by DTI. The greatest point of the method is to enable obtaining novel clustering images called DTcIs, that can give visual grading of glioma and be helpful in differentiating between LGGs and HGGs without pathological information. Our new approach could lead to more accurate non-invasive grading and more appropriate treatment.