Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Sep 1.
Published in final edited form as: J Ultrasound Med. 2014 Sep;33(9):1597–1604. doi: 10.7863/ultra.33.9.1597

Noninvasive Assessment of Liver Fibrosis Using Ultrasound-based Shear Wave Measurement and Comparison to Magnetic Resonance Elastography

Heng Zhao 1, Jun Chen 2, Duane D Meixner 2, Hua Xie 3, Vijay Shamdasani 4, Shiwei Zhou 3, Jean-Luc Robert 3, Matthew W Urban 1, William Sanchez 5, Matthew R Callstrom 2, Richard L Ehman 2, James F Greenleaf 1, Shigao Chen 1
PMCID: PMC4145616  NIHMSID: NIHMS614477  PMID: 25154941

Abstract

Objective

Magnetic Resonance Elastography (MRE) has excellent performance in detecting liver fibrosis and is becoming an alternative to liver biopsy in clinical practice. Ultrasound techniques based on measuring the propagation speed of the shear waves induced by acoustic radiation force also have shown promising results for liver fibrosis staging. The objective of this study was to compare ultrasound-based shear wave measurement with MRE.

Methods

In this study, fifty patients (22 males and 28 females, age 19–81) undergoing liver MRE exams were studied using a Philips iU22 ultrasound scanner modified with shear wave measurement functionality. For each subject, 27 shear wave speed measurements were obtained at various locations in the liver parenchyma away from major vessels. The median shear wave speed from all measurements was used to calculate a representative shear modulus μ for each subject. MRE data processing was done by a single analyst blinded to ultrasound results.

Results

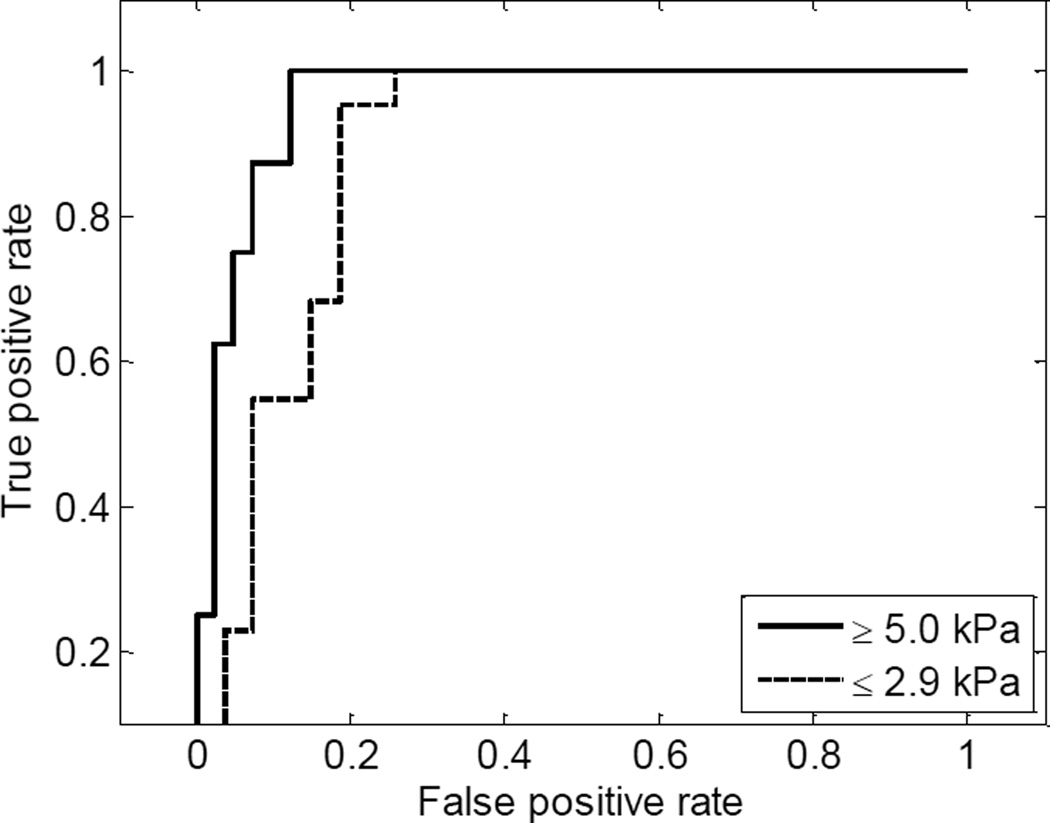
Results showed that ultrasound and MRE measurements were correlated (r = 0.86, P < 0.001). Receiver operating characteristic (ROC) analysis was applied to the ultrasound measurement results with the MRE diagnosis as the “ground truth”. The area under the ROC curve for separating patients with minimum fibrosis (defined as shear modulus μMRE ≤ 2.9 kPa) was 0.89 (95% confidence interval [CI]: 0.77–0.95), and the area under the ROC curve for separating patients with advanced fibrosis (defined as μMRE ≥ 5.0 kPa) was 0.96 (95% CI: 0.87–0.99).

Conclusions

Results indicate that the ultrasound shear wave measurement correlates with MRE and is a promising method for liver fibrosis staging.

Keywords: Ultrasound, Shear Wave, Liver fibrosis, MRE

INTRODUCTION

Liver fibrosis and cirrhosis are the response of chronic liver injury caused by viral, autoimmune, drug-induced, cholestatic, or metabolic disease [1]. Liver cirrhosis affects hundreds of millions of patients worldwide. In the United States, about 100,000 people are diagnosed annually for the first time with chronic liver disease and cirrhosis [2], which accounts for over 30,000 deaths each year [3]. Staging of liver fibrosis is crucial for assessing prognosis and treatment decision making.

Liver biopsy is considered as the standard tool for the diagnosis and staging of liver fibrosis [4]. However, it is an invasive procedure that can cause discomfort and present risks to patients. Also, liver biopsy is subject to sampling variability due to its small sample size [5] as well as histologic interpretation variability [6].

Mechanical testing results have shown mechanical properties of in vivo or ex vivo human liver tissues are associated with liver fibrosis [7–9]. Therefore, noninvasive techniques that evaluate liver mechanical properties have great potential for liver fibrosis staging, and they are more suitable for screening, monitoring, and follow-up.

Magnetic Resonance Elastography (MRE) [10] uses external mechanical vibrations to generate shear waves inside the tissue from which the tissue elasticity is measured. Extensive clinical studies have demonstrated that MRE has excellent performance for liver fibrosis staging [11–13]. A meta-analysis showed that the area under receiver operating characteristic (ROC) curve was 0.98 (95% confidence interval [CI]: 0.97–0.99) for separating F0–F1 vs. F2–F4, where F is the METAVIR fibrosis score (i.e., F0 to F4 covers a range from no fibrosis to cirrhosis) [14]. MRE quantifies tissue elasticity over a relatively large area of the liver, and therefore does not suffer from sampling or interpretation variability like liver biopsy.

Ultrasound dynamic elastography techniques also have shown great potential because they have good correlation with liver fibrosis staging, and in addition can be performed at a relatively low cost and are widely available. Among the available techniques, Fibroscan (or transient elastography) has been widely used for studying liver fibrosis [15, 16]. However, it requires a dedicated machine which is not compatible with clinical ultrasound scanners, and lacks imaging guidance for its measurements. Recently, more techniques based on shear waves induced by acoustic radiation force have been developed that are compatible with clinical scanners, including Acoustic Radiation Force Impulse (ARFI) [17, 18], Supersonic Shear Imaging (SSI) [19, 20], and Shearwave Dispersion Ultrasound Vibrometry (SDUV) [21]. Most of the studies using these techniques have shown promising performances in liver fibrosis staging.

Some studies have compared the liver fibrosis staging performance of Fibroscan with MRE [22, 23]. But very few studies have compared ultrasound radiation force induced shear wave measurements with MRE [24].

In this study, fifty patients undergoing liver MRE exams were studied using a Philips iU22 ultrasound scanner (Philips Healthcare, Andover, MA) modified with shear wave measurement functionality. Because this was a prospective study comparing ultrasound shear wave measurement with MRE, no biopsy was performed on these patients. The recorded ultrasound radiofrequency (RF) data were analyzed offline automatically using a robust method based on cross-correlation without human intervention. MRE data processing was done by a single analyst blinded to ultrasound results. The Pearson product-moment correlation coefficient was used to evaluate the correlation between ultrasound and MRE results. The performance of the ultrasound shear wave measurement for separating minimum fibrosis (defined as shear modulus μMRE ≤ 2.9 kPa) and advanced fibrosis (defined as μMRE ≥ 5.0 kPa) was assessed by calculating the area under the ROC curves.

MATERIALS AND METHODS

Subjects

The prospective study was approved by the institutional review board (IRB) of the Mayo Clinic and written consent was obtained from each participating subject. Fifty patients (28 women and 22 men; age range, 19–81 years) with liver disease were studied between December 2011 and October 2012. Thirty-six patients underwent ultrasound shear wave measurement on the same day as the MRE test, 13 patients went through both MRE and ultrasound tests within a week, and one patient had the ultrasound test one month after the MRE test. The clinical indications of liver MRE for the 50 patients determined by clinicians are summarized in Table 1.

Table 1.

Summary of the indications of liver MRE for the 50 patients in this study

Pathological Conditions Number of patients
Chronic hepatitis C 21
Abnormal liver function 8
Autoimmune hepatitis 5
Fatty liver disease (nonalcoholic) 6
Primary biliary cirrhosis 2
Primary sclerosing cholangitis 2
Hepatitis B 2
Other liver diseases 4
Open in a new tab

Ultrasound Shear Wave Measurement

Measurements of liver tissue elasticity were obtained by 4 sonographers (12, 16, 17, and 26 years of experience) in the liver by using a curvilinear transducer (C5-1, operating frequency range 1–5 MHz, Philips Healthcare, Andover, MA) through intercostal spaces with the subject lying supine with right arm abduction. The operator positioned the probe using real-time B-mode imaging to locate a large liver region free of major vessels. Then the operator selected the measurement location with a cursor moved by a trackball. Subjects were instructed to suspend breathing while the operator pressed a button that launched the data acquisition sequence. Time for each single acquisition was less than 0.1 second. After each acquisition, the machine paused until the beamformed radiofrequency data recording was complete. For each subject, 27 acquisitions were obtained from 3 image planes (by slightly adjusting the probe angle in elevational direction) with 9 acquisitions evenly distributed in each image plane (3 depths × 3 lateral locations). The total measurement time was approximately 15 minutes.

The iU22 was modified to produce shear waves and track them using the pulse sequence similar to that used in a previous study [21]. The sequence started with a couple of detection pulses followed by a push pulse and an ensemble of detection pulses after the push. Each acquisition comprised five such detection-push-detection cycles. The push pulse had a center frequency of 2.5 MHz and duration of several hundred microseconds. The focal depth was determined by the measurement location with an F-number of 2. For detection, five lateral locations were evenly spaced on the right side of the push axis. The distance from the push axis to the first lateral location was the same as the distance between two adjacent lateral locations, which can vary as a function of depth since the probe is curvilinear. Pulse repetition frequency at each lateral location was 1.6 kHz and the tracking pulse center frequency was 2.5 MHz. The acoustic and thermal outputs complied with U.S. Food and Drug Administration safety regulations [25]. The mechanical index of the push pulse was about 1.3.

Ultrasound Data Processing

From the recorded RF data, the axial shear wave displacements were estimated using cross-correlation (CC) speckle tracking method [26]. The CC window size was 1 mm and shifted one sample (24 µm sample distance at 32 MHz sampling rate) for each calculation (97.6% overlap). Then the raw displacement signals were mapped to the uniform time grid using spline interpolation and band-pass filtered to remove background motion and noise.

The displacement data within the focal zone (the focal depth ±5 mm) were analyzed using a robust shear wave speed estimation method that combines the CC [27] and the time-of-flight method [17]. At each depth, time delays were found between all possible pairings of the five lateral locations (e.g. location 1–2, 1–3, 1–4, 1–5, 2–3, 2–4, 2–5, 3–4, etc.). The time delays were calculated by finding the maximum in the CC function of any two temporal shear wave signals. The estimated delays with CC coefficients lower than 0.8 were deemed as unreliable and rejected. Linear regression was then applied to all the remaining measured delays against their corresponding distance and the slope was used to calculate the shear wave speed. The corresponding distance between the locations multiplied by the CC coefficient was used as the weighting of the measured delay for linear regression. The linear fitting results with R2 less than 0.6 were also rejected.

The shear wave speeds were calculated using the same method at 21 different depths within the focal zone (the focal depth ±5 mm with 0.5 mm step), from which a mean value was calculated and any results differing from the mean value by over 30% were rejected as outliers. From the remaining results, a mean value was calculated again to represent that acquisition. For each subject, the median value of the shear wave speed from all the 27 acquisitions was used as a final result of that subject. Then the shear modulus μ was estimated from the shear wave speed cs based on the following equation:

μ=ρ·cs2 (1)

where ρ is density which is close to 1000 kg/m3 for all soft tissues [28, 29]. Equation (1) assumes the medium is locally isotropic, homogeneous, incompressible, and the shear wave frequency is low and narrowband. These assumptions should be reasonable for this study, considering that most liver fibrosis is diffuse, and the ROI we used was small (about 5 mm × 10 mm).

MRE Measurement

In this study, the MRE exams for all the subjects were performed using 1.5T MRI scanners (GE Healthcare, Milwaukee, WI). The subject was laid on the scanner table in a supine position and an acoustic passive driver was secured on the abdomen by an elastic belt wrapped around the body. The passive driver was connected to an acoustic speaker system which provided a harmonic mechanical vibration at 60 Hz. The MRE used gradient echo 2D imaging sequence with a field of view (FOV) of 32–42 cm, slice thickness = 10 mm, and number of slices = 4. An MR phase-contrast method was used to acquire images of wave propagation in the liver which were processed by inversion algorithms for a liver elastogram (stiffness map). Regions of interest (ROIs) were manually drawn on the liver elastograms where the shear wave signal-to-noise ratio was high and there were no non-liver tissue or large blood vessels. Mean (standard deviation) liver stiffness values were measured from the ROIs.

Statistical Analysis

Pearson product-moment correlation was used to assess the correlation between MRE and the ultrasound shear wave measurement results [30]. A value of P < 0.05 was considered indicative of statistical significance. Clinical cut-points routinely used at our institute were applied to MRE results to classify patients with minimum (defined as μMRE ≤ 2.9 kPa, normal liver or inflammation) and advanced (defined as μMRE ≥ 5.0 kPa, stage 4 fibrosis or cirrhosis) fibrosis. Then the MRE classification result was used as a “ground truth” to evaluate the performance of the shear moduli obtained from ultrasound-based measurements in differentiating minimum fibrosis and advanced fibrosis using the areas under the ROC curves.

RESULTS

Fig. 1 shows the interface of the shear wave data acquisition on iU22. The measurement location was outlined by the white box that can be moved by the operator using the trackball. Fig. 2 shows the filtered shear wave signals from the five locations at the push focal depth (30 mm) from one acquisition of a patient. Time delays between the signals from different locations can be observed. The shear wave speed was estimated using linear regression of the time delays between each combination of the lateral locations against their distance as shown in Fig. 3. For each acquisition, shear wave speed was measured at multiple depths (focal depth ± 5 mm with 0.5 mm step) as shown in Fig. 4. The mean and standard deviation of the measured shear wave speeds for this acquisition were 1.83 ± 0.17 m/s. After rejecting the outliers using the method described in Data Processing, the mean and standard deviation of the measured shear wave speeds from 27 acquisitions were put together as shown in Fig. 5 and the median value was used to calculate shear modulus for each patient.

Fig. 1.

Fig. 1

Open in a new tab

The interface of the shear wave data acquisition on iU22. The measurement location outlined by the white box can be selected by the operator using the trackball.

Fig. 2.

Fig. 2

Open in a new tab

Representative shear wave signals from the five locations at the push focal depth (30 mm) of one acquisition from a patient after band-pass filtering to remove the background motion and the noise.

Fig. 3.

Fig. 3

Open in a new tab

Linear regression of the time delays between every pair of the five locations calculated using CC.

Fig. 4.

Fig. 4

Open in a new tab

Shear wave speeds measured at different depths from one acquisition. The mean and standard deviation of the measured shear wave speeds were 1.83 ± 0.17 m/s.

Fig. 5.

Fig. 5

Open in a new tab

Mean and standard deviation of the measured shear wave speeds from 27 acquisitions of one subject.

MRE could not be obtained from one patient due to iron overload. Shear moduli measured using MRE and the ultrasound shear wave measurement for each of the other 49 patients were plotted against each other in Fig. 6. Pearson product-moment correlation coefficient between the MRE and ultrasound results was 0.86 (95% CI: 0.76–0.92) with P < 0.001, indicating the correlation was significant. According to MRE results, 22 patients were diagnosed with minimum fibrosis (μMRE ≤ 2.9 kPa), 8 patients with advanced fibrosis (μMRE ≥ 5.0 kPa), and 19 patients with moderate fibrosis (2.9 kPa < μMRE < 5.0 kPa). For the ultrasound results, the area under the ROC curve for separating patients with minimum fibrosis (μMRE ≤ 2.9 kPa) was 0.89 (95% CI: 0.77–0.95), whereas the area under the ROC curve for separating patients with advanced fibrosis (μMRE ≥ 5.0 kPa) was 0.96 (95% CI: 0.87–0.99).

Fig. 6.

Fig. 6

Open in a new tab

MRE and ultrasound shear wave measurement results of 49 patients. The linear fitting shows they are correlated with a correlation coefficient of r = 0.86.

DISCUSSION

From the 49 patients undergoing liver MRE, significant correlation was found between the ultrasound shear wave measurement results and MRE results. The ultrasound shear wave measurement also had good performances in separating patients with minimum fibrosis (μMRE ≤ 2.9 kPa) and patients with advanced fibrosis (μMRE ≥ 5.0 kPa).

The ultrasound shear wave measurement method and MRE have been validated by mechanical testing using phantoms [31, 32]. The liver shear modulus measured using ultrasound shear wave measurement in this study ranged from 1.16 kPa to 26.08 kPa, which was comparable to the reported ranges using Fibroscan (1.12–23.03 kPa, converted from Young’s modulus) [15], ARFI (0.49–21.16 kPa, converted from shear wave speed) [18], and SSI (1.50–11.32 kPa, converted from Young’s modulus) [19]. Mechanical testing results from ex vivo tissue samples also had similar range (approximately 3–20 kPa, converted from storage modulus at 1 Hz) [9].

In this study, a robust shear wave speed estimation method was developed to measure shear wave speed based on the time delays between all the possible pairings of the locations. Conventional shear wave elastography methods calculate time delays between one location and each of the other locations (e.g. location 1–2, 1–3, 1–4, and 1–5). In this case, if the quality of the ultrasound signal from location 1 was poor, then no reliable shear wave speed could be calculated from this set of data. Our method ensures that the entire dataset would not be compromised by the poor signal quality from one or two locations. Distance multiplied by CC coefficient was used as the weighting for linear regression. Higher CC coefficient indicates higher confidence in delay estimation. Therefore, pairs with higher CC coefficient receive higher weighting. In the presence of noise, the measured delay between two locations is the summation of the real delay Δt and the disturbance of noise δ, (Δt + δ). Assuming a relatively constant δ for all measurements, pairs with larger distance should have higher Δt and thus less relative error (δ/Δt). Therefore, pairs with larger distance were given higher weighting in this study. If no weighting was used, the fitting result would be more sensitive to noise presented in unreliable pairs with low CC coefficient or pairs with shorter distance and presumably larger relative error. Fig. 8 compares the results from all the acquisitions of one patient using the robust estimation method with the results using conventional method in which time delays were calculated between the first and the rest of the locations and no weightings were used for linear regression. For the robust method, the variation of the results was within 19% of the mean value, whereas for the conventional method the variation was 31%.

Fig. 8.

Fig. 8

Open in a new tab

The measured shear wave speeds for one patient using the robust shear wave speed estimation method and the conventional method. For the robust method, the variation of the results was within 19% of the mean value, whereas for the conventional method the variation was 31%.

Our study used multiple measurements to quantify liver elasticity for each patient (27 acquisitions × 21 shear wave speed measurements at different depths = 567 measurements). Therefore, CC coefficient, R2 of linear regression, and the speed variation along depth were used as quality control to keep more reliable results, among which the median value was used as the final result. These thresholds were selected empirically but blinded to MRE results. After applying these quality control measures, among 49 patients, 40 patients still had over 280 remaining measurements (averaged more than 10 measurements for each acquisition). The remaining measurements for each of the other 9 patients were over 140 (averaged more than 5 measurements for each acquisition). Therefore, the remaining results were still sufficient even if some of the results were discarded. Other studies have used the ratio between interquartile range and median value as quality control [33, 34]. Here we used a similar approach to keep the most consistent measurement results among results from different depths. Because the shear waves were generally consistent within the focal zone, the measured shear wave speeds should not vary much through depth. Therefore, rejecting the outliers along depth should not have a strong impact on the final results. As shown in Fig. 4, the variation among different depths within the same acquisition was relatively small and generally less than the differences among acquisitions obtained at different measurement locations.

A constant tissue density of 1000 kg/m3 was used to calculate shear modulus from shear wave speed based on Equation (1). To our knowledge, no liver density change due to fibrosis has been reported, and all the liver fibrosis studies assume a constant density. Because mass density of different soft tissues does not change much [29], we do not expect significant variation for liver tissues with different fibrosis stages. Even if the density did vary among different patients, the comparison between ultrasound and MRE measurements would still be valid, because both methods assume a fixed tissue density. Therefore, the comparison was essentially about the shear wave speed which would not be impacted by the tissue density.

Equation (1) ignores viscosity when calculating the shear modulus from the shear wave speed. The liver tissue is viscoelastic [35] and the dispersion effect [36] has implications on measurement results, which means measured shear wave speed increases with the shear wave frequency. The shear waves induced by acoustic radiation force generally have a higher center frequency than the 60 Hz shear waves generated by the mechanical vibration in MRE. Therefore, the measured shear wave speeds should be higher with ultrasound than with MRE, resulting in higher shear moduli using the ultrasound shear wave measurement, as shown in Fig. 6. Such differences were consistent with the reported values of the studies using an ultrasound radiation force based method [19] and the MRE method [12]. For liver fibrosis staging, this difference may not be important, because we are only looking for the correlation between shear wave measurement and the disease state. A previous study shows that the performance of liver fibrosis staging was not compromised even when viscosity was ignored [21]. On the other hand, Quantitative Imaging Biomarkers Alliance (QIBA) founded by Radiological Society of North America (RSNA) has been working on standardization of shear wave measurement across different imaging modalities [37].

Another possible reason for higher shear moduli measured using ultrasound shear wave method might be the diffraction effect [38]. When the measurement area is close to the push beam area, the size of the push beam becomes non-negligible and can cause overestimation of the shear wave speed. In our study, in order to capture shear waves with higher amplitude, the shear wave speed was measured approximately from 1 mm to 6 mm away from the push axis, where the effect of the push beam was more significant. Therefore, the shear wave speed could be somewhat overestimated especially for very stiff livers. On the other hand, the overestimation for very stiff livers should not compromise the performance for fibrosis staging, since they would be categorized as advanced fibrosis anyway.

In this study, only 8 patients were diagnosed with advanced fibrosis (μMRE ≥ 5.0 kPa), which was determined by the distribution of patients undergoing liver MRE exam in this study. Therefore, the ROC curve for separating patients with advanced fibrosis was based on a relatively small sample size, which was one of the limitations of this study.

Besides the offline shear wave measurement method used in this study, the iU22 scanner was also equipped with real-time processing functionality. Preliminary evaluation of real-time processing of the ultrasound data also suggested good correlation with the MRE measurements. More complete studies using iU22 real-time shear wave measurement will be presented in the future.

CONCLUSION

In this study, fifty patients with liver MRE were studied using the iU22 ultrasound scanner modified with shear wave measurement functionality. The shear moduli measured by ultrasound were compared to the MRE results. The ultrasound-based shear wave measurement showed a significant correlation with MRE, and was able to separate the patients with minimum fibrosis (μMRE ≤ 2.9 kPa) and the patients with advanced fibrosis (μMRE ≥ 5.0 kPa), indicating that the ultrasound radiation force based shear wave measurement is a promising tool for non-invasive liver fibrosis staging.

Fig. 7.

Fig. 7

Open in a new tab

The ROC curves of discriminating minimum fibrosis (μMRE ≤ 2.9 kPa) and advanced fibrosis (μMRE ≥ 5.0 kPa) using clinical routine cut points for MRE. The area under the ROC curve for separating minimum fibrosis was 0.89, whereas the area under the ROC curve for separating advanced fibrosis was 0.96.

ACKNOWLEDGMENTS

This work was supported by NIH grants DK082408, EB001981, and EB002167. The content is solely the responsibility of the authors and does not necessarily represent the official views of NIH. Mayo Clinic and some of the authors have financial interest in the technology described here.

REFERENCES

  • 1.Friedman SL. Liver fibrosis -- from bench to bedside. J Hepatol. 2003;38(Suppl 1):S38–S53. doi: 10.1016/s0168-8278(02)00429-4. [DOI] [PubMed] [Google Scholar]
  • 2.HHS, CDC, NCHS. National hospital discharge survey. 2010 [Google Scholar]
  • 3.Murphy SL, Xu J, Kochanek KD. National Vital Statistics Reports. 2013 [Google Scholar]
  • 4.Bravo AA, Sheth SG, Chopra S. Liver biopsy. N Engl J Med. 2001;344:495–500. doi: 10.1056/NEJM200102153440706. [DOI] [PubMed] [Google Scholar]
  • 5.Afdhal NH. Biopsy or biomarkers: is there a gold standard for diagnosis of liver fibrosis? Clin Chem. 2004;50:1299–1300. doi: 10.1373/clinchem.2004.035899. [DOI] [PubMed] [Google Scholar]
  • 6.Regev A, Berho M, Jeffers LJ, Milikowski C, Molina EG, Pyrsopoulos NT, et al. Sampling error and intraobserver variation in liver biopsy in patients with chronic HCV infection. Am J Gastroenterol. 2002;97:2614–2618. doi: 10.1111/j.1572-0241.2002.06038.x. [DOI] [PubMed] [Google Scholar]
  • 7.Yeh WC, Li PC, Jeng YM, Hsu HC, Kuo PL, Li ML, et al. Elastic modulus measurements of human liver and correlation with pathology. Ultrasound Med Biol. 2002;28:467–474. doi: 10.1016/s0301-5629(02)00489-1. [DOI] [PubMed] [Google Scholar]
  • 8.Mazza E, Nava A, Hahnloser D, Jochum W, Bajka M. The mechanical response of human liver and its relation to histology: an in vivo study. Med Image Anal. 2007;11:663–672. doi: 10.1016/j.media.2007.06.010. [DOI] [PubMed] [Google Scholar]
  • 9.DeWall RJ, Bharat S, Varghese T, Hanson ME, Agni RM, Kliewer MA. Characterizing the compression-dependent viscoelastic properties of human hepatic pathologies using dynamic compression testing. Phys Med Biol. 2012;57:2273–2286. doi: 10.1088/0031-9155/57/8/2273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Magnetic-Resonance Elastography by Direct Visualization of Propagating Acoustic Strain Waves. Science. 1995;269:1854–1857. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
  • 11.Yin M, Talwalkar JA, Glaser KJ, Manduca A, Grimm RC, Rossman PJ, et al. Assessment of hepatic fibrosis with magnetic resonance elastography. Clin Gastroenterol Hepatol. 2007;5:1207–1213. e2. doi: 10.1016/j.cgh.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Huwart L, Sempoux C, Vicaut E, Salameh N, Annet L, Danse E, et al. Magnetic resonance elastography for the noninvasive staging of liver fibrosis. Gastroenterology. 2008;135:32–40. doi: 10.1053/j.gastro.2008.03.076. [DOI] [PubMed] [Google Scholar]
  • 13.Huwart L, Peeters F, Sinkus R, Annet L, Salameh N, ter Beek LC, et al. Liver fibrosis: non-invasive assessment with MR elastography. NMR Biomed. 2006;19:173–179. doi: 10.1002/nbm.1030. [DOI] [PubMed] [Google Scholar]
  • 14.Wang QB, Zhu H, Liu HL, Zhang B. Performance of magnetic resonance elastography and diffusion-weighted imaging for the staging of hepatic fibrosis: A meta-analysis. Hepatology. 2012;56:239–247. doi: 10.1002/hep.25610. [DOI] [PubMed] [Google Scholar]
  • 15.Sandrin L, Fourquet B, Hasquenoph JM, Yon S, Fournier C, Mal F, et al. Transient elastography: a new noninvasive method for assessment of hepatic fibrosis. Ultrasound Med Biol. 2003;29:1705–1713. doi: 10.1016/j.ultrasmedbio.2003.07.001. [DOI] [PubMed] [Google Scholar]
  • 16.Castera L, Vergniol J, Foucher J, Le Bail B, Chanteloup E, Haaser M, et al. Prospective comparison of transient elastography, Fibrotest, APRI, and liver biopsy for the assessment of fibrosis in chronic hepatitis C. Gastroenterology. 2005;128:343–350. doi: 10.1053/j.gastro.2004.11.018. [DOI] [PubMed] [Google Scholar]
  • 17.Palmeri ML, Wang MH, Dahl JJ, Frinkley KD, Nightingale KR. Quantifying hepatic shear modulus in vivo using acoustic radiation force. Ultrasound Med Biol. 2008;34:546–558. doi: 10.1016/j.ultrasmedbio.2007.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Boursier J, Isselin G, Fouchard-Hubert I, Oberti F, Dib N, Lebigot J, et al. Acoustic radiation force impulse: a new ultrasonographic technology for the widespread noninvasive diagnosis of liver fibrosis. Eur J Gastroenterol Hepatol. 2010;22:1074–1084. doi: 10.1097/MEG.0b013e328339e0a1. [DOI] [PubMed] [Google Scholar]
  • 19.Bavu E, Gennisson JL, Couade M, Bercoff J, Mallet V, Fink M, et al. Noninvasive in vivo liver fibrosis evaluation using supersonic shear imaging: a clinical study on 113 hepatitis C virus patients. Ultrasound Med Biol. 2011;37:1361–1373. doi: 10.1016/j.ultrasmedbio.2011.05.016. [DOI] [PubMed] [Google Scholar]
  • 20.Muller M, Gennisson JL, Deffieux T, Tanter M, Fink M. Quantitative Viscoelasticity Mapping of Human Liver Using Supersonic Shear Imaging: Preliminary in Vivo Feasability Study. Ultrasound Med Biol. 2009;35:219–229. doi: 10.1016/j.ultrasmedbio.2008.08.018. [DOI] [PubMed] [Google Scholar]
  • 21.Chen S, Sanchez W, Callstrom MR, Gorman B, Lewis JT, Sanderson SO, et al. Assessment of liver viscoelasticity by using shear waves induced by ultrasound radiation force. Radiology. 2013;266:964–970. doi: 10.1148/radiol.12120837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Oudry J, Chen J, Glaser KJ, Miette V, Sandrin L, Ehman RL. Cross-validation of magnetic resonance elastography and ultrasound-based transient elastography: a preliminary phantom study. J Magn Reson Imaging. 2009;30:1145–1150. doi: 10.1002/jmri.21929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Motosugi U, Ichikawa T, Araki T, Matsuda M, Fujii H, Enomoto N. Bayesian prediction for liver fibrosis staging: combined use of elastography and serum fibrosis markers. Hepatology. 2013;58:450–451. doi: 10.1002/hep.26144. [DOI] [PubMed] [Google Scholar]
  • 24.Yoon JH, Lee JM, Woo HS, Yu MH, Joo I, Lee ES, et al. Staging of hepatic fibrosis: comparison of magnetic resonance elastography and shear wave elastography in the same individuals. Korean J Radiol. 2013;14:202–212. doi: 10.3348/kjr.2013.14.2.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.AIUM/NEMA. Revision 2. Laurel, MD: American Institute of Ultrasound in Medicine; 2009. Standard for real-time display of thermal and mechanical acoustic output indices on diagnostic ultrasound equipment. [Google Scholar]
  • 26.Lubinski MA, Emelianov SY, O'Donnell M. Speckle tracking methods for ultrasonic elasticity imaging using short-time correlation. IEEE Trans Ultrason Ferroelectr Freq Control. 1999;46:82–96. doi: 10.1109/58.741427. [DOI] [PubMed] [Google Scholar]
  • 27.McLaughlin J, Renzi D. Shear wave speed recovery in transient elastography and supersonic imaging using propagating fronts. Inverse Probl. 2006;22:681–706. [Google Scholar]
  • 28.Yamakoshi Y, Sato J, Sato T. Ultrasonic imaging of internal vibration of soft tissue under forced vibration. IEEE Trans Ultrason Ferroelectr Freq Control. 1990;37:45–53. doi: 10.1109/58.46969. [DOI] [PubMed] [Google Scholar]
  • 29.Duck FA. Physical Properties of Tissue: A Comprehensive Reference Book. London: Academic Press; 1990. [Google Scholar]
  • 30.Pearson K. Mathematical contributions to the theory of evolution. III. Regression, heredity and panmixia. Philos Trans Royal Soc London Ser A. 1896;187:253–318. [Google Scholar]
  • 31.Amador C, Urban MW, Shigao C, Qingshan C, Kai-Nan A, Greenleaf JF. Shear Elastic Modulus Estimation From Indentation and SDUV on Gelatin Phantoms. IEEE Trans Bio-med Eng. 2011;58:1706–1714. doi: 10.1109/TBME.2011.2111419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Hamhaber U, Grieshaber FA, Nagel JH, Klose U. Comparison of quantitative shear wave MR-elastography with mechanical compression tests. Magn Reson Med. 2003;49:71–77. doi: 10.1002/mrm.10343. [DOI] [PubMed] [Google Scholar]
  • 33.Cassinotto C, Lapuyade B, Ait-Ali A, Vergniol J, Gaye D, Foucher J, et al. Liver Fibrosis: Noninvasive Assessment with Acoustic Radiation Force Impulse Elastography--Comparison with FibroScan M and XL Probes and FibroTest in Patients with Chronic Liver Disease. Radiology. 2013;269:283–292. doi: 10.1148/radiol.13122208. [DOI] [PubMed] [Google Scholar]
  • 34.Ferraioli G, Tinelli C, Dal Bello B, Zicchetti M, Filice G, Filice C. Accuracy of real-time shear wave elastography for assessing liver fibrosis in chronic hepatitis C: a pilot study. Hepatology. 2012;56:2125–2133. doi: 10.1002/hep.25936. [DOI] [PubMed] [Google Scholar]
  • 35.Liu Z, Bilston L. On the viscoelastic character of liver tissue: experiments and modelling of the linear behaviour. Biorheology. 2000;37:191–201. [PubMed] [Google Scholar]
  • 36.Chen S, Fatemi M, Greenleaf JF. Quantifying elasticity and viscosity from measurement of shear wave speed dispersion. J Acoust Soc Am. 2004;115:2781–2785. doi: 10.1121/1.1739480. [DOI] [PubMed] [Google Scholar]
  • 37.Hall TJ, Milkowski A, Garra B, Carson P, Palmeri M, et al. RSNA/QIBA: Shear wave speed as a biomarker for liver fibrosis staging. 60th IEEE International Ultrasonics Symposium; Prague. 2013. Czech Republic. [Google Scholar]
  • 38.Song P, Zhao H, Manduca A, Urban MW, Greenleaf JF, Chen S. Comb-push ultrasound shear elastography (CUSE): a novel method for two-dimensional shear elasticity imaging of soft tissues. IEEE Trans Med Imaging. 2012;31:1821–1832. doi: 10.1109/TMI.2012.2205586. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES