The Impact on CT Dose of the Variability in Tube Current Modulation Technology: a Theoretical Investigation

Abstract

Body CT scans are routinely performed using tube-current-modulation (TCM) technology. There is notable variability across CT manufacturers in terms of how TCM technology is implemented. Some manufacturers aim to provide uniform image noise across body regions and patient sizes, whereas others aim to provide lower noise for smaller patients. The purpose of this study was to conduct a theoretical investigation to understand how manufacturer-dependent TCM scheme affects organ dose, and to develop a generic approach for assessing organ dose across TCM schemes. The adult reference female extended cardiac-torso (XCAT) phantom was used for this study. A ray-tracing method was developed to calculate the attenuation of the phantom for a given projection angle based on phantom anatomy, CT system geometry, X-ray energy spectrum, and bowtie filter filtration. The tube current (mA) for a given projection angle was then calculated as a log-linear function of the attenuation along that projection. The slope of this function, termed modulation control strength, α, was varied from 0 to 1 to emulate the variability in TCM technology. Using a validated Monte Carlo program, organ dose was simulated for five α values (α = 0, 0.25, 0.5, 0.75, and 1) in the absence and presence of a realistic system mA limit. Organ dose was further normalized by volume-weighted CT dose index (CTDI_vol) to obtain conversion factors (h factors) that are relatively independent of system specifics and scan parameters. For both chest and abdomen-pelvis scans and for 24 radiosensitive organs, organ dose conversion factors varied with α, following second-order polynomial equations. This result suggested the need for α-specific organ dose conversion factors (i.e., conversion factors specific to the modulation scheme used). On the other hand, across the full range of α values, organ dose in a TCM scan could be derived from the conversion factors established for a fixed-mA scan (h_FIXED). This was possible by multiplying h_FIXED by a revised definition of CTDI_vol that accounts for two factors: (a) the tube currents at the location of an organ and (b) the variation in organ volume along the longitudinal direction. This α-generic approach represents an approximation. The error associated with this approximation was evaluated using the α-specific organ dose (i.e., the organ dose obtained by using α-specific mA profiles as inputs into the Monte Carlo simulation) as the reference standard. When the mA profiles were constrained by a realistic system limit, this α-generic approach had errors of less than ~20% for the full range of values. This was the case for 24 radiosensitive organs in both chest and abdomen-pelvis CT scans with the exception of thyroid in the chest scan and bladder in the abdomen-pelvis scan. For these two organs, the errors were less than ~40%. The results of this theoretical study suggested that knowing the mA modulation profile and the fixed-mA conversion factors, organ dose may be estimated for a TCM scan independent of the specific modulation scheme applied.

1. Introduction

To promote the appropriate use of CT radiation and avoid unnecessary exposure, various institutions are actively developing dose monitoring programs (Cook et al., 2010; Li et al., 2011e; Christianson et al., 2012). Such programs automatically extract quality assurance dose quantities, such as volume-weighted CT dose index (CTDI_vol), from the patient’s dosimetry report. They can further track these dose quantities over time. However, as quality assurance dose quantities do not represent patient dose (McCollough et al., 2011), they cannot be used to compare dose across examination types or patient sizes. Therefore, it is necessary to convert quality assurance dose quantities into organ dose. Multiple studies in chest and abdominal CT have shown that the conversion factors from CTDI_vol to organ dose (denoted as h factors) have an exponential relationship with body diameter (Turner et al., 2011; Li et al., 2011b; AAPM). Furthermore, for organs fully-encompassed by the primary radiation beam, h factors do not depend strongly on scan parameters (Li et al., 2011b) and scanner models (Turner et al., 2010). These desired properties suggest that h factors may be built into dose monitoring programs to allow organ dose to be monitored for individual patients. However, existing h factors are mainly limited to fixed-tube-current examinations.

Recently a number of research groups have investigated how tube current modulation (TCM) impacts dose and dose conversion coefficients (Huda et al., 2008; van Straten et al., 2009; Angel et al., 2009a; Angel et al., 2009b; Schlattl et al., 2010; Zanca et al., 2011; Khatonabadi et al., 2012; Rendon et al., 2013; Khatonabadi et al., 2013a; Rupcich et al., 2012). For example, Schlattl and colleagues (Schlattl et al., 2010) published h factors associated with TCM examinations for four adult phantoms and various examination types. Their study used the modulation scheme described by Kalender et al. (Kalender et al., 1999), i.e., the tube current at the source position φ_s was modulated with the square root of the attenuation measured at source position φ_s−180°. For angular modulation, this scheme has been shown to provide the minimum noise at a given dose (Gies et al., 1999). However, this scheme only represents one implementation of the TCM technology. There is notable variability across CT manufacturers in terms of how TCM technology is implemented. Some manufacturers aim to provide uniform image noise across body regions and patient sizes, whereas others aim to provide lower noise for smaller patients and higher noise for larger patients. The dependence of h factors on modulation scheme is currently unknown. Methods to estimate organ dose in TCM scans also have not been tested across modulation schemes (Khatonabadi et al., 2013a).

In this theoretical study, we focused on chest and abdomen-pelvis CT, two examination types that frequently use TCM. A validated Monte Carlo program was combined with realistic human anatomy to simulate organ dose and compute CTDI_vol-to-organ dose conversion factors (i.e., h factors). Our purpose was two-fold: (1) to evaluate how different implementations of the TCM technology affect h factors in chest and abdomen-pelvis CT and (2) to develop a generic approach for assessing organ dose across modulation schemes.

2. Methods and materials

2.1. Theory

The exact TCM principles employed by various CT manufacturers are proprietary and not publicly available. However, an earlier investigation (Keat, 2005) conducted by the ImPACT group (National Health Service CT Evaluation Centre, London, UK) provided important insight into the underlying theory. In the ImPACT study, the automatic exposure control systems of four CT manufacturers (GE, Siemens, Philips, and Toshiba) were evaluated using a cone-shaped phantom, representing body sizes ranging from smaller than a newborn child to larger than an average-sized adult. Their study showed that for three of the manufacturers (GE, Siemens, and Toshiba), the logarithm of tube current (mA) increases roughly linearly with phantom diameter (d),

$$\ln \mathrm{mA}=b+md.$$ (1)

A similar relationship was not available for the Philips system included in the ImPACT study because at the time of the study, the Philips system adjusted tube current from one patient to another, but did not vary tube current within a patient scan. It was further shown in the ImPACT study that in Equation 1, the intercept b depended on the choice of scan parameters (e.g., pitch, noise index setting for a GE system, and standard deviation setting for a Toshiba system). In contrast, the slope m was shown to be generally independent of scan parameters for a given manufacturer; however, it differed from one manufacturer to another. For the Siemens system using the CAREDose4D package (Flohr, 2011), m was also shown to depend on the CAREDose4D adaptation strength (e.g., weak, average, and strong). Equation (1) can be reformatted as

$$\mathrm{mA}=e^b\cdot e^{md}=e^b\cdot {\left(e^{\mu d}\right)}^{\alpha },$$ (2)

where μ denotes the effective attenuation coefficient of the phantom in a given CT beam, and thus e^μd represents the attenuation of the patient. As a first-order approximation, Equation 2 suggests that the different implementations of TCM may be modeled generically as

$$\mathrm{mA}=\beta \cdot A^{\alpha },$$ (3)

where A is the attenuation (A = I₀/I) of the patient for a given projection, i.e., the ratio of x-ray intensity before (I₀) and after (I) being attenuated by the patient. In Equation 3, α controls the strength of the modulation, which differs from one implementation (i.e., one manufacturer or modulation setting) to another. For example, α =1 results in constant noise in all measured CT projections and consequently uniform noise across body regions and patient sizes. In contrast, α =0.5 results in higher noise in high-attenuation projections and consequently higher noise in high-attenuating body regions and larger patients. For angular modulation, α = 0.5 has been shown to provide the minimum noise at a given dose (Gies etal., 1999). Lastly, α = 0 corresponds to no modulation or a fixed-tube-current scan. Therefore, the variability in TCM technology and its effect on CT dose may be studied by varying the value of α from 0 to 1.

Earlier studies showed that the dose conversion factors do not depend strongly on scan parameters(Li et al., 2011b) or scanner models (Turner etal., 2010). Therefore, they also donot depend strongly on the proportionality constant β( = e^b) in Equation 3. For this reason, the effect of TCM scheme (i.e., the effect of α) on dose conversion factors can be studied using a representative CT system and are presentative set of scan parameters.

2.2. Computational phantom

In this study, the effect of α was investigated by estimating organ dose for a computational phantom using Monte Carlo simulations. The computational phantom was the adult reference female extended cardiac-torso (XCAT) phantom (Segars et al., 2010). The female phantom was chosen because female patients are more radiosensitive than male patients (NRC, 2006). The phantom was initially created based primarily on the Visible Human data from the National Library of Medicine. Defined by flexible nonuniform rational B-spline (NURBS) surfaces, the phantom was later transformed to match body measurements and organ volumes for a 50^th percentile (height and weight) female. Figure 1 illustrates the surface-rendered views of this phantom. The arms of the phantom were raised above the head to mimic the usual patient posture during a chest or abdomen-pelvis CT scan.

Figure 1.

Surface-rendered views of the XCAT female reference phantom.

For input into Monte Carlo simulations, the phantom was voxelized at 3.45-mm isotropic resolution with the skin modeled as a single voxel layer on the surface of the phantom. This voxel size was chosen because it represented a reasonable tradeoff between phantom resolution and memory requirement, storage space requirement, as well as simulation speed. The voxelized phantom (weight: 74 kg, height: 170 cm, average chest diameter: 29.3 cm, average abdomen-pelvis diameter: 27.5 cm) had 44 organs each labeled by a unique integer identification number. A list of these organs has been reported in an earlier publication (Li et al., 2011d); with the exception of salivary glands, lymphatic nodes, and oral mucosa, the list included all the radiosensitive organs defined by ICRP Publication 103 (ICRP, 2007)

2.3. Tube current modulation profiles

A method was developed to generate tube current (mA) modulation profiles based on the attenuation of the phantom. Defining the gantry angle at the start of a CT scan as zero, the gantry angle at any z location was calculated as

$$\theta =\frac{z-z_o}{S}2\pi ,$$ (4)

where z_o is the starting z location of the CT scan and S denotes table increment per gantry rotation. For a CT scan covering three full rotations, θ ranged between 0 and 6π. The effective mAs (mAs divided by pitch) at a given gantry angle was calculated as

$$\mathrm{eff}\_{\mathrm{mAs}}_{\theta }=\mathrm{eff}\_{\mathrm{mAs}}_{ref}{\left(\frac{A_{\theta }}{A_{ref}}\right)}^{\alpha },$$ (5)

where A_θ denotes the attenuation at gantry angle θ, i.e., the attenuation of the polyenergetic x-ray beam by the bowtie filter and the phantom, and A_ref is the reference attenuation, defined in this study as the attenuation of the polyenergetic x-ray spectrum by 34-cm of water as well as the center of the bowtie filter. The effective mAs value corresponding to A_ref is denoted in Equation 5 as eff_mAs_ref. It will be referred to as the reference effective mAs of the scan.

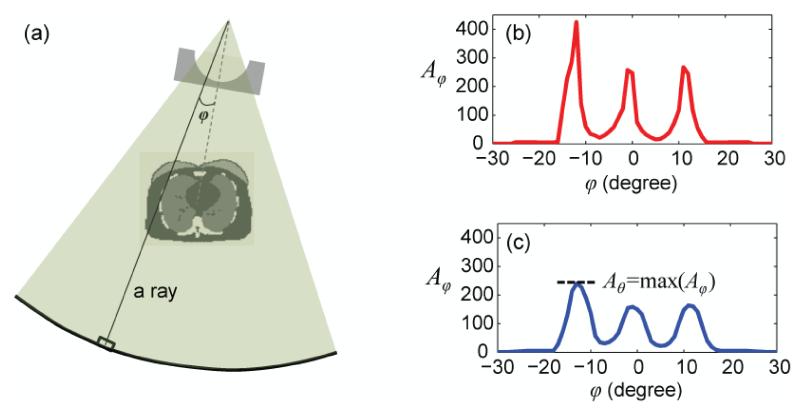
To determine A_θ for a given gantry angle θ (corresponding to a given z location per Equation 4), the attenuation along each ray (Figure 2a) was first calculated as

$$A_{\phi }=\frac{\sum _i{E}_i{N}_i}{\sum _i{E}_i{N}_i\exp (-\sum _{j\in \left\{\text{patient}\right\}}\mu (materia{l}_j,E_i)\Delta l_j-\sum _{k\in \left\{\text{bowtie}\right\}}\mu (materia{l}_k,E_i\left)\Delta l_k\right)},$$ (6)

where the subscript φ is the angular position of the ray (or the detector element) along the fan-angle direction (Figure 2a), E_i denotes the center of the i^th energy bin in the polyenergetic x-ray spectrum, and N_i denotes the (relative) number of photons in the i^th bin. The subscript j indices the patient voxels along the ray, and the subscript k indices the different bowtie filter materials along the ray. μ is linear attenuation coefficient, and Δl denotes the path length of the ray in a given patient voxel or bowtie material. The numerator and the denominator in Equation 6 correspond respectively to the signals at the detector element without and with attenuations from the patient and the bowtie filter. Therefore, A_φ is the attenuation along the ray “measured” by the corresponding detector element (Figure 2). The attenuation for a given gantry angle θ was defined as

$$A_{\theta }=\max \left(A_{\phi }\right),$$ (7)

the maximum A_φ across all detector elements after smoothing A_φ using a 5-cm rectangular filter to minimize the influence of noise (Figure 2).

Figure 2.

The method used to determine the attenuation at a given gantry angle θ. (a) The attenuation calculation took into account the geometry of the CT system, the fan angle of the X-ray beam, the polyenergetic X-ray energy spectrum, and the attenuation through the bowtie filter and the phantom anatomy. (b) The attenuation was first calculated for individual rays and plotted as a function of the angular position φ of the ray (or the detector element) along the fan-angle direction. (c) The attenuation profile was smoothed to minimize the influence of noise. The peak value was taken as the attenuation at a given gantry angle θ.

A computer program (Matlab, R2010a; Mathworks, Natick, MA) was written to perform the calculations described above. The Matlab function fanbeam was used to calculate ${\sum }_{j\in \left\{\text{patient}\right\}}\mu (materia{l}_j,E_i)\Delta l_j$. The detector elements were assumed to space equally along a circular arc with an angular spacing Δφ of one degree. Bowtie filter geometry was defined as

$$pl=f\left(\phi \right),$$ (8)

where pl is the path length through each filter material. From Equation 8, Δl_k (see Equation 6) at any φ was calculated using interpolation.

Using the above method, five mA modulation profiles were generated for α values of 0, 0.25, 0.5, 0.75, and 1, assuming that the phantom underwent a chest CT scan on a 128-slice CT system (SOMATOM Definition Flash, Siemens Healthcare, Forchheim, Germany) at tube voltage of 120 kVp, helical pitch of 0.8, detector configuration of 2×64×0.6 mm, reference effective mAs of 150, and rotation time of 0.5 second. The polyenergetic x-ray spectrum at the exit of x-ray tube, the bowtie filtration (standard filter for adult body scans), and the geometry of the CT system provided by the manufacturer were used to generate the mA modulation profiles. The same method and parameters were used to generate five mA modulation profiles for an abdomen-pelvis CT scan. Typical of clinical scan coverage, the chest scan extended from 1 cm above lung apex to 1 cm below lung base, and the abdomen-pelvis scan extended from 1 cm above the superior edge of the liver to 1 cm below the inferior edge of the ischium. The overranging distance was assumed to be zero.

In a clinical CT system, the behavior of TCM is often complex and constrained by system tube current limits. Taking the CAREDose4D package of Siemens Healthcare (Flohr, 2011) for example, prior to a TCM scan, longitudinal modulation profiles in two orthogonal directions (anteroposterior and lateral directions) are determined based on a localization radiograph (Siemens, 2006). Their average is calculated as the Z profile, which serves as a constraint for the real-time modulation (Siemens, 2006). During the TCM scan, a combined longitudinal and angular modulation profile (XYZ profile) is generated in real time based on measured patient attenuation, satisfying the system mA limit as well as the constraint that the pre-calculated Z profile is the average of the XYZ profile in each rotation (per communication with the manufacturer). In this study, ten constrained mA modulation profiles were also generated, emulating the behavior of CAREDose4D. At each z location, in addition to A_θ, the attenuations along the anteroposterior and lateral directions, denoted as A_AP and A_LAT, were also determined and used to calculate eff_mAs_AP and eff_mAs_LAT per Equation 5. The average of eff_mAs_AP and eff_mAs_LAT, i.e.,(eff_mAs_AP + eff_mAs_LAT) × 0.5, was further averaged across all the z locations within a rotation to obtain a Z profile. To emulate the behavior of CAREDose 4D, within each rotation, the XYZ profile was shifted slightly so that its average matched the Z profile. If the Z profile exceeded the system limit (833 mA at 120 kVp), it was clipped to serve as a constraint for the XYZ profile. If the XYZ profile in a given rotation exceeded the system limit, the average of the profile remained unchanged whereas the amplitude of its modulation was scaled down to respect the system limit.

A total of twenty mA modulation profiles were generated, representing two scan types (chest and abdomen-pelvis scans), five modulation schemes (α values of 0, 0.25, 0.5, 0.75, and 1), and two conditions (unconstrained and constrained mA conditions).

2.4. Organ dose simulations

Organ dose received by the phantom was simulated using a Monte Carlo program for the above CT system, scan parameters and mA modulation profiles. The Monte Carlo program was previously developed and validated for simulating dose associated with fixed-mA scans for the same CT system (Li et al., 2011c; Tian et al.). In the original program, the effect of x-ray source motion during a helical scan was modeled by randomly sampling gantry angle θ with uniform probability from a range between 0 and the maximum gantry angle θ_max(e.g. α_max = 6π for a scan of three rotations). In this study, the Monte Carlo program was extended to model TCM scans. The mA modulation profile, mA(θ) was converted to a probability distribution function

$$p\left(\theta \right)\propto mA\left(\theta \right)0<\theta <{\theta }_{\max },$$ (9)

from which gantry angle (i.e., photon incident angle) was sampled using the Walker’s aliasing algorithm (Walker, 1977).

Monte Carlo simulation was performed for each of the twenty mA modulation profiles. Energy deposited in organs and tissues was tallied and used to calculate dose. Because bone marrow and bone surface were not explicitly modeled in the XCAT phantom, the following methods were used to assess dose to these two organs. To assess dose to the red bone marrow, volume-averaged photon fluence spectrum was tallied individually at each skeletal site and used to calculate dose to the red bone marrow via the fluence-to-dose conversion coefficients published by Cristy and Eckerman (Cristy and Eckerman, 1987). A single active marrow dose was then calculated as its skeletal average using the age-dependent fractional distribution of active marrow tabulated in ICRP Publication 89 (ICRP, 2002). Dose to the bone surface was approximated by the mass-weighted average of dose to the homogenous bones as recommended by Lee et al. (Lee et al., 2006).

Each mA modulation profile was simulated with 500 million photon histories using a single processor on a 2.3 GHz Linux server with 20 GB of random access memory (RAM). In terms of simulation time, each simulation took approximately an 11-hour runtime resulting in relative dose errors of less than 0.5% for organs in the scan coverage and less than 10% for other organs.

2.5. Effect of TCM scheme on dose conversion factors

As mentioned in the Introduction Section, the conversion factors from CTDI_vol to organ dose (h factors) have several desired properties, which lend them to practical clinical applications. To examine the effect of TCM scheme on h factors, the organ dose values obtained for each modulation profile were normalized by CTDI_vol to calculate the unitless h factors,

$$h=\frac{\text{organ dose}(\mathrm{mGy}∕100\mathrm{mAs})}{{\mathrm{CTDI}}_{\mathrm{vol}}(\mathrm{mGy}∕100\mathrm{mAs})}.$$ (10)

Here CTDI_vol (mGy/100mAs) was simulated using the above mentioned Monte Carlo program for the CT system and scan parameters used in this study. It agreed with measured value to within 10% (Tian et al.). To examine the effect of TCM scheme, h factors for various organs were plotted against α and correlated with α using nonlinear regression analysis.

2.6. Evaluation of approximation methods

Provided that α value can be determined for a given TCM scan, the relationship between h and α may be used to obtain the organ dose conversion factors appropriate for the TCM scheme used. Alternatively, it was postulated that approximation methods may be used to take advantage of the existing organ dose conversion factors for fixed-mA scans, h_FIXED (Khatonabadi et al., 2011; Li et al., 2011a; Khatonabadi et al., 2013a). The accuracy of three approximation methods was evaluated. The first method simply ignored the effect of TCM and was formulated as

$$D_{\mathrm{TCM}}^{\text{approx}}=h_{\text{FIXED}}\times {\mathrm{CTDI}}_{\mathrm{vol}},$$ (11)

where CTDI_vol is the CTDI_vol value displayed on the CT scanner console for a TCM scan, which is determined from the average mA value of the entire scan.

The second method was motivated by recent research (Khatonabadi et al., 2011; Li et al., 2011a; Khatonabadi et al., 2013a), which suggested that organ dose associated with a TCM scan may be approximated as

$$D_{\mathrm{TCM}}^{\text{approx}}=h_{\text{FIXED}}\times {\left({\mathrm{CTDI}}_{\mathrm{vol}}\right)}_{\text{organ}},$$ (12)

where(CTDI_vol)_organ is the CTDI_vol computed from the average mA values of all the axial slices containing the organ, i.e.,

$${\left({\mathrm{CTDI}}_{\mathrm{vol}}\right)}_{\text{organ}}=\frac{{\langle \mathrm{mA}\rangle }_{\text{organ}}}{{\langle \mathrm{mA}\rangle }_{\text{scan}}}{\mathrm{CTDI}}_{\mathrm{vol}}.$$ (13)

This method took into consideration that the average mA value at the location of an organ may differ substantially from the globally averaged mA value of the entire scan.

A refinement to the second method, the third method was formulated as

$$D_{\mathrm{TCM}}^{\text{approx}}=h_{\text{FIXED}}\times {\left({\mathrm{CTDI}}_{\mathrm{vol}}\right)}_{\text{organ, weighted}},$$ (14)

where (CTDI_vol)_{organ, weighted} is the CTDI_vol computed from the organ volume-weighted average mA value of all the axial slices containing the organ, i.e.,

$${\left({\mathrm{CTDI}}_{\mathrm{vol}}\right)}_{\text{organ, weighted}}=\frac{{\langle \mathrm{mA}\rangle }_{\text{organ, weighted}}}{{\langle \mathrm{mA}\rangle }_{\text{scan}}}{\mathrm{CTDI}}_{\mathrm{vol}},$$ (15)

$${\langle \mathrm{mA}\rangle }_{\text{organ,weighted}}=\frac{\sum _{z\in \left\{\text{organ}\right\}}{\mathrm{mA}}_z\cdot V_z}{\sum _{z\in \left\{\text{organ}\right\}}{V}_z},$$ (16)

where mA_z is the mA value at location z and V_z is the organ volume in the axial slice at location z (proportional to the number of organ voxels at this location). The third method took into consideration that certain organs, such as lung, vary in size considerably along the z direction. For such organs, dose is proportional to volume-weighted average mA (Figure 3).

Figure 3.

For organs that vary in size considerably along the z direction, dose is proportional to volume-weighted average mA. The rectangular box represents a cylindrical body section. The rectangular stripes represent organ volumes in contiguous CT slices. d denotes the dose per unit mA in a fixed-mA scan. V_i is organ volume in slice i. mA_i is tube current at the location of slice i. is organ density. E_i is energy deposited in V_i. D is organ dose in a TCM scan.

The accuracy of each approximation method was evaluated by calculating the discrepancy between $D_{\mathrm{TCM}}^{\text{approx}}$ and D_TCM (the organ dose obtained by using α-specific mA profiles as inputs into the Monte Carlo simulation) and examining the variation of this discrepancy as a function of modulation control strength α.

Hereafter, we will use the term “inside organs”, “peripheral organs”, and “outside organs” to refer to organs located on the inside, the periphery, and the outside of the scan coverage, respectively. The term “distributed organ” will be used to refer to organs distributed throughout the body (e.g., red bone marrow and skin). For chest and abdomen-pelvis CT scans, inside and peripheral organs account for around 90% of the effective dose (Li et al., 2012). The three approximation methods were evaluated for such organs.

3. Results

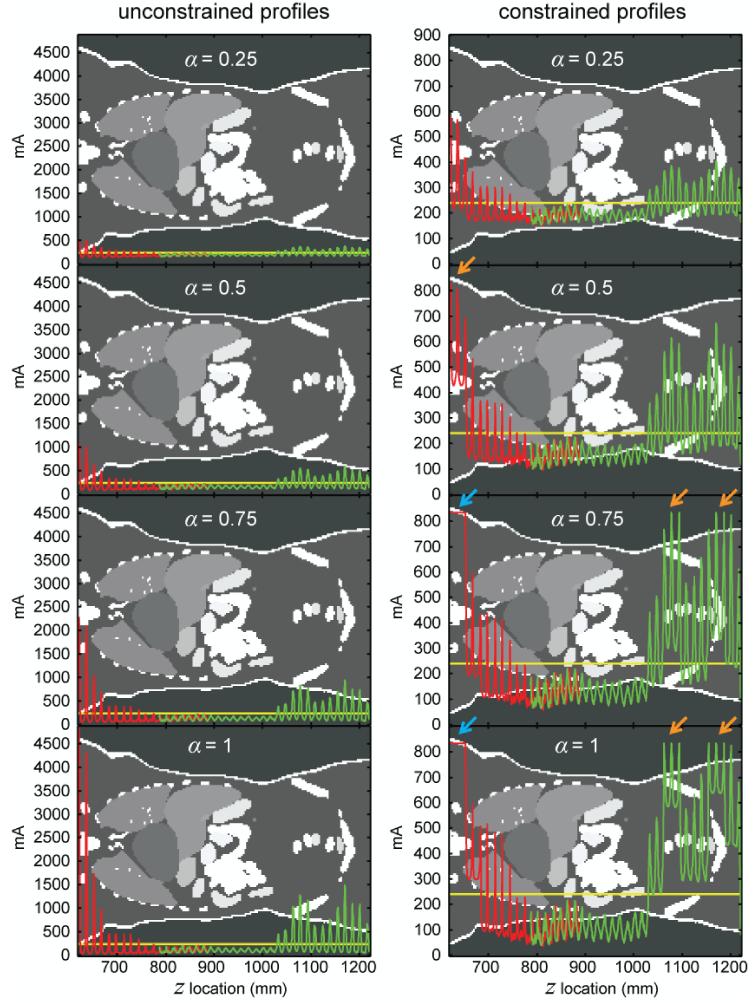
Figure 4 illustrates the mA modulation profiles associated with two scan types (chest and abdomen-pelvis scans), five modulation schemes (α values of 0, 0.25, 0.5, 0.75, and 1), and two conditions (unconstrained and constrained mA conditions). As can be expected from Equation 5, the amplitude of the modulation increased with increasing α. For chest CT, the unconstrained mA profiles exceeded the system limit (833 mA) around the shoulder region for α values of 0.5, 0.75, and 1. For abdomen-pelvis CT, this occurred around the pelvic region for α values of 0.75 and 1. At locations where the unconstrained mA profiles exceeded the system limit, the corresponding constrained mA profiles had a reduced modulation amplitude or zero modulation amplitude (arrows in Figure 4).

Figure 4.

Theoretical tube current (mA) modulation profiles generated for the XCAT female reference phantom under unconstrained and constrained conditions for chest (red) and abdomen-pelvis (green) CT scans. The two scans had an overlap of around 10 cm (z locations between 787 mm and 890 mm). At each z location in the overlapped region, the gantry angle (tube position) was different for the two scans, resulting in a difference in calculated attenuation (A_θ) and a corresponding mA difference. α controls the strength of the modulation as defined in Equation 3. The horizontal (yellow) line in each figure (240 mA) corresponds to the reference mA of the two scans. It also represents the constant tube current when α=0. At locations where the unconstrained mA profiles exceeded the system limit, the corresponding constrained mA profiles had a reduced modulation amplitude (orange arrows) or zero modulation amplitude (blue arrows). The grayscale image in the background is a single coronal plane taken about half-way in between the anterior and posterior surfaces of the phantom. The grayscale values in the image represent arbitrary organ tags.

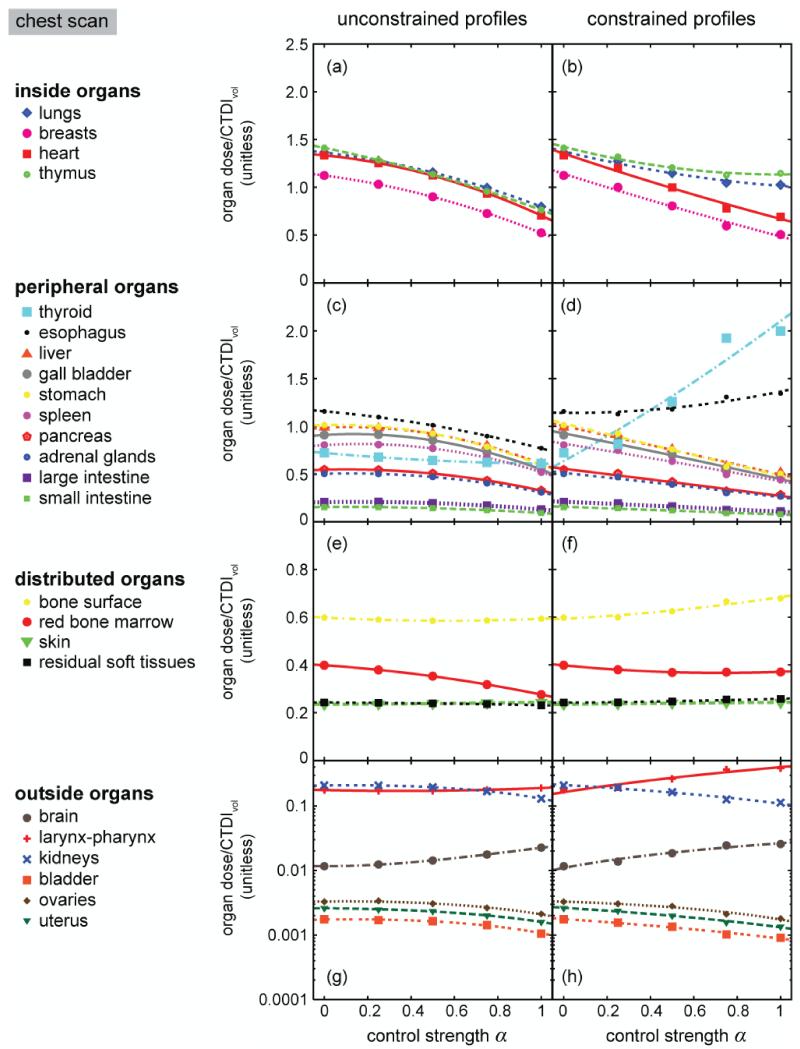
For both types of CT scans and all the radiosensitive organs, the variations of h with can be described by second-order polynomial equations under both unconstrained and constrained conditions (Figures 5 and 6, Tables 1-4). In chest CT, when CTDI_vol was held constant, increasing reduced the dose received by inside organs (i.e., lungs, breasts, heart, and thymus). Such was also the case for peripheral organs with two notable exceptions: the dose received by thyroid and esophagus increased with increasing when mA profiles were constrained by a system limit (Figure 5d). In abdomen-pelvis CT, when CTDI_vol was held constant, increasing decreased the dose received by inside and peripheral organs with the exception that the dose received by three organs in the pelvic region (bladder, uterus, and ovaries) increased with increasing (Figures 6a and 6b). For these three organs, the dose increase was more pronounced under the constrained condition. When CTDI_vol was held constant, the dose received by distributed and outside organs also varied with α, but the absolute values of the variations were small.

Figure 5.

Organ dose conversion factors as functions of modulation control strength α for a chest CT scan of the XCAT female reference phantom under unconstrained and constrained conditions. Curves in the plots represent second-order polynomial fits to the data (see fitting parameters in Tables 1 and 2).

Figure 6.

Organ dose conversion factors as functions of modulation control strength α for an abdomen-pelvis CT scan of the XCAT female reference phantom under unconstrained and constrained conditions. Curves in the plots represent second-order polynomial fits to the data (see fitting parameters in Tables 3 and 4).

Table 1.

Relationship between organ dose conversion factors (h factors) and modulation control strength (α), h = a + bα + cα², for the chest CT scan of the XCAT female reference phantom. mA modulation profiles are unconstrained.

	a	b	c	root-mean-square of residuals
inside
lungs	1.364610	−0.267555	−0.300147	0.001822
breasts	1.124090	−0.296075	−0.306274	0.003499
heart	1.334590	−0.220907	−0.409414	0.002767
thymus	1.413100	−0.463884	−0.186951	0.002552
periphery
thyroid	0.721679	−0.199957	0.088355	0.000470
esophagus	1.157420	−0.202643	−0.185829	0.003655
liver	0.984985	0.118477	−0.494930	0.002434
gall bladder	0.909644	0.133628	−0.495937	0.002670
stomach	1.013240	0.054449	−0.472743	0.001825
spleen	0.803284	0.141776	−0.423591	0.003134
pancreas	0.546265	0.055109	−0.274115	0.001006
adrenal glands	0.503715	0.059847	−0.254631	0.001417
large intestine	0.206345	0.034499	−0.111384	0.000354
small intestine	0.155140	0.014573	−0.077170	0.000393
distributed
bone surface	0.598185	−0.048014	0.042690	0.000463
red bone marrow	0.398188	−0.061083	−0.061496	0.000372
skin	0.235222	0.003455	0.004981	0.000111
residual soft tissue	0.242454	−0.003886	−0.007569	0.000140
outside
brain	0.011671	−0.000199	0.011003	0.000091
larynx-pharynx	0.175996	−0.031837	0.045541	0.000714
kidneys	0.207629	0.027093	−0.104841	0.000578
bladder	0.001739	0.000231	−0.000903	0.000034
ovaries	0.003317	0.000291	−0.001520	0.000085
uterus	0.002599	−0.000125	−0.000878	0.000032

Table 4.

Relationship between organ dose conversion factors (h factors) and modulation control strength (α), h = a + bα + cα², for the abdomen-pelvis CT scan of the XCAT female reference phantom. mA modulation profiles are constrained.

	a	b	c	root-mean-square of residuals
inside
liver	1.265400	−0.638703	−0.120265	0.013013
gall bladder	1.400040	−0.689331	−0.147075	0.014794
stomach	1.209730	−0.672198	−0.077942	0.012249
spleen	1.263650	−0.588961	−0.148128	0.012853
pancreas	1.34700	−0.648606	−0.084329	0.012106
adrenal glands	1.190130	−0.635750	−0.076245	0.012666
kidney	1.374690	−0.654802	−0.119295	0.014253
large intestine	1.412100	−0.397288	0.029570	0.014533
small intestine	1.426140	−0.476319	−0.005086	0.014991
bladder	1.053540	−0.114844	0.885912	0.024355
ovaries	1.063560	0.136186	0.382991	0.014231
uterus	1.103640	−0.041237	0.673072	0.024415
periphery
lungs	0.456328	−0.300766	−0.002674	0.004738
breasts	0.418616	−0.277784	−0.003166	0.004772
esophagus	0.377211	−0.241031	−0.007022	0.004720
heart	0.707089	−0.482898	0.005874	0.007597
distributed
bone surface	0.850485	0.031005	0.079422	0.000547
red bone marrow	0.576685	−0.031726	0.056790	0.001729
skin	0.368457	0.007789	−0.003575	0.000163
residual soft tissue	0.483451	0.000660	0.033109	0.001171
outside
brain	0.000855	−0.000508	−0.000035	0.000012
thyroid	0.036194	−0.025852	0.001987	0.000417
larynx-pharynx	0.016331	−0.010476	0.000118	0.000300
thymus	0.157139	−0.100731	−0.003107	0.001711

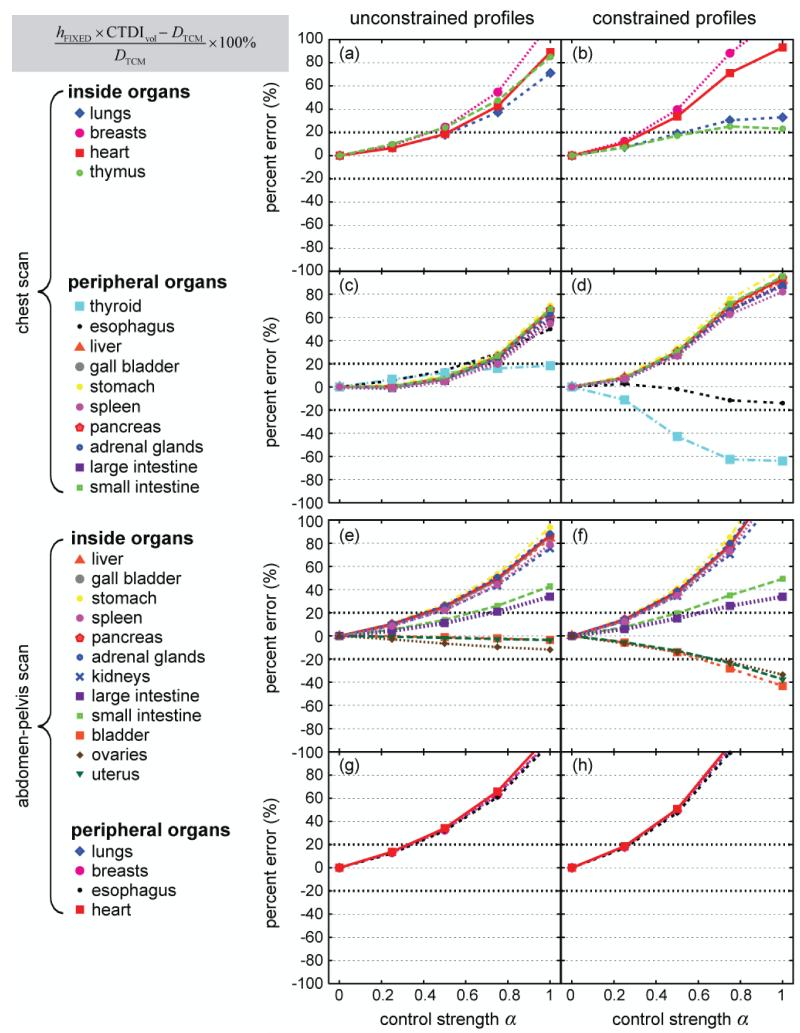
To evaluate the accuracy of the three approximation methods, D_TCM (the organ dose obtained by using α-specific mA profiles as inputs into the Monte Carlo simulation) was used as the reference standard. For both chest and abdomen-pelvis CT scans, h_FIXED × CTDI_vol was generally a poor estimate of D_TCM (Figure 7). The discrepancy between the two (i.e., the error associated with the first approximation method) increased with increasing α. The largest errors (~200%) were found under the constrained condition; they were the errors associated with heart dose and breast dose in the abdomen-pelvis scan when α=1 (exceeding the y range shown in Figure 7).

Figure 7.

Discrepancy between h_FIXED × CTDI_vol and D_TCM as a function of modulation control strength α. Data points are connected by lines for easy visualization. All data points are plotted over the same y range of [−100%, 100%] to allow the trends of the data to be better visualized. The data points cut off by the upper boarders of the plots represent percent errors greater than 100%.

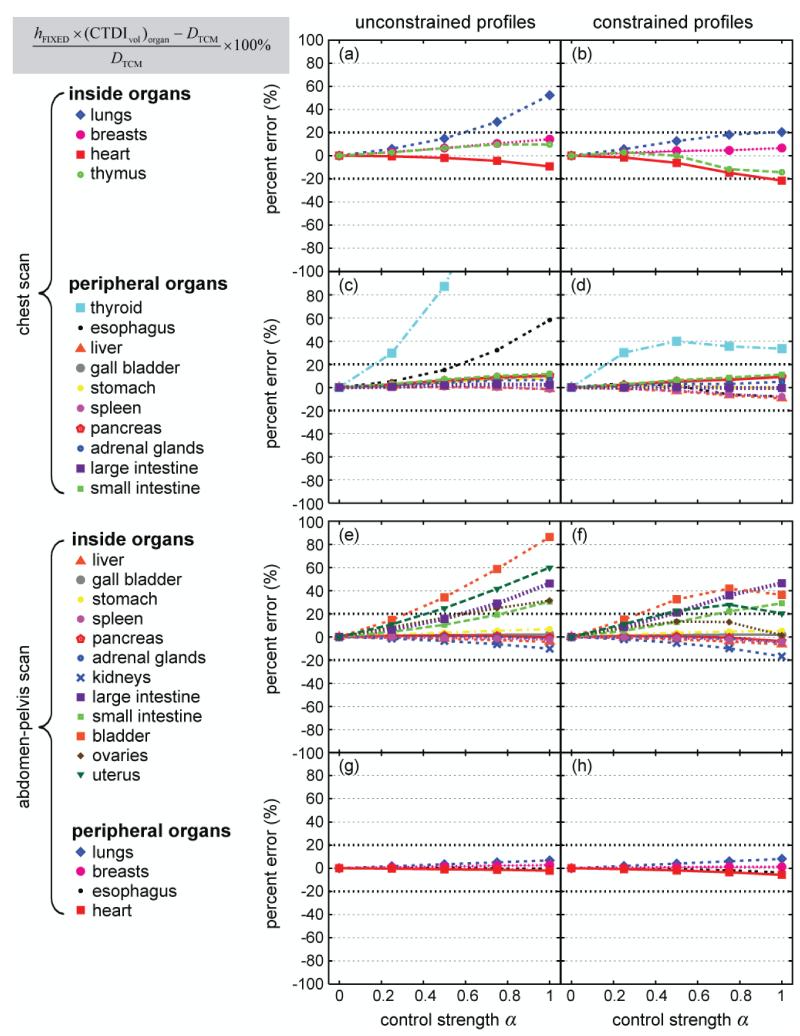
In general, the second approximation method, h_FIXED × (CTDI_vol)_organ, significantly improved the accuracy of dose estimation (Figure 8). However, there were notable exceptions. When mA profiles were unconstrained, using h_FIXED × (CTDI_vol)_organ significantly increased the errors associated with thyroid dose in the chest CT scan and the dose received by bladder, uterus, and ovaries in the abdomen-pelvis scan. Under the constrained condition (right column of Figure 8), the maximum error was ~50%.

Figure 8.

Discrepancy between h_FIXED × (CTDI_vol)_organ and D_TCM as a function of modulation control strength α. Data points are connected by lines for easy visualization. All data points are plotted over the same y range of [−100%, 100%] to allow the trends of the data to be better visualized. The data points cut off by the upper boarders of the plots represent percent errors greater than 100%.

Lastly, h_FIXED × (CTDI_vol)_{organ, weighted} provided the most accurate estimate of D_TCM under the constrained condition (Figure 9). The errors were less than ~20% across all the values with the exception of thyroid dose in the chest scan and bladder dose in the abdomen-pelvis scan. For these two organs, the errors were less than ~40%.

Figure 9.

Discrepancy between h_FIXED × (CTDI_vol)_{organ, weighted} and D_TCM as a function of modulation control strength α. Data points are connected by lines for easy visualization.

4. Discussion

In this study, we performed a theoretical investigation to understand how the variability in TCM technology affects organ dose conversion factors in chest and abdomen-pelvis CT. To the best of our knowledge, this work represents the first attempt to describe the different implementations of TCM technology using a unified mathematical framework. It also represents the first attempt to develop a reasonably generic approach for assessing organ dose across different modulation schemes.

This theoretical study showed that in chest and abdomen-pelvis CT, organ dose conversion factors (h factors) can be fitted to second-order polynomial equations of the modulation control strength. This is true under both unconstrained and constrained mA conditions. This result suggested that if an value can be established for a given CT system or modulation scheme, then the polynomial equations may be used to determine the h factors appropriate for the modulation scheme used.

In the chest CT scan, when CTDI_vol was held constant, the total number of photons outputted by the source was a constant. The higher the value α was, the more photons were distributed in the high-attenuation region (i.e., the shoulder region) and less photons in the low-attenuation region (i.e., the middle of the chest). This explained the decline of organ dose with increasing α for most inside and peripheral organs (Figures 5a-5d). Under the unconstrained condition, thyroid dose decreased very slightly with changing α (Figure 5c). This can be explained by the fact that although the shoulder region had an overall increase in photon flux with increasing α, the increase occurred in the lateral direction; the anteroposterior (AP) direction had a decrease in photon flux with increasing α(Figure 4, left column). Because the dose received by the thyroid was mostly affected by the beam in the AP direction, thyroid dose did not increase proportionally with an overall increase in photon flux at the shoulder region. Under the constrained condition (Figure 4, right column), whenever the mA limit was reached, the amplitude of the modulation around the shoulder region was reduced (α=0.5) or diminished to zero (α=0.75 and 1). As a result, the mA and hence the photon flux in the AP direction increased, resulting in increased thyroid dose with increasing α (Figure 5d). For the same reason, the dose received by esophagus, a centrally-located tubular organ, also increased with increasing α (Figure 5d).

In the abdomen-pelvis CT scan, the bony pelvic region was the high-attenuation region. What occurred in the shoulder region in the chest scan similarly occurred in the pelvic region in the abdomen-pelvis scan. Under the unconstrained condition, the dose received by the bladder, uterus, and ovaries only varied slightly with changing α (Figure 6a); however, under the constrained condition, increasing α increased the mA and hence the photon flux in the AP direction, resulting in a pronounced increase in the dose received by these three pelvic organs (Figure 6b).

The polynomial dependence of h factors on α further indicated that for most organs, significant dose estimation errors are introduced if one ignores the effect of TCM and simply uses h_FIXED × CTDI_vol to approximate organ dose (Figure 7). The errors are appreciable (up to ~50%) even for α=0.5, consistent with the results of Schlattl et al. (Schlattl et al., 2010). Because the average mA value at the location of an organ may differ substantially from the globally averaged mA value of the entire scan, h_FIXED × (CTDI_vol)_organ provides a better approximation to D_TCM (Figure 8). The utility of (CTDI_vol)_organ was recently reported by Khatonabadi et al. (Khatonabadi et al., 2013a), who studied the actual modulation profiles from a single clinical CT system (Sensation 64, Siemens Healthcare, Forchheim, Germany). Khatonabadi and colleagues showed that for large organs in the scan coverage, D_TCM/(CTDI_vol)_organ correlated better with patient diameter than D_TCM/CTDI_vol. This is consistent with our finding that D_TCM/(CTDI_vol)_organ approximates to h_FIXED, which has been shown in earlier studies (Turner et al., 2011; Li et al., 2011b) to correlate well with patient diameter for large organs in the scan coverage. However, because (CTDI)_{vol organ} is calculated as a simple average of the mA values at the location of an organ, it has two limitations: (a) it ignores the variation of organ volume along the z direction and (b) it ignores the non-uniform distribution of photon flux in the x-y plane and the interplay of which with organ size and location in the x-y plane. The first limitation can be overcome with the use of (CTDI_vol)_{organ, weighted}. As illustrated in Figure 3, when organ volume varies considerably along the z direction, organ dose is proportional to volume-weighted average mA, instead of a simple average. For example, lung dose in chest CT and the dose received by large and small intestines in abdomen-pelvis CT were significantly improved when (CTDI_vol)_{organ, weighted} was used in place of (CTDI_vol)_organ. However, neither new derivative of CTDI_vol overcomes the second limitation. Thus, they have limited utility in correcting dose errors for thyroid and bladder, both located centrally in asymmetrical regions of the body, where photon flux is highly non-uniform in the x-y plane.

It should be noted that although (CTDI_vol)_{organ, weighted} provides the most accurate dose estimates, its calculation requires slice-by-slice organ segmentation, which is more cumbersome than the calculation of (CTDI_vol)_organ, which only requires knowledge of the organ starting and ending locations. As shown in Figure 8, for certain organs, the use of (CTDI_vol)_organ already reduces the errors in dose estimation to within 20% across the full range of α value. For such organs, determining (CTDI_vol)_{organ, weighted} via slice-by-slice organ segmentation would not be necessary.

In summary, under the theoretical framework (i.e., Eq 3), we proposed two approaches for estimating organ dose from TCM scans.

1. The first approach is scanner-specific. Because organ dose conversion factors are second-order polynomial equations of α, estimating organ dose for a specific CT system requires the use of an α value specific to the TCM technology implemented on that CT system. Organ dose is estimated as

   $$D_{\mathrm{TCM}}=h_{\alpha }\times {\mathrm{CTDI}}_{\mathrm{vol}},$$ (17)

   whereh_α is an α-specific organ dose conversion factor appropriate for the TCM technology and the body size of the patient.
2. The second approach is scanner-generic. Organ dose is approximated as

   $$D_{\mathrm{TCM}}^{\text{approx}}=h_{\text{FIXED}}\times {\left({\mathrm{CTDI}}_{\mathrm{vol}}\right)}_{\text{organ,weighted}},$$ (18)

   where h_FIXED is the scanner-independent organ dose conversion factor published for fixed-tube-current scans, and independent of the specific CT system (or modulation scheme) used, (CTDI_vol)_{organ, weighted} is calculated from patient images using the organ volume information as well as the tube currents at the location of the organ (e.g., extracted from the DICOM headers of individual patient images). A method to automatically extract local tube current information was recently reported (Khatonabadi et al., 2013b).

Our study has several limitations. First, we did not explicitly estimate α values for specific CT systems used clinically. As indicated by Equation 3, to estimate α for a given CT system or modulation setting, one needs to measure tube current (mA) for two distinct known attenuations from a TCM scan. The body and head CTDI phantoms provide two distinct attenuations, which can be determined for a given CT beam by calculating the signal ratio between the peripheral detector channel (no attenuation) and the central detector channel (maximum attenuation). Such calculations can be readily performed by the CT manufacturers, which have ready access to the raw detector signals. Ordinary users of a CT system generally do not have access to the raw signals from CT detectors. An alternative approach is to measure the attenuations of the two CTDI phantoms using a radiographic system, the x-ray beam of which can be hardened to match the half-value layer (HVL) of a CT beam. The raw (unprocessed) images from the radiographic system provide information about the detector signals in the absence and presence of a CTDI phantom. It is possible that even for a single CT system or modulation setting, α may not have a single value, but may vary over a small range based, for example, on patient size. In that case, tube current should be measured for more than two distinct known attenuations. A taper-shaped phantom, such as the one developed by the ImPACT group (Keat, 2005) or Duke University (Wilson et al., 2013) can be used for this purpose. Although the ImPACT study (Keat, 2005) suggested that the variability in TCM technology can be described by a single parameter α, that study was based on a non-anthropomorphic phantom. It is possible that the complex behaviors of modern TCM technologies when applied to actual patients need to be modeled by more than one parameter. A separate study involving CT systems from major manufacturers as well as anatomically realistic anthropomorphic phantoms is needed to fully establish the feasibility of α and assess its clinical variability.

Another limitation of our study is that the constrained modulation profiles were generated to emulate the behavior of a single TCM algorithm (i.e., CAREDose 4D). Other TCM algorithms may apply mA constraints differently. However, the main effect of applying constraints is that the mA has an upper limit and cannot always reach its desired values. Therefore, the results we obtained using the constrained TCM profiles, although not specific for other TCM algorithms, are indicative of their effects in the presence of a tube current limit. It should be noted that the specific mA limit we applied (i.e., mA is limited to 833 mA at 120 kVp) represents the capacities of the current CT systems. Future CT systems may allow higher mA limits, making the unconstrained profiles more representative of clinical reality.

Third, the TCM profiles generated in our study, although resembling the looks of the actual TCM profiles published by earlier authors (Angel et al., 2009a; Angel et al., 2009b; Khatonabadi et al., 2013a), do not indicate an exact match. For example, in the work of Khatonabadi and colleagues (Khatonabadi et al., 2013a), tube current was shown to increase dramatically at the interface of chest and abdomen regions. This trend was not apparent in the TCM profiles generated in this study for the reference XCAT female phantom (Figure 4). This could be due to the anatomical difference between this reference phantom and the patient in the earlier study. It could also be caused by a discrepancy in lung density. In this study, we assumed the lung density to be the density of an inflated lung (0.26 g/cc) (ICRU, 1992). This value may be higher than the density of a patient’s lungs during a chest CT scan following a forced inhalation. However, the main reason for the difference between theoretical and actual TCM profiles lies in the fact that actual TCM profiles are often complex and do not strictly follow theoretical predictions. A notable example can be found in the study of Khatonabadi et al., which showed that at the beginning of a TCM scan, over multiple rotations, the amplitude of the modulation may not reflect the variation in patient attenuation at that location. Furthermore, an overshoot of tube current may exist at the beginning of a TCM scan. Such complex and erratic behaviors were not modeled in our study. Furthermore, for certain CT systems, tube current may be determined based on attenuation only for selected projections (e.g., anteroposterior and lateral projections). Simple interpolation may be used to determine the tube currents for other projections. Therefore, care should be taken when using the h factors published in this study to estimate organ dose for patient scans. It is also desirable to further test the accuracy of the last two approximation methods using actual TCM profiles downloaded from the scanners made by different manufacturers.

Lastly, h factors were found in earlier studies to depend strongly on patient size, notably patient diameter (Turner et al., 2011; Li et al., 2011b) and obesity level (Ding et al., 2012; Li et al., 2012). Thus, the fitting parameters in Tables 1-4 only apply to the adult reference female XCAT phantom and patients with a similar body habitus as this phantom. For the patient population at large, h factors are multi-dimensional functions of body size metrics and the TCM scheme, which needs to be substantiated in future studies.

5. Conclusion

This theoretical study showed that in chest and abdomen-pelvis CT scans employing TCM, the conversion factors from CTDI_vol to organ dose can be represented as second-order polynomial functions of the modulation control strength. Ignoring the effect of TCM can lead to dose errors as large as ~200%. Organ dose in a TCM scan, however, may be derived from the conversion factors established for a fixed-mA scan (h_FIXED) across the full range of modulation control strength. This is possible by multiplying h_FIXED by a revised definition of CTDI_vol that accounts for two factors: (a) the tube currents at the location of an organ and (b) the variation in organ volume along the longitudinal direction.

Table 2.

Relationship between organ dose conversion factors (h factors) and modulation control strength (α), h = a + bα + cα², for the chest CT scan of the XCAT female reference phantom. mA modulation profiles are constrained.

	a	b	c	root-mean-square of residuals
inside
lungs	1.375860	−0.551437	0.190154	0.024848
breasts	1.141080	−0.714861	0.059541	0.043005
heart	1.353670	−0.766875	0.082191	0.046108
thymus	1.424480	−0.584082	0.294456	0.026723
periphery
thyroid	0.636686	1.251970	0.213765	0.219080
esophagus	1.141700	−0.017802	0.240344	0.040624
liver	1.002990	−0.493152	−0.014561	0.041311
gall bladder	0.926471	−0.443064	−0.035577	0.041818
stomach	1.030640	−0.560232	0.012905	0.041956
spleen	0.818472	−0.365333	−0.027094	0.033860
pancreas	0.556102	−0.277750	−0.006902	0.023673
adrenal glands	0.512740	−0.238435	−0.016311	0.021335
large intestine	0.210207	−0.095756	−0.009039	0.009465
small intestine	0.157911	−0.079203	−0.002574	0.006919
distributed
bone surface	0.593390	0.046099	0.044261	0.011857
red bone marrow	0.397753	−0.086233	0.059646	0.002418
skin	0.234989	0.011149	−0.003015	0.000617
residual soft tissue	0.241694	0.007750	0.008835	0.002210
outside
brain	0.010950	0.016294	−0.000802	0.001700
larynx-pharynx	0.163409	0.199425	0.036355	0.031569
kidneys	0.211393	−0.098434	−0.004630	0.008683
bladder	0.001772	−0.000954	0.000062	0.000061
ovaries	0.003298	−0.000848	−0.000713	0.000138
uterus	0.002645	−0.001307	−0.000022	0.000081

Table 3.

Relationship between organ dose conversion factors (h factors) and modulation control strength (α), h = a + bα + cα², for the abdomen-pelvis CT scan of the XCAT female reference phantom. mA modulation profiles are unconstrained.

	a	b	c	root-mean-square of residuals
inside
liver	1.61430	−0.411973	−0.167074	0.004215
gall bladder	1.395170	−0.458111	−0.189514	0.004049
stomach	1.05970	−0.459071	−0.126999	0.004046
spleen	1.59430	−0.3640 3	−0.194097	0.003788
pancreas	1.230780	−0.434770	−0.139968	0.003932
adrenal glands	1.186910	−0.430694	−0.128970	0.004947
kidney	1.370560	−0.410191	−0.182816	0.005064
large intestine	1.407040	−0.208729	−0.149568	0.002937
small intestine	1.40980	−0.267179	−0.160579	0.003264
bladder	1.041400	0.004044	0.034654	0.001295
ovaries	1.056160	0.156678	−0.010919	0.003653
uterus	1.09850	0.033794	0.007512	0.000836
periphery
lungs	0.45480	−0.211854	−0.027479	0.001445
breasts	0.417106	−0.193100	−0.026206	0.001582
esophagus	0.37595	−0.168005	−0.027486	0.001846
heart	0.704750	−0.343900	−0.034815	0.002675
distributed
bone surface	0.850058	0.019129	0.033545	0.000399
red bone marrow	0.575945	−0.020934	0.012577	0.000023
skin	0.368490	0.006185	−0.002013	0.000092
residual soft tissue	0.48944	0.003821	0.000771	0.000005
outside
brain	0.000852	−0.000330	−0.000085	0.000007
thyroid	0.035969	−0.017929	−0.001177	0.000146
larynx-pharynx	0.016384	−0.008650	0.000640	0.000038
thymus	0.156648	−0.069301	−0.013086	0.000694