Abstract
The relationship between the dose of an effector and the biological response frequently is not described by a linear function and, moreover, in some cases the dose-response relationship may change from positive/adverse to adverse/positive with increasing dose. This complicated relationship is called “hormesis”. This paper provides a short analysis of the concept along with a description of used approaches to characterize hormetic relationships. The whole hormetic curve can be divided into three zones: I – a lag-zone where no changes are observed with increasing dose; II – a zone where beneficial/adverse effects are observed, and III – a zone where the effects are opposite to those seen in zone II. Some approaches are proposed to analyze the molecular components involved in the development of the hormetic character of dose-response relationships with the use of specific genetic lines or inhibitors of regulatory pathways. The discussion is then extended to suggest a new parameter (half-width of the hormetic curve at zone II) for quantitative characterization of the hormetic curve. The problems limiting progress in the development of the hormesis concept such as low reproducibility and predictability may be solved, at least partly, by deciphering the molecular mechanisms underlying the hormetic dose-effect relationship.
Keywords: hormesis, reactive oxygen species, mechanisms, components
“That which does not kill us makes us stronger.”
Friedrich Nietzche, German philosopher, XIX century.
INTRODUCTION
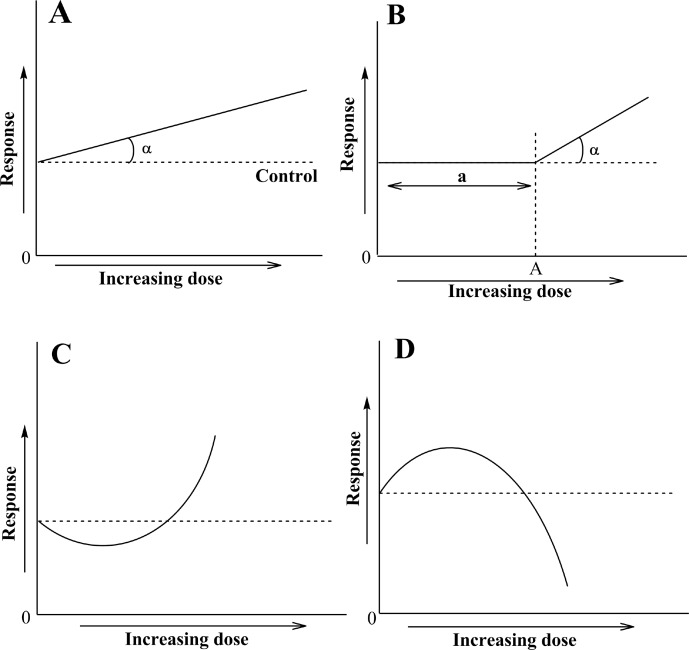
The relationship between the dose of an effector and the biological response that it elicits is a cornerstone of basic and applied disciplines of physiology, biochemistry, toxicology and pharmacology; indeed, its importance is illustrated by the existence of specialized scientific journal dedicated to this phenomenon (Dose-Response, http://www.dose-response.com). Two models of dose-response relationships are commonly used (Calabrese et al. 1987; Calabrese and Baldwin 1998; Calabrese 2008, 2013a, b; Gaman et al. 2011; Ristow and Schmeisser 2011; Cox 2012; Deng et al. 2012; López-Martínez and Hahn 2012; Calabrese et al. 2012; Demirovic and Rattan 2013). In the first one, called the linear model, the registered endpoint shows a linear dependence on the dose of the effector (Figure 1A); this is also called the linear non-threshold model (Hadley 2003). The α-angle can vary widely and depends on many factors including the model type, specific conditions used and the properties of effectors. It is based on cumulative effects of single acts of interaction between the effector and the biological subject. However, in many cases the response cannot be linearly extrapolated to “zero” dose. In these cases, the observed effects may only begin to be observed from a certain (threshold) dose (X = A) with different distances from the beginning of the abscissa (X = 0) (Figure 1B). This relationship is called the “threshold model”. The distance “a” seen in Figure 1B is called the “lag phase” and may reflect the operation of defense mechanisms that prevent an immediate response by organisms.
FIGURE 1.
Dose-response relationships: (A) the linear model, (B) the threshold (linear) model, (C) the J-shaped model, and (D) the inverted U-shaped model, or inverted J-shaped model. The dashed line shows initial level of the response being measured (endpoint). Description in the text.
The theoretical material presented above may be illustrated by the examples on the effects of reactive oxygen species (ROS) on biological systems (Lushchak 2011). In order to evaluate the antioxidant capacity of an organism, it is usually necessary to challenge the organism with oxidants at certain doses (concentrations). Endogenous antioxidants can prevent oxidation of molecular targets, but when a certain dose of oxidant is reached, the antioxidant potential will be exceeded and oxidative damage will take place. In this case, the situation demonstrates a threshold character as seen in Figure 1B where “a” represents the capacity of the system to tolerate changes provoked by inducers. Similar to the situation described for Figure 1A, the α-angle is again variable. However, in many cases the dose-response relationship at low doses does not follow either the linear (Figure 1A) or the threshold (Figure 1B) model. Rather, it shows changes in opposite directions over zones of low and high doses. These relationships where low doses of an effector trigger responses opposite to high ones are called “hormetic”, from the Greek hórm?sis meaning “rapid motion, eagerness” (or the ancient Greek hormáein “to set in motion, impel, urge on”). Two main types of these dependences have been described. One is called J-shaped (Figure 1C) and the other is inversed U-shaped (Figure 1D) (Hadley 2003; Cook and Calabrese 2006; Calabrese 2008). The inversed U-shaped hormetic relationship might be more correctly named inversed J-shaped, because it is asymmetric and is cut off at the “zero” point of the abscissa. Actually, it does not matter very much how it is called, as long as we clearly recognize the character of the relationship.
Although the hormetic relationship was first described more than a century ago (Schulz 1888, cited after Calabrese and Baldwin 1998), for various reasons it was largely ignored until about the last decade when it was analyzed in detail by E. Calabrese and colleagues. Previously, we have not mentioned which type of effector induces a certain type of hormetic response, or what was used as the “endpoint” or biological effect. This is because there are huge numbers of possibilities. The effector could be either chemical or physical in nature (e.g. different compounds, temperature, physical exercise, radiation, light, etc.) whereas the endpoint may be virtually any biologically important parameter including survival time, fecundity, organism mass and length, stress resistance, blood pressure, enzyme activity, protein levels, fuel reserves, etc. Depending on the endpoint selected, dose-response curves can differ for the same organism or under the same conditions.
In the present paper, I do not investigate the details of the effector-endpoint relationship in different systems. There are excellent, detailed and readily available publications on this topic by the research groups of E. Calabrese (Calabrese and Baldwin 1998; Calabrese 2008), S. Rattan (Rattan and Demirovic 2009; Rattan 2012; Demirovic and Rattan 2013), E. le Bourg (Le Bourg 2009; Le Bourg and Rattan 2009), L. Partridge (Gems and Partridge 2008) as well by others (Radak et al. 2005; Birringer 2011; Brigelius-Flohé and Flohé 2011; Pijl 2012). Instead, my analysis focuses on just one of the hormetic relationships, the case of the inversed J-shape (Figure 1D), the most frequently found relationship in biological systems. This relationship shows that, at low doses, effectors enhance the response parameter, but with an increase in effector dose the effect becomes less pronounced until no further increment in effect is found, and finally the parameter of interest begins to decrease back to the initial (control) level or to an even lower value. This paper aims to analyze the main parameters involved in causing the inverted J-shape relationship in order to propose some clues for its quantitative characterization.
1. “CLASSIC” DESCRIPTION OF THE HORMETIC CURVE
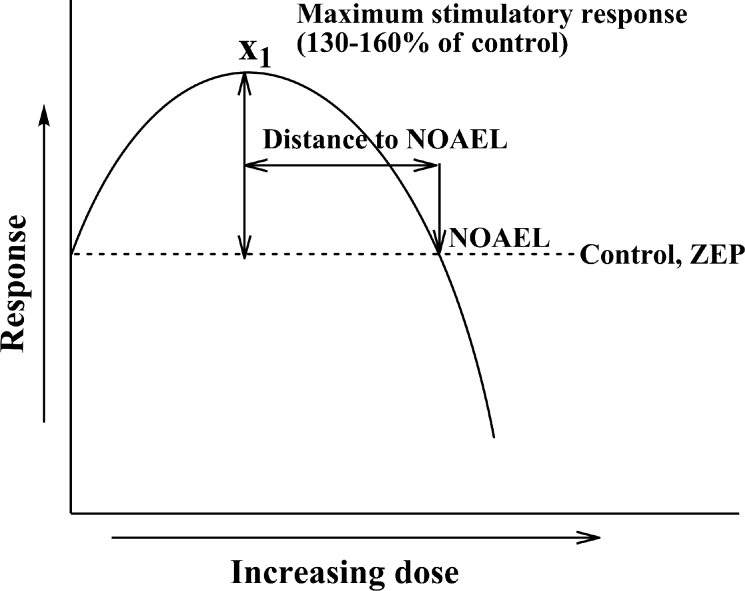
To develop some system and objectivity in hormesis research, E. Calabrese and L. Baldwin (1998) used specific criteria to create a database of articles related to the problem. For that, they analyzed approximately 8000 dose-response studies taking into account such criteria as the strength of the study, design features, magnitude of the low dose stimulation, statistical significance, and reproducibility of the findings. Usually the hormetic dose-response is supposed to be reliably described as stimulation in the low dose zone, followed by inhibition at high doses (Calabrese 2008). The typical stimulatory effect reaches about 30-60% above the control level and in most cases the maximum stimulatory response was less than twice the control value (Figure 2). Furthermore, in most cases, the zero equivalent point (ZEP; where the response changes from stimulation to inhibition) was reached within a 100-fold increase in dose (Calabrese 2008). However, in some cases, a very broad stimulatory range exceeding 1000-fold was found. The stimulatory range causing expected (positive medical effect) is usually defined as a therapeutic window. However, in some cases the effects of low doses may be deleterious like in example where antitumor drugs stimulate tumor growth at low doses and only high doses inhibit it (cited after Calabrese 2005). Calabrese (2008) stated that “the hormetic stimulatory zone is graphically contiguous with the pharmacologic/toxicologic threshold”. Inter-individual variation may complicate the use of hormetic-based therapies due to the possibility of the desired therapeutic dose being a toxic dose to some individuals. This variation must be taken into account and corrected by monitoring specific parameters.
FIGURE 2.
“Classic” presentation of the dose-response hormetic curve. Abbreviations used: NOAEL – no observable adverse effect level – the dose of inducer where no observable effect is seen; ZEP – zero equivalent point. Description in the text.
The point where an effector-induced positive (or negative) effect of a treatment reverses itself is a cornerstone of the hormetic hypothesis. The two ranges of doses/concentrations meet at specific point where no effect is observed and this point is commonly known as the “no observable adverse effect level” (NOAEL), a term commonly used in medicine. The NOAEL is also applicable to analysis of hormetic curves (Figure 2).
The information given in this section above is a short description of the hormetic hypothesis extensively propagated by E. Calabrese and colleagues. This hypothesis may be very productive not only due to its application to basic science interests, but also due to numerous applications to adaptation studies and pharmaceutical research. However, the concept has also been subjected to serious critique (Thayer et al. 2005) which may further simulate its development. In addition, the concept may be actively applied to “classic” toxicology and therapy.
To my mind, the first and the most attractive thing about the hormesis concept is its potential possibilities for use in analyzing the ability of organisms to adapt to adverse effectors via stimulation of endogenous protective systems. The second important issue involves the concept that low or very low doses of effectors may induce less adverse effects or side-effects than “classically” used doses in “official” medicine thereby potentially minimizing the development of various pathologies and even fatalities. These points are related to the Hippocratic Oath “I will prescribe treatment to the best of my ability and my judgment for the good of the sick and never for harmful or illicit purpose”.
2. “IDEALIZED” HORMETIC CURVES AND THEIR COMPONENTS
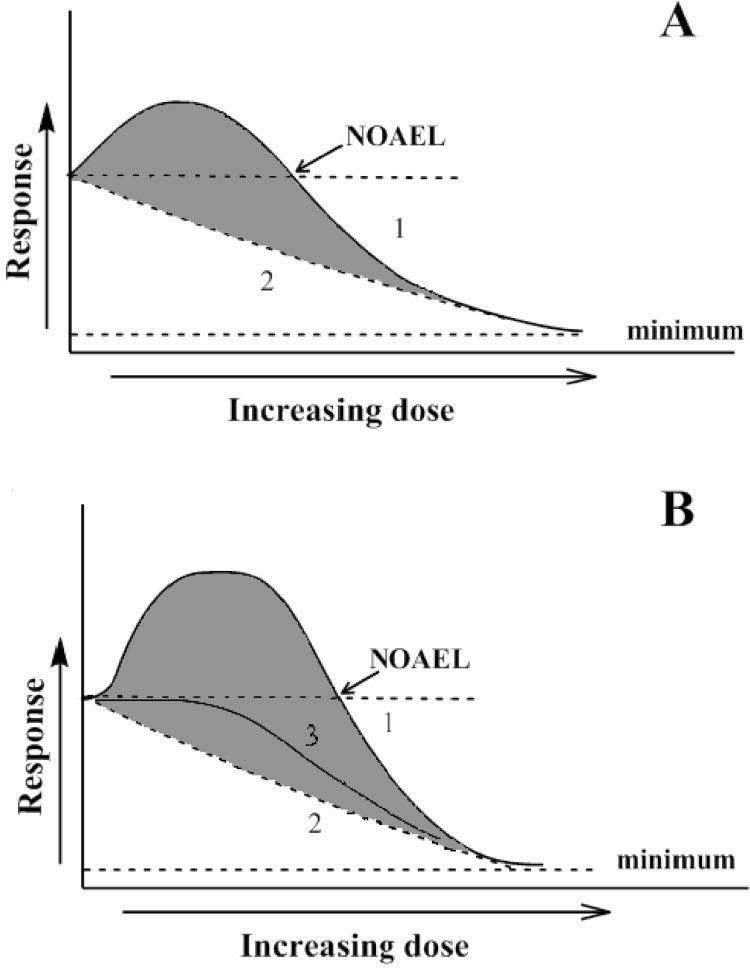
From a theoretical point of view, the hormetic curve consists of a minimum of two components. The negative inhibitory effect of the inducer (Figure 3A, line 2) occurs at all doses applied, but at low doses it is negligible and masked by the activatory effect. When the two processes – inhibition and activation – are superimposed, the net effect on the response parameter (endpoint) being monitored as it is depicted by curve 1 (Figure 3A). Although the effector is the same for both processes mentioned – inhibition and activation – and basic chemical mechanisms of the effects caused may be potentially similar, the primary targets or modified molecules usually differ. The exponentially declining component represents one or several target systems critically important for the development of the registered endpoint. In the simplest case, the process is described by a first order (or pseudo-first order) declining exponential function (Figure 3A, curve 2). Depending on the nature of the selected endpoint, the curve may or may not approach zero. The second process is related to the increase in defense potential induced by the same effector. Again, either one or more systems can be involved, but to simplify the analysis an idealized dose-response curve can be envisioned that deals with only one system. So, the system is initially activated and to a certain extent may increase tolerance leading to an observation of improved function. However, higher doses of the effector also may inactivate regulatory pathways responsible for enhancing function, thereby leading to a decrease or disappearance of the observed system activation and a decline in the registered response parameter.
FIGURE 3.
Two- (A) and three-component (B) curves demonstrating the components contributing to the total hormetic curve. Curve 1 – general hormetic dose-response; 2 – pure negative effects of the effector, and 3 – negative (suppressive) effects in the presence of operating defense mechanisms. Description in the text.
Living organisms possess defense systems to prevent their injury by many factors. Therefore, the two-component system described above does not often match the real response in nature. The defense systems also contribute to the net hormetic response observed with increasing dose of the inducer. At very low effector doses, a defense system successfully prevents injury and, hence, no observable effects occur. When the threshold of the activatory system (responsible for the upregulation of defense mechanisms) is reached, a researcher may observe an increased response to the dose followed by the well-known hormetic curve (Figure 3B, line 1). Now let us analyze the components that provide this “idealized” hormetic curve (Figure 3B). From basic logic and data from many experiments, the damage component described above by a first order declining curve always exists (Figure 3B, line 2). Since the defense system can, to a large extent, prevent damage to the critically important endpoint parameter, line 3 demonstrates the idealized relationship connecting the response registered with the dose applied, under conditions where a defense system virtually does not operate. Curve 3 in Figure 3B shows the superposition of damaging effects of the effector and protective system(s) defending the organism against the deleterious effects of the effector. In my opinion, this three-component system (Figure 3B) describes the dose-response relationship in most cases. It is clear that the real situation in living organisms may be much more complicated and the net response probably includes many other components. However, in radiobiology, for example, it is accepted that in certain cases one system is the critically important target affected by radiation and most of the registered biological responses depend on that system (Greenberger et al. 2003). In hormesis, the situation also may be similar and the question raised will be covered below.
3. EXPERIMENTAL AND MATHEMATICAL APPROACHES TO ANALYZE THE HORMETIC CURVE
Analysis of many thousands of hormetic curves was carried out by Calabrese and colleagues (Calabrese and Baldwin 1998, 2001; Calabrese and Blain 2011). In the present work, I would like to demonstrate potential approaches to analyze the components responsible for the formation of the complicated dose-response relationships that are observed. Interested readers can find more information on this topic in review articles (Hadley 2003; Calabrese 2008) and the references therein on earlier model studies such as the interaction of two functionally antagonistic receptor populations activated by the same agonist (Szabadi 1977) or the regulation of G-protein coupled receptors by agonists and antagonists (Järv 1995).
To make analysis easier, we will start with the two-component system (Figure 3A). How can the researcher discriminate experimentally between the two processes involved – activatory and inhibitory? An appropriate way to begin would be to block the process of activation of defense systems and then analyze the inactivation process. There are at least two potential approaches to do that. One of them is to disrupt potential pathways responsible for the activation process. Theoretically, if the function can be switched off without lethal consequences, it should be possible to inactivate the adaptive activation response pathway at the level of receptors, transmitters, target systems, etc. Nowadays, there are many experimental approaches to construct organisms with genetically inactivated regulatory pathways. For example, it is well known that in baker’s yeast, the Yap1 protein regulates the transcription of genes involved in the response to reactive oxygen species (ROS), such as hydrogen peroxide (Semchyshyn 2009; Lushchak 2010; Semchyshyn and Lozinska 2012). In the yeast strain with a defective YAP1 gene, the cells adapt to increased H2O2 levels very poorly and, as a result, they are more sensitive to this toxicant. My laboratory (Bayliak et al. 2006) and others (Stephen et al. 1995) found that in response to incubation with low H2O2 concentrations yeast mutants with a defective YAP1 gene did not increase tolerance to H2O2, whereas the “wild” strain showed increased tolerance and enhanced viability. Similarly, the involvement of YAP1 protein in the adaptive response of yeast to nitric oxide exposure was also reported (Lushchak et al. 2010). Recently, two stress-regulated systems, involving the regulatory proteins Yap1 and Msn2/4, were shown to be responsible for the hormetic yeast response to different concentrations of a preparation of the medicinal herb Rhodiola rosea (Bayliak et al. 2013). In general, then, if an organism can be engineered to switch off the systems responsible for the activation of defense mechanisms against a toxicant or physical stressor, one could produce an organism that would not be able to develop the hormetic response (or at least not the full response).
The second experimental approach that could be used to dissect the components responsible for an observed hormetic dose-response curve would be to inhibit protein or mRNA biosynthesis or other processes directly or indirectly responsible for the increase in tolerance. Again, it is relatively easy to apply this approach to cell cultures or unicellular organisms like bacteria or yeast, but with multicellular organisms the situation is much more complicated. Although two-component hormetic curves may be more the exception than the rule, this simplified model may help us to clearly understand the processes involved and identify potential experimental approaches. It is also supported by the understanding that in many cases mostly one system is critically important to provide endpoint response to effector exposure. I mean here that one may approximate the resulting action to effects on one organ that is critically important for surviving under the specific condition. For example, in many cases where exposure to toxicants occurs, it is the liver or kidney that may be the primary target, whereas brain and heart are well protected and would not be substantially affected.
Now the question arises: how can we derive quantitative parameters of the involvement of processes that result in a hormetic dose-response relationship? As mentioned above, it is sometimes possible to experimentally inactivate the system(s) responsible for the development of the hormetic relationship. This inactivation may be accomplished either via the use specific gene deletion strains or by inhibiting protein or mRNA synthesis to get a dose-response curve without an activation component, i.e. producing only the declining (inhibitory) curve. In the control condition, however, the system provides the full hormetic curve. The results from these two conditions (control vs inactivated) can be superimposed, as seen in the two-component system (Figure 3A, curve 1 vs 2). Subtraction of the values of curve 2 from those of curve 1 therefore shows the contribution of the activation of defense systems to the total hormetic function (shaded area). To some extent, a similar analysis can be carried out even without manipulation with the systems responsible for adaptation, but this can be less accurate. By analogy to many biological and chemical processes, one may assume that at the far right-hand side of the hormetic curve (Figure 3A), the response is purely an inhibitory one and follows a first order dependency. Using this part of the total curve, it is therefore possible to get parameters for the needed equation by taking into account the “zero” dose point, i.e. extrapolate the right-hand portion of the curve to the ordinate at X = 0. It is clear that too many factors should be ignored or approximated by this method, but in this way we can quantitatively analyze the role of certain components of the total dose-response relationship.
As with the “idealized” two-component system, we can apply similar logic to analyzing a three-component system (Figure 3B). The first order decline function is also present here (Figure 3B curve 2). However, the operation of protective mechanisms does not let us observe the negative effects neutralizing them. Therefore, a lag-phase may be identified and, furthermore, at higher doses of the effector, curve 3 may virtually merge with curve 2. Of course, curve 1 describes the overall process. It is potentially possible to determine curve 3 (Figure 3B) experimentally using specific genetic constructs or inhibitors of processes leading to enhanced resistance, as it was described above for the two-component system.
After analysis of the overall hormetic curve, some quantitative approaches can be used to describe this curve using mathematical tools.
4. QUANTITATIVE CHARACTERISTICS OF THE HORMETIC CURVE
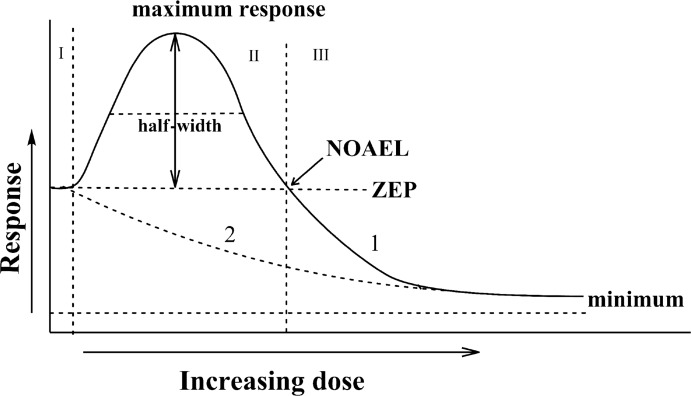
In this section again we will deal with the approximated “idealized” hormetic dose-response relationship for a two-component system (Figure 3A), but for convenience this figure is redrawn to show specific features needed for the analysis (Figure 4). The whole hormetic curve may be divided into three zones: I – the lag-zone where no observable changes occur; II – the zone where beneficial/adverse effects are observable, and III – the zone where the effects observed at zone II are reversed. Previously developed approaches (Hadley 2003; Calabrese 2008) are discussed along with the introduction of additional characteristics.
FIGURE 4.
“Idealized” hormetic curve to depict quantitative features of the hormetic relationship. Zones described are: I – lag zone – no observable effects at low effector doses, II – zone of beneficial/adverse effects, III – zone of changes opposite to zone II – zone of adverse/beneficial effects. Description in the text.
Zone I, where no observable effects are registered, is typically rather narrow relative to the broader zones II and III. It is supposed that traditional approaches to evaluate the effects of interest in zone I are rather weak (below sensitivity level). In this case, the range of doses which are not sensed (or perhaps more correctly – where the effects are not registered due to sensitivity limits of traditionally used approaches) cannot be defined accurately, and only the border of zone II may be used to determine its right-hand position. Zone II represents the range of doses that constitute the “hormetic zone” (Calabrese 2008), i.e., where increases or decreases in the parameter of interest occur. This zone is located between zone I (lag zone) and the NOAEL point – i.e. the dose where no observable effect is found. Two characteristics of this zone are generally discussed in the literature – its width and maximum response. Since these two characteristics do not provide information on the parameters of steepness (slope) of the curve, I propose to add one more characteristic – the half-width, defined as the width at the point of half-maximum response. The NOAEL point is not ideal for characterizing the hormetic curve, but it can be used to define the upper limit on the zone where the effects of interest are observed.
Zone III, in my opinion, should be described differently from the “classic” presentation of the hormetic curve. It is important to note here that zone III typically strongly approximates a first order exponential decay curve at highest doses of the inducer (the right-hand portion). Depending on the endpoint, system used and many other factors, this part of the hormetic curve tends to asymptote – either to zero at the ordinate axis (Y = 0), or to a certain asymptote (Y = A) reflecting minimum function. This lowest part of the hormetic curve can be used to calculate parameters of an exponential decay curve with extrapolation to the place where the ordinate value crosses the ZEP (Y value at X = 0).
The approach described above extends the number of parameters that can be used to provide a quantitative description of the hormetic curve (Figure 4). After calculation of the asymptote, i.e. either the minimum value or zero on the Y-axis, it is then possible to calculate the area under the hormetic curve 1. Similarly, the area under curve 2 can be calculated and used to characterize the adverse effects of the effector. Finally, subtracting the area under curve 2 from the area under the hormetic curve 1 provides a measure of the activation characteristics. These characteristics include both the preexisting defense potential and the defense potential induced by the effector.
In summary, then, a variety number of parameters can potentially be calculated to provide a highly detailed description of the hormetic dose-response relationship (Figure 4). These include the maximum response, hormetic range, half-width range, and NOAEL, minimum (asymptote) level, the areas under curves 1 and 2 and the defense potential (area 1 minus area 2).
5. PROBLEMS AND PERSPECTIVES
It is clear that the hormesis concept provides many important clues to diverse basic and applied fields of biology, toxicology and medicine. The main problems related to the concept still remain in the low reproducibility of the results and their low predictability. The observed effects often depend on many parameters particularly on the physiological state of the organisms. Several aspects need special attention in this field to make it more reliable. First, the molecular mechanisms underlying the hormetic dose-effect relationship should be delineated in different organisms and tissues, because it is absolutely clear now that they differ. This approach may provide clues to make the concept more evidence-based. Second, although there are already some mathematical approaches used to characterize hormetic curves (Belz and Piepho 2012), more accurate tools are needed. Third, in some cases, triphasic dose-response relationships were found (Imlay and Linn 1986; Choi et al. 2012; Semchyshyn 2014), which will need clarification to determine if they are special cases of “typical” hormetic curves, or if hormetic curves at low dose ranges may include one more component usually missed or overlooked for different reasons.
Acknowledgments
The author is grateful to Drs. H. Semchyshyn, D. Gospodaryov and M. Bayliak for critical analysis of the manuscript and to J. Storey for editorial review. The idea of this work was formulated and discussed with many colleagues owing to financial support and great facilities provided by the Institute for Advanced Study, Delmenhorst, Germany for the author.
REFERENCES
- Bayliak M, Semchyshyn H, Lushchak V. Effect of hydrogen peroxide on antioxidant enzyme activities in Saccharomyces cerevisiae is strain-specific. Biochemistry (Mosc) 2006;71(9):1013–1020. doi: 10.1134/s0006297906090100. [DOI] [PubMed] [Google Scholar]
- Bayliak MM, Burdyliuk NI, Izers’ka LI, Lushchak VI. Concentration-dependent effects of Rhodiola rosea on long-term survival and stress resistance of yeast Saccharomyces cerevisiae: the involvement of Yap1 and Msn2/4 regulatory proteins. Dose-Response. 20132013 doi: 10.2203/dose-response.13-013. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belz RG, Piepho HP. Modeling effective dosages in hormetic dose-response studies. PLoS One. 2012;7(3):e33432. doi: 10.1371/journal.pone.0033432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birringer M. Hormetics: dietary triggers of an adaptive stress response. Pharm Res. 2011;28(11):2680–2694. doi: 10.1007/s11095-011-0551-1. [DOI] [PubMed] [Google Scholar]
- Brigelius-Flohé R, Flohé L. Basic principles and emerging concepts in the redox control of transcription factors. Antioxid Redox Signal. 2011;15(8):2335–2381. doi: 10.1089/ars.2010.3534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese EJ. Cancer biology and hormesis: human tumor cell lines commonly display hormetic (biphasic) dose responses. Crit Rev Toxicol. 2005;35(6):463–582. doi: 10.1080/10408440591034502. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ. Hormesis and medicine. Br J Clin Pharmacol. 2008;66(5):594–617. doi: 10.1111/j.1365-2125.2008.03243.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese EJ. Biphasic dose responses in biology, toxicology and medicine: accounting for their generalizability and quantitative features. Environ Pollut. 2013a;182:452–460. doi: 10.1016/j.envpol.2013.07.046. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ. Hormesis: Toxicological foundations and role in aging research. Exp Gerontol. 2013b;48(1):99–102. doi: 10.1016/j.exger.2012.02.004. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ, Baldwin LA. Hormesis as a biological hypothesis. Environ Health Perspec. 1998;106(Suppl 1):357–362. doi: 10.1289/ehp.98106s1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese EJ, Baldwin LA. Hormesis: a generalizable and unifying hypothesis. Crit Rev Toxicol. 2001;31(4–5):353–424. doi: 10.1080/20014091111730. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ, Blain RB. The hormesis database: the occurrence of hormetic dose responses in the toxicological literature. Regulatory Toxicology and Pharmacology. 2011;61(1):73–81. doi: 10.1016/j.yrtph.2011.06.003. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ, McCarthy ME, Kenyon E. The occurrence of chemically induced hormesis. Health Phys. 1987;52(5):531–541. doi: 10.1097/00004032-198705000-00002. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ, Stanek EJ, 3rd, Nascarella MA. A detailed re-assessment supports the conclusion of the paper that hormesis is commonly observed in the Ames assay. Mutat Res. 2012;747(1):157. doi: 10.1016/j.mrgentox.2012.04.008. [DOI] [PubMed] [Google Scholar]
- Choi VW, Yum EH, Konishi T, Oikawa M, Cheng SH, Yu KN. Triphasic low-dose response in zebrafish embryos irradiated by microbeam protons. J Radiat Res. 2012;53(3):475–481. [PubMed] [Google Scholar]
- Cook R, Calabrese EJ. The importance of hormesis to public health. Cien Saude Colet. 2006;12(4):955–963. doi: 10.1590/s1413-81232007000400017. [DOI] [PubMed] [Google Scholar]
- Cox LA., Jr Hormesis for fine particulate matter (PM 2.5) Dose Response. 2012;10(2):209–218. doi: 10.2203/dose-response.11-040.Cox. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demirovic D, Rattan SI. Establishing cellular stress response profiles as biomarkers of homeodynamics, health and hormesis. Exp Gerontol. 2013;48(1):94–98. doi: 10.1016/j.exger.2012.02.005. [DOI] [PubMed] [Google Scholar]
- Deng Z, Lin Z, Zou X, Yao Z, Tian D, Wang D, Yin D. Model of hormesis and its toxicity mechanism based on quorum sensing: a case study on the toxicity of sulfonamides to Photobacterium phosphoreum. Environ Sci Technol. 2012;46(14):7746–7754. doi: 10.1021/es203490f. [DOI] [PubMed] [Google Scholar]
- Gaman L, Stoian I, Atanasiu V. Can ageing be slowed? Hormetic and redox perspectives. J Med Life. 2011;4(4):346–351. [PMC free article] [PubMed] [Google Scholar]
- Gems D, Partridge L. Stress-response hormesis and aging: “that which does not kill us makes us stronger”. Cell Metab. 2008;7(3):200–203. doi: 10.1016/j.cmet.2008.01.001. [DOI] [PubMed] [Google Scholar]
- Greenberger JS, Epperly MW, Gretton J, Jefferson M, Nie S, Bernarding M, Kagan V, Guo HL. Radioprotective gene therapy. Curr Gene Ther. 2003;3(3):183–195. doi: 10.2174/1566523034578384. [DOI] [PubMed] [Google Scholar]
- Hadley C. What doesn’t kill you makes you stronger. A new model for risk assessment may not only revolutionize the field of toxicology, but also have vast implications for risk assessment. EMBO Rep. 2003;4(10):924–926. doi: 10.1038/sj.embor.embor953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imlay JA, Linn S. Bimodal pattern of killing of DNA-repair-defective or anoxically grown Escherichia coli by hydrogen peroxide. J Bacteriol. 1986;166(2):519–527. doi: 10.1128/jb.166.2.519-527.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Järv JJ. A model of nonexclusive binding of agonist and antagonist on G-protein coupled receptors. J Theoret Biol. 1995;175:577–582. doi: 10.1006/jtbi.1995.0166. [DOI] [PubMed] [Google Scholar]
- Le Bourg E. Hormesis, aging and longevity. Biochim Biophys Acta. 2009;1790(10):1030–1039. doi: 10.1016/j.bbagen.2009.01.004. [DOI] [PubMed] [Google Scholar]
- Le Bourg E, Rattan SI. Is hormesis applicable as a pro-healthy aging intervention in mammals and human beings, and how? Introduction to a special issue of Dose-Response. Dose Response. 2009;8(1):1–3. doi: 10.2203/dose-response.09-052.LeBourg. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Martínez G, Hahn DA. Short-term anoxic conditioning hormesis boosts antioxidant defenses, lowers oxidative damage following irradiation and enhances male sexual performance in the Caribbean fruit fly, Anastrepha suspensa. J Exp Biol. 2012;215(12):2150–2161. doi: 10.1242/jeb.065631. [DOI] [PubMed] [Google Scholar]
- Lushchak OV, Inoue Y, Lushchak VI. Regulatory protein Yap1 is involved in response of yeast Saccharomyces cerevisiae to nitrosative stress. Biochemistry (Mosc) 2010;75(5):629–664. doi: 10.1134/s0006297910050135. [DOI] [PubMed] [Google Scholar]
- Lushchak VI. Oxidative stress in yeast. Biochemistry (Mosc) 2010;75(3):281–296. doi: 10.1134/s0006297910030041. [DOI] [PubMed] [Google Scholar]
- Lushchak VI. Adaptive response to oxidative stress: Bacteria, fungi, plants and animals. Comp Biochem Physiol C Toxicol Pharmacol. 2011;153(2):175–190. doi: 10.1016/j.cbpc.2010.10.004. [DOI] [PubMed] [Google Scholar]
- Pijl H. Longevity. The allostatic load of dietary restriction. Physiol Behav. 2012;106(1):51–57. doi: 10.1016/j.physbeh.2011.05.030. [DOI] [PubMed] [Google Scholar]
- Radak Z, Chung HY, Goto S. Exercise and hormesis: oxidative stress-related adaptation for successful aging. Biogerontology. 2005;6(1):71–75. doi: 10.1007/s10522-004-7386-7. [DOI] [PubMed] [Google Scholar]
- Rattan SI. Rationale and methods of discovering hormetins as drugs for healthy ageing. Expert Opin Drug Discov. 2012;7(5):439–448. doi: 10.1517/17460441.2012.677430. [DOI] [PubMed] [Google Scholar]
- Rattan SI, Demirovic D. Hormesis can and does work in humans. Dose Response. 2009;8(1):58–63. doi: 10.2203/dose-response.09-041.Rattan. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ristow M, Schmeisser S. Extending life span by increasing oxidative stress. Free Radic Biol Med. 2011;51(2):327–336. doi: 10.1016/j.freeradbiomed.2011.05.010. [DOI] [PubMed] [Google Scholar]
- Semchyshyn H. Hydrogen peroxide-induced response in E. coli and S. cerevisiae: Different stages of the flow of the genetic information. Central European J Biol. 2009;4(2):142–153. [Google Scholar]
- Semchyshyn H. Hormetic concentrations of hydrogen peroxide but not ethanol induce cross-adaptation to different stresses in budding yeast. Int J Microbiol. 20142014:485792. doi: 10.1155/2014/485792. (5 pages) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semchyshyn HM, Lozinska LM. Fructose protects baker’s yeast against peroxide stress: Potential role of catalase and superoxide dismutase. FEMS Yeast Res. 2012;12(7):761–773. doi: 10.1111/j.1567-1364.2012.00826.x. [DOI] [PubMed] [Google Scholar]
- Stephen DW, Rivers SL, Jamieson DJ. The role of the YAP1 and YAP2 genes in the regulation of the adaptive oxidative stress responses of Saccharomyces cerevisiae. Mol Microbiol. 1995;16(3):415–423. doi: 10.1111/j.1365-2958.1995.tb02407.x. [DOI] [PubMed] [Google Scholar]
- Szabadi E. Model of two functionally antagonistic receptor populations activated by same agonist. J Theor Biol. 1977;69:101–112. doi: 10.1016/0022-5193(77)90390-3. [DOI] [PubMed] [Google Scholar]
- Thayer KA, Melnick R, Burns K, Davis D, Huff J. Fundamental flaws of hormesis for public health decisions. Environ Health Perspect. 2005;113(10):1271–1276. doi: 10.1289/ehp.7811. [DOI] [PMC free article] [PubMed] [Google Scholar]