Comparing Like with Like: The Power of Knowing Where You Are

Abstract

Magnetic resonance imaging can now provide human brain images of structure, function, and connectivity with isotropic voxels smaller than one millimeter, and thus much smaller than the cortical thickness. This resolution, achievable in a scan time of less than 1 h, enables visualization of myeloarchitectural layer structure, intracortical variations in functional activity—recorded in changes in blood oxygenation level dependent signal or cerebral blood volume CBV—and intracortical axonal orientational structure via diffusion-weighted magnetic resonance imaging. While recent improvements in radiofrequency receiver coils now enable excellent image data to be obtained at 3T, scanning at the ultra-high field of 7T offers further gains in signal-to-noise ratio and speed of image acquisition, with a structural image resolution of about 300 μm. These improvements throw into sharp question the strategies that have become conventional for the analysis of functional imaging data, especially the practice of spatial smoothing of raw functional data before further analysis. Creation of a native cortical map for each human subject that provides a reliable individual parcellation into cortical areas related to Brodmann Areas enables a strikingly different approach to functional image analysis. This proposed approach involves surface registration of the cortices of groups of subjects using maps of the longitudinal relaxation time T1 as an index of myelination, and methods for inferring statistical significance that do not entail spatial smoothing. The outcome should be a far more precise comparison of like-with-like cortical areas across subjects, with the potential to greatly increase experimental power, to discriminate activity in neighboring cortical areas, and to enable correlation of function and connectivity with specific cytoarchitecture. Such analyses should enable a far more convincing modeling of brain mechanisms than current graph-based methods that require gross over-simplification of brain activity patterns in order to be computationally tractable.

Introduction

It is an important goal of imaging neuroscience to develop well-grounded mechanistic models of the function of neural circuits. To achieve this, it is clearly vital to be able to associate localized changes in brain activity, and the end points of axonal pathways, with specific well-characterized neural substrates. Physical mechanisms exist only in physical objects, in this case individual human subjects: A multi-subject averaged brain image is no longer a physical object, but is only an abstraction that is incapable of function. A mechanism based on such an average can be proposed, but obviously cannot be experimentally tested on an averaged brain. Instead, it should be tested on data from each individual brain. To reveal actual mechanisms, network analysis clearly needs to be carried out on individual subject data, and only then generalized across a group of subjects.

The rebirth of scientific interest in myeloarchitecture, now implemented using high-resolution structural magnetic resonance imaging (MRI), holds the promise of deeper insights into principles of cortical organization. Once the location of changes in brain activity in a given subject's brain can be identified via their own native myelin-based cortical atlas, the corresponding cytoarchitecture can be looked up in a concordance atlas. When combined with high-quality crossing-fiber diffusion-weighted magnetic resonance imaging tractography, such information could provide an empirical basic for a mechanistic explanation of brain function.

To promote this goal, building on the insights described in the papers of a Special Issue of Neuroimage published in 2014 (Turner and Geyer, 2014), we describe strategies to provide increasingly complete in-vivo native cortical and subcortical atlases of individual human subjects, in which the boundaries of many cortical areas are clearly identified. For such strategies to bear fruit, however, changes should be made in how functional imaging data are normally analyzed. Commonly employed practices of spatial smoothing of image data before statistical analysis, with clumsy comparisons across subjects, prevent assignment of specific neural substrates to specific functions, and directly result in many false-positive apparent activations. It is likely that such practices have resulted in serious misinterpretations of functional magnetic resonance imaging (fMRI) data over the past fifteen years. Since better methods are now becoming available, they should be abandoned as soon as possible.

Toward a Native Cortical Map for Each Human Subject—The “In-Vivo Brodmann Mapping/Triple Jump” Approach

Despite two centuries of neuroanatomy and the genius of pioneers such as Ramon y Cajal, we are still very unsure of the nature and function of the component parts of the human brain. It is clear that brain gray matter can be categorized as cortical and subcortical, and subcortical regions such as the amygdala, the basal ganglia, striatum, and thalamus can be subdivided into nuclei with specific connections and well-understood developmental pathways (Swanson, 2012). We can even make some testable inferences regarding the role that each nucleus plays in the coordinated activity of the brain (Forstmann et al., 2011).

With regard to the white matter and the cortical gray matter, we are on weaker ground. The typical poverty of our understanding of the organization of white matter fibers in the human brain is revealed; for instance, by the widely held assumption over the decade 2000–2010 that most of this tissue can be considered to comprise a small number of highly coherent axonal fascicles, with infrequent fiber crossings. A few minutes spent examining histological samples of brain tissue stained for myelin with a good optical microscope reveals that this assumption is obviously incorrect. The “small world” connectivity (Hilgetag et al., 2000) of a brain, indeed, implies a very large number of short connections between brain areas, and a smaller number of longer connections (Schüz and Braitenberg, 2002), which may well be quite coherent, but are inevitably crossed frequently by connections between other brain regions (Jeurissen et al., 2013). Diffusion-weighted MRI techniques that have been available since 2010 are starting to provide a much more realistic picture of white matter organization (Jones et al., 2013; Wedeen et al., 2012).

The situation is even worse when it comes to cortical gray matter. As recently summarized by Elston and Garey (2013), Triarhou (2013), and Nieuwenhuys (2013a, 2013b), the 0.23 m² area of gray matter in the human brain has been known for more than a century to show many compact subregions (Brodmann areas) defined by their distinctive cytoarchitecture and myeloarchitecture (Brodmann, 1909; Elliot Smith, 1907; Vogt and Vogt, 1919). Ideally, a mechanistic explanation that enables valid prediction requires a clear definition of the given mechanism's components, their specific functional roles, and how these sub-functions are integrated into the operation of the mechanism as a whole. Some would argue (Mikula et al., 2012; personal communication) that reasonably accurate predictions may only be achievable when we can specify components at a nanometer scale across the entire brain. However, given the comparatively uniform structure of cortical areas and the anatomical discriminability of subcortical nuclei, it may be more pragmatic to start with these as the units of analysis and mechanistic modeling. This would limit the number of components to no more than 200, which along with more than 20 different neurotransmitters, neuropeptides, and corticosteroids should already provide a requisite level of complexity (Lohmann et al., 2013).

Consensus remains to be built, however, regarding how many such cortical regions can and should be distinguished, and there is an urgent need for a useful concordance atlas between myeloarchitecture and cytoarchitecture in the same cadaver human brains. Research in the human myeloarchitecture has made little progress in a century (Nieuwenhuys, 2013a, 2013b). Although details of myeloarchitecture are often far more easily visible than in cytoarchitecture, such as the heavily myelinated stria of Gennari in the primary visual cortex (observable even with the naked eye), there has been little speculation or research regarding the functional role of specific myeloarchitecture in each cortical area (but see Glasser et al., 2014). Some important details of cortical connections have been carefully researched, such as the respective inputs and outputs to and from other brain regions and the spinal cord, although the variations between cortical areas of the horizontal bands of myelinated cortical fibers comprising the Exner stripe and the two Bands of Baillarger remain unexplained. The arrangement of cytoarchitectural features within the cortex is no better explained, although terms such as “granular” and “agranular,” “allocortex” and “isocortex” give the impression that the mode of operation of specific types of cortex is already well understood. Even though different networks may be able to ostensibly perform the same task (Price and Friston, 2002), it is obvious that brain areas with different microarchitecture have different information processing competences (Shepherd, 2009). However, current methodologies for functional data analysis pay little regard to the precise division of labor that this would imply, as will be discussed next.

It would, thus, be a major leap forward if it were possible to generate an individual-specific map of genuine cortical microstructure in vivo and correlate it with cortical function in the same brain. This is for at least two reasons. The first is that like could always be compared with like in group studies—averaging of structural and functional results could be performed in an area-wise manner, without spatial smoothing. The second reason that this goal is desirable is that it may enable connection of the findings of systems neuroscience with those of cellular neuroscience; for instance, explanation of the functional competence of some specific cortical area in terms of its neuronal makeup and configuration. In recent years, two advances are bringing us closer to this ambitious goal. The first is the dramatic improvement in the quality of in-vivo MRI scans, as already mentioned. Even at 3T, use of a 32-element radio frequency (RF) receiver coil has dramatically increased signal-to-noise ratios (SNRs), and at 7T, structural images of entire brains can be obtained with better than 0.5 mm isotropic resolution (Trampel et al., 2011). Functional blood oxygenation level dependent (BOLD) contrast changes can be mapped with 0.65 mm isotropic resolution (Heidemann et al., 2012). The second advancement is based on the observation that maps of the longitudinal relaxation time T1 effectively indicate the presence of myelin and closely resemble myelin-stained histological sections (Dick et al., 2012; Geyer et al., 2011; Sereno et al., 2013; Turner, 2011, 2013), whereas differences in cytoarchitecture are detectable with MRI only in rare instances such as the unique islands of large neurons in layer II of the entorhinal cortex (Augustinack et al., 2005). Research by Cécile and Oskar Vogt, pioneers in the field of myeloarchitecture in the first half of the twentieth century, has shown that there is a great degree of concordance between structural parcellations of the cortex based on differences in myeloarchitecture and those in cytoarchitecture (Vogt and Vogt, 1919). Myelo- and cytoarchitecture are not two parallel universes but two different views of the same universe.

“In-vivo Brodmann mapping” (Geyer et al., 2011) exploits the longitudinal relaxation time T1 and reveals cortical microstructure by showing, similar to myelin-stained histological sections, differential gray matter myelination. Cortical areas known from postmortem studies to be heavily myelinated such as primary motor, somatosensory, auditory, visual cortex, or area V5-MT (Clarke and Miklossy, 1990; Hopf, 1955, 1956; Hopf and Vitzthum, 1957) are easily discernible from surrounding less myelinated regions. In addition, a “triple jump” approach enables us to validate the myelin-based in vivo maps with “classic” histology data ex vivo, and—what is even more important—to define precise borders between cortical areas: Formalin-fixed postmortem tissue blocks of the human cortex are scanned with a 7T MRI sequence that produces T1 maps, sectioned with a microtome, sections are stained for myelin sheaths or cell bodies, and the MR architecture is correlated with myelo- and cytoarchitecture. This approach makes it possible (1) to define a cortical area based on myelo- and cytoarchitecture, (2) to extract the “MR fingerprint” of this area ex vivo, and (3) to transfer this “fingerprint” to living brains and define this area in vivo. As an example, this technique has been successfully used to map microstructural borders between cortical areas in the pre- and postcentral gyrus, especially the functionally important border between primary motor (Brodmann's area 4) and somatosensory (area 3a) cortex. Here, a sharp drop in T1 values at the base of the precentral gyrus of a formalin-fixed tissue block (ex vivo) coincides with an increase in myelin density in a histological section of the same block immunostained for myelin basic protein (myeloarchitecture). In an accompanying section stained for cell bodies (cytoarchitecture), this position is characterized by an increase in gray matter thickness, a disappearing inner granular layer, and emerging giant pyramidal (Betz) cells—which altogether marks the border between area 3a and area 4. A T1 map of the central sulcus region in a living subject (in vivo) also shows a sharp drop in T1 values and an increase in cortical thickness at the base of the precentral gyrus. The position and MR parameters of this border in vivo match the corresponding border between area 3a and 4 ex vivo (Geyer, 2013; Geyer et al., 2011).

The justification for terming this myelin-based approach “in-vivo Brodmann mapping” [which refers to cytoarchitecture, the cell-architectonic technique used by Brodmann for mapping the cortex; see Brodmann (1909) and Garey (2006) for an English translation] comes from the writings of Cécile and Oskar Vogt, who repeatedly stressed the great degree of topographical concordance between areal borders based on differences in myelo- and cytoarchitecture. See also the comprehensive reviews of earlier myeloarchitecture research in Nieuwenhuys (2013a, 2013b). In a schematic drawing of the pre- and postcentral gyrus, published by Vogt and Vogt (1919, p. 394), they present a pictorial synopsis of the topography of cortical areas and their borders as defined by cyto- and myeloarchitecture. There is a precise spatial correspondence, for example, in the fundus region of the central sulcus between cytoarchitectonic area 4 (primary motor cortex) and myeloarchitectonic area 42, cytoarchitectonic area 3a and myeloarchitectonic area 67, and cytoarchitectonic area 3b (primary somatosensory cortex) and myeloarchitectonic area 69. Of course, this sketch represents only a tiny sample of the entire cerebral cortex and borders were defined solely by subjective visual inspection through the microscope—the only technique available at that time. Extending this concordance mapping between cyto- and myeloarchitecture to the entire cerebral cortex, and verifying areal borders with objective analysis techniques is under rapid development. The articles by Bazin et al. (2014) and Waehnert et al. (2014) present first and very promising results in this direction.

Thus, “in-vivo Brodmann mapping” based on high-field MRI can detect functionally important borders such as the one between primary motor (area 4) and somatosensory (area 3a) cortex ex vivo and—more importantly—also in vivo. This will continue to be an integral step toward individual-specific microanatomical brain maps, with the great potential to make direct correlations between microstructure and function in living human brains.

Spatial Smoothing: A Critique

Using MRI and BOLD contrast, Kwong et al. (1992) localized functional activity in the human brain with a much better spatial resolution than O-15 PET, MRI's functional precursor. With the advent of fMRI, the inadequacy of gross sulcal and gyral brain anatomy for precise location of specific cortical areas became much more apparent. Cortical areas are defined cytoarchitecturally only in cadaver brains, but human brains naturally show considerable variability, both in the pattern of sulcal folding and generally in the relative locations of cortical areas on the sulci and gyri. While some areas such as primary visual or primary motor cortex are quite well defined by their sulcal location (Fischl, 2013; Fischl et al., 2008), their spatial extent can still vary dramatically across subjects. Since MRI data were then incapable of defining cortical features, the spatial localization of brain activity was initially specified using the work of Talairach and Tournoux (1988), who projected the cytoarchitecturally defined Brodmann areas onto the external cortex of the brain of an elderly French woman. The usefulness of this work lay mainly in the definition of a three-dimensional coordinate system, which could be used to suggest locations of Brodmann areas in other brains. The invention of MRI by Mansfield and Lauterbur in the early 1970s made it feasible to project this Talairach map onto any desired living brain, which could be scanned with a spatial resolution of about 1 mm by the time of Kwong's discovery in the early 1990s. The coordinate system defined by Talairach was subsequently replaced by Montreal Neurological Institute (MNI) coordinates (Le Goualher et al., 1999).

Leading imaging neuroscience laboratories, such as the FIL in London, then developed the now-current methodology, which attempts to link brain location, neuroanatomy, and function at a spatial scale of about 8 mm—which is about as close as anyone dared to expect that corresponding cortical areas could be located across brains. The strategy of spatial smoothing, using a Gaussian smoothing kernel of typically about 8 mm, was fundamental to this approach. This had the following very important benefits: (1) it often considerably improved the SNR of functional data; (2) it enabled very simple analytic equations (Worsley et al., 1992) to be used for assessing the statistical significance of measured brain activity, and thus for thresholding the resulting group images to provide spatial activation maps; and (3) after structural brain images had been spatially normalized into a standard template brain registered within MNI space, smoothing enabled the residual mismatch of actual cortical areas, so that positive results could be anticipated from group averaging across normalized brains.

Such maps could then be interpreted in relation to the psychological task paradigm experienced by the human subjects, and discussed in the context of the rapidly growing body of results obtained using a similar strategy. From this perspective, it is clear that at the time of discovery of BOLD fMRI in the early 1990s, the methodology just outlined was driven by necessity. MRI scanner resolution for structural in-vivo brain images was about 1 mm, unable to resolve details within the 3 mm thickness of the cortex, and BOLD functional imaging could provide adequate quality images with no better than 3 mm isotropic resolution. In 1995, affordable lab computers required 30 min or more to analyze time series of fMRI even with the simplistic methods for assessing significance that were then recommended. MRI using any type of sequence has never been good at depicting variations in cortical cytoarchitecture, and very few researchers were aware in 1992 that it could be made quite sensitive to myeloarchitectural details (Clark et al., 1992).

The situation these days is very different: (1) scanners with a field strength of 3T and higher, along with vastly more sensitive phased array RF receiver coils, give much improved sensitivity, so that enough contrast-to-noise ratio is often available without spatial smoothing; (2) by virtue of Moore's Law, 18 years of improvement in computer speed and capacity have made practicable many alternative methods for assessing statistical significance (such as correct implementations of False Discovery Rate), rendering spatial smoothing unnecessary; and (3) a deeper understanding of the importance and scope of myeloarchitecture enables identification of cortical areas within each human subject, so that smoothing is increasingly unnecessary to ensure overlap across subjects.

To illustrate the weakness of traditional methods for analysis of fMRI data, we summarize important human brain characteristics, and review and critique the implicit and explicit assumptions embedded within these traditional methods. Several of the papers in the 2014 Neuroimage Special Issue show that relatively detailed parcellation of the cortex can be performed into regions comparable to those identified by Brodmann, which can then plausibly be taken as brain components with definable processing competences (see also Bridge et al., 2005, and Sánchez-Panchuelo et al., 2012). We outline the crucial features of more suitable analysis and richer modeling strategies based on such components, and finally discuss the multiple benefits of such a scientific paradigm shift for understanding human brain function.

As a reminder of what a human brain is really like, there are about 10¹¹ neurons, about 10¹¹ glial cells, and on the order of 10¹⁴ synaptic connections (cf. Lent et al., 2012). The cerebral cortex can be parcellated into probably more than 100 areas of recognizably different cyto- and myeloarchitecture. Each area is axonally connected to at least 10 other areas, and to several thalamic nuclei, basal ganglia, and specific cerebellar regions. Many cortical areas have sharp boundaries (less than 1 mm in thickness), and since brain areas and even sparsely encoding separate neurons can be selectively activated by appropriate combinations of stimuli, brain activity cannot be assumed in general to be spatially smooth. However, for most tasks, many brain areas are jointly in operation, due to the intense connectivity. No neurons are more than about eight synapses apart, and most are separated by no more than five synapses.

Significant local activity takes place on time scales from 1 msec to minutes and days, and inter-area transit times for action potentials are about 10–50 msec. The brain itself is nonstationary: its connections are dynamic. A stationary brain would be useless to its organism. The strengths of synaptic connections are continually changing and the concentration patterns of modulatory neurotransmitters, neuropeptides, and corticosteroids, which strongly modulate brain network activity, vary diurnally and with situations. New dendrites and terminal axons are continually growing and new synapses are being formed; while simultaneously other synapses are lost, dendrites are reabsorbed, and neurons die.

Thus, the facts that stable, reproducible neurovascular responses to carefully controlled tasks can be observed, and that these can be replicated across subjects, should be considered somewhat surprising, and in themselves worthy of scientific curiosity. That many tasks require concerted activity among large assemblages of neurons is clearly evident, but this should not exclude the possibility that increased (or decreased) task-related activity of small numbers of neurons, perhaps spatially distributed, may have an enormous impact on how a task is performed.

Readers also need to be reminded of certain biophysical facts regarding brain activity, and its detection with MRI techniques. Gray matter has an energy demand (and corresponding blood volume) about four times greater than that of white matter. This energy demand is supplied by glucose and oxygen in blood delivered by capillaries and terminal arterioles, branching almost entirely from arteries lying on the pial surfaces. Blood that has delivered these metabolic substrates is drained from the cortex by pial veins (Turner, 2002). Since the BOLD signal is proportional to the blood volume in each voxel, as well as to the change in blood oxygenation (Menon et al., 1995), one can expect much larger changes in BOLD signal to arise from the cortex, especially at the cortical surface, than in white matter. It is, thus, a good assumption that apparently activated voxels lying in white matter, cerebrospinal fluid (CSF), or bone are, in fact, false positives. As regards the smoothness of the BOLD signal, since the cortex is never more than 4 mm thick, the maximum spatial smoothness that can be expected in the trans-cortical direction is this value, 4 mm. In fact, rapid spatial variations of BOLD signal have been reliably observed over shorter distances—across cortical layers (Koopmans et al., 2010) and cortical columns (Yacoub et al., 2008). It might be expected that that the draining vein effect (Turner, 2002) might blur out such high spatial frequency effects—but the surface veins carrying deoxygenated blood that could give rise to spurious signals are relatively discrete and can, thus, be edited out of the image (Yacoub et al., 2008). It should be mentioned that this may entail loss of some more localized activity arising from cortical capillaries. Boundaries between cortical areas are often narrower than the cortical thickness, and tracking BOLD activation time courses across voxels often shows abrupt changes at such cortical boundaries. The point-spread function of BOLD within the primary visual cortex has been measured to be less than 2 mm full-width half maximum (Shmuel et al., 2007). Statistically based estimates of the spatial smoothness of BOLD activation (Kiebel, 1999) entirely fail to take account of the physics of brain tissue and of the MRI acquisition.

Typical in-vivo MRI and fMRI image parameters, as used in standard functional studies in magnetic fields of 3T and below

In the late 1990s, most labs studying brain function using MRI converged on a standard protocol for imaging. This was especially helpful for cognitive neuroscience studies of perception, cognition, and motor control, because it made reasonably good use of the current MR scanner capabilities, and enabled straightforward comparisons to be made between studies performed at different laboratories. While some variations on this theme continue to be used, in relation to specialized hypotheses and specific brain areas (such as early visual areas), a convention was rapidly agreed on. In broad terms, this consists of acquisition of structural images of entire volunteer subject brains with 1 mm isotropic resolution, using the T1-weighted magnetization prepared rapid acquisition gradient-echo MRI sequence, followed by acquisition of functional data using gradient-echo echo-planar imaging sensitive to BOLD contrast, at about 3 mm isotropic resolution.

The 1 mm isotropic resolution structural images are often used for voxel-based morphometry (VBM) studies of comparative morphometry (Ashburner and Friston, 2000), and recently especially for exploring neural plasticity. Segmented gray matter images are usually smoothed using a Gaussian kernel of approximately 10 mm, in order to construct a fictitious parameter described as “grey matter density,” which can be compared across the appropriately normalized brains of a group of subjects using standard statistical tests relying on Gaussian Random Field theory. It can be mentioned here that this construction of gray matter density results in an inextricable confounding of cortical thickness and the intensity of gray matter signal, known to reflect myelin density in T1-weighted and T2*-weighted images. Thus, there is no way of knowing whether inter-group differences found in VBM result from differences in cortical thickness or cortical myelination.

The functional images are analyzed using the apparatus of the Design Matrix and the general linear model (GLM) (Friston et al., 1995). As described earlier, spatial smoothing is an integral feature of this analysis strategy.

Current analysis methods are unable to make effective use of ultra-high field-MRI data

Since 1995, the number of cognitive neuroscience studies that utilize neuroimaging techniques has increased exponentially. Between 1995 and 2000, a very widespread consensus emerged regarding acceptable strategies for analysis of fMRI data, led by the work of Friston at the Institute of Neurology in London. These strategies were embodied in software packages such as SPM (Ashburner, 2012), FSL (Jenkinson et al., 2012), and BrainVoyager (Goebel, 2012). It was clearly of great benefit to this young research field to have such consensus, but it can now be argued that this was often a case of premature closure, given the continual improvement in the brain image data available. AFNI (Cox and Hyde, 1997) is a laudable example of a package that allows the researcher a wider range of choices of strategy. However, this requires much greater detail to be supplied of the guiding assumptions when the results of analysis are reported, and a consensus has yet to be reached of the most appropriate strategy.

To make this explicit, let us consider the stages of data analysis that are recommended in using SPM8 for a standard neurocognitive study. The first step is, of course, to acquire the fMRI data, as a series of 300–600 brain volumes, each taking about 2 sec to acquire, while a well-controlled brain task is performed. It is considered that results which can be generalized to a subject group or an entire population require scanning about 16 subjects, a number just large enough to enable estimation of inter-subject variance.

The next steps in analysis immediately involve a set of explicit and implicit assumptions regarding brain mechanisms and brain spatial organization. This set of assumptions is commonly adopted (whether they are aware of it or not) by users of all data analysis packages, such as SPM, FSL, that use spatial smoothing and probabilistic atlases.

Problematic assumptions of standard fMRI analysis

Smoothing is required for statistical inference

It is commonly assumed that statistical inference using fMRI data can only be performed if the image is smoothed by a kernel thrice the size of the acquired voxels. Gaussian Random Field theory requires such smoothness for valid estimation of the statistical significance of brain activations. With the standard acquisition voxels of about 3 mm, this means that a smoothing of 8 mm or more is usually applied. The result, after statistical thresholding, is generally a relatively formless blob of voxels that are considered functionally active. Since the perimeter of such blobs is anatomically meaningless, only the points at which significance is maximal are usually reported. The time course of activity at such points is considered to summarize the activity of the entire blob.

One implication of this assumption is the tacit acceptance of the idea that Neural Mass Modeling (Friston, 2008) is valid everywhere in the brain, at a scale of 8 mm or more. Instead of modeling individual neurons, this approach approximates a group of neurons by its average properties and interactions. This raises the important neurophysiological question: Is there a spatial scale for which Neural Mass Modeling might be reliably valid? Spatial smoothing lumps together the highly specific and well-localized task-related changes of blood oxygenation observable with fMRI, such that only the locations of the maxima of the thresholded smoothed map of t-scores are attributed any physical meaning. If Neural Mass Modeling were valid on a spatial scale of 8 mm, smoothing on this scale might be appropriate, but there is compelling evidence that this assumption is generally incorrect. To take but a few examples, a columnar structure with a scale of 1 mm or less is found in primary visual and somatosensory cortices, where the perceptually relevant “neural fields” are certainly smaller than 1 mm in extent; and the brain is equipped with many spatially organized maps, again with a scale of 1 mm, such as the retinotopic, tonotopic, and somatotopic maps in the cortex and thalamus. Smoothing to 8 mm is likely to obscure this functionally crucial detail, and the common practice of smoothing data of individual subjects before they are even examined by the experimenter means that one would never be aware of this problem.

When data are smooth enough that the residuals after fitting to some model can be described as a Gaussian Random Field, the Worsley et al. (1992) formula enables a very robust and computationally quick evaluation of significance. Given the vast amount of data to be analyzed in a typical fMRI experiment, the speed of this operation was very appealing in the mid 1990s.

However, can statistical inference be performed without smoothing? The answer is, yes, of course. The basis of all statistical inference is repeated measures, which enables the computation of the mean and the variance of each measured variable. A normal fMRI experiment, consisting of a time course of hundreds of brain volumes, provides many samples of the signal in each image voxel of the brain for each condition, and thus, in principle, contains all the information needed to assess significance. Spatial smoothing might help by effectively performing a local average of the functional signal, which would improve the SNR, and hence sensitivity, if the noise were random and uncorrelated across voxels. However, most of the apparently randomly fluctuating component of the BOLD signal at a typical spatial resolution arises from more-or-less spatially correlated variations in neuronal activity (Bianciardi et al., 2009), not from random stochastic thermal noise.

As already mentioned, it is quick and easy to make whole-brain statistical inferences on spatially smooth data. However, Moore's Law and the remarkable reduction in the cost of computing hardware mean that much more appropriate, albeit more elaborate methods for assessing significance in functional data, without smoothing, are now feasible (Lee et al., 2012). Based mainly on the concept of False Discovery Rate (Benjamini and Hochberg, 1995), these methods still have to account for the fact that in comparing the intensities of images voxel by voxel, many statistical inferences are made simultaneously. Significance estimates should, therefore, be corrected for multiple comparisons, which is not straightforward when data are not smooth.

Brain architecture is conserved across brains at a scale of 8 mm, and is defined by a probabilistic brain atlas valid for all adult brains

The variability across brains of the relationship between microarchitectonically different cortical areas and their gross anatomical location has been well known for more than a century (Elliot Smith, 1907). Even when brain image volumes are normalized quite precisely using nonlinear warping techniques, corresponding brain areas may fail to overlap by as much as 10 mm (Geyer et al., 1999, 2000). One increasingly popular strategy is to use the probabilistic atlas by Eickhoff et al. (2005), which defines a set of brain areas on an internationally agreed template brain using data from ten cadaver brains that have been parcellated by cytoarchitecture into the equivalent of Brodmann areas. The probabilistic atlas depicts boundaries between areas on the template brain corresponding to the maximum probability that a given voxel will belong to a given brain area. However, an examination of the source overlap maps that show the data from all ten brains reveals that some Brodmann areas show very few concordant voxels.

Thus, it is invalid to assign a Brodmann location to the maximum t-score from a smoothed activation—in the general sense that it is quite improbable that in any particular brain the peak activation actually lies within the specified Brodmann area, whether the data have been smoothed or not.

At this point, it can be strongly emphasized that volumetric cadaver brain maps of cytoarchitecture, such as the BigBrain (Amunts et al., 2013), are of very slender value in the vitally important task of in-vivo cortical parcellation, for the simple reason that while MRI is exquisitely sensitive to variations in cortical myelination, it is almost incapable of discriminating cytoarchitecture. While it may sometimes be useful to access digitally the cytoarchitecture of some morphologically defined region in the single cadaver BigBrain that was assembled from histological slices, this work falls far short of the requisite cortical parcellation concordance atlas which could have been compiled decades ago.

The importance of a given brain area for a specific task is indicated only by a positive mean activity, on a scale of 8 mm

Most BOLD fMRI cognitive studies show thresholded maps of the positive BOLD signal, along with tables of activation maxima in MNI space. However, pattern classification techniques can decode reliably from patterns of scale 1 mm (Bode et al., 2011), which include decreases of BOLD signal as well as increases. It should not be surprising that localized decreases of neuronal activity in a given cortical area should have informational relevance for other brain areas.

Lateral inhibition (reviewed in Beck and Hallett, 2011; von Békésy, 1967) is a well-known neural strategy that enhances edge detection and focuses spatial attention, for instance, in the visual system. It is not known how often a brain typically uses such a means of attentional focusing. For a small area of activation, smoothing by 8 mm is likely to include an area of negative BOLD corresponding to lateral inhibition, and thus reduce the apparent amplitude of the activation. For instance, in the primary visual cortex, regions of positive BOLD activation are usually surrounded by a ring of negative BOLD signals, over cortical distance scales of several millimeters (Shmuel et al., 2006). Obscuration of this ring by smoothing incurs the obvious risk that a vital component of the mechanism of vision will remain undiscovered (see also Harvey et al., 2013).

Activity in any given brain voxel is statistically independent from any other brain voxel

Many fMRI analyses, whether using SPM, FSL, AFNI, or BrainVoyager, are conducted using the GLM, which treats each image voxel as independent, except insofar as the image is spatially smooth. The solution of the GLM entails formulation of a Design Matrix, which includes time series of all covariates of interest and of no interest. Computation of the pseudo-inverse of the design matrix then provides least-squares-fit best estimates of the linear dependences (betas) of the data time course in each voxel on the covariates of interest and of no interest. To estimate the statistical significance of the coefficients of variation thus obtained, spatial smoothness should be taken into account. In SPM, this is estimated statistically from the residuals after the GLM fit, and its value is used in correcting the final voxel-by-voxel significance estimates for multiple comparisons. Once this has been performed, cluster size can be used to obtain an additional estimation of significance, which clearly enables the use of lower values for the z-score or t-score in computing significance thresholds.

The GLM has proved to be a very powerful tool in objectively identifying brain regions in which significant changes in BOLD contrast take place in controlled experimental conditions (Monti, 2011). However, at a conceptual level, its validity is fundamentally compromised by the well-established fact that a brain (of any species) is intrinsically multivariate in operation. It is the very dependence of activity in one group of neurons on the activity in a different group of neurons that enables a brain to function. Even the brain of a fly is intrinsically multivariate in operation. Any neuron projects to several other neurons, often in a variety of areas. Synchronized synaptic input at any neuron from many other neurons is required to trigger delivery of an action potential. Analyses that ignore these trivially obvious facts will never be capable of providing insights into brain mechanisms.

Attempts to include spatial covariance using graph theory with an artifactually small number of nodes, such as Dynamic Causal Modeling (critiqued by Lohmann et al., 2012) or Granger Causality (Goebel et al., 2003), are unlikely to do justice to the complex detail of neural performance. Recent work using unusually long averaging times per volunteer subject in a simple fMRI study have shown that time-locked activity can be detected in 95% of gray matter voxels, when the data are not smoothed (Gonzalez-Castillo et al., 2012). This result suggests that conventional fMRI analyses are likely to incur a very large number of false negative findings. The appearance of simplicity provided by spatial smoothing and conservative thresholding of fMRI data may be highly misleading.

Fortunately, as mentioned earlier, multivariate analytic techniques—brain decoding—have recently come to the forefront (Formisano and Kriegeskorte, 2012; Kriegeskorte et al., 2006) and offer access to coordinated spatial patterns of brain activity, which manifest themselves most particularly in the numerous cortical maps (retinotopic, tonotopic, and somatotopic maps) in which variations in perceptual parameters become spatially encoded in brain networks. In such analyses, spatial smoothing is rarely explicitly performed, though an effective smoothing is implicit in “searchlight” methods for pattern classification (Kriegeskorte et al., 2006). It should be pointed out that such techniques would produce no results if the activity in each voxel was uncorrelated.

Gray matter, white matter, and CSF are considered equally likely, as possible locations of changed brain activity

After BOLD fMRI data have been spatially smoothed by 8 mm, analyzed and the resulting t-statistic map has been thresholded (typically at p<0.05 corrected for multiple comparisons), it is usually overlaid on a high-resolution gray-scale T1-weighted image of the brain, inviting assignment of the spatial localization of the activations found. Sadly, the activated region usually then has the topology of a distorted sphere, rather than the ∼3 mm thick curved surface corresponding to the cortical gray matter. Thus, it is inevitable that many voxels in the high-resolution map which are CSF, bone, or white matter are then labeled as a part of the activated region. In point of fact, all such voxels are false positives: there can be no activation in them.

If a given voxel's task-related variance is smaller than a statistical threshold of p<0.05, after correction for multiple comparisons, it can play no role in the task performance

This assumption infringes one of the fundamental principles of experimental science: Absence of evidence does not constitute evidence of absence. The just-cited paper of Gonzalez-Castillo et al. (2012) shows that at least for some experimental paradigms, longer data collection and averaging of more samples reveals activation in a much greater number of voxels. The critical question arises, by what criteria can it be decided which of these voxels are most important for the performance of the given experimental task? Should an activated region of limited extent, but strong BOLD contrast, so that when spatially smoothed it expands over a wide area, be considered more vital to some task performance than a much larger area of voxels with activations which fail to reach the arbitrary threshold of p<0.05 corrected?

It can be strongly argued that attempting model fits to data with many false negatives is just as pointless as trying to fit data with many false positives (as with Assumption 5).

The position of the maximum t-score of a thresholded activated area completely defines its localization

It is customary to display fMRI results in tabular form, giving coordinates of maximal activation in MNI space. With the typical 8 mm spatial smoothing, this maximum will be located close to the centroid of the activated volume. Any other spatial parameters of the activated area are very difficult to interpret anatomically, particularly when much of the thresholded volume fails even to lie within gray matter. However, especially when group average data are considered, the maximum t-score itself may lie in a part of the brain that cannot be identified with any particular cortical area. For example, if the crown of a gyrus and each of its banks are activated in some particular study, the maximum will lie in white matter somewhere within the gyrus, where there is, in fact, no change of BOLD contrast. If one of the goals of functional neuroimaging is to associate function with specific brain architecture, the MNI coordinates cited in such a study can provide no useful information whatever.

It should be noted that the strategies criticized here have generally been restricted to imaging studies related to cognitive neuroscience and human subjects. Even in humans, there is an extensive body of fMRI research, beginning with the retinotopic studies of Engel et al. (1994), that has explored the functional anatomy of occipital cortex using little or no smoothing, and group data were combined after separate detailed analysis of the data from each subject. The same is true for many fMRI studies of animal brain, ranging from rat (Silva et al., 1999) to cat (Zhao et al., 2006), to macaque brain (Logothetis et al., 1999). In such studies, it has been vital to respect the distinction between spatial extent and amplitude, and the underlying neuroanatomy is typically sufficiently well understood that there is no likelihood of conflating distinct brain regions. Thus, the difficulties that have encouraged reckless smoothing have mainly arisen when the so-called “higher” brain functions of humans—cognition, emotion, attention, and language—have been the object of study.

Keys to New Analysis Methods

A more powerful strategy is clearly desirable for neuroimaging studies of human cognition. One important concept might be the idea of “cortical competence,” that is, the description of the relationship between input and output streams of action potentials for any given clearly identifiable area of cortex—and for completeness, the linked concept of “nuclear competence,” with regard to the deep brain nuclei such as the thalamic nuclei and the basal ganglia. The explicit assumption is made, following the great 20th century neuroanatomists, that myeloarchitecture and cytoarchitecture are not epiphenomenal, as one might gather from contemporary research publications, but are closely related to the transformational properties of specific areas. A careful study of cyto- and myeloarchitecture may afford important clues regarding such competences. The fact that some details of myeloarchitecture can be observed in vivo, and correlated with task-related activation, invites attempts at interpretation of why it varies across cortical areas.

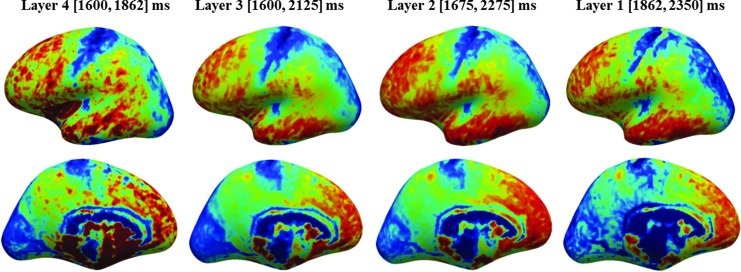
We suggest the following routine procedures to replace existing conventions, in order to facilitate the mechanistic modeling of the functional roles of specific well defined cortical areas: (1) in-vivo brain imaging at a submillimeter resolution of structure, function, and connectivity; (2) in-vivo cortical parcellation; (3) voxel encoding (Huth et al., 2012; Vu et al., 2011) or multivariate analysis; and (4) across-subject averaging by anatomically defined regions of interest. This latter operation can be greatly assisted by the use of surface cortical registration driven by the matching of cortical T1 maps. This has been shown to align equivalent heavily myelinated cortical areas across subjects with remarkable precision (Tardif et al., 2013). Figure 1 (provided by Tardif) shows the result of such a surface alignment based on T1 maps, for an average of five brains, scanned at 0.5 mm isotropic resolution at 7T. Here, the surfaces at each of four cortical depths, calculated using the methods of Waehnert et al. (2014), have been separately aligned across the five subjects. A great deal of conserved myeloarchitectural detail can be seen, which will enable a quite specific assignment of functional activity to known cortical areas.

FIG. 1.

Group averaged human brain in-vivo T1 map (n=5) at different cortical depths, from the gray/white boundary to the pial surface. The T1 contrast between cortical areas varies with cortical depth, and reveals evidence of area-specific myeloarchitecture. Computed from images acquired at 0.6 mm isotropic resolution at 7T, using the MP2RAGE imaging sequence (Data provided by Tardif). See Tardif et al. (2013) for details.

In the analysis of functional data, it should be noted that spatial smoothing should be strictly avoided, except possibly at the final stage of presentation of data after analysis—and then only within the cortical sheet. This approach clearly enables a much closer association of function and connectivity with each distinct cortical and deep brain area. Obvious advantages are the greatly increased statistical power provided by the region-of-interest analysis across subjects, and the continued separation of spatial extent and amplitude as independent variables.

It is important to recognize that cognitive neuroscientific analysis of human brain function could be productive at a much coarser spatial scale. However, such understanding can only be validated once it has become clear what approximations a coarse-grain approach entails, and what justifies the ignoring of neuroanatomical details. So far, high-resolution functional studies of animal brain have offered little support for the sweeping generalizations inherent in Neural Mass Modeling at the spatial scale of 8 mm.

Beyond this, fundamental research on the neuroscience of cognition should progress far more rapidly when cortical areas supporting specific psychological tasks can be more unambiguously identified. Currently, standard functional image analysis methodology is unable even to assign brain activity to a particular bank of a sulcus, once averaging has been performed across human brains. The great power of spatial mapping of brain activity for understanding when differently labeled tasks are, in fact, the same, and when apparently similar tasks are actually dissociated, can only be used to its fullest when the neuronal substrate of brain functional activity has been properly identified. Meta-analysis, already showing great promise, should really take off when such correlations have even been partly established.

Author Disclosure Statement

No competing financial interests exist.