Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Aug 27.
Published in final edited form as: Cancer Causes Control. 2011 Nov 25;23(1):175–185. doi: 10.1007/s10552-011-9866-9

Comparing the Benefits of Screening for Breast Cancer and Lung Cancer Using a Novel Natural History Model

Ray S Lin 1,2, Sylvia K Plevritis 1
PMCID: PMC4146530  NIHMSID: NIHMS404193  PMID: 22116537

Abstract

To estimate the impact of early detection of cancer, knowledge of how quickly primary tumors grow and at what size they shed lethal metastases is critical. We developed a natural history model of cancer to estimate the probability of disease-specific cure as a function of tumor size, the tumor volume doubling time (TVDT) and disease-specific mortality reduction achievable by screening. The model was applied to non-small cell lung carcinoma (NSCLC) and invasive ductal carcinoma (IDC), separately. Model parameter estimates were based on Surveillance Epidemiology and End Results (SEER) cancer registry datasets and validated on screening trials. Compared to IDC, NSCLC is estimated to have a lower probability of disease-specific cure at the same detected tumor size, shed lethal metastases at smaller sizes (median: 19mm for IDC vs. 8 mm for NSCLC), have a TVDT that is almost half as long (median: 252 days for IDC vs. 134 days for NSCLC). Consequently, NSCLC is associated with a lower mortality reduction from screening at the same screen detection threshold and screening interval. In summary, using a similar natural history model of cancer, we quantify the disease-specific curability attributable to screening for breast cancer, and separately lung cancer, in terms of the TVDT and onset of lethal metastases.

Keywords: Breast Neoplasms; Lung Neoplasms; Cancer Screening (Early Detection of Cancer); Computer Simulation; Mathematical Model (Models, Theoretical)

INTRODUCTION

Cancer affects more than one million people each year and is the second leading cause of death in the United States (1). Screening for cancer is based on the rationale that detecting and treating cancer at early, asymptomatic stages will prevent cancer deaths. However, clinical trials have shown that cancer screening prevents cancer deaths in some cases, such as mammographic screening for breast cancer, but not in other cases, such as chest radiographic screening for lung cancer (2).

To understand the probability of disease-specific cure from early detection, two critical questions need to be answered: (i) How small does cancer need to be detected to ensure that the disease has not progressed to an incurable state? and (ii) How quickly does the disease progress from a curable to incurable state? We propose a novel natural history model of cancer to answer these questions. In this report, we present the model, describe its properties, and apply it separately to the estimate the efficacy of screening for two different cancers: invasive ductal carcinoma (IDC) and non-small cell lung carcinoma (NSCLC). We focused on these diseases because they have had different screening recommendations for the past 30 years. In the case of breast cancer, mammography has been recommended ever since randomized controlled trials (RCTs) of screening demonstrated a reduction in breast cancer mortality. However, in the case of lung cancer, no RCTs of chest radiography has demonstrated a reduction in lung cancer mortality; consequently, lung cancer screening by chest radiography has not been recommended. The differences in the impact of mammographic and chest radiographic screening on their associated disease-specific mortality rates is due to a variety of factors, among them are biological differences in these diseases, and characteristics of the screening tests. Even though it is well known that the biology of lung and breast cancer differ, the goal of our work is to quantify specific biological differences of these diseases and demonstrate how these biological differences may explain a difference in disease-specific mortality reductions attributable to screening, when the characteristics of the screening tests are similar.

MATERIALS AND METHOD

Natural History Model Formulation and Assumptions

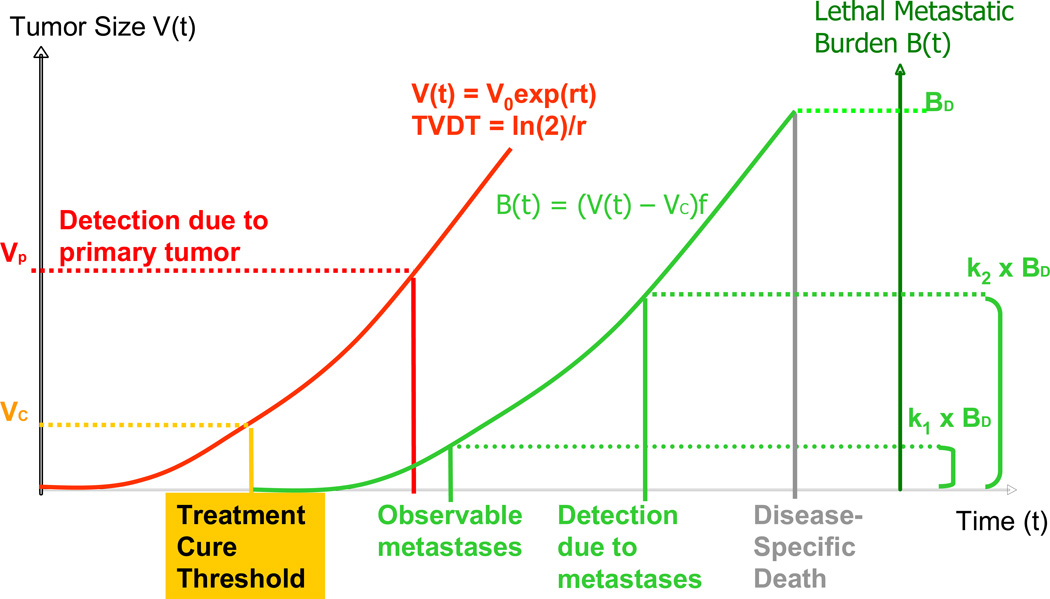
We propose the natural history model of cancer shown in Figure 1; the formulation and assumptions are described below.

Figure 1.

Figure 1

Open in a new tab

Natural history model of cancer: The volume of the primary tumor V(t) grows exponentially with tumor volume doubling time, TVDT, and the treatment cure threshold occurs at size VC. Patients detected and treated at or before VC are cured of their disease; otherwise, lethal metastatic burden B(t) will grow exponentially from VC in proportion (f) to the primary tumor and become the cause of cancer death at a maximal metastatic tolerance level BD. The lethal metastatic burden becomes observable when it reaches a fraction (k1) of BD . A patient detected after this moment is regarded as having advanced staged. A patient is detected from either the primary tumor or metastasis, dependent on which prompts detection present first. The primary tumor is detected at size VP, and the lethal metastatic burden is detected when it reaches a fraction (k2) of BD.

Growth of Primary Tumor

We assume that growth of primary tumor volume grows exponentially, starting from a volume V0 at time t=0 and the growth rate be denoted by r.

The tumor volume at time t, V(t), is

V(t)=V0exp(rt)fort≥0

We chose V0 = 1 mm3. Note the tumor has a constant tumor volume doubling time (TVDT) equal to ln(2)/r.

Treatment Cure Threshold

We define the “treatment cure threshold” of cancer as the primary tumor volume at which the disease transitions from being curable to incurable, assuming standard of care following detection. Here “curable vs. incurable” is disease-specific curability, meaning that the patient would never die from their specific disease if detected and treated at or before the treatment cure threshold. At the treatment cure threshold, we represent the primary tumor volume by VC. The corresponding time, represented by TC, is

TC=1rln(VCV0)forVC>V0

TC and all time related terms henceforth are relative to t=0 when the primary tumor volume is expressed as V0.

Based on our model assumptions, patients diagnosed and treated at or before the treatment cure threshold will be cured and will not die of their cancer; otherwise, they die of that cancer regardless of treatment, unless they die of other causes first. The actual cause of death can be evaluated by considering disease-specific cause of death and other cause death as competing risks, but that is not objective of this study.

Lethal Metastatic Burden

We assume the lethal metastatic burden starts increasing at the treatment cure threshold, thereby we are implicitly excluding metastasis that may be eradicated or controlled by systemic treatment when treated before the onset of the lethal metastatic burden. We assume the lethal metastatic burden grows in proportion (f) to the growth of the primary tumor, and continues to grow even after the primary tumor is detected and removed. The lethal metastatic burden at time t, denoted by B(t), is computed as:

B(t)=(V(t)−VC)fifV(t)≥VCB(t)=0ifV(t)<VC

We assume if the patient is not diagnosed and treated before the treatment cure threshold, the lethal metastatic burden becomes the cause of death at the maximal lethal metastatic burden, represented by BD, unless the patient dies of other causes first. If diagnosed before the treatment cure threshold, the patient is cured of that specific cancer; otherwise, the time of disease-specific death TD can be expressed as:

TD=1rln(VC+BD/fV0).

Symptomatic Detection

We assume that disease is symptomatically detected either due to the primary tumor or the lethal metastatic burden, dependent on which presents with symptoms first.

  1. The primary tumor is detected at size VP at time TP, where detection is attributed to the occurrence of symptoms or an incidental finding under routine medical care.

  2. The lethal metastatic burden prompts detection when it reaches a fraction (k2) of the maximal lethal metastatic burden BD. Let this burden be denoted by BM, the corresponding time and the volume of the primary tumor be denoted by TM and VM respectively. Then
    BM=BDk2VM=VC+BM/f=VC+BDk2/fTM=1rln(VMV0)=1rln(VC+BDk2/fV0)
    Let the time and volume of primary tumor at clinical detection are denoted by TE and VE respectively,
    TE=min(TP,TM)VE=min(VP,VM)=min(VP,VC+BDk2/f).

Observable Metastasis and Clinical Staging

We assume patients are clinically staged with advanced disease if lethal metastastic burden is detected at symptomatic detection. We assume that lethal metastastic burden becomes clinicially detectable when it reaches a fraction (k1) of BD. Let this burden be denoted by BA, and the corresponding time and the volume of the primary be denoted by TA and VA, respectively. Then

BA=BDk1VA=VC+BA/f=VC+BDk1/fTA=1rln(VAV0)=1rln(VC+BDk1/fV0)

Patients diagnosed at and after TA are regarded as having advanced staged disease and assumed to be incurable of their disease with existing treatment; patients detected before TA are regarded as having early staged disease and can be cured of their disease only if detected and treated before the treatment cure threshold. Let the observed clinical stage at detection be denoted by A, where A =0 for early stage, and A =1 for advanced stage, then

A=I(TE<TA)=I(VE<VA)=I(VP<VC+BDk1/f)

where I(.) is an indicator function.

Disease-Specific Survival time from Symptomatic Detection

Disease-specific survival time S is the length of time measured from symptomatic detection TE to disease-related death TD. If a patient is symptomatically detected due to their primary tumor, but detected before the treatment cure threshold, we assume they are cured of their disease. If a patient is symptomatically detected due to primary tumor but after the treatment cure threshold, then their disease-specific survival is as follows:

S=TD−TE=1rln(VC+BD/fV0)−1rln(VPV0)=1rln(VC+BD/fVP).

If a patient is symptomatically detected due to the lethal metastatic burden, then we assume their disease is incurable and their disease-specific survival is as follows:

S=TD−TE=1rln(VC+BD/fV0)−1rln(VMV0)=1rln(VC+BD/fVC+BDk2/f)

Estimation of the Cancer Progression Timeline and Likelihood of Disease-specific cure

We define the cancer progression timeline as a sequence of time points that include the treatment cure threshold time TC, symptomatic detection time TE, cancer death time TD, and time points when the tumor reaches specific tumor diameters of interest (e.g., 5mm). As previously mentioned, all times are relative to t=0 when the primary tumor volume is expressed as V0.

The likelihood of disease-specific cure in the absence of screening is estimated as the proportion of patients who are symptomatically diagnosed before the treatment cure threshold, that is,

Pr(TE<TC)

assuming patients are treated immediately following detection. This quantity is expected to reproduce the disease-specific cure fraction, which is essentially captured by a flattening of the disease-specific survival curve.

Screen Detection Threshold

By comparing the treatment cure threshold to the tumor size detection threshold of a given screening test, we can estimate the proportion of patients whose disease is curable by early detection. We define the “screen detection threshold” of the screening test as the smallest tumor size detectable by the screening test; it is assumed to characterize the screening test detection characteristics in this analysis.

Opportunity Window for Early Detection

We define the “opportunity window for early detection” as the time interval between the time that the tumor reaches the screen detection threshold and the time that it reaches the treatment cure threshold (3). If the screen detection threshold occurs before the treatment cure threshold and the screening test is conducted within the opportunity window for early detection, the tumor will be screen detected early enough to cure the patient of their disease. However, if the screening test is conducted before the onset of the opportunity window for early detection, the tumor will be missed because it is below the screen detection threshold. Before undergoing a subsequent screening, the patient may be symptomatically detected (and recorded as an “interval cancer case”), but may be cured of their disease, if symptomatic detection occurs within or after the opportunity window for early detection. On the other hand, if the screening test occurs before symptomatic detection but after the opportunity window for early detection, the patient will be screen detected but will not be cured of their cancer.

The length of the opportunity window for early detection depends on the screen detection threshold as well as the growth rate of the tumor. The smaller the screen detection threshold and the slower the tumor grows, the longer the opportunity window for early detection will be. Given a screening program of periodic examinations, by comparing the length of the opportunity window for early detection to the screening interval (e.g. annual or biennial), we estimate the proportion of patients who are cured of their disease by early detection followed by treatment.

Estimation of Natural History Model Parameters

All the events in our natural history model of cancer are determined by seven variables, namely VC, VP, r, BD, f, k1, and k2, as defined above and in Figure 1. Because BD and f cannot be identified uniquely from the SEER data (described below), the ratio BD/f is modeled instead. The variables VC, VP, r, BD /f, are assumed to be stochastic in order to allow for variation across individuals. In other words, for a given individual, the values for these variables are randomly drawn from probability distributions as described next. The size of the primary tumor at detection VP and the growth rate of tumor volume r are assumed to have bivariate lognormal distribution with mean (µ1, µ2), variance (σ1, σ2), and correlation coefficient ρ; the treatment cure threshold VC is assumed to have a Weibull distribution with shape parameter c1 and scale parameter c2; and the ratio BD/f is assumed to have a Weibull distribution with shape parameter b1 and scale parameter b2. The two coefficients (k1, k2), related to observable metastasis (k1) and detection due to metastasis (k2), are assumed constant for a specific cancer type.

Parameters estimates were based on the maximum likelihood method (4, 5), using data from the SEER-Nine Registry (1). To more directly compare estimates of the natural history of NSCLC and IDC, we fitted the model to SEER data during the calendar years when there was no to minimal effect of screening and adjuvant therapy for either disease. Because we fit our natural history model to patient data in the absence of screening and adjuvant treatment, we can only use the natural history model to analyze the effect of screening on patients who would have been clinically detected in the absence of screening and under no or minimal effect of adjuvant therapy. The parameter estimation method and model properties are described in the Supplement.

Modeling the Natural History of Non-Small Cell Lung Carcinoma

SEER NSCLC Data Used for Model Parameter Estimation

Parameters of the natural history model for NSCLC were estimated using SEER data on 52,660 Caucasian male patients who were diagnosed with malignant non-small cell lung or bronchus carcinoma between 1988 and 2003. We did not include patients diagnosed before 1988 in order to avoid potential inconsistency due to a change of coding strategy in SEER. The analysis was limited to Caucasians because it is the largest ethnic group with lung cancer in the SEER database; estimates for other ethnicities were poor due the lower number of cases. The analysis was limited to males, because external validation dataset from the Mayo Lung Project (described below) was limited to males only; estimates for females were estimated (not presented) and found to be similar to males, except for a slightly larger TVDT of adenocarcinoma computed for females. Histology types were identified using ICD-O-3 codes, and patients were excluded if their survival information or histology type was missing. Disease stage was derived based on AJCC staging system the 3rd edition (1988). Early stage was defined as AJCC Stage I/II whereas advance stage was defined as AJCC stage III/IV. Table 1 summarizes the characteristics of the study population. Since regular screening for lung cancer has never been recommended in the U.S., the impact of screening in SEER is assumed to be negligible. In addition, the impact of adjuvant therapy for NSCLC is assumed to be negligible because lung disease-specific survival has improved by less than 3% over the last three decades (6).

Table 1.

Characteristics of the SEER study population

NSCLC* IDC*
Year of diagnosis 1988--2003 1975--1979
Gender Male Female
Sample size 52,660 20,474
Mean age at diagnosis (yr) 68 61
Mean tumor size at diagnosis (cm)** 4.4 2.5
Advance stage at diagnosis ** (%) 60 5
Median survival (yr) 0.7 >30
NSCLC* IDC*
Year of diagnosis 1988--2003 1975--1979
Gender Male Female
Sample size 52,660 20,474
Mean age at diagnosis (yr) 68 61
Mean tumor size at diagnosis (cm)** 4.4 2.5
Advance stage at diagnosis ** (%) 60 5
Median survival (yr) 0.7 >30
Open in a new tab
*

Histology types are identified using ICD-O-3 codes: Non-small cell lung carcinoma (NSCLC): 8078, 8012/3, 8070–8076, 8410, 8141, 8143, 8147; Invasive ductal carcinoma (IDC):

**

Excluding patients with missing tumor size or stage.

NSCLC Model Validation Based on the Mayo Lung Project

The NSCLC model was validated based on the Mayo Lung Project (MLP), which was a randomized controlled trial performed to evaluate the effect of chest radiography screening on lung cancer mortality on male smokers (7, 8). We performed a Monte Carlo simulation of MLP based on the NSCLC model with parameters estimated from SEER. The inputs for this simulation included age distribution at study entry, baseline NSCLC incidence rate, rate of incidental chest radiography examinations, and the screen detection threshold of chest radiography in terms of tumor diameter. These inputs were estimated based on our previous research (9). Lung cancer specific survival obtained in our simulation was compared against the observed survival in the control arm of MLP.

Modeling the Natural History of Invasive Ductal Carcinoma

SEER IDC Data Used for Model Parameter Estimation

Parameters of the IDC model were estimated based on SEER, using the same nine registries as the NSCLC model (1). We included 20,474 Caucasian female patients from SEER, who were diagnosed with invasive ductal carcinoma between 1975 and 1979. These calendar years represent a time period where the impact of screening and adjuvant therapy was negligible (10, 11). Histology types were identified using ICD-O-3 codes, and patients were excluded if their survival information or histology type was missing. Disease stage was derived based on SEER historical staging system. Local or regional stage in SEER historical staging system was considered as early stage, and SEER historical distant stage was considered as advanced stage. The characteristics of the study population are summarized in Table 1.

IDC Model Validation Based on the Health Insurance Plan Breast Cancer Screening Program

The IDC model was validated based on the Health Insurance Plan screening program (HIP). HIP is a RCT performed to evaluate the effect of screening mammography on breast cancer mortality (12). We performed a Monte Carlo simulation of HIP based on our IDC model. We simulated the screened participants who were diagnosed with IDC during 1975 to 1979. The inputs for this simulation included the age distribution at study entry and baseline IDC incidence rate. Patient survival predicted by our simulation was compared to the observed survival in the HIP.

RESULTS

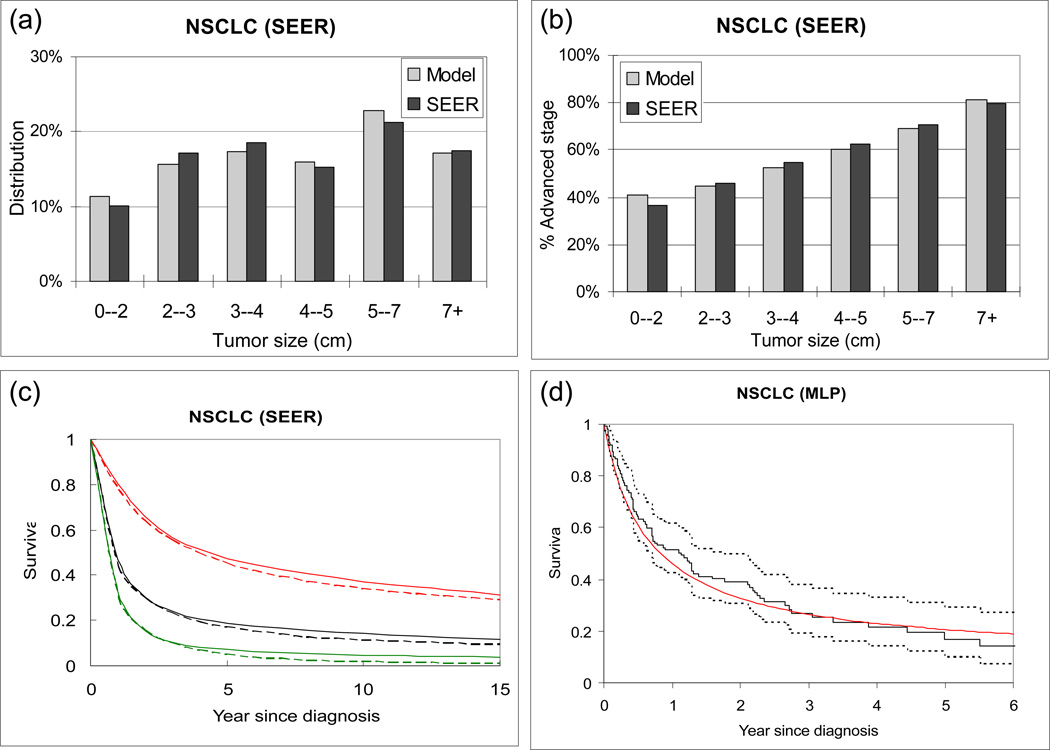
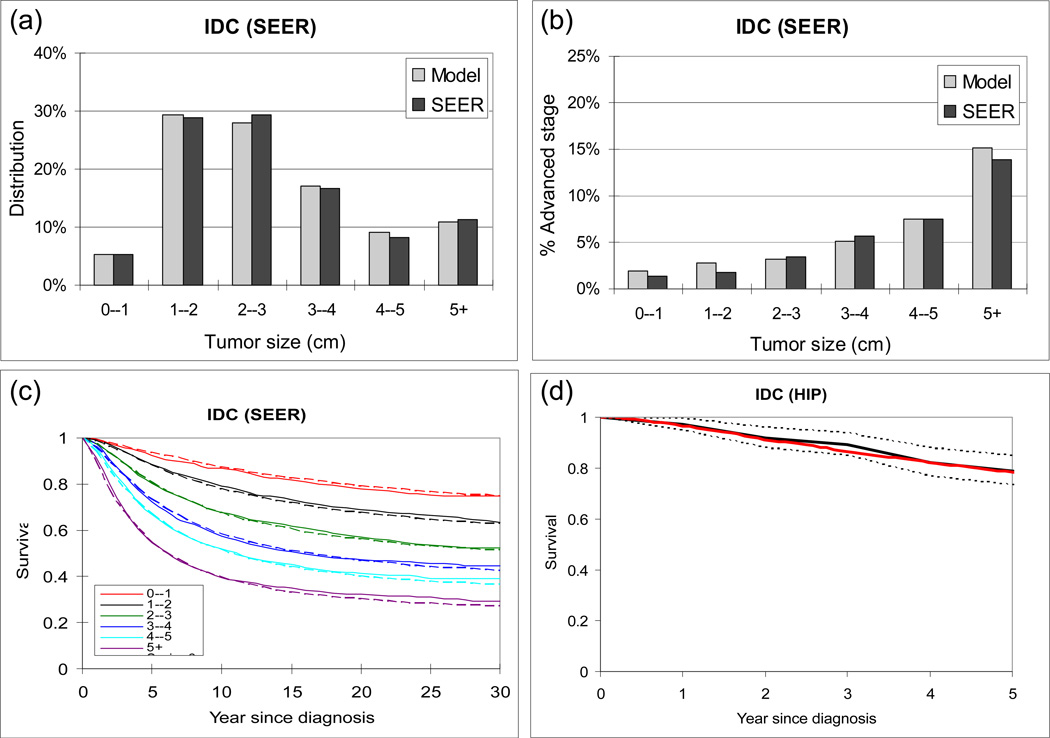
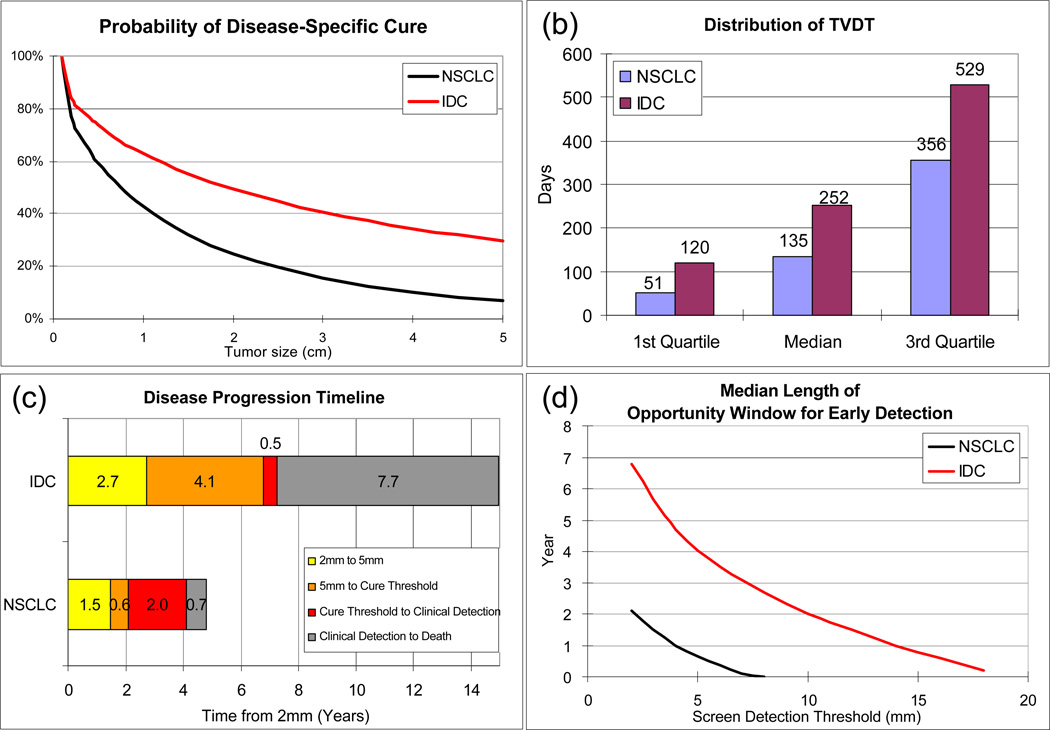
Our natural history model produces a good fit to SEER data, by tumor size, stage distribution, and patient survival for IDC (Figure 2(a-c) and NSCLC (Figure 3(a-c)). It reproduces the survival of the control group in the MLP for NSCLC (Figure 2(d)) and HIP for IDC (Figure 3(d)). When using our natural history model to evaluate the effect of early detection among patients who would be clinical detected in the absence of screening and not treated with adjuvant therapy, the following results are obtained. For a given primary tumor size at screen detection, the estimated probability of disease-specific cure by tumor size for NSCLC and IDC is compared (Figure 4(a)) and IDC is found to have a higher probability of disease-specific cure than NSCLC. For tumors screen detected when 1cm or greater, the probability of disease-specific cure for IDC is at least 20% higher than NSCLC. This difference is primarily due to the difference in the estimated treatment cure threshold (median: 19 for IDC vs. 8mm for NSCLC). In other words, our model-based analysis suggests that NSCLC sheds lethal metastases at smaller sizes than IDC. In addition, in the absence of screening and adjuvant therapy, IDC presents with symptoms at smaller tumor sizes than NSCLC (25mm for IDC vs. 50mm for NSCLC), and has a higher estimated probability of disease-specific cure (44% for IDC vs. 6% for NSCLC). Based on our analysis, the probability of disease-specific cure can be increased to 61% for NSCLC and 74% for IDC if tumor is screen detected and treated at 5 mm in diameter (Figure 4(a)). Such a low screen detection threshold has a larger relative impact on probability of disease-specific cure for NSCLC than IDC. For example, dropping the screen detection threshold from 15mm to 5mm may increase the probability of disease-specific cure by 97% for NSCLC (31% at 15mm vs 61% at 5mm) versus 35% for IDC (55% at 15mm to 74% at 5mm).

Figure 2.

Figure 2

Open in a new tab

Model validation for non-small cell lung carcinoma (NSCLC), symptomatically detected in the absence of screening. (a) Distribution of tumor size (diameter in cm) predicted by model (grey) and observed in SEER (black). (b) Proportion of advanced stage diseases (stratified by tumor size) predicted by model and observed in SEER. (c) Disease-specific survival predicted by model (dashed curves) and observed in SEER (solid curves). The red, green and black curves represent early stage, advanced stage, and all cases, respectively. (d) Disease-specific survival predicted by model (red solid curve) vs. observed in the MLP control arm (black solid curve). The black dotted curves represent 95% confidence interval of MLP.

Figure 3.

Figure 3

Open in a new tab

Model validation for invasive ductal carcinoma (IDC) symptomatically detected in the absence of screening. (a) Distribution of tumor size (diameter in cm) predicted by model (grey) and observed in SEER (black). (b) Proportion of advanced stage diseases (stratified by tumor size) predicted by model and observed in SEER. (c) Disease-specific survival predicted by model (dashed curves) and observed in SEER (solid curves). The red, green and black curves represent early stage, advanced stage, and all cases, respectively. (d) Disease-specific survival predicted by model (red solid curve) vs. observed in the HIP non-screened participants diagnosed from 1975 to 1979 (black solid curve). The black dotted curves represent 95% confidence interval of HIP.

Figure 4.

Figure 4

Open in a new tab

Comparison of the model-based predictions of the impact of screening for non-small cell lung carcinoma (NSCLC) versus invasive ductal carcinoma (IDC), among patients who would have been symptomatically detected in the absence of screening. (a): Probability of disease-specific cure by tumor size at screen detection. (b): Distribution of tumor volume doubling time (TVDT) in days, represented as the 1st quartile, median, and the 3rd quartile. (c): Disease progression timeline, where the median length of the following time intervals are presented: progression from 2 mm to 5 mm, from 5mm to the treatment cure threshold, from the treatment cure threshold to clinical detection, and from clinical detection to disease-specific death. (d): Median length of opportunity window for early detection as a function of the screen detection threshold (mm).

Next we compared IDC and NSCLC in terms of the TVDT (Figure 4(b)), the disease progression timeline (Figure 4(c)), and the median length of opportunity window for early detection (Figure 4(d)). The estimated median TVDT of IDC is almost twice as long as that of NSCLC (median: 252 days for IDC versus 134 days for NSCLC). These estimates are consistent with literature for non-screened population: median 7 to 9 months for breast cancer (13, 14) versus our estimate of 8 months; and 120 to 157 days for IDC (15, 16) versus our estimate of 134 days. Given the differences in the treatment cure threshold and the TVDT, IDC and NSCLC progress through critical time points differently. Starting from 5mm in diameter, NSCLC reaches the treatment cure threshold faster (median: 0.6 years for NSCLC versus 4.1 years for IDC). Starting from the treatment cure threshold, NSCLC is asymptomatic while incurable for longer duration (median: 2.0 years for NSCLC vs. 0.5 years for IDC). Starting from symptomatic detection, NSCLC progresses to disease-related death faster (median: 0.7 year for NSCLC vs. 7.7 years for IDC).

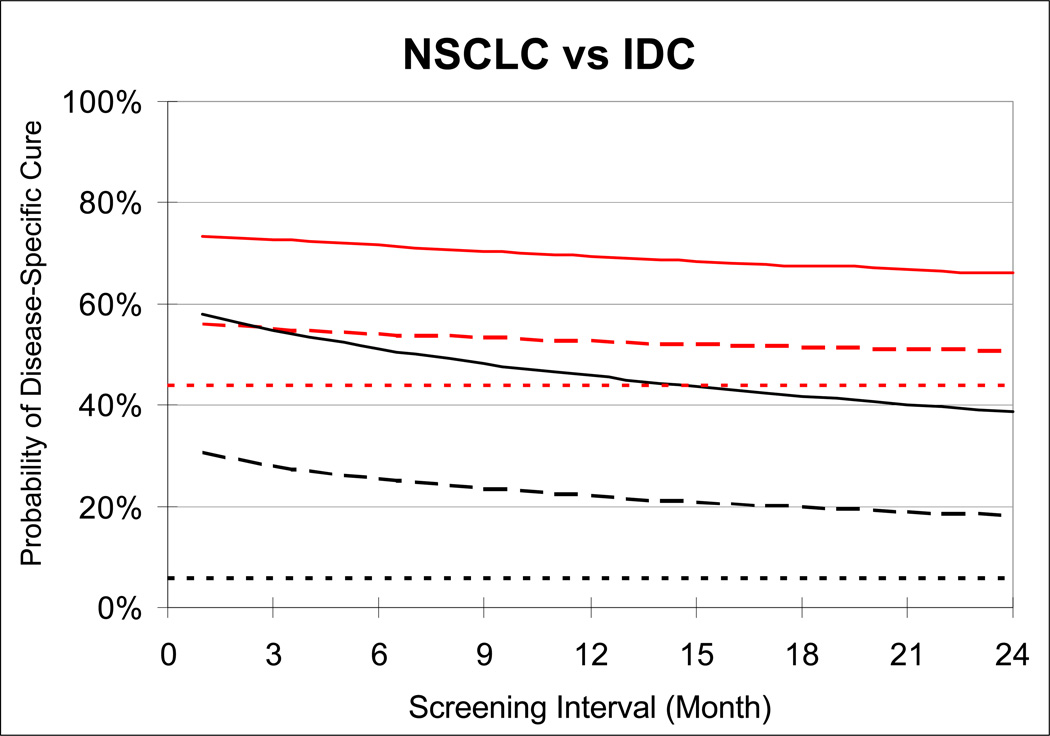
Because the treatment cure threshold is lower for IDC and its TVDT is longer, the opportunity window for early detection is longer for IDC than NSCLC (Figure 4(d)), making IDC a disease that is more easily detectable by screening. For any screen detection threshold and screening interval, IDC is a more curable disease than NSCLC (Figure 5). This finding is consistent with prior clinical trials that examined the effectiveness of mammographic screening for breast cancer (12) and chest radiographic screening for lung cancer (7, 8). Although mammography and chest radiography are different examinations they both rely on X-ray imaging and, based on our estimates, have similar median screen detection thresholds (our estimates range from 15 to 17 mm, data not shown). Yet the breast cancer trial HIP (12) demonstrated a roughly 20% cancer mortality reduction whereas the lung cancer trial MLP showed no benefit (7, 8). For IDC, in the absence of adjuvant therapy, our model predicts that with an annual screening program with a test whose screen detection threshold is 15mm, 55% of the breast cancer patients are cured of their disease (Figure 5), compared to 44% in the absence of screening. This represents a 19.6% breast cancer mortality reduction, which is consistent with the HIP trial. In contrast, chest radiography had less potential to reduce lung cancer mortality. Even if chest radiography had a screen detection threshold of 15 mm, then it is operating well above the median treatment cure threshold of NSCLC, which is 8 mm. This suggests that there is no feasible screening program for a chest radiography program that could detect tumor small enough to cure the majority (>50%) of the patients of their disease, regardless of the screening frequency. In fact, the MLP showed no mortality reduction due to radiographic screening even though screening was conducted every 4 months for 6 years. If the screen detection threshold for chest radiography were close to 17 mm, screening every 4 months corresponds to a roughly 23% probability of disease-specific cure according in our model (Figure 5). Given the probability of disease-specific cure of NSCLC is 6% in the absence of screening, our analysis suggests that of the mortality reduction due screening in MLP may be roughly as high as 18% for NSCLC. Because 20% of the cases in MLP were small cell lung carcinoma (SCLC), which are known to be less curable than NSCLC, our model would predict a mortality reduction less than 18% for MLP. Moreover, the actual trial included prevalence screen in the control arm, and non-perfect compliance, which would further lower our estimate from an 18% mortality reduction. Because MLP was powered for a 20% mortality reduction, the fact that MLP did not observe a significant effect of chest radiography screening is consistent with our findings.

Figure 5.

Figure 5

Open in a new tab

Estimated probability of disease-specific cure for NSCLC (black curves) and IDC (red curves) in the absence of screening (dotted curves) and under two alternative screening detection thresholds (solid curves: 5mm; dashed curves: 15mm) and screening intervals (1 to 24 months). The disease-specific mortality reduction from screening is computed as difference between the probability of disease-specific cure in the presence and absence of screening divided by one minus the probability of disease-specific cure in the absence of screening. All estimates are limited to patients who would have been symptomatically detected in the absence of screening.

DISCUSSION

We presented a natural history model of cancer that estimates how early the primary tumor and how often to screen asymptomatic individuals so that the primary tumor is detected early enough to prevent disease-specific death among patients who would have been clinically detected with the disease in the absence of screening and under no or minimal effect of adjuvant therapy. We compared model-based predictions for IDC and NSCLC. Our analysis suggests that NSCLC starts to shed lethal metastases when it is roughly one-half of the diameter of a IDC and the median TVDT of IDC is almost twice as long as that of NSCLC. These differences alone appear to explain why breast cancer screening has been more effective than lung cancer screening with conventional radiographic screening in past clinical trials. HIP trial produced positive results for breast cancer screening with mammography and the MLP trial produced negative findings for lung cancer screening with chest radiography. In the case of lung cancer screening, the National Lung Screening Trial (17, 18) recently reported mortality reduction of 20% in an annual screening program using low-dose helical computed tomography (CT). We do not yet have enough information to provide model-based predictions for NLST; however, we have modeled the Mayo CT screening trial (19, 20) and predicted a 25% mortality reduction (preliminary data not shown) relative to no screening.

Our natural history model of cancer provides a new approach of assessing the potential benefit of cancer screening. Previous models of the natural history of cancer have been developed to answer somewhat related but different questions. Models proposed by Geddes (16), Tubiana (13), and Michaelson (21) use TVDT reported by empirical studies to infer patient survival, tumor size and the time course of lethal metastasis; Kimmel et al. introduced the concept of “cure versus no-cure” and estimated the relationship between tumor size and metastases (22, 23); Tan et al. introduced the concept of treatment cure threshold as “fatal diameter” to estimate the progression and likelihood of cure of breast cancer (24). We model treatment cure threshold and the time course of lethal metastasis jointly: treatment cure threshold determines the time point when the metastatic burden starts growing whereas the ratio BD/f decides how fast the burden grows. This approach enables us to jointly estimate the treatment cure threshold and TVDT based on survival data. Intuitively, the probability of disease-specific cure is informed by the tail of the survival curve and TVDT is inferred mainly based on the shape of the survival curve and tumor size at detection.

The main limitation of any model-based analysis of screening, including ours, is that it relies on a variety of modeling assumptions. First, we assume that the tumor grows exponentially. Previous studies have shown this is an appropriate assumption for some cancer types (such as lung cancer (25, 26)), but the growth of the primary tumor may also slow down at large sizes and follow Gompertzian growth (27). Because our model demonstrated both internal and external validity, the exponential growth model appears to be a reasonable first order approximation for both NSCLC and IDC. Our model also assumes that advanced staged disease is not curable. This assumption holds in most cancer types, and we define “advanced disease” by choosing a clinical stage where patients have a very low likelihood of disease-specific cure. Our current analysis does not account for a variety of factors that may affect the disease progression, such as smoking behavior for NSCLC or estrogen receptor status for IDC). However, these factors can be modeled easily using our approach as long as data becomes available. Regarding the performance of a screening test, our current model characterize the sensitivity of a test as a function of tumor size; however, we do not account for other factors that may affect sensitivity, such as tumor location-. Moreover, our analysis also does not consider the false positive findings from screening.

An advantage of our approach is that it estimates the survival benefit of screening among cases symptomatically detected reported in SEER. Consequently, we are not considering the possibility that screening may also generate overdiagnosed cases which will likely increase the disease-specific curability without changing disease-specific mortality. For this reason alone, our model-based analysis may provide a less biased estimate of screening benefit than that inferred from a single-armed screening study (28, 29). Because single-armed screening studies lack a control group, their estimates of the survival benefit of screening are subject to biases such as over-diagnosis, lead-time bias and length bias (30–33).

Our model can be extended to study the potential impact of novel molecular biomarkers, based on blood, urine and exhaled breath condensates as noninvasive screening for early detection (34–37). Already our work suggests that if a molecular biomarker were available for frequent screening, it may have a greater impact on NSCLC than IDC, due to the lower treatment cure threshold and faster TVDT of NSCLC. As more data becomes available to characterize the performance of molecular biomarkers, our model may be extended to incorporate these biomarkers by relating the biomarker level to the primary tumor size, or using the biomarker level as a measure of the extent of metastases, or both. One mathematical model that relates blood biomarker levels to tumor size (38) can be combined with our model, because it relates tumor size to disease-specific curability, to bridge the connection between biomarker levels and survival outcomes. Similarly, our model may be extended to incorporate molecular biomarkers that are being developed to detect metastases, such as circulating tumor cells in the peripheral blood and disseminated tumor cells in the bone marrow (39, 40). In this manner, our model has a potentially broad range of roles to assess the potential impact of new early detection strategies on cancer mortality.

Supplementary Material

Supplement

Acknowledgements

The authors gratefully acknowledge funding from NIH 1R01CA105366, NIH 1U01CA088248 and the Canary Foundation (Grant Number 40675). The authors also gratefully acknowledge helpful discussions with Drs. Bronislava Sigal, Michael Gould and Amar Das, and Santhosh Kasavajjala.

REFERENCE

  • 1.SEERStat* Surveillance, Epidemiology, and End Results (SEER) Program (www.seer.cancer.gov) SEER*Stat Database: Incidence - SEER 17 Regs Limited-Use + Hurricane Katrina Impacted Louisiana Cases, Nov 2007 Sub (1973–2005 varying) - Linked To County Attributes - Total U.S., 1969–2005 Counties, National Cancer Institute, DCCPS, Surveillance Research Program, Cancer Statistics Branch, released April 2008, based on the November 2007 submission.
  • 2.Smith RA, Cokkinides V, Brawley OW. Cancer screening in the United States, 2008: a review of current American Cancer Society guidelines and cancer screening issues. CA: A Cancer Journal for Clinicians. 2008;58:161–179. doi: 10.3322/CA.2007.0017. [DOI] [PubMed] [Google Scholar]
  • 3.Brown PO, Palmer C. The preclinical natural history of serous ovarian cancer: defining the target for early detection. PLoS Medicine. 2009;6 doi: 10.1371/journal.pmed.1000114. e1000114-e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Chia YL, Salzman P, Plevritis SK, Glynn PW. Simulation-based parameter estimation for complex models: a breast cancer natural history modelling illustration. Statistical Methods in Medical Research. 2004;13:507–524. doi: 10.1191/0962280204sm380ra. [DOI] [PubMed] [Google Scholar]
  • 5.Nelder JA, Mead R. A simplex method for function minimization. Computer Journal. 1965;7:308–313. [Google Scholar]
  • 6.Alberg AJ, Ford JG, Samet JM. Epidemiology of lung cancer: ACCP evidence-based clinical practice guidelines. Chest. ((2nd edition)) 2007;132:29S–55S. doi: 10.1378/chest.07-1347. 29S-55S. [DOI] [PubMed] [Google Scholar]
  • 7.Marcus PM, Bergstralh EJ, Fagerstrom RM, et al. Lung cancer mortality in the Mayo Lung Project: impact of extended follow-up. Journal of the National Cancer Institute. 2000;92:1308–1316. doi: 10.1093/jnci/92.16.1308. [DOI] [PubMed] [Google Scholar]
  • 8.Marcus PM, Bergstralh EJ, Zweig MH, Harris A, Offord KP, Fontana RS. Extended lung cancer incidence follow-up in the Mayo Lung Project and overdiagnosis. Journal of the National Cancer Institute. 2006;98:748–756. doi: 10.1093/jnci/djj207. [DOI] [PubMed] [Google Scholar]
  • 9.Pashkevich MA, Sigal BM, Plevritis SK. Modeling the transition of lung cancer from early to advanced stage. Cancer Causes Control. 2009;20:1559–1569. doi: 10.1007/s10552-009-9401-4. [DOI] [PubMed] [Google Scholar]
  • 10.Cronin KA, Yu B, Krapcho M, et al. Modeling the dissemination of mammography in the United States. Cancer Causes Control. 2005;16:701–712. doi: 10.1007/s10552-005-0693-8. [DOI] [PubMed] [Google Scholar]
  • 11.Mariotto A, Feuer EJ, Harlan LC, Wun LM, Johnson KA, Abrams J. Trends in use of adjuvant multi-agent chemotherapy and tamoxifen for breast cancer in the United States: 1975–1999. J Natl Cancer Inst. 2002;94:1626–1634. doi: 10.1093/jnci/94.21.1626. [DOI] [PubMed] [Google Scholar]
  • 12.Chu KC, Smart CR, Tarone RE. Analysis of breast cancer mortality and stage distribution by age for the Health Insurance Plan clinical trial. Journal of the National Cancer Institute. 1988;80:1125–1132. doi: 10.1093/jnci/80.14.1125. [DOI] [PubMed] [Google Scholar]
  • 13.Tubiana M, Pejovic MH, Koscielny S, Chavaudra N, Malaise E. Growth rate, kinetics of tumor cell proliferation and long-term outcome in human breast cancer. International Journal of Cancer. Journal International Du Cancer. 1989;44:17–22. doi: 10.1002/ijc.2910440104. [DOI] [PubMed] [Google Scholar]
  • 14.Weedon-Fekjaer H, Lindqvist BH, Vatten LJ, Aalen OO, Tretli S. Breast cancer tumor growth estimated through mammography screening data. Breast Cancer Research: BCR. 2008;10 doi: 10.1186/bcr2092. R41-R. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Arai T, Kuroishi T, Saito Y, Kurita Y, Naruke T, Kaneko M. Tumor doubling time and prognosis in lung cancer patients: evaluation from chest films and clinical follow-up study. Japanese Lung Cancer Screening Research Group. Japanese Journal of Clinical Oncology. 1994;24:199–204. [PubMed] [Google Scholar]
  • 16.Geddes DM. The natural history of lung cancer: a review based on rates of tumour growth. British Journal of Diseases of the Chest. 1979;73:1–17. [PubMed] [Google Scholar]
  • 17.National Cancer Institute. The National Lung Screening Trial. [cited Nov 2010] Available from: http://www.cancer.gov/clinicaltrials/noteworthy-trials/nlst.
  • 18.National Lung Screening Trial Research Team . Aberle DR, Berg CD, et al. The National Lung Screening Trial: overview and study design. Radiology. 2011;258:243–253. doi: 10.1148/radiol.10091808. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Swensen SJ, Jett JR, Hartman TE, et al. CT screening for lung cancer: five-year prospective experience. Radiology. 2005;235:259–265. doi: 10.1148/radiol.2351041662. [DOI] [PubMed] [Google Scholar]
  • 20.Swensen SJ, Jett JR, Sloan JA, et al. Screening for lung cancer with low-dose spiral computed tomography. American Journal of Respiratory and Critical Care Medicine. 2002;165:508–513. doi: 10.1164/ajrccm.165.4.2107006. [DOI] [PubMed] [Google Scholar]
  • 21.Michaelson JS, Silverstein M, Wyatt J, et al. Predicting the survival of patients with breast carcinoma using tumor size. Cancer. 2002;95:713–723. doi: 10.1002/cncr.10742. [DOI] [PubMed] [Google Scholar]
  • 22.Flehinger BJ, Kimmel M, Melamed MR. Natural history of adenocarcinoma-large cell carcinoma of the lung: conclusions from screening programs in New York and Baltimore. Journal of the National Cancer Institute. 1988;80:337–344. doi: 10.1093/jnci/80.5.337. [DOI] [PubMed] [Google Scholar]
  • 23.Kimmel M, Flehinger BJ. Nonparametric estimation of the size-metastasis relationship in solid cancers. Biometrics. 1991;47:987–1004. [PubMed] [Google Scholar]
  • 24.Tan SYGL, van Oortmarssen GJ, de Koning HJ, Boer R, Habbema JDF. The MISCAN-Fadia continuous tumor growth model for breast cancer. Journal of the National Cancer Institute. Monographs. 2006:56–65. doi: 10.1093/jncimonographs/lgj009. [DOI] [PubMed] [Google Scholar]
  • 25.Detterbeck FC, Gibson CJ. Turning gray: the natural history of lung cancer over time. Journal of Thoracic Oncology: Official Publication of the International Association for the Study of Lung Cancer. 2008;3:781–792. doi: 10.1097/JTO.0b013e31817c9230. [DOI] [PubMed] [Google Scholar]
  • 26.Schultz EM, Silvestri GA, Gould MK. Variation in experts’ beliefs about lung cancer growth, progression, and prognosis. Journal of Thoracic Oncology: Official Publication of the International Association for the Study of Lung Cancer. 2008;3:422–426. doi: 10.1097/JTO.0b013e318167146b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Laird AK. Dynamics of tumor growth. British Journal of Cancer. 1964;13:490–502. doi: 10.1038/bjc.1964.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Henschke CI, McCauley DI, Yankelevitz DF, et al. Early Lung Cancer Action Project: overall design and findings from baseline screening. Lancet. 1999;354:99–105. doi: 10.1016/S0140-6736(99)06093-6. [DOI] [PubMed] [Google Scholar]
  • 29.Henschke CI, Yankelevitz DF, Libby DM, Pasmantier MW, Smith JP, Miettinen OS. Survival of patients with stage I lung cancer detected on CT screening. The New England Journal of Medicine. 2006;355:1763–1771. doi: 10.1056/NEJMoa060476. [DOI] [PubMed] [Google Scholar]
  • 30.Bach PB, Jett JR, Pastorino U, Tockman MS, Swensen SJ, Begg CB. Computed tomography screening and lung cancer outcomes. JAMA: The Journal of the American Medical Association. 2007;297:953–961. doi: 10.1001/jama.297.9.953. [DOI] [PubMed] [Google Scholar]
  • 31.Patz EF, Goodman PC, Bepler G. Screening for lung cancer. The New England Journal of Medicine. 2000;343:1627–1633. doi: 10.1056/NEJM200011303432208. [DOI] [PubMed] [Google Scholar]
  • 32.Bach PB. Lung cancer screening. Journal of the National Comprehensive Cancer Network: JNCCN. 2008;6:271–275. doi: 10.6004/jnccn.2008.0022. [DOI] [PubMed] [Google Scholar]
  • 33.Bach PB. Is our natural-history model of lung cancer wrong? The Lancet Oncology. 2008;9:693–697. doi: 10.1016/S1470-2045(08)70176-1. [DOI] [PubMed] [Google Scholar]
  • 34.Gold DV, Goggins M, Modrak DE, et al. Detection of early-stage pancreatic adenocarcinoma. Cancer Epidemiol Biomarkers Prev. 2010;19:2786–2794. doi: 10.1158/1055-9965.EPI-10-0667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Kanojia D, Garg M, Gupta S, Gupta A, Suri A. Sperm-associated antigen 9, a novel biomarker for early detection of breast cancer. Cancer Epidemiol Biomarkers Prev. 2009;18:630–639. doi: 10.1158/1055-9965.EPI-08-0629. [DOI] [PubMed] [Google Scholar]
  • 36.Gordian E, Ramachandran K, Reis IM, Manoharan M, Soloway MS, Singal R. Serum free circulating DNA is a useful biomarker to distinguish benign versus malignant prostate disease. Cancer Epidemiol Biomarkers Prev. 2010;19:1984–1991. doi: 10.1158/1055-9965.EPI-10-0287. [DOI] [PubMed] [Google Scholar]
  • 37.Conrad DH, Goyette J, Thomas PS. Proteomics as a method for early detection of cancer: a review of proteomics, exhaled breath condensate, and lung cancer screening. Journal of General Internal Medicine: Official Journal of the Society for Research and Education in Primary Care Internal Medicine. 2008;23(Suppl 1):78–84. doi: 10.1007/s11606-007-0411-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Lutz AM, Willmann JK, Cochran FV, Ray P, Gambhir SS. Cancer Screening: A Mathematical Model Relating Secreted Blood Biomarker Levels to Tumor Sizes. PLoS Medicine. 2008;5 doi: 10.1371/journal.pmed.0050170. e170-e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Cristofanilli M, Budd GT, Ellis MJ, et al. Circulating tumor cells, disease progression, and survival in metastatic breast cancer. The New England Journal of Medicine. 2004;351:781–791. doi: 10.1056/NEJMoa040766. [DOI] [PubMed] [Google Scholar]
  • 40.Cristofanilli M, Hayes DF, Budd GT, et al. Circulating tumor cells: a novel prognostic factor for newly diagnosed metastatic breast cancer. Journal of Clinical Oncology: Official Journal of the American Society of Clinical Oncology. 2005;23:1420–1430. doi: 10.1200/JCO.2005.08.140. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplement
NIHMS404193-supplement-Supplement.doc (55KB, doc)

RESOURCES