Abstract
Background and Purpose
The middle cerebral artery (MCA) bifurcation is a preferred site for aneurysm formation. Wider bifurcations angles have been correlated with increased risk of aneurysm formation. We hypothesized a link between the presence of MCA aneurysms and the angle morphology of the bifurcation.
Methods
3D rotational angiography volumes of 146 MCA bifurcations (62 aneurysmal) were evaluated for angle morphology: parent-daughter angles (larger daughter-Φ1, smaller daughter-Φ2), bifurcation angle (Φ1+Φ2), and inclination angle (γ) between the parent vessel axis and the plane determined by daughter vessels axes. Statistics were evaluated using Wilcoxon rank-sum analysis and area under the ROC curve (AUC).
Results
Aneurysmal bifurcations had wider inclination angle γ (median 57.8° vs. 15.4°; p<0.0001). 75% of aneurysmal MCAs had γ>10°, compared to 25% non-aneurysmal. Φ1, Φ2, but especially Φ1+Φ2 were significantly larger in aneurysmal bifurcations (median 171.3° vs. 98.1°; p<0.0001). 67% of aneurysmal bifurcations had Φ1+Φ2>161°, compared to 0% non-aneurysmal MCAs. An optimal threshold of 140° was established for Φ1+Φ2 (AUC=0.98). 68% of aneurysms originating off the daughter branches. 76% of them originated off the branch with the largest branching angle, specifically if this was the smaller daughter branch. Wider Φ1+Φ2 correlated with aneurysm neck width, but not dome size.
Conclusion
MCA bifurcations harboring aneurysms have significantly larger branching angles, and more often originate off of the branch with the largest angle. Wider inclination angle is strongly correlated with aneurysm presence, a novel finding. The results point to altered WSS regulation as a possible factor in aneurysm development and progression.
Keywords: Optimality, intracranial aneurysm, bifurcation geometry
Introduction
Intracranial aneurysms are not present at birth, but are rather pathological conditions acquired during life, usually during adulthood. Recent research have evaluated the basic mechanisms of aneurysm initiation and formation, with a focus on hemodynamic patterns, which has been suggested to play an essential role in aneurysm formation1-3. The apex of bifurcations, where the vessel wall is exposed to the highest wall shear stress (WSS) and spatial wall shear stress gradient (WSSG), is a location where saccular cerebral aneurysms arise with high frequency. The hemodynamic environment at the bifurcation apex is highly dependent on the bifurcation geometry4 and WSS is minimized in cases where the bifurcation follows the optimality principles of minimum work 5-7. The principle of minimum work provides an optimization model for the growth and adaptation of biological systems5, 6. Previous studies have shown arterial bifurcations in animals and humans, including the cerebral arterial tree, to follow this principle8-11 which decrees the optimal relationship between the bifurcation angle and the relative size of the daughter vessels. Changes in bifurcation morphology were previously linked to changes in hemodynamic forces at the bifurcation apex. Specifically, wider bifurcation angles have been associated not only with aneurysmal presence, but also with particular hemodynamic characteristics previously associated with an increased risk of aneurysm formation12.
The middle cerebral artery (MCA) bifurcation is a preferred site for aneurysm formation. Studies have estimated that MCA aneurysms represent between 18% and 36% of all intracranial aneurysms13. MCA aneurysms account for approximately 30% of the aneurysms presenting with acute subarachnoid hemorrhage and for 16% of all giant aneurysms14. Because of the high prevalence of MCA aneurysms, detection of local morphological patterns more prone to aneurysm formation could help assist in risk assessment of aneurysm initiation.
Recent studies have shown a significant difference in branching angles between MCA bifurcations which harbor aneurysms compared to bifurcations without aneurysmal involvement15-17. These findings suggest that the geometry of branching angles might play a role in aneurysm formation. However most studies were limited by the small sample of aneurysmal MCA bifurcations15, 16. To the best of our knowledge the morphological differences between aneurysmal and non-aneurysmal MCA bifurcations have not been thoroughly investigated. The objective of this study is to evaluate the morphology of MCA bifurcations with and without aneurysm involvement and to determine a possible link between aneurysm presence and bifurcation angles.
Methods
Patient Selection
3D volumetric datasets of patients presenting with intracranial aneurysms within a period of eight years were included. Mycotic and fusiform aneurysms were excluded. MCA bifurcations without aneurysmal involvement were gathered from patients with aneurysms at other locations and separately from a group of healthy individuals who had undergone cerebral angiography for different purposes (excluding patients with familial history of intracranial aneurysms). Data on patient age, gender, smoking status, hypertension, hyperlipidemia, and aneurysm rupture status was collected from a prospectively maintained database. The study was approved by Tufts Health Sciences Campus Institutional Review Board.
Data Acquisition
3D cerebral angiograms were obtained from either Philips Integris (Bothell, WA) or Siemens Artis (Malvern, PA) biplane systems and reconstructed using the manufacturers' clinical software package. 3D volumetric datasets were analyzed using Amira visualization software platform version 5.4 (FEI Visualization Sciences Group, Burlington, MA). Gradient edge-detection filtering was used to enable threshold-independent measurements18.
Morphological Feature Extraction
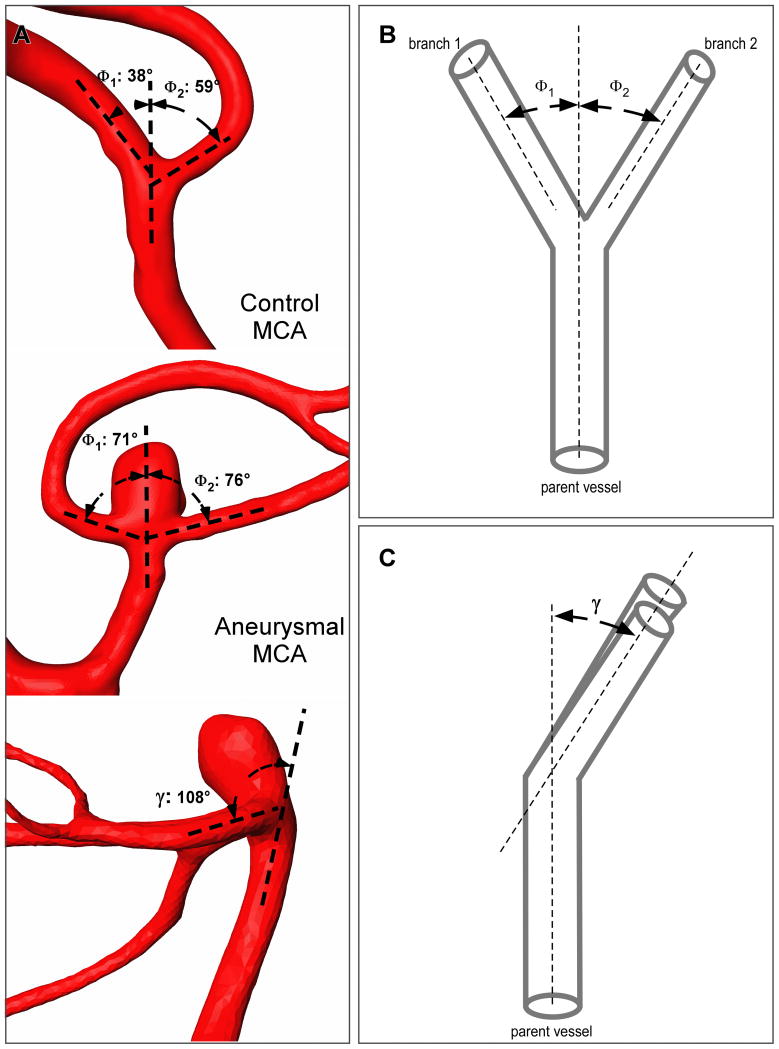
The branching angles were measured on longitudinal 2D cut-planes placed through the center of both the parent and daughter branches. This approach is similar to the one employed by other similar studies15-17, and has the advantage that the angle measurement are easily obtainable during the 3D rotational angiography, making it practical for clinical applications. By convention, the angle between parent vessel and the larger daughter vessel was termed Φ1, whereas the angle between parent vessel and the smaller vessel was termed Φ2 (Figure 1). Additionally, the angle between the parent vessel and both daughter branches was measured to obtain the angle between two planes (γ angle). The location of origin was noted for every aneurysm as either originating purely off of the larger or smaller daughter branch or off the apex of the bifurcation.
Figure 1.
(A) Measurement of branching angles in a control MCA bifurcation (patient with no aneurysms), a non-aneurysmal MCA bifurcation (patient with aneurysms at other locations), and an aneurysmal MCA bifurcation. (B) Schematic drawing of a bifurcation showing measurement of branching angles: Φ1 between parent vessel main axis and largest daughter vessel (branch 1) axis and Φ2 with the axis of the smallest branch (branch 2). (C) Schematic drawing of a bifurcation (lateral view) which shows measurement of the inclination angle (γ) between the parent vessel plane and the daughter branches plane.
Statistical Analysis
JMP version 10.0 (SAS Institute, Carey, NC) was used for statistical analysis, with significance assumed for p < 0.05. Bifurcations were divided into 3 categories for analysis: control bifurcations from patients without aneurysms, non-aneurysmal bifurcations from patients with aneurysms at other locations (no MCA), and aneurysmal bifurcations harboring aneurysms. All variables were tested independently using ANOVA and post-hoc Student's t-test for normal distributed data, and Wilcoxon rank-sum test for non-normal distributed data. Statistics for non-normal distributed data are reported as median and interquartile range (IQR). The relative correlation between parameters (branch angles, age, and aneurysm morphology) was evaluated by multivariate analysis using least square linear regression. Whenever data was available on both aneurysmal and non-aneurysmal contralateral MCA bifurcation within the same patient, a separate pair matched analysis was carried out to compare the corresponding angles. Receiver operator characteristics (ROC) analysis was performed to determine the area under the curve (AUC) index, as well as optimal cutoff values, for Φ1, Φ2, Φ1+ Φ2, and γ. Finally the data was again analyzed after exclusion of ruptured aneurysms to address possible vasospasm distorting the findings.
Results
Patient Demographics
A total of 353 aneurysms in 282 patients were identified. After exclusion of mycotic and fusiform aneurysms a total of 62 MCA bifurcation aneurysms were available of which 13 had previously ruptured. Non-aneurysmal MCA bifurcations were evaluated in 84 patients (57 from patients with aneurysms at other locations and 27 from healthy control patients). In a subset of 16 patients data on both aneurysmal and normal contralateral MCA bifurcation could be obtained. Mean age of the entire population was 56.6 (range 30 – 92 years old) with 97 bifurcations from female patients (67 %). Mean ages for the three bifurcation groups were: (1) the aneurysmal group 57.6 (range 30-92 years), (2) non-aneurysmal MCA in patients with aneurysms in other locations 53.5 (range 31-85 years), and (3) control MCA in patients with no aneurysms 58.8 (range 30-85 years). Because the angle of healthy cerebral bifurcations have been previously shown to increase with age, only control bifurcations from patients older than 30 years old were included in analysis. There was no statistical difference between the mean ages of the three bifurcation groups.
Bifurcation Morphology
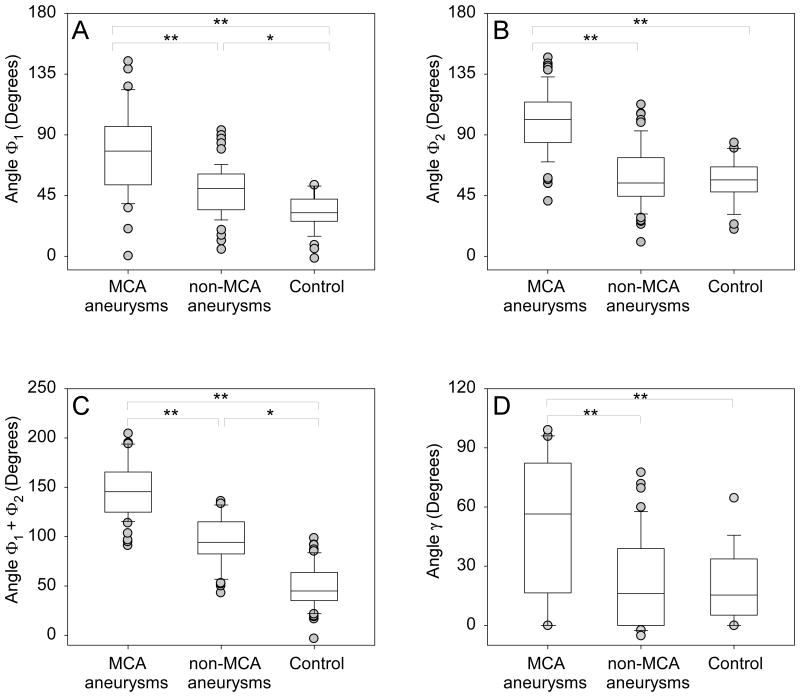
Angles Φ1 and Φ2 were significantly wider in aneurysmal MCA bifurcations compared to bifurcations without aneurysm involvement (Figure 2). Median Φ1 was 77.5° (IQR 52.9 – 96) for bifurcations with aneurysms, but only 40.3° (IQR 32 – 56.7) for bifurcations with no aneurysms (p < 0.001). Median Φ2 was 101.7° (IQR 84.5 – 115.6) for bifurcations with aneurysms, but only 55.4° (IQR 45 – 68.9) for bifurcations with no aneurysms (p<0.001). The total bifurcation angle Φ1+ Φ2 was significantly larger in aneurysmal MCA bifurcations compared to MCA bifurcations with no aneurysms (median 171.3°, IQR 150.8 – 191.5 vs. 98.1°, IQR 86.7 – 115.9; p<0.001). None of the non-aneurysmal bifurcations had a total bifurcation angle of more than 161°, however 67% of aneurysmal bifurcations did. Also no aneurysmal bifurcation had a total bifurcation angle of less than 121°. Exclusion of ruptured aneurysms did not affect the results (data not shown).
Figure 2.
Statistical differences between control, non-aneurysmal, and aneurysmal MCA bifurcation subgroups for angles (A) Φ1, (B) Φ2, (C) total bifurcation angle Φ1 + Φ2 and (D) inclination angle γ. ** represents p<0.001, whereas * represents p<0.04.
As shown in Table 1, within the non-aneurysmal group, Φ1 was significantly wider in patients with aneurysms at other locations (median 50.2°) compared to control patients (median 32.3°; p<0.001) (Figure 2). Φ1+ Φ2 was also significantly wider in non-aneurysmal MCA from patients with aneurysms in other locations (median 103.6°) compared to control MCA (median 92.1°; p=0.009). However, there was no difference in Φ2 (median 54.3° in patients with aneurysms in other locations vs. 56.6° in controls).
Table 1.
Univariate statistical analysis using Wilcoxon rank-sum test. Shown are median and interquartile range for control, non-aneurysmal MCA in patients with aneurysms at other locations, and aneurysmal middle cerebral artery bifurcations.
| Control MCA (no aneurysms) (n = 27) |
Non-aneurysmal MCA (non-MCA aneurysms) (n = 57) |
Aneurysmal MCA (n = 62) |
p value | |
|---|---|---|---|---|
| Φ1 | 32.3° (26 – 42.4) | 50.2° (34.5 – 61) | 77.5° (52.9 - 96) | <0.001 |
| Φ2 | 56.6° (47.7 - 66.3) | 54.3° (44.5 - 73.1) | 101.7° (84.5 - 115.6) | <0.001 |
| Φ1 + Φ2 | 92.1° (76.2 - 97.7) | 103.6° (91.85 - 124.4) | 171.5° (150.8 - 191.5) | <0.001 |
| γ | 15.4° (5.2 – 33.7) | 16.1° (0 – 38.9) | 57.8° (16.5 – 82.3) | <0.001 |
The inclination angle γ, formed between the parent vessel axis and the plane containing the axes of the two daughter vessels, was significantly wider in aneurysmal bifurcations (median 57.8°, IQR 16.5 – 82.3 vs. 15.4°, IQR 0.5 – 36.2; p<0.001). There was no statistical significance within the non-aneurysmal bifurcations when γ was compared between control (no aneurysm) and non-aneurysmal MCA bifurcations in patients with aneurysms in other locations (p=0.73).
In pair matched analysis, aneurysmal MCA bifurcations had significantly wider bifurcation angles compared to their non-aneurysmal contralateral counterparts (Table 2). This was true for Φ1 (median 75.34° aneurysmal vs. 51.2° contralateral), for Φ2 (median 105.5° aneurysmal vs. 53.5° contralateral), but also for angle γ (median 69.2° aneurysmal vs. 30.5° contralateral). When compared to other non-aneurysmal MCA bifurcations, MCA contralateral to an aneurysmal bifurcation had significantly wider Φ1 compared to controls (median 51.2° vs. 32.3°; p=0.004). Contralateral Φ1 was similar to that of non-aneurysmal MCA bifurcations from patients with aneurysms in other locations (p=0.92). Φ2 and γ were not different between the contralateral MCA and other non-aneurysmal bifurcations.
Table 2.
Matched pair analysis for aneurysmal and non-aneurysmal contralateral MCA bifurcations within same patients; n = 16, shown are median with interquartile range.
| Contralateral MCA | Aneurysmal MCA | P-value | |
|---|---|---|---|
| Φ1 | 51.2° (37.1 - 57.7) | 75.4° (42.5 - 83.575) | 0.02 |
| Φ2 | 53.5° (42.5 - 64.9) | 105.5° (85.2 - 123.4) | <0.001 |
| Φ1+ Φ2 | 104.5° (92.2 - 121.8) | 172.1° (150.2 - 197.3) | <0.001 |
| γ | 30.5° (0 - 51.4) | 69.2° (19.4 - 84.9) | 0.009 |
Optimal Discriminating Angle Thresholds
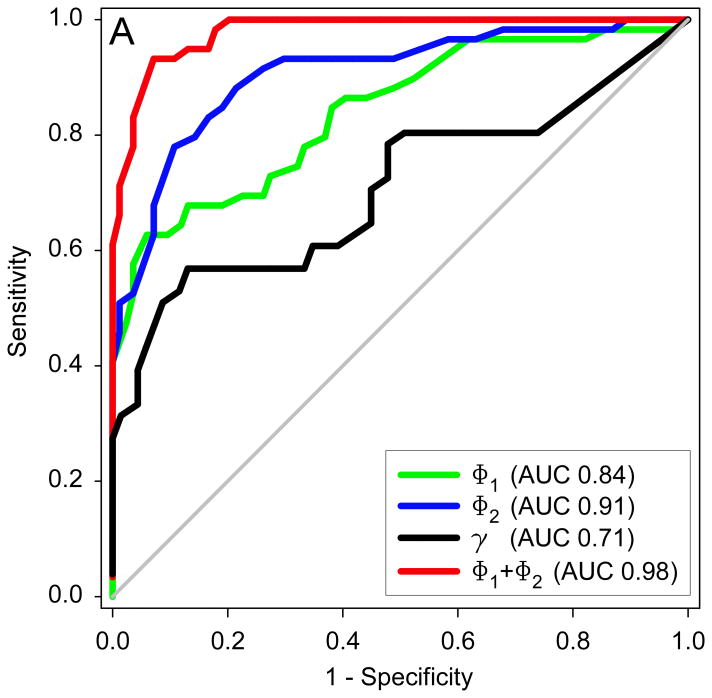
Optimal angle threshold values distinguishing between MCA bifurcations with and without aneurysms were determined by employing Receiver Operating Characteristic (ROC) analysis (Figure 3A). The total bifurcation angle Φ1+ Φ2 was the best performer in discriminating between aneurysmal and non-aneurysmal MCA. The resulting optimal Φ1+ Φ2 threshold was 140° (AUC = 0.98), with 93% sensitivity and 93% specificity. The optimal Φ1 threshold was 69° (AUC = 0.84), resulting in a sensitivity of 63% and specificity of 96%. The optimal Φ2 threshold was 83° (AUC = 0.91), resulting in a sensitivity of 78% and specificity of 91%. The optimal γ threshold was 56° (AUC = 0.71), resulting in a sensitivity of 53% and specificity of 91%.
Figure 3.
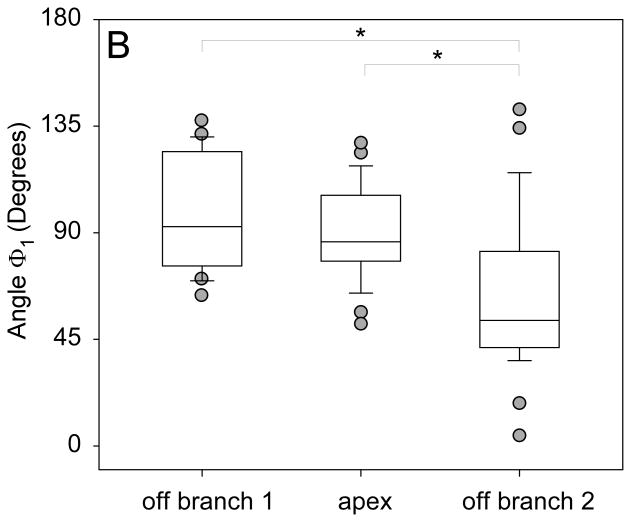
(A) Receiver operator characteristics plot showing the performance of all bifurcation angles in discriminating between aneurysmal and non-aneurysmal MCA bifurcations. AUC represents area under the ROC curve. (B) Graph showing significantly larger Φ1 for bifurcations in which the aneurysm originated off of the larger branch compared to bifurcations where the aneurysm originated off of the smaller branch. (C) Graph showing significantly larger Φ2 for bifurcations in which the aneurysm originated off of the smaller branch compared to bifurcations where the aneurysm originated off of the larger branch or the middle of the bifurcation.
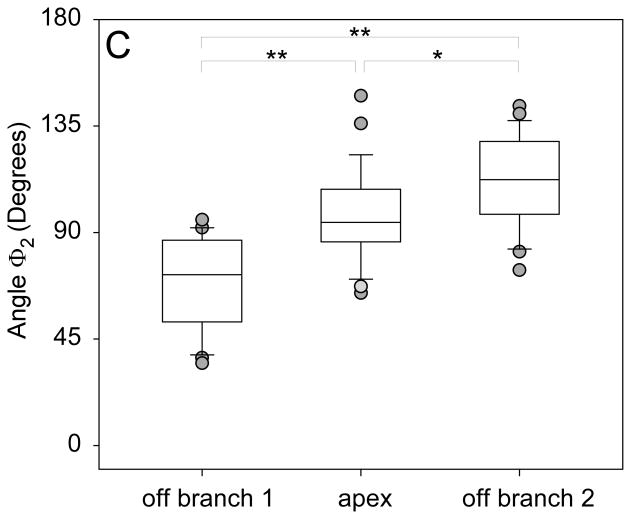
Aneurysm Location and Size
The aneurysm location was as follows: 10 (16 %) originated off the larger daughter branch, 32 (52 %) off the smaller branch and 20 (32 %) off the apex of the bifurcation. Pair matched analysis comparing Φ1 and Φ2 based on aneurysm location showed that the aneurysm consistently originated off the vessel corresponding to the larger angle (Table 3). When the aneurysm originated off the larger daughter, Φ1 was significantly wider than Φ2 (median 92.6° vs. 72.1°, p=0.04) (Figure 3B). When the aneurysm originated off the smaller daughter, Φ2 was significantly wider than Φ1 (median 112.3° vs. 53°, p<0.001) (Figure 3C). However when the aneurysm originated at the apex there was no statistical difference between Φ1 and Φ2 (median 86.1° vs. 94.3°, p=0.19). Although not statistically significant, the inclination angle γ was larger in aneurysms originated at the bifurcation apex compared to aneurysms originated off one of the daughter vessels (p=0.08).
Table 3.
Univariate statistical analysis using Wilcoxon rank-sum test. Shown are median and interquartile range for aneurysms originating off the larger daughter, off the smaller daughter branch, or off the apex of the bifurcation.
| Aneurysm originates off larger daughter (n = 10) |
Aneurysm originates off apex (n = 20) |
Aneurysm originates off smaller daughter (n = 32) |
P-value | |
|---|---|---|---|---|
| Φ1 | 92.6° (75.95 - 124.25) | 86.1° (78 - 105.8) | 53° (41.5 - 82.15) | <0.001 |
| Φ2 | 72.1° (52.25 - 86.75) | 94.3° (86.05 - 108.25) | 112.3° (97.7 - 128.45) | <0.001 |
Mean aneurysm size was 6.43±2.63 mm with a neck size of 4.46±1.33 mm. Φ1 and Φ2 were not correlated to the aneurysm size. However, Φ1 was positively correlated to the aneurysm neck (p=0.02). In addition, Φ1+Φ2 was highly correlated to the aneurysm neck (p=0.006). The inclination angle γ was not statistically correlated to aneurysm morphology.
Age and Gender
Φ1 was positively correlated with age in aneurysmal MCA (p=0.001) and in non-aneurysmal MCA from patients with aneurysms in other locations (p=0.02), but not in controls (p=0.65). In contrast, Φ2 was not correlated with age in any of the groups. Similarly, angle γ showed no age dependency in any of the groups. Similar to Φ1, the total bifurcation angle Φ1+ Φ2 was positively correlated with age in aneurysmal MCA (p=0.02) and in non-aneurysmal MCA from patients with aneurysms in other locations (p=0.04), but not in controls (p=0.21).
Regarding gender differences, there were no statistical differences between males and females in any of the three groups analyzed: aneurysmal, non-aneurysmal MCAs with aneurysms in other locations, and healthy controls.
Smoking, Hypertension and Hyperlipidemia
Overall 21% of the bifurcation samples were from patients currently smoking (45% had a smoking history). In the aneurysmal MCA group, 30% samples were from current smokers (65% had smoking history). In contrast, in the non-aneurysmal group, only 14% of the samples were from current smokers (30% had a smoking history). The difference in smoking status between aneurysmal and non-aneurysmal samples was statistically significant both for current smokers (p=0.02) and for smoking history (p<0.001). Both in the smoking and nonsmoking groups, angles Φ1, Φ2, Φ1+ Φ2 and γ were significantly wider in aneurysmal MCA compared to non-aneurysmal MCA bifurcations. Moreover, in the nonsmoking group, Φ1 was significantly wider in patients with aneurysms at other locations compared to control patients (p<0.02). Importantly, within the aneurysmal group, non-smokers had significantly wider Φ1 (median 84.7°, IQR 61.3 – 115.2 vs. 58.5°, IQR 42.2 – 79.1; p=0.002) and Φ1+ Φ2 (median 182.3°, IQR 159.8 – 216.5 vs. 155.2°, IQR 143.5 – 171.6; p=0.001) compared to smokers. This was not observed in the non-aneurysmal group where there was no statistical difference in any of the angles between smokers and nonsmokers. It should be noted that even when aneurysmal nonsmokers were excluded, the aneurysmal bifurcations still had significantly wider Φ1, Φ2, Φ1+ Φ2 and γ angles compared to non-aneurysmal bifurcations (p<0.001).
Overall, 54% of the bifurcation samples were from patients with hypertension. 70% of the aneurysmal MCA bifurcations were from patients with hypertension compared to 42% in the non-aneurysmal group (p<0.001). Regardless of hypertension status, angles Φ1, Φ2, Φ1+ Φ2 and γ were significantly wider in aneurysmal MCA compared to non-aneurysmal bifurcations. Moreover, there was no angle difference between patients with hypertension compared to patients with no hypertension.
Overall, 22% of the bifurcation samples were from patients with hyperlipidemia. 23% of the aneurysmal MCA bifurcations were from patients with hyperlipidemia compared to 20% in the non-aneurysmal group (p=0.66). Regardless of hyperlipidemia status, angles Φ1, Φ2, Φ1+ Φ2 and γ were significantly wider in aneurysmal MCA compared to non-aneurysmal bifurcations. Moreover, there was no angle difference between patients with hyperlipidemia compared to patients with no hyperlipidemia.
Multivariate Statistical Analysis
Multivariate analysis employing least square linear regression was used to determine the relative dependency of the variables. The analysis showed Φ1 to be independently predicted by aneurysm presence (p<0.001), age (p=0.005), and current smoking status (p=0.007), but not by gender, hypertension, hyperlipidemia, or the width of the aneurysm neck. Similarly, Φ1+ Φ2 was independently predicted by aneurysm presence (p<0.001), age (p=0.01), and current smoking status (p=0.02), but not by gender, hypertension, hyperlipidemia, or the width of the aneurysm neck. In contrast, Φ2 and γ were independently predicted solely by aneurysm presence (p<0.001).
Imaging Acquisition Analysis
Out of 146 MCA bifurcations, 86 bifurcations (34 aneurysmal) have been evaluated on 3D cerebral angiograms obtained from Philips Integris imaging system, and 60 bifurcations (28 aneurysmal) have been evaluated on angiograms obtained from Siemens Artis. In order to determine the impact of acquisition system on statistical findings, the statistical analysis was repeated within the two subgroups. Regardless of the acquisition origin, all angles evaluated here were significantly wider for aneurysmal compared to non-aneurysmal MCA bifurcations with identical statistical performance. When only aneurysmal bifurcations were compared, there was no statistical difference between angiograms acquired from Philips Integris, compared to those acquired from Siemens Artis. This was true for Φ1 (median 77° vs. 76.4°; p=0.40), Φ2 (median 103.3° vs. 95.2°; p=0.41), and Φ1+ Φ2 (median 171.2° vs. 167.2°; p=0.78). Similarly, when only non-aneurysmal bifurcations were compared, there was no statistical difference between angiograms acquired with the two systems for Φ1 (median 50.4° vs. 48°; p=0.87), Φ2 (median 57.2° vs. 49°; p=0.30), and Φ1+ Φ2 (median 106.1° vs. 97°; p=0.46).
Discussion
Previous studies have investigated the possible correlation between the angles formed by parent and daughter vessels and aneurysm presence at the MCA bifurcation15-17. Ingebrigtsen et al.16 evaluated the geometry of bifurcations in the circle of Willis and showed that aneurysmal bifurcations had wider bifurcation angles compared to non-aneurysmal geometries, though the analysis was limited to 14 aneurysmal bifurcations including not only middle cerebral but also internal carotid and basilar arteries. Similarly, Bor et al.15 reported that aneurysmal bifurcations in the circle of Willis (including 10 MCA) had narrower lateral angles compared to non-aneurysmal geometries. Finally, Sadatomo et al.17 showed that aneurysmal MCA bifurcations had smaller lateral angles and higher lateral angles ratio compared to non-aneurysmal bifurcations.
Unlike earlier reports, this study focused specifically on MCA bifurcations which are end-vessel type without collateral supply from anterior or posterior communicators. The study also was concerned uniquely on the geometry of the bifurcation at the actual point of blood flow impingement. Whereas other studies evaluated lateral bifurcation angles, here we use not only individual angles between parent and daughter vessels (Φ1 and Φ2), but also total bifurcation angle to describe the bifurcation. Total bifurcation angle was previously shown to determine the hemodynamic environment of bifurcations following stent-mediated treatment19. In addition, this study introduced the overall inclination angle between the parent vessel axis and the plane formed by the axes of the daughter vessels. Because recent studies suggested that aneurysm initiation reflects not only local, but also global characteristics of the vasculature20, 21, we hypothesized (1) a link between the presence of MCA aneurysms and the angle morphology of the bifurcation, and (2) a link between aneurysms presence at locations other than the MCA bifurcation and the morphology of the MCA bifurcation.
All evaluated angles were significantly wider in aneurysmal compared to non-aneurysmal MCA bifurcations. Among non-aneurysmal MCA bifurcations, the angle between the parent vessel and the larger daughter, as well as the total bifurcation angle, were significantly wider in patients with aneurysms at other locations compared to patients without any aneurysms (control patients). No control patient had a total bifurcation angle larger than 116° and no aneurysmal MCA bifurcation had a total bifurcation angle of less than 121°. Similarly, none of the patients with aneurysms at other locations had a total bifurcation angle larger than 161°. In contrast, 67% of the aneurysmal bifurcations were wider than 161°. Interestingly, the bifurcation angles of non-aneurysmal MCA bifurcations contralateral to aneurysmal MCAs were not only significantly smaller compared to the corresponding counterparts, but also significantly wider compared to control patients. In fact, the non-aneurysmal contralateral MCA bifurcations had similar morphology to that of the non-aneurysmal MCA bifurcations in patients with aneurysms at other locations. These findings suggest a more global arterial weakening at bifurcation sites throughout the cerebral circulation.
Smoking is a well-documented risk factor for cerebral aneurysm formation22 and this study showed that in smokers, aneurysms formed at narrower bifurcation angles compared to nonsmokers (p=0.001). To the best of our knowledge ours is the first report of this phenomenon. The finding suggests that the added risk of smoking may have resulted in a decrease of the angle threshold for aneurysm formation. Sill aneurysmal MCA bifurcations in smokers were significantly wider compared to MCA bifurcations in controls and in patients with aneurysms in other locations.
A novel finding in this study is the increased inclination angle in MCA bifurcations that harbor aneurysms. A small inclination angle means that the daughter branches are in line with the parent vessel. However when the inclination angle increases, the daughter branches make a sharper turn from the parent vessel and thus deviate from the inflow of blood. We had hypothesized that such an increase in angle could lead to aneurysm formation, since it would cause a deviation of the blood flow and of its location of impact on the vessel wall and cause changes in WSS and WSSG. We indeed found a significant increase in the inclination angle between aneurysmal and non-aneurysmal MCA bifurcations.
We hypothesize that because branching angles are relatively larger in diseased bifurcations, the blood stream has to deviate more profoundly at that point. Finlay et al23 have described a collagen tendon-like medial pad which is thought to protect the apex of the bifurcation where the flow is divided into the daughter branches and the highest WSS and WSSG is supposed to occur. Meng et al.2 studied canine arteries and described the presence of an “intimal pad” in the impingement region where the flow-jet hits the bifurcation tip. This intimal pad was a healthy reaction of the endothelium for protection of itself against high WSS and WSSG. When branching angles increase, the impingement region shifts away from the bifurcation apex12 where the arterial wall is protected from these forces. Higher branching angles lead to dispersal of the high WSS and WSSG impact zone on the adjacent arterial wall, away from the protection at the bifurcation apex onto the more vulnerable arterial wall of the daughter vessel. These conditions of high WSS and WSSG have been shown to lead to aneurysm formation2, 24. Consequently, detection of bifurcations with such deviant morphology could potentially enable follow-up for longitudinal risk evaluation of aneurysm initiation. Further testing of this hypothesis requires in-depth computational fluid dynamics studies which will be the focus of future research. Prospective studies are required to elucidate any causal versus associative relationship.
Study Limitations
Given the retrospective nature of our study, we cannot conclude that wider bifurcation angles preceded aneurysm formation, because aneurysm formation might have altered bifurcation morphology itself. Prospective analysis of a small set of MCA bifurcations15 seem to suggest that indeed wide branching angles precede aneurysm initiation. However, to the best of our knowledge, no conclusive data has yet been presented to conclusively address this issue. Moreover, while this study showed a strong correlation between the MCA bifurcation angles and aneurysm presence, no cause and effect relation can be conclusively determined. The possibility remains that aneurysm formation is an epiphenomenon to wider bifurcations rather than a direct consequence to higher risk bifurcation morphology. Further investigations are required in order to clarify the potential utility and applicability of the middle cerebral artery bifurcation angle assessment in cerebral aneurysm risk stratification analysis.
Conclusions
MCA bifurcation harboring aneurysms have significantly wider bifurcation and inclination angles compared to non-aneurysmal bifurcations. Moreover, patients with aneurysms at locations other than MCA, have significantly wider MCA angle configurations compared to control patients with no cerebral aneurysms. A bifurcation angle of 140° was established as a highly accurate optimal threshold to distinguish between MCA bifurcations with and without aneurysms. Control MCA bifurcations from patients with no cerebral aneurysms have smaller bifurcation angles compared to non-aneurysmal bifurcations from patients with aneurysms in other locations, suggesting a global morphological risk for aneurysm formation. In smokers, MCA bifurcation aneurysms occur at smaller bifurcation angles compared to non-smokers. Overall, our data suggest that the angle morphology of the MCA bifurcation might play an important role in the formation of MCA aneurysms and may be indicative of aneurysm presence at other locations.
Acknowledgments
Sources of Funding: This work was supported by a grant from the National Institutes of Health (NIH-R21HL102685).
Disclosures: The senior author (A.M.M.) has received unrestricted research funding by ev3 Inc., Microvention Inc., Siemens Inc., and Stryker Inc. for research unrelated to the submitted work.
References
- 1.Meng H, Tutino VM, Xiang J, Siddiqui A. High wss or low wss? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: Toward a unifying hypothesis. [Accessed May 31, 2013];AJNR Am J Neuroradiol. 2013 doi: 10.3174/ajnr.A3558. published ahead of print April 18, 2013. http://www.ajnr.org/content/early/2013/07/04/ajnr.A3558.full.pdf. [DOI] [PMC free article] [PubMed]
- 2.Meng H, Wang Z, Hoi Y, Gao L, Metaxa E, Swartz DD, et al. Complex hemodynamics at the apex of an arterial bifurcation induces vascular remodeling resembling cerebral aneurysm initiation. Stroke. 2007;38:1924–1931. doi: 10.1161/STROKEAHA.106.481234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sforza DM, Putman CM, Cebral JR. Hemodynamics of cerebral aneurysms. Annual Review of Fluid Mechanics. 2009;41:91–107. doi: 10.1146/annurev.fluid.40.111406.102126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hassan T, Timofeev EV, Saito T, Shimizu H, Ezura M, Matsumoto Y, et al. A proposed parent vessel geometry-based categorization of saccular intracranial aneurysms: Computational flow dynamics analysis of the risk factors for lesion rupture. J Neurosurg. 2005;103:662–680. doi: 10.3171/jns.2005.103.4.0662. [DOI] [PubMed] [Google Scholar]
- 5.Murray CD. The physiological principle of minimum work: I. The vascular system and the cost of blood volume. Proceedings of the National Academy of Sciences of the United States of America. 1926;12:207–214. doi: 10.1073/pnas.12.3.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Murray CD. The physiological principle of minimum work: Ii. Oxygen exchange in capillaries. Proceedings of the National Academy of Sciences of the United States of America. 1926;12:299–304. doi: 10.1073/pnas.12.5.299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rosen R. Optimality principle in biology. Butterworths; London: 1967. [Google Scholar]
- 8.Zamir M. Cost analysis of arterial branching in the cardiovascular systems of man and animals. Journal of theoretical biology. 1986;120:111–123. doi: 10.1016/s0022-5193(86)80021-2. [DOI] [PubMed] [Google Scholar]
- 9.Zamir M, Brown N. Internal geometry of arterial bifurcations. J Biomech. 1983;16:857–863. doi: 10.1016/0021-9290(83)90010-6. [DOI] [PubMed] [Google Scholar]
- 10.Zamir M, Wrigley SM, Langille BL. Arterial bifurcations in the cardiovascular system of a rat. The Journal of general physiology. 1983;81:325–335. doi: 10.1085/jgp.81.3.325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rossitti S, Lofgren J. Optimality principles and flow orderliness at the branching points of cerebral arteries. Stroke. 1993;24:1029–1032. doi: 10.1161/01.str.24.7.1029. [DOI] [PubMed] [Google Scholar]
- 12.Alnaes MS, Isaksen J, Mardal KA, Romner B, Morgan MK, Ingebrigtsen T. Computation of hemodynamics in the circle of willis. Stroke. 2007;38:2500–2505. doi: 10.1161/STROKEAHA.107.482471. [DOI] [PubMed] [Google Scholar]
- 13.Inagawa T, Hirano A. Autopsy study of unruptured incidental intracranial aneurysms. Surgical Neurology. 1990;34:361–365. doi: 10.1016/0090-3019(90)90237-j. [DOI] [PubMed] [Google Scholar]
- 14.Smith R, Zubkov Y, Tarassoli Y. Middle cerebral artery aneurysms Cerebral aneurysms. Springer; US: 1994. pp. 146–160. [Google Scholar]
- 15.Bor AS, Velthuis BK, Majoie CB, Rinkel GJ. Configuration of intracranial arteries and development of aneurysms: A follow-up study. Neurology. 2008;70:700–705. doi: 10.1212/01.wnl.0000302176.03551.35. [DOI] [PubMed] [Google Scholar]
- 16.Ingebrigtsen T, Morgan MK, Faulder K, Ingebrigtsen L, Sparr T, Schirmer H. Bifurcation geometry and the presence of cerebral artery aneurysms. Journal of Neurosurgery. 2004;101:108–113. doi: 10.3171/jns.2004.101.1.0108. [DOI] [PubMed] [Google Scholar]
- 17.Sadatomo T, Yuki K, Migita K, Imada Y, Kuwabara M, Kurisu K. Differences between middle cerebral artery bifurcations with normal anatomy and those with aneurysms. Neurosurg Rev. 2013;36:437–445. doi: 10.1007/s10143-013-0450-5. [DOI] [PubMed] [Google Scholar]
- 18.Bescos JO, Slob MJ, Slump CH, Sluzewski M, van Rooij WJ. Volume measurement of intracranial aneurysms from 3d rotational angiography: Improvement of accuracy by gradient edge detection. AJNR Am J Neuroradiol. 2005;26:2569–2572. [PMC free article] [PubMed] [Google Scholar]
- 19.Gao B, Baharoglu MI, Cohen AD, Malek AM. Y-stent coiling of basilar bifurcation aneurysms induces a dynamic angular vascular remodeling with alteration of the apical wall shear stress pattern. Neurosurgery. 2013;72:617–629. doi: 10.1227/NEU.0b013e3182846d9f. discussion 628-619. [DOI] [PubMed] [Google Scholar]
- 20.Maltete D, Bellien J, Cabrejo L, Iacob M, Proust F, Mihout B, et al. Hypertrophic remodeling and increased arterial stiffness in patients with intracranial aneurysms. Atherosclerosis. 2010;211:486–491. doi: 10.1016/j.atherosclerosis.2010.04.002. [DOI] [PubMed] [Google Scholar]
- 21.Schimansky S, Patel S, Rahal J, Lauric A, Malek AM. Extradural internal carotid artery caliber dysregulation is associated with cerebral aneurysms. Stroke. 2013;44:3561–3564. doi: 10.1161/STROKEAHA.113.001762. [DOI] [PubMed] [Google Scholar]
- 22.Juvela S, Poussa K, Porras M. Factors affecting formation and growth of intracranial aneurysms: A long-term follow-up study. Stroke. 2001;32:485–491. doi: 10.1161/01.str.32.2.485. [DOI] [PubMed] [Google Scholar]
- 23.Finlay HM, Whittaker P, Canham PB. Collagen organization in the branching region of human brain arteries. Stroke. 1998;29:1595–1601. doi: 10.1161/01.str.29.8.1595. [DOI] [PubMed] [Google Scholar]
- 24.Tardy Y, Resnick N, Nagel T, Gimbrone MA, Jr, Dewey CF., Jr Shear stress gradients remodel endothelial monolayers in vitro via a cell proliferation-migration-loss cycle. Arterioscler Thromb Vasc Biol. 1997;17:3102–3106. doi: 10.1161/01.atv.17.11.3102. [DOI] [PubMed] [Google Scholar]