Computation of flow through the oesophagogastric junction

Abstract

Whilst methods exist to indirectly measure the effects of increased flow or gastro-oesophageal refluxing, they cannot quantitatively measure the amount of acid travelling back up into the oesophagus during reflux, nor can they indicate the flow rate through the oesophago-gastric junction (OGJ). Since OGJ dysfunction affects flow it seems most appropriate to describe the geometry of the OGJ and its effect on the flow.

A device known as the functional lumen imaging probe (FLIP) has been shown to reliably measure the geometry of and pressure changes in the OGJ. FLIP cannot directly measure flow but the data gathered from the probe can be used to model flow through the junction by using computational flow dynamics (CFD). CFD uses a set of equations known as the Navier-Stokes equations to predict flow patterns and is a technique widely used in engineering. These equations are complex and require appropriate assumptions to provide simplifications before useful data can be obtained. With the assumption that the cross-sectional areas obtained via FLIP are circular, the radii of these circles can be obtained. A cubic interpolation scheme can then be applied to give a high-resolution geometry for the OGJ.

In the case of modelling a reflux scenario, it can be seen that at the narrowest section a jet of fluid squirts into the oesophagus at a higher velocity than the fluid surrounding it. This jet has a maximum velocity of almost 2 ms^-1 that occurs where the OGJ is at its narrowest. This simple prediction of acid ‘squirting’ into the oesophagus illustrates how the use of numerical methods can be used to develop a better understanding of the OGJ. This initial work using CFD shows some considerable promise for the future.

INTRODUCTION

The Giome is a subset of the Physiome project, which was originally proposed by Bassingthwaighte in 1995[1]. The Giome Project initiated by Gregersen represents a method for obtaining an integrated understanding of the human gastrointestinal (GI) tract based on bioengineering models[2]. To use this method to advance our understanding of the GI tract, it will be necessary to generate new computational models and capture data pertinent to these models. The output from the functional lumen imaging probe (FLIP) is potentially one of these sources of data for sphincteric regions in the GI tract.

In patients where compliance of the sphincter is not ideal, control of reflux is not optimal. Often oesophago-gastric junction (OGJ) dysfunction is the prime suspect in this phenomenon, which effects up to 44% of the population in the western world. It is logical to deduce that an increase in sphincter compliance will result in increased flow through the OGJ. Measuring flow directly in the oesophago-gastric junction in vivo would prove very difficult, especially because it must be accessed from the oral or nasal cavity. This review looks at another option for predicting flow parameters in the OGJ.

FLIP

Recently, a device known as the FLIP has been shown to reliably measure the geometry of and pressure changes in the OGJ by using a distensibility technique[3-6]. FLIP can measure the geometric data needed to model flow through the junction. The concept of measuring flow by a distensibility technique is not new[7] but the acquisition and analysis of FLIP data seems much easier than with any other known technique. Thus, FLIP could provide a practical solution with the potential for clinical use in the future.

Data from FLIP provides a platform for carrying out numerical flow analysis, where the complexities of flow through the junction could be represented using a technique known as computational flow dynamics (CFD).

CHARACTERISTICS OF THE OGJ

At the OGJ, the oesophagus opens into the stomach. It is important that backflow of stomach secretions into the oesophagus is controlled at the OGJ opening only transiently to allow passage of the swallowed food into the stomach. The diaphragmatic hiatus, through which the oesophagus passes at the OGJ, has a role in this valvular mechanism[8].

Several structures are important in maintaining a barrier at the OGJ. The lower oesophageal sphincter (LOS) forms part of the OGJ structure. The intrinsic muscles of the distal oesophagus and the sling fibers of the proximal stomach make up the internal mechanism structures of the LOS. The muscles of the diaphragm that connect to the OGJ make up the crural diaphragm and this constitutes the external LOS mechanism structures. The tissue that connects the distal oesophagus to the crural diaphragm is known as the phreno-oesophageal ligament[9].

The OGJ can be distinguished from the body of the oesophagus by its behavior pattern. There is an increase in the tone of the circular muscle in this region. The sphincter relaxes in response to a swallow and this usually precedes the arrival of a contraction wave travelling down the oesophagus. This phase of relaxation is followed by a short-lasting elevation of pressure above resting values[10]. In recent years it has been known that the sphincter sometimes relaxes even when a swallow does not occur. These relaxations are known as transient lower oesophageal sphincter relaxations (tLOSRs)[11]. Pressures in the abdominal and thoracic cavities are involved in creating the barrier, as well as the exact intra-abdominal location of the junction. Time and posture are also important factors.

It is clear that the OGJ and the components that affect its function as a valvular region between the stomach and oesophagus have a complex interaction. In normal healthy individuals this region provides adequate protection from the effects of acid and non-acid liquids refluxing or back-flowing up into the oesophagus.

REFLUX IN GENERAL

Gastro-oesophageal reflux disease (GORD) symptoms are very common in the general population affecting up to 44% of the US population at least once a month and 20% of the population once a week[12-14]. It has been shown that patients suffering from GORD have a lower health related quality of life than patients with angina and mild heart failure[15]. There is solid evidence that incompetence or dysfunction of the OGJ is a primary determinant of GORD. Three mechanisms at the OGJ lead to an increased number of acid reflux events associated with GORD: tLOSRs, free reflux during periods of low LOS pressure and deglutitive relaxation of the LOS[11,16-18].

Other methods exist to indirectly measure the effects of increase flow or refluxing. The most widely used of these are 24 h pH studies and intraluminal impedance. Studies of 24 h pH indicate the amount of time the oesophagus is exposed to an acidic environment in a 24 h period. However, they cannot quantitatively measure the amount of acid travelling back up into the oesophagus nor can they indicate the flow rate. Intraluminal impedance on the other hand demonstrates the presence of liquids, solids and gases in different longitudinal segments of the oesophagus, hence giving flow patterns related to refluxing but still without precise data on flow.

WHY PREDICT FLOW IN THE OGJ?

By using data gathered with FLIP, it is possible to predict the flow patterns that occur during a reflux event. By analysing the predicted flow patterns, a variety of information can be obtained, such as shear stresses along walls, which may contribute to the tissue damaging potential of acid. With a better understanding of the flows that develop in the area of the oesophago-gastric junction, knowledge of its function will be improved. To model the type of flow behaviour observed in the OGJ, a set of equations known as the Navier-Stokes equations is required (See appendixI). These equations are complex and therefore require computational numerical analysis to obtain useful data. By making appropriate assumptions, however, simplifications to the equations are made.

METHODS AND ASSUMPTIONS

CFD simulation is a process that has been used successfully in the engineering industry, particularly aerospace, for many years. CFD analysis has become advanced enough that it is no longer considered as simply an evaluation tool. It is increasingly being used in the design process of everything from aircraft to racing cars. In recent years, the technology has been applied to the flow within arteries and the respiratory system of the human body. For this application, the way a CFD simulation is preformed can be broken down into 4 basic steps, as shown in Figure 1.

Figure 1.

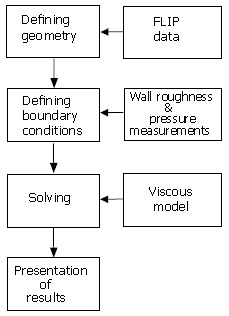
Flow diagram of CFD process.

Defining geometry

The data gathered by a FLIP probe provides, at the current stage of development, eight cross-sectional areas. By making the assumption that these cross-sectional areas are circular, then the radii of these circles can be obtained. By utilising these radii as X co-ordinates and the distances of the electrode pairs from the ends of the probe as Y co-ordinates, it is possible to construct a 2D representation of the geometry of the OGJ, as shown in Figure 2A.

Figure 2.

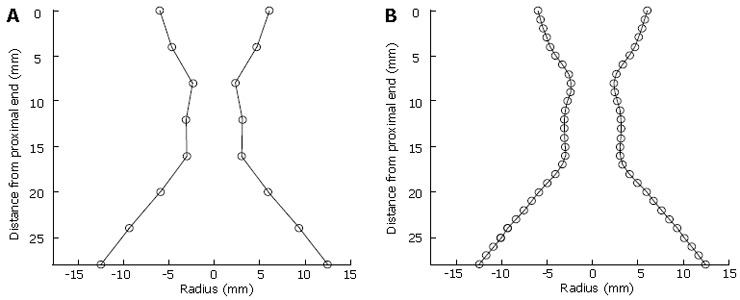
A: OGJ geometry as extracted from FLIP. B:Interpolated OGJ geometry.

The data gathered from FLIP probes is currently limited in that it can only gather information at eight points with a 4 mm separation. However, by using a cubic interpolation scheme, a higher resolution image of the OGJ can be obtained (Figure 2B).

The final step in defining the geometry of the problem is to provide a mesh or grid (Figure 3) over which the CFD solver can perform its calculations. To do this, the geometric data above is imported into a modelling program where the parameters of the mesh, such as cell shape and resolution, are set before being created over the geometry. Generally speaking, higher resolutions result in more accurate results but require greater computational time. Similarly, a carefully designed grid will yield better results but will require more man-hours.

Figure 3.

Example of a CFD mesh.

Defining boundary conditions

The second stage in performing a CFD analysis is to define the boundary conditions along each edge/wall of the geometry and to define the operating fluid. For the sample illustrated in this work, this results in a total of 5 definitions (2 walls, 2 edges and the fluid).

For the purposes of a simple CFD simulation, the assumption is made that the flow field consists of a single fluid, and that this fluid fills the field entirely. The physical parameters, such as density and viscosity of this fluid, must be set. For the general case it can be assumed that the operating fluid is liquid water. This has very similar viscosity and density characteristics to the saline used in the FLIP probe from where the data was acquired.

The walls present a unique problem for this CFD simulation. It is known from basic flow dynamics that boundary layers, which are areas of slower moving fluid, form along these walls. The behaviour of these layers has a large effect on the overall flow dynamics and can cause turbulent flows in regions of fast moving fluid. In order to properly simulate these walls it is necessary to define a roughness length. Since the FLIP probe cannot provide this information, a value of 120 nm for the oral mucosa was assumed[19].

The proximal edge is an imaginary wall that defines the top of the area where the data is collected. The flow of the fluid is not stopped by this wall, but its presence allows the flow behaviour along this edge of the problem to be defined. The most important parameter to be defined along this wall is the hydrostatic pressure. If this hydrostatic pressure is higher than that at the distal edge, it will drive fluid down through the junction. Conversely, if this pressure is lower it will allow fluid to flow upwards from the stomach.

The FLIP probe measures two manometric pressures. These measurements are used to identify the position of the OGJ, but the proximal pressure measurement can also be used to estimate the pressure along the proximal edge of the problem.

The distal edge is similar in most respects to the proximal edge but is located along the bottom of the problem. The second pressure measurement on the FLIP probe is located within the balloon and during the placement of the probe within the OGJ it is temporarily dropped to a position below the junction and into the stomach. As the gastric pressure does not vary greatly during an examination, the balloon pressure at this point can be used to define the pressure along the distal edge of the problem.

Practical assumptions

In order to be sure that the result obtained is an accurate representation, the flow at the exit of the system must be fully developed. In the case of the OGJ, this is generally facilitated by extending the problem upwards into the oesophagus and downwards into the stomach. By doing this, the OGJ becomes the central core of the problem and hence any problems that may be encountered due to the proximity of the proximal and distal edges are removed. An example of such geometry is shown in Figure 2B, where the oesophagus is assumed to have a resting diameter equal to the uppermost diameter recorded by the FLIP probe and the geometry of the cardia and stomach are estimated from illustrations. It is necessary to acknowledge these changes when estimating the pressures on the data recorded by the FLIP probe.

Following the above method and using the grid illustrated in Figure 3, a preliminary CFD simulation was performed. The conditions for this simulation were as follows (all pressures relative to atmospheric): (1) Pressure at lower limit of stomach, 10 cmH₂O; (2) Pressure in the oesophagus, 0 cmH₂O; (3) Roughness length of walls, 120 nm (estimated from data on oral mucosa); (4) Operating fluid, water.

Solving

Before calculations can begin it is necessary to define a few more parameters, which are the solution type and the viscous model to be used.

For the rudimentary simulation shown here, the flow does not change with time and hence a steady state solver was used. Whilst this does not reflect the true complexity of the situation, it provides a decent estimation that can be used to develop an understanding in preparation for more complex problems. For a dynamic problem, it is possible to simulate the motion of the OGJ walls. In these cases, where the geometry is allowed to move with successive time steps and thus provides a more representative model, an unsteady solver will be used in the future.

The way in which the thickness, or viscosity, of the fluid is modelled in a CFD simulation is via a viscous model. Each model makes different simplifications to the governing equations of fluid flow, and has an effect on the number of equations that must be solved over the cells defined by the mesh. It is therefore important to select a model that is appropriate to the problem. For a smooth, simplistic flow a laminar model can be chosen, which provides a fast calculation. For flows that feature turbulent areas, a more complex viscous model is required. In these cases there are a variety of models available from the faster κ-ε solver to the more accurate Reynolds Stress solver. A balance between speed and accuracy must be struck when selecting the solver to be used.

After these parameters have been set, the calculation can be started. This is a complex process, known as iteration, where calculations must be performed over each cell in the mesh and then repeated using the results from one calculation to start the next. When the difference between a given result and the one before it is small enough, it is taken as an acceptable estimation and is called convergence. At this point the calculations are complete and the results can be presented.

Presentation of results

The CFD solver provides information on a variety of parameters describing the flow, such as hydrodynamic and hydrostatic pressures as well as flow velocities and vectors of the operating fluid. These results can be plotted on contour plots (Figure 4) to provide a picture of how these parameters vary through the flow field allowing an understanding of the flow itself.

Figure 4.

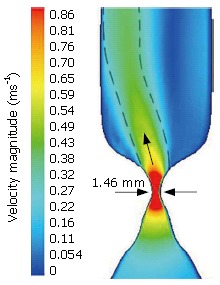
Velocity Magnitude (m/s) through the OGJ and into the oesophagus (limited to 0.9 m/s).

RESULTS

Figure 4 illustrates a contour plot of velocity magnitude. In this situation, the stomach pressure is higher than the pressure in the oesophagus. This causes the flow to move upwards, which represents the situation that occurs in reflux. It can be observed in this plot that as the flow moves upwards towards the oesophagus, its velocity increases whilst the cross-sectional area decreases as predicted by the continuity equation. The velocity of the flow then reaches a maximum of almost 2 m/s at the narrowest section of the OGJ, which has a diameter of 1.46 mm.

DISCUSSION AND PERSPECTIVES

This initial work using a CDF analysis of the OGJ shows some promise for the future. For the case shown above, it can be seen that at the narrowest section, a jet of fluid emerges at a higher velocity than the fluid surrounding it. This jet, illustrated by a green to light blue colouring in Figure 4, does not travel vertically and is seen to brush against the left side of the oesophagus. The cause of this deflection from vertical is the bend between the cardia and the stomach. This illustrates how the geometry surrounding the OGJ must be considered for an accurate analysis. The prediction of this jet of fluid corresponds with anecdotal evidence of acid ‘squirting’ into the oesophagus as the OGJ relaxes during tLOSRs and illustrates how the use of numerical methods can be used to further understanding of the OGJ operation.

The presented model is of a 2D nature, which provides only a general picture of the flow in the OGJ. In the future, the possibilities of CFD analysis will allow a fully 3D model to be constructed, including dynamic changes in the geometry of the OGJ and surrounding geometry, which is more representative of reality. With these improvements, the numerical analyses will produce better results and greater knowledge of the nature and complexity of flow through the OGJ.

APPENDIX I

The Navier-Stokes Equations are the series of equations that describe the relationship between the pressure and viscous forces acting on a fluid particle and its acceleration.

Math 1

Math 1.

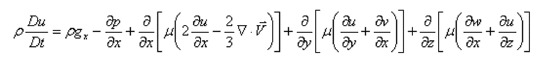
Math(A1).

The X-Component of the Navier-Stokes Equations

Since these are differential equations, only the most basic of fluid flows can be solved via hand methods. This means that the solution to these equations must be sought via numerical methods in a field known as Computational Fluid Dynamics. When attempting to solve the Navier-Stokes equations for a fluid flow, it is generally necessary to discretise a problem into a grid or mesh. By doing this, it is possible to define a complex problem as a collection of simpler computations that can be solved simultaneously to obtain a solution. In reality, the solution obtained via this method will contain imbalances (or residuals) between the different cells of the mesh. By repeating these calculations, and using the results from the previous calculation as a starting point each time, these residuals can be reduced until they can be considered negligible.