Mechanics of flow and mixing at antroduodenal junction

Abstract

The morphology of tissue structures composing the pyloric orifice is thought to play a role in effectively mixing aqueous gastric effluent with duodenal secretions. To understand the physical mechanisms leading to efficient digestion requires computational models that allow for analyses of the contributions of individual structural components. Thus, we have simulated 2-D channel flows through representative models of the duodenum with moving boundary capabilities in order to quantitatively assess the importance of notable features. A well-tested flow solver was used to computationally isolate and compare geometric and kinematic parameters that lead to various characteristics of fluid motion at the antroduodenal junction. Scalar variance measurement was incorporated to quantify the mixing effectiveness of each component. It was found that the asymmetric geometry of the pyloric orifice in concert with intermittent gastric outflow and luminal constriction is likely to enhance homogenization of gastric effluent with duodenal secretions.

INTRODUCTION

The gastric outlet to the small intestine or antroduodenal junction is thought to influence the effectiveness of mixing and subsequent absorption of nutrients in the gastrointestinal tract[1-3]. Following ingestion of meals, the stomach secretes gastric juice containing protein-denaturing hydrochloric acid and pepsinogen, and effectively grinds the mixture with a series of strong muscular contractions to produce a slurry of small solid particles and gastric juice known as chyme. Peristaltic contractions in the sinus of the stomach then serve to transport chyme distally into the small intestine, where further enzymatic catalysis, transport, and digestion continue[1-4]. The objective of this study is to determine what role, if any, the morphology of the antroduodenal junction (Figure 1) plays in affecting transport and dynamic mixing of nutrients in the proximal duodenum. For this purpose we computed the flow of gastric effluent in silico, modeling a set of experiments that were conducted on the cat gut in vitro[5].

Figure 1.

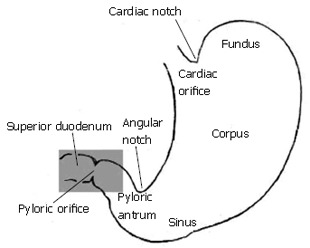
The region of interest (highlighted in grey) includes gastric outlet, or antrum, pylorus, and superior duodenum.

The pylorus is comprised of a collection of tissue structures that connect the antrum to the duodenum. Its luminal diameter is controlled by a sphincter muscle complex that sets the resistance to bulk gastric effluent by regulating the tone of the pyloric orifice. During gastric digestion, the proximal and distal pyloric muscle loops occlude the pyloric lumen, preventing premature discharge of unprocessed material to the duodenum. Once the stomach has completed its task of breaking down large solid agglomerates into smaller particles, the pylorus relaxes and peristaltic contractions in the antrum begin to force chyme distally. At this point, antral contraction waves approach the pyloric orifice and, along with the sphincter complex and mucosal folds, cause steady constriction of the pyloric lumen. Chyme continues to be forcibly transported through this lumen until it is fully occluded, a process thought to potentiate an effluent jet into the superior duodenum[1-3]. To date, it seems that no specific attention has been paid to how the geometry and contractile activity of the pylorus might impact gastric outflow and mixing in the first part of the duodenum, although mixing of chyme with duodenal contents (in particular pancreaticobiliary secretions) is essential for digestion and absorption to proceed[3]. The purpose of this study is to examine, through computer modeling and simulation, the mechanics of flow and mixing in the antroduodenal junction.

COMPUTATIONAL MODELING OF TRANSPORT AND MIXING IN ANTRODUODENAL REGION

Laboratory in vivo and in vitro experiments provide a great deal of information regarding the function of various components of the GI tract. However, better understanding the mechanics requires development of quantitative models that allow precise and isolated effects of these components to be more thoroughly investigated. Such models must include the essential physical mechanisms pertinent to the physiology of the overall system. Clearly, inclusion of all the known mechanisms acting in the GI tract leads to a highly complex dynamical system. While a 3-dimensional transient model of the entire system would best reproduce actual physical behavior, there is much physical insight to be revealed in simple models that allow for examination of specific features over a range of flow and geometric parameters. This approach is being taken presently, with emphasis on morphology and dynamic properties of the pylorus.

In these preliminary calculations we examined the basic aspects of fluid mechanics across the gastric outlet in simplified models of its geometry. Several cases were constructed and analyzed in order to assess the importance of individual aspects of anatomical structure and kinematics. Flow calculations were performed in a series of channel-like domains (Figure 2) representing the distal antrum and superior duodenum, separated by various configurations of the pylorus. The particular aspects being evaluated are: (1) How does the pulsatile nature of gastric outflow affect the dynamics of nutrient transport and mixing? (2) What are the geometric features of the antro-duodenal junction that enhance or suppress transport/mixing in that region? (3) To what extent does wall motion in concert with pulsatile gastric outflow (aspect 1) through different geometric configurations (aspect 2) lead to enhanced transport and mixing?

Figure 2.

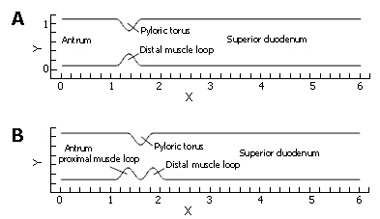
Two representative channel domains used in flow calculations: (A) relaxed pylorus; (B) "notched" configuration resulting from tonicity of pyloric torus and both muscle loops.

To examine the aspects 1-3 listed above, flow fields were computed in the following configurations:

(A) steady flow through a relaxed (symmetric) pylorus; (B) pulsatile flow through a relaxed pylorus; (C) pulsatile flow through a closing pylorus; (D) pulsatile flow through a static pylorus, with asymmetry produced by tonicity of the proximal and distal pyloric muscle loops along with the pyloric torus; (E) pulsatile flow through a similarly asymmetrical, but closing pylorus; and (F) In addition, some of these cases varied in a range of gastric outflow rates or effluent viscosities alternately to determine the effect of the pylorus on homogenization of the chyme of different consistencies, more precisely different viscosities.

Computational methods for solving equations of flow around moving boundaries in the manner chosen here have been thoroughly validated in several papers[6-9].

Following fluid mechanical conventions, the governing equations are “non-dimensionalized” or normalized, by dividing dimensional quantities based on their corresponding representative scales in order to reveal parametric relationships to govern the physical behavior. In our cases, length L^* is normalized by the characteristic unit length of the focal region (i.e. nominal diameter of the duodenum), velocity V* by the maximum inflow velocity in the gastric pulse V_max, and time t* by L/V_max . This normalization leads to an important non-dimensional quantity known as the Reynolds number, Re = (LV)/ν, where ν is the kinematic viscosity of the fluid. Physically, when the Reynolds number is very small, viscous effects dominate over fluid inertia. The Reynolds number for all cases in this investigation varied from Re = 1 (low) to Re = 333 (moderate), the upper-bound value obtained from duodenal dimensions and flow rates of normal saline was introduced into the cat gut in vitro[5]. In moderate Reynolds number flows (Re = 100 to Re = 1000), the presence of relatively strong laminar vortical fluid patterns is expected. It is widely recognized by fluid mechanicians that such vortical patterns can lead to intense fluid mixing, particularly if they possess temporal and spatial variations[10-12].

The flow field equations solved in our level-set models include the standard Navier-Stokes (continuity and momentum) equations (Eqs. 1 and 2), where is a non-dimensional fluid velocity vector with u*, ν* (x- and y- velocity) components in 2D.

Math 1

Math 1.

Math(A1).

Math 2

Math 2.

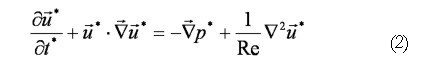
Math(A2).

Based on the available data and non-dimensional techniques described above, the channel height in the antral and duodenal regions was set at 1.0 unit length, with the overall channel length from the inlet to the exit of 6.0 units. The 2D computational domain for all cases was discretized into square Eulerian grid elements measuring 0.05, 0.025, or 0.0125 units length per side depending on the level of mesh refinement demanded by localized fluid motion to obtain a suitable solution[13].

For each model involving temporal variation of fluid velocity in digestive systems, a pulsatile inlet velocity condition was imposed to represent rudimentary flow characteristics generated by periodic antral contractions (Figure 3). Nondimensional inlet velocity V* varied in a sinusoidal manner between 0.0 and 1.0, and the frequency of oscillation was set to f = 0.4 per time unit so that one pulse would have a total duration of 2.5 time units (corresponding to in vitro experimental data on cats[5].) To complete the cycle, each pulse was separated by a quiescent period (V* = 0.0) of 1.0 time unit, giving a total cycle duration of t* = 3.5. The quiescent phase was principally designed to represent the refractory period during which pyloric relaxation and return to an open position occur, but it was retained in all cases, with or without dynamic wall events, to make the results more directly comparable.

Figure 3.

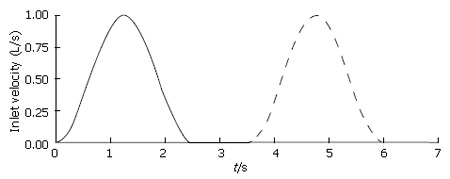
Temporal variation of inlet velocity.

In addition to the standard flow variables (velocities and pressure), a conserved species of transport equation was implemented to measure the spatial gastric effluent homogenization with duodenal contents. Mixing effectiveness was quantified in each case by calculating the scalar variance[14] of an evolving species (marked fluid region) that was initialized as a block measuring 1.0 unit in length and 0.5 unit in height, with a concentration of 1.0 (Figure 4). The species was given a negligible diffusivity of D* = 0.0001, being vertically centered around the domain’s longitudinal axis with the front (right) side of the block giving the same horizontal coordinates as the distal terminus of the antrum. These scalar species blocks were evolved in each of the flow fields by solving the transport equation[15]:

Figure 4.

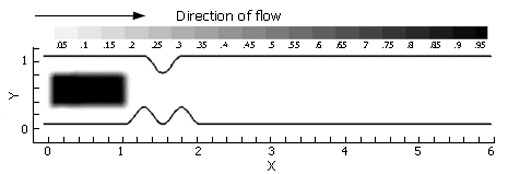
The scalar species block was initialized identically for each case evaluated.

Math 3

Math 3.

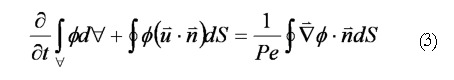
Math(A3).

In Eq. 3, represents scalar species concentration, Pe = (U₀L)/D is the Peclet number (the ratio of convective to diffusive transport in the fluid continuum), and U₀ represents the characteristic bulk fluid velocity (ranging from 0.0 to V_max). Clearly, a small diffusivity coefficient results in very little diffusive transport, implying that the scalar species simply advects along fluid streamlines.

Math 4

Math 4.

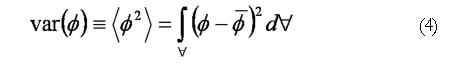
Math(A4).

The scalar species variance calculated for each case is defined by In EΦ 4, is the volume of the computational domain and is the volume averaged concentration of the initial species block, i.e.

Math 5

Math 5.

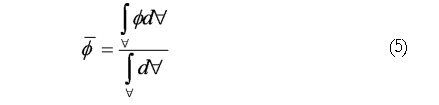
Math(A5).

In our 2-D computations, "volume" is the area. The concept of scalar variance is clarified by considering a rectangular domain of species concentration zero (no species present), and initialized with a scalar species block of concentration 1.0, or 100^°, Φ^- (Figure 5A.)

Figure 5.

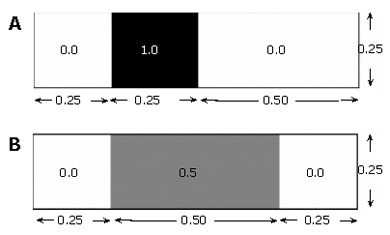
Illustrative example of scalar variance calculation: (A) initial and (B) final states, each with a mean concentration of 0.25.

Φ^- =﹙0.0×﹙0.75×0.25﹚＋1.0×﹙0.25×0.25﹚﹚/﹙﹙0.75×0.25﹚＋﹙0.25×0.25﹚﹚=1/4

The mean 〈Φ²〉=﹙0.0 - 0.25﹚²×﹙0.75×0.25﹚＋﹙1.0 - 0.25﹚²×﹙0.25×0.25﹚=3/64 concentration of the field in this state is: which gives a variance of In a field that has become twice as "well mixed" (Figure 〈Φ²〉=﹙0.0 - 0.25﹚²×﹙0.5×0.25﹚＋﹙0.5 - 0.25﹚²×﹙0.25×0.25﹚=1/64 5B), the variance decreases with the increased level of species homogenization.

In this way, the variance approaches zero as perfect mixing is nearly achieved.

COMPUTATIONAL RESULTS

Steady flow across gastric outlet through a relaxed pylorus

Volumetrically, a large portion of gastric emptying aqueous material is believed to occur across an initially relaxed pylorus[1-4]. In a relaxed state, the torus and distal muscle loop of the human pylorus form a lumen of about 1 cm in diameter between the antrum and duodenum, whose diameters are several times larger[3]. To isolate the effect of such a localized channel narrowing on flow, steady flow behavior (at Re = 333) was computed through the channel (Figure 2A). This calculation was designed to establish a baseline for comparison with forthcoming cases exhibiting pulsatility. The flow is from left to right, i.e. the antrum (inlet) lies to the left of the pylorus and the duodenum to the right. A constant velocity of V* = 1.0 was imposed at the channel inlet, with the resultant flow of 10.0 time units to propagate through the domain in order to achieve steady-state conditions. After this initial period, the scalar species marker was introduced as described previously and allowed to pass through the channel domain to the exit (Figure 6).

Figure 6.

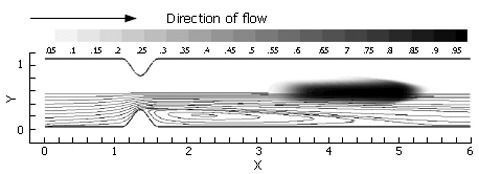
Passage of a passive scalar marker through a relaxed pylorus under steady flow conditions, with inlet velocity set to V* = 1.0 and Re = 333. In this image, 2.0 time units have passed, with the marked fluid exhibiting vertical compression toward and horizontal stretching along the symmetry axis in the weak jet created by the pyloric constriction. Aside from an increase in surface area due to longitudinal stretching, no mixing is seen in this case.

As anticipated from this steady flow case, the flow field consists of a pair of recirculation zones distal to the pylorus (Figure 7) and only one is shown with streamlines due to symmetry. While the marker fluid is distorted, it is essentially unmixed as it passes into the superior duodenum. This is primarily due to the lack of dynamic vortical activity in the flow. Vorticity is limited to the separating region distal to the pylorus, and segregated from the rest of the flow by a separatrix[10,16,17]. The separatrix thus blocks the passage of bulk advecting fluid into the recirculation zone, and vice versa, the ability to effectively mix different regions of fluid is severely limited unless some mechanism for disrupting the manifold (i.e. the separatrix) between the recirculating zone and the core flow is put into action. This is provided by pulsatility (intermittent gastric outflow) as shown below.

Figure 7.

Scalar species distribution following the active phase of one inlet pulse (t = 2.5 time units, Re = 333), illustrating vortical stretching and resultant increase in interfacial area between regions of concentration 1.0 and 0.0.

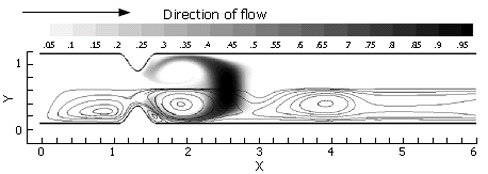
Pulsatile flow across gastric outlet through a relaxed pylorus

Pulsatile inflow conditions were imposed next (Figure 3) on a channel that was identical to the one evaluated in the steady flow. Pulsatility in the flow has apparently increased the mixing a great deal over the steady flow solution, and in a relatively small spatial region (Figure 7). Streamlines illustrate a pattern of dynamic vortex behavior absent in the previous case. In the pulsatile flow, jet development through the pylorus is coincident with vortex growth and strengthening in the distal recirculation zones; the marked fluid is entrained by vortices as they gain momentum and push the separatrix further into the jet region. As the inlet flow decelerates, mean flow through the channel decelerates as well. This leads to "shedding" of the vortices, i.e. the vortices detach from the wall distal to the pylorus and carry away downstream, and a new pair of vortices forms at the next flow pulse, leading to a periodic vortical flow field in the superior duodenum. Vortex formation and shedding from the divergent distal aspect of the pylorus provide a key mechanism for drawing the scalar species into the sheet; the separatrix between regions of large-scale advection and recirculation has been disrupted during the deceleration phase of the cycle, allowing the marked species to become entrained in the vortical flow.

Pulsatile flow across gastric outlet through a closing pylorus

Transport of gastric effluent induced by periodic antral contractions occurs in concert with the closure of pyloric orifice, and fluid is forced through a narrowing lumen. To isolate the contributions made by this narrowing to the mixing process, a model was constructed identically to that described in the previous section, but with the inclusion of pyloric closure. In this model, temporal motion of the solid boundary defining the pyloric geometry varied quasi-sinusoidally, e.g. the pylorus was in its fully open position at the beginning of a pulse cycle, and closed by the time the inlet velocity returned to zero at the end of the active part of the cycle. Temporally sinusoidal reopening of the pylorus was set to take place during the 1.0 time unit refractory period marking the end of the cycle.

Immediately, one can see the enhanced mixing achieved by closure of the pyloric lumen in concert with flow pulsatility (Figure 8). The jet flow affected by the narrowing lumen gives locally advecting fluid a great deal of axial momentum, while the recirculation zones grow concurrently with the increasing obstruction. This effectively leads to large regions of vorticity, which act to stretch marked fluid along the domain’s axis in addition to rolling it into sheets within each vortex. Prominent secondary vortices are also observed in this case, possessing a rotational sense opposite to the primary vortices. This leads to further stretching and folding of the scalar field.

Figure 8.

Scalar species passage through a narrowing pylorus (Re = 333): t = 2.5 time units; the pyloric lumen is occluded and inlet velocity has returned to 0.0. The thin, high velocity jet affected by the narrow lumen has led to rapid growth of a strong vortex pair, which sheds and propagates downstream as the bulk flow is halted.

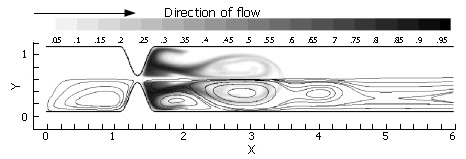
Pulsatile flow across gastric outlet through a static asymmetric pylorus

In the previous three sections, three ingredients were examined that concertedly lead to increases in the degree of fluid mixing in a channel flow, namely, some sorts of partial obstruction leading to convergence and subsequent divergence of the flow, pulsatility, and wall motion. So far, however, we have only covered highly simplified, symmetric geometries to make this point. In reality, with increased tonicity, the positioning of the proximal and distal pyloric muscle loops lead to a "notched" pyloric configuration when viewed in two-dimensional longitudinal sections (Figure 9). In the next case, we seek to capture the effect of this geometric feature of the pylorus on flow into the proximal duodenum. Figure 10 illustrates the static asymmetric pylorus increasing mixture of the scalar field over its symmetric counterpart. As fluid is accelerated through the pylorus, the resultant efflux is directed away from the centerline due to geometric asymmetry. As the jet evolves downstream and diverges further from the axial midline, it collides with the upper wall of the channel and is subsequently deflected away toward the lower wall. This results in a meandering pathway of bulk advection, demarcated by vortices which are staggered in the channel and free to occupy the whole channel width rather than being mirrored symmetrically. The resulting path of the fluid jet (advected scalar) is highly contorted, leading to longer residence time，i.e.,streamlines within the domain are much longer and take more time to traverse, and stretching of fluid elements, and therefore to enhanced mixing.

Figure 9.

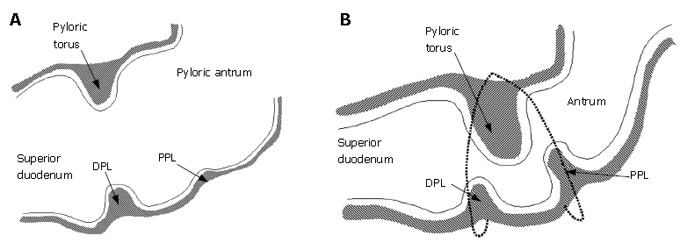
A: Relaxed pylorus; B: 2-D asymmetry is produced by tonicity of both pyloric muscle loops in the contracted state.

Figure 10.

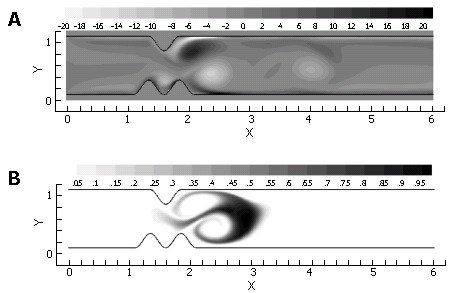
Vorticity (A) and scalar field (B) after 2.5 time units at Re = 333. Inlet velocity has returned to 0.0 and vortices have shed from divergent surfaces distal to the lumen.

Pulsatile flow across gastric outlet through a closing asymmetric pylorus

Asymmetry is seen to be a significant contributor to mixing effectiveness. Next, all of the mechanisms (pulsatility, asymmetry, pyloric closure) were involved by examining the effect of closure of an asymmetric pylorus.

Immediately evident is the fact that the mechanisms of pulsatility, asymmetry and pyloric closure concertedly lead to significant enhancement of mixing. Figure 11 shows that after a single gastric pulse, the scalar marker species has become much more homogenized. It is noteworthy that this homogenization not only occurs rapidly, but takes place within a small spatial region as well; scaling with the human GI system, the level of mixing seen in this case would occur within a 4-5 cm segment of the proximal duodenum[3], even neglecting the presence of prominent geometric features such as the duodenal cap and mucosal folds in the channel.

Figure 11.

A temporal progression of scalar species (left) and vorticity (right) during one complete inlet pulse cycle (3.5 time units) through the closing asymmetric pylorus: A: t = 1.25 time units, with the vortical jet becoming apparent as inlet velocity is maximized and luminal narrowing occurs; B: t = 2.5 time units. The lumen is fully closed, and the inlet velocity has returned to 0.0; C: t = 3.5 time units. The pylorus has returned to its original open state during the 1.0 time unit refractory period. Strong, stable regions of vorticity remain, entraining weaker unstable vortices and further stretching the species.

Mixing effectiveness attributed to geometric and dynamic properties

To quantify scalar mixing, the commonly employed scalar variance measures were obtained during each flow calculation. For each of the cases above, normalized scalar variance (computed using Eq. 4) was plotted for one complete pulse cycle to directly compare the mixing effectiveness of each flow. In Figure 12, the scalar variance measurement of the 5 cases is plotted. Dynamic behavior of the pylorus, combined with pulsatility, clearly results in effective mixing. Imperfections in the form of channel asymmetry enhance this phenomenon even more; the physical structure of the pylorus appears to have a significant effect in mixing patterns, at least in the Reynolds number (i.e. the fluid viscosity) regime corresponding to saline in the cat gut examined in vitro[5].

Figure 12.

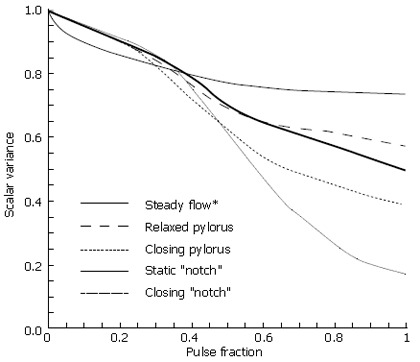
Scalar variance plots of each case through one complete pulse cycle; Re = 333.

Mixing effectiveness attributed to Reynolds number

Chyme viscosity can vary considerably based upon a meal’s solid fraction[1-3,5], with more viscous solutions yielding lower Reynolds numbers. Thus, the Reynolds number varied over several orders of magnitude to study the effects of viscosity in our model (Figure 13). For brevity, results are limited to Re variations in the fifth and final case involving a closing and asymmetric pylorus.

Figure 13.

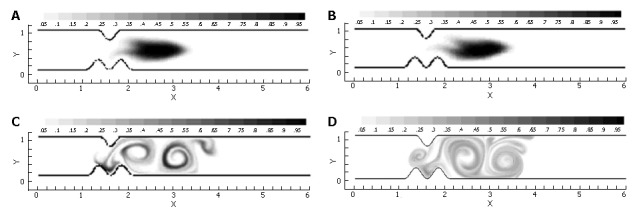
Scalar species plots following one pulse cycle through a closing, asymmetric pylorus at four different Reynolds numbers: A: Re = 1; B: Re = 10; C: Re = 100; D: Re = 333.

As seen from the scalar variance plot in Figure 14, the flows with Reynolds numbers of order 1 and order 10 lack the momentum necessary to overcome viscous stresses in the fluid and generate vorticity, leaving the initial scalar species blocks largely intact as they progress through the channel. Advection begins to dominate as chyme viscosity decreases, resulting in a large degree of fluid stretching, vortex formation and hence, mixing. Scalar variance plots help quantify this shift in behavior, and leave one to conclude that pyloric structure may not play a large role in the homogenization of dense meals without adequate dilution.

Figure 14.

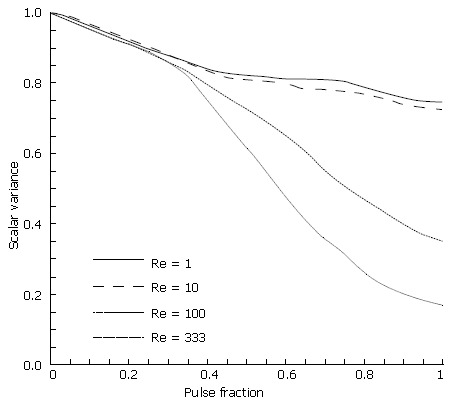
Scalar variance of asymmetric pylorus model at four different Reynolds numbers.

CONCLUSIONS

The lumen of the gastroduodenal junction has a complex geometry which changes with the contractile activity of gastroduodenal musculature in response to the pH, osmolarity, caloric density and mechanical properties of the luminal contents[1-3]. Here we focused on the contribution likely to be made by several specific anatomical parameters (like the notching of pyloric lumen produced by its muscle loops), and by some specific functional parameters (steady versus intermittent gastric outflow). We also compared the results between aqueous and more viscous luminal contents. Our results indicate that intermittent gastric outflow in combination with the complex geometry and motion of the pyloric lumen is likely to enhance duodenal mixing of aqueous fluids, facilitating rapid chemical digestion and subsequent absorption of nutrients in the duodenum. More viscous meals may remain unmixed and will necessarily involve contractions of the duodenum to provide any significant homogenization.

ACKNOWLEDGEMENTS

The authors wish to acknowledge support from the Veterans Administration, and the valuable insight provided by Dr. Konrad Schulze at VAMC and UIHC, Iowa City, which enabled the conduct of this work.