Dashboard Systems: Implementing Pharmacometrics from Bench to Bedside

Abstract

In recent years, there has been increasing interest in the development of medical decision-support tools, including dashboard systems. Dashboard systems are software packages that integrate information and calculations about therapeutics from multiple components into a single interface for use in the clinical environment. Given the high cost of medical care, and the increasing need to demonstrate positive clinical outcomes for reimbursement, dashboard systems may become an important tool for improving patient outcome, improving clinical efficiency and containing healthcare costs. Similarly the costs associated with drug development are also rising. The use of model-based drug development (MBDD) has been proposed as a tool to streamline this process, facilitating the selection of appropriate doses and making informed go/no-go decisions. However, complete implementation of MBDD has not always been successful owing to a variety of factors, including the resources required to provide timely modeling and simulation updates. The application of dashboard systems in drug development reduces the resource requirement and may expedite updating models as new data are collected, allowing modeling results to be available in a timely fashion. In this paper, we present some background information on dashboard systems and propose the use of these systems both in the clinic and during drug development.

INTRODUCTION

Personalized medicine identifies patient characteristics predictive of therapeutic response and uses this information to optimize doses to each patient based on these characteristics (1). Examples of patient characteristics enabling treatment individualization include age, weight, organ (e.g., hepatic) function and various biomarkers (e.g., genomic). Personalized medicine aligns well with population pharmacokinetic and pharmacodynamic (PK/PD) modeling (2), which also focuses on identification of predictive factors in drug exposure and/or response. PK/PD modeling is also central to model-based drug development (MBDD).

Utilization of biomarkers for patient care has been limited by the lack of decision-support tools integrating biomarker data with other patient specific information to generate treatment recommendations (3). PK/PD modeling enables integration of multiple patient characteristics in a drug-specific decision-support framework, and has been combined with web-based applications providing a user-friendly interface, or “dashboard” for evaluating patient data, updating PK/PD models, and summarizing/visualizing data and model predictions (4). Dashboard systems may offer improved means of tailoring treatment for individual patients, particularly for drugs with highly variable exposure or narrow therapeutic windows. Applications similar in concept to dashboards, where clinical trial data are integrated with PK/PD models, may be advantageous as platforms for facilitating implementation of MBDD and informing decisions. Dashboard systems can be used to manage and monitor studies implementing adaptive dosing designs to achieving specific exposure or response. This paper reviews the potential of dashboard systems in patient care and drug development.

CURRENT DOSING PARADIGMS

Flat Dosing

In “flat” dosing, all patients receive the same dose. However, variability in response can arise from pharmacokinetic or pharmacodynamic differences such as genetic subpopulations that rapidly clear a drug, or are more sensitive to its effects. If factors such as weight affect clearance, then small patients will be over-dosed and high weight patients will be under-dosed using this paradigm. Figure 1 depicts the relationship between administered dose and exposure with several dose regimens. When a covariate such as weight affects clearance, exposure can be highly variable with flat dosing. Flat dosing is often a response to difficulties in developing, marketing and safely using a medication with multiple dose strengths.

Fig. 1.

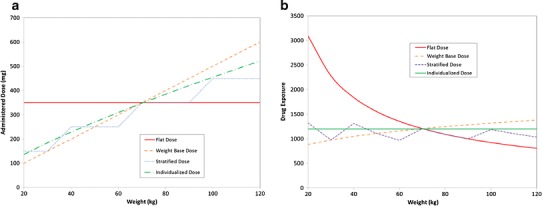
Example of differences between patient exposure following different dose metrics. In this figure, several dose metrics are tested, a flat dose, weight-based dose (mg/kg), stratified dosing and individualized dosing. The underlying clearance model was CL = 0.29 × (weight/70)^0.75. Panel A is the administered dose for each regimen. Panel B is the associated patient exposure. Because clearance is related to weight, the exposure is very high with a flat dose regimen. However, dosing based on milligrams per kilogram assumes a linear relationship between clearance and weight, which is incorrect. Thus, low weight patients have much lower exposure than high weight patients. With stratified dosing, the exposure is more consistent over the range of weights examined. As might be expected, individualized dosing provides consistent exposure across all weights

Adjustment for Body Size

Dosing is commonly based on body size. However, dosing based on milligrams per kilogram often results in sub-therapeutic exposures in low weight patients (Fig. 1), particularly in pediatric patients (5,6) because the relationship between drug clearance and weight (if it exists) is rarely linear or simple (7). This finding has been confirmed for many compounds, including infliximab (8,9). The US FDA produced a guidance document on dose selection for FTIH studies (10) suggesting initial dose selection based on bodyweight (e.g., mg/kg) to scale exposure seen in nonclinical studies to safe levels in humans. While this document is not specifically aimed at providing guidance for dose selection, many monoclonal antibodies (MAbs) use milligrams per kilogram dosing. A recent review (11) found that only 3 of 26 marketed MAbs had clearance linearly related to weight; 8 were dosed on a milligrams per kilogram basis and 2 of these had no weight effect identified on clearance.

Doses based on body surface area (BSA) are similarly problematic; although this is approach is common in oncology. Compared to weight-based dosing, BSA-based dosing assumes somewhat less influence of body size on kinetics. Egorin published a review on BSA-based dosing for antineoplastic agents (12). The variability in exposure with this dosing approach is not always improved over milligrams per kilogram.

Stratified Dosing

Stratified dosing employs flat doses administered over specified ranges of body weight, which often helps ensure appropriate exposure when body size impacts clearance, and may be particularly relevant for pediatric patients (6). This approach has the benefit of reducing the over- and under-dosing seen with flat dosing and dosing based on body size.

Adaptive Dosing

Adaptive dosing (titration) uses doses that are increased or decreased based on observed effect. Some compounds such as epoetin (a biologic agent used to treat anemia) are dosed based on specific hemoglobin measurement. The dose algorithm is complex, and although the approach works well to control hemoglobin, the complexity of the dose strategy can give rise to dose errors and adjustment takes time to determine. Computer-based dose support improves the percentage of patients staying within the target range of hemoglobin often with lower doses than manual adjustment provided (13), and increased staff efficiency without negatively impacting safety (14). Computer-guided dosing may substantially improve patient management and clinical efficiency.

DEFINITION OF DASHBOARD SYSTEMS

Automobile dashboards organize and present information in simple, interpretable formats. Similarly, software packages that integrate information and calculations about therapeutics from multiple components into a single display for clinical use are referred to as dashboards. For example, patient management dashboards might obtain information from electronic medical records, laboratories, clinicians and patients themselves and present it as though arising from the same source. Hewlett Packard developed the first dashboard system, a tool for customizing Windows desktops (15).

“Dose calculators” have been in existence since the late 1950s, although most of these early systems calculated radiological doses (16). One of the earlier dashboard systems in clinical use focused on pediatric antineoplastic dosing (4) and the number of dashboard systems has grown over time. Until recently, computational needs of individualized dosing limited its utility in practice. The application of Bayesian forecasting has been shown to result in therapeutic improvements, for example the number of patients whose trough phenytoin levels were within target range was higher with Bayesian forecasting (63.6% of troughs), compared with conventional dose adjustment (34.0%) (17). Most dashboard systems available for clinical use deal with aminoglycoside antibiotics and warfarin, although there is one (Knowledgebase) dealing with pediatric oncology dosing. A list of some dashboard systems is provided in Table I.

Table I.

Overview of Some Current Dashboard Systems

Software	Bayesian updating	Bayesian forecasting	Bayesian averaging	Dose	Use	Drugs	Website
MM-USC*PACK BestDose (18)	Yes	Yes	No	Yes to target exposure	PK only	Aminoglycosides, digoxin	http://lapk.org.bestdose.php
APK systems (18)	Yes		No	Yes to target AUC	Simple PK only	Aminoglycosides	http://www.rxkinetics.com/apk.html
Abbottbase (19)	Yes	Yes	No	Yes, to an AUC	PK only	Aminoglycosides	NA
Drugcalc (20)	Yes	No	No	Yes to an AUC	PK only	Aminoglycosides	http://www.testandcalc.com/drugcalc/index.asp
Dosecalc (21)	No	No	No	Yes to an AUC	PK only		NA
MW/Pharm (22)	Yes	Yes	No	Yes	PK only	180 drug models	http://www.mwpharm.nl/main.htm
CHOP Pediatric Knowledgebase Dashboard (4)	Yes	Yes	No	Yes through forecast	?	Pediatric oncology (methotrexate)	http://pkb.chop.edu/index.php
NZ FirstDose Dashboard (23)	No	Yes	No	Yes	PK only	Amikacin and vancomycin	http://www.firstdose.org/
TCIworks (19)	Yes	No	No	No	PK only	Gentamycin, enoxaparin and user supplied	http://www.tciworks.info/
Baysient Dose Evaluation system (24)	Yes	Yes	Yes	Yes, multiple	PK and PD	Any	NA

Note that this is a listing of only several dashboard systems. For a complete review of system performance see (18)

We will not cover regulatory aspects of dashboards. Related topics that will not be covered are emergence of computerized Clinical Decision Support systems (25,26) and implementation of electronic medical records systems (27).

Relationship to Population Models

Therapeutic dashboard systems are generally built around population models (2). The population model embodies the current state of knowledge about the kinetics (or dynamics) of a drug and is comprised of three components:

1. The structural model (e.g., a one-compartment pharmacokinetic model) providing a (ideally) mechanistic description the time-course of measured response.

2. Stochastic models quantitating the distribution of unexplained variability in an observed population such as between-subject variability or residual variability.

3. Covariate models quantitating the influence of explainable factors including demographics or disease on individual response.

Dashboard systems are user-friendly programs for accessing models for simulations of kinetics (or dynamics) for an individual patient, with the predictions of the model refined using information about the individual patient. The greater the size and diversity of the database used to construct the underlying model, the greater the chance that the model will be able to return useful and accurate individual patient predictions. However, the often untested assumption is that a particular population model will continue to describe data from a patient into the future, and that the model captures all important sources of variability (both explainable and unexplainable). When the underlying patient condition changes, model predictions may contain substantial errors. For example, while a pharmacokinetic model may have been appropriate for a patient in the past, following a cardiac infarct (major reductions in cardiac output and drug clearance) forecast concentrations are likely to be substantially under-estimated.

INDIVIDUALIZED FORECASTS

Individual data can refine population model predictions for a patient in two ways: Covariate relationships identified during model building or Bayes updating based on individual data. Figure 2 illustrates how both methods work together to improve individual patent forecasting.

Fig. 2.

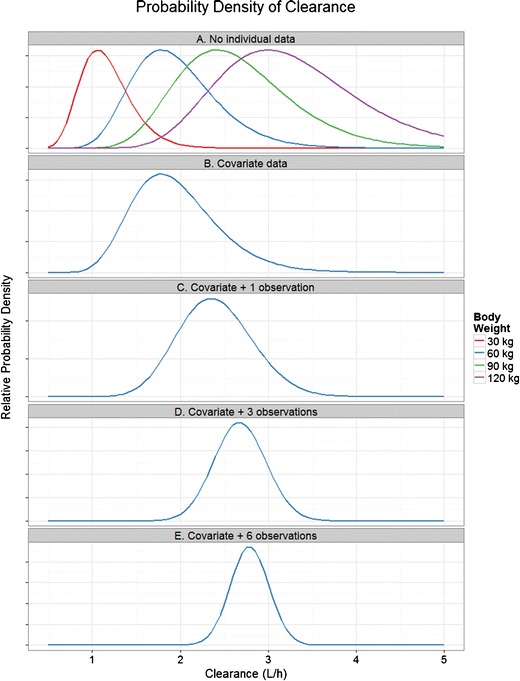
An example of the contribution of individual data to Bayes forecasts. The example uses a simple one parameter, one covariate model for the steady-state drug concentration (C _ss) of a chronically administered drug: C _ss = DoseRate/(CL × (WT/70)^0.75). CL is a log-normally distributed population parameter with a population value of 2 L/h and a between-subject variability of 25%. WT is a covariate for body weight affecting CL via an allometric relationship, where the standard body weight is 70 kg. DoseRate is the average steady-state dose rate—set at 10 mg/h, proportional residual error for the model was 20%. We wish to forecast the clearance of the drug (so that individual C _ss can be estimated). Panel A shows the probability densities for CL for the case where no individual information is known about the patient (densities are normalized to the same peak value for clarity). There are a variety of possible distributions for CL, depending on the unknown body weight of the patient. Panel B shows the distribution of CL with covariate data. The patient has a weight of 60 kg, eliminating other candidate distribution curves. Panel C shows the distribution of CL with covariate data and a single observation of C _ss in the patient (C _ss was found to be 4 mg/L, lower than the expected value of 5.6 mg/L for a 60 kg subject). The distribution has therefore moved to the right, reflecting higher individual clearance and has become narrower, reflecting more certainty about the individual value of CL. Panels D and E show the distribution of CL with covariate data and 3 and 6 observations of C _ss in the patient. Note that as more individual data are available, the uncertainty in the distribution of CL reduces (i.e., the distributions are narrower)

Covariates

Covariates (e.g., patient factors) modify the value of a model parameter (e.g., CL, V) depending on the value of the covariate (Fig. 2). The inclusion of covariate relationships in a model generally implies that covariates provide a better fit of the data and that parameter BSV is reduced. This effectively converts unexplainable to explainable variability at the population level; reducing parameter uncertainty for individual patients for whom covariate values are known. Depending on the drug and data used to build the model, the contribution of covariates to reductions in unexplainable variability can vary from nothing (i.e., no covariates found), to substantial. When no covariates are found, this may imply that the factors causing variability between patients were not possible to measure, or were not available during analysis.

Bayes Update of Models with Individual Data

Most software packages for individualizing therapy utilize Bayesian methods to help predict individual responses to varying treatments. Bayesian inference is a method in which Bayes’ rule is used to update the probability estimate for a hypothesis as additional data are obtained. From a Bayes perspective, the interpretation of a data point is seen to have contributions from the truth (the underlying process, described by a model), error (intra-individual, inter-individual, inter-study, residual etc.) and prior knowledge.

$$\mathrm{data}=\mathrm{truth}+\mathrm{error}+\mathrm{prior}\mathrm{knowledge}.$$ 1

Typically, software packages utilize a combination of one or more: Bayesian updating, Bayesian forecasting and Bayesian model averaging.

Bayes Updating

Bayesian updating is important for dynamic analysis of data collected over time and is a special case of curve-fitting, with its own objective function to compare data, prior values and model predictions. Bayes Theorem balances the contribution of new data and prior parameter values in estimating the new “updated” model parameters. A single data point in an individual is given less weight during fitting if it deviates substantially from what has happened before, and given more weight as additional data points support the finding. Similarly, parameter values are given less weight if they deviate substantially from the prior parameter values inherent in the population model (Fig. 2).

Bayes’ rule can be applied iteratively. After observing data, the resulting posterior value can then be treated as a prior, and a new posterior probability computed from the next set of new evidence. This procedure is termed Bayesian updating or “Bayesian learning” (28).

Bayes Model Averaging

Bayesian model averaging (29) offers a systematic method for checking the robustness of one’s results to alternative models. The standard practice of selecting a single model from some class of models and then making inferences based on this model ignores model uncertainty and can not only impair predictive performance but may overestimate the strength of evidence. Bayesian model averaging allows model uncertainty to be incorporated into inference. The idea behind Bayesian model averaging is to make inferences based on a weighted average over a model space including several models. While model averaging is usually conducted during initial model development, it can be implemented using a “mixture of models” or “indescribable model” approach where the software determines the most likely model for a given patient during Bayesian updating (30). This approach accounts for model uncertainty in predictions and parameter estimates. Thus, resulting estimates incorporate model uncertainty and may better reflect the true uncertainty in parameter estimates.

Bayes Forecasting

Bayesian forecasting (31) uses updated individual parameters to predict the likely exposure and response that a specific patient will exhibit with varying proposed dose regimens based on individual parameter estimates obtained via Bayesian model averaging and/or Bayesian updating. However, when the software does not have the capacity to do Bayesian updating then forecasts are based on patient covariates, which is generally less precise.

BASIC CONCEPTS IN BAYES ESTIMATION

Bayes’ Theorem allows manipulation of conditional probability. Figure 3 illustrates the concept of conditional probabilities using an example where 1,000 patients were tested for whether they had Single Nucleotide Polymorphism (S) or were wild-type (W). They were also tested for positive (P) or negative (N) response to a drug. The conditional probability that a patient would not respond to the drug (N) given that the patient is known to carry SNP1 (S) has the notation Pr(N|S) where Pr denotes a probability. Pr(N|S) can be calculated (Fig. 3) as the joint probability Pr(N&S) divided by the marginal probability Pr(S). Bayes Theorem allows the calculation of Pr(N|S) if the reverse conditional probability that a patient has SNP1 given they are a non-responder, Pr(S|N), is known.

$$\begin{array}{c}\hfill Pr\left(\mathrm{N}|\mathrm{S}\right)=Pr\left(\mathrm{S}|\mathrm{N}\right)\times Pr\left(\mathrm{N}\right)/Pr\left(\mathrm{S}\right)\hfill \\ \hfill \mathrm{Posterior}=\mathrm{Likelihood}\times P\mathrm{rior}/\mathrm{Data}\hfill \end{array}$$ 2

Fig. 3.

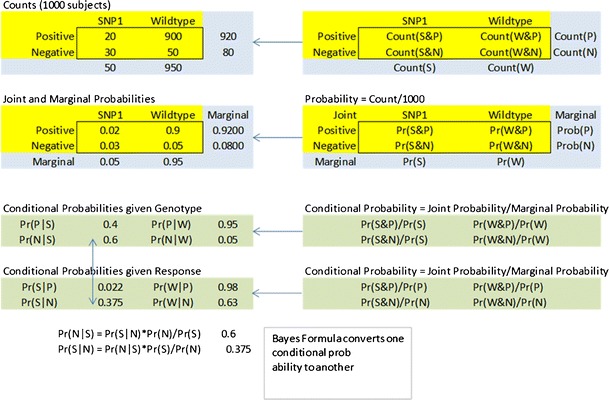
Conditional probabilities and Bayes theorem. One thousand patients were tested for the presence of a particular SNP (possible values are SNP1 present (S) or wild-type (W)) and were also tested for response to a drug (possible values are positive response (P) or negative response (N)). A two-way table of the counts for each of the four possible outcomes is converted to the joint and marginal probabilities (Pr) by dividing by the total number of subjects. There are two types of conditional probabilities—the conditional probability of a drug response given the genotype is known, and the conditional probability of the genotype given the drug response is known. Bayes formula allows the conversion between the two types of conditional probability

We wish to forecast the probability that a new patient will have a negative response to the drug. If we have no information about the patient, our prior probability is the probability of a negative response if the SNP status is unknown is Pr(N) = 0.08 (8%). However, if we test and have new data that the patient carries SNP1, the probability of this being the case, Pr(S) = 0.05 (5%). The updated estimate of the probability that the patient will have a negative response is the conditional probability Pr(N|S). Bayes Theorem requires knowledge of the likelihood, Pr(S|N), however, this is Pr(S&N)/Pr(N) and is therefore 0.03/0.08 = 0.375. Using Eq. 2:

$$Pr\left(\mathrm{N}|\mathrm{S}\right)=0.375\times 0.08/0.05=0.6$$ 3

The forecast probability of a negative response for the patient has moved from a prior (before adding data) value of 8% to a posterior (after the data) value of 60%. One piece of individual data (genotype) substantially changed expectations for this patient.

Figure 3 shows discrete data summarized as probabilities. For continuous data (e.g., drug concentrations) probabilities are replaced with probability densities. Probability density reflects the chance that a given number comes from a given distribution, and is easily calculated using functions in common computer software (e.g., dnorm in R, NORMDIST in Excel). For example, for a normal distribution with a mean of 2 and a standard deviation of 0.5, the probability density of an observed value of 1 is from the distribution is 0.108, of 2 is 0.798 and of 3 is 0.108. Hence, an observed value of two is very likely to be from the distribution, while one and three are less so. An observed value of 5 has a probability density of 1 × 10⁻⁸, which is very unlikely to arise from the distribution.

Probability densities are a fundamental part of the Bayes objective function used for Bayes forecasting with population models. An objective function returns a single number that summarizes the difference between model predictions and data (2). Generally, the objective function is structured so that lower numbers implies better fit, and a curve-fitting process is used to find a set of parameter values for an individual that gives the lowest objective function value for a particular data set. For Bayes forecasting, the objective function takes a modified form of Bayes Formula:

$$\mathrm{Posterior}\propto \mathrm{Likelihood}\times \mathrm{Prior}$$ 4

The Posterior reflects the overall probability density that a model is true after observing some data, and is what we seek to optimize. Note the Data term of Eq. 2 is a constant in the fitting process, and can be neglected for the purpose of optimization. The objective function therefore has two distinct components. Using a PK model as an example:

The Likelihood reflects the overall probability density of a set of observed concentrations in an individual given a distribution representing the model predicted concentrations with residual error. It is calculated from the product of probability densities for each observed data point.

The Prior reflects the overall probability density for a particular set of parameter values given the prior distributions of the parameters in the population. It is calculated from the product of probability densities for the current parameter value from a distribution representing the population variability of the parameter (inherent in the population model).

The different contributions of the Likelihood and the Prior to the objective function are explored in Fig. 4. Factors favoring the Prior in the objective function include: few data points, high residual error and low population variability. Factors favoring the Data include: many data points, low residual error and high population variability.

Fig. 4.

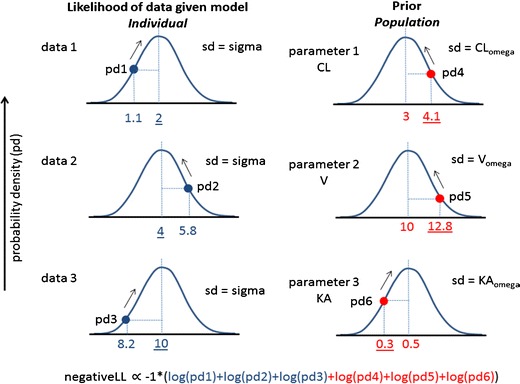
Maximum likelihood estimation for Bayes forecasting. A population pharmacokinetic model with three population parameters (CL, V, and KA) is available for a drug. Three concentration data points are available in a patient given the drug. In Bayes forecasting, a curve-fitting algorithm tries various individual values of CL, V, and KA for the patient to find the minimum value of the Bayes objective function. There are two components of the objective function—one that expresses the difference between the model predicted concentration and the observed concentration data (left column) and one that expresses the difference between the population values of CL, V, and KA and the current model estimate for the individual parameters (right column). The plots show the probability density distribution for each case (assuming a normal distribution). For the left column, each distribution is centered on the model predicted concentration and has variability described by sigma, the residual variability of the population model. The probability density for each observed data point is calculated—the better the fit of the data, the closer each data point is the center of the distribution. For the right column, each distribution is centered on the population parameter value and has variability described by omega, the previously observed variability of the parameter within the population. The probability density for current individual parameter values is calculated—the closer each individual parameter value is to the center of their distribution, the more the patient is considered to be consistent with the previously observed population. The objective function is derived from the product of all the probability density values shown. For computational convenience, the objective function is the negative log likelihood as shown

POTENTIAL BENEFITS AND OUTSTANDING PROBLEMS

Forecasting software such as USC*PACK and MW/PHARM have been available as personal computer software for some years (32). Increased interest and utilization of dashboard systems may be driven by the concurrence of opportunities for expanding forecasting beyond therapeutic drug monitoring, the wider adoption of applications on smart phones and tablets, electronic patient records, cloud computing and user-friendly web-based interfaces for powerful data analysis software (33).

Applications in Drug Development

Drug development costs have escalated dramatically in recent years (34) and new therapeutic drug approvals have declined (35). These findings suggest a need for more efficient approaches to drug development. The Critical Path Opportunities document released by the US Food and Drug Administration (FDA) in 2006 supported the use of modeling and simulation to evaluate clinical trial designs, as well as the use of innovative trial designs (36).

MBDD develops, evaluates, and utilizes models describing pharmacokinetics, pharmacodynamics and disease progression to facilitate quantitative decision-making during drug development. Among the key components of MBDD are improved, innovative trial designs, establishment of quantitative decision criteria, and assessment of trial performance metrics relative to these criteria (37). Although implementation of MBDD has increased rapidly, significant hurdles remain to widespread acceptance of MBDD in industry, including the need for timely availability of model-based analyses, improved communication of results and greater alignment with project teams and stakeholders (38).

Applications similar in concept to dashboard systems, where PK/PD models and clinical trial data are integrated for seamless model updates and visualization for better and faster decision-making, could be envisioned as valuable tools for more successful implementation of MBDD. Drug development dashboard systems may be utilized in a manner similar to that in clinical practice when individualization of dose is required during a clinical trial, based on the design or objectives of the trial. Such trial designs may include adaptive designs where models are used to forecast the likely outcome of dosing a specific patient with a given dose, and the dose adjusted according to pre-specified criteria, such as a target concentration (concentration-controlled) or a target effect (effect-controlled). Individual dose adjustments to achieve safe and efficacious exposure are also needed for drugs with narrow therapeutic indices requiring therapeutic drug monitoring and have been in use since the early 1990s (39). The ability to accurately adjust a patient’s dose to achieve a specified endpoint could substantially shorten the period of time needed to identify appropriate doses for further clinical evaluation.

Innovative designs for clinical trials in patients prior to Phase 3 have included interim analyses to enable improved decisions either at the level of the trial, drug, or portfolio. Types of trial-level decisions at interim analyses may include (1) stopping for futility if low probability of success is predicted based on interim data, (2) stopping if target response is achieved at interim, and (3) adaptive changes to the trial, such as number of subjects, number of dose groups, and duration of treatment, to increase the probability of success (40). These evaluations need to be made in a timely manner, since continuation of the trial is dependent on well-informed decisions. Dashboard-type platforms that access trial data from the clinical database in specified formats for running or updating models, and visualizing outputs, have the potential to facilitate rapid modeling inputs during interim analyses. Additionally, dashboard systems may facilitate review of modeling results and decisions by independent data monitoring committees that are usually composed of non-modelers. In double-blind trials, such a committee is typically utilized for data review and communication with the blinded study team.

There are considerations that must be given for implementation of adaptive designs. The FDA classifies adaptive designs into well-understood designs (e.g., the typical group sequential design) and less well-understood designs (e.g., the adaptive dose finding and two-stage phase I/II (or II/III) seamless adaptive designs) (41). Although adaptive designs offer flexibility, high flexibility may result in the study being classed as a less well understood design. With such studies, statistical inference is often difficult to obtain, leading to the use of adaptive designs in early “learning” (e.g., Phase 1 and 2) trials rather than in later “confirming” (e.g., Phase 3) studies. For example, consider a Phase I dose escalation study to evaluate a new antineoplastic agent where the primary objective is to determine the maximum tolerated dose for subsequent trials. In this scenario, there are two choices for dose escalation: an algorithm-based traditional dose escalation rule (TER) design and a model-based continual re-assessment method (CRM) design. While CRM designs typically utilize traditional statistical models of dose and toxicity to step through a pre-determined dose range, they can also be linked via dashboard systems to select doses based on PK/PD models, emulating existing dashboard systems in clinical use (4). In the CRM trial design, the next enrolled patient will be assigned to the dose that is close to the estimated MTD from updated models, which incorporates the individual patient’s demographic, pharmacokinetic, and pharmacodynamic information. Such dashboard driven CRM designs can incorporate dose escalation/de-escalation and stopping rules which are updated as more information is gathered.

The acceptance of MBDD as a viable development tool has spread, but has never been fully implemented due in part to lack of familiarity with modeling, ineffective communication of modeling results, limited resources, and timelines necessary to complete modeling and simulation activities (42,43). However, dashboard systems allow non-modelers to utilize previously developed models, enhancing their utility during a clinical trial and improving familiarity with modeling. Data from dashboard systems can be downloaded in formats that are appropriate for modeling packages, reducing resource requirements for formatting and cleaning data, allowing earlier initiation of modeling and simulation, and timely delivery of updated results for upcoming protocols. When integrated with electronic case report forms and laboratory databases, dashboards represent an efficient means of integrating and utilizing ongoing trial data to select appropriate doses with minimal effort on the part of the clinical study staff.

Drug development dashboard systems would have to be designed to preserve study blinding, and algorithms for dose changes would also have to be developed with the same goal. Thus, dashboard systems used during drug development would be fundamentally different from those used in clinical practice. These systems would also be expected to be updated as information is accrued about the drug, refining dose recommendations and to allow tracking of important biomarkers and disease metrics. In addition, dashboard systems can be designed to include applications for internal decision making as well as applications for dosing at clinical study sites. The former could include more complex elements, such as stochastic models (e.g., models that include between and within subject variability) and probabilistic outputs to track the feasibility of the drug achieving a particular outcome, while the latter would be simpler and similar to clinical dashboards.

The use of dashboard systems allows implementation of MBDD by the project team, and when applied to adaptive designs, allows for correction of erroneous assumptions, rapid selection of promising doses, and use of emerging information. MBDD has been proposed as a means to shorten drug development time. The use of dashboard systems should allow smoother integration of MBDD into drug development and coupled with adaptive design methods, provide tools to proactively modify trials, avoiding testing ineffective or unsafe doses. An advantage of using dashboard systems in clinical study sites may be fewer dosing and data errors, and may be particularly relevant for pediatric studies, where doses are often based on covariates.

For new drugs developed prospectively where therapeutic drug monitoring is expected to be necessary, a dashboard system could potentially be co-developed with the drug and implemented in practice post-approval as a companion medical device to ensure safe and effective dosing in patients post-marketing. Such systems would require regulatory clearance but the documentation required for regulatory review is similar to documentation needed for validation and is part of any quality lifecycle management for software. Lastly, dashboard systems developed by the manufacturer may be helpful as a central resource that could be updated and shared by all health care providers.

Applications in Clinical Use

A Pharmacokinetic System—Infliximab

The treatment of inflammatory bowel diseases (IBD) with infliximab provides an example of a drug that could benefit from a dashboard system. Factors known to impact on the PK/PD, and hence, safety and efficacy of infliximab, include body weight, concomitant use of immunosuppressive drugs (e.g., methotrexate) which affect clearance and decrease probability of anti-drug antibodies (ADA) formation, the degree of systemic inflammation which can be reflected by the serum albumin concentration, C-Reactive Protein (CRP) TNF, and disease severity and type (44). Collectively, these factors account for part of the differences in PK and clinical efficacy observed after standard dosing. A population pharmacokinetic model for infliximab in IBD has been developed by Xu et al. (8) where patient weight, sex, albumin and ADA status were identified as important covariates.

The management of IBD patients typically initially uses standard infliximab dose regimens with modification by clinical presentation and measured infliximab concentrations in plasma. Doses are given intravenously 2–8 weeks apart. Recent findings have shown that infliximab concentrations measured immediately before the next dose (trough concentration) have special significance. In steroid-resistant ulcerative colitis patients (45), infliximab trough concentrations above the threshold of assay detection were associated with higher remission rates (from 15 to 69%), endoscopic improvement and less surgical intervention. Therefore, successful management of IBD may be attributed to maintaining trough concentrations above a target. While this task is complicated by changes in patient disease status which has a feedback effect on infliximab concentrations, it is a classical pharmacokinetic problem which is readily addressed in the research setting. However, to date this technology has been unavailable to physicians in clinical practice.

A prototype dashboard system for infliximab implementing the population model of Xu et al. (8) has been developed. Figure 5 shows dashboard output tracking the time-course of key covariates, allowing a clinician to see trends. Figure 6 shows the time-course of observed and forecast infliximab concentrations based on a Bayes updated model using all observed infliximab concentrations. A separate plot shows key trough concentrations and a nominal threshold trough concentration. The dashboard system allows clinicians to simulate proposed doses of infliximab ensuring trough concentrations stay above the target.

Fig. 5.

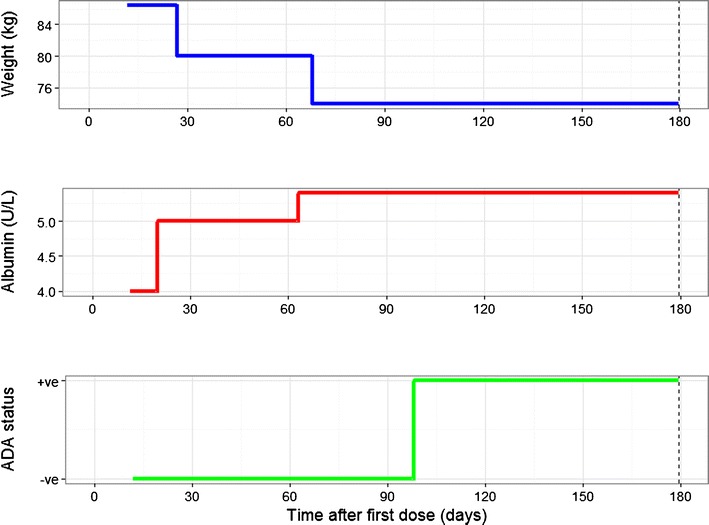
Covariate “dashboard” for an ulcerative colitis patient receiving infliximab. This plot shows how three key covariates known to affect the pharmacokinetics of infliximab change over time. Lack of efficacy may result in weight loss as seen in the first plot. The dose given may not be adequate leading to more severe disease and increased clearance of infliximab. Improvement in the disease may be reflected in the serum albumin returning to the normal range and the potential to reduce the dose of infliximab. The development of ADA may require an increase in the dose of infliximab or a change of medication

Fig. 6.

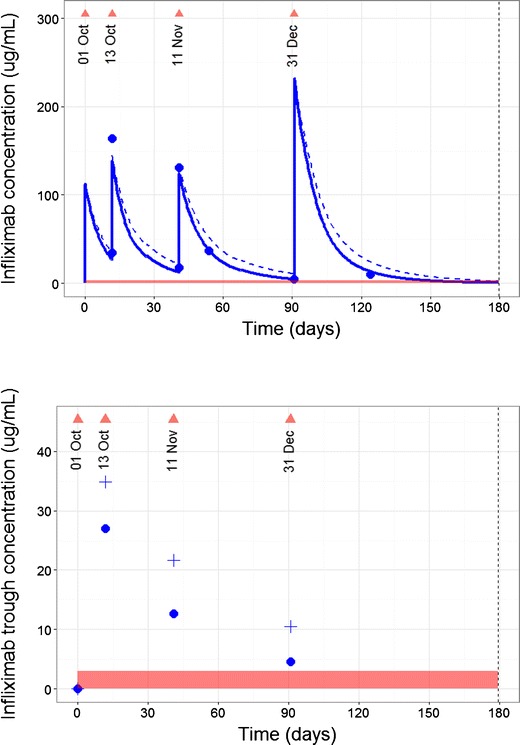
Predicted and forecast infliximab concentrations. Upper: The predicted and actual infliximab concentrations (blue dots) for a patient and were used to update a population PK model using Bayes estimation. The triangles are infliximab doses. The horizontal axis shows days since the commencement of infliximab treatment. The dashed line shows the predicted group infliximab concentration for a patient with matching covariate characteristics (e.g., Fig. 5) giving the individual infliximab time-course shown by the solid line. Although the peak from the dose given on 31 Dec was greater than previous doses, it was not sufficient to give trough concentrations above target by the time of next clinic visit. Lower: The predicted infliximab trough concentrations for the patient. The vertical line indicates “now”, the time of the current clinic visit. The four triangles show clinic visits with an infliximab dose. The crosses show the predicted group infliximab trough concentration for a patient with matching characteristics (e.g., Fig. 5). The individual infliximab trough concentrations following a Bayes update of the model are shown by the circles. Trough concentrations for this patient are lower than expected based on a matching individual in the population (group prediction), suggesting a higher than expected clearance. The model now accounts for this higher clearance for forecasting future doses

In addition to maintaining therapeutically effective concentrations, the associated expectation is that outcomes will improve, allowing more patients to achieve remission. Given the rising costs of healthcare, and the consideration of outcome-related reimbursement (46), the use of dashboards may become a method by which drug use, outcomes and costs are improved.

A Pharmacodynamic System—DAS28

Dashboards have potential to help clinicians interpret individual patient pharmacodynamic data. For example, the 28-joint Disease Activity Score (DAS28) is increasingly used to track rheumatoid arthritis (RA) activity. A common first-line protocol for RA is “triple therapy” with methotrexate, sulfasalazine and hydroxychloroquine where doses are adjusted according to disease activity and intolerance (47,48). Early DAS28 reductions are associated with long-term joint preservation and reduced disability (49) such that effective disease control shortly after diagnosis results in long-term retardation of disease progression (50,51). If initial therapy fails, biological agents are typically introduced (52).

The DAS28 trajectory during triple therapy could be described using an empirical population model based on data from 263 early RA patients (53). DAS28 typically showed an immediate exponential drop from baseline to a new value over a year or more of treatment (Fig. 7). The model showed good predictive performance (Fig. 7), but had considerable BSV in rate and extent of DAS28 change, and high residual error. The model therefore embodies prior population knowledge about the DAS28 trajectory with triple therapy, but shows patient trajectory can range between rapid, substantial improvement to slow worsening of symptoms. The clinical challenge is to accurately identify patients who respond slowly and/or poorly to triple therapy so that other treatments can be utilized. The high residual variability in DAS28 suggests a potential risk of basing decisions on “noise” rather than true changes in disease status, suggesting decision making based on one observation is inappropriate. Two prior DAS28 may reveal more of a pattern for the patient, but when and how often should DAS28 be evaluated? Bayesian forecasting has the potential to address some of these questions in a research setting, and the potential to be implemented in a dashboard system as a means to forecast disease trajectory measured by DAS28 for individual patients. As more DAS28 data become available, the accuracy of Bayes forecasts improves, but not all individual data are equal. Table II summarizes a simulation study investigating forecasting accuracy of the DAS28 model. The relationship between true and Bayes predicted change in DAS28 from baseline at 60 weeks is summarized by the R² value for the regression of true versus predicted value. With no individual data, the Bayes forecast is poor (Schedule 1, R² = 3%) while with the impractical scenario of weekly DAS28 the forecast is excellent (Schedule 2, R² = 90%). The forecast has little improvement if only individual baseline (Time = 0) data are available (Schedule 3, R² = 5%). There is marginal improvement by adding more DAS28 observations, but observation timing is important. Three observations within 6 weeks of treatment show marginal improvements in the forecast (Schedule 5, R² = 11%), but three observations within 26 weeks of treatment substantially improved the forecast 60 week DAS28 (Schedule 6, R² = 43%).

Fig. 7.

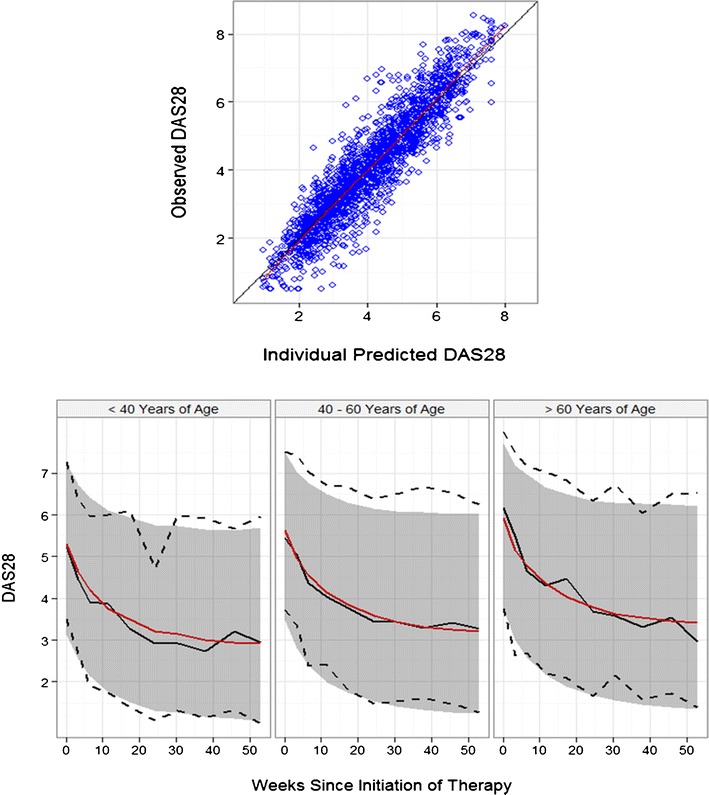
A population model for DAS28 score during triple therapy. A population model of the time-course of DAS28 during triple therapy for RA (53). The model is an empirical description of the time-course of DAS28 after the initiation of triple therapy: DAS28_t = BASE + EX1 × (1 − e ^{− EX2. t}) where BASE, EX1 and EX2 are population parameters described by a central population value and inter-subject variability. Upper: the observed DAS28 versus individual predicted DAS28 showed good agreement, indicating that the model could find a time-course of DAS28 that was an acceptable description of most patients. Lower: Visual Predictive Check (VPC) of the model facetted by patient age. The observed data is represented by a black solid line (median), and the black dashed lines (90% confidence intervals). The simulated DAS28 is represented by the red solid line (median) and the gray shaded area (90% confidence intervals). The model predictions overlay the observed data with good agreement, and show the progressive drop in DAS28 from the baseline value to a new treated level

Table II.

Improved Forecasting of DAS28 Trajectory with Individual Data

DAS28 observation schedule	No. of DAS28 scores	R2 60 week change in DAS28 true versus predicted (%)
Schedule 1. None	0	3
Schedule 2. Weeks 0–60 at weekly intervals	61	90
Schedule 3. Week 0	1	5
Schedule 4. Weeks 0, 3	2	10
Schedule 5. Weeks 0, 3, 6	3	11
Schedule 6. Weeks 0, 12, 26	3	43

A simulation study where Bayesian forecasting was used to predict the DAS28 after 60 weeks of triple therapy for each patient (n = 9996). The prior was the population model of Wojciechowski (53), while various observation schedules for individual DAS28 data were examined, ranging from 0 to 61 observations for each patient. The relationship between true and Bayes predicted change in DAS28 from baseline at 60 weeks is summarized by the R² value for the regression of true versus predicted value

These initial findings illustrate the substantial body of work needed before PD forecasting becomes practical as a clinical tool. Robust, validated disease metrics and population models are needed, as well as a clear understanding of how they can be used in dashboard systems (e.g., optimal collection of individual data) to maximally benefit both clinicians and patients.

CONCLUSIONS

The concept of dashboard systems for therapeutics is intuitively appealing with potential benefits ranging from improved efficacy and safety to improving clinical efficiency. However, development, validation and implementation of dashboards are challenging. They are expensive to develop, and who should bear this cost? To what extent do their benefits and disadvantages need to be defined to appease clinicians, patients, pharmaceutical and insurance companies and regulators? Is using a randomized clinical trial to support every version of every dashboard system for every drug scientifically necessary? It has been argued that benefits of some interventions are self-evident without formal evidence, as has been highlighted in a light-hearted meta-analysis of parachutes (54). The difficulties in defining costs and benefits for software-based devices are further illustrated by Target Controlled Infusion pumps for the intravenous anesthetic propofol which, while not approved for commercial use in the USA, have been widely adopted elsewhere (55). Despite challenges, research and commercialization of dashboards is ongoing motivated by the belief that current dose strategies for many therapeutics can be improved, benefitting patients.