Abstract
Quantitative prediction of the impact of chronic kidney disease (CKD) on drug disposition has become important for the optimal design of clinical studies in patients. In this study, clinical data of 151 compounds under CKD conditions were extensively surveyed, and alterations in pharmacokinetic parameters were evaluated. In CKD patients, the unbound hepatic intrinsic clearance decreased to a similar extent for drugs eliminated via hepatic metabolism by cytochrome P450, UDP-glucuronosyltransferase, and other mechanisms. Renal clearance showed a similar decrease to glomerular filtration rate, irrespective of the contribution of tubular secretion. The scaling factor (SF) obtained from the interquartile range of the relative change in each parameter was applied to the well-stirred model to predict clearance in patients. Hepatic and renal clearance could be successfully predicted for approximately half and two-thirds, respectively, of the applied compounds, showing the high utility of SFs. SFs were also introduced to a physiologically based pharmacokinetic (PBPK) model, and the plasma concentration profiles of 12 model compounds with different elimination pathways were predicted for CKD patients. The PBPK model combined with SFs provided good predictability for plasma concentration. The developed PBPK model with information on SFs would accelerate translational research in drug development by predicting pharmacokinetics in CKD patients.
Electronic supplementary material
The online version of this article (doi:10.1208/s12248-014-9626-3) contains supplementary material, which is available to authorized users.
KEY WORDS: model-based drug development, modeling and simulation, PBPK, pharmacokinetics, renal impairment
INTRODUCTION
Chronic kidney disease (CKD) is a worldwide public health problem with global increase in the number of patients (1,2). CKD is associated with multiple physiological changes and, hence, alters the pharmacokinetics (PK) of drugs, which could cause adverse effects (3–5). According to the survey of new molecular entities approved from 2003 to 2007 by the US Food and Drug Administration (FDA), half of the orally administered compounds with altered drug disposition in patients with renal disease were predominantly eliminated by non-renal pathways such as hepatic metabolism or biliary excretion (6). In 2010, the FDA issued a draft guidance emphasizing the need to perform clinical studies on drugs that are eliminated by non-renal mechanisms as well as the renal route in patients with renal impairment (7). For pharmaceutical industries, quantitative prediction of the impact of CKD on drug disposition has become important for the optimal design of clinical studies in patients including careful dosage adjustment to avoid possible side effects.
Recently, physiologically based pharmacokinetic (PBPK) modeling and simulation has increasingly gained importance to provide a rational design for first-in-human studies (8). PBPK modeling is, generally, constructed based on a bottom-up approach, which needs a large number of input parameters such as plasma protein binding and metabolic intrinsic clearance (CLintH), in addition to physicochemical properties and physiological parameters. With regard to hepatic failure, quantitative variations in the activity or content of cytochrome P450 (CYP) enzymes have been reportedly available alongside alternation of physiological parameters, and such information are successfully applied to PBPK models to describe the PK in liver cirrhosis (9,10).
On the other hand, the effects of chronic renal failure (CRF) on PK have been evaluated mainly in animal models (11,12). Based on the accumulated evidence from in vitro and in vivo studies, the mechanisms underlying the alternation of PK can be explained as follows (3,4): uremic toxins such as indoxyl sulfate, parathyroid hormone, and cytokines, all of which are highly increased in the serum of chronic renal failure patients, are involved in either the transcriptional or translational modifications or direct inhibition of CYP enzymes or transporters. The elevated concentrations of parathyroid hormone in chronic renal failure lead to the down-regulation of hepatic drug-metabolizing enzymes including CYP enzymes through activation processes like nuclear factor-κB. Since various mechanisms are complexly intertwined, it is difficult to quantitatively evaluate these parameters in CKD condition, which are necessary for the bottom-up approach, based on in vitro systems and in vivo animal models for individual drugs.
Meanwhile, the top-down approach, which is based on the actual changes in PK parameters derived from clinical data, would become a useful tool to predict drug dispositions in CKD patients by the PBPK model. Rowland et al. quantitatively estimated the microsomal content of CYP1A2, CYP2C8, CYP2C9, CYP2C19, and CYP3A4 enzymes in CKD condition (13), by the back calculation of in vivo hepatic clearance (CLH) to CLintH including the correction of differences in plasma protein binding, and predicted the PK of paroxetine, diltiazem, and repaglinide in patients. The same input parameters for CYP enzyme abundance in CKD condition were also utilized by Zhao et al., who prepared an expanded PBPK model by incorporating the hepatic uptake process (14). Furthermore, the simulation of the changes in plasma concentrations of solifenacin in CKD patients employed a factor of 0.6, which was estimated from the difference in in vivo clearance (CL) between healthy volunteers (HV) and CKD patients (15). Although these PBPK models informed by the top-down approach allow successful predictions of PK in CKD patients for certain drugs, the reduction of CLintH or in vivo CL in CKD patients in these models is derived from a limited number of clinical studies.
Importantly, taking complex mechanisms into consideration, a relatively large dataset encompassing an equally large number of drugs is essentially required for the top-down approach, and the change ratios of PK parameters obtained from the differences between CKD patients and HV should be applied as scaling factors (SF) to the prediction of the plasma concentrations in the PBPK model. In the present study, we extensively collected clinical data of CKD patients for a variety of drugs that are non-renally and/or renally eliminated, and the utility of the obtained SFs in the PBPK model was evaluated by comparing the predicted and observed changes in PK parameters and plasma concentration profiles in CKD patients.
MATERIALS AND METHODS
Data Collection
The clinical data for 151 compounds, for which PK parameters in HV and both moderate and severe CKD patients were available, were collected from the literature or the PharmaPendium database (Elsevier, NY, USA; https://www.pharmapendium.com/). Moderate and severe CKD are generally defined by a glomerular filtration rate (GFR); 30 to 59 mL/min/1.73 m2 for moderate and 15 to 29 mL/min/1.73 m2 for severe CKD. The collected PK parameters were as follows: unbound fraction in plasma (fp), fraction excreted unchanged in urine (fe), an apparent volume of distribution at a steady state (Vss), CL, area under the plasma concentration-time curve (AUC) after oral dosing, and the elimination half-life (t1/2). These data were summarized as supplemental data (Supplementary Table S1). In silico parameters such as lipophilicity (clogP), pH-dependent measure of lipophilicity (clogD), and basic and acidic dissociation constants (pKa) were calculated from structural information using CLOGP, version 4.82 (Daylight Chemical Information Systems Inc., CA, USA) and Pallas, version 4.4.1 (CompuDrug Inc., AZ, USA). The compounds were divided into acidic, basic, and neutral classes based on the differences between the clogD values at pH 6.5 and 7.4 (∆clogD) as indicated by the following equation:
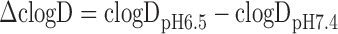 |
1 |
Compounds with positive and negative ∆clogD values were classified as acidic and basic, respectively. Compounds with ∆clogD values of zero were assumed to be neutral. As blood to plasma concentration ratio (RB) values of most compounds were not available from the literature data, they were assumed to be 0.6 for acidic compounds and 1 for the other, basic and neutral, compounds (16–18). Unbound fraction in blood (fB) was calculated by dividing fp by RB. The information on hepatic elimination mechanisms including the contribution of CYP enzymes was obtained from the literature or FDA approval packages.
Dataset for the Evaluation and Prediction of CL Alterations
To evaluate the alteration of unbound CLintH (CLUintH) in disease conditions, the 1st dataset was used as a training set. The 1st dataset consists of PK data after oral administration for 76 compounds that are mainly eliminated via the hepatic route (fe < 0.4; averaged value, 0.05). Then, the SF for CLUintH obtained from the 1st dataset was applied to the well-stirred model together with those for fp and renal blood clearance (CLR), and predictabilities for CLs in CKD conditions were confirmed using the 2nd dataset as a validation set. The 2nd dataset, which is independent from the 1st dataset, consists of intravenous data of 40 compounds eliminated via both renal and non-renal routes (averaged fe value, 0.50). In addition, within the 2nd dataset, the compounds, for which plasma concentration-time profiles were available, were used for the validation of a PBPK model combined with the SFs in CKD patients. The summary of 1st and 2nd datasets was shown in the supplemental data (Supplementary Table S2).
Alterations of the PK Parameters in CKD Patients
Collected fp and Vss in patients with moderate and severe CKD were compared with those in HV to produce the relative percentages (RP) for each disease stage as shown in the following equation:
 |
2 |
CLR was obtained from the literature information or calculated from plasma CL after intravenous dosing as shown in the following equation:
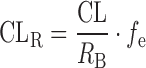 |
3 |
The CLR in patients with moderate and severe CKD was compared with those in HV, and the RPs in each disease stage were obtained in the same manner as fp and Vss.
For alterations in CLintH, as enough data of intravenous PK profiles in hepatically cleared drugs were not available, RPs were obtained from dose-normalized AUC after oral dosing in the 1st dataset. The theory underlying this calculation was derived from the well-stirred liver model and shown by the following equation:
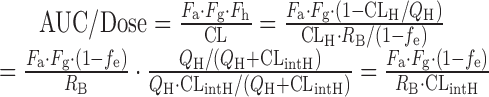 |
4 |
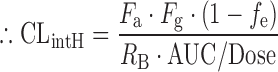 |
5 |
where QH is the hepatic blood flow, Fa is the fraction moving into enterocytes, Fg is the fraction escaping gut-wall elimination, and Fh is the fraction escaping hepatic elimination. Assuming that Fa, Fg, and RB were not altered in the CKD condition, the RP of CLintH was obtained as shown by the following equation:
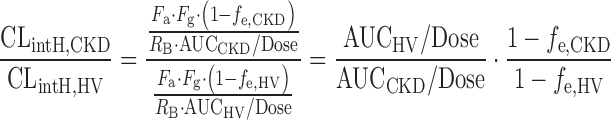 |
6 |
Finally, RPs for CLUintH were calculated using the corresponding mean RP for the fp of acidic, basic, and neutral drugs under moderate and severe CKD conditions obtained in this study as shown in the following equation:
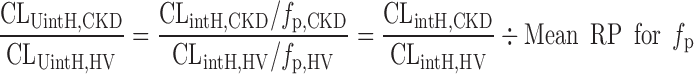 |
7 |
The RPs in CLR and CLUintH were obtained from compounds with fe values of >0.4 (mainly eliminated via the kidney) and <0.4 (mainly eliminated via the liver), respectively.
Prediction of CL in CKD Patients
The predictabilities for CLs in CKD condition were validated with the 2nd dataset. The SF for CLR, fp, and CLUintH in patients with moderate and severe CKD, which represent the relative difference under the disease conditions compared to HV, was obtained as follows. The SF for CLR was defined as the relative changes of GFR ranges under each disease condition. Although GFR is generally defined as a range of 15 to 30 mL/min/1.73 m2 for severe CKD, the lower limit of 10 mL/min/1.73 m2 was used for the calculation of SF, because patients with GFR below 15 mL/min/1.73 m2 were often included in this survey. For HV, a GFR of 125 mL/min/1.73 m2 was used for calculation (19). The SFs for fp and CLUintH were assumed to be equal to the interquartile ranges of the RP of each parameter in the disease states obtained in this study. The parameters under disease conditions (CLR,CKD, fp,CKD, and CLUintH,CKD) were calculated by multiplying those under healthy conditions by the SFs.
To predict CLH under CKD conditions (CLH,CKD), the following simple well-stirred equation incorporating fp,CKD and CLUintH,CKD was used:
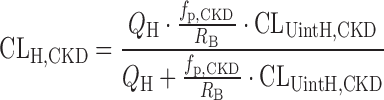 |
8 |
It was assumed that QH and RB values are not altered under CKD conditions. By combining these CLR,CKD and CLH,CKD, the total CL under the disease condition (CLCKD) was predicted as expressed by the following equation:
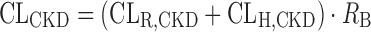 |
9 |
Prediction of Plasma Concentrations in CKD Patients
Within the 2nd dataset, the compounds, for which plasma concentration-time profiles after intravenous dosing were available, were used for the validation of a PBPK model combined with the SFs in CKD patients. The structure of the PBPK model and physiological parameters used are shown in Supplementary Fig. S1 and Supplementary Table S3, respectively. The framework of the PBPK model had previously been reported (20), that is, the model is composed of 11 tissue compartments (lungs, adipose tissue, bones, brain, heart, muscles, kidneys, spleen, liver, skin, and small intestine), which are linked by venous and arterial blood pools. Perfusion rate-limited kinetics were assumed, and each tissue was represented by a single well-stirred compartment. The liver and kidney were considered as the elimination sites. The principles of mass balance equations for non-eliminating tissues, liver, and kidney are indicated by the following differential equations:
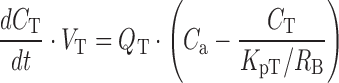 |
10 |
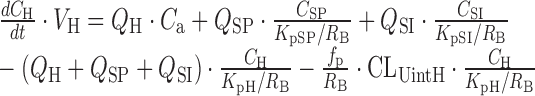 |
11 |
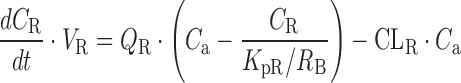 |
12 |
where V is the volume, Q is the blood flow, C is the concentration, Kp is the tissue to plasma concentration ratio, and for subscripts, T is for tissue, a is for artery, H is for hepatic, SP is for spleen, SI is for small intestine, and R is for renal.
Firstly, the PBPK model was constructed using the observed fp, CLUintH, and CLR to simulate the plasma concentration-time profiles after intravenous dosing in HV. The Kp values for HV in each tissue was calculated by the tissue composition-based equations proposed by Rodgers et al. (21,22), using clogP, pKa, and fp. A uniform factor obtained from the comparison of the predicted and observed Vss was applied to the calculated Kp values for the adjustment of PK profiles in HV (20). The SFs for fp, CLUintH, and CLR were then introduced to obtain the parameters under CKD conditions, and the plasma concentrations in patients were simulated. Note that the Kp values of CKD patients were recalculated by the same procedure using fp,CKD.
The PK parameters (Vss, CL, and t1/2) were estimated by the non-compartmental analysis of simulated plasma concentrations in both HV and patients, and RP of these parameters in disease states were calculated. Model construction, simulation of plasma concentrations, and non-compartmental analysis were performed by Phoenix WinNonlin, version 6.3 (Pharsight, CA, USA).
RESULTS
Alterations of fp and Vss in CKD Patients
The RPs of fp and Vss in CKD patients compared with HV are shown in Fig. 1 and are summarized in Table I. For acidic and neutral compounds, the fp increased in CKD patients with the median RP of 109 to 115% for moderate and 134 to 135% for severe CKD, indicating that the extent of change in the fp depended on the progression of disease. On the contrary, the fp for basic drugs showed no significant changes with the median RP of 99 to 104%. For the Vss, no pronounced differences between the disease states or drug properties were observed with the median RP of 95 to 107%. The interquartile ranges of the RP for the obtained fp in each class of drug presented in Table I were used as the SFs for the prediction of CL, CLR, CLH, and PK in CKD patients. Given that the alteration of Vss was not found under any disease conditions and the Vss was generally determined by the fp and physicochemical properties in PBPK models, the SF of Vss was not taken into consideration for PK prediction.
Fig. 1.
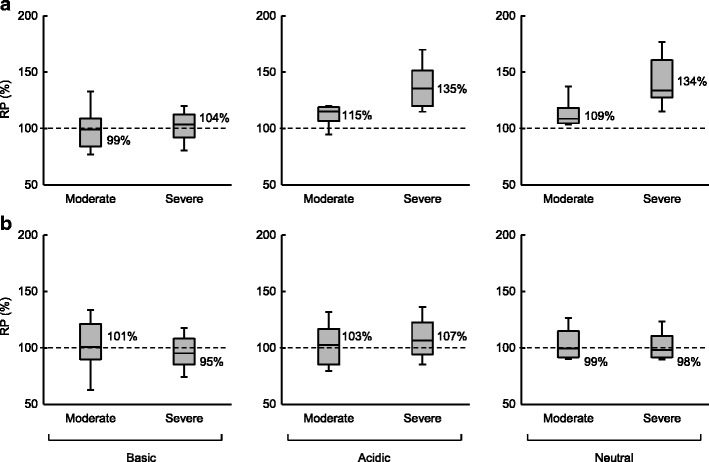
RP of f p (a) and V ss (b) in moderate and severe CKD. In the boxes, the middle lines represent the median values, the top and bottom margins represent the 75th and 25th percentiles, and the top and bottom whiskers represent the 90th and 10th percentiles. The percentages on the right of the boxes represent median values
Table I.
Alteration of f p and V ss in Moderate and Severe CKD
| Parameter | CKD stage | Group | n | RP (%) | |||
|---|---|---|---|---|---|---|---|
| Median | (Interquartile range) | Mean | (SD) | ||||
| f p | Moderate | Basic | 28 | 99 | (84–109) | 100 | (23) |
| Acidic | 13 | 115 | (107–119) | 112 | (12) | ||
| Neutral | 10 | 109 | (105–118) | 118 | (25) | ||
| Severe | Basic | 26 | 104 | (92–113) | 103 | (21) | |
| Acidic | 16 | 135 | (120–151) | 139 | (25) | ||
| Neutral | 10 | 134 | (127–161) | 147 | (39) | ||
| V ss | Moderate | Basic | 13 | 101 | (90–121) | 103 | (32) |
| Acidic | 17 | 103 | (85–117) | 104 | (23) | ||
| Neutral | 10 | 99 | (92–115) | 109 | (26) | ||
| Severe | Basic | 17 | 95 | (85–108) | 99 | (28) | |
| Acidic | 19 | 107 | (94–123) | 110 | (27) | ||
| Neutral | 12 | 98 | (92–111) | 107 | (28) | ||
CKD chronic kidney disease, RP relative percentage, f p unbound fraction in plasma, V ss volume of distribution at a steady state
Alteration of CLR in CKD Patients
The RPs of CLR in CKD patients compared with HV are shown in Fig. 2 and Table II. The CLR showed a disease state-dependent reduction with median RP of 31% for moderate and 12% for severe CKD. The alterations in CLR were within the range of change for GFR (24 to 47% for moderate and 8 to 23% for severe CKD). Compounds with lower and higher unbound CLR (CLR/fB) than GFR, which can be considered to be predominantly eliminated by glomerular filtration and tubular secretion, respectively, showed similar changes in the CLR, as determined by the median RP of 35 versus 31% for moderate and 13 versus 11% for severe CKD. This finding indicated that the alterations in CLR can be predicted based on the GFR regardless of the elimination mechanism. Therefore, instead of the interquartile ranges of the RP of CLR, the ranges of GFR to be defined in moderate and severe CKD were applied as the SF for the prediction of CLR and PK in CKD patients.
Fig. 2.
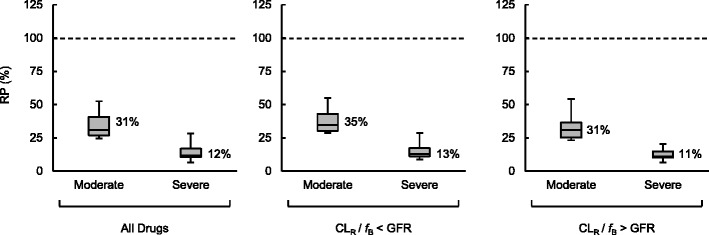
RP of CLR in moderate and severe CKD. In the boxes, the middle lines represent the median values, the top and bottom margins represent the 75th and 25th percentiles, and the top and bottom whiskers represent the 90th and 10th percentiles. The percentages on the right of the boxes represent median values
Table II.
Alteration of CLR and CLUintH in Moderate and Severe CKD
| Parameter | CKD stage | Group | n | RP (%) | |||
|---|---|---|---|---|---|---|---|
| Median | (Interquartile range) | Mean | (SD) | ||||
| CLR | Moderate | All drugs | 25 | 31 | (27–41) | 36 | (14) |
| CLR/f B < GFR | 10 | 35 | (30–43) | 39 | (12) | ||
| CLR/f B > GFR | 15 | 31 | (25–37) | 34 | (15) | ||
| Severe | All drugs | 25 | 12 | (10–17) | 14 | (8) | |
| CLR/f B < GFR | 11 | 13 | (11–17) | 16 | (9) | ||
| CLR/f B > GFR | 14 | 11 | (10–15) | 13 | (6) | ||
| CLUintH a | Moderate | All drugs | 64 | 68 | (55–82) | 69 | (20) |
| CYP substrates | 36 | 68 | (56–89) | 72 | (22) | ||
| UGT substrates | 11 | 67 | (61–86) | 69 | (16) | ||
| Others | 17 | 68 | (53–76) | 63 | (16) | ||
| Severe | All drugs | 68 | 62 | (48–80) | 64 | (21) | |
| CYP substrates | 42 | 65 | (48–80) | 66 | (23) | ||
| UGT substrates | 10 | 59 | (47–68) | 59 | (16) | ||
| Others | 16 | 60 | (51–72) | 63 | (19) | ||
CKD chronic kidney disease, RP relative percentage, CL R renal blood clearance, CL UintH unbound intrinsic clearance, f B unbound fraction in blood, GFR glomerular filtration rate, UGT UDP-glucuronosyltransferase, CYP cytochrome P450
aRPs of CLUintH were obtained from the 1st dataset
Alteration of CLUintH in CKD Patients
The RPs for CLUintH in CKD patients compared with HV were obtained from the 1st dataset and are shown in Fig. 3 and Table II. In both disease stages, a similar extent of decrease in CLUintH was noted for CYP and UDP-glucuronosyltransferase (UGT) substrates and drugs eliminated via other mechanisms, with the median RP of 67 to 68% in moderate and 59 to 65% in severe CKD conditions. The change in CLUintH was unlikely dependent both on the disease stage of CKD and the elimination mechanism in the liver. Consequently, the median RP of CLUintH for all examined drugs was calculated as 68% (interquartile range, 55 to 82%) in moderate and 62% (interquartile range 48 to 80%) in severe CKD, and these interquartile ranges were used as the SFs for the following predictions of CLH and PK in CKD patients.
Fig. 3.
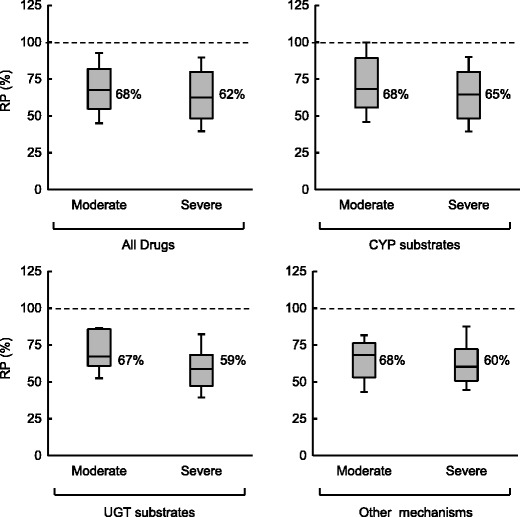
RP of CLUintH in moderate and severe CKD obtained from the 1st dataset. In the boxes, the middle lines represent the median values, the top and bottom margins represent the 75th and 25th percentiles, and the top and bottom whiskers represent the 90th and 10th percentiles. The percentages on the right of the boxes represent median values
Prediction of CLs in CKD Patients
The present study demonstrated that there were relatively large variations in the alterations of CLR and CLH between the examined compounds, and therefore, CLs in the 2nd dataset were predicted using SFs based on the interquartile ranges analyzed for the CLUintH and fp. The SFs for CLR, CLUintH, and fp used in the present study are summarized in Table III. The predicted and observed mean RP of CLR, CLH, and CL in CKD patients compared with HV and the success rates of the prediction are shown in Table IV. The predicted mean RPs were in good agreement with the observed values for CLR (36 vs 43% in moderate and 16 vs 21% in severe CKD), CLH (75 vs 73% in moderate and 79 vs 69% in severe CKD) and CL (54 vs 52% in moderate and 45 vs 43% in severe CKD). When the range of the predicted CLs included the observed data, the prediction was defined to be successful. The percentages of compounds that were successfully predicted were 66 to 70% for CLR, 47 to 48% for CLH, and 67 to 68% for CL.
Table III.
SFs for CLR, CLUintH, and f p for the Prediction of CL and PK in CKD
| Parameter | Group | Moderate CKD (%) | Severe CKD (%) |
|---|---|---|---|
| CLR | All drugs | 24–47 | 8–23 |
| CLUintH | All drugs | 55–82 | 48–80 |
| f p | Basic | 84–109 | 92–113 |
| Acidic | 107–119 | 120–151 | |
| Neutral | 105–118 | 127–161 |
CKD chronic kidney disease, CL R renal blood clearance, CL UintH unbound intrinsic clearance, f p unbound fraction in plasma
Table IV.
Predicted and Observed RP of CLs in CKD Patients and Success Rates of the Prediction
| CKD stage | Parameter | n | Mean RP (%) | Success rate (%) | |||
|---|---|---|---|---|---|---|---|
| Observed | Predicted | Successfully predicteda | Over-predictedb | Under-predictedc | |||
| Moderate | CL | 34 | 52 | 54 | 68 | 12 | 21 |
| CLR | 32 | 43 | 36 | 66 | 22 | 13 | |
| CLH | 33 | 73 | 75 | 48 | 18 | 33 | |
| Severe | CL | 36 | 43 | 45 | 67 | 8 | 25 |
| CLR | 33 | 21 | 16 | 70 | 21 | 9 | |
| CLH | 34 | 69 | 79 | 47 | 15 | 38 | |
The predictabilities for CLs were evaluated using the 2nd dataset
CKD chronic kidney disease, RP relative percentage, CL clearance, CL R renal blood clearance, CL H hepatic clearance
aThe predicted range included the observed change
bThe predicted range was greater than the observed change
cThe predicted range was smaller than the observed change
Prediction of Plasma Concentrations in CKD Patients
The plasma concentration-time profiles after intravenous dosing of 12 model compounds in HV, moderate, and severe CKD were simulated by the PBPK model incorporating the SFs under the disease conditions. The predicted range and mean observed RP for CL, Vss, and t1/2 in CKD patients are summarized in Table V. The simulated plasma concentration-time curves of six drugs (the best and worst predicted compounds in each group; mainly eliminated via the renal, non-renal, and mixed routes) are also described in Fig. 4. In case the range of the predicted parameters included the observed values, the compounds were classified as showing successful prediction. For the CL prediction in CKD patients, 10 (83%) and 7 (58%) of 12 compounds were regarded to show successful prediction in moderate and severe CKD, respectively. The alterations of t1/2 in CKD patients were also well-predicted by the PBPK model, accompanied with successful predictions in 9 (75%) and 8 (67%) of 12 compounds under moderate and severe CKD conditions, respectively.
Table V.
Predicted and Observed RP of CL, V ss, and t 1/2 in 12 Model Compounds in CKD by the PBPK Model
| Disease stage | Compound | f e | CL | V ss | t 1/2 | |||
|---|---|---|---|---|---|---|---|---|
| Observed | Predicted | Observed | Predicted | Observed | Predicted | |||
| Moderate CKD | Isepamicin | 1 | 40 | 24–47 | 171 | 98–105 | 387 | 208–438 |
| Zanamivir | 0.90 | 38 | 28–52 | 101 | 101–105 | 234 | 199–363 | |
| Cefepime | 0.88 | 37 | 28–53 | 129 | 99–103 | 307 | 193–350 | |
| Cidofovir | 0.86 | 26 | 29–54 | 115 | 101–102 | 468 | 182–330 | |
| Enprofylline | 0.82 | 32 | 31–56 | 74 | 105–113 | 226 | 185–298 | |
| Carumonam | 0.78 | 41 | 32–58 | 117 | 104–110 | 220 | 185–315 | |
| Meropenem | 0.77 | 39 | 32–56 | 111 | 101–102 | 251 | 175–301 | |
| Tomopenem | 0.57 | 34 | 34–65 | 105 | 89–120 | 365 | 135–344 | |
| Cefotetan | 0.49 | 46 | 43–73 | 99 | 101–103 | 193 | 141–236 | |
| Batanopride | 0.20 | 94 | 52–84 | 121 | 96–110 | 121 | 109–179 | |
| Cyclophosphamide | 0.19 | 71 | 54–87 | 121 | 104–113 | 188 | 130–191 | |
| Lidocaine | 0 | 77 | 67–95 | 101 | 97–99 | 135 | 101–134 | |
| Severe CKD | Isepamicin | 1 | 20 | 8–23 | 184 | 98–103 | 944 | 424–1,252 |
| Zanamivir | 0.90 | 23 | 13–34 | 108 | 107–115 | 425 | 336–784 | |
| Cefepime | 0.88 | 22 | 14–35 | 139 | 102–110 | 574 | 313–722 | |
| Cidofovir | 0.86 | 11 | 15–37 | 93 | 103–105 | 842 | 274–641 | |
| Enprofylline | 0.82 | 8 | 17–40 | 71 | 114–135 | 797 | 298–564 | |
| Carumonam | 0.78 | 21 | 19–39 | 102 | 111–112 | 416 | 275–562 | |
| Meropenem | 0.77 | 23 | 18–37 | 117 | 102–102 | 463 | 261–535 | |
| Tomopenem | 0.57 | 17 | 24–51 | 78 | 88–110 | 366 | 170–452 | |
| Cefotetan | 0.49 | 33 | 33–72 | 87 | 104–109 | 209 | 150–307 | |
| Batanopride | 0.20 | 63 | 47–80 | 98 | 95–106 | 177 | 111–190 | |
| Cyclophosphamide | 0.19 | 44 | 49–81 | 92 | 113–114 | 241 | 139–229 | |
| Lidocaine | 0 | 45 | 65–96 | 88 | 96–97 | 192 | 99–136 | |
Values in italic form represent successfully predicted cases
CKD chronic kidney disease, RP relative percentage, f e fraction excreted unchanged in urine, CL clearance, V ss volume of distribution at a steady state, t 1/2 elimination half-life
Fig. 4.
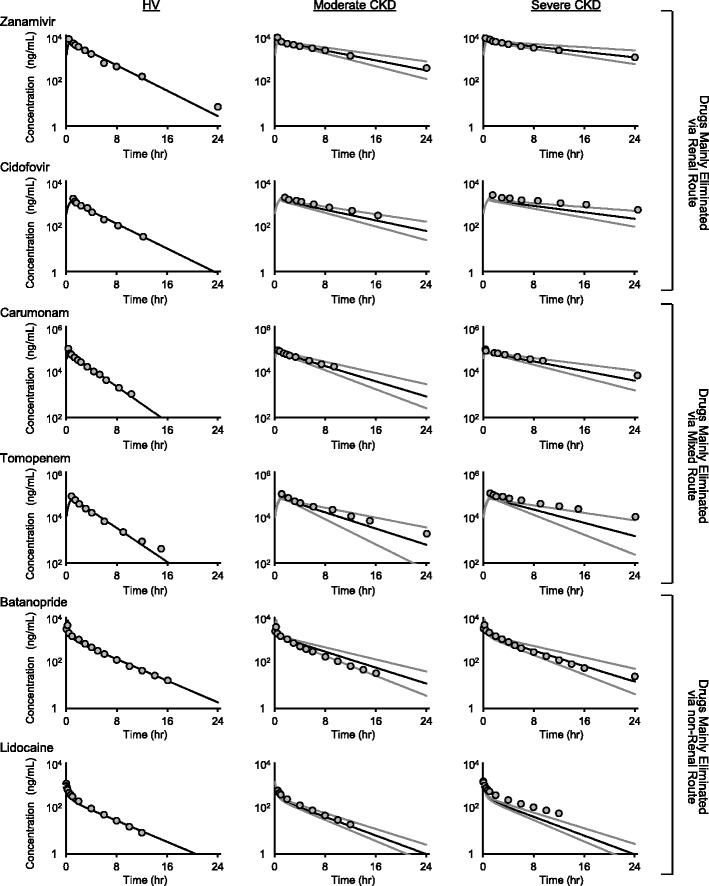
Examples of plasma concentration-time simulations after intravenous dosing in HV and CKD conditions by the PBPK model combined with SFs. The black lines represent averaged predicted curves. The gray lines represent the predicted ranges of plasma concentrations. The gray circles are observed concentrations of each model compound. Best (zanamivir, carumonam, batanopride) and worst (cidofovir, tomopenem, lidocaine) cases of prediction in each group of drugs mainly eliminated via renal route, mixed route and non-renal route are presented
DISCUSSION
In the present study, we extensively collected clinical data of 151 compounds with various pharmacokinetic properties and analyzed the impact of CKD on different PK parameters. Notably, for altered hepatic elimination, clinical data of over 70 compounds were comprehensively analyzed. The CLUintH of compounds that are eliminated via hepatic metabolism by CYP, UGT, or other mechanisms decreased to a similar extent in CKD patients as to HV. CLR showed a similar decrease to GFR irrespective of the involvement of tubular secretion. The RP in each parameter under different disease conditions showed large variations, which might involve a variety of mechanisms. Therefore, SFs based on the interquartile range estimated by a statistical analysis of the RP were applied to the well-stirred model to predict the CLs in CKD patients. CLH and CLR were successfully predicted for approximately half and two-thirds of the compounds, respectively. Importantly, the SFs for CLUintH obtained from the 1st dataset were validated using the different datasets (the 2nd dataset) in the prediction of CLs. The plasma concentration-time curves of 12 model compounds in CKD patients were also well-predicted by the application of the SFs into the PBPK model, as demonstrated by the relatively high success rates for CL and t1/2.
During the drug development stage, a perspective evaluation for the influence of CKD on the PK of new molecular entities has become a critical issue for the pharmaceutical industries. Since multiple factors are complexly intertwined in the alteration of the PK under CKD conditions, we employed the top-down approach rather than the bottom-up approach based on in vitro and in silico data. Some authors have proposed PBPK models incorporating the CLUintH reduction in CKD patients based on the top-down approach; however, these models were derived from a limited number of clinical data (13–15). On the other hand, one advantage of this study is that SFs based on an interquartile range derived from a relatively large number of clinical data are employed and would have a possibility for encompassing widely ranging PK alterations by various mechanisms in CKD.
Plasma protein binding is a governed factor to PK behavior and is known to vary depending on the plasma concentrations of the binding proteins as well as several other factors in CKD patients such as the competition of the binding sites by metabolites that have accumulated as a result of reduced renal function or the denaturation of albumin itself due to uremic toxins (23). Strougo et al. demonstrated that the albumin plasma concentration tended to decrease, but the median α1-acid glycoprotein level in the plasma was 1.4 times higher in patients with moderate to severe CKD compared to the control group (15). In this study, acidic and neutral compounds clearly exhibited an increase in fp in patients with severe CKD probably due to a decrease in the plasma concentration of albumin to which these classes of compounds mainly bind (24). Regarding basic compounds, it was assumed that fp would decrease if the α1-acid glycoprotein plasma level increases in severe CKD in theory; but in practice, the fp of some compounds almost remained constant or increased in moderate and severe CKD, which is probably due to multiple mechanisms. Importantly, Vss was almost consistent for all of the examined compounds regardless of the increase of fp in acidic and neutral drugs possibly because these classes of compounds have relatively small distribution volume which is not sensitive to the alteration of plasma protein binding.
In general, the renal tubular secretion is reportedly known to involve various transporters including organic anion transporters 1 (OAT1) and 3 (OAT3), organic cation transporter 2 (OCT2), and multidrug resistance protein 2 (MRP2) (25). An animal study using CRF rats demonstrated the alteration of hepatic and intestinal protein expression levels of multidrug resistance 1 (MDR1) and MRP2 (4). However, there is no literature on the up- or down-regulation of proteins or mRNA expression levels of those transporters in the kidneys of CKD patients. Interestingly, the impact of CKD on glomerular filtration and on renal tubular secretion was not different, and the RP of CLR for compounds that undergo tubular secretion was proportional to GFR. This finding provides insight into CLR prediction, namely that GFR is still a dominant factor to predict CLR regarding renal tubular secretion in addition to glomerular filtration.
Unexpectedly, the percentage reduction of CLUintH in CKD patients relative to that in HV was not affected by the disease progress and was within a similar range for CYP and UGT substrates. The result was in agreement with the findings reported by Zhang et al., who showed that there were no significant differences in the AUC changes between CYP and non-CYP substrates in CKD patients (6). In addition, the RPs of CLUintH for typical substrates of CYP1A2, CYP2C9, and CYP3A did not differ in CKD patients except for CYP2D6 that slightly showed the lower RP (data not shown). Rowland et al. also evaluated the RPs for CYP1A, CYP2C9, CYP2D6, and CYP3A4 (13). The estimated RPs were decreased by the progression of the disease and appeared to be slightly lower than the corresponding median data in our study. In hepatocytes prepared from rats with CRF, down-regulation was found for CYP2C11 and CYP3A1/2, but not for CYP1A2 and CYP2D proteins (26). There may be species differences in the down-regulation of CYP enzymes between humans and rats. It has not yet been attempted to investigate a change in UGT expression level by the CRF condition in preclinical studies.
One of our objectives of this study was to acquire SFs based on a relatively large amount of clinical data to develop a universal prediction model by the top-down approach. To increase the number of compounds, the RP for the reduction of hepatic elimination was estimated from the oral AUC, which was in contrast to Rowland’s method using a small number of intravenous PK data (13). The alterations of CLUintH under CKD conditions were evaluated assuming that the Fa and Fg are not affected by CKD. The Fa and Fg are controlled by passive absorption, transporter-mediated influx and efflux, and metabolism mainly by CYP3A in humans. It has been reported that P-glycoprotein and some CYP enzymes including CYP3A are down-regulated in the small intestine of animal models of CRF (27,28), which leads to the increase of Fa and Fg in the disease condition. CYP3A substrates among our dataset were regarded as relatively high Fh compounds, and this implied that Fg of these compounds were also high and that the effect of the alternation of Fg on the estimation of SF was limited. It is important to note that the applicability of SFs derived from the oral AUC was proven by a relatively high success rate for CL in different datasets after intravenous dosing, which shows a minor effect of the alterations of Fa and/or Fg on RPs’ estimation. In this study, however, as PK alterations of midazolam, which is known as the typical substrate of CYP3A with a significant intestinal first-pass metabolism (29), could not be evaluated because both moderate and severe CKD data were not separately available, further discussion would be needed for the effect of the alteration of Fg in the disease conditions.
Another assumption in obtaining the SF for CLUintH is that RB value does not change in the disease condition. Since RB is a function of fp which increased by up to approximately 50% in neutral drugs in the disease condition, the alteration of RB could have an impact on the determination of SF for CLUintH. However, relatively high plasma protein binding of drugs in the 1st dataset (averaged value of known fp, 0.11) indicated low distribution to blood cell, and the impact of the change of RB on SF seems to be minor. In addition, regarding compounds that strongly bind to α1-acid glycoprotein, the change of fp due to increased plasma binding protein level in the disease condition would give an impact to SF for CLUintH. Further analysis on the alteration of fp in patients would be required for such compounds.
Some drugs are known to be mainly eliminated via hepatic transporters such as organic anion transporting polypeptides (OATPs) (30), but the number of such compounds included in the current dataset was so limited. Consequently, the estimated SF is unlikely to reflect a change in the hepatic uptake activity; hence, the insufficient dataset for the liver uptake via transporters could be one of the reasons for the over-prediction of CL.
The PBPK model with SFs based on an interquartile range estimated in the present study was used for the simulation of the plasma concentration profiles of 12 model compounds with widely ranging fe values. Consequently, the plasma concentrations of the 12 model drugs seemed to coincide with the observed data, and this was supported by a relatively high accuracy of CL and t1/2, which were successfully predicted for 58 to 83% and 67 to 75% compounds, respectively, in CKD patients. These data suggest the utility of SFs with an interquartile range on PK prediction in CKD patients of drugs eliminated by different pathways. For the prediction of Vss, only two compounds in each moderate and severe CKD condition were successfully predicted. Since the prediction of Vss is based on the alteration of fp in the PBPK model, an improved prediction method of fp in disease condition would lead to a better predictability of Vss.
More recently, translational research, which involves the translation of efficacy and PK data from preclinical to clinical studies via modeling and simulation cycles, occupies an important position in drug development (31,32). We have proposed the tiered approach, which consists of four steps based on modeling and simulation of PBPK models to predict human PK from drug discovery to first-in-human studies (20). In the last step, the measured plasma concentration profile in HV allows us to optimize the PBPK model by the integration of comprehensive in vitro and in vivo information. Such a PBPK model developed through modeling and simulation would become a key tool to evaluate intrinsic factors (age, gender, race, disease, and genetic polymorphism) on human PK in clinical studies. In the draft guidance, FDA recommends that pharmaceutical companies conduct either “the reduced PK study” in end-stage renal disease patients or “the full PK study” for more detailed evaluation in mild, moderate, and severe CKD patients to assess the possible impact of CKD on drug disposition under development (7). The new method with SFs derived by the top-down approach would provide a rationale for the selection of the appropriate study as well as dose adjustment through predicting the PK profile in patients from that in HV and also accelerates the implementation of model-based drug development that is deeply associated with decision-making based on PK profile prediction and risk assessment of toxicity.
CONCLUSION
We collected the large dataset regarding PK parameters in CKD patients and comprehensively described large variations in the alterations in PK parameters. Consequently, the SFs with an interquartile range were successfully derived from PK parameters in the disease conditions by the top-down approach. The predictability of the PBPK model combined with the SFs was validated using 12 model compounds with various PK profiles. The developed PBPK model with information on SFs would play an important role in the translational research in drug development.
Electronic Supplementary Material
(PDF 70.1 kb)
References
- 1.Coresh J, Selvin E, Stevens LA, Manzi J, Kusek JW, Eggers P, et al. Prevalence of chronic kidney disease in the United States. JAMA. 2007;298:2038–47. doi: 10.1001/jama.298.17.2038. [DOI] [PubMed] [Google Scholar]
- 2.2013 USRDS annual data report. Available from: www.usrds.org/adr.aspx.
- 3.Dreisbach AW. The influence of chronic renal failure on drug metabolism and transport. Clin Pharmacol Ther. 2009;86:553–6. doi: 10.1038/clpt.2009.163. [DOI] [PubMed] [Google Scholar]
- 4.Nolin TD, Naud J, Leblond FA, Pichette V. Emerging evidence of the impact of kidney disease on drug metabolism and transport. Clin Pharmacol Ther. 2008;83:898–903. doi: 10.1038/clpt.2008.59. [DOI] [PubMed] [Google Scholar]
- 5.Sun H, Frassetto L, Benet LZ. Effects of renal failure on drug transport and metabolism. Pharmacol Ther. 2006;109:1–11. doi: 10.1016/j.pharmthera.2005.05.010. [DOI] [PubMed] [Google Scholar]
- 6.Zhang Y, Zhang L, Abraham S, Apparaju S, Wu TC, Strong JM, et al. Assessment of the impact of renal impairment on systemic exposure of new molecular entities: evaluation of recent new drug applications. Clin Pharmacol Ther. 2009;85:305–11. doi: 10.1038/clpt.2008.208. [DOI] [PubMed] [Google Scholar]
- 7.Draft guidance for industry: pharmacokinetics in patients with impaired renal function—study design, data analysis, and impact on dosing and labeling (2010). Available from: www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/ucm204959.pdf.
- 8.Zhao P, Zhang L, Grillo JA, Liu Q, Bullock JM, Moon YJ, et al. Applications of physiologically based pharmacokinetic (PBPK) modeling and simulation during regulatory review. Clin Pharmacol Ther. 2011;89:259–67. doi: 10.1038/clpt.2010.298. [DOI] [PubMed] [Google Scholar]
- 9.Edginton AN, Willmann S. Physiology-based simulations of a pathological condition: prediction of pharmacokinetics in patients with liver cirrhosis. Clin Pharmacokinet. 2008;47:743–52. doi: 10.2165/00003088-200847110-00005. [DOI] [PubMed] [Google Scholar]
- 10.Johnson TN, Boussery K, Rowland-Yeo K, Tucker GT, Rostami-Hodjegan A. A semi-mechanistic model to predict the effects of liver cirrhosis on drug clearance. Clin Pharmacokinet. 2010;49:189–206. doi: 10.2165/11318160-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 11.Belpaire FM, Rosseel MT, Vermeulen AM, De Smet F, Bogaert MG. Stereoselective pharmacokinetics of atenolol in the rat: influence of aging and of renal failure. Mech Ageing Dev. 1993;67:201–10. doi: 10.1016/0047-6374(93)90123-9. [DOI] [PubMed] [Google Scholar]
- 12.Mukai H, Morino A. Effects of renal insufficiency and aging on the pharmacokinetics of a phenethylamine class alpha(1A)-adrenoceptor agonist NS-49. Int J Pharm. 1999;185:37–43. doi: 10.1016/S0378-5173(99)00142-8. [DOI] [PubMed] [Google Scholar]
- 13.Rowland Yeo K, Aarabi M, Jamei M, Rostami-Hodjegan A. Modeling and predicting drug pharmacokinetics in patients with renal impairment. Expert Rev Clin Pharmacol. 2011;4:261–74. doi: 10.1586/ecp.10.143. [DOI] [PubMed] [Google Scholar]
- 14.Zhao P, Vieira Mde L, Grillo JA, Song P, Wu TC, Zheng JH, et al. Evaluation of exposure change of nonrenally eliminated drugs in patients with chronic kidney disease using physiologically based pharmacokinetic modeling and simulation. J Clin Pharmacol. 2012;52(1 Suppl):91S–108. doi: 10.1177/0091270011415528. [DOI] [PubMed] [Google Scholar]
- 15.Strougo A, Yassen A, Krauwinkel W, Danhof M, Freijer J. A semiphysiological population model for prediction of the pharmacokinetics of drugs under liver and renal disease conditions. Drug Metab Dispos. 2011;39:1278–87. doi: 10.1124/dmd.110.037838. [DOI] [PubMed] [Google Scholar]
- 16.Akabane T, Tabata K, Kadono K, Sakuda S, Terashita S, Teramura T. A comparison of pharmacokinetics between humans and monkeys. Drug Metab Dispos. 2010;38:308–16. doi: 10.1124/dmd.109.028829. [DOI] [PubMed] [Google Scholar]
- 17.Nakamori F, Naritomi Y, Hosoya K, Moriguchi H, Tetsuka K, Furukawa T, et al. Quantitative prediction of human intestinal glucuronidation effects on intestinal availability of UDP-glucuronosyltransferase substrates using in vitro data. Drug Metab Dispos. 2012;40:1771–7. doi: 10.1124/dmd.112.045476. [DOI] [PubMed] [Google Scholar]
- 18.Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J Pharm Sci. 2002;91:129–56. doi: 10.1002/jps.10005. [DOI] [PubMed] [Google Scholar]
- 19.Davies B, Morris T. Physiological parameters in laboratory animals and humans. Pharm Res. 1993;10:1093–5. doi: 10.1023/A:1018943613122. [DOI] [PubMed] [Google Scholar]
- 20.Sayama H, Komura H, Kogayu M, Iwaki M. Development of a hybrid physiologically based pharmacokinetic model with drug-specific scaling factors in rat to improve prediction of human pharmacokinetics. J Pharm Sci. 2013;102:4193–204. doi: 10.1002/jps.23726. [DOI] [PubMed] [Google Scholar]
- 21.Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94:1259–76. doi: 10.1002/jps.20322. [DOI] [PubMed] [Google Scholar]
- 22.Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95:1238–57. doi: 10.1002/jps.20502. [DOI] [PubMed] [Google Scholar]
- 23.Dreisbach AW, Lertora JJ. The effect of chronic renal failure on drug metabolism and transport. Expert Opin Drug Metab Toxicol. 2008;4:1065–74. doi: 10.1517/17425255.4.8.1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kwong TC. Free drug measurements: methodology and clinical significance. Clin Chim Acta. 1985;151:193–216. doi: 10.1016/0009-8981(85)90082-8. [DOI] [PubMed] [Google Scholar]
- 25.Inui KI, Masuda S, Saito H. Cellular and molecular aspects of drug transport in the kidney. Kidney Int. 2000;58:944–58. doi: 10.1046/j.1523-1755.2000.00251.x. [DOI] [PubMed] [Google Scholar]
- 26.Leblond F, Guévin C, Demers C, Pellerin I, Gascon-Barré M, Pichette V. Downregulation of hepatic cytochrome P450 in chronic renal failure. J Am Soc Nephrol. 2001;12:326–32. doi: 10.1681/ASN.V122326. [DOI] [PubMed] [Google Scholar]
- 27.Leblond FA, Petrucci M, Dubé P, Bernier G, Bonnardeaux A, Pichette V. Downregulation of intestinal cytochrome p450 in chronic renal failure. J Am Soc Nephrol. 2002;13:1579–85. doi: 10.1097/01.ASN.0000017575.50319.77. [DOI] [PubMed] [Google Scholar]
- 28.Naud J, Michaud J, Boisvert C, Desbiens K, Leblond FA, Mitchell A, et al. Down-regulation of intestinal drug transporters in chronic renal failure in rats. J Pharmacol Exp Ther. 2007;320:978–85. doi: 10.1124/jpet.106.112631. [DOI] [PubMed] [Google Scholar]
- 29.Komura H, Iwaki M. In vitro and in vivo small intestinal metabolism of CYP3A and UGT substrates in preclinical animals species and humans: species differences. Drug Metab Rev. 2011;43:476–98. doi: 10.3109/03602532.2011.597401. [DOI] [PubMed] [Google Scholar]
- 30.Shitara Y, Maeda K, Ikejiri K, Yoshida K, Horie T, Sugiyama Y. Clinical significance of organic anion transporting polypeptides (OATPs) in drug disposition: their roles in hepatic clearance and intestinal absorption. Biopharm Drug Dispos. 2013;34:45–78. doi: 10.1002/bdd.1823. [DOI] [PubMed] [Google Scholar]
- 31.Huang SM, Abernethy DR, Wang Y, Zhao P, Zineh I. The utility of modeling and simulation in drug development and regulatory review. J Pharm Sci. 2013;102:2912–23. doi: 10.1002/jps.23570. [DOI] [PubMed] [Google Scholar]
- 32.Zhang L, Pfister M, Meibohm B. Concepts and challenges in quantitative pharmacology and model-based drug development. AAPS J. 2008;10:552–9. doi: 10.1208/s12248-008-9062-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF 70.1 kb)


