Cardiac Electrophysiological Dynamics From the Cellular Level to the Organ Level

Abstract

Cardiac alternans describes contraction of the ventricles in a strong-weak-strong-weak sequence at a constant pacing frequency. Clinically, alternans manifests as alternation of the T-wave on the ECG and predisposes individuals to arrhythmia and sudden cardiac death. In this review, we focus on the fundamental dynamical mechanisms of alternans and show how alternans at the cellular level underlies alternans in the tissue and on the ECG. A clear picture of dynamical mechanisms underlying alternans is important to allow development of effective anti-arrhythmic strategies.

Introduction

The cardiac action potential is the single cellular level electrical signal that triggers contraction of the heart.1 Under normal conditions, the originating activation signal comes from a small bundle of tissue in the right atrium called the sinoatrial node (SAN). The action potentials generated by the SAN initiate an excitatory wave that, in healthy tissue, propagates smoothly through a well-defined path and causes excitation and contraction in the ventricles. In disease states, the normal excitation pathway is disrupted and a variety of abnormal rhythms can occur, including cardiac alternans, a well-known precursor to sudden cardiac death.

Cardiac alternans was initially documented in 1872 by a German physician, Ludwig Traube.2 He observed contraction of the ventricles in a strong-weak-strong-weak sequence even though the pacing frequency was constant. Clinically, alternans manifests as alternation of the T-wave on the ECG, typically in the microvolt range. It is well established that individuals with microvolt T-wave alternans are at much higher risk for arrhythmia and sudden cardiac death.3–7 In this review, we focus on the fundamental dynamical mechanisms of alternans and show how alternans at the cellular level underlies alternans in the tissue and on the ECG. A clear picture of physiological mechanisms underlying alternans is important to allow development of effective anti-arrhythmic drugs. It is also important to understand dynamical mechanisms because while the cardiac action potential is composed of multiple currents, each of which confers specific properties, revelation of dynamical mechanisms provides a unified fundamental view of the emergent phenomena that holds independently of specific current interactions. By analogy, in classical mechanics, the equation describing motion is independent of the properties and material of the car, boat, dog etc. under study. The same is true for the dynamics of alternans, which can originate at the cellular or subcellular level in the cardiac ventricular myocyte.

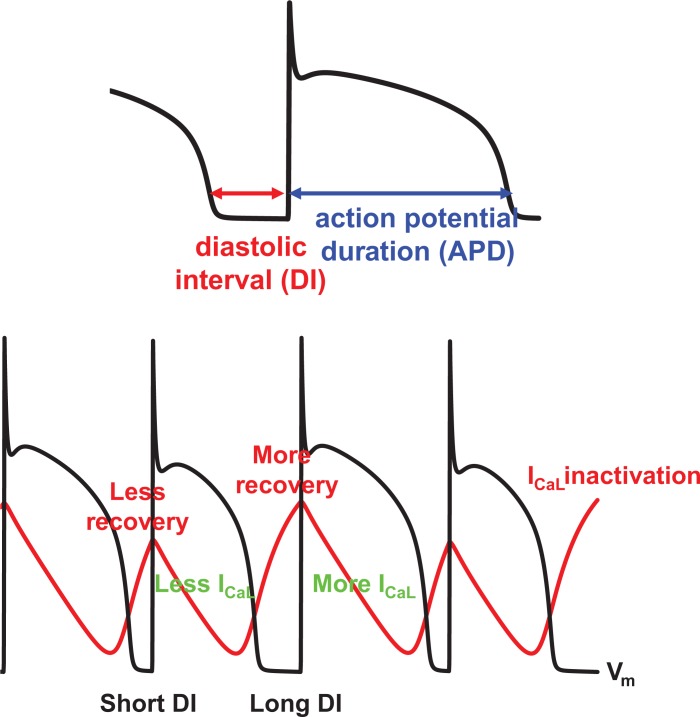
The ventricular myocyte is an excitable cell providing the cellular level electrical activity that underlies cardiac contraction. Under resting conditions, the membrane potential is about −80 mV. When the cell is stimulated, sodium (Na) channels open and the membrane potential goes above 0 mV. Then, a few ms later, the inward current L-type calcium (Ca) current activates and maintains depolarization of the membrane potential. During this action potential plateau, several types of outward current potassium (K) channels also activate. Depending on the balance between inward and outward currents, the action potential duration (APD) is determined. The diastolic interval (DI) that follows cellular repolarization describes the duration the cell resides in the resting state until the next excitation. During the DI, channels recover with kinetics determined by intrinsic time constants. APD restitution defines the relationship between the APD and the previous DI (Fig. 1 top panel). In most cases1, the APD becomes longer as the previous DI becomes longer due to recovery of the L-type Ca channel (Fig. 1, bottom panel), and thus the APD restitution curve has a positive slope.

Figure 1.

(Top): APD and DI. (Bottom): The physiological mechanism of APD alternans involves recovery from inactivation of I_CaL.

Action Potential Duration Restitution

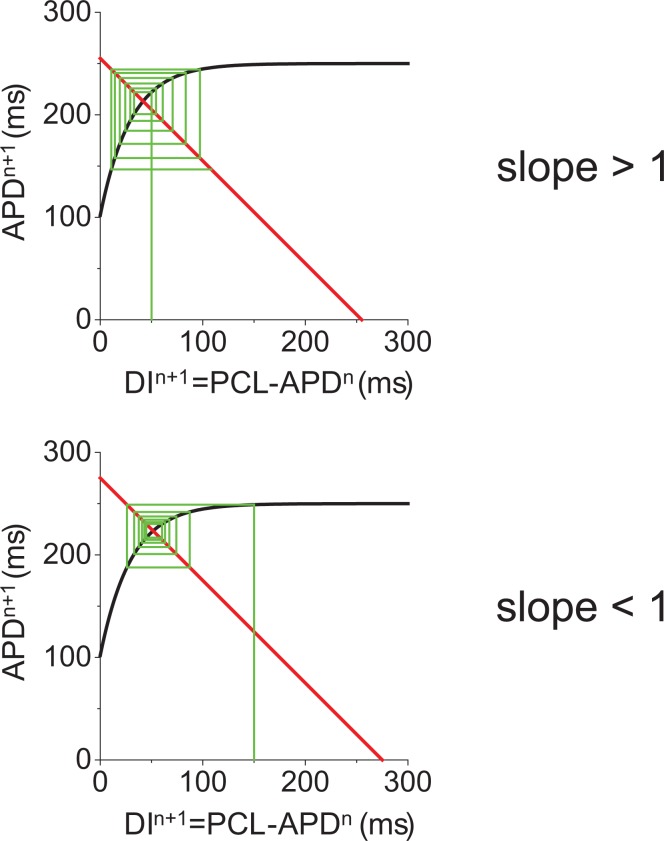
In 1968 Nolasco and Dahlen showed graphically that APD alternans occurs when the slope of the APD restitution curve exceeds unity.8 Why is the steepness of the slope important? As shown graphically in Figure 2, APD alternans amplitude is multiplied by the slope of the APD restitution curve in each cycle. If the slope is less than one, let’s say 0.9, then, any alternans will attenuate (i.e. 0.9*0.9*0.9 … goes to 0). On the other hand, when the slope is larger than one, then the alternans amplitude will be amplified until the average slope reaches 1 or the cell shows a 2:1 stimulus to response ratio. Although APD restitution is useful, there are cases that cannot be explained by APD restitution alone. For example, APD alternans has been shown to occur even when the slope is less than one.9 Also there are cases when APD alternans does not occur even when the slope is larger than one.10,11 The one-dimensional mapping between APD and DI also fails to explain quasi-periodic oscillation of the APD.12,13

Figure 2.

APD restitution and dynamical mechanism of APD alternans.

Calcium Driven Alternans

A strong-weak-strong-weak oscillation in contraction implies that the Ca transient (CaT) is alternating. Until 1999 it was assumed that if the APD is alternating then the CaT alternates because the CaT follows APD changes. However, Chudin et al showed that CaT can alternate even when APD is kept constant during pacing with a periodic AP clamp waveform.14 This implies that the intracellular Ca cycling has intrinsic nonlinear dynamics. A critical component in this process is the sarcoplasmic reticulum (SR), a subcellular organelle that stores Ca inside the cell. When Ca enters a cell through the L-type Ca channel (or reverse mode Na-Ca exchanger (NCX),15,16 ryanodine receptors open and large Ca releases occur from the SR (Ca induced Ca release).17 The amount of Ca release steeply depends on SR Ca load.18,19 This steep relation between Ca release and SR Ca load is the key to induce CaT alternans.20 A one-dimensional map between Ca release and SR calcium load can be constructed to describe the relationship21 similar to the map used in APD restitution.

Subcellular Alternans

A number of experimental and computational studies have been undertaken to identify molecular mechanisms of CaT alternans by identifying the specific components in the calcium cycling process critical to formation of CaT alternans. These components include SR Ca leak and load, Ca spark frequency and amplitude, and rate of SR refilling. For example, experiments have shown that alternation in diastolic SR Ca is not required for CaT alternans.24 In addition, stochastic openings of ryanodine receptors (RyR) lead to Ca sparks that occur randomly, not in an alternating sequence that would be expected to underlie Ca alternans. So, how do local random sparks and constant diastolic SR calcium load lead to global CaT alternans? Mathematical models with detailed representations of subcellular Ca cycling have been developed in order to elucidate the underlying mechanisms.22,23 Modeling studies have shown that even when SR Ca load is not changing, RyRs, which are analogous to I_CaL in APD alternans, recover gradually from refractoriness. As RyR availability increases (for example during a long diastolic interval) a single Ca spark from a RyR will be larger in amplitude and recruit neighboring Ca release units to generate more sparks. The large resultant CaT causes depletion of the SR and when complete recovery of RyRs does not occur prior to the arrival of the next stimulus, the subsequent CaT will be small. This process results in an alternans of CaT amplitude from beat-to-beat.

Coupling Between the Membrane Potential and Subcellular Calcium Dynamics

Importantly, the membrane voltage and intracellular Ca cycling are coupled via Ca sensitive channels such as the L-type Ca channel and the sodium-calcium exchanger (NCX). The membrane voltage dynamics and the intracellular Ca dynamics are bi-directionally coupled.27 One direction is from voltage to Ca. As the DI becomes longer, the CaT usually becomes larger since the recovery time for the L-type Ca channel in increased and the SR Ca release becomes larger. The other direction is from Ca to voltage. Here we consider two major currents, NCX and I_CaL. As the CaT becomes larger, forward mode NCX becomes larger and prolongs APD. On the other hand, as the CaT becomes larger, I_CaL becomes smaller due to Ca-induced inactivation, and thus, larger CaT shortens the APD. Therefore, depending on which current dominates, larger CaT can prolong or shorten APD. If a larger CaT prolongs (shortens) the APD, then the coupling is positive (negative).27 The coupled dynamics of the membrane voltage and the intracellular Ca cycling can be categorized by the instability of membrane voltage (steep APD restitution), instability of the intracellular Ca cycling (steep relation between Ca release versus SR Ca load), and the coupling (positive or negative).27 If the coupling is positive, alternans is electromechanically concordant (long-short-long-short APD corresponds to large-small-large-small CaT sequence) regardless of the underlying instability mechanism. On the other hand, if the coupling is negative, alternans is electromechanically concordant in a voltage-driven regime. However, if alternans is Ca driven, alternans becomes electromechanically discordant (long-short-long-short APD corresponds to small-large-small-large CaT sequence). It is also possible to induce quasi- periodic oscillation of APD and CaT when voltage and Ca instabilities contribute equally.27

Alternans in Higher Dimensions

Tissue level alternans in APD28 and CaT29 also occur and here we describe how the dynamical mechanism of alternans at the single cell level determines the phenomena in tissue. Spatially discordant alternans (SDA) where APDs in different regions of tissue alternate out-of-phase, is more arrhythmogenic since it causes large gradients of refractoriness and wave-break, which can initiate ventricular tachycardia and ventricular fibrillation.28 How is SDA induced?

As the APD is a function of the previous DI, conduction velocity (CV) is also function of the previous DI (CV restitution)30,31 since the action potential propagation speed depends on the availability of the sodium channel. As the DI becomes shorter, sodium channels have less time to recover. Therefore, in general, as the DI becomes shorter, the CV becomes slower. When tissue is paced rapidly, action potentials propagate slowly near the stimulus, and thenaccelerate downstream as the DI becomes longer. This causes heterogeneity in APD (APD is shorter near the stimulus). During the following tissue excitation, APD becomes longer and the CV becomes faster at the pacing site then gradually APD becomes shorter and the CV becomes slower. The interaction between steep APD restitution and steep CV restitution creates SDA.30–33 This mechanism applies only when the cellular instability is voltage driven.

When the cellular instability is Ca driven, the mechanism of SDA formation is different. If the voltage-Ca coupling is negative, SDA can form without steep APD and CV restitution.34 The mechanism can be understood as follows. First, when cells are uncoupled, alternans of APD and Ca are electromechanically discordant. If two cells are alternating in opposite phases, once these cells are coupled by voltage, due to electrotonic coupling, the membrane voltage of both cells is synchronized and thus APD becomes the same. This synchronization of APD amplifies the difference of CaT between two cells (Fig. 5 in).34 In other words, it desynchronizes CaT2. This instability mechanism is also found in subcellular SDA.35

In the case where the instability is Ca driven and the coupling is positive, there are several interesting distinctive phenomena that can occur. First, the profile of SDA of Ca contains a much steeper gradient at the node (point in space where no alternans occurs–cells downstream of the node are alternating out of phase with those upstream of the node) compared to the case of voltage driven SDA.36 Thus, the cellular mechanism of instability can be identified by evaluating the steepness of the alternans amplitude gradient in space around the node. When the cellular instability is voltage driven, the steady-state wavelength (separation of nodes in space) depends on electrotonic coupling between cells and the steepness of APD and CV restitution, regardless of the initial conditions. However, if the cellular instability is Ca driven, the location of nodes depends on the pacing history, which includes pacing cycle length and other parameters affected by pacing frequency. In this case, once the node is formed, the location of the node may be fixed, especially when Ca instability is strong.37 Such anex planation may apply to recent experimental results.38

Summary

In this review, we described how the origin of alternans at the cellular level (voltage driven, Ca drive, coupling between voltage and Ca) affects the formation of spatially discordant alternans at the tissue level. Cardiac alternans is a multi-scale emergent phenomenon. Channel properties determine the instability mechanism at the cellular level. Alternans mechanisms at cellular level determine SDA patterns at the tissue level. In order to understand alternans and develop anti-arrhythmic drug and therapy, multi-scale modeling of the heart is useful,39–41 which is increasingly enabled by emerging technologies such as general-purpose computing on graphics processing units (GPGPU)42 and cloud computing.

Glossary

Abbreviations

APD

action potential duration

Ca

calcium

CaT

calcium transient

CV

conduction velocity

ECG

Electrocardiogram

GPGPU

general-purpose computing on graphics processing units

K

potassium

Na

sodium

NCX

sodium-calcium exchanger

RyR

ryanodine receptor

SAN

sinoatrial node

SDA

spatially discordant alternans

SR

sarcoplasmic reticulum