Complex Pathways in Folding of Protein G Explored by Simulation and Experiment

Abstract

The B1 domain of protein G has been a classic model system of folding for decades, the subject of numerous experimental and computational studies. Most of the experimental work has focused on whether the protein folds via an intermediate, but the evidence is mostly limited to relatively slow kinetic observations with a few structural probes. In this work we observe folding on the submillisecond timescale with microfluidic mixers using a variety of probes including tryptophan fluorescence, circular dichroism, and photochemical oxidation. We find that each probe yields different kinetics and compare these observations with a Markov State Model constructed from large-scale molecular dynamics simulations and find a complex network of states that yield different kinetics for different observables. We conclude that there are many folding pathways before the final folding step and that these paths do not have large free energy barriers.

Introduction

The B1 domain of protein G is one of the best-studied model systems of protein folding. Although it is fairly small and therefore accessible to various types of computational modeling, it has a mixed secondary structure, high stability, and relatively slow folding kinetics that make it comparable with much larger proteins. Previous measurements of folding kinetics on the millisecond timescale have found Arrhenius-type kinetics that suggest a simple two-state folding picture (1), but the presence of nonlinearity in some measurements of the folding chevron plot have led some to argue the presence of an intermediate state (2,3). One folding study with submillisecond time resolution found a kinetic process ∼ 500 μs (4). This study used ultra-rapid mixing with a dead-time of 170 μs and one type of folding probe, tryptophan (Trp) fluorescence, so it is unlikely that anything but a single intermediate could be determined. In this study we have reexamined the folding of this protein using mixers that mix up to 20 times faster and a variety of folding probes that yield a much more complex folding picture on the submillisecond timescale. Additionally, we investigated the folding of this protein by using a Markov State Model (MSM) built on ∼ 50 ms of molecular dynamics (MD) simulations. Models such as the one presented have been successful at comparing with experiment and providing atomic-level detail of folding reactions (5–7). From the perspective of multiple experimental probes as well as the simulations, protein G cannot be said to be a simple two- or three-state folder.

Materials and Methods

Protein expression and purification

The plasmids were transformed into BL21(DE3) Escherichia coli (E. coli) cells for expression. A single colony was picked from the transformants, grown in 5.0 mL starter cultures, inoculated into 1L cultures and incubated for ∼ 17 h in the presence of ampicillin. Protein expression was induced by 1.0 mM isopropyl-β-D thiogalacoside (IPTG), followed by incubation for an additional ∼ 6 h. The cells were harvested by centrifugation for 20 min at 4000 rpm and 4°C, and the pellets resuspended in buffer (50 mM NaH₂PO₄, 300mM NaCl, 20mM imidazole, 5mM β-mercaptoethanol) at pH 8.0, 4°C. The cells were lysed with a Misonix 3000 Sonicator (Farmingdale, NY), and pelleted at 12,000 rpm for 20 min at 4°C. The protein was purified by anion-exchange chromatography and by gel filtration on a Hi-Prep 16/60 Sephacryl S200 column. For most experiments the protein was buffer-exchanged into a solution of 100 mM potassium phosphate at pH 7 and 6 M GdnHCl. The protein concentration was 100 μM for fluorescence and fast photochemical oxidation of protein (FPOP) experiments and 1 mM for circular dichroism (CD) experiments.

Microfluidic mixer fabrication

The basic design of the “T” mixer was first described by Knight et al. (8) and was optimized by Hertzog et al. (9). This design takes advantage of small channel dimensions to keep the dynamics in the laminar flow regime, even for high velocities, resulting in mixing times of as low as 8 μs (10,11). However, some data were collected with lower flow rates and longer mixing times to achieve a longer observation time. The observation channel is 10-μm wide and 500-μm long. The fluid dynamics in the chip are simulated with Comsol Multiphysics (Comsol, Stockholm, Sweden). The channels were etched in 500-μm-thick fused silica wafers using reactive ion etching with polysilicon as a mask. Inlet and outlet holes were drilled with a diamond-tipped drill. The channels were first prebonded to a 170-μm-thick fused silica wafer after a reverse RCA cleaning, and then fused together at 1100°C. The mixer is mounted on a manifold, which contains solution reservoirs for each channel in the chip. The flow rate of each channel is controlled by air pressure above the reservoir using computer-controlled pressure transducers (Marsh Bellofram Type 2000, Newell, WV). At the fastest flow rates reported, the sample consumption is ∼ 4 μL/h of the protein and 400 μL/h of folding buffer.

To measure circular dichroism, a larger mixer was used, which completely mixes the buffer and protein solution in a larger volume. The “serpentine” mixer relies on chaotic advection in the laminar flow regime to mix three streams as they turn multiple corners (12). Fabrication is the same as described above for the T-mixer except the final depth was 20 μm. Solutions were fed by two computer-controlled syringe pumps (KDS200, KD Scientific, Holliston, MA). The mixing time was ∼ 300 μs and the total flow rate was 250 μL/min.

Folding of the B1 domain of protein G was prompted by dilution of 6 M GdnHCl. In the T-mixer the mixing time was ∼ 8 μs and dilution of denaturant was 100× (10,11,13). In the serpentine mixer the mixing time was ∼ 300 μs and the dilution of both protein and denaturant was 5× (6,14). Folding was then monitored from the earliest observable time to 1 to 4 ms, depending on the type of measurement.

Tryptophan fluorescence

The UV fluorescence of a folding protein is monitored with a specially designed confocal microscope (15). An Argon-Ion laser (Lexel Laser 95-SHG, Lexington, KY) at 257 nm enters an inverted microscope (Olympus IX51, Melville, NY) as a collimated beam and is focused to a 1-μm spot by a 0.5 NA UV objective (OFR 40x-266, Newton, NJ) inside the mixer. For a linear flow speed of 1 m/s, the 1-μm spot results in a maximum time resolution of 1 μs. Fluorescence intensity is collected by the same objective and sent through a dichroic mirror (Chroma 300dclp, Brattleboro, VT) to a photon counter (Hamamatsu H7421-40, Hamamatsu City, Japan). The mixer manifold is mounted on a three-axis piezoelectric scanner (Mad City Labs Nano-LP100, Madison, WI), which scans the chip over the objective 100 μm in each direction and a motorized microscope stage (Semprex, Campbell, CA) that moves the chip by 80 μm down the channel.

A typical experiment begins with a scan of the exit channel imaged by the photon counter to locate the 100 nm jet of fluorescent protein. The chip is typically scanned 10 μm across the exit channel and 500 μm down the linear section of the exit channel. This corresponds to ∼ 500 μs of folding time at an initial flow rate of 1 m/s without substantial diffusion of the protein out of the jet. Alternatively, long time courses can be obtained by slowing the flow rate to as low as 0.125 m/s. The overall intensity as a function of time can be obtained from a scan by averaging the fluorescence intensity of the jet in ∼ 1 μm regions, the size of the excitation beam. To correct for a large decrease in fluorescence in the mixing region because of formation of the protein jet, a control experiment is performed in which the protein in 6 M GdnHCl is mixed with 6 M GdnHCl and the fluorescence observed. This trace is divided point-by-point into the folding trace, as shown in Figs. 1 A and B.

Figure 1.

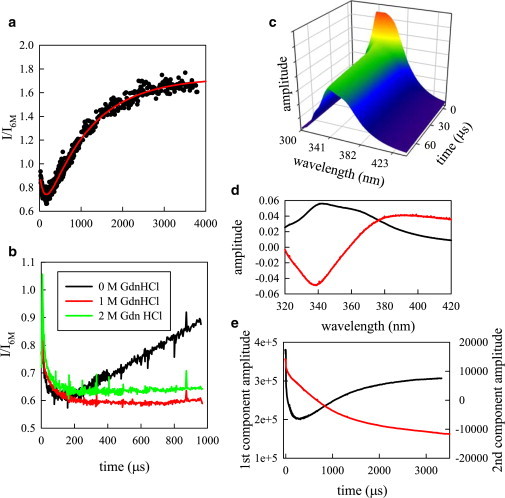
Folding kinetics of protein G as measured by Trp fluorescence. (A) Fluorescence in 0 M GdnHCl scaled to the unfolded protein (in 6 M GdnHCl) as measured by the photon counter (black points). Measurements made with three flow rates (1, 0.5, and 0.125 m/s) are overlaid. The red line is a fit to two exponentials with opposing amplitudes. (B) Fluorescence scaled to the unfolded protein for three final concentrations of denaturant. When fitted to a single exponential, the fast decay time constants are 74 μs (red) and 42 μs (green). (C) Time-resolved fluorescence emission as measured by the spectrograph and charged coupled device (CCD). (D) Two most significant spectral components determined by singular value decomposition (SVD). The first component (black line) is the average spectrum of all measurements and the second component (red line) is the blue shift of the spectrum as the protein folds. (E) Time resolved amplitudes of the first (black) and second (red) SVD components. To see this figure in color, go online.

Fast photochemical oxidation of protein

The setup of FPOP is similar to the fluorescence experiment (16). The protein in 6 M GdnHCl was flowed through the center channel and mixed with potassium phosphate buffer from the side channel to initiate folding. In addition, 15 mM hydrogen peroxide was added into the side channels to provide hydroxyl radicals. To reduce the OH radical lifetime to ∼ 1 μs, glutamine was added in both center and side channels as a scavenger (17). The glutamine concentration was 2 mM for flow rates of 1 m/s and 20 mM for flow rates of 0.5 m/s. The 258 nm laser with ∼ 5 mW power was focused onto a 1-μm diam. region of flow jet inside the exit channel of mixer. Within the laser focus hydrogen peroxide was photolyzed to produce hydroxyl radicals and exposed amino acid residues of protein were oxidatively modified. The laser sat at the same spot on the jet for a period of time, depending on the flow rate, to accumulate enough labeled protein for analysis. The 100 μL solution was collected in 20 min at a flow rate of 1 m/s. The laser was then moved to another position and another sample was collected. Each sample was collected in an Eppendorf tube containing 20 μL of 100 nM catalase and 70 mM methionine to remove excess H₂O₂ after FPOP. The sample was left at room temperature for 10 min before storing at 5°C to allow the complete decomposition of hydrogen peroxide by catalase. The samples were desalted and concentrated with a C18 ZipTip before mass spectrometry analysis.

A Waters (Milford, MA) Quattro Premier mass spectrometer was coupled to a Acquity HPLC system. A Waters Symmetry Beta Basic CN column (10 × 1 mm, 5-μm particle size) was used at room temperature. The injection volume was 10 to 20 μL, and the HPLC flow rate was 0.1 mL/min achieved by using the gradient from 2% acetonitrile (98% water) with 0.1% formic acid to 75% acetonitrile over 12 min, then back to 2% acetonitrile followed by a 3-min reequilibration step. Mass spectra were acquired by using electrospray ionization in the positive ion mode. The capillary voltage, extractor voltage, and cone voltage were set at 3.17 kV, 5 V, and 25 V, respectively. The flow rates of the cone gas and desolvation gas were 30 and 600 L/h, respectively. The source temperature and desolvation temperature were 120 and 350°C, respectively. Data were acquired with MassLynx 4.1 and processed for calibration and for quantification of the analytes with QuanLynx software, Millford MA.

Circular dichroism

For measurement of circular dichroism an instrument was constructed with similar design to some commercial instruments but with accommodations for the mixing chip. Light from a 150 Watt xenon arc lamp (Newport model 6254, Irvine, CA) housed inside a Newport Oriel Universal Arc Lamp Housing (model 67005) and connected to a Newport Universal Arc Lamp Power Supply (model 69907), was passed through a Cornerstone 260, 1/4 meter monochrometer tuned to the desired wavelength. The unpolarized light was then linearly polarized by a Rochon prism (CVI Laser Corp., Albuquerque, NM) and converted to circularly polarized light after passing through a photoelastic modulator (Hinds Instruments PEM 100 Controller, Hillsboro, OR). The oscillation of the photoelastic modulator produces both right and left circularly polarized light once per cycle (f = 50 kHz). The polarized light is focused onto the exit channel of the mixing chip with a 25-mm lens, captured and collimated with a 35-mm lens, and finally focused with a 20-mm lens onto a Hinds Instruments Avalanche Photodiode Detector (model APD-100) and a Stanford Research SR810 DSP lock-in amplifier (Stanford Research Systems, Sunnyvale, CA). The ellipticity was determined from the ratio of the AC and DC components of the detected signal. The mixing chip was mounted on a New Focus (Santa Clara, CA) Closed Loop Picometer Driver computer-controlled two-dimensional translation stage to position the exit channel in front of the beam at different distances from the mixing region.

Molecular dynamics simulation

Molecular dynamics (MD) simulations of the B1 domain of protein G were run using the GROMACS (18,19) molecular dynamics package on the Folding@home distributed computing network (20). The amber96 force field (21,22) was used with a GB/SA implicit solvent model (23). Covalent bonds involving hydrogen were constrained using the LINCS algorithm (24). Roughly half the simulations were begun from an extended chain and the other half from the crystal structure (PDBID: 1GB1) (25). A Langevin integrator was used at 370 K with a timestep of 2 fs. Snapshots were saved every nanosecond. A total of 4600 trajectories (each of which were at least 5-ms long) were collected for an aggregate simulation time of 50 ms. The terminal oxygen was dropped in half of the simulations, leading to a -1 charge rather than a -2 charge, but this difference should be minimal.

Markov state model construction and analysis

An MSM was used to analyze the simulations. Briefly, an MSM attempts to model a protein’s dynamics as a memory-less jump process between discrete regions in phase space (26,27). There are two components to the construction process: 1), define the discrete states given the dataset and 2), estimate the probability of transition from each state to any other states in some time, τ (referred to as the lag time). The MSMs discussed herein were built using the MSMBuilder package (27).

To define the state space, each conformation was represented as a single vector whose entries corresponded to the distance between all possible residue pairs. This distance was taken to be the minimum distance between the two residues’ heavy atoms. Only residue pairs separated by at least two other residues were considered. This representation was then analyzed using the time-structure-based independent component analysis (tICA) to determine the linear combination of residue-residue distances that decorrelated the slowest. This method is analogous to principal component analysis (PCA) but maximizes the autocorrelation function of a projection rather than that projection’s explained variance (28).

By only considering the top N solutions to the tICA problem (tICs), conformations can be represented in a coordinate system that separates conformations along the slowest decorrelating degrees of freedom. Many state decompositions were built by using the k-centers clustering algorithm in the reduced tICA subspace of at most 18 tICs. A model built with 25,000 states and six tICs was used for calculating the experimental observable time-traces, and a 20-state model built using Ward clustering (29) on a tenth of the trajectories and six tICs was used to generate the free energy surface. The 25,000 state model was built using the sliding window approach for counting transitions, whereas the 20-state model was built without sliding window. For a discussion of the pros and cons of sliding window, refer to Prinz et al. (26).

To judge the quality of the MD dataset, we can compare MSMs built on subsets of the trajectories. The 20-state model was built on only 10% of the trajectories but exhibited a folding timescale similar to the timescale calculated in the 25,000-state model (300 μs versus 900 μs). This is evidence that the dataset has at least sampled the timescales in the 100s of microsecond regime.

Once the state space is defined, the transition probabilities (i.e., the probability of transferring to a state j given from a state i) were calculated using a maximum likelihood estimator described in Beauchamp et al. (27). This transition matrix, T, determines the dynamics of the system. The characteristic relaxation timescales (t_i) are given as follows:

$$t_i=-\frac{\tau }{\log {\lambda }_i},$$

where τ is the lag time (the time between transitions in the MSM) and λ_i is the i^th eigenvalue of the transition matrix. These timescales correspond to global relaxations in the state space toward the equilibrium distribution. For example, in folding simulations the slowest timescale generally corresponds to transitions between unfolded states and the folded state.

The transition matrix can be used to transform a distribution over states, p_t, to a new distribution, p_t+τ, determined by the individual transition probabilities from each state. This process can be written entirely in terms of the eigenvalues and left $\left({\varphi }_i\right)$ and right $\left({\psi }_i\right)$ eigenvectors of T as follows:

$$\begin{array}{c}{p}_{t+\tau }=p_0{T}^n\\ =\sum _{i=1}^{\text{∞}}{\lambda }_i^n\left(p_0\cdot {\psi }_i\right){\varphi }_i\\ =\sum _{i=1}^{\text{∞}}\exp \left[-\frac{n\tau }{t_i}\right]\left(p_0\cdot {\psi }_i\right)\left({\varphi }_i\right)\end{array}$$

These probability distributions can be calculated for many time points and used to simulate an experiment. For example, the solvent accessible surface area of Trp43 was computed for every snapshot in the dataset. For each state in the MSM, the average Trp43 solvent accessible surface area (SASA) was computed. By computing the ensemble average Trp43 SASA according to $p_{t+\tau }$, we can compute the average Trp43 SASA of the ensemble as a function of time (let the vector r be the average Trp43 SASA for each state) as follows:

$$\begin{array}{c}{\langle r\rangle }_{p_{t+n\tau }}=r\cdot p_{t+n\tau }\\ ={\sum }_{i=1}^{\text{∞}}\exp \left[-\frac{n\tau }{t_i}\right]\left(p_0\cdot {\psi }_i\right)\left({\varphi }_i\cdot r\right)\end{array}$$

As given by the above equation, the ensemble average is a sum of single exponential terms, whose timescales are governed by the MSM’s eigenvalues and amplitudes by the dot product of the initial distribution with the right eigenvector and a particular observable’s projection onto the left eigenvector.

For the results discussed herein the initial distribution was defined by states whose root mean square deviation (RMSD) was greater than 4 nm from the folded state defined by PDBID 1GB1 (25). As can be seen above, the starting distribution will affect the relative exponential amplitudes but not their timescales. The qualitative behavior (e.g., amplitude signs) did not change significantly when adjusting the initial distribution by changing the 4-nm cutoff, or by using a cutoff based on the radius of gyration.

The define secondary structure of proteins (DSSP) program (30) was used to assign secondary structural elements to each residue in each conformation. Residues assigned an “H” (helix) were considered helical, and those assigned a “B” (isolated beta bridge) or an “E” (extended beta strand) were considered to be in sheets.

Results

Multiple experiments reveal multi-exponential relaxations for the folding of WT protein G

Trp fluorescence was monitored by both total intensity and its full emission spectrum. Upon dilution, the total intensity decreased within 100 μs and then rose to the native intensity over 4 ms (Fig. 1 A). The intensity was also monitored for folding reactions in a higher concentration of denaturant. This change in denaturant had little effect on the fast decay, however the slow rise in fluorescence became significantly slower (Fig. 1 B). The final folding step has previously been observed to depend on denaturant (1,4,31), which is consistent with the slow rise observed here. These observations are consistent with those reported by Park et al., using a slower mixer and different solvent conditions though the timescales reported in this study are slightly faster (4).

The full time-resolved emission spectrum (Fig. 1 C) was analyzed by singular value decomposition (SVD), which had two significant components (Fig. 1 D and E). The first component is the average spectrum that exhibits kinetics identical to those seen by measuring total fluorescence in the photon counter. The second component is the difference spectrum between the average spectrum and the spectrum at each time point. The dispersion shape shows how the spectrum shifts to lower wavelengths as the protein folds. This shift occurred with two phases. The slow phase was the same as that for the intensity, but the fast phase was approximately four times faster.

FPOP probes the solvent exposure of the protein as it folds by transiently producing OH radicals, which modify the side chains of various amino acids (Met, Cys, Trp, Phe, Tyr, His, Pro, Leu, and Ile are the most likely). Samples collected for different time points of OH exposure are analyzed with mass spectrometry. The typical curve shows several peaks separated by 16 mass units, the size of one oxygen atom from the OH radical (Fig. 2 A). When the protein is denatured in 6 M GdnHCl, the first four peaks (unmodified, 1, 2, and 3 OH) are fairly evenly populated. Within the mixing time, the unmodified and 1 OH peaks rise and the 2 and 3 OH peaks drop, indicating the chain is compacting with the change in solvent conditions (Fig. 2 B). The rise of the 1 OH peak indicates the average structure is more solvent exposed than the folded structure. Then the unmodified peak continues to rise whereas the other peaks decay. The data for all four peaks were globally fit to two exponential decays with lifetimes of 72 and 653 μs.

Figure 2.

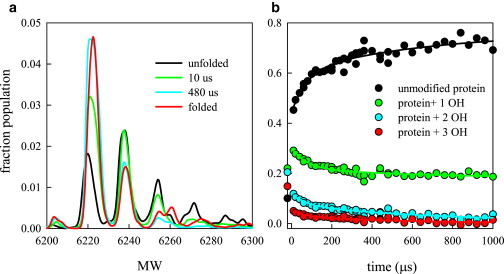
Folding kinetics of protein G as measured by fast photochemical oxidation. (A) Representative mass spectra of the unfolded and folded protein and two points along the folding pathway. (B) Total population within the four largest peaks as a function of time. To see this figure in color, go online.

CD spectra in 1.25 M GdnHCl collected at various times after mixing show a continuous shifting in spectral shape over time (Fig. 3 A). SVD analysis yields three significant spectral components (see Fig. 3 B). The first component looks generally like an α-helix spectrum, although with more amplitude at 208 than at 222 nm. The second component is comparable with a β-sheet spectrum and the third component appears to be a linear combination of helix and sheet. The time dependency of the first component (Fig. 3 C) rises with a lifetime of 304 μs, whereas the second component rises within the mixing time then decays after 1 ms, although this behavior may not be statistically significant. Since the folding time at 1.25 M GdnHCl is 50 ms, the observed kinetics do not include the final folding step.

Figure 3.

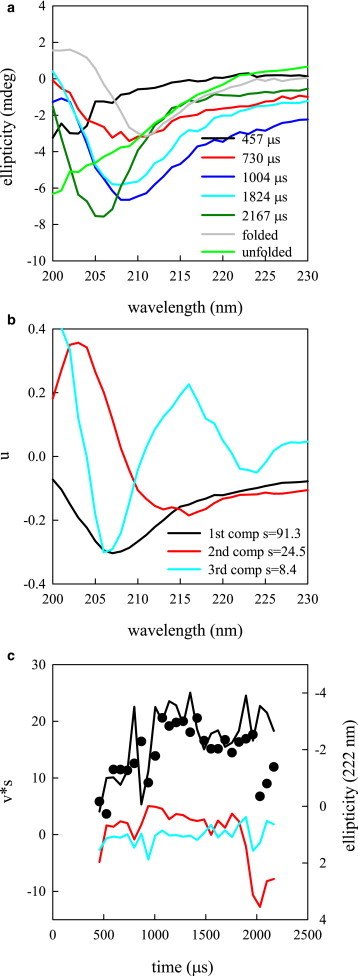
Folding kinetics of protein G as measured by circular dichroism. (A) Representative CD spectra of the unfolded, folded protein, and multiple points along the folding pathway. (B) Three most significant spectral components determined by SVD. (C) Time resolved amplitudes for the three most significant components using the same legend as in (B) (lines). The black points are the ellipticity at 222 nm. To see this figure in color, go online.

Molecular dynamics simulations qualitatively agree with experimental timescales

MD simulations were analyzed using MSMBuilder. We built many MSMs, varying the number of tICs employed as well as the number of states. Despite the large parameter space, most models had qualitatively similar eigenspectra. The slowest eigenvector of each model was associated with folding and had a timescale between 300 and 900 μs, which is in agreement with the slow (∼ 1 ms) timescales observed in the above experiments. Each model also had a multitude of faster (∼ 10 μs) timescales. For each model, we computed observables corresponding to each of the experiments performed. All models exhibited qualitatively similar traces (though the relative timescales and amplitudes changed slightly).

As a proxy for measuring the Trp fluorescence, we calculated the total SASA for Trp in each state in the MSM. We suspect that native interactions do not quench the fluorescence since the native state has a higher intensity than the unfolded state. The average Trp SASA time series produced from the various MSMs (see Methods section) was consistently a double exponential decay. The slow decay came from the folding timescale (300 to 900 μs). The fast decay (∼ 1 to 10 μs) had an amplitude that was opposite in sign to the folding timescale, which is consistent with the amplitude from the Trp fluorescence experiments (Fig. 4 A). However, this eigenprocess was much too fast to be directly compared with the experimentally observed fast phase. As implicit solvent has been observed to artificially stabilize compact states, this speed-up could be attributable to the simulation parameters. It is also possible that the actual process observed in the experiment was simply not observed in the simulation. The range of timescales reported above refer to a range defined by the timescale calculated using the 20-state model versus the 25,000-state model.

Figure 4.

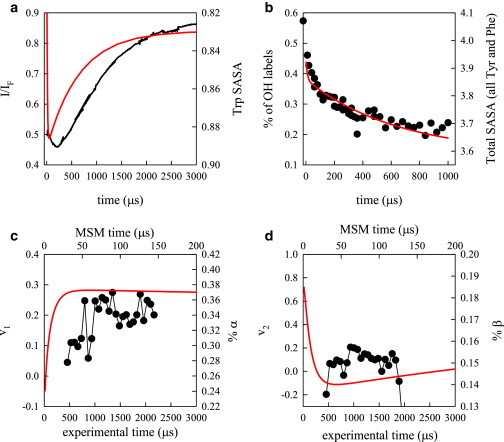
Comparison of experimental (black lines and points) with MSM (red lines) observables. The left axes correspond to experiment and the right axes correspond to calculation. (A) Trp fluorescence (scaled to the folded steady-state fluorescence) and Trp SASA. (B) FPOP labeled peak population and total SASA for all Tyr and Phe residues. (C) Most significant SVD component of CD spectra and % α-helix. (D) Second most significant SVD component of CD spectra and % β-sheet. To see this figure in color, go online.

Determining the labeling rate in FPOP to compute experimental observables is problematic because the rates of labeling for each type of amino acid are not known as a function of that residue’s SASA. However, Xu et al. has estimated rates for free amino acids, which gives a rank ordering of residues most likely to be labeled (32). The five most likely residues to be labeled are Cys, Tyr, His, Met, and Phe in that order. Protein G contains no Cys, His, or Met so we simply added the SASA of all Tyr and Phe residues and compared that with the sum of all labeled peaks over time (Fig. 4 B). These results are qualitatively similar to the experimental FPOP results, as the MSM predicts a double exponential, but once again the fast phase is too fast.

Computing secondary structure from the MSM is quite straightforward, but deconvolving CD spectra into types of secondary structure is not. Because the two most significant SVD components correspond roughly to α-helix and β-sheet spectra, respectively (Fig. 3 C), we plot those against calculated helix and sheet structure from the MSM in Figs. 4 C and D. The helix observable and the first SVD component roughly agree qualitatively, but the timescale in the MSM is ∼ 20-fold faster. This could be attributed to two causes: 1), the measurement was made in 1.25 M GdnHCl, 20 times more than the Trp fluorescence and FPOP measurements, which could make the rates slower (the final folding rate has been measured to be ∼ 10 times slower than at 0 M GdnHCl) and 2), the force field used in the simulations is known to highly stabilize secondary structure, which would make the MSM predictions faster than experiment. The β-sheet prediction and second SVD component show similar behavior. The MSM gains β-sheet at very early times, loses it and then regains it again, whereas the experiment gains β-sheet and then loses it, and the last step of regaining β-sheet in the folded state is not observed.

Markov state model reveals two major folding pathways

We built a 20-state model with Ward clustering on 10% of the trajectories and without using the sliding window approach to counting transitions (this is necessary because of the scaling of Ward clustering) to produce a qualitative picture of the protein folding process in protein G. This model had a similar eigenspectra to the previous models, with a folding timescale of ∼ 300 μs. Because there are fewer states, the folding process is distilled down to only the most important states.

We used transition path theory (TPT) to determine the folding pathways through the MSM (7,33). The result of TPT is a set of paths that connect the unfolded to the folded states without backtracking, which means we would only observe “on-pathway” intermediates using this analysis. We defined the unfolded state as the two most extended states. There were largely just two pathways that connected these extended states to the folded state. Both paths began with rapid collapse to a number of unfolded states with many nonnative contacts and nonnative secondary structure. From this collapsed unfolded state, the two paths diverged. The first path formed the N-terminal hairpin alone whereas the second path formed the C-terminal hairpin. From these intermediates, both pathways converged to one of two intermediates with both terminal hairpins formed. In one of these intermediates, the 1-4 sheet is also partially formed, but in both the hydrophobic core is mostly not packed as it is in the native state. The final step consisted of forming the remaining hydrophobic core contacts.

These two pathways are illustrated as a two-dimensional “free energy” surface in Fig. 5. The axes of this surface were selected to depict the difference between the main folding pathways. The two axes monitor the number of contacts formed in the N- and C-terminal hairpins. Each state was represented as a single Gaussian whose mean and variance were calculated by the sample means and variances within the state in this two-dimensional space. The full equilibrium probability was then calculated by summing the Gaussians with weights corresponding to the MSM equilibrium populations. A free energy was calculated by taking the minus log of the probability.

Figure 5.

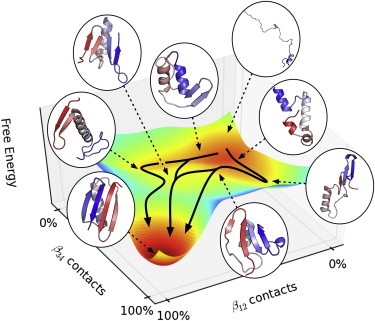
Free energy landscape predicted by the MSM. The x- and y-axes are the number of native contacts in the N- and C-terminal hairpins, respectively. To see this figure in color, go online.

It is important to note that this surface cannot be used to calculate transition state barriers, as the rates between the states are not determined by the equilibrium probability as calculated, but from the MSM transition probabilities. Nonetheless, the figure provides a qualitatively useful description of the two pathways observed in the MSM. It is possible that the projections used in Fig. 5 are not perfect and so the two paths we report in this study could be split further into additional paths with a different projection. Finally, depending on the resolution of the MSM, it will be possible to split these two pathways into many additional pathways, but we believe that the high-level view depicted in Fig. 5 is a useful picture to describe the folding of protein G.

Discussion

Using rapid mixing and multiple probes we have characterized the folding paths for the B1 domain of protein G on the submillisecond timescale. Previous work has shown that the last stage of folding is independent of the experimental probe and the rate exhibits strong exponential dependence on denaturant concentration. With a free energy barrier estimated to be 4 to 5 kcal/mol, it is unlikely that multiple pathways could be observed of the last folding step. However, earlier steps could have much lower barriers and display more heterogeneity depending on how folding is observed. In this work we have used four distinct probes (total Trp fluorescence emission, Trp fluorescence spectral shift, photochemical oxidation, and circular dichroism) and found a variety of kinetic processes. The earliest phase (or phases) falls within the mixing time of the T-mixer so is likely faster than 8 μs and is observed for Trp spectral shift and FPOP. This phase probably represents a rapid collapse of the unfolded chain because of the change in solvent, which has been observed for most proteins in a ultrarapid mixer (10,15,34). Nonspecific hydrophobic collapse has been estimated to be as fast as 80 ns (35). After the mixing time each probe shows a statistically distinct phase before 1 ms as summarized in Table 1. Finally, the Trp fluorescence and spectral shift show the final folding step at ∼ 1 ms. Because of time resolution limitations of FPOP and CD, this phase was not observed with those probes, but we assume they would also reflect this step because the final folding step has such a high free energy barrier (1,3).

Table 1.

Kinetic timescales from fitted experimental data

Folding probe	τ1 (μs)	τ2 (μs)	Fraction fast rate amplitude
Fluorescence intensity	126 ± 7a	1097 ± 24a	0.26b
Fluorescence spectral shift	32 ± 2c	1098 ± 4a	0.092
FPOP	72 ± 24d	653 ± 106d	0 OH: 0.44
			1 OH: 0.67
			2 OH: 0.39
			3 OH: 0.47
CD (1st SVD component)		304 ± 144

^aFit over range of 0.01 to 4 ms.

^bf = |A₁|/(|A₁|+|A₂|).

^cFit over range of 0.01 to 1 ms.

^dErrors from the global fit were determined as the range over which the sum of squared residuals changed by less than 20%.

The results presented in this work clearly show that a two-state model is not appropriate for understanding the full folding path of protein G. An intermediate has been proposed before based on curvature in the chevron plots of millisecond folding rates measured by stopped-flow mixing and observation of a submillisecond process in Trp fluorescence (3,4), although other measurements have disputed this claim (31). Recent comparison of experimental rates with MD simulations have determined this intermediate is on pathway (2). However, a simple three-state system such as U↔I↔N cannot account for the multitude of rates measured in this work by different probes. Indeed, Camilloni et al. has found nonnative contacts as well as three separate pathways in a ratcheted simulation of protein G folding (36). On the other hand, Hori et al. have constructed a free energy landscape of protein G using a coarse-grained model that shows a reasonably funneled landscape near the native state but many energy minima far from the native state, including a completely misfolded state that must largely unfold before progressing to the native state (37). Different trajectories show different pathways to the native state. This picture seems in reasonable agreement with the spectrum of rates observed in the present study.

The MSM we construct is the most detailed view of protein G folding, exploring 25,000 different states. The calculated experimental observables agree qualitatively with the observed experiments, in that both observe double exponential relaxations and turnover in signals. Looking just at productive folding processes, the MSM reveals a folding reaction that can proceed via several states along two different paths. In the MSM, either terminal hairpin can form first, followed by the remaining structure. We cannot say with confidence that either path is favored significantly more than the other.

The MSM eigenspectrum has a large gap between the slowest and next slowest timescales, which would appear as two-state behavior to experiments with low (>1 ms) time resolution. However, apparent two-state kinetics does not imply that there are really only two states. Lane et al. has shown that this type of spectrum is the hallmark of a folding free energy landscape in which the native state free energy is significantly lower than any other state and the mean first passage time between nonnative states is relatively slow (38). Protein G appears to satisfy these conditions. First, the native state in the low denaturant concentrations measured here is clearly the most stable state. Second, Waldauer et al. and Voelz et al. have measured extremely slow reconfiguration of unfolded states (under native conditions) in Acyl-coenzyme A-binding protein (ACBP) and the B1 domain of protein L (14,39). We have not measured reconfiguration for protein G, but Singh et al. showed that proteins L and G had similar reconfiguration rates for various concentrations of denaturant (40), so it is reasonable to assume reconfiguration is slow for protein G under the conditions in which we measure folding. Thus, protein G can appear to have two states by certain observations while still retaining an underlying complexity of many different folding pathways with similar timescales that manifest in the experimental observables as various fast (< 1 ms) phases. These results demonstrate the necessity of examining many experimental observables and using simulation data to give complete picture of folding for even fairly small proteins.