A spatial scan statistic for multinomial data

Abstract

As a geographical cluster detection analysis tool, the spatial scan statistic has been developed for different types of data such as Bernoulli, Poisson, ordinal, exponential and normal. Another interesting data type is multinomial. For example, one may want to find clusters where the disease-type distribution is statistically significantly different from the rest of the study region when there are different types of disease. In this paper, we propose a spatial scan statistic for such data, which is useful for geographical cluster detection analysis for categorical data without any intrinsic order information. The proposed method is applied to meningitis data consisting of five different disease categories to identify areas with distinct disease-type patterns in two counties in the U.K. The performance of the method is evaluated through a simulation study.

1. Introduction

Spatial scan statistics are widely used for geographical cluster detection and inference. Different types of discrete or continuous data can be analyzed using spatial scan statistics for Bernoulli, Poisson [1], ordinal [2], exponential [3, 4] and normal [5, 6] models. The Bernoulli and Poisson models are among the most popular models for discrete data in geographical disease surveillance such as disease prevalence, incidence or mortality. The ordinal model is used for categorical data with intrinsic order information such as cancer stage or grade. The exponential model has been developed for survival data (with or without censoring), and the normal model for continuous outcome such as babies’ birth weight.

Another interesting data type is multinomial. For example, one may be interested in identifying non-random spatial patterns in the distribution of the types of meningitis in a study area when there are five different types of the disease. While there is abundant literature on the statistical analysis of geographical pattern for count data in spatial epidemiology (see e.g. [7–9] for general review), methods directly applicable to multinomial data are few. An example is the study by Ohno et al. [10] who evaluated clustering of categorical areal data by examining adjacent areas with concordant (i.e. identical) categories using chi-square tests.

Here, we are interested in finding geographical clusters where the disease-type distribution is statistically significantly different from the rest of the map. If the type of disease has an ordinal structure, the ordinal model can be used. If not, it does not make any sense to use it. Another option is to dichotomize the types of disease into only two categories and apply the Bernoulli model, but there is loss of information in dichotomization.

Multinomial data have been analyzed using conditional autoregression (CAR) modeling to study spatial patterns of, for example, gene frequencies [11] and childhood co-morbidity in Malawi [12]. CAR modeling can also be used for spatial cluster detection, as shown by Kazembe et al. [12]. However, cluster detection procedure in such methods is primarily exploratory, by, for example, examining residual patterns on the map by eye, and they do not provide formal testing or inference on individual clusters that were detected. Spatial scan statistics, on the other hand, are based on hypothesis-testing framework and provide statistical inference on individual clusters. We think of the two types of methods as complementary for different purposes rather than as competing methods.

In this paper, we propose a spatial scan statistic for multinomial data, which can be used for spatial cluster detection analysis for categorical data without intrinsic order information. As a motivating example, meningitis data from Nottingham and Derby counties in the United Kingdom (U.K.), which contain five different types of the disease, are introduced in Section 2. The data were first analyzed using the Bernoulli-based spatial scan statistic after dichotomization of the disease type. Five separate analyses were performed on five different dichotomizations of one category versus the others. In Section 3, a spatial scan statistic for multinomial data is described and the analysis results of meningitis data using the proposed method are presented. As the spatial scan statistics for other models, the test statistic is based on a likelihood ratio test and is evaluated using the Monte Carlo hypothesis testing. The performance of the proposed method is evaluated through a simulation study in comparison with the ordinal and Bernoulli models in Section 4. The paper ends with a general discussion in Section 5.

2. Meningitis data

2.1. The data

The meningitis data were collected as part of a national 3 year multi-center study carried out by the U.K. meningococcal carriage group whose objectives were to identify risk factors for meningococcal carriage among 14 000 teenagers in the U.K. as well as examine the effect of meningococcal serogroup C conjugate vaccine that was offered to all persons below 18 years old in the U.K. We obtained records for meningitis cases among students from the selected schools in Nottingham and Derbyshire counties for the years 1999–2001. There were a total of 594 meningitis cases and their locations were linked to the spatial data using home address postcodes. The spatial data consist of easting and northing in meters for the centroid of each postcode. Owing to some errors in the data (e.g. incorrect postcodes due to typing errors), 87 cases could not be linked to the spatial data resulting in 507 total cases for the study. Most cases were assigned to unique locations (postcodes), whereas some cases share the same locations. A total of 475 distinct postcodes were used. The disease was classified into one of the five major categories ST-213 complex, ST-22 complex, ST-23 complex/cluster A3, ST-41/44 complex/lineage 3, and ST-53 complex. The number of cases in each category is listed in Table I.

Table I.

The number of meningitis cases in Nottingham and Derbyshire counties, U.K. (1999–2001), by type of disease.

Category	Meningitis type	n	Per cent
1	ST-213 complex	78	15.4
2	ST-22 complex	119	23.5
3	ST-23 complex/cluster A3	50	9.8
4	ST-41/44 complex/lineage 3	179	35.3
5	ST-53 complex	81	16.0
Total		507	100.0

The purpose of the study is to identify non-random spatial patterns in the distribution of the types of meningitis in the two counties. Especially, we want to identify areas in which the disease-type distribution is statistically significantly different from the remaining areas.

2.2. Cluster detection analysis using the Bernoulli model

As an alternative, the Bernoulli-based spatial scan statistic can be used to search for clusters with high or low rates of each category of the meningitis type (versus the other categories) after dichotomization. The Bernoulli model has been described in detail by Kulldorff [1] and here we provide a brief summary. Let Z be a scanning window in a study area and let p and q be the probability of being a case of a particular disease type inside the window Z and outside the window, respectively. The null hypothesis of no clustering is written as H₀ : p = q and the alternative as H₀ : p>q for high rates (or p<q for low rates). The test statistic of the Bernoulli model for a given window Z is

$${\lambda }_Z={\left(\frac{o_Z}{n_Z}\right)}^{o_Z}{\left(1-\frac{o_Z}{n_Z}\right)}^{n_Z-o_Z}{\left(\frac{O-o_Z}{N-n_Z}\right)}^{O-o_Z}{\left(1-\frac{O-o_Z}{N-n_Z}\right)}^{(N-n_Z)-(O-o_Z)}I()$$

where o_Z and n_Z are the number of cases of a particular disease type and the number of all observations, respectively, inside the window Z, and O and N are the corresponding totals in the whole study area. The indicator function I() is equal to one if o_Z /n_Z >(O − o_Z)/(N − n_Z) when searching for clusters with high rates and the opposite inequality applies when searching for clusters with low rates. The region associated with the maximum of the test statistic is defined as the most likely cluster and the statistical significance is determined by the Monte Carlo hypothesis testing as described by Kulldorff [1].

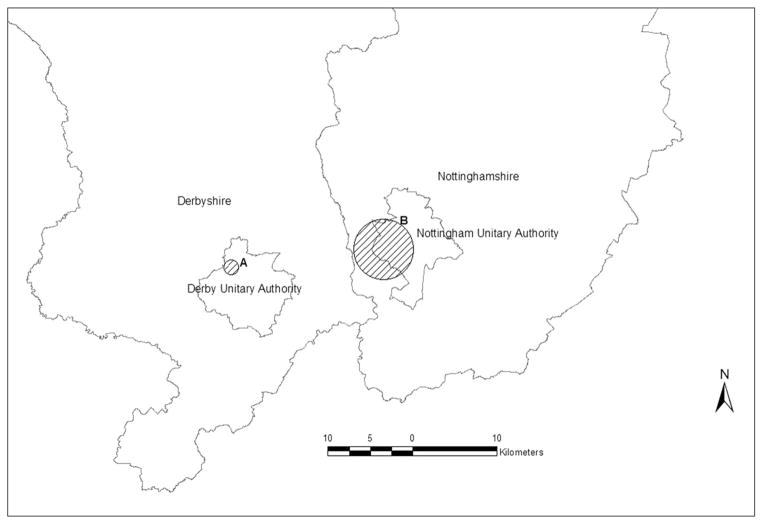
The disease category of meningitis data was dichotomized as 1 vs the others, 2 vs the others, and so on, and the Bernoulli model was applied to each of dichotomizations. The most likely cluster from each analysis is listed in Table II. Significant clusters were detected when the disease category was dichotomized as 1 vs the others (cluster A) and 5 vs the others (cluster B). Those clusters are presented in Figure 1. Cluster A is an area with high rates of category 1 and cluster B is an area with high rates of category 5.

Table II.

Cluster detection analysis results for meningitis data in Nottingham and Derbyshire counties, U.K., using the Bernoulli model with dichotomized categories. (See Figure 1.)

	Radius (m)	# Obs	RR	LLR	p-value
Category 1 versus the others (Cluster A)	1745	18	4.94	12.70	0.003
Category 2 versus the others	2866	5	1.17	7.33	0.332
Category 3 versus the others	11908	71	0.00	7.98	0.114
Category 4 versus the others	3108	15	0.00	6.66	0.481
Category 5 versus the others (Cluster B)	7124	139	3.00	14.49	0.001

^#Obs is number of total observations. RR is relative risk, computed as the ratio of the proportions of the number of cases out of total number of cases inside the cluster versus outside. LLR is log-likelihood ratio.

Figure 1.

Spatial cluster detection analysis results for meningitis data in Nottingham and Derbyshire counties, U.K., using the Bernoulli model with dichotomized categories (See Table II.).

3. Spatial scan statistic for multinomial data

3.1. Test statistic

Suppose we have K categories for types of a disease on a study area consisting of I sub-regions such as counties or postcodes. Let c_ik be the number of observations belonging to category k in sub-region i (k = 1, …, K, i = 1, …, I). The null hypothesis of no clustering can be expressed as the probability of being in category k is the same in all part of the study area for all k = 1, …, K. Then we search for regions where the disease-type distribution is statistically significantly different from the remaining regions. The spatial scan statistic is based on a likelihood ratio test for comparing a potential cluster versus the remaining areas. The potential cluster is one of the scanning windows constructed first on a study area. Here, a circular-shaped area centered at the centroid of each sub-region is considered as a scanning window, which is denoted by Z. We calculate the test statistic for each scanning window and find the window that maximizes the likelihood ratio test statistic as the most likely cluster. As described by Jung et al. [2], the collection of scanning windows is a parameter space for the cluster, over which the likelihood ratio is maximized.

The likelihood function for the multinomial model is written as

$$L(Z,p_1,\dots ,p_K,q_1,\dots ,q_K)\propto \prod _{k=1}^K\left(\prod _{i\in Z}{p}_k^{c_{ik}}\prod _{i\notin Z}{q}_k^{c_{ik}}\right)$$

where p_k and q_k are the probabilities of being in category k inside window Z and outside the window, respectively (k = 1, …, K). Note that Σ_k p_k = Σ_k q_k = 1. Under the null hypothesis, these probabilities are the same for each category.

$$H_0:p_1=q_1,\dots ,p_K=q_K$$ (1)

The alternative hypothesis is that there exists at least one category for which the probabilities are not the same. Let c_i(= Σ_k c_ik) be the total number of observations in sub-region i, C_k(=Σ_i c_ik) be the total number of observations in category k, and C(=Σ_k Σ_i c_ik) be the total number of observations in the whole study area. The likelihood ratio test statistic is expressed as

$$\lambda =\frac{{max}_{Z,H_a}L(Z,p_1,\dots ,p_K,q_1,\dots ,q_K)}{{max}_{Z,H_0}L(Z,p_1,\dots ,p_K,q_1,\dots ,q_K)}=\frac{{max}_{Z}L(Z)}{L_0}$$

with

$$L_0=\prod _k\prod _i{\widehat{p}}_{o_k}^{c_{ik}}=\prod _k{\left(\frac{C_k}{C}\right)}^{{\sum }_i{c}_{ik}}=\prod _k{\left(\frac{C_k}{C}\right)}^{C_k}$$

where p̂_ok = C_k/C(=q̂_ok) is the maximum likelihood estimator (MLE) of p_k(= q_k) under the null hypothesis, and with

$$L(Z)=\prod _k\left(\prod _{i\in Z}{\widehat{p}}_k^{c_{ik}}\prod _{i\notin Z}{\widehat{q}}_k^{c_{ik}}\right)$$

where p̂_k and q̂_k are the MLEs of p_k and q_k, respectively, under the alternative hypothesis, which are simply the proportion of the number of observations in category k to the total number of observations inside the scanning window and outside, respectively. That is, ${\widehat{p}}_k={\sum }_{i\in Z}{c}_{ik}/{\sum }_k{\sum }_{i\in Z}\stackrel{\text{let}}{=}{C}_k(Z)/C(Z)$ and q̂_k = Σ_i≠Z c_ik/Σ_kΣ_i≠Z c_ik = (C_k −C_k(Z))/(C − C(Z)). Note that L₀ is constant over all scanning windows since it depends only on the total number of observations in each category (C₁, …, C_K). For a given window Z, we calculate the log-likelihood ratio test statistic as

$$log{\lambda }_Z=\sum _k\left\{C_k(Z)log\left(\frac{C_k(Z)}{C(Z)}\right)+(C_k-C_k(Z))log\left(\frac{C_k-C_k(Z)}{C-C(Z)}\right)\right\}-\sum _k{C}_{k}log\left(\frac{C_k}{C}\right)$$

and the window associated with the maximum of log λ_Z is the most likely cluster.

To evaluate the statistical significance of the most likely cluster, we use the Monte Carlo hypothesis testing [13] since the distribution of the spatial scan statistic cannot be obtained in a closed analytical form. Under the null hypothesis, a large number of random data sets are generated and the test statistic is calculated for each random data set. The Monte Carlo-based p-value is then determined as the rank of the test statistic among all data sets divided by the number of all data sets (one added to the number of simulated data sets). When generating random data sets under the null hypothesis, we condition on the total number of observations in each category. First, the locations of C₁ observations are randomly selected over all possible locations and the selected C₁ observations are assigned to category 1. Next, C₂ of remaining observations are randomly selected and assigned to category 2. We keep doing the procedure until C_K−1 observations are selected and assigned to category K−1 and then, the remaining C_K observations are assigned to category K. This way, the inference is only about the purely spatial distribution of the observations, with no interest in the proportion of observation in each category. In other words, the null hypothesis is simply that the spatial location of each observation is independent of the category to which it belongs, and there is no hypothesis about how many observations are there in each category.

Besides the most likely cluster, it may be interesting to inspect secondary clusters with high values of likelihood ratio. The statistical significance of secondary clusters are also evaluated in the same way as the most likely cluster. That is, the likelihood ratio of secondary clusters are compared with those of the most likely clusters from the random data sets. In this way, secondary clusters are evaluated on its own strength regardless of the other clusters. Secondary clusters are reported when there is no geographical overlap with other reported clusters with higher values of likelihood ratio.

3.2. Comparison with Bernoulli and ordinal models

If there are only two categories (K = 2), we get the existing Bernoulli-based scan statistic as a special case when we are searching for clusters with either high or low rates. The Bernoulli model could be used for multinomial data after dichotomization. However, there would be loss of information and it may not be clear how to dichotomize or be necessary to consider all possible dichotomization. The result interpretation from several different models would also not be very clear.

The null hypothesis for the ordinal model is the same as that for the multinomial model, whereas the alternative hypothesis for ordinal model is written as H_a : p₁/q₁≤ ··· ≤p_K /q_K (or H_a : p₁/q₁≥ ··· ≥p_K /q_K) to ensure that detected clusters represent areas with high (or low) rates of more serious status of outcome than the remaining areas. The random data set generation procedure for the Monte Carlo hypothesis testing for the ordinal model and the multinomial model is basically the same.

Using the multinomial model, we search for clusters without considering ‘high’ or ‘low’ rates. The detected clusters are areas where the distribution of categories is statistically different from the rest of the map. We may instead list the categories in the order of dominance in terms of the relative risk of each category inside the cluster compared with outside.

3.3. Cluster detection analysis of meningitis data using the multinomial model

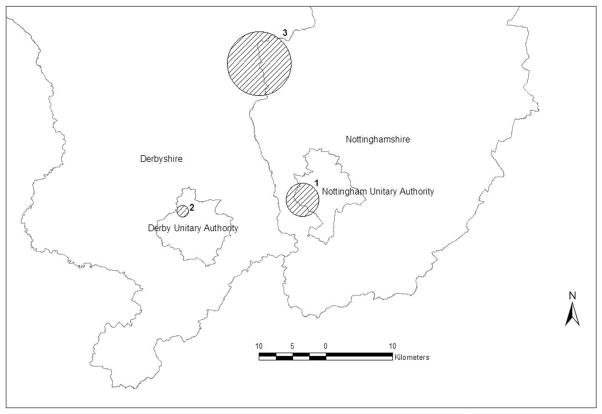
Using the proposed method of spatial scan statistic for multinomial data, we searched for spatial clusters where the meningitis-type distribution is statistically significantly different from the remaining regions in the two counties. Three clusters were detected and the detailed information on the clusters is presented in Table III. Figure 2 displays the location and the size of the clusters on the map. Cluster 1 is the most likely cluster and the others are secondary in order of statistical significance. The most likely cluster is a region where disease category 5 (ST-53 Complex) is the most dominant in terms of relative risk. The risk of being a case of category 5 is three times higher inside the cluster compared with outside. In cluster 2, disease category 1 (ST-213 Complex) is the most dominant and the risk of being category 1 is almost five times higher than outside the cluster. While in clusters 1 and 2 a certain category is quite prevailing than the other categories, the relative risk of being each disease type in cluster 3 is not that severely different. Given the overall proportion of each meningitis type (Table I), the relative risk of 3 for category 5 in cluster 1 and that of 5 for category 3 in cluster 2 are quite extreme.

Table III.

Cluster detection analysis results for meningitis data in Nottingham and Derbyshire counties, U.K., using the multinomial model. (See Figure 2.)

	Radius (m)	# Obs	RR in each category	LLR	p-value
Cluster 1	4948	56	(0.21, 0.82, 0.00, 1.07, 3.00)	18.10	0.001
Cluster 2	1745	18	(4.94, 0.23, 0.55, 0.62, 0.00)	14.44	0.033
Cluster 3	9546	37	(0.51, 1.83, 0.00, 1.51, 0.00)	14.10	0.041

^#Obs is number of total observations. RR is relative risk, computed as the ratio of the proportions of the number of cases in each category out of total number of cases inside the cluster versus outside. LLR is log-likelihood ratio.

Figure 2.

Spatial cluster detection analysis results for meningitis data in Nottingham and Derbyshire counties, U.K., using the multinomial model. (See Table III.)

Compared with the results from the analysis using the Bernoulli model in Section 2, cluster 2 is exactly the same as cluster A and cluster 1 is inside of cluster B. However, cluster 3 was not detected using the Bernoulli model with any dichotomization. As seen in Table III, there are no cases of category 3 or 5 in cluster 3 and the relative risk for categories 2 and 4 is less than 2 without an extreme relative risk of a certain category. Such clusters could not be detected using the Bernoulli model with dichotomized categories.

3.4. Covariate adjustment

It is sometimes important to adjust the analysis for confounders. To illustrate how this can be done, we adjust the meningitis analysis for community-level socio-economic deprivation. A variable called Mosaic UK was obtained from Mosaic Public Sector, which classifies every U.K. postcode into 1 of 61 distinct types [14]. According to a paper by Ward [14], Mosaic UK can be linked to the indices of deprivation and we used a deprivation variable with a higher value indicating a more deprived area. It would be interesting to see if the cluster detection analysis results will be affected by the variable. For categorical covariates, one option is to adjust by doing a multivariate scan statistic analysis using multiple data sets stratified by the categorical covariate level as proposed by Kulldorff et al. [15]. With 61 categories, it makes more sense to treat the variable as continuous. Using a generalized linear models approach as proposed by Jung [16] is a more flexible option to adjust for all types of covariates. Suppose we have constructed J scanning windows and denote jth scanning window by Z_j. Let U_ji be an indicator variable indicating whether the ith individual’s location belongs to Z_j (U_ji = 1) or not (U_ji = 0). Note that the index i here is for 507 individuals, not the postcodes as in Section 3.1 Denote ith individual’s deprivation value by x_i and consider the following model:

$$log\left(\frac{{\pi }_{ik}}{{\pi }_{i1}}\right)={\alpha }_k+{\theta }_{Z_j,k}{U}_{ji}+{\beta }_k{x}_i,k=2,\dots ,K$$

where π_ik is a probability that ith individual belongs to category k. Using this generalized logits model, we can compare the mean of the outcome (a vector of probabilities for each category) for the individuals having the same covariate information inside versus outside the window Z_j through the parameters θ_Zj,_k. It can be easily verified that H₀ : θ_Zjk =0, k = 2, …, K is equivalent to (1). The alternative hypothesis can be written as there is at least one k such that θ_Zjk ≠ 0. The log-likelihood ratio test statistic for comparing the alternative versus the null is calculated for each j and the area associated with the largest value of the test statistic is the most likely cluster. Statistical significance of detected clusters is obtained in the same manner as described in Section 3.1. For further details on using this approach for covariate adjustment, please refer to the paper by Jung [16].

The adjustment did not affect the meningitis clusters, which were identical to the ones shown in Figure 2. That does not mean that the adjustments were unnecessary, as we can now state that the clusters cannot be explained (solely) by community-level socio-economic levels.

4. Power, sensitivity, and positive predicted value

We conducted a simulation study to evaluate the performance of the proposed method in terms of statistical power, sensitivity, and positive predicted value (PPV). We used the meningitis data for geographical location (postcode). Removing one case each from seven randomly chosen postcodes among those having more than one case, we used 500 cases in total to make data generation easy in simulations. True clusters centered at the centroid of cluster 1 (Figure 1) were created under various scenarios with a radius of 5467 and 5009 m, respectively. There are 80 case s included in the larger cluster and 60 cases in the smaller one. We considered H₀ : p = q= (0.25,0.25,0.25,0.25) as the null hypothesis assuming four categories. To compare the proposed multinomial model with the ordinal and the Bernoulli models, several different alternative hypotheses were tested: A: p= (0.05,0.25,0.35,0.45), B: p= (0.05,0.25,0.25,0.45), C: p= (0.10,0.10,0.40,0.40) and D: p= (0.15,0.15,0.15,0.55). Note that these alternatives reflect an ordinal structure in the clusters and it is expected that the ordinal model outperforms the multinomial model in these situations. To see if the multinomial model outperforms the ordinal model in other situations, the ordinal model was also evaluated under unordered alternatives: A′ :p= (0.45,0.05,0.35,0.25), B′ :p= (0.45,0.05,0.25,0.25), C′ :p= (0.40,0.10,0.40,0.10) and D′ :p= (0.15,0.55,0.15,0.15). Four different Bernoulli models were applied after the categories were dichotomized: category 1 vs the others, category 2 vs the others, category 3 vs the others and category 4 vs the others. Since the multinomial model and the Bernoulli models with four dichotomizations do not depend on the ordering structure, they have to perform the same for each pair of alternatives (A and A′, …, D and D′) and were not evaluated additionally under the unordered alternatives.

Under the null hypothesis, 125 cases out of 500 were randomly selected first and assigned to category 1, 125 cases out of the remaining 375 were randomly selected and assigned to category 2, 125 cases out of the remaining 250 were randomly selected and assigned to category 3, and the remaining 125 cases were assigned to category 4. Under the alternative, the same procedure was done for each alternative inside the cluster and outside separately. For H_a : p = (0.05,0.15,0.35,0.45) with the larger cluster, for example, 4 randomly selected cases were assigned to category 1, 12 randomly selected cases were assigned to category 2, 28 cases to category 3, and 36 cases to category 4 inside the cluster, and 105 randomly selected cases each were assigned to one of four categories outside the cluster. For unordered alternatives A′, …, D′, we shuffled the order of categories in the data sets generated under alternatives A, …, D instead of generating new data sets.

We first generated 10 000 random data sets under the null hypothesis to obtain the critical values at the significance level (α) of 0.05 and 0.01 for each model. Then, 1000 random data sets were generated under each alternative hypothesis to estimate power, sensitivity, and PPV. Power was estimated as the proportion of the number of rejected data sets out of 1000 at α= 0.05 and α= 0.01 and the results are presented in Table IV. Sensitivity and PPV for spatial scan statistics were introduced by Huang et al. [3] and also used by Jung et al. [2] to evaluate the geographical precision of the detected cluster. Sensitivity was defined as the proportion of the number of cases correctly detected among the cases in the true cluster and PPV as the proportion of the number of cases belonging to the true cluster among the cases in the detected cluster. Sensitivity and PPV were computed only for the data sets rejected at the significance level of 0.05 and the averages of them are presented in Table V.

Table IV.

Estimated power of the multinomial, ordinal, and Bernoulli models at the significance level of 0.05 and 0.01.

Ha	α= 0.05							α= 0.01
	Multi	Ord	Ord*	Br1	Br2	Br3	Br4	Multi	Ord	Ord*	Br1	Br2	Br3	Br4
80 cases in cluster
A: p= (0.05,0.15,0.35,0.45)	1.000	1.000	0.383	1.000	0.073	0.070	0.450	1.000	1.000	0.111	0.764	0.016	0.017	0.151
B: p= (0.05,0.25,0.25,0.45)	0.958	1.000	0.299	1.000	0.048	0.052	0.449	0.646	1.000	0.074	0.769	0.012	0.009	0.157
C: p= (0.10,0.10,0.40,0.40)	1.000	1.000	0.395	0.263	0.236	0.144	0.132	0.745	1.000	0.113	0.096	0.067	0.040	0.041
D: p= (0.15,0.15,0.15,0.55)	1.000	1.000	0.300	0.070	0.081	0.073	1.000	0.811	1.000	0.078	0.013	0.024	0.016	1.000
60 cases in cluster
A: p= (0.05,0.15,0.35,0.45)	0.901	1.000	0.245	0.723	0.060	0.048	0.217	0.513	0.938	0.070	0.322	0.015	0.012	0.066
B: p= (0.05,0.25,0.25,0.45)	0.492	0.931	0.175	0.720	0.038	0.049	0.223	0.221	0.492	0.042	0.335	0.008	0.008	0.062
C: p= (0.10,0.10,0.40,0.40)	0.596	0.965	0.224	0.148	0.140	0.099	0.084	0.250	0.568	0.041	0.032	0.034	0.020	0.022
D: p= (0.15,0.15,0.15,0.55)	0.693	1.000	0.181	0.060	0.068	0.070	1.000	0.329	0.663	0.040	0.011	0.017	0.014	0.902

Multi=multinomial model, Ord=ordinal model, Ord*=ordinal model tested under unordered alternatives A′ :p= (0.45,0.05,0.35,0.25), B′ :p= (0.45,0.05,0.25,0.25), C′ :p= (0.40,0.10,0.40,0.10), D′ :p= (0.15,0.55,0.15,0.15), Br1= Bernoulli model for category 1 (versus the others), Br2=Bernoulli model for category 2 (versus the others), Br3=Bernoulli model for category 3 (versus the others), Br4= Bernoulli model for category 4 (versus the others).

Table V.

Estimated sensitivity and positive predicted value of the multinomial, ordinal, and Bernoulli models.

Ha	Sensitivity							PPV
	Multi	Ord	Ord*	Br1	Br2	Br3	Br4	Multi	Ord	Ord*	Br1	Br2	Br3	Br4
80 cases in cluster
A: p= (0.05,0.15,0.35,0.45)	0.896	0.898	0.563	0.876	0.250	0.273	0.596	0.887	0.890	0.611	0.838	0.222	0.325	0.683
B: p= (0.05,0.25,0.25,0.45)	0.854	0.877	0.518	0.876	0.069	0.057	0.625	0.838	0.863	0.579	0.835	0.101	0.128	0.668
C: p= (0.10,0.10,0.40,0.40)	0.853	0.873	0.535	0.624	0.569	0.429	0.370	0.840	0.859	0.559	0.553	0.500	0.485	0.480
D: p= (0.15,0.15,0.15,0.55)	0.837	0.861	0.487	0.313	0.304	0.314	0.878	0.864	0.883	0.494	0.293	0.243	0.239	0.898
60 cases in cluster
A: p= (0.05,0.15,0.35,0.45)	0.844	0.866	0.425	0.851	0.238	0.204	0.507	0.829	0.852	0.491	0.745	0.157	0.211	0.587
B: p= (0.05,0.25,0.25,0.45)	0.791	0.832	0.402	0.845	0.077	0.099	0.521	0.706	0.760	0.394	0.732	0.063	0.086	0.568
C: p= (0.10,0.10,0.40,0.40)	0.772	0.832	0.501	0.547	0.516	0.319	0.299	0.754	0.818	0.449	0.396	0.348	0.413	0.350
D: p= (0.15,0.15,0.15,0.55)	0.742	0.814	0.410	0.249	0.202	0.255	0.845	0.775	0.844	0.392	0.184	0.141	0.193	0.870

Multi=multinomial model, Ord=ordinal model, Ord*=ordinal model tested under unordered alternatives A′ :p=(0.45,0.05,0.35,0.25), B′ :p= (0.45,0.05,0.25,0.25), C′ :p= (0.40,0.10,0.40,0.10), D′ :p= (0.15,0.55,0.15,0.15), Br1= Bernoulli model for category 1 (versus the others), Br2= Bernoulli model for category 2 (versus the others), Br3= Bernoulli model for category 3 (versus the others), Br4= Bernoulli model for category 4 (versus the others).

As expected, the ordinal model performs better than the multinomial model for ordered alternative hypotheses. The ordinal model has higher power, sensitivity, and PPV than the multinomial model in every situation of ordered alternatives. The multinomial model attains relatively high power with the larger cluster although the power with the smaller cluster under alternatives B, C, and D is not very high. Still, the multinomial model seems to detect the correct cluster fairly well. The sensitivity and PPV for the multinomial model and the ordinal model are very comparable. For unordered alternatives, on the contrary, the ordinal model performs very poorly. Power is less than 40 per cent and sensitivity and PPV are also very low compared with the multinomial model. The Bernoulli models performs well with certain dichotomization in extreme conditions. The situations in which the Bernoulli model attains highest power are alternatives A and B for category 1 and alternative D for category 4. In such cases, the Bernoulli model performs better than the multinomial and ordinal models. However, the performance of the Bernoulli model in the other situations is not very good. For alternative C, none of the four Bernoulli models perform well.

5. Discussion

We have proposed a spatial scan statistic for multinomial data, which is very useful for geographical cluster detection analysis for categorical data without any intrinsic order information. The detected clusters are the areas where the distribution of the category is statistically significantly different from the remaining region in a study area. The Bernoulli-based scan statistic may be used for such data with dichotomized categories, but we have to consider different models as many as the number of categories if we dichotomize the categories into one category versus the others. As seen in the meningitis data example, different clusters were detected from different models and not all the clusters detected using the multinomial-based scan statistic were identified using the Bernoulli-based scan statistic.

The simulation study suggests that the multinomial model has good power for different types of divergence from the null hypothesis and detects clusters fairly precisely, although the ordinal model attains higher power, sensitivity, and PPV when there is intrinsic ordinal structure in the data. However, without such an ordinal structure, the multinomial model performs much better than the ordinal model. Although the Bernoulli model with dichotomized categories performs very well in some situations, problems of using the Bernoulli model for multinomial data are that there would be loss of information in dichotomization and that it may not be clear how to dichotomize. Also, without an extreme probability of certain category, the Bernoulli model may not perform very well with any dichotomization. We also conducted another simulation study for a smaller sample size (N = 200) and a smaller cluster (number of cases in the cluster= 40) by randomly selecting 200 locations from the original data. The overall patterns were similar to the results presented here although power, sensitivity, and PPV are a bit lower for each model.

We have briefly introduced a generalized linear model approach for covariate adjustment. For the meningitis data, we assumed the simple linear relationship between the logits for the disease category and the covariate treated as continuous, which may not be appropriate in some cases. Still, it can be a useful method for covariate adjustment for the multinomial-based scan statistic. It might be more interesting to see if the cluster detection analysis results are affected by other covariates, such as age or gender, when available.

The proposed method can be used in many other applications in addition to disease surveillance. For example, one may want to search for areas with a different plant distribution when there are multiple types of trees or plants in a region. Other examples may be found in politics or criminology: when people vote for multiple political parties in an election, areas with the most distinct voting pattern are of interest. For multiple types of crimes (burglary, homicide, vandalism, assault, etc.), one may want to search for areas with distinct crime patterns. In some application the primary interest may not be whether there are statistically significant clusters, but which area is the most different from the rest of the region.

Although we have ordinal data, we do not necessarily have to consider the ordinal structure all the time when searching for clusters. For example, one may be simply interested in finding if the distribution of cancer stage in a certain area is statistically significantly different from the remaining areas instead of finding clusters with high rates of more serious stage when a higher stage indicates more serious status of disease. Then, we may identify which stage is the most prevailing or the least in terms of the relative risk of each stage in the detected clusters compared with outside the clusters. It can be revealed that the detected clusters are in fact areas with high rates of more serious stage than the surrounding areas. The multinomial model will be of more general use than the ordinal model in the sense that the multinomial model can be used for categorical data with or without ordinal structure, whereas the ordinal model can be used only for ordinal data.

The proposed method has been presented for purely spatial analysis in this paper, but it can also be used for space–time data using a cylindrical scanning window with the base representing space and the height representing time. Computation of the test statistic, the Monte Carlo hypothesis-testing procedure, and other algorithms will remain the same. The space–time scan statistic may be used for a single retrospective analysis [17] or for a prospective surveillance with repeated analyses [18].

The spatial scan statistic for multinomial data has been implemented into the freely available software SaTScan, which can be downloaded from www.satscan.org.