A model-based parallel origin and orientation refinement algorithm for cryoTEM and its application to the study of virus structures

Abstract

We present a model-based parallel algorithm for origin and orientation refinement for 3D reconstruction in cryoTEM. The algorithm is based upon the Projection Theorem of the Fourier Transform. Rather than projecting the current 3D model and searching for the best match between an experimental view and the calculated projections, the algorithm computes the Discrete Fourier Transform (DFT) of each projection and searches for the central section (“cut”) of the 3D DFT that best matches the DFT of the projection. Factors that affect the efficiency of a parallel program are first reviewed and then the performance and limitations of the proposed algorithm are discussed. The parallel program that implements this algorithm, called PO²R, has been used for the refinement of several virus structures, including those of the 500 Å diameter dengue virus (to 9.5 Å resolution), the 850 Å mammalian reovirus (to better than 7 Å), and the 1800 Å paramecium bursaria chlorella virus (to 15 Å).

1. Introduction

Electron microscopy has been widely used to obtain the 3D structures of viruses at low to moderate resolutions (about 10–30 Å) (see Baker et al., 1988; Cheng et al., 1995; review by Baker et al., 1999). In recent years, there has been a concerted effort to push the limits of electron microscopy and extend the resolution of structure determinations well beyond 10 Å and ultimately to near atomic or atomic resolution (van Heel et al., 2000). At the same time, there is a significant need to develop more powerful tools to study the organization of genetic material in virus cores, as well as virus structures that do not exhibit icosahedral symmetry.

New methods have recently been proposed that address the computational challenges posed by high resolution reconstruction of the 3D electron density map of viruses. (While computational challenges are the main concern of this paper, bear in mind that high resolution reconstruction poses numerous other challenges, related to specimen preparation, imaging and image processing, and so on.) Some of these challenges relate to the refinement of algorithms to: (i) eliminate some of the artifacts introduced by the electron microscope, (ii) cope with very low signal to noise ratio of information gathered experimentally, (iii) screen out particle projections which would distort the result, and (iv) determine an accurate and unbiased measure of the resolution of the final result. A different group of challenges stem from the need to handle the large quantity of experimental data required for high resolution reconstruction of large macromolecular structures.

The procedure for 3D virus structure determination in cryoTEM considered in this paper consists of a few basic steps:

• Step AExtract individual particle projections from micro-graphs and identify the center (origin) of each projection.
• Step BDetermine the approximate orientation of each projection with respect to a defined coordinate system.
• Step CRefine the origin and the orientation of each projection at a specified level of resolution.
• Step DCompute a 3D reconstruction of the electron density of the macromolecule.

This paper focuses primarily on the procedures designed to determine the rotational and translational alignment parameters for individual particle images (Step C). Ab initio reconstruction methods are used to create a model of the electron density map and to determine the approximate specimen orientation comparable to each experimental view. With such model-based methods, Steps C and D are executed iteratively until the 3D electron density map cannot be further improved at a given spatial resolution; then the resolution r is increased in gradual increments. Tens of iterations are necessary at a given resolution; one cycle of iteration for a medium size virus may take days. Currently, it may take many months and sometimes years to obtain an electron density map at resolutions in the 5–8 Å realm. Best results are obtained for highly symmetrical particles, such as spherical viruses, because the icosahedral symmetry inherent for such particles leads to redundancies in the Fourier transform data and that, in turn, aids the orientation search process. The 3D reconstruction of hepatitis B virus capsid (Böttcher et al., 1997; Conway et al., 1997) at 7–9 Å resolution required the inclusion of several thousand particle projections. It was estimated that approximately 2000 particle images are necessary for the reconstruction of a virus with a diameter of 1000 at 10 Å resolution (Rossmann and Tao, 1999) and such estimates correlate well with our own experience with many virus reconstructions. A much larger number of images is required to achieve much higher resolutions.

We present a model-based approach and a parallel algorithm for the origin and orientation refinement of experimental views used for 3D reconstruction in cryoTEM. An important advantage of our algorithm is a straightforward implementation of the contrast transfer function (CTF) correction. The CTF summarizes the specific condition of the electron microscope at the time a micrograph is taken and allows us to correct the distortion of the data introduced by the measuring instrument.

Thousands, or more, particle projections are used in a high-resolution reconstruction of a virus structure. Thus, several sets of micrographs are collected and particle projections from different micrographs must be corrected using different CTF functions. Our method uses Cartesian coordinates for the electron density map while the traditional methods (Crowther et al., 1970) use cylindrical coordinates and Fourier–Bessel transforms. Our interpolation algorithms allow us to apply distinct CTF corrections and weights to the experimental data points used to calculate the electron density for a non-integral grid point.

The parallel program that implements this algorithm, called PO²R, has been used for the refinement of several virus structures, including those of the 500 Å diameter dengue virus (to 9.5 Å resolution), the 850 Å mammalian reo-virus (to better than 7 Å), and the 1800 Å paramecium bursaria chlorella virus (to 15 Å). In this paper, we provide only highlights of the structure determination for these viruses to illustrate the use of our program. Several papers (Yan et al., 2005; Zhang et al., 2005) provide a detailed analysis of the reconstruction process and the results for these virus structures.

1.1. Basic concepts and related work

We introduce a few concepts necessary to rigourously define the problem of origin and orientation refinement. An electron density map is a function D : ℝ^𝟛↦ℝ with a compact support (A function has compact support if it is zero outside a compact set. A set in a finite dimensional space is compact if it is closed and bounded.). It associates a real number, the electron density, to a point in space with coordinates (x, y, z). A 2D projection Vⁱ (x, y) of the 3D electron density map D(x, y, z) at an orientation Oⁱ characterized by three angles (θⁱ, ϕⁱ, and ωⁱ) is given by the following expression:

$$V^i(x,y)={\int }_{-\infty }^{+\infty }D(R({\theta }^i,{\varphi }^i,{\omega }^i){[x,y,z]}^{\mathrm{T}})\mathrm{d}\mathrm{z},$$

where R (θⁱ, ϕⁱ, ωⁱ) is a three-dimensional rotation matrix. The collection of all projections Vⁱ (x, y) is called a sinogram of D (x, y, z) (Kak and Slaney, 1988).

Given a projection Vⁱ (x, y), call $x_0^i,y_0^i$ the coordinates of the center. Given a set of m 2D projections we are able to reconstruct the electron density map accurately if we know precisely the five coordinates $({\theta }^i,{\varphi }^i,{\omega }^i,x_0^i,y_0^i)$ of each projection.

The “common line” method was developed some 35 years ago (Crowther et al., 1970). Consider two projections, Vⁱ and V^j of the electron density map D (x, y, z) of an icosahedral particle on planes p_i and p_j. The normal vectors of the two planes correspond to orientations Oⁱ and O^j, respectively. All 1D projections of D (x, y, z) onto a line passing through the origin in a plane p_i corresponding to orientation Oⁱ can be computed from the 2D projection Vⁱ. Two planes p_i and p_j intersect, thus there is a line, “the cross-common line” of the two planes for which the projections Vⁱ and V^j agree. Searching for the cross-common lines of experimental views is prone to errors owing to the high noise level in each individual particle image.

van Heel (1984) introduced the use of image classification as a means to objectively analyze particle images obtained by electron microscopy. Projection images identified as arising from particles with similar orientations were classified into a single class and these could be summed to form an average image. The average image had higher signal to noise ratio; it exceeded that for any individual images in the same class. With a sufficient number of these class averages, a 3D reconstruction could be computed. Also Harauz and Ottensmayer (1984) conceived the idea of using a computer-generated model of the electron density to aid the process of determining the relative orientations of projections using an iterative procedure. The basic idea of this approach is to generate projections of the existing model at many orientations and compare an experimentally obtained projection (view) with all calculated projections. The experimental view is assigned the known orientation of the calculated projection that has the “best score.” A fair number of sequential algorithms based upon the same idea have been developed since; see Frank (1996) for a comprehensive review of angular refinement techniques known in the mid 1990s. These algorithms differ in terms of:

• The transforms used. Most algorithms use the Discrete Fourier Transform (DFT) domain, others use the Fourier–Bessel or the Radon Transform domain (Radon, 1917).

• The coordinate system used. Cylindrical coordinates are generally used for particles with icosahedral or dihedral symmetry. We prefer Euclidian coordinates because this choice allows us to implement the CTF correction in a straightforward manner; indeed, different CTF corrections apply to experimental values coming from different micrographs and when we interpolate to determine the transform of the electron density at a lattice point it is easier to apply different weights to these values.

• The order in which rotational and translational alignment is performed.

• The “metrics” used to define the “distance” between a calculated projection and an experimental view. These metrics depend upon the space and the coordinate systems used.

• The transformation of the input data—the set of experimental views—prior to the actual origin and orientation refinement (e.g., wavelet filtering in (Saad, 2003)). The strategies used to eliminate experimental data corresponding to distorted views, and/or views with a very low signal to noise ratio.

• The CTF correction method used to transform the experimental image data.

• The region of the electron density map used to generate the calculated projections. Ideally, for spherical viruses one should only form a projection image of the reconstructed density map for those portions of the structure that are highly organized (e.g., the icosahedrally symmetric capsid shell). In practice, we carry out the comparison in the DFT domain and we use only the spatial frequencies in a limited range, f_min ≤ f ≤ f_max with f = 1/r and r the resolution.

• The ability to exploit additional information (e.g., the symmetry or the structure of the virus).

• The level of integration of the alignment, 3D reconstruction, and CTF correction. Since many iterations are necessary at each resolution, we should integrate these functions. Rather than having several codes/programs, we could have a library of functions and then combine these functions, without the need to write-out at the end of one step and then read-in at the beginning of the next step the intermediate results.

1.2. The need for parallel algorithms for high resolution reconstruction

The consequences of Moore’s law (the number of transistors on a chip doubles every 18 months or so; for many years this translated into doubling the speed of the processor during the same interval of time) have benefited computational scientists for nearly 40 years. Hence, with virtually no additional effort, we can expect to solve increasingly larger problems without any change of the algorithms, or the code, because faster processors (processors with higher clock rates) and larger physical memories would become available. Technological barriers posed by heat dissipation and leakage effects of solid-state devices are very likely to limit in the immediate future the clock rate, thus the speed of processors. Indeed, the power consumption is proportional with a power (2 to 3) of the clock rate increase depending upon the technology. If we double the speed of a processor, then its power consumption and the heat generated by the device could increase by a factor of eight.

A chip will be populated with more processors running at today’s or slightly higher speeds. Consequently, if we want to solve increasingly challenging computational problems we have no choice but to migrate to concurrent (parallel) computations.

In this paper, we define medium resolution to correspond to the range 10 ≤ r ≤ 20 Å and high resolution when r ≤ 10 Å. High resolution reconstruction provides more accurate data for fitting atomic models. The higher the desired resolution is for a reconstruction of a particle of diameter D, the smaller the pixel size must be, which necessitates a larger box size for each particle projection. Also, the number of particle projections needed to compute a 3D reconstruction with isotropic resolution must substantially increase with finer resolutions (Table 1). A dramatic increase in the memory and secondary storage is required when the desired resolution increases from 12 to 6 Å, and then to 3 Å for a virus with icosahedral symmetry and a diameter of about 850 Å (see Table 1). The analysis of the complexity of the algorithms for origin and orientation refinement presented in Section 2.3 indicates a similar rate of increase in the computing power (CPU cycles) needed to carry out the computations.

Table 1.

Amount of data and the corresponding increase in memory requirements for high resolution reconstruction of reovirus (D = 850 Å)

Resolution (Å)	12	6	3
Pixel size (Å)	4	2	1
Particle image size (pixels)	2562	5122	10242
Memory/particle image	256 kB	1 MB	4 MB
Number of particle images	103	104	106
Memory/data set	256 MB	10 GB	4 TB
3D map size (pixels)	2563	5123	10243
Memory/3D map	64 MB	0.5 GB	4 GB

1kB = 10³ bytes, 1MB = 10⁶ bytes, 1GB = 10⁹ bytes, 1 TB = 10¹² bytes. As of 2005, high end PCs typically have 2–4 GB of physical memory and 40–200 GB of secondary storage (disk).

Some of the considerations that affect the amount of computer resources, memory and CPU cycles, necessary for high resolution reconstruction are outlined below.

1. The pixel size, p, should satisfy the Nyquist condition: p ≤ r/2. For example, for r = 6 Å, the pixel size should be no larger than 3 Å. A more precise calculation of the pixel size has to take into account the minimum step size of a scanning microdensitometer and the magnification of the image. For example, for a scanner with a minimum step size of 7 µm (=70,000 Å), when the image magnification is 63,000, the pixel size is 1.1 Å (70,000/63,000).

2. The projection of a particle with diameter D should be embedded into a box of dimension no smaller than D + D′ (Rosenthal and Henderson, 2003). Here, the extra box size D′ = 2λΔf/r with λ the wavelength of the electrons (0.02 Å for 300 keV electrons) required to achieve a resolution limit r and Δf the defocus level. When Δf = 15,000 Å and r = 3 Å then D′ = 200 Å. In the case of reovirus (D = 850 Å), the minimum box dimensions required to achieve 3 Å resolution is (850 + 200)/1.1 = 955 pixels. Thus, the particle image size will be about 1024 × 1024 pixels.

3. For a virus with icosahedral symmetry and under ideal conditions the number of unique projections, N, required to achieve a desired resolution, r, is quite small (N = πd/60r) (Crowther et al., 1970). For example, for reovirus, 20 projections would be needed and for PBCV—Paramecium bursaria Chlorella virus—40 projections would be needed. Under real conditions (i.e., for low contrast images with significantly low signal to noise ratio) the number of projections necessary for high resolution (r ≤ 10 Å) reconstruction is several orders of magnitude larger than for the reconstruction at medium resolution (10–20 Å).

From the foregoing discussion, it is clear that the structure determination of viruses and other large macromolecular complexes at high resolution leads to data- and compute-intensive problems that require resources well beyond those available on a single processor system. The orientation and origin refinement (rotational and translational alignment) is probably the most challenging computational problem posed in data processing for 3D reconstruction. Thus, there is an imperative need to develop parallel algorithms and programs to solve the alignment problem on clusters of PCs and/or computational grids.

There are two major reasons to develop a parallel algorithm for solving a computational problem: (i) to reduce the computation time by distributing the load among the P nodes of a parallel system, and (ii) to reduce the physical memory requirements for individual nodes.

While there are shared-memory parallel systems (e.g., SGI Origin 3000 supercomputer), such systems tend to be rather expensive. Distributed-memory systems such as clusters of PCs are less expensive and thus more popular. Such a system consists of a set of nodes (a node typically has 2–4 processors with a clock rate of 2.5–3.0 GHz that share a common memory of 2–4 GB) and an interconnection network which allows the nodes to communicate at high speed (a gigabit switch allows data transfer rates of up to 1 Gbps).

1.3. Factors that influence the efficiency of parallel algorithms

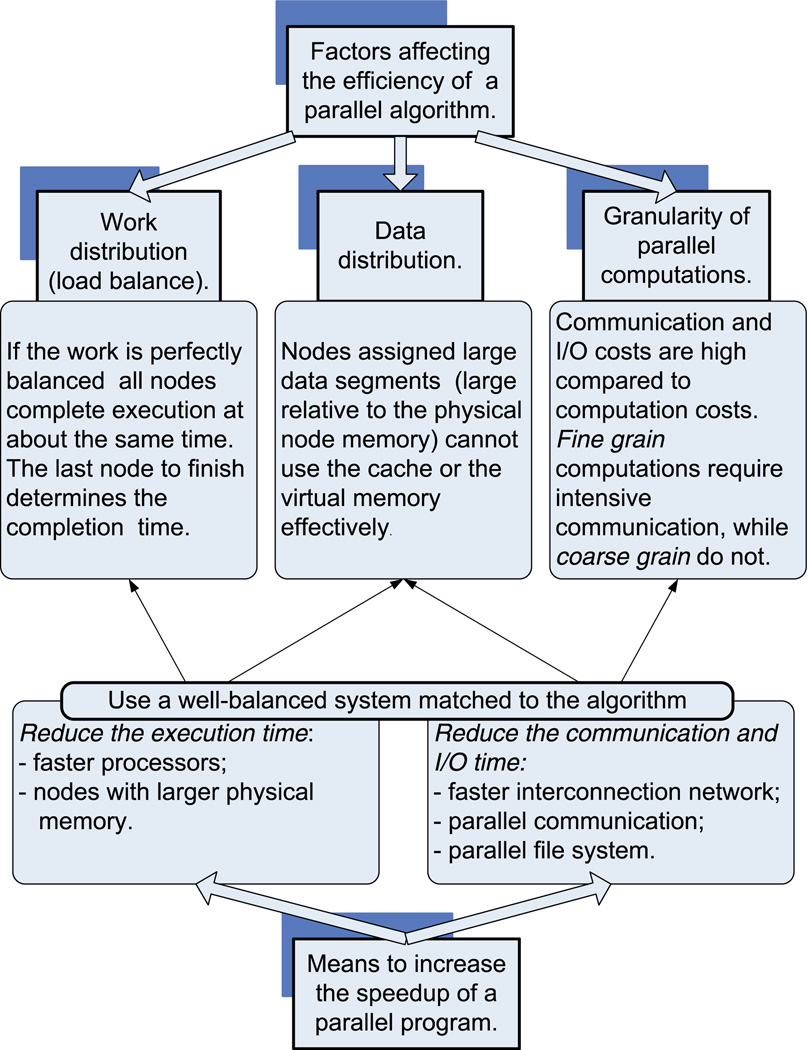
There are many concerns related to the efficiency of a parallel algorithm for a distributed-memory system, such as load distribution and data distribution across the nodes (Fig. 1). The efficiency of a program that implements a parallel algorithm is measured by the speedup. If T₁ is the computation time in one node and T_P is the computation time when using P nodes, the speedup is defined as: $S=\frac{T_1}{T_P}$. To be more precise, we talk about the speedup of an implementation of a parallel algorithm on a particular system. For example, if the program implementing the algorithm presented in this paper requires 100 h on a single node of a shared-memory system and only 2 h on 100 nodes we have achieved a speedup of S^shmem = 50 while the maximum speedup would be $S_{\text{opt}}^{\text{shmem}}=100$. The program implementing the same algorithm on a cluster of workstations may need 4 h to complete on a cluster with 100 nodes of the same type and with the same configuration (memory, disk, I/O) as in the previous example; in this case, the speedup would only be S^cluster = 25. In some cases, we could observe a superlinear speedup. For example, the running time of the problem requiring 100 h on a single node could be less than one hour when running on 100 nodes; in this case the speedup would be S > 100. The superlinear speed-up is often a consequence of a better performance of the memory system, namely a more efficient utilization of the cache, and/or virtual memory (less paging) for each node.

Fig. 1.

Factors affecting the efficiency of a parallel algorithms and the means to increase the speedup of a parallel program.

When there is a load imbalance among the nodes, the speedup is considerably smaller than optimal, where S_opt = P. High communication latency among nodes is another factor that can lead to inefficient execution of a parallel program and low speedup. Indeed, during the time required to send a single byte of data across the interconnection network of a parallel system the processor can execute several million instructions. Yet, many parallel algorithms require a substantial level of communication among nodes. For example, to compute the DFT of a 3D density map corresponding to the model we can partition the data in z-slabs (sets of adjacent x–y planes) and distribute the slabs among the P nodes. Then, we compute 2D DFTs of individual x–y planes (as 1D DFT along x followed by 1D DFT along y). The next step involves a global exchange when each node sends a block of its own data to every other node and, in turn, receives a block of data from every other node. At the end of this communication phase, each node ends up with say y-slabs (sets of adjacent x–z planes) and can perform a 1D DFT along z. If individual nodes are assigned slabs with very different numbers of planes, then the load is imbalanced. Even if we are able to balance the load by assigning an equal number of planes to each node, the speedup will not be linear due to the inherent communication costs of the algorithm.

Given the above considerations, data should be distributed carefully across nodes to minimize communication costs. For example, distributing the electron density map in our alignment algorithm could result in excessive communication; as is discussed later (Section 2.3), we have to construct cross-sections with different orientations in the 3D DFT of the electron density map, thus we need access to the entire map in each node. A solution is to keep a copy of the entire (or up to certain resolution) 3D DFT of the electron density map in every node. In this case, we trade off space for communication latency, therefore data replication in each node reduces the need of nodes to communicate with each other and increases space costs.

Space limitations are of major concern regardless of whether the algorithm is sequential or parallel. If the amount of local cache and of physical memory available for program code and data structures falls below a certain threshold, then the execution time could increase dramatically because the caching strategies as well as the virtual memory replacement algorithms may no longer be able to hide the considerably larger latency of primary storage (in case of cache management), or secondary storage devices (in case of virtual memory management).

For example, it is unfeasible to keep the 10 GB required for the image data set at 6 Å resolution (see Table 1) in the virtual memory of a system with physical memory of 1 GB. On the other hand, when we distribute the data across 100 nodes, the space requirement for each node reduces to 100 MB (=10 GB/100 nodes). At that time when analysis of structures by cryoTEM methods at 3 Å resolution becomes feasible (here the electron density map could be 4 GB or more for larger viruses, as seen in Table 1), the strategy to replicate the electron density in every node requires systems with considerably larger physical memory per node (10 GB or more). To reduce memory requirements we have to distribute the 3D DFT map across nodes. In this case, we trade off communication cost for space, therefore data distribution reduces the space and increases the communication costs.

The system we choose to run a parallel program should be well balanced and match the algorithm. Consider, for example, a situation involving fine grain computation, in which the nodes communicate frequently with one another. In this instance, to our dismay we observe that, if computations are performed on a system with faster processors and an interconnection network with the same speed as our current system, the speedup may actually decrease. The same effect could be observed if the new system does not have enough cache and/or physical memory in each node to match the faster processors. In both cases, the mismatch between the computation bandwidth (number of computer instructions executed per second) and the communication, memory, or input/output (I/O) bandwidth (number of bytes transferred per second between two nodes, or between the memory and the CPU, or between the I/O device and memory) simply slows down the computation; the faster CPU ends up waiting for the slower system components to finish their tasks.

Parallel algorithm and program development is a highly non-trivial process. It is rare that a sequential algorithm can be parallelized without major alterations of the logic and of data structures used. In addition to numerous tradeoffs inherent to the design of a parallel algorithm, various traps (e.g., race conditions and deadlocks) posed by concurrent execution arise and must be properly handled. Even worse, families of algorithms must be developed to solve a particular problem wherein each algorithm is tailored to a particular system architecture and system configuration and a range of problem sizes (Marinescu et al., 2001). Any of these aspects may frustrate the desire to switch from sequential to concurrent computations. Sequential computations require very little understanding of computer architecture. On the other hand, parallel (concurrent) computations are difficult to master, yet offer the only practical alternative for data-intensive problems, similar to those posed by structural biology (see Rao et al., 1995).

The parallel orientation refinement algorithm developed at NIH several years ago (Johnson et al., 1994) uses a sequential algorithm to process independently individual experimental views. Our algorithm (i) makes no assumptions about the symmetry of the object; (ii) constructs cross-sections of the DFT of the electron density map instead of projecting the current model and then performing a 2D DFT of each projection; (iii) uses a multi-resolution rotational and translational refinement scheme; and, finally, (iv) uses a sliding window mechanism similar to that described in an earlier study (Baker et al., 1997). The algorithm is used in conjunction with our 3D reconstruction algorithm in Cartesian coordinates for objects without symmetry (Lynch et al., 1999; Marinescu et al., 2001; Marinescu and Ji, 2003).

2. A parallel algorithm for origin and orientation refinement

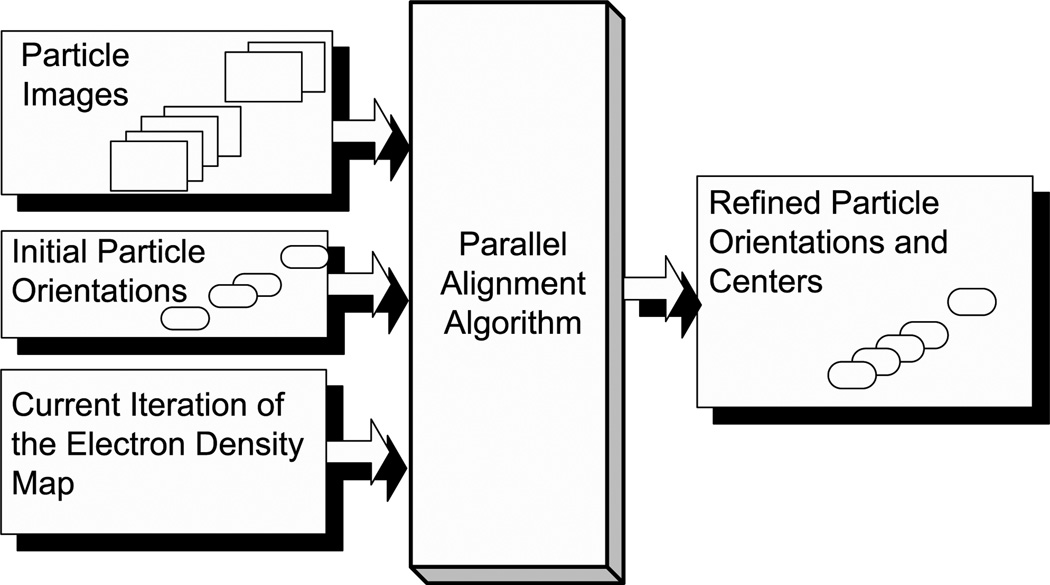
Data flow in the origin and orientation refinement algorithm is illustrated in Fig. 2. The main computation steps of the algorithm discussed in Section 2.2 are schematically represented in a flow chart (Fig. 3).

Fig. 2.

The input and the output of the origin and orientation refinement algorithm.

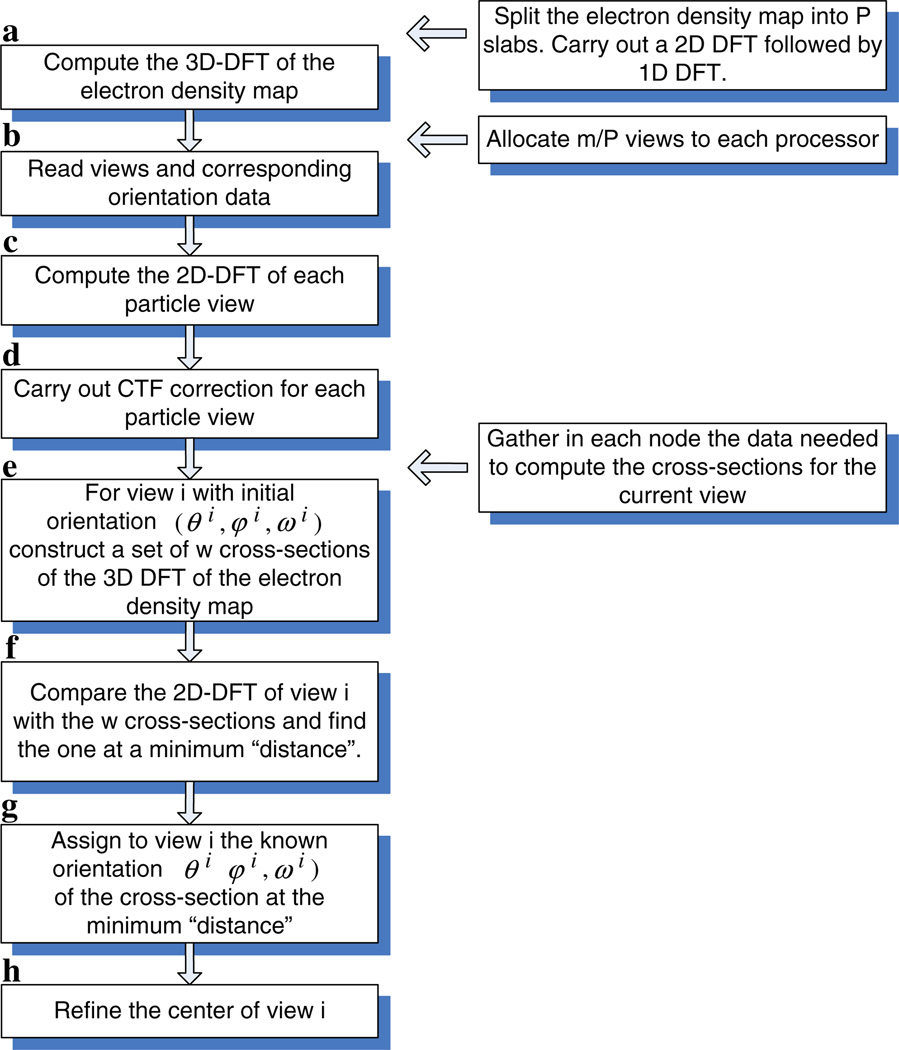
Fig. 3.

The main computation steps for the sequential algorithm (left). The data distribution across nodes for the parallel version of the algorithm (right).

2.1. Terms and notations

We use the following terms and notations:

• D is the current version of the electron density map of size l³.

• 𝒟 = DFT (D) is the 3D DFT of the electron density map.

• 𝒞 is a set of 2D planes of 𝒟 by interpolation in the 3D Fourier domain.

• ℰ = {ℰ¹, ℰ², … ℰ^q, … ℰ^m} with 1 ≤ q ≤ m is the set of m experimental views; each view is of size l × l pixels.

• ℱ = {ℱ¹, ℱ², … ℱ^q, … ℱ^m} is the set of 2D DFTs of experimental views. Here, ℱ^q = DFT (ℰ^q) for 1 ≤ q ≤ m.

• $O_{\text{init}}=\{O_{\text{init}}^1,O_{\text{init}}^2,\dots ,O_{\text{init}}^q\dots ,O_{\text{init}}^m\}$ is the set of initial orientations, one for each view. $O_{\text{init}}^q=\{{\theta }_{\text{init}}^q,{\varphi }_{\text{init}}^q,{\omega }_{\text{init}}^q\}$.

• $O_{\text{refined}}=\{O_{\text{refined}}^1,O_{\text{refined}}^2,\dots ,O_{\text{refined}}^q\dots ,O_{\text{refined}}^m\}$ is the set of refined orientations, one for each view, $O_{\text{refined}}^q=\{{\theta }_{\mathrm{\mu }}^q,{\varphi }_{\mathrm{\mu }}^q,{\omega }_{\mathrm{\mu }}^q\}.$.

• P is the number of nodes available for program execution. Note that parallel I/O could reduce the I/O time but in our algorithm we do not assume the existence of a parallel file system. To avoid contention a master node typically reads an entire data file and distributes data segments to the nodes as needed.

• Given a 3D lattice D of size l³ we define a z-slab of size z-slab_size to be a set of consecutive z-slab_size xy-planes. One can similarly define x- and y-slabs.

• The resolution of the electron density map is denoted by r.

• The window size, the range of values for the rotational or for the translational search, is denoted by w.

2.2. Informal discussion of the algorithm

The origin and orientation refinement algorithm implemented in the PO²R program is designed for a distributed-memory system, such as a cluster of PCs. The algorithm is embarrassingly parallel, as each experimental view can be processed independently by a different processor. On a shared-memory system we would need one complete copy of the electron density map and of its 3D DFT. On a distributed memory system the electron density map and its 3D DFT are replicated on every node or groups of nodes with shared memory in order to reduce communication costs. An alternative is to implement a shared virtual memory where 3D “bricks” of the electron density or its DFT are loaded into each node when they are needed, in a manner that has been developed for analysis of crystallographic data (Cornea-Hasegan et al., 1993).

Our new algorithm makes direct use of the Projection Theorem. A 2D DFT of each experimental view is first computed, then CTF corrections are applied, and the corrected 2D DFT is finally compared with a series of central-sections of the 3D DFT of the current reconstructed (‘model’) density map. This series of central sections is chosen to assure that their orientations span the current best estimate of the object’s orientation (Ji et al., 2003).

A “distance” metric is then computed, which provides a quantitative measure of the correspondence between the 2D DFT of an experimental view and each of the calculated cross-sections of the 3D DFT of the model. A successful search identifies the calculated cross-section that most closely matches (i.e., is at minimum “distance” from) the 2D DFT of the selected experimental view. The “distance” is computed as a function of the real and imaginary parts of two 2D arrays of complex numbers. A “matching operation” consists of two steps: (1) construct a cross-section of 𝒟 with a given orientation and (2) compute the distance between the 2D DFT of the experimental view, ℱ^q, and the computed cross-section.

Besides the “distance” metric, we also employ three other metrics to compare the 2D cut and the 2D DFT of an experimental view: (1) the amplitudes of both 2D DFTs; (2) the phases of both 2D DFTs; (3) the correlation coefficient of both DFTs. Our tests suggest that “distance” metric is preferable over the others.

The orientation of an object that is viewed in projection in a particular image is specified by three angles (θ, ϕ, ω) (Klug and Finch, 1968). Given an initial orientation of an experimental view, a search is conducted within a restricted range for each of these angles, first in steps of 1°, then in finer (0.1°) steps around the more precise value obtained during the previous iteration, and finally in 0.01° steps (Table 2). A similar shrinking search window strategy is used to refine the centers (origins) of the experimental views. This graded-grid search reduces the number of matching operations for a single experimental view. The advantage of this approach is clearly illustrated by an example: consider a search that is restricted to just the θ angle and assume that the initial estimate for θ is 65°, that the search domain spans from θ = 60° to θ = 70° and a refinement step of 0.01° is used. This hypothetical example would require 1000 matching operations compared to the 30 that would be needed in a graded-search procedure, and hence would consume roughly 33 (=1000/30) times more CPU cycles and increase accordingly the execution time. The difference between the two approaches becomes much more dramatic when a full three-angle search is performed, in which case the computed cost for a single-step search rises to a factor of 37 × 10³ (=(1000/30)³). The graded-search procedure reduces the number of matching operations for a single experimental view by more than four orders of magnitude. As has been discussed, with the prospects of needing several thousand or more experimental views to reconstruct a 3D electron density map at high resolution, the final savings in terms of CPU cycles and execution time are substantial.

Table 2.

The time for different steps of the origin and orientation refinement for reovirus using 7937 projections with 511 × 511 pixels/projection running on 42 CPUs

Refinement step size (degree)	1	0.1	0.01
3D DFT (min)	2	2	2
Read images (min)	23	23	23
DFT analysis (min)	2	2	2
Refine time (min)	220	280	264
Total time (min)	247	307	291

DFT size is 768³. Refinement step sizes of 1°, 0.1°, and 0.01° were implemented. For each refinement cycle the search range for each of the three angles θ, ϕ, and ω is 11 times the step size. For example if θ = 49° and the step size is 0.1°, then the search range would be from 48.5° to 49.5°.

A graded search, and, for that matter, any heuristic used to solve a global optimization problem (e.g., simulated annealing, genetic algorithms, neural networks), runs the risk of leading to a local, rather than global optimum. Yet, the algorithm presented in this paper only refines the coarse orientation obtained in a previous step of the structure determination. This problem is not discussed in depth in this paper. We note however, that the coarse orientation search starts with no a priori knowledge of the orientation of each view and leads to a set of coarse orientations after several iterations. As a precaution, we repeat the process starting from different sets of random orientations, and, if the results are consistent, then we decide that indeed we have found the optimal coarse orientation of each view.

Our algorithm implements a sliding window strategy that reuses and hence eliminates the need to recalculate cuts of the 3D DFT of the electron density map. During computation of the distance metric between an experimental view and a set of calculated cross-sections, if the corresponding set of orientation values at minimum distance occurs near the edge of the search window, the window is re-centered and a new grid of metrics is computed.

The algorithm we have developed requires fewer arithmetic operations and less space than traditional model-based methods. With traditional methods, 𝒪(l³) operations are needed to calculate a projection and 𝒪(l² log l²) are needed to calculate 2D DFT from the projection. Conversely, to obtain a cross-section from a 3D DFT lattice of dimension l³, we need only compute the 3D DFT of the reconstructed density map once, and then 𝒪(l²) arithmetic operations are sufficient to calculate each cross-section. We can also save space; when computing the cross-sections for a range of angles we need data in the 3D DFT domain only within the cone (θ_min − Δ_θ, ϕ_min − Δ_ϕ, ω_min − Δ_ω) ≤ (θ, ϕ, ω) ≤ (θ_max + Δ_θ, ϕ_max + Δ_ϕ, ω_max + Δ_ω). Yet, implementing this space-saving strategy requires substantial bookkeeping.

One advantage of this algorithm is that it does not incorporate any assumptions about the symmetry of the object, but has the potential to detect symmetry if present. A future enhancement of the algorithm will incorporate the detection of symmetry. When the symmetry is known, the search process for orientation determination can be restricted to a smaller angular domain, the asymmetric unit. We consider the more challenging case when the information regarding the symmetry of the virus particle is not available. The method described here provides a means to study the structure of the symmetric protein shell and also the structure of asymmetric objects. Moreover, if the virus exhibits symmetry this method allows us to determine the symmetry group.

The size of the search space 𝒫 is very large; if the initial orientation of an experimental view, ℰ^q is given by O^q = {θ^q, ϕ^q, ω^q} then the cardinality of the set 𝒫 is:

$$|𝒫|=\frac{{\theta }_{\text{max}}^q-{\theta }_{\text{min}}^q}{r_{\text{angular}}}\times \frac{{\varphi }_{\text{max}}^q-{\varphi }_{\text{min}}^q}{r_{\text{angular}}}\times \frac{{\omega }_{\text{max}}^q-{\omega }_{\text{min}}^q}{r_{\text{angular}}}.$$

This step requires 𝒪(l² × |𝒫|) arithmetic operations. For example, if the desired angular precision is r_angular = 0.1° and the search range is 0 < (θ, ϕ, ω) < π for all three angles (the range is limited to the range 0 < θ < π because of the singularities in the Euler angle system of coordinates at θ = 0 and θ = π), then the size of the search space is very large: |𝒫| ≈ (1800)³ ≈ 5:8 × 10⁹.

The algorithm incorporates a straightforward way to apply CTF corrections. Each experimental view is CTF corrected before orientation refinement (see Marinescu and Ji, 2003). To compensate for the attenuation of Fourier amplitudes at high spatial frequencies for EM-derived data, an amplification function was also applied to the DFTs of experimental images and to the 3D model. The amplification function is defined by the heuristic inverse temperature factor. The magnitude of the temperature factor is selected by closely monitoring the shapes of the Fourier shell correlation coefficient curves computed from two independent reconstruction maps.

An important advantage of our algorithm for orientation refinement is a straightforward implementation of the CTF correction (see Marinescu and Ji, 2003). We also apply to the 2D DFT of each experimental view the CTF correction and an attenuation factor which takes into account the inverse temperature factor. We also multiply the 3D DFT of the electron density map with an inverse temperature factor before computing the cuts. The magnitude of the inverse temperature factor is selected by trial and error using the correlation factor between two electron density maps (in our case between the ones using only odd and even experimental views) as the optimization criteria.

2.3. Formal description of the algorithm

The “distance” metric between the following two l × l arrays of complex numbers, ℱ = [a_{j, k} + ib_{j, k}]_{1≤j, k≤l}, and 𝒞 = [c_{j, k} + id_{j, k}]_{1≤j, k≤l}, with $i=\sqrt{-1}$. is computed as:

$$d(ℱ,𝒞)=\frac{1}{l^2}\sum _{j=1}^l\sum _{k=1}^l\sqrt{({[a_{j,k}-c_{j,k}]}^2+{[b_{j,k}-d_{j,k}]}^2)}.$$

To determine the distance, d(ℱ, 𝒞) at spatial resolution r we use only the Fourier coefficients up to $\frac{1}{r}$; thus the number of operations is reduced accordingly.

The orientation refinement algorithm consists of the following steps (see Fig. 3):

• Step a
  Construct 𝒟, the 3D DFT, of the electron density map.

  1. The master node reads all z-slabs of the entire electron density map D.
  2. The master node sends to each of the other nodes a z-slab of the electron density map D of size $t_{\text{slab}}=\lceil \frac{1}{P}\rceil$.
  3. Each node carries out a 2D DFT calculation along the x- and y-directions on its z-slab.
  4. A global exchange takes place after the 2D DFT calculation and each node ends up with a y-slab of size t_slab.
  5. Each node carries out a 1D DFT along the z-direction in its y-slab.
  6. Each node broadcasts its y-slab.

After the all-gather operation each node has a copy of the entire 𝒟. To perform calculations at resolution r we only keep a subset of the 𝒟, within a sphere of radius $\frac{1}{r}$. This step requires a total of 𝒪(l³ × log₂(l³)) arithmetic operations and 𝒪(l³) words of memory in each node.

• Step b
  Read in groups of views and the corresponding orientation data.

  1. Read in groups of $m\prime =\lceil \frac{m}{P}\rceil$ views, ℰ, from the file containing the 2D views of the virus, and distribute them to all the processors. The amount of space required to store the experimental views on each processor is: m′ × (b × l²) with b the number of bytes per pixel. In our experiments b = 2 or 4.
  2. Read the orientation data file containing the initial orientations of each view, $O_{\text{init}}=\{O_{\text{init}}^1,O_{\text{init}}^2,\dots ,O_{\text{init}}^q\dots ,O_{\text{init}}^m\}$. Distribute the orientations to processors such that a view ℰ^q and its orientation $O_{\text{init}}^q$, 1 ≤ q ≤ m, are together.

At a given angular resolution we perform the following operations for each experimental view ℰ^q, 1 ≤ q ≤ m:

• Step cCompute ℱ^q. Each processor carries out the transformation of the m′ views assigned to it. This step requires 𝒪(l² × log₂(l²)) arithmetic operations for each experimental view and 𝒪(l²) words of memory for the data.
• Step d
  Perform the CTF-correction of the DFT of each view ℱ^q, 1 ≤ q ≤ m. Use the CTF-factor, τ^q to correct every Fourier coefficient $(a_{j,k}^q,b_{j,k}^q)$ of ℱ^q and obtain a new value $({\alpha }_{j,k}^q,{\beta }_{j,k}^q)$:

  • ${\alpha }_{j,k}^q+i{\beta }_{j,k}^q=(a_{j,k}^q+i{b}_{j,k}^q)\times {\tau }_{j,k}^q$,
  • 1 ≤ (j, k) ≤ l,
  • 1 ≤ q ≤ m.

Note that the views originated from the same micrograph have the same CTF-factor, τ^q. This step requires 𝒪(l²) operations for each experimental view.

• Step e
  Given:

  1. the experimental view ℰ^q with the initial orientation $O_{\text{init}}^q=\{{\theta }_{\text{init}}^q,{\varphi }_{\text{init}}^q,{\omega }_{\text{init}}^q\}$,
  2. the search domain,

     • $0\le {\theta }_{\text{min}}^q\le {\theta }_s^q\le {\theta }_{\text{max}}^q\le \pi$,
     • $0\le {\varphi }_{\text{min}}^q\le {\varphi }_s^q\le {\varphi }_{\text{max}}^q\le 2\pi$,
     • $0\le {\omega }_{\text{min}}^q\le {\omega }_s^q\le {\omega }_{\text{max}}^q\le 2\pi$.

Construct a set of 2D-cuts of 𝒟 from the 3D DFT of electron density map by interpolation in the 3D Fourier domain. Call ${𝒞}^q=\{{𝒞}_1^q,{𝒞}_2^q,\dots {𝒞}_s^q,\dots {𝒞}_w^q,\}$ the set of planes spanning the search domain for ℰ^q. Call $O_s^q=\{{\theta }_s^q,{\varphi }_s^q,{\omega }_s^q\}$ the orientation of the cut ${𝒞}_s^q$.

Call w the number of calculated cuts in 𝒟 for a given angular search range and angular resolution. w = w_θ × w_ϕ × w_ω. Typical values are w_θ = w_ϕ = w_ω = 10, thus w = 1000.

This step requires 𝒪(w × l²) arithmetic operations for each experimental view.

• Step f
  Compute the distance of ℱ^q to every ${𝒞}_s^q$ and find the minimum distance.

  1. Determine the distance of ℱ^q to every ${𝒞}_s^q,d_s^q=d({ℱ}^q,{𝒞}_s^q)$ for 1 ≤ s ≤ w. This requires 𝒪(w × l²) arithmetic operations for each experimental view.
  2. Compute the minimum distance: $d_{\mathrm{\mu }}^q=\text{min}\{d_1^q,d_2^q,\dots ,d_w^q\}$. Call $O_{\mathrm{\mu }}^q$ the orientation of the cut ${𝒞}_{\mathrm{\mu }}^q$,

     $$O_{\mathrm{\mu }}^q=\{{\theta }_{\mathrm{\mu }}^q,{\varphi }_{\mathrm{\mu }}^q,{\omega }_{\mathrm{\mu }}^q\}.$$

     This requires 𝒪(w) arithmetic operations for each experimental view.
  3. If any of the three angles corresponding to the minimum distance cut $O_{\mathrm{\mu }}^q=({\theta }_{\mathrm{\mu }}^q,{\varphi }_{\mathrm{\mu }}^q,{\omega }_{\mathrm{\mu }}^q)$ is at the edge of the original search domain defined in step (f), redefine the search domain. Make $O_{\mathrm{\mu }}^q$ the center of the new search domain, and repeat step (f).

Call n_window the number that we slide the window with. Then the total number of operations required for each view in this step is: 𝒪(n_window × w × l²).

• Step gAssign to experimental view ℰ^q the orientation of the minimum distance cut, $O_{\mathrm{\mu }}^q$.
• Step h
  Refine the position of the center of the 2D DFT.

  1. Move the center of ℰ^q, $(x_{\text{center}}^q,y_{\text{center}}^q)$ within a box of size 2δ_center using the current orientation and determine the best fit with the minimum distance cut ${𝒞}_{\mathrm{\mu }}^q$. For each new value of the center $(x_{\text{center},\mathrm{i}}^q,y_{\text{center},\mathrm{i}}^q)$, determine the distance to ${𝒞}_{\mathrm{\mu }}^q$:

     $$d_{\mathrm{\mu },i}^q=d({ℱ}_i^q,{𝒞}_{\mathrm{\mu }}^q).$$
  2. Find the minimum distance: $d_{\mathrm{\mu },\text{opt}}^q=\text{min}\{d_{\mathrm{\mu },1}^q,d_{\mathrm{\mu },2}^q,\dots d_{\mathrm{\mu },n_{\text{center}}}^q\}$, where n_center is the number of center locations considered. For example, if we use a 3 × 3 box n_center = 9.
  3. If the $(x_{\text{center},\text{opt}}^q,y_{\text{center},\text{opt}}^q)$ is at the edge of the search box redefine the search box. Make $(x_{\text{center},\text{opt}}^q,y_{\text{center},\text{opt}}^q)$ the center of a new search box, and repeat step h.
  4. Correct ℰ^q to account for the new center.

The total number of operations required for each view in this step is: $𝒪(n_{\text{center}}\times {\delta }_{\text{center}}^2\times l^2)$.

• Step iWait for all nodes to finish processing at a given angular resolution.
• Step jRepeat the computation for the next angular resolution until the final angular resolution is obtained. Then: $O_{\text{refined}}=\{O_{\text{refined}}^1,O_{\text{refined}}^2,\dots ,O_{\text{refined}}^q\dots ,O_{\text{refined}}^m\}$ is the set of refined orientations, one for each view $O_{\text{refined}}^q=\{{\theta }_{\mathrm{\mu }}^q,{\varphi }_{\mathrm{\mu }}^q,{\omega }_{\mathrm{\mu }}^q,x_{\text{center},\text{opt}}^q,y_{\text{center},\text{opt}}^q\}$.
• Step kWrite out the refined orientation file.

As has been discussed (Section 2.1), a structure determination is an iterative process. Refinement is carried out in stages, involving incremental steps to progressively higher resolutions. At resolution r, the most recently refined orientations and centers are used to obtain a new reconstructed density map. This new map is then used to compute a new model 3D DFT, which provides the data for the next round of orientation and origin refinement. This process is repeated until no further improvements as measured by distance or other metrics are obtained. Then the analysis is performed at a slightly higher resolution as long as the refinement leads to progressively better reconstructions. For example, the process may be initiated at relatively low resolution (e.g., 30 Å), and refinement then iterated until no further improvements are observed. The next step is to assess the actual reconstruction resolution using the correlation between two electron density maps (e.g., obtained separately from the odd and even experimental views). For example, at some stage it may be that the reconstruction resolution has reached 20 Å. Then, either this value, or a slightly higher resolution, say 19.9 Å, is used as the new target resolution and refinement is resumed and iterated until no further improvement of the electron density map is achieved. This process continues until the resolution cannot be further increased.

2.4. Zero fill and interpolation errors

The piecewise constant interpolation method discussed in (Lynch et al., 2003) lies at the core of our parallel algorithm presented in Section 2.3. Interpolation in the Fourier domain is required to construct “cuts” at precise orientations through the model 3D DFT and to compare them with the 2D DFTs of the experimental particle images. The same interpolation method was implemented in the parallel 3D reconstruction algorithm in Cartesian coordinates (Lynch et al., 2003; Marinescu and Ji, 2003). In this case the interpolation is used to compute the 3D DFT of the electron density map, knowing the values at non-integral grid points. These non-integral grid points correspond to the intersection of the planes representing the 2D DFT of particle projections with the 3D grid.

Details of the interpolation algorithm are presented elsewhere (Lynch et al., 2003); here we address the problem of embedding a 2D pixel frame of size p × p pixels into a larger array of size w × w (w = kp, k > 1) with the extra entries set equal to zero, before computing the 2D DFT of the pixel frame. Similarly, we consider embedding a 3D electron density map of size l × l × l into a larger volume of size w × w × w with the extra array entries set equal to zero, before computing the 3D DFT of the current electron density map. This operation, called zero filling or floating, affects the accuracy of interpolation as described below.

Computing a 2D DFT reduces to the computation of two sets of 1D DFTs and a 3D DFT reduces to the computation of three sets of 1D DFTs. Thus it is sufficient for this discussion to merely consider 1D transformations of length w. As has already been demonstrated (Lynch et al., 2003), and as expected, zero filling reduces the size of the interpolation errors because it leads to over-sampling in the Fourier domain.

We performed several experiments with synthetic data to show that interpolation errors can be reduced by increasing the value of the zero-fill aspect ratio, k. In the simplest test, we reconstructed a solid sphere of unit density from 2D projections, using increasingly larger values of k and examined the density distribution in the resulting object.

We performed experiments for several sets of values of the following parameters: the number of grid points p on a side of the p × p pixel frame; the diameter d = αp, 0 < α < 1, of the sphere; the number m of randomly oriented frames (projections); and the zero-fill aspect ratio, k. The input p × p pixel frame was enlarged to a kp × kp array with zero-fill. The orientation of its 2D DFT was selected randomly for the m projections. The object was reconstructed at the points of a p × p × p grid. We determined the maximum and minimum pointwise error for various values of the parameters. To learn how the error varied with radius, we computed the mean square error (square root of the sum of the squares of the error) in a set of annular regions inside the test object.

Before the 2D DFT of the pixel frame is computed, the pixel values are embedded in a larger frame with all extra grid points set equal to zero. Errors as a function of the zero-fill aspect ratio k are listed in Table 3. The mean square error decreases from 20–25% for k = 1 to about 2% for k = 4. For a fixed k, when the ratio [diameter/(frame edge)] is kept nearly constant (about 0.79), the mean square error changes only slightly for different pixel frame sizes. In Table 3 the minimum and maximum values of the computed density inside the sphere are also listed. Variations in the reconstructed density are reduced as the aspect ratio increases (Table 3).

Table 3.

Mean square percent error (σ) inside reconstructed uniform spheres and the effect of the zero-fill aspect ratio k on the ratio γ = minimum/maximum reconstructed density of a sphere

Aspect ratio	p = 41	p = 61	p = 81
	d = 32	d = 48	d = 64
	m = 20100	m = 45150	m = 80802
k = 1	σ = 20.16%	σ = 23.38%	σ = 24.41%
	γ = 0.57/1.00	γ = 0.50/1.01	γ = 0.48/1.00
k = 2	σ = 6.92%	σ = 7.97%	σ = 7.77%
	γ = 0.86/1.00	γ = 0.84/1.01	γ = 0.84/1.01
k = 4	σ = 1.63%	σ = 2.11%	No data
	γ = 0.97/1.00	γ = 0.96/1.01

Input: m projections, onto p × p pixel frames, of a sphere having diameter d and unit density.

3. Algorithm limitations and timing results

Lynch observes that “a uniform selection of search points, (θ + Δθ) and (ϕ + Δϕ) results in a grossly non-uniform Euclidian spacing in the (h, k, l) space” (Lynch, 2004).

Indeed, the finite element of the surface area of a sphere with radius R is ΔA = R² sin (θ) ΔθΔϕ. A point on the sphere is characterized by its “latitude” and “longitude”, it is at the intersection of the circle θ = constant (whose radius is equal to zero at the North Pole when θ = 0 and R at the equator, when θ = 90°) and the circle ϕ = constant (whose radius is constant and equal to R). The length of an arc of constant Δϕ is ΔL_ϕ = Δϕ2πR sin θ. ΔL_ϕ is different for different latitudes (values of θ). The length of an arc of constant Δθ, 0 < θ < 180° is ΔL_θ = Δθ2πR. When Δθ = Δϕ the ratio

$$\eta =\frac{\mathrm{\Delta }{L}_{\varphi }}{\mathrm{\Delta }{L}_{\theta }}=\frac{\mathrm{\Delta }\varphi 2\pi R\text{sin}\theta }{\mathrm{\Delta }\theta 2\pi R}=\text{sin}\theta$$

varies significantly, it is equal to 1 for θ = 90°, 0.707 for θ = 45°, and 0.0017 for θ = 0.1°.

A solution is to transform to a different range of angles, then use equi-angular spacing Δθ = Δϕ and finally re-map the results to the original domain. The transformations suggested in (Lynch et al., 2003) are:

1. If 0° ≤ θ ≤ 45° then map this range to 45° ≤ θ′ ≤ 90° by the transformation

   • x′ = z, y′ = y, z′ = −x.
2. If 135° ≤ θ ≤ 180° then map this range to 90° ≤ θ′ ≤ 135° by the transformation

   • x′ = −z, y′ = y, z′ = x.

In addition to the complexity analysis and various tests with synthetic data we carried out several more experiments to assess the quality of the solution and the performance of our programs. The ultimate test of a new algorithm is reflected by the final resolution that can be obtained using the algorithm; this discussion is deferred for Section 4.

A rigorous comparison of the performance of the PO²R program with similar programs would be informative but is not practical at this stage. Such a comparison at minimum requires unrestricted access to a sizeable number of benchmark data sets, but such benchmark data are not available. Even a qualitative comparative analysis would be rather difficult to perform. To our knowledge there are no published results produced by parallel alignment algorithms for structures as large as the ones we report in this paper. Moreover, it would be unfair to compare a parallel program with a sequential one, or to compare a program that does not make any assumption about the symmetry of the virus particle with one that assumes the presence of symmetry. The memory and CPU rate (MIPS or Mflops) of even the most powerful single processor systems available today are insufficient to run our algorithm, or any sequential algorithm, for high resolution origin and orientation refinement of the virus structures presented in this paper.

The objectives of our experiments have thus far been threefold: (a) to verify the validity of our results, (b) to determine if the new algorithms enhance our ability to improve the resolution of structure determinations, and (c) to profile execution time and identify the most time-consuming phases of our algorithm.

The following procedure has been adopted as a means to investigate alignment errors produced by our algorithm:

1. Download structure factor data from the Protein Data Bank (http://www.rcsb.org/pdb/) and convert it to an electron density map;

2. Project the electron density map of the chosen structure at several orientations;

3. Apply the algorithm to determine the view orientation of the projected structure;

4. Compute the alignment errors by comparing the known orientation of the projection with the one determined experimentally.

In all tests with noise-free data carried out at random orientations 10° ≤ (θ, ϕ) ≤ 80° and ω= 0°, the precise orientation (no error) was obtained for refinement step sizes of 1°, 0.1° and 0.01°. Even for a refinement step size Δ_θ,ϕ = 0.001°, the error was no larger than 2Δ_{θ, ϕ}.

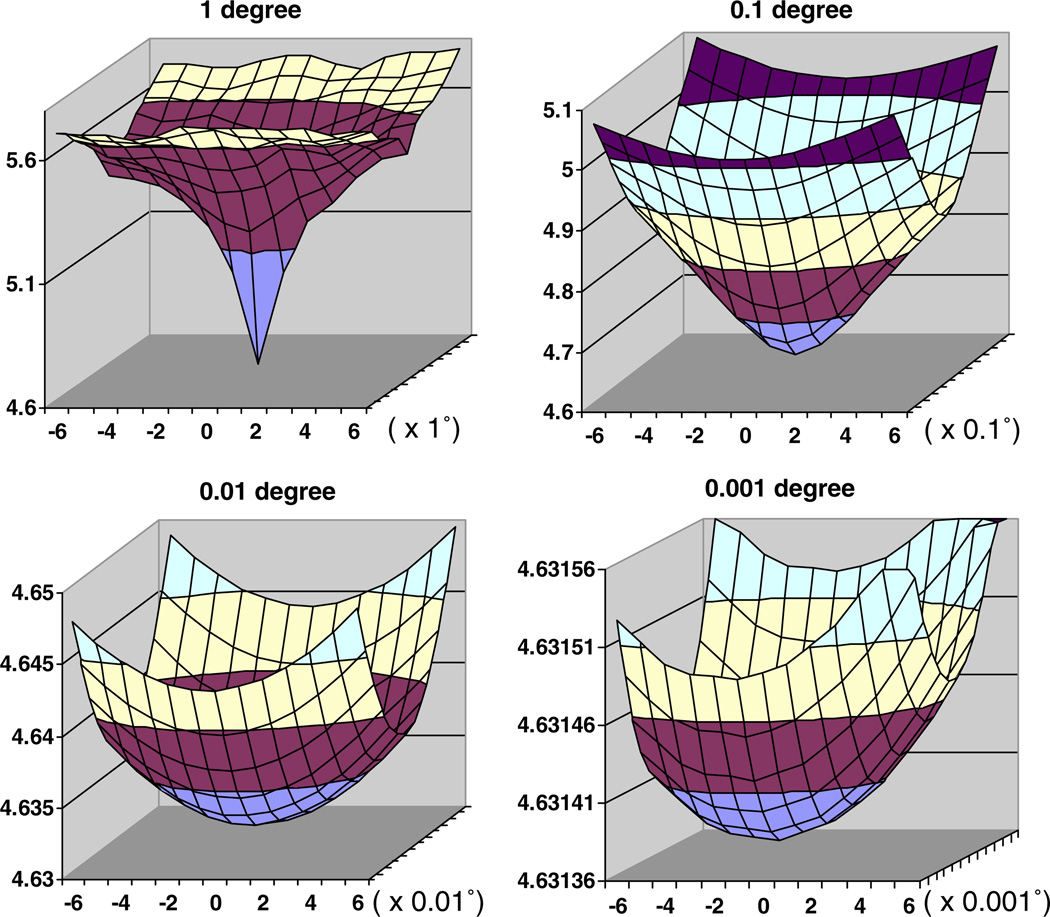
Next, we studied the behavior of the “distance,” Δ_{θ, ϕ}, between calculated cross-sections and an error-free view at a known orientation (Fig. 4). This distance reflects the error in finding the correct orientation. In the absence of interpolation errors, the distance at the center of our plots for noise-free data should be 0.0. Indeed, we are considering higher order interpolation schemes to reduce interpolation errors, instead of the piecewise constant interpolation scheme currently implemented. The plots of the “distance” between the 2D DFT of the cross-sections several Δ_θ,ϕ apart from the exact orientation and the 2D DFT of the cross-section with the precise orientation for Δ_θ,ϕ equal to 1°, 0.1°, 0.01°, and 0.001° show increasing details of the surface. Notice that the range of the values on the vertical axis in Fig. 4 is increasingly smaller and viewed at the same scale the surface ∑(Δ_θ,ϕ,θ,ϕ) for 0.001° step size would look perfectly flat.

Fig. 4.

The “distance” between the 2D DFT of the cross-sections several Δ_θ,ϕ apart from the exact orientation and the 2D DFT of the cross-section with the precise orientation for Δ_θ,ϕ equal to 1°, 0.1°, 0.01°, and 0.001°. In our experiments ω = 0° and 10° ≤ (θ, ϕ) ≤ 80°, the 3D map size is 511 × 511 × 511, and the Fourier space size is 768 × 768 × 768. The “distance” is plotted versus the equi-angular spacing for the two angles θ and ϕ (ω is fixed) in a horizontal plane. The figures show only the range for θ, (−6,…,0,…,+6)× the refinement step size, 1°, 0.1°, 0.01°, and 0.001°. The range for ϕ is identical and it is not shown for lack of space. As we move to increasingly smaller step size we show only the tip of the curve. For example, only the bottom most section of the surface (colored in gray) for the 1° curve is shown at the next smaller step size curve, 0.1°. Notice that the range of the values on the vertical axis is increasingly smaller and viewed at the same scale the surface for 0.001° step size would look perfectly flat. The “distance” converges as we decrease the refinement step Δ_θ,ϕ,ω from 1°, to 0.1°, to 0.01°, and finally to 0.001°.

Our experiments have demonstrated that the orientation parameters for noise-free data can be perfectly refined for refinement step sizes no smaller than 0.01°. In fact, interpolation errors when calculating the projections and the cross-sections become noticeable only for a refinement step size of 0.001°; we can refine the angles to a precision of 0.002°. The execution time increases considerably when a refinement step size of 0.001° is used and such precision is not necessary for any of the virus structures we have studied.

Consider now the execution time required by the parallel program when implementing the algorithms discussed here. For this study, measurements were performed on a cluster of 44 dual processing nodes and a front-end. Each node included two 2.4 GHz Intel Xeon processors and a 512 kbyte L1 cache in each processor. The peak rate of this system is 211.2 Gflops (88 processors × 2.4 GHz/processor). Each node has 3 GB of physical memory, a 30 GB disk, and 2 Gbps Ethernet ports. The front-end consists of a dual processor machine with 2 GB of primary memory, a RAID secondary storage of 280 GB and 4 Gbps Ethernet ports. The interconnection network is a HP Pro-curve switch 4108gl with 48 Gbps Ethernet ports. The total cost of the system acquired in mid 2003 was about $140,000.

The profile of sample execution times for origin and orientation refinement shows slight variations in these times (Table 2). Execution time is data dependent. The sliding window, consisting of the set of calculated cross-sections, has to be adjusted when the best match with the experimental view occurs at the edge of the window and this event may occur at any refinement step size. Partition of the cluster can also create some of the discrepancies in execution times. For the experiments reported here, the PO²R program was run on 42 out of 44 nodes. Programs running on the remaining nodes share the communication bandwidth and the file system with the nodes running PO²R and thus affect the actual running time for PO²R. The running time would be shorter than the one reported here if PO²R had exclusive usage of the system. However, in most instances production environments space share and/or time share a cluster.

The time to: (i) compute the 3D DFT of the model, (ii) read the input data, and (iii) compute the 2D DFTs of all experimental views constitutes about 10% of the total execution time (27/247, 27/307, 27/291). The time to perform these steps varies only slightly when the refinement step size is decreased from 1° to 0.1° and then to 0.01°. If we used a high performance computer with a parallel file system instead of a cluster of workstations, then individual nodes could read the data in parallel and this would reduce the I/O time possibly by one order of magnitude. In this instance, it might also be advantageous to compute the 2D DFTs of the experimental views only once, store them on the secondary storage device, and read them for the next refinement step size. With a cluster of workstations, it would be desirable to first run a pre-processing program that would distribute all experimental views to the nodes and store them on the local disk at each node. For this situation, the reading time for the computations at 0.1° and 0.01° step sizes would decrease significantly. Nevertheless, the impact of this optimization upon the total execution time would be relatively modest, and probably less than 4%.

The time required to compute the necessary cross-sections and compare them with the experimental data (denoted as the refine time in Table 2) comprises the bulk of the execution time.

As has been noted, a limited range of spatial frequencies (f) is used to compare the 2D DFT of an experimental view with a cross-section of the model 3D DFT. In our experiments the spatial frequencies are in the range 1 ≤ f ≤ 384 and we used only frequencies in the range 53 ≤ f_l ≤ 248. Hence, significant reduction of the execution time can be realized if Fourier filtering is employed.

Some 100 iterations (each iteration includes refinements with step sizes 1°, 0.1°, and 0.01°), were necessary to refine the structure of reovirus from about 7.6 Å resolution to obtain the results reported in the next section. This required about 1400 hours, or close to 60 days of running time on 42 nodes of the PC cluster. This of course motivates us to consider further optimizations of the algorithm.

4. High resolution studies of virus structures

The PO²R program has been used by us and others to investigate the structures of several viruses. This includes viruses of medium to moderate size such as dengue virus (DENV: 500 Å diameter) and mammalian reovirus (MRV: 850 Å), and relatively large ones such as chiloiridescent virus (CIV: 1850 Å) and paramecium bursaria chlorella virus 1 (PBCV-1: 1900 Å). For DENV, refinement with PO²R began with a reconstructed density map at 24 Å resolution (Kuhn et al., 2002), and has resulted more recently in a structure at 9.5 Å resolution (Zhang et al., 2003b). PO²R has also been used to refine the structure of MRV from about 7.6 Å resolution to better than 7 Å, and refine the structure of PBCV-1 from about 26 Å resolution to 15 Å (Yan et al., 2005). Brief synopses of our investigations of DENV, MRV and PBCV-1 illustrate a few examples where the new algorithm has successfully enhanced structure determinations.

4.1. Dengue virus

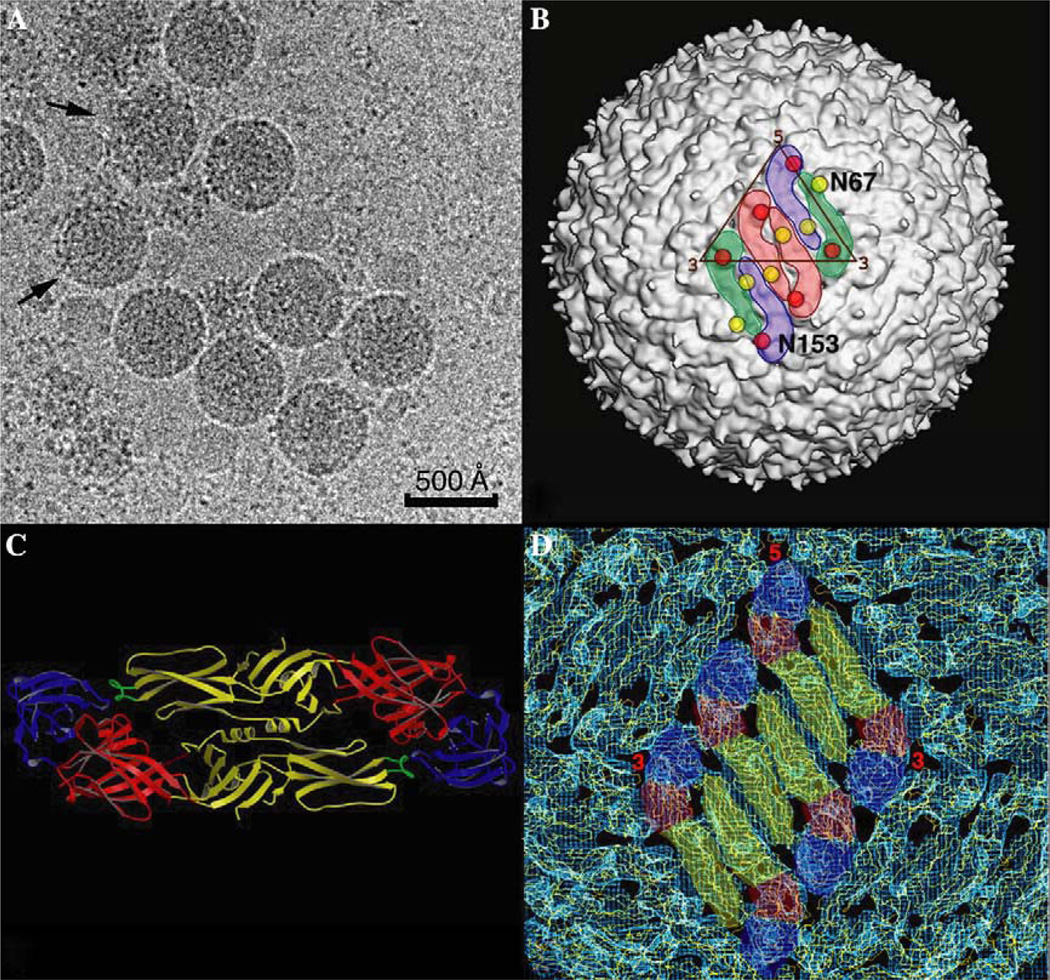
DENV (Flaviviridae family) is an enveloped, plus sense RNA virus that has an icosahedral capsid (500 Å diameter) with a smooth surface morphology (Fig. 5A).

Fig. 5.

DENV Structure. (A) Micrograph of vitrified DENV sample shows particles with a spherical morphology and a smooth outer surface. DENV particles are quite fragile, as evidenced by a significant fraction of disrupted particles (arrows) in the sample. Images of such particles were eliminated from the image reconstruction process. (B) Shaded-surface view of the DENV reconstruction at 14 Å resolution. The outlines of three E protein dimers (arranged in herringbone pattern) are highlighted in color with the dimer at the icosahedral 2-fold axis highlighted in pink and the dimers at a quasi-2-fold axes highlighted in green and blue. The locations of the two carbohydrate moieties in each E protein are depicted with red (residue N153) and yellow (residue N67) circles, respectively. (C) Ribbon diagram of the atomic structure of the E protein dimer (Zhang et al., 2004) with domains I, II and III is colored red, yellow and blue, respectively. The fusion peptide at the tip of domain II is colored green. (D) Atomic modeling of the DENV structure. The a-carbon backbone model of the ecto-domains of the E protein dimer were fitted into the 14 Å DENV reconstruction. The color scheme is the same as that used in (C).

Mature virions contain multiple copies of three different structural proteins: glycoprotein E (495 a.a.) (Modis et al., 2003; Zhang et al., 2004), membrane protein M (75 a.a.), and capsid protein C (100 a.a.) (Ma et al., 2004). Each E protein consists of an ecto-domain (395 a.a.), a stem (about 55 a.a.) and a transmembrane anchor (about 45 a.a.), whereas the M protein contains a small ecto-domain (about 38 a.a.) and transmembrane anchor (about 37 a.a.) (Zhang et al., 2003b). The E ecto-domain has a long, thin morphology and forms dimers in crystals (Fig. 5B) (Modis et al., 2003; Zhang et al., 2004) and (Zhang et al., 2005) in virions (Fig. 5C) (Kuhn et al., 2002; Zhang et al., 2003b).

The structure of DENV virus was recently determined using cryoTEM and image reconstruction methods to 9.5 Å resolution (Zhang et al., 2003b). The starting model for the refinement of the high resolution DENV structure was an earlier reconstruction of DENV that had been determined to 24 Å resolution (Kuhn et al., 2002). To obtain the high resolution structure, an additional set of cryoTEM images was recorded and added to the set used to reconstruct the DENV structure at 24 Å resolution (Table 4). Images of unstained, vitrified DENV virus samples were recorded in a FEI/Philips CM200 field emission gun electron microscope under low dose conditions (about 25 electrons/Ų) at a nominal magnification of 50,000. Micrographs were digitized in a scanning microdensitometer at a step size of 7 µm and the pixels were twofold bin-averaged to yield an effective step size of 2.8 Å at the specimen. The Fourier–Bessel reconstruction method (Crowther, 1971; Fuller et al., 1996) was used to compute three dimensional maps from images. The effective resolution of maps derived in this way was determined from independent reconstructions (e.g., Baker et al., 1999) and employing both phase agreement (<50°) and Fourier shell correlation coefficient threshold (>0.5) criteria.

Table 4.

Data statistics for two DENV reconstructions

	DENV24a	DENV9.5b
Number of micrographs	25	78
Number of particle images	526	1691
Defocus range (µm)	0.79–1.92	0.8–4.8
Starting model	CL&CCLc	DENV24
Refinement program	PFTd	PO2R
Resolution of refined map (Å)	24	9.5

^aDENV₂₄ is the 24 Å DENV virus reconstruction (Kuhn et al., 2002) and was the starting model for PO²R refinement.

^bDENV_9.5 is the 9.5A Å reconstruction (Zhang et al., 2003b).

^cDerived by use of common lines and cross-common lines procedures (Fuller et al., 1996).

^dPolar Fourier transform algorithm (Baker and Cheng, 1996).

The use of PO²R has lead to a reconstruction at a much higher resolution (9.5 vs 24 Å), and hence finer details of the DENV structure are interpretable and molecular boundaries are better defined (Fig. 6). The 9.5 Å DENV map (DENV_9.5) shows clear densities that can be attributed to the membrane bilayer, 180 copies of glycoprotein E and 180 copies of envelope protein M. The carbohydrate moieties on the E proteins, which were not distinguished at 24 Å, were clearly visible at the surface of the virus in the 9.5 Å reconstruction. Also, individual domains in each E protein and the β-barrel structures in the first and the third domains were clearly depicted in the DENV_9.5 reconstruction. Conversely, in the 24 Å reconstruction (DENV₂₄), only holes between the two E molecules in the dimer interface could be recognized, and the molecular boundaries between the E protein dimers could not be resolved.

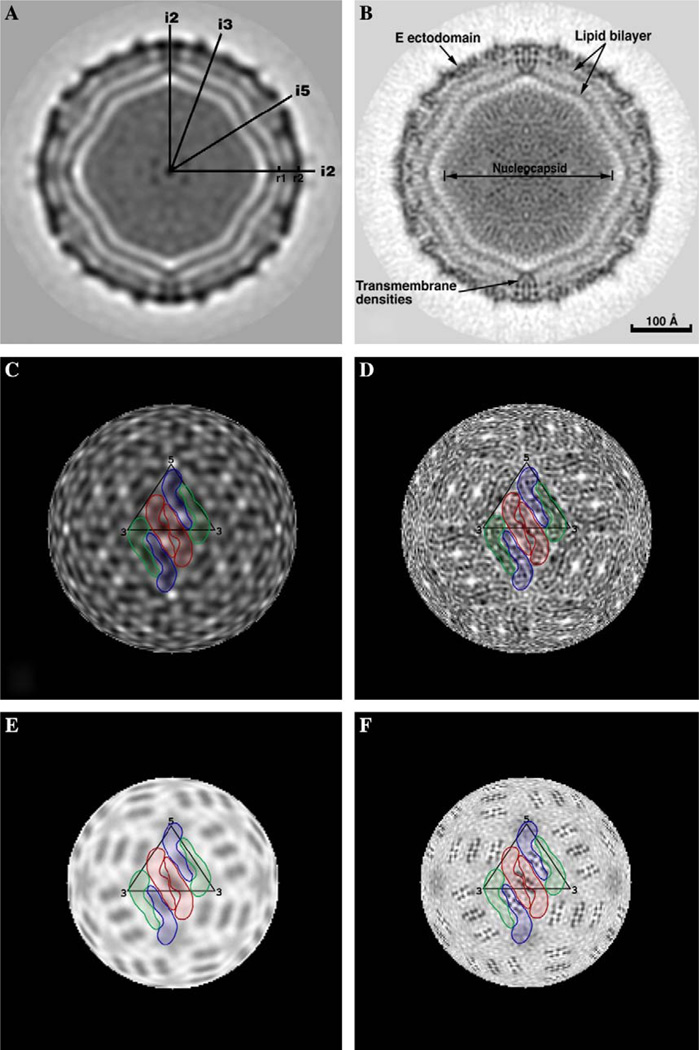
Fig. 6.

Comparisons of the DENV₂₄ (A, C, E) and DENV_9.5 (B, D, F) reconstructions without inverse temperature factor. (A) Equatorial section from DENV₂₄ reconstruction. The darkest densities correspond to protein, lipid and nucleocapsid components. Icosahedral 2-, 3-, and 5-fold axes are labeled i2, i3 and i5, respectively. The mark at r1 identifies the center of the membrane bilayer at radius 185 Å. The center of mass in the outer protein shell, comprised of the E protein ecto-domains at radius 221 Å, is labeled r2. (B) Same as (A) for DENV_9.5. The scale bar is the same for all panels. (C) Radial projection of DENV₂₄ at a radius of 221 Å (r2 position in (A)). Three E protein dimers are highlighted in colors (same scheme used in Fig. 5B). (D) Same as (C) for DENV_9.5. The herringbone pattern of E protein dimers is evident at this resolution. (E) Same as (C) at a radius of 185 Å (r1 position in (A)). The transmembrane domains of the E and M proteins are not resolved. (F) Same as (E) for DENV_9.5. The eight dark, punctate features (in four groups of two) associated with each dimer are attributed to eight transmembrane helices, with two copies attributed to each E and M monomer.

Though not resolved in DENV₂₄, distinct features corresponding to the stem and transmembrane anchor regions of the E protein were observed in the DENV_9.5 reconstruction. Likewise, densities attributed to the stem and transmembrane regions of the M (membrane) protein were also identified in the higher resolution DENV map. The lack of distinct spikes in mature DENV particles creates one of the biggest challenges in the image reconstruction process, because the presence of large, well-defined features often facilitates the refinement of origin and orientation parameters. Successful refinement algorithms are those that are very sensitive to small variations in the projected images of particles viewed in slightly different orientations. The PO²R program has provided a useful means to refine the DENV structure to subnanometer resolution.

4.2. Reovirus

The PO²R program is well suited for extending the resolution of existing reconstructed density maps, even when no new image data are available. This was true in our investigation of the structure of the mammalian reovirus (MRV), where the use of PO²R was instrumental in extending the resolution from 7.6 Å (Zhang et al., 2003a) to 7.0 Å and better (Zhang et al., 2005). Mammalian reoviruses (Reoviridae family) are non-enveloped, double-strand RNA (dsRNA) viruses. MRV virions contains ten dsRNA segments and two concentric capsid shells with an outer diameter of 850 Å. The outermost layer contains 200 μ1₃σ3₃ heterohexamers arranged with incomplete T = 13 quasi-symmetry. Beneath this lies the T = 1 reovirus core, comprised of 60, 150, and 120 copies of the λ2, σ2, and λ1 viral protein subunits, respectively.

In an earlier study of MRV, a reconstructed map of T3D virions had been refined to 7.6 Å (T3D_7.6) through use of a program called OOR (orientation and origin refinement) (Zhang et al., 2003a). Based on correlation with atomic models derived from X-ray crystal structure studies, in this map it was possible to recognize all 342 α-helices (five or more residues) and all 92 β-sheets (three or more strands) in the viral subunits within one asymmetric unit of the icosahedral structure (Zhang et al., 2003a). The PO²R algorithm was subsequently used to refine the origin and orientation parameters for the set of images from which the T3D_7.6 reconstruction was computed and this has enabled us to improve the quality of the T3D map to 7.0 Å (T3D_7.0) and higher (see Figs. 7 and 8, Table 5 in Zhang et al., 2005). All of the secondary structural features seen in the T3D_7.6 map appear more clearly in the T3D_7.0 map, which testifies to the robustness of the new PO²R algorithm. The new map also reveals details of several loop structures, and more importantly reveals several new structural features in the μ1 protein that were invisible in the μ1₃σ3₃ heterohexamer X-ray structure where portions of μ1 are presumably disordered and flexible. Among the new features, spoke and hub-like structures are formed by the C-terminal residues of μ1 at the so-called P2- and P3-channels in the outer capsid, a U-shaped loop structure is formed by residues 72–96, and the stretch of eight residues at the N-terminus follow a radial trajectory from the base of the μ1 subunit upwards to the mouth of a hydrophobic cavity in μ1 that is believed to accommodate the N-terminal myristoyl group. These new features of μ1 are believed to contribute to virus stability and the process of cell entry (see Figures in Zhang et al., 2005).

Fig. 7.

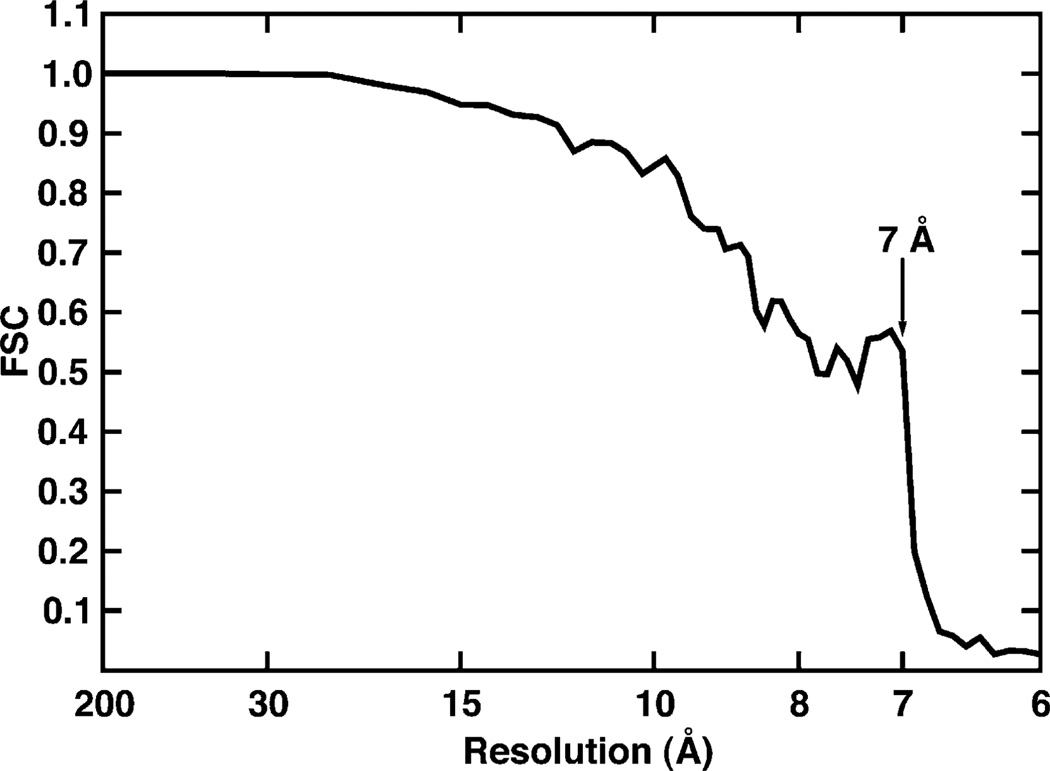
Fourier shell correlation (FSC) plot for MRV T3D virion data. The FSC curve was calculated using T3D maps separately computed from the ‘odd’ and ‘even’ images (e.g., Baker et al., 1999). The effective resolution of the current reconstruction was estimated to be about 7.0 Å (FSC = 0.535 at 7.0 Å). The sharp drop in the FSC curve is a consequence of only using transform data up to approximately 7.0 Å resolution for data refinement, but even and odd maps were computed to higher resolution limits to generate the FSC plot.

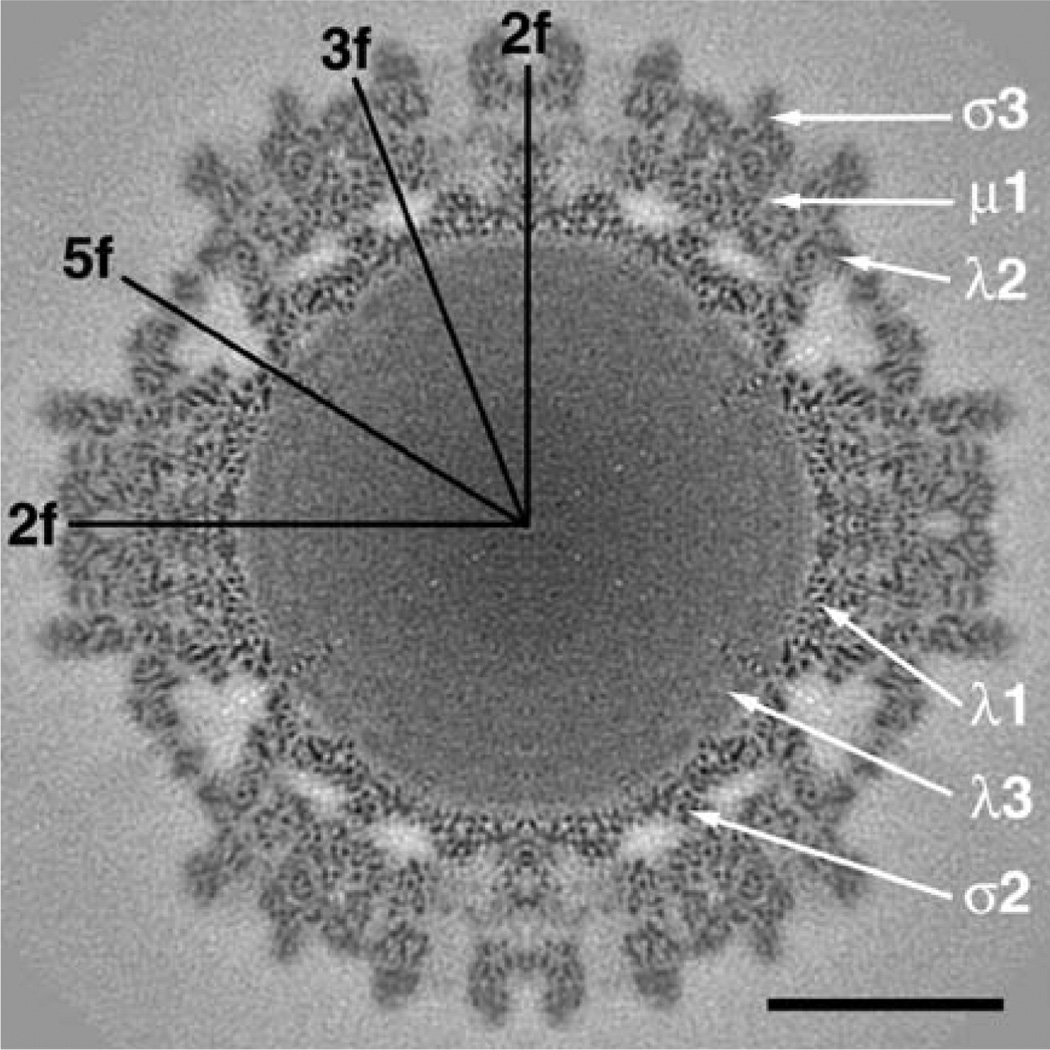
Fig. 8.

Equatorial section from the cryoTEM T3D_7.0 map. The map was computed to a Fourier cutoff of 1/6.7 Å, with structure factor amplitudes gradually attenuated (Gaussian function) to background level between spatial frequencies of 1/7.0 and 1/6.7 Å. In addition, an inverse temperature factor of 1/400 Ų was imposed to enhance the high spatial frequency features in the map. Icosahedral 2-, 3-, and 5-fold axes are indicated along with the approximate positions of six of the T3D structural proteins. Scale bar = 200 Å.

Table 5.

Data statistics for two MRV reconstructions

	T3D7.6	T3D7.0
Number of micrographs	54	54
Number of particle images	7939	7939
Defocus range (µm)	1.3–3.2	1.3–3.2
Starting model	T1L18a	T3D7.6b
Refinement program	OOR	PO2R
Resolution of refined map (Å)	7.6	7.0

^aUnpublished reconstruction of reovirus T1L at 18 Å resolution.

^bPublished 7.6 Å resolution reconstruction of reovirus T3D virions (Zhang et al., 2003a).

4.3. PBCV-1

The PO²R program is particularly well suited for projects that demand significant computer resources. Recent improvements in resolving the structures of several different, very large (>1800 Å diameter), icosahedral viruses have only been made possible through the use of this parallelized refinement protocol. Here we briefly summarize the progress obtained in our structural studies of paramecium bursaria chlorella virus 1 (PBCV-1).

PBCV (genus Chlorovirus, family Phycodnaviridae) infects certain unicellular, exsymbiotic, chlorella-like green algae (Van Etten, 2003). PBCV-1 virions are quite massive (about 1 × 10⁹ Da and over 200 times larger in volume than the common cold virus, human rhinovirus) and contain a linear 330 kbp dsDNA genome and about 50 different proteins. An earlier cryoTEM analysis of PBCV-1 yielded a 3D reconstruction at 26 Å resolution (PBCV₂₆), and demonstrated that the protein capsid has an icosahedral morphology and a maximum diameter of 1900 Å between fivefold vertices (Yan et al., 2000). The bulk of the capsid consists of 1692 capsomers, of which 1680 are trimeric and 12 are pentameric. These capsomers are arranged on a T = 169d (h = 7, k = 8) quasi-symmetric lattice (Yan et al., 2000).

Until recently, we were stymied in our attempts to improve the resolution of the PBCV-1 reconstruction much beyond what had been accomplished previously (Yan et al., 2000). This was due at least in part because both serial and parallel versions of our standard model-based refinement (Baker and Cheng, 1996) and Fourier–Bessel reconstruction (Fuller et al., 1996) routines were incapable of handling the memory demands of processing larger numbers of large images at higher and higher resolution limits. The use of PO²R and a new, parallelized reconstruction program, P3DR (Marinescu and Ji, 2003; Marinescu et al., 2001), have enabled us to improve the PBCV-1 structure determination to 15 Å resolution (Yan et al., 2005) (Table 6).

Table 6.

Data statistics for two PBCV-1 reconstructions

	PBCV26	PBCV15
Number of micrographs	15	45
Number of particle images	356	1000
Defocus range	1.8–2.6 µm	1.4–3.6 µm
Starting model	CL&CCLa	PBCV26b
Refinement program	PFTc	PO2R
Resolution of refined map	26 Å	15 Å

^aDerived by use of common lines and cross-common lines procedures (Fuller et al., 1996).

^bPublished 26 Å resolution reconstruction of PBCV-1 virions (Yan et al., 2000).

^cPolar Fourier transform algorithm (Baker and Cheng, 1996).

Our current reconstruction of PBCV-1 (PBCV₁₅) reveals much more detail of the capsid morphological features compared to that observed in the previous (PBCV₂₆) reconstruction (Fig. 9). The higher resolution map has permitted us to build a more accurate atomic model of the capsid based upon knowledge of the crystal structure of the major capsid protein, Vp54 (Nandhagopal et al., 2002). Indeed, the fine structural details that characterize the PBCV₁₅ density map act to highly constrain the range of possible fits of the Vp54 atomic model into the map. At this and even higher resolutions, such atomic fitting experiments will provide a means to define the presence and locations of several minor capsid proteins.

Fig. 9.

Comparison of 3D image reconstructions of PBCV-1 at low (A and B) and moderate (C) resolutions without inverse temperature factor. (A) Shaded-surface view of PBCV₂₆ reconstruction, viewed along a 3-fold axis of symmetry. (B) Magnified view of the area outlined in (A) showing the close-packed arrangement of doughnut-like capsomers. At 26 Å resolution, the trimeric nature of each capsomer is difficult to recognize. (C) Same area as in (B), but for a view of the PBCV₁₅ reconstruction. At 15 Å resolution, the trimeric character of each capsomer becomes obvious as all capsomers exhibit a clearly defined hexagonal base that is topped with three, tower-like protrusions.

The challenges inherent in refining and reconstructing the structures of large macromolecular complexes like PBCV-1 at moderate resolutions and beyond are fairly obvious. PBCV-1 represents one of the largest, most complex viruses ever studied using cryo-reconstruction methods and its structure determination even at relatively moderate resolution (better than 20 Å) has proved to be challenging in terms of algorithm development and use of computer resources. In fact, with the current set of approximately 1000 images (Table 6) and taking into account the large image size (699² pixels = 2MB), we are unable to refine and reconstruct the PBCV-1 structure even at quite low resolution using a single processor computer. Hence, we have had to rely on the development of newer, parallel programs such as PO²R and P3DR (Marinescu and Ji, 2003) to process data of this magnitude and to do it within reasonable time frames. As investigations move to higher resolutions, which necessitate use of many more images and with smaller pixel and larger box sizes, the processing requirements expand very rapidly and parallelized programs become indispensable tools.

5. Summary and future work

Numerous computational challenges for cryoTEM exist. The most significant are (i) optimize the algorithms for particle identification, origin and orientation refinement, and 3D reconstruction to allow reconstruction at the highest possible resolutions (5 Å or better); (ii) support reconstruction of asymmetric objects at these resolutions; (iii) optimize the algorithms to reduce the computation time by several orders of magnitude. In this paper we report on the development, testing, and utilization of a parallel algorithm for origin and orientation refinement that addresses some of these challenges.

The parallel algorithm (PO²R) described here was designed for a distributed memory, parallel architecture. We first compute a 2D DFT of each experimental view, apply a CTF correction to it, and then compare the corrected 2D DFT with a series of central-sections of the 3D DFT of the current reconstructed density map. These sections are chosen such that their orientations span the current best estimate of the object’s orientation.

The algorithm does not make any assumptions about the symmetry of the object, but can detect symmetry if it is present. Test experiments show that we can refine the orientation of noise-free data without any errors with a refinement step size at least down to 0.01°; interpolation errors for noise-free data become noticeable only for a refinement step size of 0.001° and smaller.

Our algorithm facilitates straightforward implementation of CTF corrections to images and thus allows for more reliable, higher resolution reconstructions. To reconstruct virus structures at very high resolution, we need very “clean” input data, thus CTF corrections must be optimized (Ji et al., 2005) and procedures must be in place to weed-out ‘bad’ images (e.g., from distorted or disrupted particles or that have very low signal to noise ratios). The PO²R program can handle images with different box or pixel sizes and also permits the use of several schemes for attenuating or amplifying the 2D DFT of each experimental view. Each of these schemes can be implemented independently, or in combination with others (as a product), and they all vary as a function of spatial frequency. The theoretical CTF associated with each image can be used to attenuate the influence of noise in the data, especially in the image transform at the nodes of the CTF where the signal-to-noise reaches its minima. Also, an inverse temperature factor by itself or in combination with other functions (e.g., (1/r)^x, where r is resolution and x is set to a value between 0.0 and 2.0) can be used to compensate in part for the rapid fall-off in amplitudes in image transforms that is a result of several microscope envelope functions (e.g., see Thuman-Commike et al., 1999).

The PO²R program has been used extensively during the past few years for 3D reconstruction of viruses with diameters ranging from 500 to 2000 Å. The program has been useful in improving virus reconstructions regardless of what the initial resolution was. PO²R refinement of DENV and PBCV-1 data began with reconstructions at relatively low resolutions (24 and 26 Å, respectively) and led to significant improvements (9.5 Å for DENV and 15 Å for PBCV-1). Though many different strategies were employed in our attempts to improve the MRV reconstruction beyond 7.6 Å resolution, only PO²R has thus far proved capable of extending the resolution to higher levels (to 7.0 Å).

Our algorithm includes several optimizations. Traditional methods require 𝒪(l³) arithmetic operations to calculate a projection and 𝒪(l² log l²) operations to calculate its 2D DFT. To extract a central-section from a 3D DFT of lattice dimension, l³, we compute the 3D DFT of the reconstructed density map only once, and then 𝒪(l²) operations will yield each central-section. The multi-resolution search employed within the PO²R algorithm provides a four orders of magnitude speedup compared with a simple, brute force linear search.

In spite of these optimizations, the computing time required to improve the resolution of a medium-sized virus such as MRV, from about 7.6 Å to better than 7.0 Å on 42 processing nodes, is about 14 h/iteration. Since the entire refinement process in this case included about 100 iterations, the total time taken to improve the resolution from 7.6 to 7.0 Å was about 1400 h, or nearly 60 days. Assuming sufficient memory were available on a single processor system, this refinement process would have taken roughly 2500 days. Conversely, if we had exclusive use of a 1000 node system, the total computing time could be reduced to 3 days or less. Sobering statistics such as these reflect that: (i) significant progress has been made; we would have been unable to address problems similar to the ones reported in this paper without a parallel algorithm; (ii) further optimization of our algorithms is needed and the use of a massively parallel system with 500 or more nodes must be considered in order to solve challenging problems in structural biology. Obviously, a substantial investment of expertise, a financial commitment, and a strong collaborative effort involving structural biologists and computer scientists is essential. To reduce the execution time by significant amounts, we need to consider the use of highly non-trivial optimizations. Use of the Radon Transform (Radermacher, 1997), new distance metrics, different interpolation techniques, and possibly a more refined search algorithm all have the potential to improve data processing. Even relatively simple strategies that have yet to be adopted, such as caching the 3D DFT cross-sections, can reduce computations.

We are currently implementing a space-saving version of the algorithm; when computing the cross-sections for a range of angles we need data in the 3D DFT domain only within the cone (θ_min − Δ_θ,ϕ_min − Δ_ϕ,ω_min − Δ_ω) ≤ (θ,ϕ,ω) ≤ (θ_max + Δ_θ,ϕ_max + Δ_ϕ, ω_max + Δ_ω). However, such a space-saving strategy requires a fair amount of bookkeeping and most likely leads to a longer execution time.

A rigorous and objective comparison of different 3D reconstruction and origin and orientation refinement algorithms is not feasible at this time. Only a standard benchmark would allow us to compare objectively (i) the quality of the solution and (ii) the time required to obtain a high resolution electron density map using different algorithms on the same set of data. Yet, the creation of a Web-based benchmark service requires the cooperation of many laboratories, full disclosure of the algorithms used for data analysis and well-documented source code implementing each algorithm.

Our most recent results include the refinement of the MRV and Sindbis to 6.9 and 8.3 Å resolution.

The PO²R and other parallel programs are available for distribution on our Web site (http://cfl.cs.ucf.edu).