Gap Junction Structures VII ^{Analysis of Connexon Images Obtained with Cationic and Anionic Negative Stains}

Abstract

Micrographs of isolated gap junction specimens, negatively stained with one molybdate, three tungstate and three uranyl stains, were recorded at low and high irradiation. Fourier-averaged images of the negatively stained gap junctions have been self-consistently scaled to identify conserved and variable features. Intrinsic features in the hexagonally averaged images have been distinguished from residual noise by statistical comparisons among similarly prepared specimens. The cationic uranyl stains can penetrate the axial connexon channel, whereas the anionic stains are largely excluded; these observations indicate that the channel is negatively charged. Variability in the extent of the axial stain penetration, and enhancement of this staining by radiation damage and heating may be accounted for by a leaky, labile channel gate. The peripheral stain concentrations marking the perimeter of the skewed, six-lobed connexon image and the stain-excluding region at the 3-fold axis of the lattice, which are seen only under conditions of low irradiation with both anionic and cationic stains, are identified as intrinsic features of the isolated gap junction structure. The stain concentrations located ~30 Å from the connexon center appear to be symmetrically related on opposite sides of the junction by non-crystallographic 2-fold axes oriented ~8° to the lattice axes at the plane of the gap. The radiation-sensitive hexagonal features seen in the negatively stained images may correspond to substructure on the cytoplasmic surfaces of the paired gap junction membranes.

1. Introduction

Gap junctions are built of hexameric connexon units, which are paired to form gated channels extending across the coupled cell membranes (Bennett & Goodenough, 1978). The pairs of connexon units can crystallize in regular two-dimensional hexagonal arrays in isolated junction membranes (Goodenough & Stoeckenius, 1972) and in physiologically uncoupled intact tissues (Raviola et al., 1980). By Fourier averaging the hexagonal junction lattices imaged in projection from low irradiation micrographs of isolated, uranyl acetate-stained mouse liver gap junctions, we have established that the pairs of connexon units are skewed in these lattices (Baker et al., 1983). This asymmetry implies that the connexons are not packed identically in the two coupled membranes. The pairs of connexon hexamers appear to be related by non-crystallographic 2-fold axes oriented about 8° to the right or left of the hexagonal lattice axes. Skewing of the connexons in gap junction lattices had also been observed in averaged images from phosphotungstate-stained specimens (Henderson et al., 1979); however, previous low-dose images from uranyl-acetate-stained junctions appeared to show mirror symmetric arrays of connexons in projection (Zampighi & Unwin, 1979; Unwin & Zampighi, 1980) corresponding to the p622 lattice symmetry expected if the connexons were arrayed in the same way in the pair of coupled membranes (Makowski et al., 1977). Recent micro-graphs of unstained dehydrated (Wrigley et al., 1984) and frozen-hydrated (Unwin & Ennis, 1984) specimens show skewed arrays of connexons, but the possibility that this appearance is an artifact due to asymmetric distortion of the two sides during preparation of the unstained specimens has not been excluded. If skewing is a consequence of the way connexon pairs crystallize in the gap junction lattice (Makowski et al., 1984a), then similar skewed arrangements should be observed in images of specimens prepared by different methods that preserve the lattice structure.

Variability in the gap junction specimens viewed in the electron microscope complicates the identification of intrinsic details in the structure. Radiation damage, fluctuations in stain distribution, specimen distortion, imaging artifacts and differences among preparations all contribute to variations in the images. Features consistently evident in the averaged images from low irradiation micrographs of uranyl-stained specimens are the stain-accessible connexon channel, the peripheral stain concentrations outlining the skewed, six-lobed connexon and the lighter-stained region at the 3-fold axis (Baker et al., 1983). The relative contrast of these features is variable even among junction domains imaged in the same micrograph. Uranyl staining of the connexon center ranges from very light to dark, and increased irradiation enhances this axial stain accumulation. Radiation damage smooths out the peripheral stain distribution leading to relatively featureless images of hexagonal or nearly circular connexon units arrayed with mirror symmetry. The locations of the characteristic features in the low irradiation micrographs showing skewed connexons are nearly invariant. These gap junction images can be represented to 25 Å resolution by a simple model with two stain-excluding domains and two stain-accessible regions arrayed with hexagonal symmetry (Baker & Caspar, 1983); differences in the stain penetration of the axial channel and in the stain exclusion bv the feature on the 3-fold axis can account for most of the image variation.

Averaging is essential to reduce the effect of random noise and local fluctuations in the specimen. Typically, in our experiments, the average extends over about 900 connexon units in well-ordered domains. Differences among such averages reflect variability in the specimens provided that the micrographs have been recorded under similar imaging conditions. Measurement of systematic variations can be made by comparison of multiple specimens in diverse situations if the different averaged images can be comparably scaled. For example, large variations in the average appearance of negatively stained domains of the hexagonally packed intermediate layers of a Micrococcus cell envelope, imaged from the same grid, have been correlated with differences in the stain-to-protein ratio measured in a scanning transmission microscope (Engel et nl., 1982). In another example of the use of comparative averaging methods, differences in the distribution of an anionic and a cationic stain in mitochondrial outer membranes have been mapped by scaling the averaged images to minimize the difference between the amplitudes of their computed Fourier transforms (Mannella & Frank, 1983, 1984).

In the present study, we have explored the range of variation of identically prepared gap junction specimens imaged at low and high irradiation with different cationic and anionic negative stains (uranyl acetate, formate and sulfate, ammonium molybdate, phosphotungstate, methyl amine tungstate and sodium silicotungstate), and we have characterized a distinctive difference in the aecessibility of the axial channel to the cationie and anionic stains. Identification of intrinsic features in the junction speeimens was facilitated by comparison of the images obtained with the variety of negative stains. Self-consistent image-scaling procedures devised for these eomparisons provide a quantitative basis for structural interpretation of conserved and variable features. Methods for calculating model projections and for factoring the cylindrical and hexagonal components of the images have been applied to locate the positions of the invariant features in the skewed connexons contrasted with the different stains.

2. Materials and Methods

(a) Junction specimens

Mouse liver gap junctions were isolated and purified as reported (Fallon & Goodenough, 1981; Baker et al .. 1983). with the exception that 5 × 10⁻⁴ M-diisopropyl fluorophosphate, 5 mg leupeptinjl/1, and 1 mg aprotinin/l (Sigma Chemical Co .. St Louis. MO) were added to all detergent solutions to inhibit endogenous proteolysis.

(b) Electron microscopy

Membrane specimens (0·1 to 0·.5 mgjml) were deposited on carbon or carbonjFormvar-coated grids by adhesion, washed with distilled water and stained for 10 to 60s with unbuffered aqueous solutions of 1% (w/v) uranyl acetate (UA1^†, pH4·2; UA2. pH6·0) 1% (wjv) uranyl sulfate, (pH 5·0), 1% (wjv) uranyl formate, (pH 5·2). I to 2% (wjv) phosphotungstic acid, (pH 4·3 and pH 6·0), (w/v) methylamine tungstate, (pH 7,6), 2·.1% (wjv) ammonium molybdate, (pH 5·2) and 4% (wfv) sodium silicotungstate, (pH 5·8). In one experiment with AM (2%, pH 6·5) all steps were carried out at 37°C.

Micrographs at minimal ( < lO to 20e⁻/Ų ) and normal ( > l00e ⁻;Ų) irradiation levels were recorded at 40,000 to 45,000 × on a Philips EM30l electron microscope at 80 kV using procedures identical to those described by Baker et al., (1983).

(c) Image processing

The methods of surveying, averaging and displaying images were similar to those used previously (Baker et al., 1983). Micrographs were surveyed by optical diffraction (Salmon & DeRosier, 1981) to assess the imaging conditions (defocus, astigmatism, specimen drift and tilt) and to identify the best-preserved specimen areas. Gap junction domains showing sharp, strong optical diffraction spots out to at least the third-order set were selected for digital image processing. Images of single lattice domains, free of noticeable defects. were digitized using an Optronics Pl000 Photoscan microdensitometer and displayed on a television raster graphics screen. Suitable areas (usually 400 × 400 pixels containing about 900 connexon images) were boxed, using the television screen cursors. and were Fourier-transformed on a VAX 11/780 minicomputer.

The positions of the diffraction maxima were fitted to a reciprocal lattice with p1 plane group symmetry and a single amplitude and phase for the structure factor at each lattice point was measured out to the fifth order. Of these 45 unique structure factors from the Fourier averaging with p1 symmetry. the 15 lowest-order terms were tabulated on reciprocal lattice plots to examine the regularity of the hexagonal symmetry. Data sets in which the amplitudes showed statistically significant departures from hexagonal symmetry, due to effects such as astigmatism or specimen distortion, drift or tilt, were discarded. The hexagonality of the p1 averaged lattices was also compared by measurement of the unit cell dimensions.

Transforms of gap junction domains, judged to be undistorted and oriented close to normal to the electron beam, were hexagonally averaged after locating the best 6-fold phase origin. The regularity of the hexagonal symmetry was assessed by computing the phase residual comparing the p6 and p1 averages. Since the phases are necessarily all 0 or 180° in the hexagonally averaged transform, as in the p2 average, the phase residual evaluated was a measure of the departure from centrosymmetry in the p1 averaged transform. This residual was defined as:

$${\Psi }_{\mathbf{R}}={(\sum _i{\left(\Delta {\Psi }_i{F}_i\right)}^2∕\sum _i{F}_i^2)}^{1∕2},$$

where ▲ψ_i is the phase difference (taken as ≤90°) between each structure factor of index i( = h, k) in the centrosymmetrically averaged transform and the corresponding term in the pl average. This residual could also have been defined in terms of the amplitude B_i of the antisymmetric components of the p1 averaged structure factor, since |Bi| = |Fi sin ▲ψ|. The origin for calculating ψ_i was chosen as the point near the connexon center that minimizes the phase residual, and this point was defined as the best 6-fold phase origin.

The sign of the first-order structure factor in the hexagonal average was taken as positive, corresponding to a positive density for stain-excluding matter. A consistent hand convention was maintained by interchanging the indices h, k and k, h if necessary. so that |F_{1, 2}| > |F_{2, 1}|. Hexagonally symmetric lattice images were computed by Fourier transforming the 15 unique p6 structure factors derived by hexagonally averaging the 45 terms from the p1 average. These images were displayed on the television graphics screen either in black and white or in color and photographed on a graphics recorder. A grey scale with 6 or 8 steps was used for the black and white displays to accentuate the contrast among the negative-stained features.

(d) Comparing images

The sets of structure factors for images of different specimens were scaled by equating Σ|F_hk| for the common structure factors. For comparison of identically stained specimens, the scaling was adjusted to minimize the R-factors between the transforms of different domains, but this did not significantly alter the scale based on equating Σ|F_hk|. These reciprocal space procedures scale similar images to have comparable densities. To scale the averaged images of specimens stained under different conditions, alternate, direct space procedures were used. In the display of different images, the densest stain feature at the periphery of the connexon of each computer graphics picture was set to the same dark level, while the least-stained region of the connexon, at about 20 to 25 Å radius, was set to the same light level. To compare circularly averaged profiles of the stain distribution. the mean peripheral contrast, rather than the maximum, was set to the same value. Scaling different images on the assumption that the maximum or the mean contrast between the stain-excluding perimeter of the connexon and the peripheral stain accumulation is constant for all staining conditions was based on the observation that this feature is less variable than the staining on the 6-fold or 3-fold axes. The scale factors obtained with the reciprocal and direct space procedures were correlated with the details of the stain distribution.

The R-factor, comparing the transforms of pairs of hexagonally averaged lattice images, denoted l and 2. which have been scaled to equate Σ|F_hk|, is defined as:

$$R_{\mathrm{f}}=\sum _i\mid F_i\left(1\right)-F_i\left(2\right)\mid ∕\sum _i\mid F_i\mid .$$

Note that the magnitude of the difference in the numerator depends on the signs F( 1) and F_i(2), which are necessarily known, unlike the usual situation in crystallography. Structure factors, F_i for weak terms in the hexagonally averaged transforms may occasionally have opposite signs for some pairs of specimens (cf. Table 2). The value of the R-factor as defined is determined predominantly by differences in amplitude of strong terms with the same sign.

Table 2.

Comparison of hexagonally averaged structure factors and mean R-Factors for each stain category of gap junction images

Stain category		UA1	UA2	US	UF	AM 37°C	PTA	AM	MAT	SST
Number of images		21	15	8	4	3	10	9	8	5
R̄f (s.d.)		0·31 (0·11)	0·24 (0·07)	0·25 (0·07)	0·33 (0·15)	0·12 (0·01)	0·26 (0·09)	0·19 (0·04)	0·10 (0·04)	0·14 (0·04
h	k	Structure factors (Fhk)
1	0	622	482	679	503	1008	1101	1103	1204	1336
1	1	–240	–618	–454	–827	–543	–274	–165	–291	–199
2	0	–433	–586	–566	–549	–279	–198	–249	–200	–329
2	1	–233	–172	–174	–47	10	–28	–16	–25	–124
1	2	–655	–422	–269	–383	–310	–356	–376	–281	–164
3	0	138	95	97	–9	186	128	200	143	12
2	2	42	8	65	–8	38	111	130	106	129
3	1	104	68	74	11	33	96	100	90	123
1	3	76	44	84	73	53	135	118	101	90
4	0	–11	–22	–46	–96	–36	–16	–9	–10	0
3	2	–12	–21	–22	–27	–24	–40	–23	–43	–36
2	3	–6	–19	–41	–39	–42	–53	–51	–44	–5
4	1	–5	–8	–4	1	6	2	–6	–3	–29
1	4	–11	–24	–14	–13	–20	–50	–37	–47	–12
5	0	–2	3	1	3	0	3	7	–2	2

The hexagonally averaged structure factors correspond to the averaged images for the 9 stain categories illustrated in the 4th column of Figs 2 and 3. The averaged structure factors were scaled by equating $\sum \mid F_{hk}\mid$. The same hand (|F_{1, 2}| > |F_{2, 1}|) has been taken for all images. The R-factors, $R_f=\sum \mid F_{hk}\left(n\right)-{\stackrel{‒}{F}}_{hk}\mid ∕\sum \mid F_{hk}\mid$, were computed by comparing the transform of domain n in each stain category with the average for that category. The mean values, R̄_f and their standard deviations (s.d.) are listed for each category.

(e) Factoring cylindrical and hexagonal components of images

The cylindrically symmetric component of the connexon image was determined by circularly averaging the calculated 2-dimensional density distribution about the 6-fold axis. This average was plotted as a function of radius out to the radius of the 2-fold axis. Beyond this distance, the circularly symmetric components of neighboring connexons overlap in the hexagonal lattice and are not easily separable. The hexagonally symmetric component of the connexon image out to the radius of the 2-fold axis was determined by subtracting the circular average from the image. This difference oscillates with hexagonal symmetry from positive to negative values and the average at any radius is necessarily zero. To display the hexagonal component of the image on the television graphics terminal, a constant term was added equal to the mean image density; since the magnitude of the hexagonal density fluctuation is small, the contrast was stretched by a factor of 1·6 relative to that of the circularly symmetric component for this display. Circular averages were displayed on the graphics terminal together with the hexagonal components superimposed on the original lattice images.

(f) Model building

Each average image was modeled in the computer using a set of circles with Gaussian density distribution to represent the 4 main features of the stained gap junctions. All models had positive weighted Gaussians to represent stain exclusion about the 3-fold unit cell position (r = 49 Å, Θ = 30°) and the position of the 6 equivalent connexon lobes (r = 23 Å, Θ = 8°), and negative terms for the 6 identical stain features delimiting the periphery of the connexon (each modeled as 2 adjacent Gaussians to produce an elliptically shaped feature: one positive at r = 28 Å, Θ = 35° and one negative at r = 32 Å, Θ = 35°), and a positive or negative feature at the 6-fold position corresponding to stain exclusion or penetration along the connexon axis (r = 0 Å). The agreement between an average and its model was most sensitive to the position and relative weights of the Gaussian circles and less sensitive to their size as long as the diameter of the Gaussians was larger than the resolution of the observed data. The set of 15 unique structure factors for the hexagonal lattice model was computed and compared with the equivalent set of structure factors for the average image being modeled. The model parameters were refined using an iterative trial-and-error procedure to minimize both the R-factor between the observed and calculated structure factors and the differences in appearance between observed and calculated images.

3. Results

(a) Appearance of micrographs

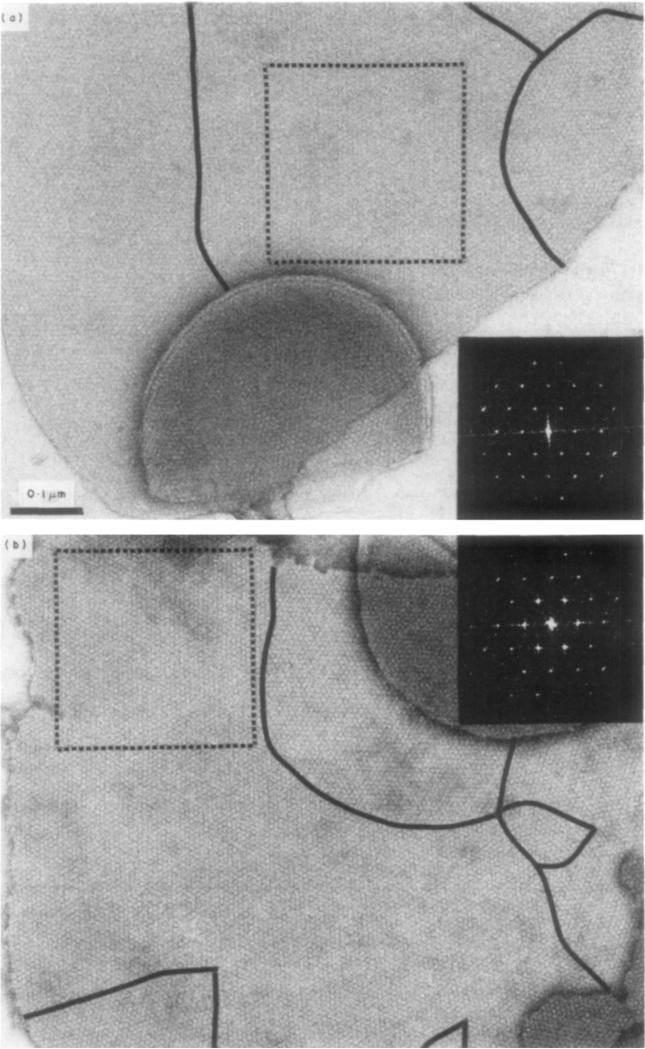
Micrographs and diffraction patterns of two of the 66 gap junction domains, recorded under low irradiation, that were digitally analyzed in this study are shown in Figure 1. The specimen in Figure 1(a), which was stained with uranyl sulfate, is one of the highest contrast, low irradiation micrographs among the uranyl-stained specimens. The specimen in Figure 1(b), which was stained with methylamine tungstate, is representative of the low-irradiation micrographs we obtained with this stain and with phosphotungstic acid and ammonium molybdate. Micrographs that we obtained with sodium silicotungstate show rather higher contrast than the other tungstate and molybdate stains.

Figure 1.

Representative micrographs recorded using minimal irradiation of gap junctions stained with (a) uranyl sulfate and (b) methylamine tungstate. Black lines mark the grain boundaries of the coherently ordered areas. These boundaries are more apparent when the images are viewed at a glancing angle, and the rows of connexons are seen along the principal lattice lines. The square regions selected for image processing are marked by broken lines and their corresponding optical diffraction patterns are shown on the right. The magnification is identical for both images. Staining conditions (at room temperature): (a) 1% uranyl sulfate, pH 5·0; (b) l% methylamine tungstate, pH 7·6. Note the optical diffraction pattern for the US-stained specimen (a) is left-handed and for the MAT-stained domain (h) iR right-handed.

The images selected for processing were of single, non-overlapped domains as shown boxed in Figure I. Most of the gap junction plaques consist of several differently oriented hexagonal lattice domains, as indicated by the grain boundaries marked in Figure 1. Comparing tungstate- and molybdate-stained junctions with uranyl-stained specimens, our observations indicate that the lattice domains contrasted with the anionic stains were, on average, smaller and somewhat more regularly ordered than those with the uranyl stains. The overall size and shape of the junction plaques were not noticeably affected by the different stains. Some of the junctions appear to be broken vesicles or flattened cup shapes (e.g. bottom of Fig. 1(a)); and the edge views of these curved junctions show the concentration of stain in the gap between the pair of coupled membranes. With all the stains used, the accumulation in the gap appears similar; but the connexon units seen in the unprocessed, low iradiation micrographs, seem more strongly contrasted with the anionic than with the uranyl stains.

(b) Unaveraged diffraction data

Diffraction patterns computed from the selected gap junction domains ( cf. Fig. 1 ), without averaging for the lattice symmetry, indicate the intrinsic periodicities of the connexon arrangements in the boxed areas. Clear diffraction maxima are observed among the first three orders of the hexagonally arrayed spots corresponding to the hexagonally indexed structure factors (1,0); (I, I) and (2,0); (I,2), (2, I) and (3,0). Beyond the fourth-order set, the amplitudes measured at lattice positions are generally close to the background noise level. Characteristic features evident in the unaveraged diffraction patterns correlate with the staining conditions. All of the tungstate- and molybdate-stained specimens show strong first-order spots and relatively weaker second-order (I, I and 2, 0) spots. whereas with the uranyl stains the first-order spots are comparable to or weaker than the second-order spots. There is significantly more variation in the ratio of the first-to-second order amplitudes among the uranyl-stained specimens than among those prepared with anionic stains.

The specimens stained with PTA, AM and MAT show a striking self-consistency in the relative amplitudes of the (I, 2) and (2, I) pair of structure factors: for the three pairs that should be related by hexagonal symmetry in each of the 3I patterns calculated, one spot is undetectable above the noise level or systematically much weaker than the other for 91 of the 93 pairs compared. In contrast, for the seven patterns from the SST -stained specimens, the ( l, 2) and (2, I) spots are more nearly equal and are relatively much weaker than the strong spot of thE:> pair in the patterns from the other anionic stains. The I5 uranyl-acetate-stained specimens examined in this study, four of the ·five uranyl-formatE:'-stained specimens, and six of the eight uranyl sulfate-stained specimens show pronounced asymmetry in the amplitudes of the (1. 2) (2, l) pairs similar to that characterized previously for 21 uranyl-acetate-stained specimens (Baker et al .. I983). Comparing different uranyl-stained specimens, there is more variation in the relativte amplitudes of the third-order spots than among the PTA-, AM- and MAT-stained specimens; nevertheless, the differences in amplitudes of the (I, 2) (2, I) pairs are generally similar for both types of stain.

Diffraction patterns computed from all negatively stained specimens exposed to electron doses in excess of ~50 e⁻ /Ų show significant decreases in the amplitudes of spots beyond the second order, together with a substantial reduction in the asymmetry of the (1,2) (2, 1) pair. With the anionic stains, the amplitude of the first-order spot remains strong relative to the second-order terms after irradiation; but with the uranyl stains, increased irradiation leads to a reduction in the amplitude of the first-order terms, coupled with an increase in that of the second-order terms.

(c) Hexagonal lattice symmetry

The regularity of the unit cell dimensions and of the amplitudes and phases of the p1 averaged structure factors provide a measure of the conservation of the hexagonal symmetry in the lattice domains selected for image processing. Measurements of the mean lattice constants, axial ratios, interaxial angles and phase residuals for the images we have compared are summarized in Table 1. There is no significant variation in lattice constant that correlates with the seven different stains applied at room temperature to the gap junction preparation used in this study. The average lattice constant for these 63 specimens (UA2, US, UF, SST, MAT, AM and PTA) is 81·2 ± 1·5 Å, which is within one standard deviation of the average for each stain. The 77·4 Å average lattice constant for the three specimens stained with ammonium molybdate at 37°0 is significantly smaller than that of the specimens from the same preparation stained at room temperature. The average lattice constant of 84 Å measured for the 21 UA1 specimens was obtained from different gap junction preparations (Baker et al., 1983). For all these specimens, the angle between the reciprocal lattice axes is very close to 60° and the two unit vectors have very nearly the same length as expected for a regular hexagonal lattice.

Table 1.

Mean lattice and symmetry parameters

Stain category	Number of images (n)	Lattice constant ā(Å) (s.d.)	Axial ratio ā*/b̄*	Interaxial angle $\stackrel{‒}{\alpha }\ast$(°) (s.d.)	Phase residual ${\stackrel{‒}{\psi }}_{\mathrm{R}}$(°) (s.d.)
UA1	21	84·0 (2·2)	0·995	60·2 (0·9)	35·0 (6·9)
UA2	15	81·9 (1·7)	1·004	60·0 (0·8)	32·2 (4.8)
US	8	80·5(0·9)	0·999	59·5 (0·8)	30·8 (7·4)
UF	5	80·4 (0·8)	0·997	60·0 (0·9)	34·7 (3·5)
SST	7	82·1 (1·1)	1·011	60·2 (0·9)	30·6 (4·1)
MAT	6	80·2 (0·5)	1·005	60·3 (0·9)	29·4 (5·4)
AM	10	81·2 (1·2)	0·997	59·8 (0·8)	26·8 (6·0)
PTA	10	82·2 (1·9)	0·978	59·9 (0·7)	31·8 (6·8)
AM 37°C	3	77·4 (1·0)	0·999	59·8 (0·2)	26·9 (9·1)

Stain categories are described in Materials and Methods. The mean p6 averaged lattice constant, ā, and the mean ratio of the p1 averaged reciprocal lattice vectors, a*/b*, and the angle α* between them were evaluated from the computed Fourier transforms of undistorted gap junction domains, each consisting of ~10³ connexon units. The phase residuals, $\stackrel{‒}{\psi }R={(\sum {\left(\Delta {\psi }_i{F}_i\right)}^2∕\sum F_i^2)}^{1∕2}$, measure the departure from centrosymmetry of the p1 averaged transforms. The standard deviations (s.d.) of ā, $\stackrel{‒}{\alpha },\stackrel{‒}{\alpha }$, and ${\stackrel{‒}{\psi }}_{\mathrm{R}}$ were computed for the n individual domain averages in each stain category.

Hexagonal lattice symmetry in the junction images selected for processing was measured by the correspondence in amplitude of the hexagonally related strong spots in the computed diffraction patterns. Selection of the domains for digital processing was based on visual survey of the micrographs and their optical diffraction patterns to locate regions with regular lattices and strong diffraction out to the third-order spots. Comparison of the 15 lowest-order structure factors computed for the 66 images averaged with p1 symmetry indicated that the departures from hexagonal symmetry for two SST specimens and one UF specimen were greater than expected from the statistics of the mean variations. These three specimens were, therefore, not included in the p6 averages. Among the 63 sets of p1 structure factors selected for hexagonally averaging the diffraction patterns from nine micrographs showed small correlated departures from hexagonal symmetry in the amplitudes of the second-order terms. which could be due to tilting of the specimens hy approximately 10° (cf. Unwin & Zampighi, 1980). The differences were, however, within the mngt> expected for statistical fluctuations; thus, tlw correlation in these variations mav be fortuitous. To make the selection of the images included in Uw hexagonal averages a reasonably unbiased sample of the micrographs that we recorded, only specimens whose transforms indicated significant distortion were excluded.

The mean phase residual comparing the p1 averaged data with the centrosymmetric average for the 63 images selected for hexagonal averaging is 30·5° with a standard deviation of 6·0°. The mean values for the nine stain categories we have analyzed (Table 1) range from 26·8° to ~5·0°. For individual domains, the phase residuals range from 19° to 42° with most values close to the mean. The hexagonal phase residual for individual domains is in the same range as the phase residuals comparing the p1 averaged images of different domains selected from the same micrograph.

The asymmetry observed in the amplitude of the (I, 2) and (2, I) structure factors corresponds to left-handed skewing of the connexon image in the lattice when |F_1,2 | >F|_2,1 and vice versa for the right-handed array, according to our convention. Of the 36 domains contrasted with anionic stains included in the hexagonal averages, 2I were right-handed, I4 left-handed and one not significantly asymmetric. Among the corresponding 27 uranyl-stained specimens. 20 were right-handed, four left-handed and three not asymmetric. In the previous analysis of 25 UAI specimens (Baker et al., I983), 12 were right-handed and I3 left-handed. The preponderance of right-handed lattices in the present study, particularly among the uranyl-stained specimens, does not appear to correlate with any differences in the right- and left-handed images. Of the 18 left-handed domains processed, 12 were from micrographs that included at least one other processed domain which was right-handed. No significant differences could be detected between the pairs of left- and right-handed images when compared with the same hand. For comparison of the hexagonal averages, all images were taken as left-handed.

(d) Averaged structure factors and images

Averaged structure factors of low irradiation images for the nine different staining conditions (UAI, UA2, US, UF, AM 37°C, PTA, AM, MAT and SST) are listed in Table 2. The choice of these categories does not imply that all images in each average are closely correlated; but these groupings provide a convenient way to compare similarities and differences among negatively stained gap junction images. The different averages listed in Table 2 were sealed by equating Σ|F_hk|. Structure factors were measured and listed for all terms out to the fifth order corresponding to a resolution of 14 Å. The data beyond the fourth order are weak and the computed images are not substantially altered if these terms are omitted. Thus. the effective resolution of these images is about 18 Å. The higher-resolution data are included. however, since comparison of the averaged structure factors. particularly for the specimens stained with PTA. AM and MAT, indicate that the measured amplitudes for most of these terms, although small. are statistically significant.

Also listed in Table 2 are the mean R-factors for the domains averaged in the nine stain categories. These R-factors were computed by comparing the hexagonally averaged transform of eaeh domain with the average transform for the category; and the individual R-factors in each category were then averaged. The mean values of R_f are listed together with their standard deviations at the bottom of Table 2. The mean R-factors range from 0·10 to 0·33, with generally smaller values and smaller standard deviations for the anionic stain categories than for the uranyl stains. The mean R-factors comparing different p6 averages are similar to the R-factors comparing the p1 and p6 averages of the same domain. Comparison of the R-faetors between different stain categories shows that these can be grouped in three classes: the uranyl stains; the anionic stains, except SST; and SST. Correlations from comparison of R-factors among the stain categories correspond to similarities and differences that are evident in the averaged images.

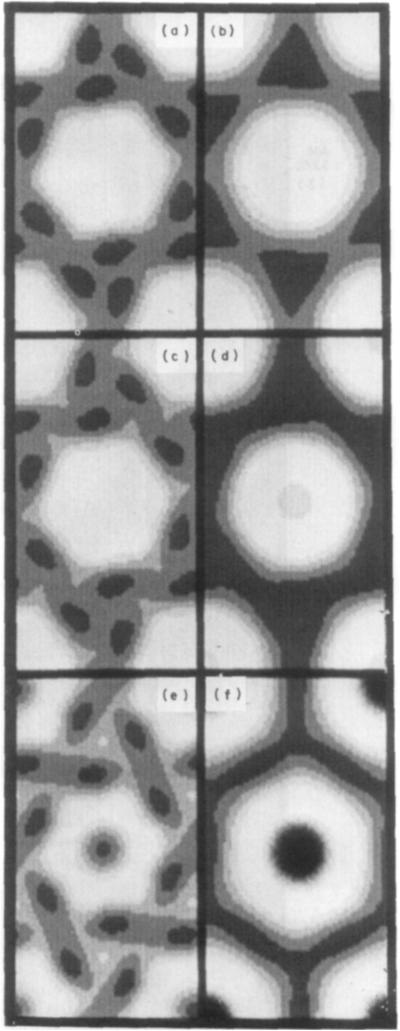
Averaged images, computed from the nine categories of averaged structure factors listed in Table 2, are shown in the fourth column of Figure 2 (uranyl stains) and Figure 3 (molybdate and tungstate stains); the first three columns in these Figures show selected hexagonally averaged images from the individual domains, which are representative of the group included in each category; and the fifth column shows computer-generated models corresponding to each average. Three of the average low irradiation images (MAT, AM and U A l) are shown again on the left in Figure 4 for comparison with averaged high irradiation images obtained from correspondingly stained specimens.

Figure 2.

Fourier-averaged, uranyl-stained gap junction images. First 3 columns: gallery of averaged individual gap junction lattice domains, such as those marked in Fig. I. Fourth column: average of individual Fourier-averaged images. Fifth column: model images constructed from features shown in Fig. 5 with the co-ordinates listed in Table 3. The number beneath each abbreviation indicates how many individual p6 averaged domains are averaged in the image in the fourth column. Individual images in the first 3 columns were selected to illustrate the range of variation of stain: junctions with the darkest connexon centers appear on the left. Contrast between the prominent stain-excluding lobes of the connexons and the densest part of the peripheral stain feature was set equal in the displays for all images. as deseribed in Materials and Methods. The images are displayed with 6 grey levels.

Figure 3.

Fourier-averaged molybdate- and tungstate-stained gap junction images. Averaged individual domains, average of averages and model images are arranged and displayed as for Fig. 2.

Figure 4.

Fourier-averaged images from micrographs obtained at low irradiation (left column) and higher irradiation (right column) of gap junction specimens stained with: (a) and (b) methylamine tungstate: (c) and (d) phosphotungstic acid; (e) and (f) uranyl acetate.

It is obvious from Figures 2 and 3 that the cationic uranyl stains and the anionic molybdate and tungstate stains interact very differently with the central part of the connexons. With the anionic stains (Fig. 3) there is, in most specimens, no detectable staining on the axis; and, in the few specimens showing some axial staining such as those prepared with AM at 37°C, the accumulation is very slight. In contrast, with the cationic uranyl stains (Fig. 2) there is accumulation on the axis in all specimens, and the amount varies from moderately light to very dark.

The distribution of the cationic and anionic stains at the periphery of the connexons is generally similar, but variations in the size and shape of the outline are observed among specimens from each category. In most low irradiation images, the connexon outline is, itself, mirror-symmetric with pronounced hexagonal lobes; and in all these specimens, the local hexagonal mirror lines are twisted by about 8° relative to the hexagonal lattice axes. This skewing is displayed as left-handed in the averaged images for uniformity of comparison. There are noticeable differences in diameter of the skewed connexon images among different specimens that do not correlate with the type of stain. The six peripheral concentrations of stain, delineating the skewed connexon outline, also generally demark a region of lighter staining at the 3-fold axes of the lattice. The SST-stained specimens show nearly circular connexon units with relatively uniform distribution of the peripheral stain; and the hexagonal connexon substructure is not very evident in some US-stained specimens. Even when the hexagonal features are weak in low irradiation micrographs, the skewing of the connexon is similar to that seen in images with a prominent six-lobed shape.

The effect of electron irradiation on the peripheral stain distribution, as illustrated in Figure 4, is similar for both anionic and cationic stains. This distribution becomes more uniform and the outline of the connexon is smoothed following irradiation greater than ~50 e⁻/Ų. Stain appears to retract from the periphery of the connexon, which takes on a relatively featureless hexagonal or nearly circular shape. When hexagonal form can still he distinguished following irradiation, the orientation is generally close to mirror-symmetric in the lattice with the hexagonal vertices pointing either toward 2-fold axes along the unit cell edge (e.g. see Fig. 4(b)) or toward 3-fold axes along the diagonal direction (e.g. see Fig. 4(f)). Irradiation affects the staining of the connexon center with cationic and anionic stains differently: uranyl staining at the connexon axis is strongly enhanced (e.g. Fig. 4(f)), whereas molybdate (Fig. 4(d)) and tungstate (Fig. 4(b)) staining at the center show little or no increase. Low irradiation micrographs, showing relatively uniform peripheral stain distribution with nearly circular connexon outlines, such as those from SST -stained specimens, are not altered very noticeably by increased irradiation.

(e) Measurement of conserved and variable features

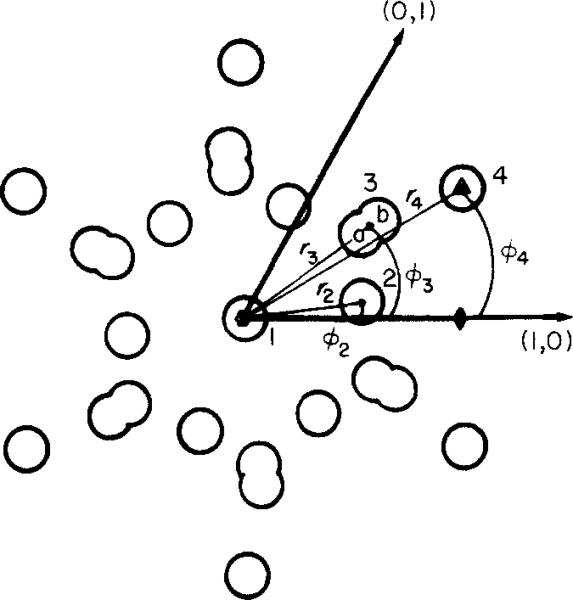
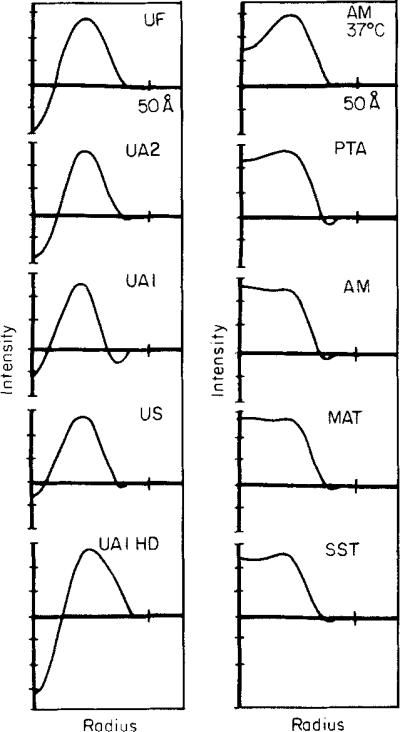
Model building and factoring the cylindrical harmonics of the projected images provide measurements of the conserved and variable features in the negatively stained gap junction structures. The parameters used to model the stain-excluding and stain-accessible regions in the connexon lattice are shown diagramatically in Figure 5; and the co- ordinates for these features selected to generate the model images shown in Figures 2 and 3 are listed in Table :3. Profiles of the circularly averaged density distribution in the connexon images are plotted in Figure 6; and the circularly and hexagonally symmetric components of the connexon images are displayed, superimposed on the corresponding lattices for the nine low irradiation stain categories and for one high irradiation condition, in Figure 7.

Figure 5.

Cylindrical co-ordinates (r_i, Θ_i) of the 4 features in the connexon model diagrammed in the hexagonal lattice. Feature l on the 6-fold axis can be positive or negative, corresponding to the stain exclusion or penetration; feature 2 is positive, representing the 6 stain-excluding lobes of the connexon; feature 3, corresponding to the 6 peripheral stain concentrations, is modeled by a positive (r_3a) and negative (r_3b) Gaussian to produce an elliptical shape; feature 4 represents stain exclusion near the 3-fold axis. The size and weight of the Gaussian features are adjusted to best fit the averaged images in Figs 2 and 3.

Table 3.

Model parameters

Model	R f	r 1	r 2	ϕ 2	r 3a	r 3b	ϕ 3	r 4	ϕ 4
UF	21·9	0·0	24·0	–8·0	27·0	33·0	–35·0	49·0	–15·5
UA2	11·6	0·0	22·3	–8·0	27·0	32·0	–35·0	49·0	–28·0
UA1	13·8	0·0	22·0	–8·0	27·0	32·0	–35·0	49·0	–30·0
US	12·0	0·0	22·0	–8·0	22·0	32·5	–35·0	49·0	–25·0
SST	12·9	0·0	22·0	–8·0	25·0	32·0	–35·0	49·0	–35·0
MAT	11·0	0·0	23·0	–8·0	28·0	32·0	–35·0	49·0	–30·0
AM	9·8	0·0	22·0	–8·0	30·5	33·4	–35·0	49·0	–30·0
PTA	16·0	0·0	22·0	–8·0	30·5	34·0	–35·0	49·0	–30·0
AM 37°C	10·7	0·0	24·0	–8·0	28·7	33·5	–35·0	49·0	–30·0

Values of R_f factors comparing the averaged images with the models displayed in Figs 2 and 3; and model co-ordinates as shown diagrammatically in Fig. 5. Radial co-ordinates (r₁ through r₄) are in ångström units measured from the 6-fold axis and angles, ϕ₂ through ϕ₄ from the [1, 0] lattice vector, are in degrees.

Figure 6.

Plots of the circularly averaged connexon unit profiles from the averaged images shown in the fourth columns of Figs 2, 3 and 4(f). The scaled images were displayed on the television screen and intensities were circularly integrated about the 6-fold axis out to the radius of the 2-fold axis of the unit cell. The plots were scaled to equate the difference in the stain-excluding density at the periphery of the connexon (20 to 25 Å radius) and the density at the 2-fold axis ( ~ 40 to 42 Å radius) for all profiles. HD (in Figs 6 and 7), high dose.

Figure 7.

Circularly and hexagonally symmetric components of averaged connexon images. The averaged connexon images from the fourth column of Figs 2 and 3 and from Fig. 4(f) are arranged centered on the vertical white lines. The image to the left of this line is the circular average evaluated out to the radius of the 2-fold axis. The image to the right of this line is the hexagonally symmetric component of the connexon image (evaluated by subtracting the circularly symmetric component from the average connexon image). The hexagonally symmetric component is displayed on a grey background corresponding to the average image density, and the contrast in this display has been stretched by a faetor of 1 ·6 relative to the original image ind its circular average. The images in this Figure are displayed using 8 grey levels.

The co-ordinates for the features in the models listed in Table 3 indicate that all the images can be fitted, to the good approximation illustrated in Figures 2 and 3, with nearly invariant locations for the stain-excluding and stain-accessible regions. The most significant variation among these models is the relative weight of the axial stain feature and the peripheral stain concentration. For the nearly circularly symmetric images, such as the SST-stained specimens, the hexagonal features in the model have been smoothed out by increasing the width of their Gaussian density distribution. These models, which have been constructed by trial-and-error to fit the projected images, are not intended as unique representations of the structures but do illustrate that differences in staining can account for most of the image variation.

The circularly averaged connexon profiles plotted in Figure 6 show the substantial variation in axial stain accumulation among the uranyl-stained specimens and the relatively uniform exclusion of the anionic stains along the axis. The peak in the stain-excluding distribution near the connexon periphery is between 20 Å and 25 Å radius for all specimens, and the outer edge, at which there is a minimum in the circularly averaged stain exclusion, is between 35 Å and 40 Å radius. The grey scale displays of the circular averages in Figure 7 show the same features evident in the plots of the radial profiles.

In Figure 7, each averaged connexon image is centered on the vertical white line and the hexagonally symmetric density fluctuation (relative to the average image density) is displayed with slightly enhanced contrast to the right. Adding the hexagonal density fluctuation to the circular component on the left, taking the average image density as zero, would regenerate the connexon image on the center line. With the contrast of this display, there is no measurable hexagonal component in the averaged SST -stained connexon image. The hexagonal component of the US and high-dose UAl specimens is relatively weak, showing up only at the first density contour level near the periphery of the connexon. The shape of the hexagonal component is similar for the UF, UAI, UA2, AM 37°C, PTA, AM and MAT specimens; among these, the hexagonal density fluctuation is strongest for UAI and comparable for the others. For these specimens, all the hexagonal components have local mirror symmetry, within the noise level of the images; and the mirror lines are skewed by 8 to 9° relative to the lattice axes. The radius of the maximum hexagonal density fluctuation is between 30 Å and 34 Å. For the US specimens, which have a weak hexagonal component, the shapes of the maxima and minima are not locally mirror-symmetric, but the twist in their orientation relative to the lattice axes is similar to the other low irradiation specimens. In contrast, the weak hexagonal component of the high-dose UAI specimen is aligned with its maximum stain-excluding region pointing toward the 3-fold axes. Figure 7 shows that for all the low irradiation connexon images with clear hexagonal features, the shape and orientation of these features are nearly invariant, even though there are variations in the circularly averaged profiles.

4. Discussion

The objective of this study was to identify details in the images of negatively stained gap junctions that represent intrinsic aspects of the structure and to correlate variations among the images with differences in the conditions of the specimens. Analysis of the noise in the images provides a measure of the scale of the significant detail that can be distinguished. The connexon units are often barely recognizable in unaveraged low irradiation images; symmetry averaging enhances the intrinsic features but may also introduce spurious detail by superposition of noise.

Preferential staining along the connexon axis by uranyl ions (Fig. 2) and virtual exclusion of tungstate and molybdate ions (Fig. 3) is the most striking difference among the averaged images that correlates with the staining conditions. Affinity for cationic stains and repulsion of anionic stains can be explained in terms of a fixed negative charge on the channel wall in the specimens we have compared. This is in accord with the evidence from permeability studies using small charged fluorescent molecules (Flagg-Newton et al., 1979; Flagg-Newton, 1980; Brink & Dewey, 1980) that there is a fixed negative charge along the channel under physiological conditions. The permeability properties of the channels in the specimens prepared for electron microscopy cannot, however, be directly assessed. Thus, there are ambiguities in the correlation of information about the structure from the negatively stained images with that from physiological studies.

The most labile features in the gap junction images, which appear intrinsic to the structure, are the concentrations of stain marking the perimeter of the skewed, six-lobed connexon and the stain-excluding region at the 3-fold axis of the lattice. Very similar hexagonal substructure is observed in the most detailed low irradiation, averaged images obtained with both uranyl and anionic: stains but, under some conditions of staining, the hexagonal detail is weak or absent and increased irradiation inevitably leads to its disappearance. Our analysis of the hexagonal substructure illustrates the utility of making quantitative comparisons among the averaged images under a variety of staining conditions.

The experimental variables considered in this study include the type of stain, its concentration and pH, the temperature of staining and the electron dose to the specimens. Temporal variations were minimized by making the stained grids from the same junction preparation within days of each other. Images of 66 domains analyzed from the low irradiation micrographs were correlated with 25 low irradiation images analyzed from a previous study (Baker et al., 1983) of six different gap junction preparations that were similarly stained with uranyl acetate. Features compared directly from the micrographs ( c:f. Fig. I) include the junction morphology, the size of the coherent hexagonal domains, the contrast in the lattice and local variations in the staining. From the computed Fourier transforms of selected domains, the lattice dimensions were measured, and the regularity of the symmetry and the magnitude of the noise were assessed. Quantitative comparisons among the Fourier-averaged images were made by scaling procedures based on equating conserved features.

(a) Image scaling

Comparison of differences in stain distribution under various conditions is influenced by the way in which the images are scaled. The strategy adopted for comparing and averaging different images obtained with the same stain was to scale the computed structure factors to equate Σ|F_hk| (Baker et al., 1983). This procedure was shown to give scale factors that are nearly the same as a direct scaling obtained by setting the maximum contrast between stain exclusion and stain concentration the same for all images. Provided that the stain distribution is similar in all specimens, these two procedures should give comparable scale factors. Significant differences in distribution are, however, observed comparing the uranyl with tungstate or molybdate stains. In this situation, scaling all images to have the same maximum contrast would give a misleading impression of the differences in stain distribution. With the uranyl-stained specimens, the densest region is generally at the connexon center, whereas the anionic stains are excluded from the center. Setting the contrast between the stain-excluding protein of the connexon and the average peripheral stain concentration the same for all averages (Fig. 6) gives a reasonable comparison.

Correlation of information about the gap junction structure from negative staining, freeze-fracture and X-ray diffraction provides an empirical basis for the image scaling procedure we have adopted. It is evident from edge views of negatively stained junctions (cf. Fig. 1(a)) that, at the periphery of the connexon, most of the contrast is due to stain accumulation in the gap. A three-dimensional reconstruction of uranyl-acetate-stained specimens clearly showed the stain accumulation in the gap but revealed no substantial substructure on the cytoplasmic surface (Unwin & Zampighi, 1980). Similarly, no prominent relief on the cytoplasmic surface was seen in freeze-etched specimens (Goodenough, 1975; Hirokawa & Heuser, 1982) or in three-dimensional reconstructions of some frozen-hydrated specimens (Unwin & Ennis, 1984). X-ray diffraction data (Makowski et al., 1982; Makowski, 1985) indicate, however, that the protein on the cytoplasmic surface is not distributed uniformly; protein domains clustered at the 3-fold axes of the lattice protrude from the surface, but the extension of this substructure is small compared to the ~30 Å width of the gap. Shallow pits and low projections on the cytoplasmic surface, arranged with the lattice symmetry, may correspond to the hexagonal details we have seen in negatively stained images, but such fine features would not substantially modify the mean peripheral contrast due to the stain in the gap. Since the gap appears to be freely accessible to negative stains, and the cytoplasmic surface has a low relief, the appearance of the connexon units in projection should be insensitive to the total thickness of stain. Increasing the amount of stain on the cytoplasmic surface would reduce the apparent contrast between the stain and the protein in the gap, but would not ehange the shape of the stain-excluding portion. This situation is different from that of the hexagonally packed intermediate layer of a bacterial cell envelope whose appearance is very sensitive to stain thickness, since the surface lattice has high projections and deep cavities (Engel et al .. 1982). On the assumption that the width of the gap is the same for all stains, scaling all the negatively stained gap junction images to have the same mean peripheral contrast corresponds to setting the effective stain thickness in the gap the same for all specimens. The contrast in the scaled images should, therefore, be proportional to the stain-excluding thickness.

The plausibility of the assumptions we have made in scaling images obtained with anionic and cationic negative stains (cf. Fig. 6) is indicated by the self-consistency of the detail seen at the periphery of connexon in specimens with well-resolved hexagonal substructure (Fig. 7). The principal difference between the two types of stain is that the mean thickness of the uranyl stains on the axis may substantially exceed that in the gap, whereas there is little or no axial accumulation of anionic stains (Fig. 6).

Curiously, the scale factors obtained for the two types of stain by equating the peripheral contrast (Fig. 6) are practically the same as those obtained by equating Σ|F_hk| (Table 2). The reason for this is that increasing the amount of stain on the axis, without altering the peripheral contrast, adds amplitude to the transform that is out of phase with the (1, 0), (3, 0) and (2, 2) structure factors, and in phase with the (1, 1 ), (2, 0), (2, 1) and (I, 2) terms. The magnitude of the changes. ■F_hk in thP structure factors diminish with increasing radius in reciprocal space. Overall, the effect is to add about as much amplitude in phase as out of phase so that Σ|F_hk| does not change significantly. although Σ|■F_hk| is substantial.

(b) Lattice constants

The computed p1 averaged transforms provide a measurement of the average unit cell parameters, the lattice symmetry and the noise level. The relative lack of variation in lattice constant with the seven different stains applied at room temperature in this study (Table 1} is somewhat unexpected considering the range of variation observed by X-ray diffraction. Lattice eonstants measured from the X-ray patterns of more than 200 different gap junction preparations (Makowski P1 al., 1984a) range from 75 to 89 Å. Within a given specimen, the variation appears small, judged from the sharpness of the equatorial reflections. The differences among these speeimens indicate that the connexon packing in the isolated junction lattices is in a delicate state of balance, which can be altered by small changes in environmental conditions in the course of specimen preparation. Since the different stains, applied under similar conditions on specimens from the same preparation did not significantly alter the lattiee constant (α = 81·2 ± 1·5 Å; Table I). it appears that thP connexon paeking Is not sensitive to ionic composition or pH under the conditions tested. The differences in stain distribution observed among these specimens cannot therefore be attributed to changes in connexon packing interactions. Furthermore, the small change in packing observed for the specimen stained with AM at 37°C, in which the lattice constant decreased by ~4 Å compared with the specimens at room temperature, did not involve substantial changes in the hexagonal substructure. The mean lattice constant measured in the previous analysis of uranyl-acetate-stained specimens (GAl) was about 2 Å greater than that of the UA2 specimens, which is comparable to the standard deviations; and the averaged connexon images are similar to each ,other. The differences noted in the size of the hexagonal lattice domains comparing specimens prepared with the anionic and cationic stains are not correlated with any obvious differences in the lattice parameters or resolution of the Fourier transforms.

(c) Symmetry and noise

Hexagonal symmetry of the lattice requires that the Fourier transform be centrosymmetric and that the symmetry-related structure factors in the three different lattice directions be equal. The departure from centrosymmetry in the pl averaged transform was measured by the phase residual comparing the p1 and p2 averages. The mean value of this phase residual, as defined (Table 1), is about 30° for all the staining conditions. Evaluation of the residual, defined by the ratio of the sum of the amplitudes of the antisymmetric part of transform to the sum of the measured amplitudes, could also have been used to compare the pl and p2 averages. This residual is similar to the R-factor comparing the p2 and p6 averaged transforms. That is, the magnitude of the antisymmetric part of the pl averaged transform is similar to the difference between the centro-symmetric part of the pl average (which is the p2 average) and the p6 average. Furthermore, these residuals comparing p1 and p6 averages are similar to those comparing p1 averages of different domains from the same grid. All these comparisons indicate that the departures from hexagonal symmetry in the pl averaged transforms are due principally to random noise in the image.

Averaging the transforms with p6 lattice symmetry reduces the noise but does not eliminate it. The residual random noise in the p6 average should be $1∕\sqrt{3}$ times that in the p2 average, which is measured by the R-factor comparing the p2 and p6 averages. R-factors comparing p2 and p6 averages are generally in the range 0·2 to 0·3 (Baker et al., Hl83); thus, the random noise in the p6 average should be ~15% of the mean signal. Another measure of random noise is provided by the R-factors comparing the transforms of different p6 averaged images of identically prepared specimens (Table 2). The most closely self-consistent sets of hexagonally detailed images we have obtained are from the MAT- and AM-stained specimens for which the mean R-factors are 0·10 and 0·19, respectively. These R-factors are similar to those expected from analysis of the departures from perfect hexagonal symmetry if these differences are due mainly to random noise.

R-factors comparing the transforms of specimens stained with uranyl salts and with PTA (Table 2) are in the range 0·24 to 0·33. These R-factors are larger than that expected from random noise. Greater variation among these specimens than among those stained with AM and MAT can be explained by differences in the staining. The averaged images of different uranyl-stained domains show substantial differences in the mean amount of stain on the axis (Fig. 2). and the PTA-stained specimens show differences in both the axial and peripheral stain distribution (Fig. 3).

Our estimate that the random noise level in the averaged images is ~15% of the mean signal suggests that features with less than 15% of the maximum contrast may not be statistically significant. We have, therefore. displayed the averaged images with either six or eight grey levels (Figs 2, 3, 4 and 7). Details that stand out in these displays are likely to correspond to genuine structural features of the connexon units in the negatively stained gap junction specimens.

(d) Connexon skewing

Analysis of the Fourier transforms of gap junction domains showing welt-resolved substructure confirms the hexagonal symmetry of the lattices. Asymmetry in the amplitude of the ( l, 2) and (2, l) pair of structure factors requires that the plane group of the lattice be p6 (Baker et al., 1983) rather than p622 as expected on the assumption that the connexons should be arrayed in the same way in the pair of coupled membranes (Makowski et al., 1977; Unwin & Zampighi, 1980). The pairs of connexons appear to be related by noncrystallographic 2-fold axes oriented about 8° to the right or left of the hexagonal lattice axes (Baker et al., 1983). In this arrangement, the connexon pairs are seen to be skewed to the left of the lattice axes when viewed from one side of the junction and skewed to the right when viewed from the opposite side. Assuming that the junctions can land on the grid with either side up, the two views should occur with equal probability.

The preponderance of right-handed skewed images among the uranyl-stained specimens in the present study is surpnsmg considering the expectation that right- and left-handed skewing should be equally likely. On this expectation, the observed 20 right, 4 left distribution is a priori 254 times less likely to occur than a 12 right, 12 left distribution. A characteristic of such a coin-toss system is that unlikely distributions will sometimes occur. Were this 20 right, 4 left distribution the only observation, we might seek reasons to explain why right skewing is favored. For example, one side of the asymmetric junction might preferentially adhere to the grid or the structure might be better preserved in the right-hand orientation. However, in view of previous measurements of a 12 right, 13 left distribution for the UA1 specimens (Baker et al., 1983), the present observations with anionic stains of a 21 right, 14 left distribution, and the very close mirror relation of right- and left-skewed averages, the expectation of equal a priori probability for right- and left-skewed images is still plausible. The observed unequal distribution of right- and left-handed forms demonstrates that the present selection of the uranyl-stained images was not biased by the expectation of equality.

(e) Variations in contrast

Micrographs of specimens prepared with the uranyl and tungstate or molybdate stains (Fig. 1) directly show differences in the stain distribution and contrast. It is not obvious why the contrast appears much lower with the uranyl than with the anionic stains, but there is a correlation between the fineness of the detail revealed in the averaged images (Figs 2 and 3) and the lack of dominant contrast of the connexon units seen in the lattice. The highest contrast was observed with the SST-stained specimens, which show, in the averaged image, a very featureless stain-excluding disk whose area is about half that of the unit cell. The uranyl images can be represented by six small stain-excluding lobes and a stain-excluding feature on the 3-fold axis contrasted with six small peripheral stain concentrations and a stain feature on the 6-fold axis (Fig. 5). To the eye this fine detail will tend to merge and be obscured by the noise in the micrograph, whereas the strong single feature in the SST-stained specimen will stand out against the background noise. The peripheral detail in the AM-, PTA- and MAT-stained specimens is similar to that resolved with the uranyl stains, but, since the anionic stains do not concentrate on the axis, the apparent contrast of the connexon units is enhanced. Perceptual differences may not, however, be the only factor determining the contrast. For example, increased irradiation of specimens showing low contrast at low irradiation eliminates fine structural detail but does not enhance the contrast (Baker et al., 1983).

Absence of structural detail in the SST-stained specimens appears to be the consequence of the high stain concentration used (4% for SST compared with 1 to 2·5% for the other stains). Micrographs obtained by Wrigley et al. (1984) with I% sodium silicotungstate at neutral pH show low contrast and very fine detail in the Fourier-averaged images. Loss of fine detail does not, however, necessarily imply low resolution as judged by the Fourier transform. The higher-order structure factors from the SST -stained specimens are comparable to those with the other stains (Table 2). The strength of these higher-order Fourier coefficients depends on the sharpness of the stain contrast as well as the fineness of the structural detail.

(f) Variations in staining of the channel

Variations in staining along the connexon axis by uranyl ions (Fig. 2) may depend on the state of the gates that control intercellular communication (Lowenstein et al., 1978; Bennett & Goodenough, 1978). X-ray diffraction studies on isolated gap junction specimens, similar to those we have examined by negative staining, show that the channels are closed to sucrose by gates near the cytoplasmic surface (Makowski et al., 1984b). Electron irradiation (Baker et al., 1983; Fig. 4(f)) and heating (Hertzberg & Gilula, 1979) enhance the staining of the channel by uranyl ions, which may result from alteration or disruption of the permeability barrier.

Our observations (cf. Fig. 1(a)) indicate that. in junctions showing light staining of the channel by uranyl ions from the average image of hundreds of connexons, there is considerable variation in the amount of axial stain in the individual connexons. Some channels may be partially opened under the conditions of preparing the negatively stained specimens, thereby allowing some association of positively charged ions from the solution with the negative charges lining the channel. Once the fixed charges are neutralized, then more neutral salt, could accumulate in wide parts of the channel. Occasional very light staining with uranyl ions may be the result of minimal disruption of the closed gates. The substantial staining by uranyl salts. often observed under low irradiation conditions. suggests that the gates are leaky enough in these negatively stained specimens to allow significant binding of stain cations to negative charges in the channel.

Anionic stains are not completely excluded from the connexon channel. For example, in the MAT-stained specimen in Figure 1(b), a few of the connexons show substantial accumulation of stain on the axis although the center appears unstained in the averaged image. The channel, when free of stain, should be more transparent to electrons than the ~150 Å thick layer of protein in the pair of connexons. Thus, a uniform density profile for the connexon unit may correspond to some stain, on average, in the channel. The enhanced axial staining with AM on heating to 37°C (Fig. :3) suggests an opening of channel gates. Axial staining with PTA, observed under low irradiation occasionally (Fig. 3). and following increased irradiation (Fig. 4), may be related to the lowered pH of the concentrated acid stain, which would reduce the negative charge on the protein, as well as to leakiness of the channel gates.

Our observations that uranyl ions are sometimes excluded and that anionic stains are occasionally accumulated on the axis indicate that the stai; distribution is not exclusively determined by the electrostatic interactions. Since the channel gates are closed to sucrose in similar gap junction preparations that were maintained hydrated for X-ray diffraction (Makowski et al., 1984b), we believe that the variable leakiness of the gates to negative stains observed in the electron microscope may be an artifact of the staining and dehydrating treatments.

(g) Circularly and hexagonally symmetric components of connexon images

Separation of the connexon images into their circularly and hexagonally symmetric components provides the basis for the image scaling (Fig. 6) and for the characterization of the hexagonal substructure (Fig. 7). The circularly averaged profiles for all the low irradiation conditions show invariance of the radius of the stain-excluding perimeter of the connexon unit and substantial variation in the mean amount of stain on the axis (Fig. 6). The profile for the high-dose UAl image shows an increase of about 5 A in the apparent connexon radius presumably due to retraction of stain as observed with other structures (Unwin, 1974). Enhanced staining of the connexon axis following irradiation must involve substantial redistribution of the stain in the specimens.

Local mirror symmetry in the hexagonal component of the images of all the specimens showing well-resolved substructure (Fig. 7) suggests that the coupled connexon pairs are related by noncrystallographic 2-fold axes in the plane of the gap (Baker et a.l.. 1983). These skewed mirror lines correspond to the local 2-fold axes seen in projection, which are oriented 8 to 9° to the right or left of the lattice axes. Local mirror symmetry cannot be a spurious result of the limited resolution since, in the average image of the US-stained specimens, the hexagonal features are seen to be slewed relative to the radial lines (Fig. 7), thereby eliminating the local mirror symmetry. Asymmetry in this US image is, however, likely to be an artifact since the strength of this hexagonal feature, which shows up only at the first step in the grey level, is comparable to the noise in the data. The noise level expected in these images is ~15% of the maximum contrast. In the displays of the hexagonally symmetric component (Fig. 7), the steps in the grey level correspond to about 8% of the maximum contrast. For the low irradiation images from the CAl, CA2, UF, AM, PTA and MAT-stained specimens (Fig. 7), the hexagonal signal is greater than ± 15% of the maximum contrast and is therefore significant compared to the noise level. The similarity in the dimensions, symmetry and eontrast of the significant hexagonal component in all these images implies that it corresponds to an intrinsic structural feature in the symmetrically related pair of eonnexon units.

The hexagonal feature is absent or weak in low irradiation images under some staining conditions (e.g. with SST and CS) and is lost or altered following increased irradiation. The magnitude of the hexagonal fluctuation in the high-dose UAl image (Fig. 7) is the order of the noise level, and its radial position and rotational orientation have shifted compared to the strong, skewed hexagonal feature in the low irradiation images. Comparison of the high irradiation images in Figure 4(b). (d) and (f) shows distinctly different orientations of the weak hexagonal feature. The faint hexagonal shape is skewed in Figure 4(d) but the hexagonal vertices point toward the lattice 2-fold axis in Figure 4(b) and toward the 3-fold axis in Figure 4(f), giving the impression of a 30° difference in orientation. Our measurements suggest that such differences could be the residual of hexagonally averaged noise in the images of specimens in which the intrinsic hexagonal features have been disordered or obliterated.

We have identified the skewed peripheral stain concentration located at a radius of ~ 30 Å from the connexon axis and the stain-excluding domain on the 3-fold axis as intrinsic features of the isolated gap junction structure imaged at low irradiation with a variety of negative stains. The stain concentrations appear symmetrically related on opposite sides of the junction by noncrystallographic 2-fold axes oriented about 8° to the lattice axes at the plane of the gap. Our observations have not established the co-ordinates of these features relative to the plane of the gap. The stain-excluding feature on the 3-fold axis may be identified with the protein domains projecting at the 3-fold axis on the cytoplasmic surfaces that have been detected by X-ray diffraction (Makowski et a.l., 1982; Makowski, 1985). The peripheral stain concentrations may correspond to shallow pits on the membrane surfaces. Studies are in progress with tilted, negatively stained specimens to determine the three-dimensional arrangement of these labile features in the gap junction structure.

5. Conclusion

Penetration of the axial connexon channel of isolated gap junction membranes by positively charged uranyl ions and exclusion of anionic stains indicate that there is a fixed negative charge along the channel. Variability in the extent of uranyl ion penetration and in the exclusion of the anionic stains suggests that the connexon channels are closed by gates that become leaky in the negatively stained specimens. The stain concentrations marking the perimeter of the skewed, six-lobed connexon and the stain-excluding region at the 3-fold axes of the lattice, seen in averaged, low irradiation images with uranyl, tungstate and molybdate stains, are intrinsic features of the gap junction structure. Identification of intrinsic features in the structure has been based on analysis of the noise in the averaged images by Fourier methods. Details in the images obtained with different stains have been compared quantitatively by scaling procedures based on equating conserved features. The hexagonal features are sensitive to the staining condition and are lost or altered following increased irradiation. The labile features may correspond to symmetrically related substructure on the cytoplasmic surfaces.