FastHap: fast and accurate single individual haplotype reconstruction using fuzzy conflict graphs

Abstract

Motivation: Understanding exact structure of an individual’s haplotype plays a significant role in various fields of human genetics. Despite tremendous research effort in recent years, fast and accurate haplotype reconstruction remains as an active research topic, mainly owing to the computational challenges involved. Existing haplotype assembly algorithms focus primarily on improving accuracy of the assembly, making them computationally challenging for applications on large high-throughput sequence data. Therefore, there is a need to develop haplotype reconstruction algorithms that are not only accurate but also highly scalable.

Results: In this article, we introduce FastHap, a fast and accurate haplotype reconstruction approach, which is up to one order of magnitude faster than the state-of-the-art haplotype inference algorithms while also delivering higher accuracy than these algorithms. FastHap leverages a new similarity metric that allows us to precisely measure distances between pairs of fragments. The distance is then used in building the fuzzy conflict graphs of fragments. Given that optimal haplotype reconstruction based on minimum error correction is known to be NP-hard, we use our fuzzy conflict graphs to develop a fast heuristic for fragment partitioning and haplotype reconstruction.

Availability: An implementation of FastHap is available for sharing on request.

Contact: sepideh@cs.ucla.edu

1 INTRODUCTION

All diploid organisms have two homologous copies of each chromosome, one inherited from each parent. The two DNA sequences of a homologous chromosome pair are usually not identical to each other. The most common DNA sequence variants are single nucleotide polymorphism (SNP). We refer to the sites at which the two DNA sequences differ as heterozygous sites. Current high-throughput sequencing technologies (Eid et al., 2009) are incapable of reading the DNA sequence of an entire chromosome. Instead, they produce a huge collection of short reads of DNA fragments. The process of inferring two DNA sequences (i.e. haplotypes) from a set of reads is referred to as haplotype assembly, which has become a crucial computational task to reconstruct one’s genome from these reads.

Haplotype assembly methods usually involve three main stages before reconstruction phase. First, a sequence aligner is used to align the reads to the reference genome. Then, only the read alignments at the heterozygous sites are kept for haplotype reconstruction. Last, reads that span multiple heterozygous sites are used to infer the alleles belonging to each haplotype. The quality of the reconstructed haplotypes may be dramatically affected by errors in sequencing and alignment. The objective, therefore, is to design algorithms that mitigate this impact and rebuild the most likely copies of each chromosome accurately. This has led to development of accurate haplotype reconstruction algorithms in the past few years. We are, however, observing a critical shift in sequencing technology where larger datasets with longer reads and higher coverage become available. This shift necessitates the development of algorithms that not only reconstruct haplotypes accurately but also require low computation time and can scale to large datasets. In this article, we introduce a new framework for fast and accurate haplotype assembly.

1.1 Motivation and related work

The past decade has witnessed much research effort on enhancing accuracy of haplotype assembly methods. The research, however, lacks a method that is not only accurate but also fast enough that can be used widely on large-scale datasets. In particular, current trends in sequencing technologies demonstrate that the sequence read lengths are being extended significantly and access to reads of up to several thousand base pair long will become a reality in near future.

Haplotype assembly approaches can be divided into two categories: (i) fragment partitioning; (ii) SNP partitioning. The fragment partitioning techniques partition the set of fragments into two disjoint sets each representing one copy of the haplotype. Examples of such techniques are FastHare (Panconesi and Sozio, 2004) and the greedy heuristic in (Levy et al., 2007). The SNP partitioning approaches such as HapCut (Bansal and Bafna, 2008), HapCompass (Aguiar and Istrail, 2012) and the approach in (He et al., 2010) rely on partitioning the SNPs into two disjoint sets and finding those variants whose corresponding haplotype bits need to be flipped to improve minimum error correction (MEC). In any of the two scenarios, an iterative process is involved. From a computational complexity point of view, the main drawback with existing techniques is that they perform much computation during each iteration of the algorithm.

HapCut (Bansal et al., 2008) is an example of the algorithms that use SNP partitioning technique to minimize MEC criterion. The process involves iteratively reconstructing a weighted graph and finding a max-cut of the graph. Clearly, most of the computation occurs in a loop. The algorithm has proved to be fairly accurate at the cost of high computation. The greedy heuristic algorithm in (Levy et al., 2007) is a fragment partitioning approach. The iteration, however, involves two major computing tasks: (i) reconstructing a partial haplotype based on the fragments that are already assigned to a partition; (ii) calculating distance between unassigned fragments and each one of the haplotype copies. FastHare (Panconesi and Sozio, 2004) is another fragment partitioning algorithm. It sorts all fragments based on their positions before execution of the iterative module. Computationally intensive tasks that occur iteratively in FastHare include (i) reconstruction of a partial haplotype based on the fragments that are already assigned to a partition; (ii) calculating distance between the current fragment and each one of the two haplotype copies.

1.2 Contributions

Our goal in this article is to develop a framework for fast and accurate haplotype reconstruction. Our approach consists of four steps: (i) we measure dissimilarity of every pair of fragments using a new distance metric; (ii) we build a weighted graph, called fuzzy conflict graph, using the introduced dissimilarity measure; (iii) we use the fuzzy conflict graph to construct an initial partition of the fragments through an iterative process; (iv) we refine the initial partitioning to further improve the overall MEC of the constructed haplotypes. More specifically, our contributions in this article can be summarized as follows.

Inter-fragment distance: We introduce a new distance metric, called inter-fragment distance, which quantifies dissimilarity between pairs of fragments. This distance measure is carefully developed to not only assign small values to the fragments that match perfectly and large values to completely different fragments but also neutralize the effect of missing alleles on final partitioning of the fragments.

Fuzzy conflict graph: We introduce the notion of fuzzy conflict graphs that are built based on the inter-fragment distances. In our graph model, each node represents a fragment and edge weights are corresponding dissimilarity measures between portions of fragments.

Fragment partitioning algorithm: We present a two-phase computationally simple heuristic algorithm for haplotype reconstruction. The first phase uses a fuzzy conflict graph to build an initial fragment partition. In the next phase, the initial partition is further refined to achieve additional improvements in the overall MEC performance of the reconstructed haplotypes.

Validation using real data: We demonstrate the effectiveness of the proposed techniques using HuRef dataset, a dataset that has been widely used in haplotype assembly literature recently. Specifically, we compare our method with several previously published algorithms in terms of accuracy (MEC measures) and scalability (execution time) performance. Our results show that FastHap significantly outperforms the previous algorithms by providing a speedup of one order of magnitude while delivering comparable or better accuracies.

Our objective is to build a fast haplotype assembly model where computationally intensive tasks are executed before execution of the iterative process. Our algorithm has the following major differences compared with the previous work: (i) our dissimilarity measure is a novel distance metric that precisely quantifies contribution of each individual fragment for haplotype assembly; (ii) we perform all distance calculations at the beginning of the algorithm and leave only computationally simple tasks to the iterative section; (iii) we perform haplotype reconstruction outside the iterative part of our algorithm.

2 MATERIALS AND METHODS

2.1 Problem statement and assumptions

We assume that the input to the haplotype assembly algorithm is a 2D array containing only heterozygous sites of the aligned fragments, called variant matrix, X, of size m × n, where m denotes the number of fragments (aligned DNA short reads) and n represents the number of SNPs that the union of all fragments cover. In the following discussion, we use x_ij to refer to the allele of fragment f_i at SNP s_j. $x_{ij}\in \{0,1,-\}$, where 0 and 1 encode two observed alleles and – denotes that fragment f_i does not cover the SNP site s_j. If there are more than two alleles observed at a given site, the two most common alleles are encoded with 0 and 1, and the remaining allele(s) are encoded by –. It is expected that most cells in X are filled with – because, in practice, each aligned fragment covers only a few SNP sites, limited by the fragment length (As discussed previously, the trend is that much longer DNA reads will be available as a result of recent technological advancements in genome sequencing).

Algorithm 1 FastHap high-level overview.

 Initialization:

 Calculate inter-fragment distance between every pair of fragments (Section 2.2)

 Store inter-fragment distances in Δ (Section 2.2)

 Use Δ to construct a fuzzy conflict graph (Section 2.3)

 ____________________________________________________________

 Phase (I): Partitioning

 Partition fragments into two disjoint sets C₁ and C₂ (Section 2.4 and Algorithm 2)

 ____________________________________________________________

 Phase (II): Refinement

 while (MEC score improves) do

  Find fragment $\widehat{f}$ with highest MEC value

  Assign $\widehat{f}$ to the opposite partition

 end while

One of the most popular approaches for haplotype assembly is to construct haplotypes based on partitioning of the fragments in variant matrix. In this case, the haplotype assembly problem consists of two steps, namely fragment partitioning and fragment merging, described as follows. While the fragment partitioning phase aims to group rows of the variant matrix into two partitions, C₁ and C₂, fragment merging is intended to combine the fragments residing in each partition, through a SNP-wise consensus process, and form two haplotypes h₁ and h₂ associated with C₁ and C₂, respectively. The resulting haplotype is typically denoted by H = {h₁, h₂}. The main objective of the haplotype assembly is, therefore, to come up with a partitioning such that the amount of error is minimized. Our focus in this article is on minimizing the MEC objective function. As mentioned previously, this problem is proved to be NP-hard (Cilibrasi et al., 2005). Thus, our goal is to develop a heuristic algorithm for the haplotype assembly problem. Our solution relies on a novel inter-fragment distance measure, a graph model for inter-fragment dissimilarity assessment and a fast graph partitioning algorithm. A high-level overview of FastHap is shown in Algorithm 1.

2.2 Inter-fragment distance

Given two variables $x,y\in \{0,1,-\}$, we define the operator ⊗ as follows.

$$x\otimes y=\{\begin{array}{ccc}0& \text{if}x=y& \\ 1& \text{if}x\ne y& \&x,y\in \{0,1\}\\ 0.5& \text{otherwise}& \end{array}$$ (1)

Definition 1 (Inter-fragment distance) —

Given a variant matrix $X_{m\times n}$ where $x_{ij}\in \{0,1,-\}$, we define inter-fragment distance, $\Delta (f_i,f_k)$, between fragments f_i = {$x_{i1},x_{i2},\dots$, x_in} and f_k = {$x_{k1},x_{k2},\dots$, x_kn} by

$$\Delta (f_i,f_k)=\frac{1}{T_{ik}}{\displaystyle \sum _{j=1}^n(x_{ij}\otimes x_{kj})}$$ (2)

where T_ik denotes the number of columns (SNPs) that are covered by either f_i or f_k in X. In fact, T_ik is a normalization factor that allows us to normalize the distance between the two fragments such that the resulting distance ranges from 0 to 1 (i.e. $0\le \Delta (f_i,f_k)\le 1$).

The inter-fragment distance metric is developed with the goal of measuring the cumulative dissimilarity between each pair of fragments across all SNP sites. The intuition behind (1) and (2) is as follows. At a given SNP site s_j, if two fragments f_i and f_k both cover it, the per-site distance is 0 if they take the same allele (suggesting they may likely belong to the same partition) and 1 if they take opposite alleles (suggesting they may likely belong to different partitions). We assign 0.5 distance if the SNP is only covered by one of the two fragments to neutralize the contribution of the missing element. If the SNP is not covered by either fragment, 0 distance is cumulated at this site. An additional benefit of this approach is that we need to examine only SNPs covered by either of the two fragments. From a computing complexity point of view, this can reduce the execution time of the distance calculation significantly.

Figure 1a shows a set of fragments spanning eight SNP sites. The resulting inter-fragment distances are shown in a symmetric distance matrix in Figure 1b. Intuitively, Δ (the distance measure between two fragments) is smaller for those fragments that need to be grouped together and larger for those that we prefer to be placed in different partitions. When distance between the two fragments is 0.5, the two fragments alone do not provide sufficient information as how they need to be partitioned.

Definition 2 (Pivot distance) —

Given a variant matrix $X_{m\times n}$, the pivot distance between any pair of fragments in {f₁, f₂, …, f_m} is λ = 0.5.

Fig. 1.

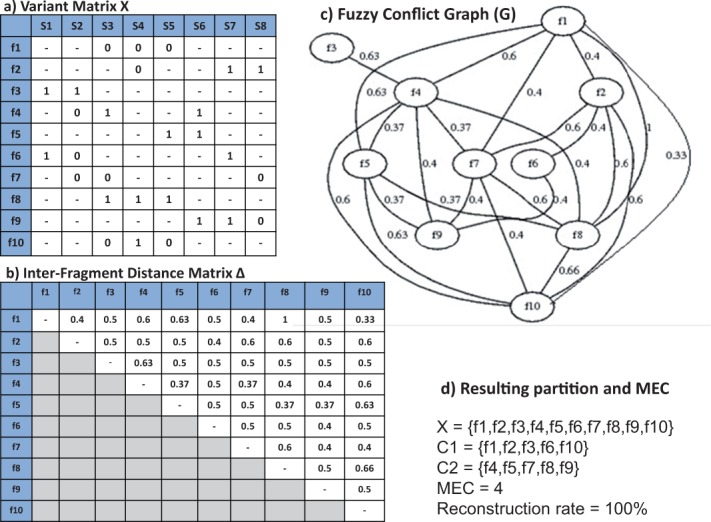
An example of variant matrix with 8 SNP sites (a), corresponding distance matrix (b), the fuzzy conflict graph associated with the variant matrix (c) and results of applying FastHap on the data (d). The graph in (c) shows only edges with non-pivot distances

The pivot λ allows us to decide whether the two fragments are dissimilar enough to be placed in separate partitions. A pair of fragments with an inter-fragment distance greater than λ is more likely to be placed in different partitions, although the final partitioning assignment is made after all pairs of fragments are examined through a partitioning algorithm. In Section 2.3, we will present a graph model that enables us to perform fragment partitioning by linking similar and dissimilar fragments through a weighted graph based on inter-fragment distance values.

2.3 FastHap graph model

In this section, we present a graph model based on the inter-fragment distance defined in (2). In Section 2.4, we will discuss how this graph model can be used to partition the fragments into two disjoint sets and construct haplotypes accordingly.

Definition 3 (Fuzzy conflict graph) —

Given a variant matrix X composed of m fragments {f₁, f₂, … , f_m} spanning n SNP sites, a fuzzy conflict graph that models dissimilarity between pairs of fragments is a complete graph G represented by the tuple (V,E,W_E). In this graph, V = {1, 2, …, m} is a set of m vertices representing the fragments in X; each edge e_l is associated with a weight w_l equal to the distance between the corresponding fragments in X.

The conflict graph introduced in this article, fuzzy conflict graph, is different from that used in previous research [e.g. the fragment conflict graph in (Lancia et al., 2001)]. A conflict graph has been conventionally defined as a non-weighted graph. Let us call it a binary conflict graph, which represents any pair of fragments with at least one mismatch in the variant matrix. For example, according to (Lancia et al., 2001), a conflict graph is a graph with an edge for each pair of fragments in conflict where two fragments are in conflict if they have different values in at least one column in the variant matrix X. There are a number of shortcomings with respect to using a binary conflict graph for haplotype assembly. The major problem with the conventional conflict graph is that it does not take into account the number of SNP sites for which the two fragments exhibit a mismatch. Two fragments are considered in conflict even if there is a mismatch at only one SNP site. In contrast, our fuzzy conflict graph aims to measure the amount of mismatch across all SNP sites of every pair of fragments. For example, consider the three fragments f₁ = {$--000---$}, f₈ = {$--111---$} and f₁₀ = {$--010---$} in Figure 1. In a binary conflict graph, all the vertices are connected because there is at least one mismatch between every pair of fragments: three mismatches between f₁ and f₈, one mismatch between f₁ and f₁₀ and two mismatches between f₈ and f₁₀. The binary conflict graph, however, treats all three edges equally. Our fuzzy conflict graph assigns weights of 1, 0.33 and 0.66 to these edges, respectively, to lead the partitioning algorithm to group f₁ and f₁₀ together.

An example of a fuzzy conflict graph based on the fragments listed in Figure 1a is illustrated in Figure 1c. For visualization, the edges with a pivot distance are not shown. The problem of dividing the fragments into two most dissimilar groups is essentially a max-cut problem (Ausiello, 1999). A max-cut partition may divide the fragments into C₁ = {f₁, f₂, f₃, f₆, f₁₀} and C₂ = {f₄, f₅, f₇, f₈, f₉} as shown in Figure 1. We note that the resulting partition may not be unique in its general case. As we will discuss in more details in Section 2.4, max-cut is an NP-hard problem, and existing techniques provide solutions that are highly suboptimal. Thus, we will leverage some properties of our fuzzy conflict graphs to develop a heuristic approach for fragment partitioning.

2.4 Fragment partitioning

As stated previously, our goal is to partition fragments into two disjoint sets such that fragments within each group are most similar and can form a haplotype with minimum MEC. Using the fuzzy conflict graph model presented in Section 2.3, a weighted max-cut algorithm needs to be used to find the optimal partition. The max-cut problem, however, is known to be NP-hard even when all edge weights are set to one (Garey and Johnson, 1990). All edges in our fuzzy conflict graph have a positive weight. There exist heuristic algorithms (Sahni and Gonzales, 1974) that produce a cut with at least half of the total weight of the edges of the graph when all edges have a positive weight. In fact, a simple $\frac{1}{2}$ − approximate randomized algorithm is to choose a cut at random. This means that each edge e_l in the fuzzy conflict graph G is cut with a probability of $\frac{1}{2}$. Consequently, the expected weight of the edges crossing the cut, W(C₁,C₂), is given by

$$W(C_1,C_2)=\frac{1}{2}{\displaystyle \sum _{l=1}^L{w}_l}\ge \frac{1}{2}OPT$$ (3)

This algorithm can be derandomized to obtain a $\frac{1}{2}$ − approximate deterministic algorithm. There exist two major shortcomings with this partitioning algorithm: (i) Unfotunately, derandomization works well only on unweighted graphs where all edges have equal/unit weights. A similar approach for a weighted graph is not guaranteed to run in polynomial time; (ii) the obtained partition is highly suboptimal with an approximation factor of $\frac{1}{2}$. Thus, we introduce a novel heuristic algorithm based on properties of fuzzy conflict graphs.

Algorithm 2 FastHap partitioning algorithm.

Require: Fuzzy conflict graph G = (V,E,W_E)

Ensure: Partition $P=[C_1,C_2]$ composed of two groups C₁ and C₂ of fragments

 (1) Delete edges with pivot weights from G

 (2) Sort remaining edges e_l in G based on their weights w_l and store results in list D

 (3) Let $e_l=(f_i,f_k)$ be the edge with the largest weight in D

 (4) Initialize partition by assigning f_i and f_k to opposite groups (e.g. C₁ = $\left\{f_i\right\}$ & C₂ = $\left\{f_k\right\}$

 while (not all vertices are partitioned) do

  (5) Let $e_l=(f_i,f_k)$ be next edge with highest weight in D such that $f_i\in P$ or $f_k\in P$

  (6) Let $f_i\in P$; if $f_i\in C_1$, then $C_2=C_2\cup \left\{f_k\right\}$, otherwise $C_1=C_1\cup \left\{f_k\right\}$

  (7) Let $e_r=(f_i,f_k)$ be next edge with lowest weight in D such that $f_i\in P$ or $f_k\in P$

  (8) Let $f_i\in P$, then if $f_i\in C_1$, then $C_1=C_1\cup \left\{f_k\right\}$, otherwise $C_2=C_2\cup \left\{f_k\right\}$

  (9) If none of e_l and e_r exist, assign each remaining fragment to the more similar set

 end while

 repeat

  (10) Let MEC be the switching error for existing partition

  (11) Let f_i be the fragment with largest switching error among all fragments in P

  (12) If $f_i\in C_1$ (alternatively $f_i\in C_2$), move f_i from to C₂ (alternatively to C₁)

  (13) Let newMEC bet the switching error for the new partition

 until ($newMEC\ge MEC$)

The FastHap partitioning algorithm is shown in Algorithm 2 and briefly explained as follows. First, the algorithm eliminates all edges with pivot weights from the fuzzy conflict graph G. Such edges do not contribute to formation of the final partition. The algorithm then sorts all edges of the graph (equivalently, pairs of the fragments) based on the edge weights and stores the results in D. An initial partition is formed by placing the two fragments with largest inter-fragment distance (associated with the heaviest edge in G) into two separate partition sets C₁ and C₂. In the next phase, the algorithm alternates between the heaviest and lightest edges and assigns adjacent vertices (associated with fragments in X) to the existing partition if either of the vertices is already assigned to the partition. An edge with highest weight results in placing the adjacent vertices in different partitions and an edge with lowest weight attempts to assign the vertices to the same partition in P. This occurs only if the chosen edge is adjacent to an already partitioned edge.

Theorem 1 —

Algorithm 2 terminates in polynomial time.

Proof —

We prove that the algorithm terminates and its running time is polynomial. Let M be the total number of edges in the given fuzzy conflict graph, respectively. During each iteration, the algorithm attempts to assign two edges (those with highest and lowest weights and adjacent to an already partitioned vertex) to the final partition P. Clearly, the iterative loop does not repeat more than M′ times. In fact, during each iteration at least one edge (i.e. e_l or e_r or both) is selected to be added to the final partition. If the algorithm cannot find such an edge, all remaining edges are allocated to the final partition and the algorithm ends. Therefore, the iterations cannot repeat more than M′ times and the algorithm will terminate after at most M′ iterations. The proof regarding computing complexity of the algorithm is as follows. Removal of edges with pivot weight in (1) in Algorithm 2 can be completed in O(M); the process of sorting the edges in instruction (2) can be done in O($M\log M$); instruction (3) takes O(1) to complete. The initialization of the partition in (4) can be done in O(1); (5) detecting the edge with the highest weight and checking if one of its vertices (i.e. fragments) is already in the partition P require O(1) and O(M), respectively, to be completed; (6) assigning the selected edge to the partition require O(1); similarly, instructions in (7) require O(1) and O(M) to finish; similar to (6), the instructions in (8) can be done in O(1). The instructions in (9) have a complexity of O(M); reading the MEC value of the partition in (10) and (13) takes O(1); instructions in (11) and (12) can finish in O(M). Given that instructions in the loop are executed at most M times, the complexity of the algorithm is O(M²).

2.5 Refinement phase

The second loop in Algorithm 2 shows second phase of the proposed haplotype reconstruction approach. The idea is to iteratively find the fragment that contributes most to the MEC score and reassign it to the opposite partition. This process repeats as long as the MEC score improves. Our experimental results show that the first phase of the algorithm performs most of the optimization in terms of MEC improvements, leaving minimal improvements for the second phase.

2.6 Fragment purging

Because the complexity of FastHap is a function of the number of fragments in the variant matrix, it is reasonable to attempt to minimize the number of such fragments by eliminating any potential redundancy before execution of the main algorithm. Therefore, FastHap uses a preprocessing phase during its initialization to combine those fragments that are highly similar. Fortunately, the inter-fragment distance measure provides a means to assess similarity between every two fragments. The criterion for combining two fragments f_i and f_k is based on the inter-fragment distance $\Delta (f_i,f_k)$ and a given threshold α. The two fragments are merged if

$$\Delta (f_i,f_k)\le \alpha$$ (4)

The purging process is straightforward. It eliminates the shorter fragments from the variant matrix. The value of α needs to be set based on the quality of data. For the dataset used in our experiments on different chromosomes, we set α experimentally and found that $\alpha =0.2$ provides the best performance.

3 VALIDATION

3.1 Setup

We used HuRef (VenterInst, 2014), a publicly available dataset, to demonstrate the effectiveness of FastHap for individual haplotype reconstruction. Our goal was to assess performance of FastHap in terms of both accuracy and speed in comparison with HapCut (Bansal and Bafna, 2008) and greedy algorithm in Levy et al. (2007). The main reason for choosing these two algorithms is that these algorithms have been historically popular in terms of accuracy and computing complexity. We ran all our experiments on a Linux x86 server computer. The server had 16 CPU cores of 2.7 GHz with 16 GB of RAM. Each algorithm performed per-block haplotype reconstruction. Each block consisted of the reads that do not cross adjacent blocks. Although haplotype assembly solutions cannot do more than random guess between two consecutive variant site that do not share any fragments, our effort in this article was to provide technology that is appropriate for longer reads in each end of paired alignment and ample insertion size to minimize disconnection between different haplotype blocks.

3.2 Dataset

The HuRef dataset used for our analysis contains reads for all 22 chromosomes of an individual, J.C. Venter. The data include 32 million DNA short reads generated by Sanger sequencing method with 1.85 million genome-wide heterozygous sites. There are too many fairly short reads of ∼15 bp (each end) while still tens of thousands of reads are long enough to cover more than two SNP sites and can be used for haplotype assembly purposes. In fact, many fragments within each block span several hundred SNP sites owing to the pair-end nature of the aligned reads. The variant matrix used for haplotype assembly was generated based on aligned short reads with paired-end method for each pair of various length (from 15 to 200 bp each end) while the insert length follows a normal distribution with a mean of 1000.

Figure 2a shows read coverage for each chromosome. Read coverage numbers are calculated by taking an average over the coverage values of all SNP sites within each chromosome. The coverage vary from 6.49 reads for chromosome 19 to 8.72 reads for chromosome 3. The average genome-wide coverage across all chromosomes is 7.43. Figure 2b shows distribution of the coverage for chromosome 20 (exemplary), which includes 39 767 SNP sites. The coverage numbers range from 1 to 20 reads. Only two SNP sites had a coverage of 20. The average coverage for chromosome 20 was 6.83.

Fig. 2.

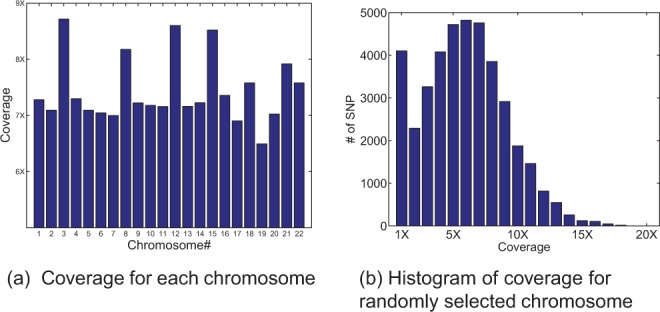
Coverage of HuRef dataset; (a) coverage for each chromosome; numbers vary from 6.49 to 8.72 for various chromosomes with an average genome-wide coverage of 7.43. (b) Histogram of coverage for chromosome 20 as an example; Y-axis shows number of SNPs, with each specific coverage shown on x-axis

Figure 3 shows several statistics on haplotype length of various chromosomes in HuRef dataset. Figure 3a shows chromosome-wide haplotype length, equivalent ally total number of SNP sites, for each chromosome. As mentioned previously, each chromosome is divided into non-overlapping blocks. Haplotype length of such blocks may vary significantly from one chromosome to another. For example, Figure 3b shows distribution of haplotype length for a subset of chromosomes with ‘small’, ‘medium’ and ‘large’ haplotypes. For instance, chromosome 8 has a number of blocks spanning >2500 SNPs. In contrast, haplotypes in chromosome 18 barely exceed 1000 SNP sites.

Fig. 3.

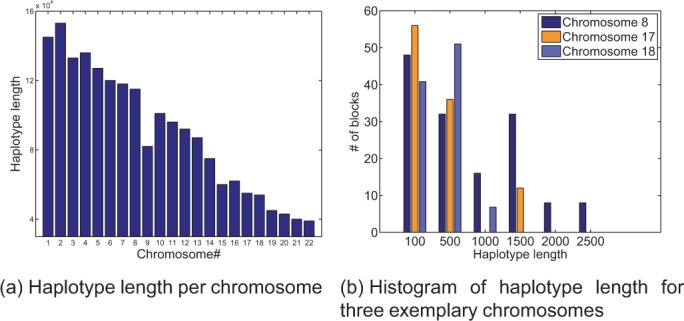
Chromosome-wide haplotype length for each chromosome (a) and histogram of per-block haplotype length for chromosomes 8, 17 and 18 as examples of chromosomes with ‘small’, ‘medium’ and ‘large’ blocks, respectively (b)

In addition to running FastHap on real HuRef data, we constructed several simulated read matrices based on HuRef data (Bansal and Bafna, 2008). A simulated dataset based on real data allows us to assess performance of the proposed algorithm and extend its capabilities by changing various parameters (e.g. error rate, coverage and haplotype length or block width). To assess the accuracy of our method, we simulated a pair of chromosome copies based on real fragments and consensus SNP sites provided by HuRef data. The variant matrix for each chromosome on HuRef data was suitably modified to generate an ‘error free’ matrix at first. This was accomplished by modifying alleles in each fragment such that it perfectly matches a predefined haplotype. To introduce errors in the variant matrix, each variant call was flipped with a probability of ε ranging from 0 to 0.25. We also modified the variant matrix to produce variant matrices of different coverage. Another change to the simulate variant matrix was to generate blocks of varying haplotype length ranging from 200 to 1000 SNPs. Such variant matrices were then used to examine how performance of different algorithms (i.e. FastHap, Greedy, HapCut) changes as a result of changes in error rate, coverage and haplotype length.

3.3 Results

Table 1 shows speed and accuracy results for all chromosomes on HuRef dataset. As it can be observed from the timing values, FastHap is significantly faster than both Greedy and HapCut. In particular, FastHap is up to 16.4 times faster than HapCut and up to 15.1 times faster than Greedy. The average speedup achieved by FastHap is 7.4 and 8.1 compared with Greedy and HapCut, respectively. In terms of accuracy performance, FastHap achieves 35.4 and 1.9% improvement in reducing switch error compared with Greedy and HapCut, respectively.

Table 1.

Comparison of FastHap with Greedy and HapCut in terms of accuracy (MEC) and execution time using HuRef dataset. Best results in each column showed in bold

	Time (min)			Speedup using FastHap		MEC (accuracy performance)
Chr	Greedy	HapCut	FastHap	versus Greedy	versus HapCut	Greedy	HapCut	FastHap
1	606	880	183	3.3	4.8	29 657	19 750	19 423
2	1001	2446	149	6.7	16.4	22 980	14 677	14 220
3	1809	1053	188	9.6	5.6	16 878	10 738	11 794
4	542	694	63	8.6	11.0	18 153	11 931	11 812
5	1381	3229	282	4.9	11.4	16 590	10 630	10 362
6	681	750	109	6.2	6.9	15 587	9992	9870
7	456	604	76	6.0	7.9	17 402	11 290	11 245
8	5052	4514	334	15.1	13.5	14 887	9845	10 830
9	2006	1747	293	6.8	6.0	13 812	9318	9204
10	667	1445	170	3.9	8.5	15 291	9906	9796
11	332	288	69	4.8	4.2	12 906	8294	8091
12	1303	1638	165	7.9	9.9	12 630	8297	7467
13	428	761	158	2.7	4.8	9312	6131	6143
14	3315	1919	383	8.7	5.0	9734	6360	5725
15	907	1137	208	4.4	5.5	13 988	9783	9695
16	157	248	42	3.7	5.9	12 621	8354	8215
17	2223	2790	246	9.0	11.3	11 157	7398	7386
18	698	798	87	8.0	9.2	8578	5043	4846
19	309	501	41	7.5	12.2	8214	5497	4886
20	326	348	32	10.2	10.9	5752	3784	3437
21	482	154	48	10.0	3.2	6611	4715	4707
22	535	128	39	13.7	3.3	8295	5864	5875
Overall	25 217	28 074	3365	7.4	8.1	301 035	197 597	195 029
	Sum over all chromosomes			Average		Sum over all chromosomes

Note. FastHap achieves speedups of 16.4 and 15.1 compared with HapCut and Greedy, respectively, is 1.9 and 35.4% more accurate than HapCut and Greedy, respectively. Statistics on coverage and haplotype length are shown in Figs 2 and 3 and further discussed in Section 3.2.

A number of parameters affect speed performance of different algorithms. In particular, number of SNP sites within each variant matrix is an important factor in many well-known algorithms such as HapCut. One advantage of FastHap is that its performance is primarily influenced by the number of fragments in the variant matrix rather than the number of SNP sites. That is, a higher read coverage allows FastHap to generate better accuracy without significant impact on its running time. In contrast, as the haplotype length grows, HapCut algorithm runs very slowly compared with FastHap. As shown in Table 1, HapCut is very slow when applied to chromosome 8 primarily owing to the large haplotype length. This is also confirmed through Figure 3b, which shows that chromosome 8 contains blocks that span >2500 SNPs. In contrast, chromosome 18, for example, can be reconstructed much faster when HapCut is used. Figure 3b shows that most of the blocks for chromosome 18 span <1000 SNP sites.

Using the simulated data described in Section 3.2, we ran FastHap on variant matrices of varying error rates and compared the reconstructed haplotypes with the true haplotypes. With this, we obtained the absolute accuracy results shown in Table 2. For brevity, results are shown only for 6 error rate values. The table shows how the absolute accuracy of the obtained haplotype is affected as a result of introduced errors. We observe that the accuracy numbers are always larger than what one may expect owing to the error rate. For example, when the error rate is 20%, one may expect an absolute accuracy of 80%, but the measured accuracy is 85.7%. This can be interpreted as follows. As the error rate (i.e. number of flipped variant calls) increases, some variant calls may become consistent with a different haplotype of higher accuracy.

Table 2.

Absolute accuracy of FastHap as a function of error rate

Error rate (ε in %)	0	5	10	15	20	25
Accuracy on HuRef (%)	100	96.2	90.3	86.0	85.7	80.6

Note. Results are obtained using variant matrix based on HuRef datasets.

Figure 4a shows the MEC score per variant call versus the simulated error rate obtained by each one of the three algorithms. The average MEC (normalized by number of variant calls) was 2.48, 2.56 and 2.86 for FastHap, HapCut and Greedy, respectively. The amount of improvement in MEC using FastHap was 13 and 2.8% compared with Greedy and HapCut, respectively. Figure 4b shows the running time of the three algorithms as the coverage varies from 5 to 20. For this experiment, the variant matrix was carefully modified to obtain the right coverage needed for the analysis. Furthermore, the obtained matrix was first made ‘error free’. We then flipped the variant calls with a probability of $\mathrm{ϵ}=0.25$ for this analysis.

Fig. 4.

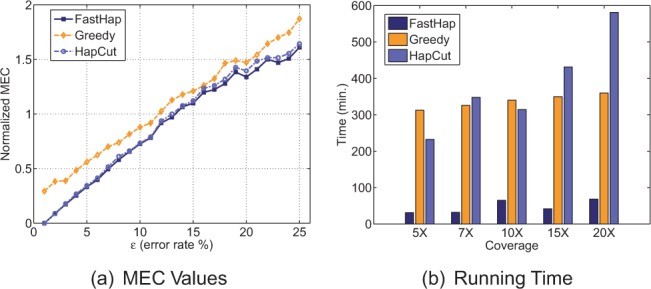
Effect of error rate and coverage on performance of different algorithms. The analysis was performed on chromosome 20 (randomly selected) of HuRef dataset. (a) Switching error (MEC) of the three algorithms under comparison as a function of error rate; (b) execution time of the algorithms as a function of coverage

To assess running time of different algorithms with respect to changes in haplotype length, variant matrices with different number of columns were built as explained previously in Section 3.2. Figure 5a shows execution time of the three algorithms as the partial haplotype length grows from 200 to 1000 SNPs. For this analysis, an injected error rate of $\mathrm{ϵ}=0.25$ was used. We note that the results are shown only for one block of data. It can be observed that the running time of HapCut increases significantly as the block width grows. That is, while HapCut can build a partial haplotype of length 200 in 25 s, its running time increases to 784 s when the length of the haplotype increases to 1000 SNPs.

Fig. 5.

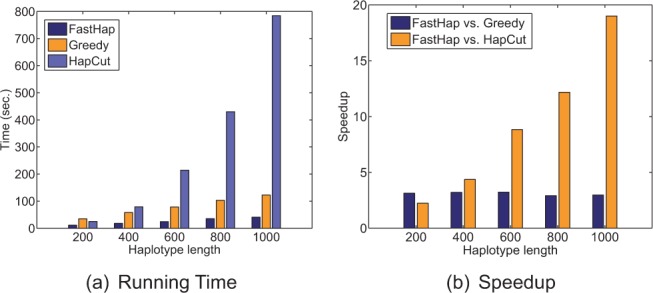
Speed performance of the three algorithms as a function of haplotype length. Analysis was performed on chromosome 20 (randomly selected) of HuRef dataset. (a) Execution time as a function of haplotype length. (b) Amount of speedup achieved by FastHap compared with Greedy and HapCut

To demonstrate superiority of FastHap partitioning algorithm over a random partitioning, we selected a subset of the dataset at random. We ran both FastHap and random partitioning algorithms on the same variant matrix 10 times and calculated percentage of improvements in MEC achieved by FastHap. The improvement numbers ranged from 12.17 to 31.64%, with an average improvement of 19.13%.

4 DISCUSSION AND FUTURE WORK

Development of efficient and scalable algorithms for haplotype assembly and reconstruction is by large an open research problem. Presence of error and missing data in the DNA short reads makes the problem challenging. Current approaches suffer from limited accuracy and are not scalable for application on large datasets. In this article, we presented design, implementation and validation of FastHap, a highly scalable haplotype assembly and reconstruction method that has shown promising results compared with the state-of-the-art assembly techniques. We presented a novel dissimilarity metric that quantifies inter-fragment distance based on the contribution of individual fragments in building a final haplotype. The notion of fuzzy conflict graph was proposed to model the haplotype reconstruction as a max-cut problem. We then introduced a fast heuristic algorithm for fragment partitioning based on the fuzzy conflict graphs. The framework lowers computing complexity of haplotype reconstruction dramatically while also outperforming accuracy performance of several popular assembly algorithms. In particular, FastHap is up to one order of magnitude faster than HapCut (Bansal and Bafna, 2008) and Levy’s greedy approach (Levy et al., 2007).

In this article, we compared FastHap with two well-known haplotype reconstruction algorithms, namely Levy’s greedy algorithm and HapCut. The greedy algorithm is historically known for its high speed while it also outperforms accuracy of other computationally simple and greedy algorithms such as FastHare (Panconesi and Sozio, 2004). HapCut, in contrast, is popular for its high accuracy, but demands much higher computational resources compared with Greedy.

Because DNA short fragments are used in the process of haplotype assembly, the number of SNPs that each short read encompasses is considered to be an important factor. As a general rule, short reads that cover less than two SNP sites are eliminated in our analysis. When two or more variant positions are spanned by a single read, or occur on paired reads derived from the same shotgun clone, alleles can be linked to identify larger haplotypes. Current sequencing technologies provide us with fragments that may or may not span multiple SNP sites. Although such reads do not link multiple SNPs, they can provide useful haplotype information for the SNP they cover. Our approach in this article does not require a preprocessing phase to eliminate such reads from further analysis.

FastHap is a heuristic approach and may result in a suboptimal solution. Yet, it can provide high-quality phasing of heterozygous variant sites. Unlike many prior works that use a randomly generate vector to seed the initial haplotype, the starting point of our algorithm is not a completely random pair of haplotypes but created using our intelligent distance measure. As demonstrated through our results, this approach would significantly improve the time complexity and accuracy of the obtained haplotypes.

Given the promising speed results that we have achieved using FastHap, we are planning to further improve the accuracy of our algorithm. We believe that the algorithm can become much smarter if a cross-optimization approach is applied where both fragment and SNP sets are considered for haplotype reconstruction/refinement.

In this article, we performed per-block analysis of speed and accuracy. As part of our future work, we plan to study how haplotypes generated from each block can be effectively combined to form genome-wide haplotypes. We also plan to study if the errors condensed by MEC values coincide when two haplotype reconstruction algorithms are compared.

With recent advancements in the sequencing technologies, access to long reads of more than few thousand bases is becoming a reality (Huddleston et al., 2014). For example, Pacific Biosciences™ released an extra-long set of DNA fragments with average read length of 8849 bp and up to 54X coverage. The dataset has recently become publicly available (PacificBiosciences, 2014). This dataset, which contains single-end long fragments, is expected to be an excellent means to demonstrate huge speed/accuracy benefits that FastHap can provide. Another example is newly released datasets based on 1000 Genome project (Siva, 2008). These datasets are also large with high-density SNP sites. Our ongoing work involves application of FastHap on such datasets.