Effects of small particle numbers on long-term behaviour in discrete biochemical systems

Abstract

Motivation: The functioning of many biological processes depends on the appearance of only a small number of a single molecular species. Additionally, the observation of molecular crowding leads to the insight that even a high number of copies of species do not guarantee their interaction. How single particles contribute to stabilizing biological systems is not well understood yet. Hence, we aim at determining the influence of single molecules on the long-term behaviour of biological systems, i.e. whether they can reach a steady state.

Results: We provide theoretical considerations and a tool to analyse Systems Biology Markup Language models for the possibility to stabilize because of the described effects. The theory is an extension of chemical organization theory, which we called discrete chemical organization theory. Furthermore we scanned the BioModels Database for the occurrence of discrete chemical organizations. To exemplify our method, we describe an application to the Template model of the mitotic spindle assembly checkpoint mechanism.

Availability and implementation: http://www.biosys.uni-jena.de/Services.html.

Contact: bashar.ibrahim@uni-jena.de or dittrich@minet.uni-jena.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Systems biology heavily relies on the precise language of reaction networks (RNs) to describe many different processes in cells and other living systems in a formal way (Kitano, 2002; Klipp et al., 2009). Molecules and reactions can be expressed in an explicit or implicit way (Danos and Laneve, 2004). These descriptions of the network only capture the static part of the model. Additionally the reactor, i.e. a collection of molecules, and the dynamics, i.e. how to apply reactions to a reactor, have to be specified.

There are many different ways to model the dynamics of the application of rules in a chemical system. To approximate the inherently stochastic evolution of chemical systems typically ordinary differential equations (ODEs) are in use (Dittrich et al. 2001). In this case, one assumes that a huge or even infinite amount of particles is present so that it is reasonable to assume continuous amounts, or more precisely, concentrations. Furthermore, usually a well-stirred reactor and time constant reaction rates as well as a sequential application of rules are presumed. Depending on the type of system different kinetics like mass action (Connors, 1990) or Michaelis–Menten kinetics (Michaelis and Menten, 1913) can be used.

When looking at qualitative properties, we are often interested in the long-term behaviour, i.e. the final states that the system is able to reach. In continuous dynamical systems, given by the ODEs, fixed points and limit cycles represent the final states of the system. Chemical organization theory (COT) (Dittrich and di Fenizio, 2007) was developed to better understand the long-term behaviour of chemical system by introducing chemically more relevant aspects and notions. Based on concepts of organization in biology (Fontana and Buss, 1994), COT was developed to deal with constructive systems, i.e. systems in which new species appear and stay over a longer period. So far, COT was applied successfully in various areas like chemical computing (Matsumaru et al., 2007), social systems (Dittrich and Winter, 2005), evolutionary game theory (Veloz et al., 2014), HIV dynamics (Matsumaru et al., 2006) or checking systems biology models for inconsistencies (Kaleta et al., 2009). The theoretical results are based on the continuous dynamics and include the observation that in every fixed point there is a chemical organization (Dittrich and di Fenizio, 2007; Peter and Dittrich, 2011).

Nevertheless their usefulness, the benefit to use differential equations with a rich arsenal of methods to find such solutions is finally limited by the fact that particle numbers are finite. Hence, obviously not all properties of a system’s behaviour can be detected. Cao and Liang (2008); Schultz et al. (2007) already made some efforts to analyse small stochastic networks by analysing effects of small numbers of molecules on the stability of switches and by proposing an algorithm to enumerate the state space for spaces with small copy numbers with a limited number of newly produced molecules, respectively. Ramaswamy et al. (2012) discovered that for small sizes of reactors, the ratio between the amounts of species in steady state can change, and hence, called this effect “discreteness-induced inversion effect”.

The inherent stochasticity of the dynamics in chemical systems gives rise to well-established models like the algorithm developed by Gillespie (1976, 1977). There the update of the molecules is based on the fact that the occurrence of a reaction depends solely on the abundance of molecules necessary for firing the reaction. Even though stochastic dynamics are much closer to a realistic system, there are additional phenomena that are mostly not considered in these standard models. Fedoroff and Fontana (2002) examine the effect of stochasticity, noise and small numbers of macromolecules and also pose the question “So how do organisms manage—and perhaps even capitalize on—molecular noise?” Halling (1989) even asks “Do the laws of chemistry apply to living cells?” In other words, are the generally used settings for chemistry, described above as the assumptions for the ODE system, correct for a living cell?

After the initial observation of molecular crowding in cells (Laurent, 1963; Laurent and Ogston, 1963), recently, even the tracking of single molecule production is possible (Elf et al., 2007; Yu et al., 2006). They discovered that proteins are produced in bursts from single messenger RNA molecules. Becskei et al. (2005) show how low molecule numbers change gene expression. Reviews on macromolecular crowding and confinement are presented in (Zhou et al., 2008; Zimmerman and Minton, 1993). On the theoretical side, there is the idea of fractal kinetics (Kopelman, 1988), and how macromolecular crowding implies these fractal kinetics (Schnell and Turner, 2004). Other influences of the geometry by the kinetics are given in (Bénichou et al., 2010).

In this article, we put an emphasis on two aspects, which we call particle effect, of discrete systems. First, a small amount of molecules of one or more species present in the reaction vessel has an effect on the dynamical long-term behaviour of the system. Second, the limitation of number of molecules in the reaction vessel is considered. We aim to detect the ability of RNs to stabilize because of the impact of small molecular number or finite reactor size. This can be achieved by extending the theory of chemical organizations.

For the extension, we look at the system in a discrete way, i.e. there is no concentration of molecules, but rather a discrete amount of them. This leads to discrete states and transitions between them given by possible sequences of reactions. The dynamics usable with this theory was chosen as general as possible, including mass action, Michaelis–Menten and maximal parallelism (Krepska et al., 2008). However, only the simplest model assuming one transition per reaction will be used in the main text. This setup yields a Markov chain model on a transition graph. Similar to COT, the definition of discrete organizations is based on the closure and self-maintenance properties. These two notions can be adapted to a discrete setup. All continuous organizations are found to be discrete chemical organizations as well. This makes the extension sound. The discrete organizations correspond to particular steady states, which we identified as caused by the described particle effects.

To distinguish between the so far developed continuous COT and the discrete one, we denote it by discrete chemical organisation theory (DOT). For the introduction of all the necessary notions in COT and Markov chains, we refer to Supplementary Sections 1 and 2, respectively. We define discrete organizations in Section 2.2. A characterisation via communication class in Supplementary Section 3 then establishes properties for small sizes of reactor vessels. For RNs with special structural properties, stronger results hold, see Supplementary Section 4. Finally we use our findings to examine the Template model of the mitotic spindle assembly checkpoint (SAC) mechanism in Section 3.2. We use a Java implementation, which is also available online. With its help, we scanned the BioModels Database (Chelliah et al., 2013) for the existence of discrete organizations, see Section 3.1.

2 METHODS

2.1 RNs and transition graphs

A RN consists of a set of molecular species and a set of reactions, which are interactions among molecules that lead to the appearance or disappearance of molecules.

Definition 1 —

Let $\mathcal{M}$ be a set and $\mathcal{R}$ be a subset of ${\mathcal{P}}_{mult}(\mathcal{M})\times {\mathcal{P}}_{mult}(\mathcal{M})$ where ${\mathcal{P}}_{mult}(\mathcal{M})$ denotes the set of multisets over $\mathcal{M}$. The pair $(\mathcal{M},\mathcal{R})$ is called RN, and we call $\mathcal{M}$ the set of molecules and $\mathcal{R}$ the set of reactions.

By applying or firing a reaction $(l,r)\in \mathcal{R}$ to a multiset s, also called a state, over $\mathcal{M}$, we mean replacing the subset l by the subset r in s. The stoichiometric coefficients of $(l,r)$ are $l_M$. We assume that the multiset considered is always large enough, i.e. that it consists of enough molecules as required on the left hand of the rule, otherwise the reaction is not applicable. Also, we will assume a maximal reactor size or maximal size of state $N_{\text{max}}$ later in our considerations; a rule cannot be applied if the resulting multiset exceeds the maximum. A limited reactor size also means a finite state space. We will use the notations from multiset theory and write $(l,r)(s)=s-l+r$ for the result of applying a reaction to a multiset.

A subset C of $\mathcal{M}$ being closed means that by applying all reactions possible in C to multisets over C we do not get molecules outside C. A subset S of $\mathcal{M}$ being self-maintaining means that reactions able to fire in S can occur at certain strictly positive rates to a multiset over $\mathcal{M}$ without reducing the number of molecules of any species of S.

Definition 2 —

A subset of $\mathcal{M}$ is a chemical organization if it is closed and self-maintaining.

The set of all states s, i.e. multisets of species, is called state space; see Figure 3 for an example. We call a set of states c a part of the state space and define the molecules present in states of the part as $\mathcal{M}(c)$. We also use this notation for species, i.e. $\mathcal{M}(s)=\mathcal{M}(\{s\})$. Analogously, the reactions firing in a part c are denoted ${\mathcal{R}}_c$.

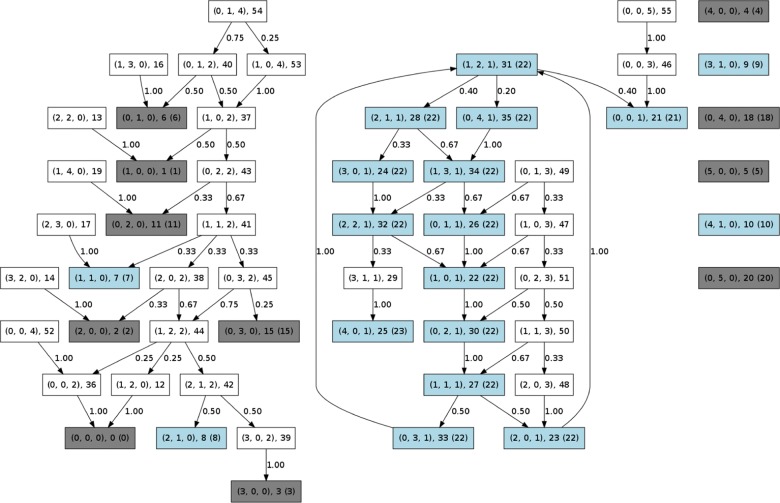
Fig. 3.

Example for our definition of pdorgs. Again, we consider the network $\mathcal{M}=\{A,B,C\}$, $\mathcal{R}=\{A+2B\to \varnothing ,A+C\to 2B+C,B+C\to A+C,$ $2C\to \varnothing \}$ with $N_{\text{max}}=5$ described in Figure 1 before. The boxes refer to the states, where, for example, $(1,2,1),31(22)$ in the top middle, means there is one element of species A, one of C and two of species B, the state has the unique number 31 and is part of the communication class with number 22. The labels at the transitions are the transition probabilities. There are the pdorgs $\{A,B,C\}$ with a generator $(1,2,1)$, $\left\{C\right\}$ with a generator $(0,0,1)$ and $\{A,B\}$ with a generator $(1,1,0)$. The light blue coloured states show the generators of the pdorgs. The grey states show the generators for the rest of organizations, namely, $\left\{A\right\}$, $\left\{B\right\}$ and $\{\varnothing \}$. We refer to the Supplementary Material, Section 5, for how they can be calculated

The following definitions are adopted from Markov chain theory; see for example (Brémaud, 1999), p. 56, and p. 71.

Definition 3 (Transition graph) —

The transition graph is a directed graph with the states as nodes and edges from a state s to a state $\stackrel{\sim }{s}$ if there is a transition, i.e. a sequence of reactions $\mathcal{R}(s,\stackrel{\sim }{s})$ transforming s to $\stackrel{\sim }{s}$.

Definition 4 (Accessible set) —

A state $\stackrel{\sim }{s}$ is said to be accessible from state s if there is a path from s to $\stackrel{\sim }{s}$. The set of states accessible from s is called accessible set from s and denoted $\text{Acc}(s)$.

2.2 Particle effects and discrete organizations

Dynamical models of RNs mostly use ODEs to describe the change in concentration of the molecular species over time. Because concentrations are a continuous abstraction of the actual amounts of molecules present, we are interested in the cases that the actual number influences the observed behaviour. The motivation for defining discrete organizations is so-called particle effects, which are the consequences of using discrete molecule numbers. They occur in two different cases.

The first case happens if there are too few particles to start a reaction, e.g. when there are reactions in the network where at least one reactant species M has a stoichiometric coefficient l_M > 1. Then, this reaction cannot fire if the amount of M is lower than l_M. When using concentrations to describe the amount of M, the effects of the not firing are not captured; see Figure 1. Taking the naive approach to just compute the solutions of the equations given by mass action kinetics leads to predicting a long-term behaviour of the concentrations, which is not possible in a real chemical system with a limited amount of molecules.

Fig. 1.

Effects of small molecular numbers. The network is $\mathcal{M}=\{A,B,C\}$, $\mathcal{R}=\{A+2B\stackrel{k_1}{\to }\varnothing ,A+C\stackrel{k_2}{\to }2B+C,B+C\stackrel{k_3}{\to }$ $A+C,2C\stackrel{k_4}{\to }\varnothing \}$, as shown in the upper part of the figure. (A) and (B) show the ODE solution corresponding to mass action kinetics with reaction rates $k_1=k_3=k_4=1,k_2=1.1$ and initial concentrations equal to 0.3 for a time interval from 0 to 100 and 500, respectively. We can see that the concentrations of all three species tend to 0, which is also a fixed point of the dynamics. To see the particle effects, we assume a total volume of molecules equal to 10 and 100 in (C) and (D), respectively. This means initially 3 or 30 copies, respectively, of every species are present. Then, because of degradation reactions, they slowly vanish. Once the concentration of C falls under 0.1 and 0.01, respectively, the destruction reaction $2C\to \varnothing$ of C is switched off. This happens approximately at time 5 and 50 in (C) and (D), respectively. Then, the system stabilizes in the (purely) discrete organization $\{A,B,C\}$; see Definitions 5 and 6. This takes of course much longer in the case of a reactor volume of 100 than 10; therefore, we used a bigger time scale in (B) and (D)

The second case occurs if the reactor is nearly full, because of the limitation of amount of molecules, reactions might also not occur. In the transition graph, this is seen in the non-existence of edges where the amount of molecules present in a state suggests that there should be a reaction possible. Also the long-term behaviour shown in Figure 2 cannot be detected with chemical organizations or analysis of the ODEs from mass action kinetics. In the only fixed point of the shown RN, the catalysts $K_1,K_2,K_3$ vanish. Only the pdorgs, see Definitions 5 and 6, hint at the possibility to stabilize the system in a small reactor in a state with all species present.

Definition 5 (Discrete organization, generator) —

A subset of species D of $\mathcal{M}$ is called discrete organization if there is a state s with

$$D=\mathcal{M}(\text{Acc}(s))$$

and there is a sequence of transitions $({\sigma }_1,\dots ,{\sigma }_k)$ such that

and $\stackrel{\sim }{s}=({\sigma }_k○\dots ○{\sigma }_1)(s)$ satisfies

Such a state s is called (internal) generator of the discrete organization.

Fig. 2.

Effects of finite reactor size. The network is $\mathcal{M}=\{A,B,C,K_1,K_2,K_3\},\mathcal{R}=\{A+K_1{\displaystyle \stackrel{k_1}{\to }}B+K_1,B+K_2{\displaystyle \stackrel{k_2}{\to }}C+K_2,C+$ $K_3{\displaystyle \stackrel{k_3}{\to }}A+K_3,$$K_1+K_2{\displaystyle \stackrel{k_4}{\to }}4C,K_2+K_3{\displaystyle \stackrel{k_5}{\to }}4C,K_1+K_3{\displaystyle \stackrel{k_6}{\to }}4C\}$, as shown in the upper part of the figure. (A) shows the ODE solution corresponding to mass action kinetics with reaction rates $k_1=k_2=k_3=1,k_4=k_5=k_6=5$ and initial concentrations equal to 0.12 for a time interval from 0 to 50. Under these conditions, the concentrations of the catalysts are the same over time. We can see that the concentrations of all three catalysts $K_1$, $K_2$ and $K_3$ tend to 0, and the other species A, B and C stabilize at some positive but distinct values. To see the particle effects when a reactor of limited size is assumed, we change the set of ODEs once the total sum of all species concentrations reaches 1. This happens at time 3 approximately. Namely, the last four reactions transforming pairs of catalysts to four copies of C are switched off. The resulting curves are shown in (B). Then, the system stabilizes in the (purely) discrete organization $\{A,B,C,K_1,K_2,K_3\}$; see Definitions 5 and 6. Furthermore, the catalysts stabilize in a small but positive concentration, and the species A, B and C tend towards the same concentration

Our definition only depends on the topological properties of the transition graph, see Definition 3, underlying the Markov chain and the topological properties of the RN. It also does not refer to the capacity of the state space. Rather, the definition is given independently of the size of state space. This makes it possible to talk about a reactor of unlimited and limited capacity.

The two requirements correspond to the closure and self-maintenance. The first ensures that we start with the species of D, and there are no new species produced or consumed in the whole accessibility set. The second ensures that there is a path of transitions using all reactions possible leading to a state with no less molecules. Of course, one discrete organization can have several generators; see also Figure 3 for examples.

Lemma 1 (Self-maintainence and discrete organizations) —

Consider the case of one reaction per transition. For a discrete organization D of $\mathcal{M}$ with a generator s the RN

$$(D,{\mathcal{R}}_{\text{Acc}(s)})=(\mathcal{M}(\text{Acc}(s)),{\mathcal{R}}_{\text{Acc}(s)})$$

is self-maintaining and hence an organization.

Proof —

We can choose a sequence of transitions or, under the hypothesis, reactions $({\sigma }_1,\dots ,{\sigma }_k)$ as in the definition of discrete organizations above. Counting the occurrence of each reaction type in the sequence, we get positive integer rates for each type of reaction. These rates show the self-maintenance.

The newly identified discrete organizations are consistent with the concept from COT, i.e. every (continuous) organization is a discrete organization.

Lemma 2 (Continuous are discrete organization) —

Consider the case of one reaction per transition. If the subset O of $\mathcal{M}$ is an organization, then there is a generator s of a discrete organization such that $O=\mathcal{M}(\text{Acc}(s))$ and ${\mathcal{R}}_O={\mathcal{R}}_{\text{Acc}(s)}$. Therefore, every organization is also a discrete organization.

Proof —

We can choose integer reaction rates for ${\mathcal{R}}_O$, which fulfil the self-maintenance condition for O. Define a sequence $({\sigma }_1,\dots ,{\sigma }_k)$ of reactions with the multiplicities equal to the rates. We can choose a state s such that $O=\mathcal{M}(s)$, and the multiplicities of species are big enough so that the sequence $({\sigma }_1,\dots ,{\sigma }_k)$ can fire.

Definition 6 (Purely discrete organization) —

The discrete organizations, which are not found in the continuous theory, are called purely discrete organizations (pdorg).

From a computation point of view, if we choose a large enough transition graph, we will find every (continuous) organization. Hence, this gives a different way of defining and computing organizations in the models using discrete molecule numbers. Of course, for most purposes, this will be considerably slower than existing implementations (Centler et al., 2008, 2010) because of the size of the state space.

We provided two ways of computing discrete organizations. First, we can use Definition 5. Second, we can check the networks $(\mathcal{M},\mathcal{R}\prime )$ for organizations where $\mathcal{R}\prime$ is a subset of $\mathcal{R}$ in which we eliminated some of the reactions of higher order. These are then candidates for discrete organizations. They are only candidates because we do not know whether there is a suitable generator. A candidate for a generator is given as in the proof of Lemma 2.

For a pdorg holds ${\mathcal{R}}_{\text{Acc}(s)}\mathrm{⊊}{\mathcal{R}}_{\mathcal{M}(\text{Acc}(s))}$. We emphasize the difference between these two sets. ${\mathcal{R}}_{\mathcal{M}(\text{Acc}(s))}$ stands for the set of reactions applicable, when only considering present species, not their numbers, whereas ${\mathcal{R}}_{\text{Acc}(s)}$ stands for the set of reactions actually applicable when also considering multiplicities. There are two possible reasons why these two sets are not equal.

First, there might not be enough molecules in any state in $\text{Acc}(s)$ to trigger a reaction, e.g. the reaction $4A\to B$ cannot fire in the state $3A$. This can only occur if at least one species, which occurs with high stoichiometry, has small molecule number. For a pdorg D with a generator s, we call it of type A if for any reaction $(l,r)\in {\mathcal{R}}_{\mathcal{M}(s)}\mathrm{\setminus }{\mathcal{R}}_{\left\{s\right\}}$, there is a species M with $s_M<l_M$.

Second, the reactor might be full. This can only occur if at least one reaction has more molecules on the right hand side than on the left hand side. Because of reactor size limitations, this overproduction might be hindered; a transition to larger states might not be possible. We call it of type B if for any reaction $(l,r)\in {\mathcal{R}}_{\mathcal{M}(s)}\mathrm{\setminus }{\mathcal{R}}_{\left\{s\right\}}$ holds $|(l,r)(s)|>N_{\text{max}}$.

An organization can be of type A as well as type B. The types correspond to the particle effects introduced in Figures 1 and 2. The existence of a connected pdorg of type A or B means that there is the potential of a steady state containing exactly these species. For the definition of type B, we need to have the possibility to limit the reactor size. Discrete organizations of type A can also exist in a reactor of unlimited size. This independence of the reactor size makes type A more realistic for a wider variety of models. We use this notion of type A and B to further filter the found pdorgs for their interest and behaviour.

The generalization of a connected chemical organization to the discrete case is easy to do. If D is a discrete organization, then $(D,{\mathcal{R}}_{\text{Acc}(s)})$ is an organization in the original sense where s is any generator state for D. Of course, for different generators, there can occur different ${\mathcal{R}}_{\text{Acc}(s)}$, and hence, different properties of the network $(D,{\mathcal{R}}_{\text{Acc}(s)})$.

Definition 7 (Connected purely discrete organization) —

A purely discrete organization D is connected if there is a generator s of D such that $(D,{\mathcal{R}}_{\text{Acc}(s)})$ is connected as a continuous chemical organization.

3 RESULTS

3.1 Scan of the BioModels Database

The BioModels Database (Chelliah et al., 2013) is a database of quantitative biological models. At the time of writing, March 2014, it consisted of 490 curated and 595 not curated models written in the Systems Biology Markup Language (Hucka et al., 2003). We use this repository to show the appearance of pdorgs. As in some of the models we found an abundance of pdorgs, we also use the notion of connected discrete organizations as an extension of the concept with the analogue name introduced in (Centler et al., 2008). Connectedness is a means to sort out organizations, which exist because of combinatorial effects; see Definition 7.

We scanned all 1085 models in the database and tried to find all discrete organizations for an $N_{\text{max}}$ of 10 if possible. For some models, the computational resources (Intel Core i7 at 3.2 GHz with 12GB of memory) were not sufficient, and within a maximal runtime of 30 min no result was found. Hence, we reduced the $N_{\text{max}}$ stepwise from 10 down to 1. The results are listed in Supplementary Table S1 and can also be found as csv file with the Supplementary Material. Of course, a model not listed might still exhibit pdorgs, but we did not find them because of the restrictions on computation mentioned.

Like this, we found that 206 of the 490 curated models and 75 of the 595 not curated have pdorgs. Among the curated models with pdorgs, only one does not exhibit any connected pdorg. All the not curated models with pdorgs also have at least one connected one. When considering a reactor of finite size and hence a state space of finite size, there are two causes for the appearance of pdorgs, as illustrated in Figures 1 and 2, respectively. We call these types A and B pdorgs, respectively; see also end of Section 2.2. Only 21 of the 205 curated models with connected pdorgs show connected pdorgs of type A. For the 75 not curated models, which exhibit connected pdorgs, we found only 7 with type A organizations. With the scan of the BioModels Database, we prove the existence of types A and B pdorgs in many stored models and hence also show the applicability of our software tool. Of course, addressing the biological relevance of the potential to go into steady state due to particle effects has to be addressed in future efforts.

3.2 The mitotic SAC mechanism—BIOMD0000000193

To ensure the fidelity of chromosome segregation of the replicated genome during cell division, the mitotic SAC delays the onset of anaphase until all chromosomes have made amphitelic tight bipolar attachments to the mitotic spindle. This checkpoint mechanism is conserved from Yeast to Human. The core protein and complexes are the same but have different concentration and live in different cell size. The mitotic checkpoint complex (MCC) composed of Mad2, Bub3, BubR1 and Cdc20 inhibits the anaphase-promoting complex to initiate progression into anaphase. The molecular mechanism has been studied using systems-level approach for both Human and partly Yeast (Ibrahim et al., 2009; Lohel et al., 2009; Ibrahim et al., 2008a,b). These models considered ODEs and also some spatial but not stochastic effects. An important pathway in these models is the formation of a complex called Bub3:BubR1:Cdc20 that is sequestering Cdc20 away and eventually inhibits the initiation of anaphase. For the full RN, see Figure 4. Our DOT approach shows that the complex Bub3:BubR1:Cdc20 must vanish to get the stable state, and this process is size limited; see Supplementary Figure S8. This is the opposite view to the explanation that this complex is kinetochore dependent (Reaction 5, switched on or off), which means it works by an external signal for specific period to sequester Cdc20. Our DOT interpretation would be that this complex enhances MCC formation and does not need to be kinetochore controlled. These predictions can influence the budding yeast rather than the human model.

Fig. 4.

Visualization of the SAC model. Eukaryotic cells have evolved a conserved checkpoint mechanism for chromosome segregation, the SAC. This checkpoint delays anaphase onset and prevents exit from mitosis until all chromosomes are properly attached and have aligned on the mitotic spindle. In many organisms, an MCC composed of Mad2, Bub3, BubR1 and Cdc20 inhibits the APC to initiate progression into anaphase. Ibrahim et al. (2009) have constructed a detailed dynamic model of MCC formation and analysed its quantitative properties. In this model, Mad2-activation at the kinetochore is commonly seen as the central part of the SAC mechanism. It is known as the “Template model”. According to this model (reactions R1, R2 and R3), Mad2 in its open conformation (O-Mad2) is recruited to unattached kinetochores by Mad1-bound Mad2 in its close conformation (C-Mad2) to form the ternary complex Mad1:C-Mad2:O-Mad2*. In this complex, O-Mad2* is the “activated” Mad2, i.e. it is stabilized in a conformation that can interact with Cdc20 to form Cdc20:C-Mad2 (Ibrahim et al., 2008a,b). O-Mad2 can bind to Cdc20 with very low affinity (reaction R6). Bub3 associates quite stably with BubR1, which has two binding sites to Cdc20. Binding of the N-terminal region of BubR1 to Cdc20 requires prior binding of Mad2 to Cdc20. Systematically, the Bub3:BubR1 complex binds to Cdc20:CMad2 to form the MCC complex (reaction R4). The other site (residues 490 and 560) of BubR1 binds Cdc20 tightly regardless of Mad2 being bound to Cdc20. Therefore, BubR1 can form a ternary complex with Bub3 and Cdc20 (reaction R5). The formation of Bub3:BubR1:Cdc20 is accelerated in the presence of unattached chromosomes and it might be that MCC forms as an intermediate complex from which O-Mad2 rapidly dissociates

4 DISCUSSION

We provided a novel method to predict possible steady states of biological models due to the occurrence of particle effects. The theoretical foundation is an extension of COT to discrete systems. More precisely, we gave the definition of discrete chemical organizations for transition graphs. This turns out to be a generalization of the concept of chemical organizations, which was originally aimed at continuous models. We called the discrete organizations not found in COT purely discrete. They represent potential steady states due to particle effects, i.e. effects of small molecular numbers and/or finite reactor size. The former effect accounts for the biological phenomena of small numbers of copies of a molecule, molecular crowding and the spatial distribution of molecules in a cell. The latter effect might seem less natural than the former because we consider reactors with an upper bound on the number of molecules they contain. However, we want to mention two classes of example situations in which this is a reasonable assumption. First, if we consider reactions that model an inflow, e.g. through channels in a membrane, we can have the situation that inflow is blocked because of the already full inside of the reactor. Second, if we model the spatial setting in a reactor, we know that single molecules occupy more space than a complex of molecules.

Furthermore, our findings complement the connection found between chemical organizations and continuous systems (Peter and Dittrich, 2011), namely, that organizations play a crucial role in the long-term behaviour of chemical reaction systems. Similarly, the theory developed herein might be adjustable to also cover particle effects on elementary modes (Schuster and Hilgetag, 1994) and cut sets (Klamt and Gilles, 2004). Because COT is based on the stoichiometric information of RNs alone, only constellations of species in the potential steady states are computed. We do not consider information on amounts or ratio of amounts as addressed in (Ramaswamy et al., 2012). Furthermore, we do not say what the concentration or amounts in the long run might be.

It is important to remark the connection between DOT and the study of RNs using Petri Nets (PN) (Murata, 1989; Petri, 1962; Yen, 2006). Namely, the PN formalism is an abstraction of parallel processes and has been shown to be equivalent to the RNs formalism. Several behavioural properties developed in PN theory, such as liveness, persistence, deadlock, etc., have shown to be relevant to the analysis of RNs (Heiner et al., 2008). Interestingly, both COT and (sur-)T-invariants of PN have been linked to the analysis of elementary modes (Schuster and Hilgetag, 1994) and cut sets (Klamt and Gilles, 2004) in RNs (Heiner et al., 2010; Kaleta et al., 2006). However, the definition of self-maintenance of COT differs from the definition of sur-T-invariants in PN theory in the choice of positive and non-negative rates, respectively. Moreover, the notion of closed set of COT has not been studied in PN theory. Hence, exploring the connections between DOT and PN might be useful to extend our knowledge of the long-term behaviour of continuous RNs, already obtained by COT (Peter and Dittrich, 2011), to the discrete domain.

The analysis of the SAC model in detail hints at the influence of a molecular complex on the cell division of Yeast, which was before not identified as important. Even though the example of palindromic DNA we described is merely a toy model, it clearly shows the inability of the known analysis tools to detect the effect of the distribution of molecules over space on the long-term behaviour. By providing an open-source tool for the search for discrete organizations, we also made it possible to find models that might be influenced by only a few copies of single molecular species. We used the tool to prove the existence of discrete organizations in many biological examples contained in the BioModels Database. Especially the appearance of connected pdorgs of type A is of interest. Also, the limitations of our implementation, like the runtime, could be addressed in a future effort.

Our newly developed discrete organization theory is a first step towards the analysis of fixed points in RNs with small molecule numbers.