TEMPI: probabilistic modeling time-evolving differential PPI networks with multiPle information

Abstract

Motivation: Time-evolving differential protein–protein interaction (PPI) networks are essential to understand serial activation of differentially regulated (up- or downregulated) cellular processes (DRPs) and their interplays over time. Despite developments in the network inference, current methods are still limited in identifying temporal transition of structures of PPI networks, DRPs associated with the structural transition and the interplays among the DRPs over time.

Results: Here, we present a probabilistic model for estimating Time-Evolving differential PPI networks with MultiPle Information (TEMPI). This model describes probabilistic relationships among network structures, time-course gene expression data and Gene Ontology biological processes (GOBPs). By maximizing the likelihood of the probabilistic model, TEMPI estimates jointly the time-evolving differential PPI networks (TDNs) describing temporal transition of PPI network structures together with serial activation of DRPs associated with transiting networks. This joint estimation enables us to interpret the TDNs in terms of temporal transition of the DRPs. To demonstrate the utility of TEMPI, we applied it to two time-course datasets. TEMPI identified the TDNs that correctly delineated temporal transition of DRPs and time-dependent associations between the DRPs. These TDNs provide hypotheses for mechanisms underlying serial activation of key DRPs and their temporal associations.

Availability and implementation: Source code and sample data files are available at http://sbm.postech.ac.kr/tempi/sources.zip.

Contact: seungjin@postech.ac.kr or dhwang@dgist.ac.kr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Many cellular events involve serial activation of cellular processes during which genes/proteins associated with the processes are up- or downregulated. Differential protein–protein interaction (PPI) networks (DNs) have been used to delineate PPIs (edges) among differentially regulated nodes (DRNs), such as up- or downregulated genes or proteins. The DNs have been considered more effective for understanding the differences between two conditions, compared with non-DNs (de la Fuente, 2010). However, the DNs delineate no temporal transition of the DRNs and/or their edges to represent serial activation of cellular processes over time. Thus, time-evolving differential PPI networks (TDNs) have been introduced to delineate (i) temporal changes in abundances or activities of DRNs (node transition), and/or (ii) formation of new edges for the DRNs and disappearance of existing edges over time (edge transition). The TDNs are essential to understand serial activation of differentially regulated cellular processes (DRPs) during a cellular event and their underlying mechanisms.

Time-course gene expression analysis can provide temporal changes in abundances of the DRNs (Hwang et al., 2009). Several interaction assays, such as yeast two-hybrid (Ito et al., 2001; Uetz et al., 2000; Yu et al., 2008) and mass spectrometry-based tandem affinity purification (Collins et al., 2007) can be used to measure PPIs among the DRNs. However, it is still challenging to experimentally identify temporal transition of the edges among the DRNs because of the limited coverage of the interactomes detected by these assays (von Mering et al., 2002).

The limitation of the experimental methods prompted us to develop a computational method to estimate TDNs. Many methods for estimation of dynamic gene regulatory networks have been developed (Kim et al., 2014). However, estimation of temporal transitions of differential PPI networks (i.e. TDNs) has been rarely studied. A couple of methods have been developed to identify differential PPI networks, which can be then used to estimate TDNs. First, a simple method to infer DNs using time-course gene expression data identifies DRNs over time and constructs a template PPI network with the known PPIs among all the DRNs (Hwang et al., 2009; Przytycka and Kim, 2010). TDNs can be then constructed by selecting the interacting DRNs with significant expression changes at each t from the template PPI network. Second, principal network analysis (PNA) identifies differential expression patterns over time and then selects DRNs and their edges (known PPIs between the DRNs) showing the differential expression patterns (Kim et al., 2011). A principal subnetwork (PS) is then constructed using both DRNs and edges selected for each differential expression pattern. Finally, TDNs can be constructed by selecting the edges in PSs for which the linked DRNs show significant expression changes at each t.

Functional interpretation of the inferred TDNs is important to understand temporal transition of the DRPs. In most of the network inference methods, it is commonly performed independently from network inference using post hoc analyses of Gene Ontology biological processes (GOBPs) of the nodes in the inferred networks (Kim et al., 2014). For example, the method proposed by Park and Bader (2012) clusters the nodes in time-evolving networks based on the similarity of temporal transitions of their edges and then links these clusters to cellular functions using GOBPs. However, none of the methods estimating DNs or TDNs integrates functional information, such as GOBPs, during the network inference such that the inferred TDNs can represent directly temporal transition of differentially regulated GOBPs and time-dependent interplays between the GOBPs, thereby facilitating functional interpretation of the TDNs.

Here, we introduce a probabilistic model for estimating Time-Evolving differential PPI networks with MultiPle Information (TEMPI). Although many methods have used probabilistic modeling for estimating network structures (Friedman et al., 2000; Ong et al., 2002; Song et al., 2009), a unique aspect of our model is that it models additionally probabilistic dependencies of GOBPs with network structures and time-course global data. By maximizing the likelihood function of the probabilistic model, TEMPI jointly estimates the TDNs showing temporal transitions of network structures with temporal activation of the GOBPs and their temporal interplays. During the network inference, TEMPI infers edges not included in the known PPIs, whereas most of the previous methods (e.g. PNA) select a subset of PPIs for estimation of TDNs from the known PPIs.

2 FRAMEWORK OF TEMPI

TEMPI uses the observed data (time-course gene expression data, known PPIs and GOBPs) as the input variables, estimates the output variables based on the probabilistic graphical model describing probabilistic dependencies among the input and output variables, and then infers TDNs using the estimated output variables. First, TEMPI uses the following three observed variables as the inputs. As the first input, TEMPI uses the time-course gene expression log₂-fold-changes (dynamic data) of n nodes at T time points, with R biological replicates (an $n\times T\times R$ array E in Supplementary Fig. S1, bottom left). Estimation of the TDNs only using E can be an underdetermined problem (De Smet and Marchal, 2010). To reduce this issue, as the second input, TEMPI uses known PPI data (an $n\times n$ adjacency matrix ${\mathit{G}}^{\mathit{I}}$ ; static data) of n nodes (Supplementary Fig. S1, top left). In TEMPI, the ${\mathit{G}}^{\mathit{I}}$ are converted into positions of n nodes in a p-dimensional latent space (a $n\times p$ positional matrix${\mathit{X}}^{\mathit{I}}$) using multidimensional scaling (MDS; Supplementary Information S1.1; Higham et al., 2008; You et al., 2010). In this study, we used the 2D latent space (Supplementary Information S1.1). MDS locates the interacting nodes closely in the latent space: for example, for nodes A–E in ${\mathit{G}}^{\mathit{I}}$ (Supplementary Fig. S1, top center), MDS located A–D closely, but E distantly from A–D in a 2D latent space. To identify TDNs, TEMPI then selects m DRNs from time-course gene expression data (Supplementary Information S1.2). TEMPI uses the $m\times p$ ${\mathit{X}}^{\mathit{I}}$ for the selected DRNs as an input. Finally, as the third input, TEMPI further uses the GOBP data (l GOBP terms assigned to m DRNs; static data), a $m\times l$ binary node-GOBP matrix T in which $t_{ik}$ = 1 when node i has GOBP k (e.g. a T for nodes A–F in Supplementary Fig. S1, top right).

Second, TEMPI uses a probabilistic graphical model (Fig. 1) that describes probabilistic dependencies (see Section 2.1) among the input observed variables ($X_o=\left\{\mathit{T},\mathit{E},{\mathit{X}}^I\right\}$) and the following output hidden variables for m DRNs at each t : (i) a $m\times p$ positional matrix ${\mathit{X}}^t$ representing positions of n nodes in a p-dimensional space at t, (ii) an $m\times m$ adjacency matrix ${\mathit{G}}^t$ representing the presence of edges between m nodes at t and (iii) a $m\times l$ node-GOBP matrix ${\mathit{A}}^t$ representing differentially regulated GOBPs at t, in which $a_{ik}^t=1$ when GOBP k is estimated to be differentially regulated for node i; otherwise, $a_{ik}^t=0$. The output hidden variables were then estimated through the optimization (see Section 2.2). Third, using the estimated outputs ($X_h=\left\{{\mathit{X}}^t,{\mathit{G}}^t,{\mathit{A}}^t\right\}$), the TDNs can be constructed as described in Section 2.3 (‘Inferred TDNs’ of Supplementary Fig. S1, bottom right). The resulting TDNs have the following characteristics: (i) a pair of interacting DRNs according to ${\mathit{G}}^I$ are likely to be linked when they share expression changes and GOBPs [e.g. the interacting A–B in ${\mathit{G}}^I$ (Supplementary Fig. S1, top left), both of which were upregulated (Supplementary Fig. S1, bottom left) and share GOBPs 3 and 6 (Supplementary Fig. S1, top right), were linked in ${\mathit{G}}^t$ at $t=1$ (Supplementary Fig. S1, bottom right)]; (ii) the links between non-interacting DRNs according to ${\mathit{G}}^I$ can be inferred when they share expression changes and GOBPs (e.g. non-interacting B–D in ${\mathit{G}}^I$, both of which were upregulated and share GOBPs 3 and 4, were linked in ${\mathit{G}}^3$ at $t=3$); and (iii) the GOBPs assigned to the interacting DRNs in T are likely to be differentially regulated (e.g. the interacting A–B at $t=1$ have GOBPs 3 and 6 in T, which are co-differentially regulated in the estimated ${\mathit{A}}^1$).

Fig. 1.

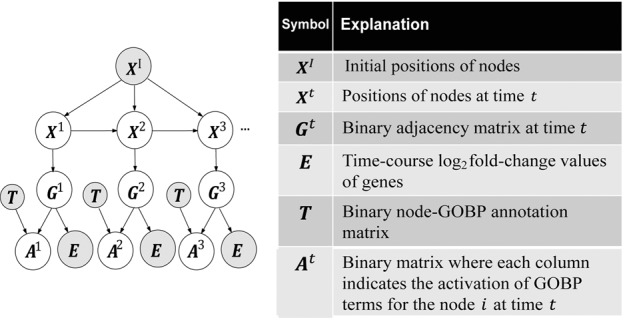
The probabilistic model describes dependencies among the observed variables $X_o=\left\{\mathit{T},\mathit{E},{\mathit{X}}^I\right\}$ and the hidden variables $X_h=\left\{{\mathit{X}}^t,{\mathit{G}}^t,{\mathit{A}}^t\right\}$

2.1 Probabilistic graphical model

The probabilistic graphical model (Fig. 1) was constructed to include the following dependencies between the input observed $X_o=\left\{\mathit{T},\mathit{E},{\mathit{X}}^I\right\}$ and the output hidden variables $X_h=\left\{{\mathit{X}}^t,{\mathit{G}}^t,{\mathit{A}}^t\right\}$: (i) ${\mathit{X}}^t$ depends on the initial positions of nodes (${\mathit{X}}^I$) and their positions at $t-1$ (${\mathit{X}}^{t-1}$) to achieve smooth transition of TDNs over time; (ii) ${\mathit{G}}^t$, a geometric graph, depends on the distances between the nodes in the latent space and thus on ${\mathit{X}}^t$; (iii) E depends on the interactions (${\mathit{G}}^t$) between the nodes based on the observation in real PPI networks that the nodes with similar expression changes are likely to interact (Grigoriev, 2001; Supplementary Fig. S2A); and (iv) ${\mathit{A}}^t$ depends on ${\mathit{G}}^t$ and the node-GOBP matrix T, based on the observation in real PPI networks that the nodes with the same GOBPs are likely to interact (Sharan et al., 2007; Supplementary Fig. S2B).

Based on these dependencies, the probabilistic model was defined by the following four submodels (see Supplementary Information S1.3 for further details of the four submodels):

• Transition model (${\mathit{P}}^{trans}$) for m nodes is defined as a product of m Gaussian distributions: ${\mathit{P}}^{trans}=P\left({\mathit{X}}^t|{\mathit{X}}^{t-1},{\mathit{X}}^I\right)=\prod _{i=1}^m\mathcal{N}\left({\mathit{x}}_i^t|{\mathit{m}}_i^t,{\mathit{\Sigma }}_i\right)$ where ${\mathit{m}}_i^t=\left({\mathit{x}}_i^{t-1}/{\sigma }_t^2+{\mathit{x}}_i^I/{\sigma }_I^2\right)/\left(1/{\sigma }_t^2+1/{\sigma }_I^2\right)$ and ${\mathit{\Sigma }}_i=[\mathbf{1}/\left(1/{\sigma }_t^2+1/{\sigma }_I^2\right)]\mathit{I}$. ${\mathit{x}}_i^t$ and I are the positional vector for node i at t and the identity matrix, respectively. ${\sigma }_t$ and ${\sigma }_I$ control the penalties of displacement of nodes from positions (${\mathit{X}}^{t-1}$) at t − 1 and initial positions (${\mathit{X}}^I$), respectively.

• Link model (${\mathit{P}}^{Link}$) is modeled as a product of Bernoulli distributions for $m\left(m-1\right)/2$ pairs of m nodes: ${\mathit{P}}^{Link}=P\left({\mathit{G}}^t|{\mathit{X}}^t\right)=\prod _{\forall \left(i,j\right)}{\left(p_{ij}^t\right)}^{g_{ij}^t}{\left(1-p_{ij}^t\right)}^{1-g_{ij}^t}$ where link probability ($p_{ij}^t$) of nodes i and j is defined by $P\left(g_{ij}^t=1\text{|}{d}_{ij}\right)=\mathcal{N}\left(d_{ij}^2\text{|}0,{\sigma }_g\right)/\mathcal{N}\left(0\text{|}0,{\sigma }_g\right)$ with $d_{ij}=||{\mathit{x}}_i^t-{\mathit{x}}_j^t||{}_2$. $p_{ij}^t$ decreases as $d_{ij}$ increases, and its decreasing rate is controlled by ${\sigma }_g.$

• Expression model (${\mathit{P}}^{expr}$) at t is defined as a weighted product of $P\left({\mathit{E}}^{\tau }|{\mathit{G}}^t\right)$ for all time points τ, where ${\mathit{E}}^{\tau }$ is the $m\times R$ log₂-fold-change matrix for m nodes, with R biological replicates at time τ, and ${\mathit{e}}_{\mathit{r}}^{\tau }$ is column r of ${\mathit{E}}^{\tau }$. $P\left({\mathit{e}}_{\mathit{r}}^{\tau }|{\mathit{G}}^t\right)$ is then modeled as the product of the mixtures of Gamma distributions for all pairs of m nodes with two sets of parameters, $\left(k_{e_1},{\theta }_{e_1}\right)$ and $\left(k_{e_2},{\theta }_{e_2}\right)$:

$$P\left({\mathit{e}}_r^{\tau }|{\mathit{G}}^t\right)={\displaystyle \prod }_{\forall (i,j)}\Gamma {\left(d_{ijr}^{\tau }|k_{e_1},{\theta }_{e_1}\right)}^{g_{ij}^t}\Gamma {\left(d_{ijr}^{\tau }|k_{e_2},{\theta }_{e_2}\right)}^{(1-g_{ij}^t)},$$

where $d_{ijr}^{\tau }=\left|e_{ir}^{\tau }-e_{jr}^{\tau }\right|+\exp \left(-{\left(e_{ir}^{\tau }\right)}^2/c\right)+\exp \left(-{\left(e_{jr}^{\tau }\right)}^2/c\right)$. k and θ are determined to produce a higher probability in the first Gamma distribution than in the second one for a small $d_{ij}^{\tau }$. Finally, we used a radial basis function kernel, $k\left(\tau ,t|v\right)=\exp \left({\left(\tau -t\right)}^2/v\right)$, to weight $P\left({\mathit{E}}^{\tau }|{\mathit{G}}^t\right)$ in its weighted product (Song et al., 2009):

$$P\left(\mathit{E}|{\mathit{G}}^t\right)={\displaystyle \prod }_{\tau =1}^T{\left({\displaystyle \prod }_{r=1}^{R}P\left({\mathit{e}}_r^{\tau }|{\mathit{G}}^t\right)\right)}^{k\left(\tau ,t|w\right)}.$$

This weighting scheme ensures (i) smooth transitions of TDNs, and (ii) a more significant dependency of ${\mathit{G}}^t$ on ${\mathit{e}}^t$ at τ = t than other τs ($\ne t$).

• Ontology model (${\mathit{P}}^{GO}$) is factorized into $P\left({\mathit{A}}^t|{\mathit{G}}^t\right)$ and $\left({\mathit{A}}^t|\mathit{T}\right):$${\mathit{P}}^{GO}=P\left({\mathit{A}}^t|{\mathit{G}}^t,\mathit{T}\right)=P\left({\mathit{A}}^t|{\mathit{G}}^t\right)P\left({\mathit{A}}^t|\mathit{T}\right)$. First, $P\left({\mathit{A}}^t|\mathit{T}\right)$ is defined by the product of Bernoulli distributions for l GOBPs of m nodes:

$$P\left(A^t|\mathit{T}\right)={\displaystyle \prod }_{i=1}^m{\displaystyle \prod }_{k=1}^l{\left(f\left(t_{ki}\right)\right)}^{a_{ki}^t}{\left(1-f\left(t_{ki}\right)\right)}^{(1-a_{ki}^t)},$$

where $f\left(t_{ki}\right)={\left(iff\left(k,\mathit{T}\right)/2·s\right)}^{t_{ki}}{ϵ}^{1-t_{ki}}$ (ϵ = 1×10⁻⁴), given an inverse function frequency $iff\left(k,\mathit{T}\right)=\log \left(m/\sum _i{t}_{ik}\right)$ that penalizes general GOBPs. The normalization constant s was defined as the maximum value of $iff\left(k,\mathit{T}\right)$. Second, $P\left({\mathit{A}}^t|{\mathit{G}}^t\right)$ was modeled as the mixture of Gamma distributions for all pairs of m nodes using two sets of parameters, $\left(k_{o_1},{\theta }_{o_1}\right)$ and $\left(k_{o_2},{\theta }_{o_2}\right)$:

$$P\left({\mathit{A}}^t|{\mathit{G}}^t\right)={\displaystyle \prod }_{\forall \left(i,j\right)}\mathit{\Gamma }{\left({\mathit{a}}_i^t{}^T{\mathit{a}}_j^t/h|k_{o_1},{\theta }_{o_1}\right)}^{g_{ij}^t}\mathit{\Gamma }{\left({\mathit{a}}_i^t{}^T{\mathit{a}}_j^t/h|k_{o_2},{\theta }_{o_2}\right)}^{\left(1-g_{ij}^t\right)},$$

where k and θ are determined to produce a higher probability in the first Gamma function than in the second one for a large ${\mathit{a}}_i^t{}^T{\mathit{a}}_j^t$.

Many previous methods have used probabilistic models for estimating the network structures using E (Friedman et al., 2000; Ong et al., 2002; Song et al., 2009). However, a unique aspect of our model is that it includes the ontology model to integrate GOBP data (${\mathit{A}}^t$ and T) during the probabilistic estimation of TDNs.

2.2 Optimization of the likelihood function

The joint probability of the graphical model at each t is defined by $P\left({\mathit{G}}^t,\mathit{E},\mathit{T},{\mathit{A}}^t,{\mathit{X}}^t|{\mathit{X}}^{t-1},{\mathit{X}}^I\right)={\mathit{P}}^{trans}{\mathit{P}}^{Link}{\mathit{P}}^{expr}{\mathit{P}}^{GO}$. The output hidden variables ($X_h=\left\{{\mathit{X}}^t,{\mathit{G}}^t,{\mathit{A}}^t\right\}$) are then estimated by maximizing the log-likelihood function of the joint distribution, $\log P\left({\mathit{G}}^t,\mathit{E},\mathit{T},{\mathit{A}}^t,{\mathit{X}}^t|{\mathit{X}}^{t-1},{\mathit{X}}^I\right)$ using variational inference (Beal, 2003). Briefly, for each t, we first calculated the lower bound of the marginal log-likelihood function, $\log P\left(\mathit{E},\mathit{T}|{\mathit{X}}^{t-1},{\mathit{X}}^I\right)$, which can be obtained by integrating the joint probability with respect to $X_h$ (Supplementary Information S1.4): for distributions of $X_h$, $Q\left(X_h\right)$, $\text{log}P\left(\mathit{T},\mathit{E}|{\mathit{X}}^{t-1},{\mathit{X}}^I\right)\ge {\int }^{\text{}}Q\left(X_h\right)\log \left(\frac{P\left(X_h,\mathit{T},\mathit{E}|{\mathit{X}}^{t-1},{\mathit{X}}^I\right)}{Q\left(X_h\right)}\right)d{X}_h$. We then used a variational approximation (Beal, 2003) to estimate the variational distribution $Q\left(X_h\right)$, assuming the independency among the variables: $Q\left(X_h\right)=Q\left({\mathit{X}}^t\right)Q\left({\mathit{G}}^t\right)Q\left({\mathit{A}}^t\right)$ where $Q\left({\mathit{X}}^t\right)=\prod _{i=1}^n\mathcal{N}\left({\mathit{x}}_i^t|{\mathit{\mu }}_i^t,{\sigma }_q^2\mathit{I}\right),$ $Q\left({\mathit{G}}^t\right)=\prod _{i=1}^{n}Ber\left(g_{ij}^t|{\xi }_{ij}^t\right),$ and $Q\left({\mathit{A}}^t\right)=\prod _{i=1}^n\prod _{k=1}^{l}Ber\left(a_{ki}^t|{\beta }_{ki}^t\right).$ In these distributions, ${\mathit{\mu }}_i^t$, ${\sigma }_q$, ${\xi }_{ij}^t$ and ${\beta }_{ik}^t$ are the variational parameters (Supplementary Information S1.5). Finally, we determined the variational parameters (${\mathit{\mu }}_i^t$, ${\xi }_{ij}^t$ and ${\beta }_{ik}^t$) such that they maximize the lower bound of the marginal likelihood function as described in Supplementary Information S1.5.

2.3 Construction of TDNs

Using these variational parameters (${\mathit{\mu }}_i^t$, ${\xi }_{ij}^t$ and ${\beta }_{ik}^t$), the output hidden variables ($X_h=\left\{{\mathit{X}}^t,{\mathit{G}}^t,{\mathit{A}}^t\right\}$) were finally estimated. At each t, first, the position $({\mathit{x}}_i^t$, column i of ${\mathit{X}}^t)$ of node i was determined as the expected value of the posterior probability of ${\mathit{x}}_i^t$ given the observed variables, P(${\mathit{x}}_i^t|X_o$). The variational distribution with the estimated variational parameters approximates the posterior probability distribution of the hidden variables given the values of the observed variables: $P(X_h|X_o)\cong Q\left(X_h\right)$. With the independency among the hidden variables, $P\left({\mathit{x}}_i^t\text{|}{X}_o\right)\cong Q({\mathit{x}}_i^t)$, $P(g_{ij}^t=1|X_o)\cong Q(g_{ij}^t=1)$ and $P\left(a_{ki}^t=1|X_o\right)\cong Q\left(a_{ki}^t=1\right)$. Thus, ${\mathit{x}}_i^t$ was determined as ${\mathit{\mu }}_i^t$, the expected value of $Q({\mathit{x}}_i^t)$. Second, nodes i and j were determined to be linked (i.e. $g_{ij}^t$ of ${\mathit{G}}^t$ = 1) when $P\left(g_{ij}=1|X_o\right)\cong Q\left(g_{ij}=1\right)={\xi }_{ij}^t$ ≥ 0.5. Using the estimated ${\mathit{X}}^t$ and ${\mathit{G}}^t$, TDNs can be constructed as geometric graphs at individual time points.

Finally, for functional interpretation of the inferred TDNs, GOBP k was determined to be differentially regulated (positively or negatively activated) at t for node i ($a_{ki}^t$ of ${\mathit{A}}^t$ = 1) when the log-likelihood ratio of posterior and prior probabilities of $a_{ki}^t=1$, $\log [P\left(a_{ki}^t=1|X_o\right)/P(a_{ki}^t=1)]\cong$ $\text{log}[Q\left(a_{ki}^t=1\right)/P(a_{ki}^t=1)]$ = $\log {\beta }_{ki}^t/f\left(t_{ki}\right)$, was significantly (P < 0.01) larger than zero. The P-value was computed using one-tailed t-test (degree of freedom = the number of nodes with GOBP k). Using the estimated ${\mathit{A}}^t$, the activation degree of GOBP k at t was estimated as the fraction of the nodes with activated GOBP k ($a_{ki}^t=1$) in the network at t among all nodes with GOBP k ($t_{ki}=1$): $\sum _i\left(a_{ki}^t·sign\left({\mathit{e}}_i^t\right)\right)/\sum _i{t}_{ki}$, where $sign({\mathit{e}}_i^t)$ is the sign of $\sum _r{e}_{ir}^t$ and r is the index of biological replicates. The sign was multiplied to distinguish positive and negative activation of GOBP k for node i at t. Furthermore, the interaction degree for two activated GOBPs k and l at t was estimated as the fraction of the inferred edges between the two sets of the nodes with activated GOBP k $(a_{ki}^t=$ 1) and activated GOBP l $(a_{li}^t=$1), respectively, in the network at t among all possible edges among the two sets of nodes with activated GOBPs k and l:

$$\left[{\displaystyle \sum }_{i,j}{g}_{ij}^t{a}_{ki}^t{a}_{lj}^{t}sign\left(sign\left({\mathit{e}}_i^t\right)+sign\left({\mathit{e}}_j^t\right)\right)\right]/\left[\left({\displaystyle \sum }_i{a}_{ki}^t\right)\left({\displaystyle \sum }_{\text{i}}{a}_{li}^t\right)\right].$$

The sum of the signs of the linked nodes i and j was included such that the edge with different signs of the linked nodes should have no contribution to the interaction degree.

3 A SYNTHETIC TDN MODEL

To demonstrate the performance of TEMPI, we generated a template PPI network and GOBPs to simulate characteristics of real yeast PPI networks and then sampled the synthetic TDN model from the template PPI network for which temporal transitions of (i) network structures and (ii) differentially regulated GOBPs associated with the TDN model are known. First, to generate a template PPI network with the characteristics of real yeast PPI networks, we used a geometric graph model with gene duplication and mutation (GEO-GD expansion model; Przulj et al., 2010; Supplementary Fig. S3A). See Supplementary Information S2.1 for the detailed procedure. The resulting template PPI network included 26 454 edges for the 3258 nodes (Supplementary Fig. S4A). This network was also used as the input PPI network (G^I). Second, to generate GOBPs with the characteristics of real yeast PPI networks, we assigned 306 GOBP labels (T) to the 3258 nodes in the template PPI network using a modified version of network module (NeMo; Rivera et al., 2010; Supplementary Fig. S3B). See Supplementary Information S2.2 for the detailed procedure. Among the 306 GOBPs, we used 103 after removing 203 GOBPs assigned to >100 or <5 DRNs, which can be too general or non-meaningful, respectively, for functional interpretation. Third, we then sampled a TDN model from the template PPI network by selecting the nodes with (i) GOBPs 60, 67 and 218; (ii) GOBPs 178, 228 and 206; and (iii) GOBPs 94, 146 and 246 at individual time points based on predefined fractions of the linked edges among the selected nodes over time (Supplementary Figs S3C and S4B). See Supplementary Information S2.3 for the detailed procedure. Finally, we generated time-course gene expression log₂-fold-changes that reflect temporal transitions of the synthetic TDN model using Metropolis–Hastings algorithm (Hastings, 1970; Supplementary Figs S3D and S4C). See Supplementary Information S2.4 for the detailed procedure.

4 RESULTS AND DISCUSSION

4.1 Application of TEMPI to the synthetic data

To evaluate performance of TEMPI, we applied it to the synthetic input data ($\mathit{T},\mathit{E},{\mathit{G}}^I$). As the input PPI data, we used the PPIs in the template PPI network (G^I; see Section 3). We first applied MDS to ${\mathit{G}}^I$ for the 3258 nodes to compute ${\mathit{X}}^I$ in 2D latent space. To identify TDNs, we then identified 616 DRNs with false discovery rates (FDRs) < 0.1 using a modified version of repeated measure-analysis of variance (RM-ANOVA) test previously reported (ElBakry et al., 2012) and maximum log₂-fold-changes > 0.58 (1.5-fold) at least at one time point (Supplementary Information S1.2) and used the ${\mathit{X}}^I$ for the 616 DRNs as an input data. For the synthetic GOBP data, we used 103 GOBPs (T) for the DRNs as described in Section 3. Finally, we used the 616×6×3 synthetic log₂-fold-changes for the DRNs as the input expression data (E). After applying TEMPI to these synthetic input data (${\mathit{X}}^I,\mathit{T},\mathit{E}$) for the 616 DRNs, the output variables (${\mathit{X}}^t,{\mathit{G}}^t,{\mathit{A}}^t$) were estimated by the optimization of the likelihood function of the probabilistic graphical model (see Section 2.2). Using the ${\mathit{X}}^t$ and ${\mathit{G}}^t$, TDNs (TEMPI- ${\mathit{G}}^{\mathit{t}}$) were inferred at individual time points (see Section 2.3).

For functional interpretation of TEMPI-${\mathit{G}}^{\mathit{t}}$, we first examined temporal activation of the 103 GOBPs represented by TEMPI-${\mathit{G}}^{\mathit{t}}$ (Fig. 2A) based on the activation degrees of the 103 GOBPs computed using the estimated ${\mathit{A}}^t$ (see Section 2.3). The activation degrees revealed that three groups of GOBPs (Groups 1–3 in Fig. 2A, left panels), among the 103 GOBPs, were differentially regulated early, mid and late over time, respectively. Notably, Groups 1–3 included GOBPs 60, 178 and 94 (Group 1); 67, 228 and 146 (Group 2); and 218, 206 and 246 (Group 3), respectively, consistent to the predefined differential regulation of the three sets of the GOBPs (Supplementary Information S2.3). For example, the high activation degree of Group 1 at t = 1 indicates that a large number of the nodes with Group 1 are linked at t = 1. The decrease of the activation degree from t = 2 indicates that decreasing numbers of the nodes with Group 1 are linked from t = 2. Moreover, the descendants of the predefined GOBPs in Groups 1–3, respectively, were partially differentially regulated. This is expected because the nodes assigned with the descendant GOBPs also have their parent GOBPs (Supplementary Fig. S3). We then examined temporal associations among the GOBPs in Groups 1–3 represented by TEMPI-${\mathit{G}}^{\mathit{t}}$ based on the interaction degrees of the GOBPs computed using the estimated ${\mathit{A}}^t$ and ${\mathit{G}}^{\mathit{t}}$ (Supplementary Fig. 2B; see Section 2.3). The interaction degrees revealed that (i) Group 1 and their descendants; (ii) Group 2 and their descendants; and (iii) Group 3 and their descendants showed early, mid and late associations among them, respectively, consistent to the predefined differential regulation of their parent GOBPs.

Fig. 2.

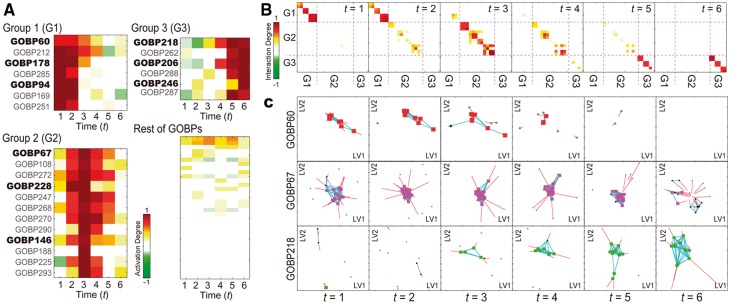
Identification of differentially regulated GOBPs and TDNs associated with the GOBPs. (A) Activation degree heat map representing temporal activation of 103 GOBPs. Differentially regulated GOBPs were categorized into Group 1 [G1-GOBPs 60, 178, 94 (bold) and their descendants (non-bold)], Group 2 (G2-GOBPs 67, 228, 146 and their descendants) and Group 3 (G3-GOBPs 218, 206, 246 and their descendants). (B) Interaction degree heat maps showing temporal associations among the GOBPs in Groups 1–3. Color bars, gradients of the activation (A) and interaction degrees (B). (C) Inferred TDNs for GOBPs 60, 67 and 218 in Group 1 (first, second and third rows, respectively). Colored nodes at each t represent the linked nodes with $a_{ki}^t=1$ for k = 60, 67 or 218. Black nodes at t represent the linked nodes with $a_{ki}^t=0$, but $t_{ki}^{}=0$ for k = 60, 67 or 218, and gray nodes at t represent colored or black nodes in ${\mathit{G}}^{\mathit{t+1}}$ or ${\mathit{G}}^{\mathit{t-1}}$. Blue and red lines at t show the edges among DRNs ($g_{ij}^t=1$) and the displacement of DRNs from t − 1, respectively

Finally, TEMPI-${\mathit{G}}^{\mathit{t}}$ (Fig. 2C) showed the transitions of nodes and edges over time from the initial network (${\mathit{G}}^I$; Supplementary Fig. S4A). Of note, because of the geometric representation of the TDNs, the linked nodes at t in TEMPI-${\mathit{G}}^{\mathit{t}}$ were moved closely to each other. The TDNs (Fig. 2C) for GOBP60 (Group 1), GOBP67 (Group 2) and GOBP218 (Group 3) correctly captured early, middle and late transitions defined in their true TDNs (Supplementary Fig. S4C).

4.2 Comparison of TEMPI with previous methods

To quantitatively assess the relative performance of TEMPI, we applied the two methods, the simple method (Hwang et al., 2009) and PNA (Kim et al., 2011) described in Section 1, to the synthetic data and identified TDNs as follows. For the simple method, as the input data, we used the synthetic E and G^I in the template PPI network. We first identified the DRNs as the nodes with the maximum fold-changes > a cutoff of 2 or 1.5. For the DRNs, we constructed a DN using the G^I. We then estimated the TDNs (Simple-${\mathit{G}}^{\mathit{t}}$) by selecting the interacting DRNs with fold-changes > the cutoff in the DN at each t or either of its neighboring time points (t − 1 or t + 1) to reflect significant smooth transitions and then by linking the selected interacting DRNs (Supplementary Information S3.1). For the PNA application, as the input data, we used the same synthetic E and G^I. PNA identified three activation patterns (H1-3 in Supplementary Fig. S5A) and then generated the three PSs (PS1-3 in Supplementary Fig. S5B) that describe interactions among the DRNs showing the three activation patterns based on the input PPIs. By selecting both DRNs and edges showing PS1-3 at each t and then combining them, we identified TDNs (PNA-${\mathit{G}}^{\mathit{t}}$) at $t=1$ –6 (Supplementary Information S3.2).

We then evaluated the performance measures (precisions, recalls and F1 scores) by comparing the TDNs inferred by the three methods with the true TDNs and compared the performance measures of TEMPI with those of these two methods. Moreover, in many species, known PPIs (G^I) are incomplete (Beyer et al., 2007). Unlike TEMPI, both the simple method and PNA predict no edges not included in G^I. Their performance can thus depend on completeness of G^I. Thus, we further examined robustness in accuracy of the inferred TDNs against incompleteness in G^I by inferring the TDNs using the three methods as randomly removing 10–90% of the PPIs in the template PPI network (G^I). Furthermore, to understand how the capability of TEMPI to predict edges not in G^I can contribute to the performance, we also compared the performance of TEMPI after removing the edge prediction capability by fixing $g_{ij}^t$ to 0 when $g_{ij}^I=0$ during the optimization of TEMPI. PNA resulted in the highest precisions, but the lowest recalls, indicating that PNA-${\mathit{G}}^{\mathit{t}}$ had less false positives (FPs), but more false negatives (FNs), compared with TEMPI and the simple method (Fig. 3A and Supplementary Table S1). By contrast, the simple method had lower precisions (more FPs), but high recalls (less FNs), compared with TEMPI and PNA. Interestingly, precisions of the three methods are robust to the amount of the removed PPIs, indicating the robust sensitivity of the methods for identifying the true links against the removal of PPIs. On the other hand, recalls of the simple method, PNA and TEMPI with no edge prediction capability linearly decreased with the increase of the amount of the removed PPIs. However, importantly, recall of TEMPI was robust up to 60% removal of the input PPIs. Based on the overall performance measure, F1 score defined as the harmonic mean of precision and recall, PNA was the best or comparable with TEMPI when the amount of the removed PPIs is <30%. However, TEMPI outperformed the other methods when the amount of the removed PPIs is >30% and showed the robust performance against the removal of the PPIs. Also, TEMPI with no edge prediction capability achieved the similar performance to PNA, and the robustness against the PPI removal disappeared. These data indicate that the edge prediction capability of TEMPI recovered the removed links in TEMPI-${\mathit{G}}^{\mathit{t}}$.

Fig. 3.

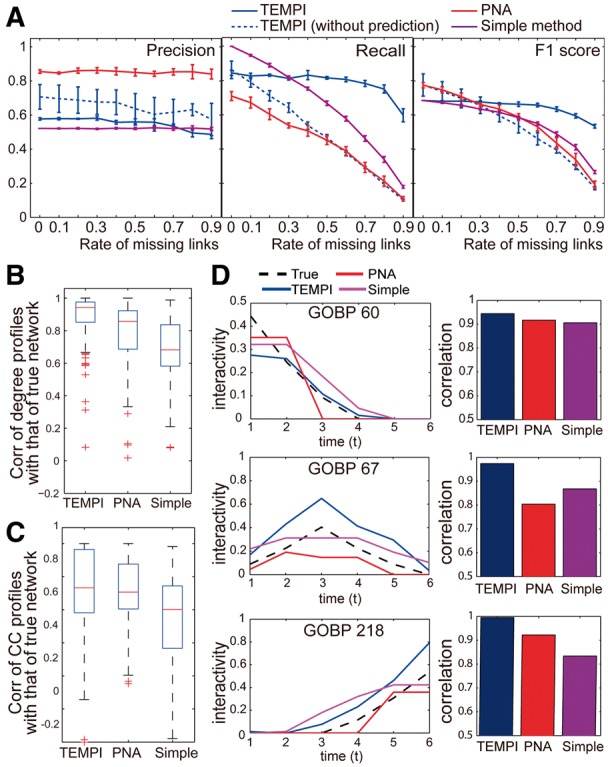
Comparison of TEMPI with two previous methods. (A) Precision, recall and F1 score for TEMPI-${\mathit{G}}^{\mathit{t}}$, PNA-${\mathit{G}}^{\mathit{t}}$ and Simple-${\mathit{G}}^{\mathit{t}}$ with up to 90% removal of the input PPIs. The performance can vary depending on which PPIs are removed. Thus, we performed 10 times of random samplings. Data are represented as mean ± SD from the samplings. (B–C) Distributions of correlations of temporal profiles of degrees (B) and CC (C) in the three ${\mathit{G}}^{\mathit{t}}$ s with those in the true ${\mathit{G}}^{\mathit{t}}$. (D) Changes in the interactivities of GOBPs 60, 67 and 218 in the three ${\mathit{G}}^{\mathit{t}}$ s and the true ${\mathit{G}}^{\mathit{t}}$ (Left) and correlations between the interactivities in the inferred ${\mathit{G}}^{\mathit{t}}$ s and the true ${\mathit{G}}^{\mathit{t}}$ (Right). See the legend for the lines used for the three methods

In addition, it is important to assess whether the three methods correctly estimate temporal transitions of topological properties in the true TDNs. Thus, we next examined the performance of the three methods in estimating transitions of the topological properties. To this end, we first selected TDNs reconstructed by the three methods when percentage of removal in input PPIs is 30% because they achieved similar F1-scores. Then, for the nodes in the ${\mathit{G}}^{\mathit{t}}$ estimated by each method, we computed (i) degree and (ii) clustering coefficient(CC) profiles over time. Then, we calculated correlations of the degree and clustering coefficient profiles with those of the true TDNs (Fig. 3B–C). The comparisons revealed that temporal transitions of the topological properties in TEMPI-${\mathit{G}}^{\mathit{t}}$, compared with PNA-${\mathit{G}}^{\mathit{t}}$ and Simple-${\mathit{G}}^{\mathit{t}}$, agreed best with those in the true TDNs. Structural changes in the ${\mathit{G}}^{\mathit{t}}$ s should be linked to transitions of cellular functions represented by the ${\mathit{G}}^{\mathit{t}}$ s over time. Thus, we examined how well structural changes in the ${\mathit{G}}^{\mathit{t}}$ s estimated by the three methods were linked to differential regulation of GOBPs 60, 67 and 218 represented in the true TDNs (Supplementary Fig. S6 for the other predefined six GOBPs). For TEMPI, as described in Section 4.1, the activation degrees of GOBPs showed that structural changes in the ${\mathit{G}}^{\mathit{t}}$ s well-represented early, mid and late differential regulation of the three GOBPs in the true TDNs (Fig. 2A). As another subjective measure previously reported (Song et al., 2009), we further defined ‘interactivity’ for each GOBP as the average number of the edges in ${\mathit{G}}^{\mathit{t}}$ among the nodes with the GOBP. For the GOBPs 60, 67 and 218, temporal changes of the interactivities obtained from TEMPI-${\mathit{G}}^{\mathit{t}}$ achieved the highest correlation with those of the true TDNs, compared with PNA-${\mathit{G}}^{\mathit{t}}$ and Simple-${\mathit{G}}^{\mathit{t}}$ (Fig. 3D). All these data together indicate that TEMPI-${\mathit{G}}^{\mathit{t}}$ represents effectively the temporal transitions in the true TDNs in the structural (Fig. 3A), topological (Fig. 3B–C) and functional (Fig. 3D) aspects, compared with the two previous methods.

4.3 Application of TEMPI to the cell cycle data

Cell cycle is a representative time-varying cellular process. Although small-scale TDNs for several molecules involved in cell cycle have been studied, large-scale TDNs for a comprehensive set of molecules for cell cycle are still largely unknown. Thus, we obtained time-course gene expression data (GSE8799) collected during the cell cycle of wild-type yeasts (Orlando et al., 2008). We first applied MDS to the high quality of known yeast PPI data (${\mathit{G}}^{\mathit{I}}$; Supplementary Information S4.1) to calculate ${\mathit{X}}^{\mathit{I}}$ in a 2D latent space for 3258 nodes. We selected the 755 DRNs with FDRs < 0.1 using the modified RM ANOVA test and maximum log₂-fold-changes > 0.58 (1.5-fold) at one time point at least. To identify TDNs, we then obtained the following input data for the 755 DRNs: (i) log₂-fold-changes (E) at six time points with two replicates, (ii) positions (${\mathit{X}}^{\mathit{I}}$) in a 2D space and (iii) 664 GOBPs (T) assigned to the 755 nodes (Supplementary Information S4.1).

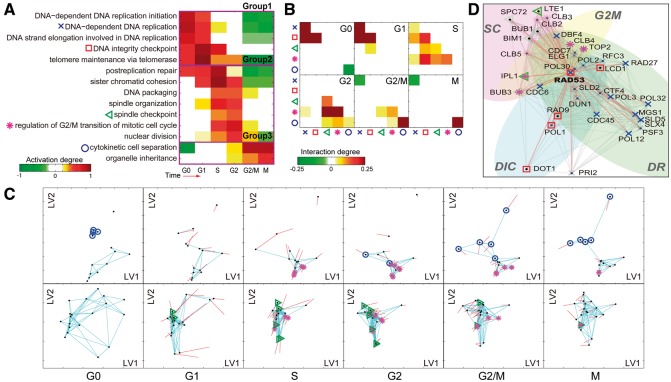
TEMPI generated ${\mathit{G}}^1$ to ${\mathit{G}}^6$ over six time points (G0, G1, S, G2, G2/M and M phases) during the cell cycle. To understand functional transition represented by TEMPI-${\mathit{G}}^{\mathit{t}}$, we first examined activation degrees of the 664 GOBPs. Among them, we focused on the 14 cell cycle–related GOBPs with pulsed changes of activation degrees, a characteristic of the cell cycle (Fig. 4A; Supplementary Information S4.2). They can be categorized into the following three groups: Group 1, early activated GOBPs with the peaks at G0 to G1 phase (DNA-dependent DNA replication initiation, DNA-dependent DNA replication, DNA strand elongation involved in DNA replication, DNA integrity checkpoint and telomere maintenance via telomerase); Group 2, middle activated GOBPs with the peaks at S to G2 phase (post-replication repair, sister chromatid cohesion, DNA packaging, spindle organization, spindle checkpoint, regulation of G2/M transition of mitotic cell cycle and nuclear division); and Group 3, late activated GOBPs with the peaks at G2/M to M phase [cytokinetic cell separation (CCS) and organelle inheritance]. The activation kinetics of these 14 GOBPs was largely consistent with their known kinetics during the cell cycle (Orlando et al., 2008; Simon et al., 2001; Spellman et al., 1998). For example, the expression of genes involved in DNA replication and repair reached peaks in G1 or S phases (Spellman et al., 1998), consistent to the kinetics of the GOBPs of DNA replication and post-replication repair in Figure 4A.

Fig. 4.

Application of TEMPI to the cell cycle data. (A) Activation degree heat map of the 14 cell cycle–related GOBPs: Group 1, cell cycle checkpoint-related GOBPs; Group 2, DNA replication-related GOBPs; Group 3, GOBPs related to the process followed by the DNA replication and Group 4, M phase-related GOBPs. The five GOBPs (DIC, SC, G2M, DR and CCS) are denoted by the indicated symbols. (B) Interaction degree heat maps of the five GOBPs. (C) TDNs showing temporal transition of the network structures for the DRNs with G2M and CCS (first row) and the DRNs with SC and G2M (second row). See Supplementary Figure S7 for TDNs for the DICs with CR. See the legend of Figure 2C for descriptions of shapes and colors of nodes and edges. (D) A detailed subnetwork including RAD53 interactors at S phase. Symbols in A were used to distinguish DRNs with the five GOBPs, and the symbols are transparent if $a_{ki}^t=0$ and solid otherwise

We then examined the interaction degrees of the GOBPs to understand time-dependent associations among GOBPs represented by TEMPI-${\mathit{G}}^{\mathit{t}}$. In this analysis, we focused on the following five GOBPs: GOBPs 1–2, DNA-dependent DNA replication (DR) and DNA integrity checkpoint (DIC) in Group 1; GOBPs 3–4, spindle checkpoint (SC) and regulation of G2/M transition of mitotic cell cycle (G2M) in Group 2; and GOBPs 5, CCS in Group 3. The interaction degrees revealed the following temporal interplays between the five GOBPs (Fig. 4B): (i) DIC and DR in Groups 1 and 2, respectively, during G0, G1 and S phases ($t=1$–3); (ii) DIC and SC, as well as DIC and G2M, in Group 1 at S phase ($t=3$); (iii) SC and G2M in Group 1 at S and G2 phases ($t=3$–4); and (iv) SC and CCS in Group 4 at G2 phase ($t=4$). Some of these interplays have been previously reported. Noh et al. (2009) reported that downregulation of G2/M transition-related genes (e.g. PLK1 and SURVIVIN) led to a defect in mitotic spindle, and Gardner et al. (1999) reported that two DIC-related genes, RAD53 and DUN1, are required for establishment and maintenance of G2/M arrest. TEMPI-${\mathit{G}}^{\mathit{t}}$ showed temporal transition of the nodes with the five GOBPs and their edges (G2M and CCS in first row of Fig. 4C, SC and G2M in second row of Fig. 4C and Supplementary Fig. S7 for individual GOBPs), consistent to the transitions of the GOBPs in Figure 4A and B.

These findings can provide novel insights into the interplays among the GOBPs during the cell cycle. TEMPI-${\mathit{G}}^{\mathit{t}}$ at S phase ($t=3$) showed the strongest associations among the GOBPs. To investigate novel insights represented by the associations, we built a subnetwork (Fig. 4D) including the nodes with the four GOBPs (DIC, DR, SC and G2M) strongly interacting at S phase ($t=3$). To reduce the complexity, we focused on the RAD53 subnetwork (Fig. 4D) including RAD53, a key molecule in DIC and DR, and its 36 interactors involved in the four GOBPs. Of the 36 interactors, only three are included in the input PPIs (${\mathit{G}}^{\mathit{I}}$), while the others are predicted. To assess the reliability of the predicted interactors of RAD53, we obtained 9850 interactions among the 755 DRNs from an independent PPI database, BioGrid (Stark et al., 2006), and confirmed that 18 of the 33 predicted interactors were previously detected by high-throughput interactome analyses, supporting the validity of TEMPI in the edge prediction. For example, TEMPI estimated the interactions of RAD53 with the 23 nodes (‘×’ nodes in Fig. 4D) involved in DR. Among them, RAD53-DBF4 and DUN1 was included in ${\mathit{G}}^{\mathit{I}}$, while the other interactions are newly predicted. Of the 21 predicted interactors, 14 (e.g. CTF4, CDC45 and CDC7) are reported to interact with RAD53 according to BioGrid. Moreover, TEMPI newly predicted the seven interactors of RAD53 involved in G2M (‘*’ nodes in Fig. 4D), where three of them (CLB2, CLB5 and IPL1) are reported to interact with RAD53 according to BioGrid. Similarly, TEMPI identified seven interactors of RAD53 involved in DIC (‘□’ nodes in Fig. 4D). Two of them (DUN1 and RAD9) were included in ${\mathit{G}}^{\mathit{I}}$, and the other five were reported to interact with RAD53 according to BioGrid. The molecules with newly predicted interactions in the RAD53 subnetwork are known to be involved in DIC, DR, SC or G2M, independently of RAD53-dependent regulation of the cell cycle at S phase. Thus, all these data indicate novel insights into potential roles of these molecules in the RAD53-dependent regulation of the cell cycle at S phase. Many subnetworks can be analyzed in the same way to generate hypotheses for novel mechanisms underlying dynamic regulation of cell cycle.

We further compared the performance of TEMPI on the cell cycle data with that of PNA. PNA produced the 10 PSs. By combining them, we generated TDNs as described above (PNA-Gs in Supplementary Fig. S8). PNA-Gs were significantly sparse, compared with TEMPI-Gs (Supplementary Fig. S8), because PNA used only the sparse real PPIs (1425 PPIs between 755 nodes) in G^I, whereas TEMPI predicted a significant number of novel edges among the DRNs (Supplementary Fig. S9A). As described above, we assessed the reliability of the predicted PPIs by examining how many of them are reported in the BioGrid database (Supplementary Fig. S9B–C). The fraction of the predicted PPIs reported in BioGrid (0.254) was significantly larger than the random expectation (0.0346). Moreover, TEMPI-${\mathit{G}}^{\mathit{t}}$ captured the larger number of cell cycle–related GOBPs (120 GOBPs) with pulsed activation patterns than PNA-${\mathit{G}}^{\mathit{t}}$ (16 GOBPs), suggesting that TEMPI-${\mathit{G}}^{\mathit{t}}$ more effectively captured cell cycle–related functional transition than PNA-${\mathit{G}}^{\mathit{t}}$ (Supplementary Fig. S9D–F). The comparison of the distribution of degrees and CC also showed that TEMPI-${\mathit{G}}^{\mathit{t}}$ is more dense and modular than PNA-${\mathit{G}}^{\mathit{t}}$ (Supplementary Fig. S9G–H). See Supplementary Information S4.3 for further details. Also, we applied TEMPI to the gene expression data collected from the mutant yeasts with defects in cell cycle, compared activation/interaction degrees of cell cycle–related GOBPs between wild-type and mutant yeasts, and examined deregulation of wild-type TEMPI-${\mathit{G}}^{\mathit{t}}$ in mutant yeasts (Supplementary Information S4.4).

4 CONCLUSIONS

In this study, we developed TEMPI that effectively estimates TDNs associated with activated GOBPs over time by integrating time-course gene expression, PPI and GOBP data. TEMPI provides activation and interaction degrees of GOBPs, facilitating the interpretation of temporal activations and interplays of GOBPs represented by the estimated TDNs. This interpretation leads to generation of TDN-driven hypotheses for key pathways regulating cellular events under investigation (see Section 4.3). Thus, TEMPI can serve as a useful tool that provides hypotheses for the mechanisms underlying functional transitions in various problems in time-varying biological systems. See Supplementary Information S5 and S6 for implementation and limitations of TEMPI, respectively, which include potential limited applicability of TEMPI to other types of interactions than PPIs, sensitivity to completeness of the input PPIs and the scalability issue.

Funding: This study was supported by National Research Foundation (NRF) of Korea (NRF-2013R1A2A2A01067464), the IT R&D Program of MSIP/KEIT (14-824-09-014, Machine Learning Center), Institute for Basic Science (CA1308), the Next-generation Biogreen21 Program (PJ009072) and Proteogenomic Research Program.

Conflict of interest: none declared.