A new statistical framework to assess structural alignment quality using information compression

Abstract

Motivation: Progress in protein biology depends on the reliability of results from a handful of computational techniques, structural alignments being one. Recent reviews have highlighted substantial inconsistencies and differences between alignment results generated by the ever-growing stock of structural alignment programs. The lack of consensus on how the quality of structural alignments must be assessed has been identified as the main cause for the observed differences. Current methods assess structural alignment quality by constructing a scoring function that attempts to balance conflicting criteria, mainly alignment coverage and fidelity of structures under superposition. This traditional approach to measuring alignment quality, the subject of considerable literature, has failed to solve the problem. Further development along the same lines is unlikely to rectify the current deficiencies in the field.

Results: This paper proposes a new statistical framework to assess structural alignment quality and significance based on lossless information compression. This is a radical departure from the traditional approach of formulating scoring functions. It links the structural alignment problem to the general class of statistical inductive inference problems, solved using the information-theoretic criterion of minimum message length. Based on this, we developed an efficient and reliable measure of structural alignment quality, I-value. The performance of I-value is demonstrated in comparison with a number of popular scoring functions, on a large collection of competing alignments. Our analysis shows that I-value provides a rigorous and reliable quantification of structural alignment quality, addressing a major gap in the field.

Availability: http://lcb.infotech.monash.edu.au/I-value

Contact: arun.konagurthu@monash.edu

Supplementary information: Online supplementary data are available at http://lcb.infotech.monash.edu.au/I-value/suppl.html

1 INTRODUCTION

A protein structural alignment is an assignment of residue–residue correspondences between the amino acids of two or more proteins, based on their 3D structure. Protein structural alignments support basic and applied research in molecular biology. For example, they reveal how protein families evolve, identify patterns of conservation in amino acid sequences that fold into similar structures, facilitate comparative modelling of structures from sequence and guide experimental solutions to structures using crystallographic molecular replacement (Konagurthu et al., 2006).

The last four decades have seen the development of many methods aimed at generating biologically meaningful structural alignments. While the number of new methods is estimated to be doubling roughly every five years (Hasegawa and Holm, 2009), several comparative studies have observed many inconsistencies and paradoxes when comparing the alignments generated by existing methods. Noteworthy among these studies are those by Michael Levitt (Kolodny et al., 2005), Liisa Holm (Hasegawa and Holm, 2009) and Manfred Sippl (Sippl and Wiederstein, 2008; Slater et al., 2013) and colleagues. A common theme emerging from all these studies is the need for a systematic framework to asses the quality of structural alignments. While a handful of quantitatively rigorous statistical models for structure comparison have been proposed for this, there is no consensus regarding their usefulness.

This is in stark contrast to the state-of-the-art in the closely related problem of aligning protein sequences, where many rigorous statistical models have been proposed to quantitatively assess sequence alignment quality (Allison et al., 1992; Altschul, 1991; Karlin and Altschul, 1990). This has, in turn, helped standardize the task of measuring sequence alignment quality and, thus, the task of generating meaningful sequence alignments.

In this work, we begin by examining the foundations of how structural alignments are currently assessed. Guided by good biological insights, current structural aligners use a scoring function to quantify the structural alignment quality. This has traditionally been achieved by combining the contributions of a small number of important criteria into an easy-to-compute scoring function. [For a comprehensive list of commonly used scoring functions, see Hasegawa and Holm (2009)].

Overwhelmingly, the two key criteria that various current measures use are coverage and fidelity. Typically, coverage measures the number of correspondences (or equivalences) in an alignment and, in some cases, also considers the number of gaps. Fidelity, measures how similarly positioned the aligned residues are. This is commonly (but not always) based on the root-mean-square deviation (RMSD) computed after the best rigid-body transformation of corresponding residues is found.

To search for the best structural alignment, the goal of the aligners is to simultaneously maximize coverage and fidelity. However, these two objectives are in direct conflict with each other. We observe that most of the current proliferation of structural alignment scoring functions arise from attempts to reconcile this conflict, that is, existing scoring functions differ mainly in how they combine these two criteria. As the reviews show, existing scoring functions do not generate consistent results, even when aligning structures that have only moderately diverged in evolution (Hasegawa and Holm, 2009; Kolodny et al., 2005; Slater et al., 2013).

Because this traditional approach of formulating a scoring function has been explored extensively over the last four decades, further development along the same lines is unlikely to provide any major breakthrough. Therefore, this field will stand to benefit by departing from the traditional approaches and exploring radically new ones. This paper is a step in this direction.

Structural alignment as an inductive inference problem. The goal of inductive inference is to propose a theory (or hypothesis) that is able to best explain the observed data. Structural alignment can thus be seen an instance of the general class of inference problems. In this context, an alignment (i.e. residue–residue correspondence) is a hypothesis that attempts to explain the residue–residue relationships between two protein structures, whose observed data is the (x, y, z) coordinates of the structures.

In general, any hypothesis has a certain (descriptive) complexity. A complex hypothesis with more free parameters can predict (or fit, explain) a greater variety of observed data than a simpler hypothesis. Therefore, in order to choose the best hypothesis for any inference problem, one is confronted with a trade-off between hypothesis complexity and its fit with the observations.

For structural alignments, this trade-off is related to the conflict between coverage and fidelity. Coverage (in various forms handled in the current scoring functions) is a crude approximation of the (alignment) hypothesis complexity. Similarly, the fidelity (or goodness of fit with the observed data) of a structural alignment is approximated using RMSD of superposition or using some distance measure. These rudimentary approximations cause the existing scoring functions to introduce several tunable parameters in an attempt to balance the contributions between coverage and fidelity of structural alignments. This has been a major source of the inconsistencies observed in alignments.

The field of statistical learning and inference provides rigorous approaches to address this trade-off systematically. In the early 1960s, several landmark papers proposed links between inductive inference and information theory (Kolmogorov, 1965; Solomonoff, 1960; Wallace and Boulton, 1968). The Minimum Message Length (MML) principle (Wallace and Boulton, 1968) provided the first practical information-theoretic criterion for hypothesis selection based on observations. It is used here to rigorously assess structural alignment quality and reliably differentiate between competing alignments.

Structural alignment quality and lossless information compression. The pioneering work of Claude E. Shannon (Shannon, 1948) provides the means to quantify information: the length of the shortest code required to transmit, losslessly, an observed event. This can be understood as the length of the shortest message needed to communicate the event losslessly between an imaginary sender (Alice) and receiver (Bob).

In this context, the structural alignment problem can be rationalized as a communication process between Alice and Bob, where Alice has access to the (x, y, z) coordinates of two protein structures and she wants to encode and transmit this information to Bob losslessly. Two possible scenarios then arise: (i) If the two are unrelated to each other structurally, Alice cannot do better than to encode and transmit the information of the two structures independently, one after another. That is, knowledge of one structure (called reference, or S) does not provide information about the other (called target, or T) and, thus, knowledge of S cannot be used to compress T. This form of independent transmission is termed here as the null model message. (ii) On the other hand, if the two structures are structurally related (i.e. there is a meaningful alignment between the two), knowledge of S reveals information about T. The more similar the structures, the more information one reveals about the other. Alice can use this similarity to compress and transmit the information of the target structure using the information of the reference. For Bob to decode the information of the target losslessly (i.e. to the precision with which Alice sees it), he will require the structural information of the reference structure plus the information of its proposed relationship (i.e. the structural alignment) with the target. This will allow Alice to encode the target more concisely than stating the target structure using a null model. We call this form of transmission, the alignment model message (to contrast it with the null model message, where the structures are transmitted independently).

We note that this information-theoretic framework for structural alignment is intuitive. If the proposed alignment relationship is a poor one, then the encoded alignment model message will be inefficient (i.e. long). Alternatively, if the alignment relationship is a good one, then the transmission of the target becomes efficient (i.e. short). Therefore, the total message length of the lossless transmission of coordinate information (using an alignment hypothesis) forms an excellent measure to assess structural alignment quality. It follows that the best alignment is the one with the shortest total message length of lossless transmission.

While we have intuitively rationalized this framework as a communication process, this message paradigm is also backed by mathematical rigour. Formally, let $\mathcal{A}$ denote some alignment between structural coordinates S and T. Using the product rule of probability over three events $\mathcal{A}$, S and T we have:

$$\begin{array}{c}P(\mathcal{A}\&S\&T)=P(\mathcal{A})\times P(S|\mathcal{A})\times P(T|S\&\mathcal{A})\\ =P(\mathcal{A})\times P(S)\times P(T|S\&\mathcal{A})\end{array}$$ (1)

where $P(\mathcal{A}\mathrm{\&}S\mathrm{\&}T)$ gives the joint probability of alignment $\mathcal{A}$ for structures S and T, $P(\mathcal{A})$ the prior probability of the alignment, $P(T|S\mathrm{\&}\mathcal{A})$ the likelihood of T given S and $\mathcal{A}$. Note, $P(S|\mathcal{A})$ is P(S) because S and $\mathcal{A}$ are assumed to be independent.

Shannon’s mathematical theory of communication (Shannon, 1948) gives the relationship between the shortest message length I(E) to communicate losslessly any observation E, and its probability P(E) as $I(E)=-\log (P(E))$. Technically, I(E) denotes the Shannon information content of E.

Restating equation 1 in terms of information content, we obtain:

$$I(\mathcal{A}\mathrm{\&}S\mathrm{\&}T)=I(\mathcal{A})+I(S)+I(T|S\mathrm{\&}\mathcal{A})$$ (2)

where transmitting the information of the reference structure S takes I(S) bits, transmitting the alignment information takes $I(\mathcal{A})$ bits and transmitting the information of the target structure T using $\mathcal{A}$ and S takes $I(T|S\mathrm{\&}\mathcal{A})$ bits.

Our message length measure has the following three key properties, which are not achieved by previous scoring functions:

1. The difference between the lengths of the messages needed to transmit the structures S and T using any two alignments, gives their log-odds posterior ratio.

   $$\begin{array}{l}I({\mathcal{A}}_1\&S\&T)-I({\mathcal{A}}_2\&S\&T)=\log \left(\frac{P({\mathcal{A}}_2\&S\&T)}{P({\mathcal{A}}_1\&S\&T)}\right)\\ =\log \left(\frac{P(S\&T)P({\mathcal{A}}_2|S\&T)}{P(S\&T)P({\mathcal{A}}_1|S\&T)}\right)=\log \left(\frac{P({\mathcal{A}}_2|S\&T)}{P({\mathcal{A}}_1|S\&T)}\right)\end{array}$$ (3)

   As a result, any two competing alignment hypotheses ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ can now be compared based on their message lengths. Therefore, the best alignment hypothesis ${\mathcal{A}}^{*}$ is the one that results in the shortest message length value of $I({\mathcal{A}}^{*}\mathrm{\&}S\mathrm{\&}T$).

2. Our measure permits a natural null hypothesis test where the statistical significance of any proposed alignment hypothesis can be estimated. Any alignment hypothesis $\mathcal{A}$ whose message length $I(\mathcal{A}\mathrm{\&}S\mathrm{\&}T)$ is worse (longer) than that of the null model message, $I(S\mathrm{\&}T)=I(S)+I(T)$, must be rejected.

3. This measure provides an objective, formal trade-off between the complexity of the alignment ($I(\mathcal{A})$) and the fidelity of the structures given the proposed alignment ($I(T|S\mathrm{\&}\mathcal{A})$). Unlike previous attempts, these terms are not ad hoc approximations, as they represent rigorous estimations of Shannon information content based on lossless encoding and compression.

2 METHODS

2.1 Computation of the null model message length

The null model message corresponds to the transmission of protein coordinates without an alignment hypothesis. (In this work, we consider only the C${}_{\alpha }$ coordinates.) We have previously defined [for a completely different problem (Konagurthu et al., 2012)] a null model encoding of coordinates along a protein chain. We will briefly summarize this approach, as elements of this encoding are used and developed further in our current work.

The null model encoding relies on the observation that the distance between successive ${\text{C}}_{\alpha }$ atoms in a protein chain is highly constrained to $3.8\pm 0.2$ (s.d.) Å. For a chain of coordinates $\{p_1,p_2,\dots ,p_n\}$, any coordinate $p_{i+1}$ can be transmitted given the previous p_i, by first transmitting the distance r_i between p_i and $p_{i+1}$ using a normal distribution $\mathcal{N}(r;\mu ,\sigma )$ stated to $\mathrm{ϵ}=0.001$ Å accuracy, with $\mu =3.8$ Å and $\sigma =\pm 0.2$ Å. ($\mathrm{ϵ}=0.001$ reflects the precision of statement of coordinate data, which is three places after the decimal point as reported in the protein data bank.). We represent the length of this encoding as $I(r_i)$. With this information transmitted, Bob now knows that $p_{i+1}$ lies on a sphere of radius r_i centred at p_i, but does not yet know where exactly on the sphere it is. Assuming that $p_{i+1}$ is distributed uniformly over the surface of the sphere, transmitter Alice can discretize the sphere’s surface into cells, each of area ${\mathrm{ϵ}}^2$. Using this discretization, $p_{i+1}$ can be transmitted as cell number $c_{i+1}$. The numbering convention of the discretization is in the shared codebook. With the knowledge of p_i, r_i and c_i, Bob can reconstruct $p_{i+1}$ to the stated accuracy. Stating the cell number takes $I(c_i)=-{\log }_2\left(\frac{{\mathrm{ϵ}}^2}{4\pi r_i^2}\right)={\log }_2(4\pi r_i^2)-2{\log }_2\mathrm{ϵ}$ bits.

When sending a chain of $C_{\alpha }$ coordinates $\{p_1,p_2,\dots ,p_n\}$ over a null model message, we assume that p₁ is the origin and, hence, does not need to be transmitted as part of the message. Even if p₁ is not assumed to be the origin, its encoding will add a fixed one-time cost to the message length. Thus, to transmit the chain of points $p_1,p_2,\dots ,p_n$ over the null model, Alice needs to send to Bob the number n of $C_{\alpha }$ atoms in the chain, followed by incrementally transmitting (using the method above) p₂ given p₁, p₃ given p₂ and so on, until all coordinates are transmitted. Alice can transmit the number n over a integer distribution. Wallace and Patrick (1993) gave an efficient code ($I_{\text{integer}}(n)$) for transmitting any positive integer n > 0.

Therefore, the total message length required to send all the coordinates over the null model message takes $I_{\text{null}}(p_1,\dots ,p_n)=I_{\text{integer}}(n)+$${\displaystyle {\sum }_{i=1}^{n-1}\left(I(r_i)+I(c_i)\right)}$ bits.

Using the above, the coordinates of structures $S=\{S_1,S_2,\dots ,S_{|S|}\}$ and $T=\{T_1,T_2,\dots ,T_{|T|}\}$ are sent as independent chains of coordinates over the null model, taking $I_{\text{null}}(S\mathrm{\&}T)=I_{\text{null}}(S)+I_{\text{null}}(T)$ bits.

2.2 Computation of the alignment model message length

Equation 2 gives the amount of information required to transmit the coordinates of structures S and T using the alignment hypothesis $\mathcal{A}$. To estimate this, the explanation message involves transmitting: the coordinates of S, the residue–residue correspondences proposed by the alignment in $\mathcal{A}$ and, finally, the coordinates of T using the information of S and $\mathcal{A}$.

2.2.1 Transmitting the coordinates of S

This is achieved by sending the coordinates of $S=\{S_1,S_2,\dots ,S_{|S|}\}$ over the null model. Therefore, $I(S)=I_{\text{null}}(S_1,S_2,\dots ,S_{|S|})$ bits.

2.2.2 Transmitting the correspondences in $\mathcal{A}$

Any alignment can be described as a string switching between three states: match (‘m’), insertion (‘i’) and deletion (‘d’) states. This alignment string can be transmitted losslessly using a first-order Markov model.

To transmit an alignment over a 3-state Markov chain, we use an approach similar to the adaptive encoding method used by Wallace and Boulton (1969) over a multinomial (n-state) distribution. The adaptive encoding here requires maintaining nine running counters, one for each possible transition probability, all initialized to 1. Traversing the alignment string left to right, for every observed transition, Alice estimates its probability by dividing the current value of the corresponding transition counter by the sum of all counters from previous to any state. After the probability is estimated, Alice encodes the current alignment state using this probability and then increments the corresponding counter by 1. The code length to encode each state is the negative logarithm of its estimated probability. Summing each transition over the entire alignment gives the code length, $I(\mathcal{A})$.

2.2.3 Transmitting the coordinates of T given S and $\mathcal{A}$

With the information of S and $\mathcal{A}$ known to Bob, Alice can now use that information to encode the coordinate information of T. Intuitively, our encoding is based on the fact that when scanning $\mathcal{A}$ from left to right, Alice views T as runs of coordinates that alternate between blocks of insertions and matches with respect to S and the stated alignment. Note that all deletion blocks (with respect to S) in T are ignored as they contain no information to be transmitted about T. More formally, let $\mathcal{A}$ yield $\{{\mathcal{I}}_1,\dots ,{\mathcal{I}}_m\}$ insertion blocks, where any ${\mathcal{I}}_k$ represents a consecutive stretch of coordinates that are inserted in T (with respect to S). Each insertion block is transmitted as a null message taking $I_{\text{ins}}(T|S\mathrm{\&}\mathcal{A})={\displaystyle {\sum }_{k=1}^m{I}_{\text{null}}}({\mathcal{I}}_k)\text{bits}.$

What remains to be sent to Bob are the coordinates in T aligned to corresponding coordinates in S, that is, the matches. Let $\{S_{i_1},S_{i_2},\dots ,S_{i_n}\}$ and $\{T_{j_1},T_{j_2},\dots ,T_{j_n}\}$ where $1\le i_1<\dots i_n\le |S|$ and $1\le j_1<\dots j_n\le |T|$, denote the ordered set of corresponding coordinates in S and T, respectively. Bob already knows S and the alignment. From the alignment information he can infer the indexes of the aligned residue–residue correspondences: (i₁, j₁), (i₂, j₂), $\dots ,$ (i_n, j_n) between S and T. Thus, Alice can use the following procedure to transmit the aligned coordinates in T. To start the procedure, the first three matched coordinates of $\{T_{j_1},T_{j_2},T_{j_3}\}$ are sent over the null model message taking: $I_{\text{startup}}(T|S\mathrm{\&}\mathcal{A})=I_{\text{null}}(T_{j_1},T_{j_2},T_{j_3})\text{bits}.$ Alice then incrementally sends the remaining aligned coordinates of T as follows. To transmit the current aligned coordinate $T_{j_{k+1}}$, Alice considers only the set of (previous plus current) aligned coordinates $\{T_{j_1},T_{j_2},\dots ,T_{j_k},T_{j_{k+1}}\}$. This set is orthogonally transformed to the set $\{{\overline{T}}_{j_1},{\overline{T}}_{j_2},\dots ,{\overline{T}}_{j_k},{\overline{T}}_{j_{k+1}}\}$, such that it minimizes the least-square error between $\{S_{i_1},\dots ,S_{i_k}\}$ and $\{T_{j_1},\dots ,T_{j_k}\}$. Using this setup, Alice can transmit ${\overline{T}}_{j_{k+1}}$ over a directional distribution on a sphere. This is achieved by first transmitting the radius $r_k=||{\overline{T}}_{j_{k+1}}-{\overline{T}}_{j_k}||$ over a normal distribution with the same procedure described for formulating a null model message. This allows Alice to state ${\overline{T}}_{j_{k+1}}$ as a point on a sphere with radius r_k centred at ${\overline{T}}_{j_k}$. However, we do not state it over a uniform distribution (which would make it a null model description), as the knowledge of correspondence of ${\overline{T}}_{j_{k+1}}$ with $S_{i_{k+1}}$ gives clues about its position on the sphere (provided the assigned correspondence is a ‘good’ one). Because Bob already knows the corresponding point $S_{i_{k+1}}$, after transmitting r_k, Alice can use a directional probability distribution to state ${\overline{T}}_{j_{k+1}}$ more concisely. In directional statistics, the von Mises–Fisher distribution gives the probability density function (PDF) on the surface of any sphere in p-dimensions. In three dimensions, the PDF on the surface of a unit sphere is (Fisher, 1953; Mardia and Jupp, 1999): $\mathcal{V}(\widehat{x};\widehat{\mu },\kappa )=\frac{\kappa }{2\pi (e^{\kappa }-e^{-\kappa })}{e}^{\kappa \widehat{\mu }·\widehat{x}}$

Using this distribution to transmit ${\overline{T}}_{j_{k+1}}$, we compute ${\widehat{x}}_{k+1}$ as the direction cosines of the vector ${\overline{T}}_{j_{k+1}}-{\overline{T}}_{j_k}$, and ${\widehat{\mu }}_{k+1}$ as the direction cosines of the vector $S_{i_{k+1}}-{\overline{T}}_{j_k}$. The probability of stating ${\overline{T}}_{j_{k+1}}$ to the required precision (that is, $\mathrm{ϵ}=0.001$ Å precision on each component) using von Mises–Fisher distribution over the surface of a 3D sphere of unit radius is then given by: $P(\widehat{x})={\mathrm{ϵ}\prime }^2\frac{\kappa }{2\pi (e^{\kappa }-e^{-k})}{e}^{\kappa \widehat{\mu }·\widehat{x}}$ where ${\mathrm{ϵ}\prime }^2=\frac{{\mathrm{ϵ}}^2}{r_i^2}$, accounting for the scaling of the sphere of radius r_i to a unit sphere. Transmission of each $T_{j_{k+1}}$ requires the concentration parameter κ. We use the maximum-likelihood estimator based on the available superposition [see Mardia and Jupp (1999)]. Therefore, the code length to state x using von Mises–Fisher is: $I_{\text{vmf}}(\widehat{x})=-\log (P(\widehat{x}))\text{bits}.$

Each ${\overline{T}}_{j_{k+1}}$ is transmitted iteratively over this procedure, which we term adaptive superposition. Thus, the message length required to transmit the matched points in T with respect to their corresponding point in S is $I_{\text{match}}(T|S\mathrm{\&}\mathcal{A})=I_{\text{startup}}(T|S\mathrm{\&}\mathcal{A})+{\displaystyle {\sum }_{i=4}^n{I}_{\text{vmf}}}({\widehat{x}}_i)\text{bits}$. Combining the message lengths of transmitting coordinates in the insertion and matched blocks gives $I(T|S\mathrm{\&}\mathcal{A})=I_{\text{ins}}(T|S\mathrm{\&}\mathcal{A})+I_{\text{match}}(T|S\mathrm{\&}\mathcal{A})\text{bits}.$ An illustration of this procedure is shown in Figure 1.

Fig. 1.

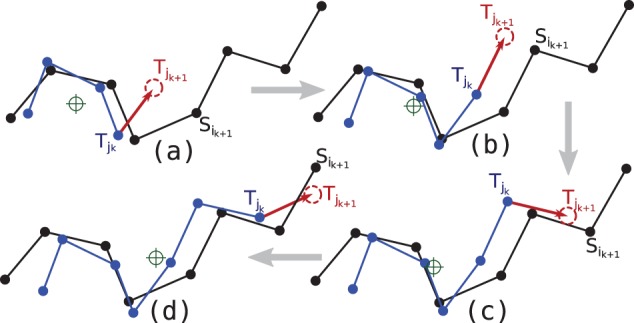
An idealized example of the adaptive superposition used to send the matched residues in T (in blue) incrementally given the knowledge of S (in black). Both structures have 8 points and are assumed here to be in one-to-one correspondence. Assume that Bob already knows the first 3 points of T. Alice sends the fourth point in T by superposing all previously matched points between the two structures. (Green crosshairs shows the rotational centre of superposition.) This orients the fourth point (in red) in T [or, more generally, $T_{j_{k+1}}$, whose deviation from its corresponding $S_{i_{k+1}}$ can be encoded over a von Mises–Fisher spherical distribution (see main text)]

2.3 Measure of alignment quality

$I(\mathcal{A}\mathrm{\&}S\mathrm{\&}T)$ is used as the measure of alignment quality. We call this measure I-value, indicating a value measuring the information content in the structural coordinates of S and T, given the structural alignment $\mathcal{A}$ as a model of compression. The smaller the I-value, the better the alignment. It follows that for competing alignments ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$, if the I-value of ${\mathcal{A}}_1$ is smaller than that of ${\mathcal{A}}_2$ by, for example, 15 bits, then ${\mathcal{A}}_1$ is 2¹⁵ times more likely than ${\mathcal{A}}_2$ (see property 1 of this measure shown in Equation 3). Further, any alignment $\mathcal{A}$ for which $I(S\mathrm{\&}T\mathrm{\&}\mathcal{A})>$ $I_{\text{null}}(S\mathrm{\&}T)=I_{\text{null}}(S)+I_{\text{null}}(T)$ can be rejected (see property 2 of this measure under ‘Structural alignment quality and lossless information compression’).

Handling shifts and rotations. So far we estimated the I-value under the rigid model of structural alignment. This model can be generalised to handle plastic deformations commonly observed in protein evolution, such as hinge rotations and shifts. Handling these deformations requires a modification in the way $I(T|S\mathrm{\&}\mathcal{A})$ is estimated under a flexible model of transmission.

Without loss of generality, assume that T contains a certain number of shifts and rotations, with respect to S, associated with its residues. In computing $I(T|S\mathrm{\&}\mathcal{A})$, alignment $\mathcal{A}$ is partitioned at the residues in T about which the shifts and rotations are defined. For example, consider below an alignment containing a hinge rotation about residue 10 of T (marked by *). Then, the alignment can be partitioned into two separate parts as follows:

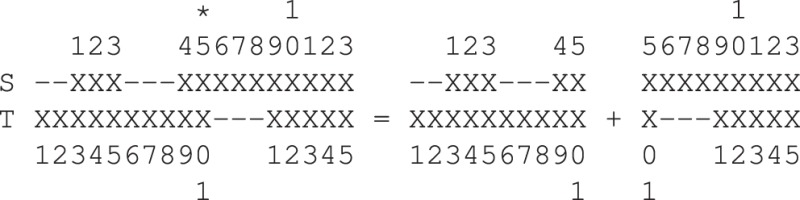
Let these partial alignments be denoted as $\mathcal{A}(T_1,\dots ,T_{10})$ and $\mathcal{A}(T_{10},\dots ,T_{15})$, identifying the start and end residue indexes in T about which the partition is defined. Then $I(T|S\mathrm{\&}\mathcal{A})$ is computed as $I(T|S\mathrm{\&}\mathcal{A}(T_1,\dots ,T_{10}))+I(T|S\mathrm{\&}\mathcal{A}(T_{10},\dots ,T_{15}))$ using the procedure described earlier. More generally, if there are k residues in T about which shifts/rotations are defined, the full alignment $\mathcal{A}$ is partitioned into k + 1 partial alignments: $\mathcal{A}(T_1,\dots ,T_{i_1}),\mathcal{A}(T_{i_1},\dots ,T_{i_2})$, $\dots ,$ $\mathcal{A}(T_{i_k},\dots ,T_{|T|})$, where $i_1<i_2<\dots <i_k<|T|$. Given these partitions, $I(T|S\mathrm{\&}\mathcal{A})$ can be computed as $I(T|S\mathrm{\&}\mathcal{A}(T_1,\dots ,T_{i_1}))$ $+\cdots +I(T|S\mathrm{\&}\mathcal{A}(i_k,\dots ,|T|)).$ This immediately poses another inference question: Given an alignment $\mathcal{A}$ of S and T, how many shifted/rotated residues does it contain? We note that adding a shift/hinge has an overhead which must pay for itself with a better fit if it is to be accepted.

Inference of shifted/rotated residues: A dynamic programming algorithm is used to optimally partition $\mathcal{A}$ minimizing $I(T|S\mathrm{\&}\mathcal{A})$.

The algorithm first constructs a matrix M of size $|T|\times |T|$ such that each cell M(i, j) ($1\le i<j\le |T|$) stores the value $I(T|S\mathrm{\&}\mathcal{A}(i,\dots ,j))$. The best partition of $\mathcal{A}$ is then computed using the following dynamic programming recurrence relationship:

$$\mathcal{P}(1,\dots ,j)=\underset{i=1}{\overset{j-1}{\min }}\{\begin{array}{ll}M(1,j),& \\ \mathcal{P}(1,\dots ,i)+M(i,j)& \forall 1\le j\le |T|\end{array}$$ (4)

where any $\mathcal{P}(1,\dots ,i)$ gives the optimal partitioning up to the ith residue in T, $1\le i\le |T|$. At the end of this procedure the value $\mathcal{P}(1,\dots ,|T|)$ gives the component message length $I(T|S\mathrm{\&}\mathcal{A})$ of Equation 2, in a way that handles shift and hinge rotations.

2.4 The time complexity of computing I-value

Using the rigid model of transmission (i.e.without handling the hinge-rotations and shift), the computation of $I(\mathcal{A}\mathrm{\&}S\mathrm{\&}T)$ is linear in the size of the alignment, as the computation of I(S), $I(\mathcal{A})$ and $I(T|S\mathrm{\&}\mathcal{A})$ are all linear. While the linearity of the first two is clear, that of $I(T|S\mathrm{\&}\mathcal{A})$ is not, as it requires repeated adaptive superpositions. However, we have recently proved sufficient statistics for the orthogonal superposition problem that allows each updated superposition to be computed as a constant-time update over the previous ones (Konagurthu et al., 2014), making the computation of $I(T|S\mathrm{\&}\mathcal{A})$, and I-value under rigid superposition, linear. On the other hand, using the flexible model which allows for hinge rotations and shifts, the computation of $I(\mathcal{A}\mathrm{\&}S\mathrm{\&}T)$ is quadratic, as it is dictated by the complexity of the dynamic program given by Equation 4.

3 RESULTS AND DISCUSSION

We have compared the quality of our I-value measure (using the flexible model described in sections 2.3) with popular scoring functions DALI, TM-Score, MI, SI, STRUCTAL, LGA_S3, GDT_TS, SAS and GSAS, using a large data set of alignments produced by the popular structural alignment methods DALI, TM-Align, LGA, CE and FATCAT. [Refer to Hasegawa and Holm (2009) for references of these scores/aligners.] Due to lack of space, we restrict our results herein to those obtained when comparing the DALI Score, TM-Score, and I-value measures, using TM-Align and DALI as the structural alignment generators. We refer to our online supplementary material for the remaining results.

Our first experiment tests the ability of the scoring functions to differentiate between pairs of structural domains that vary along the hierarchical groups defined by SCOP (Lo Conte et al., 2000)—Class, Fold, Superfamily and Family. To do this, we randomly selected a set of 500 ‘pivot’ domains from SCOP and, for each of these pivots, we randomly selected five other domains whose relationship with the pivot varies progressively: (i) Same-Family, (ii) Same-Superfamily (but not Family), (iii) Same-Fold (but not Superfamily and Family), (iv) Same-Class (but different below this level) and (v) Decoy (or different-Class). This results in a collection of 500 × 5 SCOP domains. We then aligned each pivot with each of its five counterparts, generating a total of 2500 alignments per alignment program. Finally, we assessed all these alignments using the selected scoring functions.

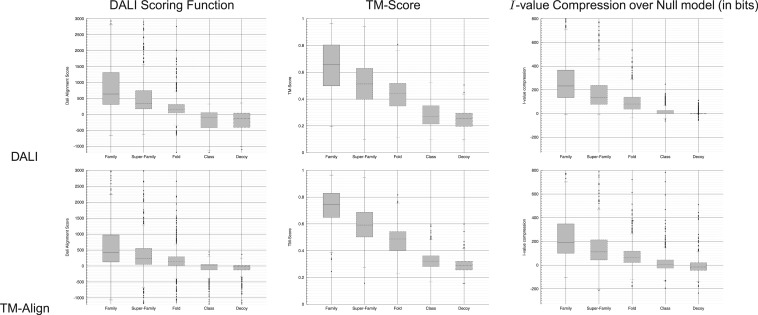
Figure 2 shows (some of) the box-whisker plots resulting from these comparisons. (As mentioned earlier, more results are given in Supplementary Table S1 of the online supplementary material.) Rows in this table denote the alignment method (DALI/TM-Align) used to generate the 2500 alignments in our collection. Columns denote the scoring function (DALI, TM-Score, I-value) used to compute the alignment score. Each cell in the table is a box-whisker plot that displays the numerical scores (as quartile marks) produced by each [alignment method, scoring function] pair, over the five groups of (500) alignments each. Note that for I-value, we show the compression gained (in bits) over the null model message length, that is, the (Null–I-value) message lengths. Thus, the greater the compression, the better the alignment. (In contrast, when using raw I-values rather than compression with respect to Null, the smaller the I-value the better the alignment.)

Fig. 2.

Table comparing the value of the DALI, TM-Score and I-value scoring functions (Columns) over 5 SCOP groups (see main text) containing 500 alignments each, generated by (rows) DALI and TM-Align programs. Note that the Y-axis uses different scales, as the range of values differ between scoring functions. Therefore, the absolute heights of the boxes cannot be compared between the box-whisker plots. However, their performance can be compared by the relative overlaps of the various quartile levels for each group with respect to others within the same box-whisker plot

A cursory inspection of these box-whisker plots indicates that, for the given alignments (which might not be the best/optimal ones), all scoring functions consistently differentiate between the SCOP groups to some extent. However, none of the scoring functions can be said to separate the SCOP groups cleanly nor to be clearly better than the others. This reflects partly the fuzzy classification boundaries of SCOP, and partly the quality of the (sub-optimal) alignments of domain pairs generated by popular alignment methods. For example, for TM-Score it has been claimed that the numerical score of < 0.5 corresponds to alignments not being in the same fold. However, we observe from the box-whisker plots in the second column of the table (the Fold group), that >3 quartiles of the alignments have a TM-score of <0.5. Inspecting the box-whisker plots at the same-Fold group, shows that a very large majority of alignments produced by DALI and TM-Align and scored using I-value are seen to be statistically significant (i.e. with Null–I-value message length > 0), with DALI alignments being more reliable than those generated by TM-Align, judging by the compression gain at the level of their respective medians. Interestingly, I-value seems to provide the smallest of variations when comparing the results obtained for the alignments generated by DALI to those generated by TM-Align.

Upon closer inspection, the results of our experiment indicate a significant degree of disagreement between the respective scores: only in 28% of the 2500 pivot-versus-counterpart alignments, all three scores agree on whether the alignment produced by DALI or by TM-Align is the best. This disagreement highlights the need for a generally accepted, rigorous alignment score. Supplementary Table S2 in the online supplementary material shows the full list of disagreeing pairs.

Our second experiment uses the set of ambiguous alignments described by Zu-Kang and Sippl (1996), as case studies for the various scoring functions ability to differentiate between very closely competing alignments. These alignments are indistinguishable in RMSD and number of equivalences (NEquiv). Table 1 compares the three scoring functions across five pairs of ambiguous structural alignments. For each scoring function, the better score of the two alignments for each pair is highlighted in bold. We again observe disagreement in two out of the five pairs between the scoring functions in their ability to decide which of the two alignments is the best. We emphasize that this discrimination is crucial for any scoring function to be useful as the basis of a search method looking for the optimal alignment.

Table 1.

Comparison between DALI score, TM-Score and I-value on ambiguous alignments reported by Zu-Kang and Sippl (1996)

Structures	Residues		Alignment ${\mathcal{A}}_1$			Alignment ${\mathcal{A}}_2$
S v. T	$|S|$	$|T|$	DALI Score	TM-Score	$I({\mathcal{A}}_1,S,T)$	Dali Score	TM-Score	$I({\mathcal{A}}_2,S,T)$
2TMVP v. 256BA	154	106	262.8	0.4871	9611.2 bits	242.6	0.4744	9614.0 bits
1TNFA v. 1BMV1	152	185	265.1	0.3815	12577.1 bits	307.3	0.3947	12463.7 bits
1UBQ v. 1FRD	76	98	161.9	0.4790	6384.8 bits	146.1	0.4518	6409.8 bits
2RSLC v. 3CHY	119	128	182.6	0.3773	9159.8 bits	206.1	0.3768	9143.5 bits
3CHY v. 1RCF	128	169	377.5	0.4960	10983.0 bits	336.4	0.4855	10961.8 bits

Note: For DALI and TM-score, the higher the score the better the alignment. For I-value, the smaller the value (or message length), the better is the alignment. Bold numbers in each row indicate the better of the two competing alignments under each of the scoring measures.

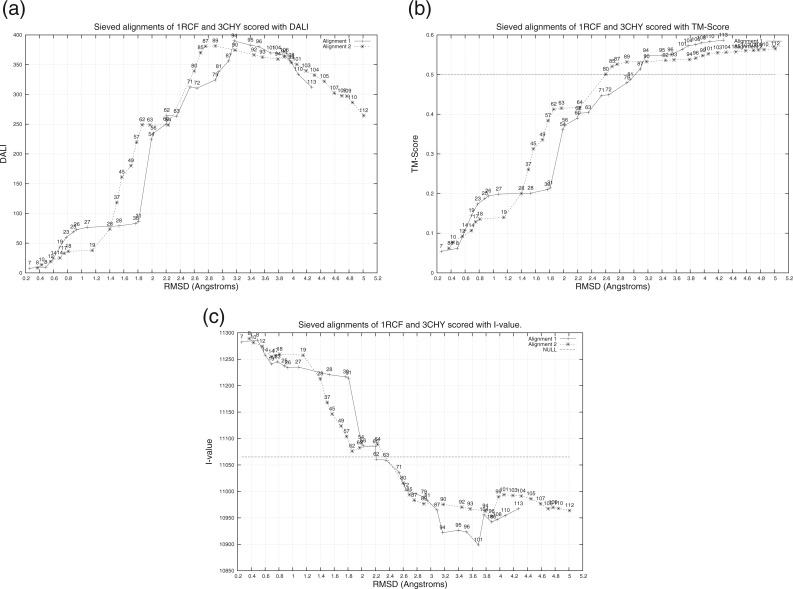
Let us illustrate the problems in using some of these scoring functions for an optimal alignment search method, using the case study of pair 3CHY v. 1RCF. To do so we ‘sieve’ each of the two ambiguous alignments using the following procedure, similar to the one described in Irving et al. (2001), to generate a number of competing alignments at varying levels of NEquiv and RMSD: (i) Compute the [NEquiv, RMSD] and corresponding DALI, TM-Score and I-value of the current alignment. (ii) Delete the worst-fitting aligned pair that appears at the end of a ‘matched block’ in the alignment, and force the deleted pair of residues to be unaligned. (iii) Repeat from Step 1 until the RMSD falls below a threshold value.

Studying the three sieving plots corresponding to DALI, TM-Score and I-value in Figure 3, it is immediately clear that TM-Score (Fig. 3b) does not produce any clear optima for this set of competing alignments to choose from. In fact, TM-Score monotonically increases towards the TM-scores of the unsieved alignments. On the other hand, I-value and the DALI score produce clear, though conflicting optima. I-value points to an optima for the sieved Alignment 1 at [NEquiv,RMSD] of [101,3.7 Å], whereas DALI points at [94, 3.17 Å]. (Superpositions based on these two alignments can be found in the online supplementary material.) This reflects the standard dilemma human experts and scoring functions face in choosing between two conflicting objectives. However, I-value objectively discriminates between the two competing alignments in terms of the lossless compression achieved. We emphasize that compression takes into account all aspects of the trade-off—descriptive complexity of the alignment hypothesis versus the quality of fit of the alignment to the structural data—that manifests in the structural alignment problem.

Fig. 3.

Sieving of the two ambiguous alignments reported by Zu-Kang and Sippl (1996) for the pair 1RCF and 3CHY. The X-axis gives the RMSD of each sieved alignment, while the Y-axis gives the scoring function used: (a) DALI, (b) TM-Score and (c) I-value. The labels in the figures correspond to the NEquiv values during sieving. For the TM-Score plot (b), the horizontal dotted line is the threshold for fold-level relationship. For the I-value plot (c), the horizontal line corresponds to the NULL model message length. The sieved alignments below this line are statistically significant

Finally, as a proof of concept, we have also developed a quadratic-time dynamic programming heuristic to search for the optimum I-value alignment. Currently this alignment heuristic is restricted to the rigid (and not flexible) model of computing the component message length $I(T|S,\mathcal{A})$. Details of the heuristic search are beyond the scope of the current article, given the page limitations. Our implementation of this alignment heuristic based on I-value is available for use from our website.

4 CONCLUSIONS

The importance of finding biologically meaningful structural alignments has led to the intensive development of methods for generating alignments and evaluating their quality. However, these methods produce conflicting results and none has been generally accepted as clearly superior.

Here we have described a measure of alignment quality, I-value, that uses the information content of messages that losslessly compress the Cα atoms of a pair of protein structures, given a proposed alignment. A lower I-value signifies a superior alignment. The method contains no adjustable parameters, as it is built on a formal Bayesian principle of minimum message length inference.

Examination of competing alignments over many pairs of protein structures demonstrates that I-value can accurately distinguish between competing structural alignments in cases in which other methods either cannot significantly distinguish the quality of these possibilities, or do not agree in the selection of a best one.

Funding: J.H.C. is supported by Australian Postgraduate Award (APA) and NICTA PhD scholarship.

Conflict of interest: none declared.