Abstract
Cellular automata are binary lattices used for modeling complex dynamical systems. The automaton evolves iteratively from one configuration to another, using some local transition rule based on the number of ones in the neighborhood of each cell. With respect to the number of cells allowed to change per iteration, we speak of either synchronous or asynchronous automata. If randomness is involved to some degree in the transition rule, we speak of probabilistic automata, otherwise they are called deterministic. With either type of cellular automaton we are dealing with, the main theoretical challenge stays the same: starting from an arbitrary initial configuration, predict (with highest accuracy) the end configuration. If the automaton is deterministic, the outcome simplifies to one of two configurations, all zeros or all ones. If the automaton is probabilistic, the whole process is modeled by a finite homogeneous Markov chain, and the outcome is the corresponding stationary distribution. Based on our previous results for the asynchronous case—connecting the probability of a configuration in the stationary distribution to its number of zero-one borders—the article offers both numerical and theoretical insight into the long-term behavior of synchronous cellular automata.
Key words: : binary lattice, cellular automata, detailed balance equation, finite homogeneous Markov chain, stationary distribution
1. Introduction
Cellular automata have been applied over time to model dynamical systems occurring in all range of organized behavior, such as statistical physics, biology, medicine, ecology, and socioeconomic interaction (Aristotelous and Durrett, 2014; Brännström and Sumpter, 2005; Clifford and Sudbury, 1973; Freire et al., 2010; Griffeath and Moore, 2002; Levy and Requeijo, 2008; Nguyen et al., 2005; O'Sullivan and Perry, 2009). They are a class of interacting particle systems, a paradigm for large dynamical systems comprising numerous particles that are allowed to interact on certain local neighborhood rules. According to Liggett, “The behavior of an interacting particle system depends in a rather sensitive way on the precise nature of the interaction. Thus most of the research that has been done in this field dealt with certain types of models in which the interaction is of a prescribed form. The unity of the subject comes not so much from the generality of the theorems which are proved, but rather from the nature of the processes which are studied and the types of problems which are posed about them” (Liggett, 2005).
Rigorously, a cellular automaton is a finite binary lattice with values 0 and 1, subject of iterative updating. In a totalistic automaton, transitions from 0 to 1 and vice versa are done locally, based only on the number of ones in some fixed-length neighborhood of the cell to be updated. If all cells in the current configuration are updated in the same time, the automaton is called synchronous; if only one cell is updated per iteration, the automaton is asynchronous. Another differentiation is given by the degree of randomness comprised by the automaton. If there is no randomness at all, the automaton is called deterministic—for example, if we update the cells one by one, from left to right, and a particular cell flips according to the majority of ones or zeros within its fixed-length neighborhood. But if the cell to be updated is chosen randomly, and/or the local transition rule involves probabilities—allowing, for example, to a cell that is currently 0 and has a majority of zeros in its neighborhood, to flip to 1 with a small probability—the automaton is called probabilistic.
At least theoretically, the probabilistic cellular automata have higher generality, and due to the fact that the current state of the automaton is solely responsible for the next state, they make the perfect candidate for Markov chain modeling.
2. Markov Chains
As introduced in Iosifescu, 2007, finite homogeneous Markov chains are stochastic processes with finite set of states 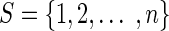 , where transition probabilities from one state to another depend only on the current position. We denote the transition probability from state i to state j by pij and gather all these probabilities into a square non-negative transition matrix
, where transition probabilities from one state to another depend only on the current position. We denote the transition probability from state i to state j by pij and gather all these probabilities into a square non-negative transition matrix
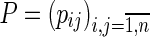 . Since elements in each row sum to one, matrix P is stochastic, and since the matrix does not change over time, the Markov chain is homogeneous.
. Since elements in each row sum to one, matrix P is stochastic, and since the matrix does not change over time, the Markov chain is homogeneous.
To the reader's convenience, we outline in the following the Markov chain prerequisites needed in our study. For a thorough introduction to the theory, see, for example, monographs (Iosifescu, 2007; Parzen, 1999).
Definition 2.1.
• A state i is called absorbing if pii = 1; that is, an absorbing state is never left once it is entered.
• A stochastic matrix P is called primitive if there is a positive integer t such that Pt is positive—that is, all entries in Pt are strictly positive.
• A stochastic matrix is called stable if all its rows are identical.
• Let p(0) be a probability vector. If p(0) is the initial probability distribution of the Markov chain with transition matrix P, then the distribution after t steps is p(t), with
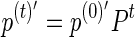 , for all t ≥ 1. If π′ = π′P, then π is called stationary distribution.
, for all t ≥ 1. If π′ = π′P, then π is called stationary distribution.• A sufficient condition for π to be the stationary distribution of P is the detailed balance equation:
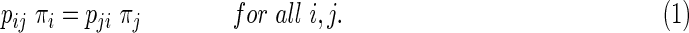 |
As pointed out in Parzen (1999), there are three main topics of interest while examining a Markov chain:
i) The short-term, time-dependent behavior—to find the transition probability matrix of a given process.
ii) The long-term, steady-state behavior—to determine conditions under which the existence of stationary distribution π is guaranteed, and to find that distribution, if possible.
iii) The analysis of first hitting time (absorption time): to study the length of time it takes the chain to pass from one set of states to another, or to enter a predefined target set.
All the above topics are of interest for cellular automata. So far, analysis has focused only on (and), yet the study of absorption time is considered by the authors of the article as an important future research direction, especially in relation to the density classification task of synchronous automata.
Theorem 2.2.
Let P be a primitive transition matrix. Then Pt converges as t → ∞ to a positive stable stochastic matrix P∞=1π′, and the rate of approach to the limit is geometric. Moreover, the limit distribution π = p(0)′P∞ has the following properties:
• is unique regardless of the initial distribution p(0);
• has positive entries on all components;
• is also the unique stationary distribution of the associated Markov chain.
An important exception from the primitive transition matrix case in Theorem 2.2 is when the Markov chain exhibits one or more absorbing states. Such situations occur frequently in synchronous cellular automata with the extreme configurations all zeros and all ones, which are the only two states of the automaton that cannot be left once they are entered. In this case, the automaton will eventually reach one of the two absorbing states, so there are only two questions to be posed:
i) Can we predict the final state of the automaton, based on the initial state?
ii) What is the journey time between the initial state and the absorbing one?
3. Asynchronous
As introduced in Section 1, there are two nonoverlapping classifications of cellular automata. One refers to the number of cells to be updated per time step, which can be either one (in the asynchronous case) or all (synchronous). The second refers to the updating mechanism itself, which can be either probabilistic or deterministic. As for the synchronous/asynchronous dichotomy, a hidden goal of this article is to break the wall between these two classes by showing that synchronous automata—at least some variants of them—behave in the long term exactly like their asynchronous counterparts!
Let us describe the Markov chain model of a probabilistic One-dimensional (1D) asynchronous cellular automaton, as introduced in Agapie et al. (2004). Consider an N-length binary string, with values 0 and 1, allowed to change at most one cell per iteration. At one time step, each cell has probability 1/N to be selected for a flip. Once selected, the local probability of flipping a cell further depends on its value and on the values of the other (L − 1) cells within its neighborhood. In Table 1 the local transition probabilities to 1 are depicted, while the local transition probabilities to 0 are to be calculated from the same table by turning the probability column upside down. Namely, if the probability of flipping to 1 from a neighborhood with k ones is ck, the probability of flipping to 0 under the same circumstances is set to (1 − ck), with 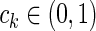 for all k.
for all k.
Table 1.
Local Transition Probability to 1, Neighborhood Size L, L Odd
| No. of ones in the neighborhood | Probability |
|---|---|
| 0 | c0 |
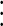 |
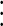 |
| (L − 1)/2 | c(L−1)/2 |
| (L + 1)/2 | 1 − c(L−1)/2 |
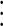 |
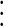 |
| L | 1 − c0 |
Nota bene, the transition 1 → 1 is also considered a flip. In the last row of Table 1, the number of ones in the neighborhood is L, so the central cell is obviously 1. Then the cell stays 1 with probability (1 − c0), or flips to 0 with complementary probability c0. We assume circular connections such that the left neighbor of the first cell is the Nth cell.
If we turn now from local to global transition probabilities, the components of transition matrix P, notice first that the Markov chain comprises 2N states–all the possible binary strings of length N. Let i be an arbitrary state (configuration). Then the asynchronous model will have exactly (N + 1) positive entries in each row; for an arbitrary row i, nonzero probabilities carry only states that differ from configuration i on maximum one cell.
The positive off-diagonal entries pij are of type (1/N)ck, respectively (1/N)(1 − ck) depending on the 0/1 value of the cell in configuration i that must be flipped in order to obtain configuration j. The diagonal term is defined as 1 minus all off-diagonal entries in the row, and is strictly positive, provided all local transition probabilities in Table 1 are in (0, 1). We have the following simple result.
Lemma 3.1.
The transition matrix of the 1D asynchronous automaton is primitive.
Lemma 3.1 and Theorem 2.2 ensure the existence of a limit distribution for the transition matrix associated to the asynchronous cellular automaton, which is also the unique stationary distribution of the respective Markov chain.
Our previous work in the field concentrated on finding the analytical formula of the stationary distribution for 1D up to 3D asynchronous cellular automata (Agapie, 2010; Agapie and Aus der Fuenten, 2008; Agapie et al. 2004), respectively on connecting our findings to the existent results from the Ising and exponential voter model (Agapie et al., 2010). The main results of the quoted articles are presented in the following.
We start with the case of an asynchronous automaton with neighborhood three, formed by the cell to be updated and its left and right neighbors. There are two Markov chain parameters in this case; we renote them ε and α, so Table 1 simplifies to only four rows, corresponding to probabilities ε, α, (1 − α), and (1 − ε).
The theorem below shows that probabilities in the stationary distribution exhibit a class property, related to the number of borders within the configuration.
Definition 3.2.
A border occurs between two different successive cells, namely (0, 1) or (1, 0). We denote by b(i) the total number of borders within configuration i.
Theorem 3.3.
The stationary distribution of P is given by π, where
 |
and Z is a normalization factor.
The computation of Z leads to a combinatorial problem, easily solved in the case of neighborhood three by the following.
Lemma 3.4.
The number of configurations with 2k borders is
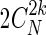 , for all
, for all
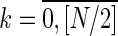 .
.
In the case of the five-neighborhood asynchronous automaton, we get one more parameter, say β, and two more active rows in Table 1, corresponding to probabilities β and (1 − β), see Table 2.
Table 2.
Local Transition Probabilities, L = 5
| No. of ones in the neighborhood | Transition Probability to 1 | Transition probability to 0 |
|---|---|---|
| 0 | ε | 1 − ε |
| 1 | α | 1 − α |
| 2 | β | 1 − β |
| 3 | 1 − β | β |
| 4 | 1 − α | α |
| 5 | 1 − ε | ε |
Yet, the extrapolation of the simple expression (2) can not be done without a further condition on ε, α, and β. This amounts to setting up the local transition probabilities such that the Markov chain satisfies the so-called detailed balance equation.
A refinement of the notion of border is needed.
Definition 3.5.
A k-border occurs between two different cells situated at distance k from each other. For example, in 001 we have a 2-border between the first and third cells and a 1-border between the second and third cells.
Theorem 3.6.
If the following holds
 |
then the stationary distribution of P is given by π, where
 |
and Z is a normalization factor.
An analogous of Lemma 3.4 is also valid.
Lemma 3.7.
The number of configurations with b order-1 borders and t order-2 borders is
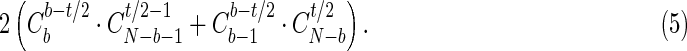 |
4. Synchronous Simulation
We test now—by means of computer simulation—whether the analytical formula of stationary distribution proved for asynchronous automata fits also the synchronous case. By definition, in a synchronous automaton all cells may change during a single iteration. Two different ways of doing that are considered.
| Sync 1: Draw a shadow configuration, filled in with the new values obtained for each cell by applying the updating rule; once completed, the shadow replaces the current configuration. |
| Sync 2: From left to right, update all the cells in the configuration using the local updating rule. |
The difference is the following: In Sync 2 the new value of a cell contributes to the local updating of its right neighbor(s), while in Sync 1 it does not. In this respect, one might say that Sync 2 is closer to an asynchronous cellular automaton than Sync 1. A variant of Sync 2 with random pick of the cell to be updated was also tested, with similar results.
As a general rule while performing computer tests, we start from an arbitrary configuration, run the cellular automaton for n iterations, then register the next n iterations for the (empirical) stationary distribution.
Consider first the three-neighborhood automaton and Formula (2) for the theoretical distribution, with scaling factor Z computed by Lemma 3.4. The parameters of the automaton are set to ε = 0.2, α = 0.4, and N = 10, for which the theoretical findings on asynchronous automata induce the following partition on the set of 210 possible configurations, with respect to the number of borders: {0, 2, 4, 6, 8, 10}.
We enforced this partition on the synchronous automata as well, by assuming that configurations sharing the same number of borders have the same probability in the stationary distribution. Next, we calculated the probabilities for Sync 1 respectively Sync 2 by summing up the relative occurrence frequencies (within the n limit configurations) of all configurations belonging to a particular class. The magnitude of n has no substantial influence on these findings—n ranging between 104 and 106 provided similar results.
As one can notice from Figure 1, this reasoning works perfectly with synchronous automaton Sync 2 but not so good with Sync 1. The difference goes beyond the graphical incongruence: not only that Sync 1 histograms depart from those of asynchronous automaton (Theory) on each class, but as a matter of fact Sync 1 does not exhibit the class property with respect to the number of borders at all!
FIG. 1.
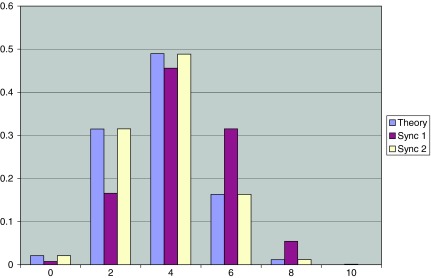
Stationary distribution for three-neighborhood synchronous automata, n = 106.
The conclusion of the three-neighborhood computer simulation is straightforward. The border-based exponential formula of the stationary distribution from Section 3 extrapolates to synchronous automata of type Sync 2, but not to Sync 1. Before giving a rigorous proof to this conjecture, we check it also on the five-neighborhood case.
A first set of tests for neighborhood five was performed by mirroring the simulation above, considering the same variants of synchronous automata, Sync 1 and Sync 2, each of fixed length N = 10 and a set of local probabilities obeying the law (3): (ε, α, β) = (0.0(8), 0.2, 0.4). Partitioning the state space with respect to the number of borders is not as straightforward as before, requiring a technical result (to improve readability, proof is omitted).
Lemma 4.1.
The partition induced by formula (5) on the neighborhood five automaton with length N = 10 is given in Table 3.
Table 3.
Partition of States for Synchronous Automaton, L = 5, N = 10
| Order-1 plus order-2 borders | 0 | 4 | 6 | 8 | 10 | 12 | 14 |
| No. of configurations | 2 | 20 | 90 | 170 | 372 | 320 | 50 |
Even if the classes in the partition differ from the previous case, the results stay the same: the empirical stationary distribution of automaton Sync 2 fits the theoretical distribution of the asynchronous case (4), while the empirical distribution of Sync 1 departs significantly from that. As before, the numerical results are not influenced by the magnitude of n, ranging from 104 to 106. The inadvertence of the border-based partition is demonstrated once more in case of Sync 1, so we can drop this automaton from the list of extrapolation candidates and concentrate on Sync 2 instead.
A second set of tests for neighborhood five was performed on Sync 2, with two different local probability settings. We compared the empirical distribution obtained for local probabilities (ε, α, β) = (0.0(8), 0.2, 0.4) against the one obtained for an arbitrary set of parameters, for example (ε, α, β) = (0.2, 0.3, 0.4). As we can notice in Figure 2, the automaton with parameters given by (3) stays close to the theoretical distribution, while the one with arbitrary parameter setting is driven away—needless to say, other arbitrary settings yielded the same behavior. It is worth mentioning that, in case of synchronous automaton Sync 2, relation (3) does not imply detailed balance equation for the corresponding Markov transition matrix. That will be explained in the next section in more detail.
FIG. 2.
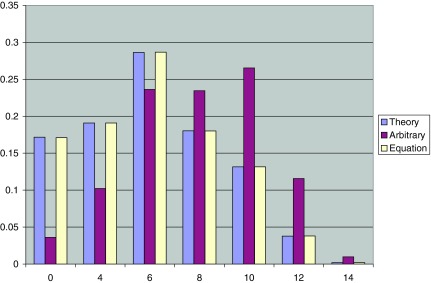
Stationary distribution for five-neighborhood synchronous automata Sync 2.
5. Synchronous Theory
Computer simulations have done their part, indicating that the stationary distribution of synchronous automaton Sync 2 obeys formula (4) of the asynchronous case, if and only if local probabilities ε, α, and β fulfill the special relation (3). That requires rigorous proof, provided in the following. As we expect the conjecture to be true for either three-, or five-neighborhood automata, we consider here the most complex situation, neighborhood five, and show that Theorem 3.6 is still valid.
To this end, we start by pointing out the differences, with respect to Markov chain modeling, between the two types of automata: synchronous and asynchronous. Even if local transitions are governed by the same rule—table 3—global transition matrix P is no longer sparse in the synchronous case. As Sync 2 is allowed to move between any two configurations in a single step, all entries in P are now positive, yet they are nothing like the positive entries of P described in Section 3.
Moreover, detailed balance equation (1)—essential to the proof of Theorem 3.6 in the asynchronous case—does not hold for synchronous automaton Sync 2. In order to see that, consider as i and j the configurations 10000 and 11111, respectively. According to (10), b1(i) = b2(i) = 2 and b1(j) = b2(j) = 0, so
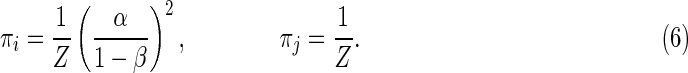 |
From Table 2, we compute transition probabilities pij and pji as
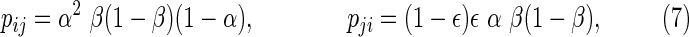 |
which gives by straightforward multiplication
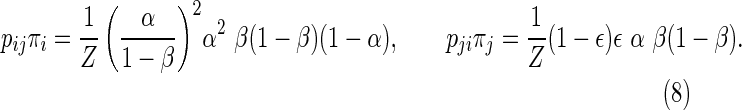 |
The application of (1) and (9) leads to α = 1 − ε; not true in general. Thus, the detailed balance equation is not fulfilled.
Theorem 5.1.
If the following holds
 |
then the stationary distribution of synchronous automaton Sync 2 is given by π
 |
with Z a normalization factor.
Proof.
As detailed balance equation is no longer valid, one needs to show that π′ = π′P, for stationary distribution π given by (10) and transition matrix P of cellular automaton Sync 2. Namely, we need to prove that
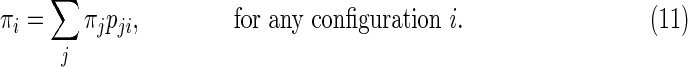 |
To improve readability, we confine to the case N = 5. A higher length automaton would not add difficulty to the proof, but only increase exponentially the dimension of transition matrix, the number of versions of equation (11) to be verified, and the number of terms in the sum at the right-hand side of each equation.
For N = 5 we have 25 possible configurations, so one needs to verify 32 versions of (11). Only one case will be demonstrated below, the one corresponding to configuration i = all ones. Proof is the same for any other configuration.
For i = 11111 we have πi = 1/Z, and as 1/Z occurs in all πj from the right-hand sum of (11), it will cancel out from both sides. We need to consider each of the 32 configurations leading to i and, for each such configuration j, calculate the product πjpji or the respective sum of products. We group the configurations with respect to the number of ones, and to shifting invariance.
Case 1: 00000 → 11111
 |
Case 2: {10000, 01000, 00100, 00010, 00001} → 11111
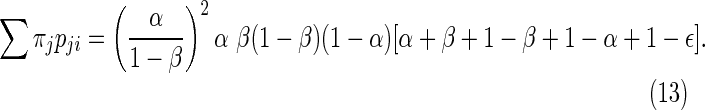 |
Case 3: {11000, 01100, 00110, 00011, 10001} → 11111
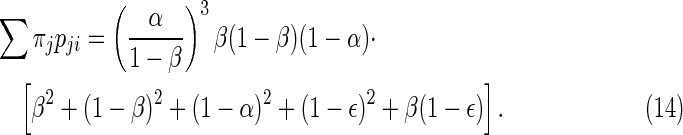 |
Case 4: {10100, 01010, 00101, 10010, 01001} → 11111
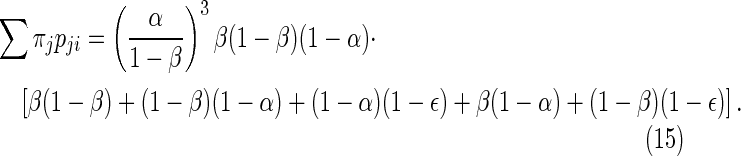 |
Case 5: {11100, 01110, 00111, 10011, 11001} → 11111
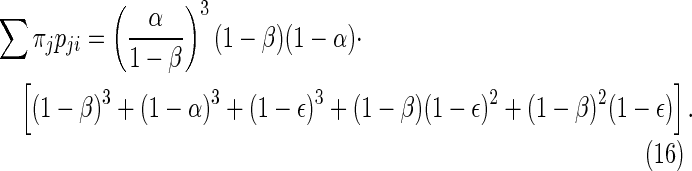 |
Case 6: {11010, 01101, 10110, 01011, 10101} → 11111
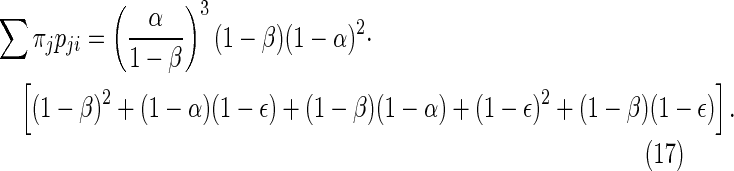 |
Case 7: {11110, 01111, 10111, 11011, 11101} → 11111
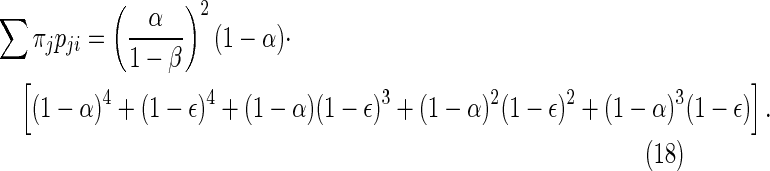 |
Case 8: {11111} → 11111
 |
Summing up (12)–(19) and imposing condition (9) on the resulting sum gives 1, which is exactly the value of πi modulo 1/Z. ■
Needless to say, Lemma 3.7 is still valid for synchronous case Sync 2, as it has nothing to do with the dynamic updating rule of the automaton.
6. Conclusion
In stochastic processes, predictability usually takes the form of a probability distribution governing the long-term behavior of the system under consideration. If one can prove an analytic formula for the stationary distribution, the problem is solved. Unfortunately, such cases are rare, and the study of cellular automata illustrates the situation perfectly. Previous work of the authors (Agapie, 2010; Agapie and Aus der Fuenten, 2008; Agapie et al., 2004) has found the stationary distribution of asynchronous automaton in closed exponential form, function of the number of borders within the configuration. The aim of the present article was to test the extrapolation of the analytical formula onto synchronous automata.
As is usually the case in complex dynamical systems, computer simulation provided significant insight into the system's long-term behavior, opening the way for rigorous mathematical proof. Out of two different synchronous automata subjected to numerical tests, one showed good resemblance with the analytical formula, while the other diverged significantly. We focused on the one that tested positive and proved that the stationary distribution obeys the same dependency on the sum of order-1 and order-2 borders as the asynchronous automaton, even if the detailed balance equation is no longer fulfilled.
The problem of finding an analytical formula for the synchronous automaton that updates all the cells in the same time—Sync 1 in Section 4—still remains open. Unfortunately, numerical simulations in that case do not indicate a grouping effect on configurations within the stationary distribution, at least not with respect to their number of borders, making the extrapolation of formula (10) intractable.
Besides seeking further extrapolation of the stationary distribution formula, an important research direction would be the stochastic analysis of absorption time—see for example, Agapie (2013) and O'Sullivan and Perry (2009)—for either synchronous or asynchronous automata converging to the extreme configuration all zeros and all ones.
7. Acknowledgment
The first author was supported by a grant of the Romanian National Authority for Scientific Research, CNCS-UEFISCDI, project number PNII-ID-PCCE-2011-0015.
Author Disclosure Statement
The authors declare they have no conflicts of interest.
References
- Agapie A.2010. Simple form of the stationary distribution for 3D cellular automata in a special case. Physica A. 389, 2495–2499 [Google Scholar]
- Agapie A., and Aus der Fuenten T.2008. Stationary distribution for a majority voter model. Stoch. Models. 24, 503–512 [Google Scholar]
- Agapie A., Agapie M., Rudolph G., et al. 2013. Convergence of evolutionary algorithms on the n-dimensional continuous space. IEEE Trans. on Cybernetics. 43, 1462–1472 [DOI] [PubMed] [Google Scholar]
- Agapie A., Höns R., and Agapie Ad.2010. Limit behavior of the exponential voter model. Math. Soc. Sci. 59, 271–281 [Google Scholar]
- Agapie A., Mühlenbein H., and Höns R.2004. Markov chain analysis for one-dimensional asynchronous cellular automata. Methodol. Comput. Appl. 6, 181–201 [Google Scholar]
- Aristotelous A.C., and Durrett R.2014. Chemical evolutionary games. Theor. Popul. Biol. 93, 1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brännström A., and Sumpter D.J.T.2005. Coupled map lattice approximations for spatially explicit individual-based models of ecology. B. Math. Biol. 67, 663682. [DOI] [PubMed] [Google Scholar]
- Clifford P., and Sudbury A.1973. A model for spatial conflict. Biometrika. 60, 581–588 [Google Scholar]
- Freire J.G., Brison O.J., and Gallas J.A.C.2010. Complete sets of initial vectors for pattern growth with elementary cellular automata. Comput. Phys. Commun. 181, 750–755 [Google Scholar]
- Griffeath D., and Moore C., eds. 2002. New Constructions in Cellular Automata, Oxford University Press, Oxford [Google Scholar]
- Iosifescu M.2007. Finite Markov Processes and Applications. Dover, New York [Google Scholar]
- Levy D., and Requeijo T.2008. Stochastic Models for Phototaxis. B. Math. Biol. 70, 1684–1706 [DOI] [PubMed] [Google Scholar]
- Liggett T.M.2005. Interacting Particle Systems, 2nd ed., Springer, New York [Google Scholar]
- Nguyen V., Mathias R., and Smith G.D.2005. A stochastic automata network descriptor for Markov chain models of instantaneously coupled intracellular Ca2+ channels. B. Math. Biol. 67, 393–432 [DOI] [PubMed] [Google Scholar]
- O'Sullivan D., and Perry G.L.W.2009. A discrete space model for continuous space dispersal processes. Ecol. Inform. 4, 5768 [Google Scholar]
- Parzen E.1999. Stochastic Processes. SIAM, Philadelphia [Google Scholar]


