Abstract
Shapes of interacting RNA complexes are studied using a filtration via their topological genus. A shape of an RNA complex is obtained by (iteratively) collapsing stacks and eliminating hairpin loops. This shape projection preserves the topological core of the RNA complex, and for fixed topological genus there are only finitely many such shapes. Our main result is a new bijection that relates the shapes of RNA complexes with shapes of RNA structures. This allows for computing the shape polynomial of RNA complexes via the shape polynomial of RNA structures. We furthermore present a linear time uniform sampling algorithm for shapes of RNA complexes of fixed topological genus.
Key words: : bijection, interacting RNA complexes, shape polynomials, topological genus, uniform generation
1. Introduction
In this article we study shapes of RNA complexes, which constitute one of the fundamental mechanisms of cellular regulation. We find such interactions in a variety of contexts, such as small RNAs binding a larger (m)RNA target, including the regulation of translation in both prokaryotes (Narberhaus and Vogel, 2007) and eukaryotes (McManus and Sharp, 2002; Banerjee and Slack, 2002; the targeting of chemical modifications (Bachellerie et al., 2002); insertion editing (Benne, 1989); and transcriptional control (Kugel and Goodrich, 2007). RNA–RNA interactions are far more complex than simple sense–antisense interactions. This is observed for a vast variety of RNA classes including miRNAs, siRNAs, snRNAs, gRNAs, and snoRNAs.
An RNA molecule is a linearly oriented sequence of four types of nucleotides, namely, A, U, C, and G. This sequence is endowed with a well-defined orientation from the 5′- to the 3′-end and referred to as the backbone. Each nucleotide can form a base pair by interacting with at most one other nucleotide by establishing hydrogen bonds. Here we restrict ourselves to Watson-Crick base pairs GC and AU as well as the wobble base pairs GU. In the following, base triples as well as other types of more complex interactions are neglected.
RNA structures can be presented as diagrams by drawing the backbone horizontally and all base pairs as arcs in the upper half-plane (Fig. 1). This set of arcs provides our coarse-grained RNA structure, ignoring any spatial embedding or geometry of the molecule beyond its base pairs.
FIG. 1.
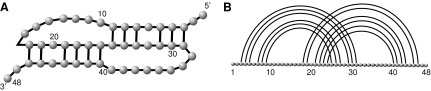
(A) An RNA secondary structure and (B) its diagram representation.
As a result, specific classes of base pairs translate into distinct structure categories, the most prominent of which being secondary structures (Kleitman, 1970; Nussinov et al., 1978; Waterman, 1978a,b). Represented as diagrams, secondary structures have only non-crossing base pairs (arcs). Beyond RNA secondary structures, we find RNA pseudoknot structures. These exhibit cross serial interactions (Rivas and Eddy, 1999). Once such cross-serial interactions are considered, the question of a meaningful filtration arises, since the folding of unconstrained pseudoknot structures is NP-hard (Lyngsø and Pedersen, 2000).
It turns out that topological genus is one such meaningful observable. The genus of pseudoknotted, single stranded RNA has been studied in Vernizzi and Orland (2005), Vernizzi et al. (2005), Bon et al. (2008), and Andersen et al. (2011), and there are several alternative filtrations of cross-serial interactions (Orland and Zee, 2002; Reidys et al., 2010, 2011).
The objects studied here are derived from RNA complexes, which are diagrams over two backbones. Distinguishing internal and external arcs, the former being arcs within one backbone and the latter connecting the backbones, RNA complexes can be represented by drawing the two backbones on top of each other (Fig. 2).
FIG. 2.
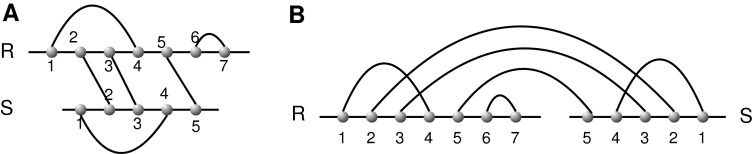
Diagram representation of an RNA complex.
We shall study shapes of RNA complexes, which are obtained by recursively removing all arcs of length one and collapsing all parallel arcs (Fig. 3).
FIG. 3.

From a 2-backbone diagram to its shape. The dashed arcs represent the rainbows (plants) of the shape.
Shapes are tailored to preserve the topological information of the molecule. The particular topologization is obtained via the notion of fat graphs, which date back to Heffter (1891). The classification and expansion of pseudoknotted RNA structures in terms of topological genus of a fat graph or double line graph were first proposed by Orland and Zee (2002) and Bon et al. (2008). In the context of RNA secondary structures, fat graphs were employed even earlier in Penner and Waterman (1993) and Penner (2004). The results of Orland and Zee (2002) are based on the matrix models and are conceptually independent. Genus, as well as other topological invariants of fat graphs, were introduced and studied as descriptors of proteins in Penner et al. (2010).
The approach undertaken here is combinatorial and follows Andersen et al. (2012). Starting with the diagram representation, we inflate each edge, including backbone edges, into ribbons. As each ribbon has two sides, and by specifying a counter-clockwise rotation around each vertex, we obtain so-called boundary cycles with a unique orientation. It is clear that we have thus constructed a surface, and its topological genus provides the desired filtration. Naturally, there are many such ribbon graphs that produce the same topological surface (by gluing the two “complementary” sides of each ribbon); this is how we obtain the desired equivalence (complexity) classes of structures.
It is easy to see that transforming an interaction structure into its shape preserves topological genus, and in Lemma 3.1, we shall see that for fixed genus g there exist only finitely many such shapes of RNA complexes. This means that for a fixed genus, there are only finitely many topologically distinct configurations, and important information is captured in the generating polynomial. In Theorem 4.5, we shall compute this polynomial and relate its coefficients to shapes of RNA structures by means of bijections relating one and two backbone shapes.
In Huang and Reidys (2014), a linear time algorithm for uniformly generating shapes of RNA structures of fixed topological genus was given. By means of the bijection of Theorem 4.2 relating one and two backbone shapes, we can use this algorithm to generate, uniformly, shapes of RNA complexes.
The article is organized as follows: In Section 2, we introduce diagrams and the basic framework in which we formulate our results. We discuss fat graphs and the topological filtration, namely, as drawing these diagrams on orientable surfaces of higher topological genus. In Section 3, we develop the concept of shapes and establish basic properties. We recall some key results on shapes of RNA structures, in particular the two-term recursion for computing their coefficients. In Section 4, we analyze shapes of RNA complexes and relate them to shapes of RNA structures. Several constructions show how to derive one from the other by specific “shape-surgery.” Here we also present the uniform generation algorithm of shapes of RNA complexes of fixed topological genus. In Section 5, we discuss specific RNA complexes, which all have a fixed shape, and in Section 6, we integrate and discuss our results.
2. Some Basic Facts
Definition 2.1.
A diagram is a labeled graph over the vertex set
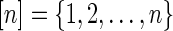 represented by drawing the vertices
represented by drawing the vertices
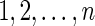 on a horizontal line in the natural order and the arcs (i, j), where i < j, in the upper half-plane. The backbone of a diagram is the sequence of consecutive integers
on a horizontal line in the natural order and the arcs (i, j), where i < j, in the upper half-plane. The backbone of a diagram is the sequence of consecutive integers
 together with the edges {{i, i + 1} | 1 ≤ i ≤ n − 1}. A diagram over b backbones is a diagram together with a partition of [n] into b backbones (Fig. 4).
together with the edges {{i, i + 1} | 1 ≤ i ≤ n − 1}. A diagram over b backbones is a diagram together with a partition of [n] into b backbones (Fig. 4).
FIG. 4.

A two-backbone diagram with 24 vertices and 12 arcs.
We shall distinguish backbone edges {i, i + 1} from arcs (i, i + 1), which we refer to as 1-arcs. Two arcs (i, j), (r, s), where i < r, are crossing if i < r < j < s holds. Parallel arcs of the form 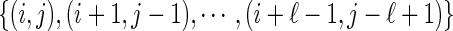 are called a stack, and ℓ is called the length of the stack. A stack on [i, j] of length k naturally induces (k − 1) pairs of intervals of the form ([i + l, i + l + 1], [j − l − 1, j − l]), where 0 ≤ l ≤ k − 2. Any of these 2(k − 1) intervals is referred to as a P-interval. An interval [i, i + 1] is called a gap if there exists a pair of subsequent backbones B1 and B2 such that i(i + 1) is the rightmost(leftmost) vertex of B1(B2). The vertex i is referred to as cut vertex. Any interval other than a gap or P-interval is called a σ-interval. Clearly, a diagram over [n] contains (n − 1) intervals of length 1, and we distinguish three types: gap intervals, P-intervals, and σ-intervals (Fig. 5).
are called a stack, and ℓ is called the length of the stack. A stack on [i, j] of length k naturally induces (k − 1) pairs of intervals of the form ([i + l, i + l + 1], [j − l − 1, j − l]), where 0 ≤ l ≤ k − 2. Any of these 2(k − 1) intervals is referred to as a P-interval. An interval [i, i + 1] is called a gap if there exists a pair of subsequent backbones B1 and B2 such that i(i + 1) is the rightmost(leftmost) vertex of B1(B2). The vertex i is referred to as cut vertex. Any interval other than a gap or P-interval is called a σ-interval. Clearly, a diagram over [n] contains (n − 1) intervals of length 1, and we distinguish three types: gap intervals, P-intervals, and σ-intervals (Fig. 5).
FIG. 5.
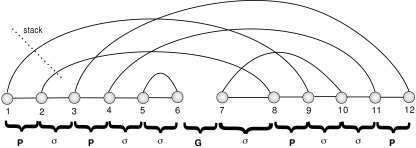
Stacks and intervals: gap intervals, σ-intervals, and P-intervals labeled by G, σ, and P, respectively. There are four stacks: {(1, 9), (2, 8)}, {(3, 12), (4, 11)}, {(5, 6)}, and {(7, 10)}.
Vertices and arcs of a diagram correspond to nucleotides and base pairs, respectively. For a diagram over b backbones, the leftmost vertex of each backbone denotes the 5′ end of the RNA sequence, while the rightmost vertex denotes the 3′ end. The particular case b = 2 is referred to as RNA interaction structures or RNA complexes. RNA complexes are oftentimes represented alternatively by drawing the two backbones on top of each other, (Fig. 6).
FIG. 6.
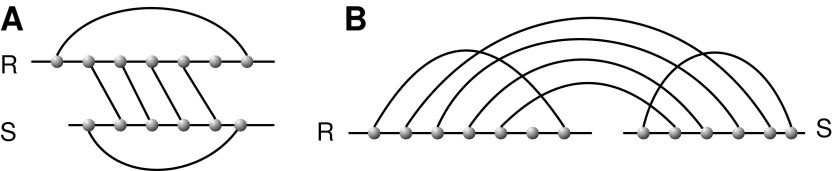
(A) An RNA complex presented by drawing the two backbones on top of each other. (B) The corresponding diagram over two backbones.
We will add an additional “rainbow-arc” over each respective backbone and refer to these diagrams as planted diagrams (Fig. 7).
FIG. 7.
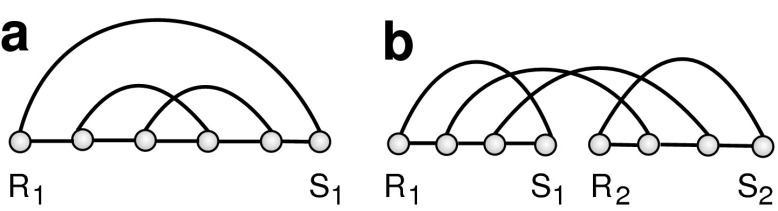
(a) A planted one-backbone diagram with the plant arc (R1, S1); (b) a planted two-backbone diagram with the plant arc {(R1, S1), (R2, S2)}.
A fat graph is a graph enriched by a cyclic ordering of the incident half-edges at each vertex and consists of the following data: a set of half-edges, H; cycles of half-edges as vertices; and pairs of half-edges as edges. The idea of half-edges stems from the observation that untwisted ribbons have two sides and are traversed in complementary directions. It is then a matter of convention to denote the terminal half of these sides as half-edge.
The specific drawing of a diagram G in the plane determines a cyclic ordering on the half edges of the underlying graph incident on each vertex, thus defining a corresponding fat graph  . The collection of cyclic orderings is called fattening, one such ordering on the half-edges incident on each vertex (Fig. 8).
. The collection of cyclic orderings is called fattening, one such ordering on the half-edges incident on each vertex (Fig. 8).
FIG. 8.

The fattening.
A fat graph  can be embedded in a compact orientable surface
can be embedded in a compact orientable surface 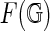 , such that its complement is a disjoint union of simply connected domains (called the faces or boundary components) and considered up to oriented homeomorphism. We can define the genus g of the fat graph by the genus of the surface. Clearly,
, such that its complement is a disjoint union of simply connected domains (called the faces or boundary components) and considered up to oriented homeomorphism. We can define the genus g of the fat graph by the genus of the surface. Clearly, 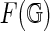 contains G as a deformation retract, and each
contains G as a deformation retract, and each 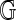 represents a cell-complex (Massey, 1967) over
represents a cell-complex (Massey, 1967) over 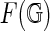 (Fig. 9).
(Fig. 9).
FIG. 9.
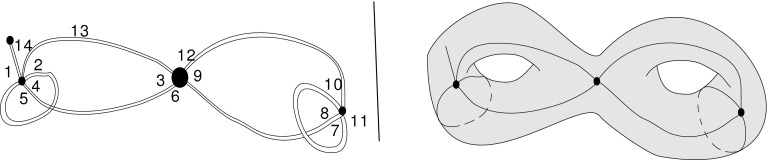
A fatgraph and its embedding.
A diagram G hence determines a unique surface  . Equivalence of simplicial and singular homology implies that Euler characteristic χ and genus g of
. Equivalence of simplicial and singular homology implies that Euler characteristic χ and genus g of  are independent of the choice of the cell-complex
are independent of the choice of the cell-complex  and given by χ = v − e + r and
and given by χ = v − e + r and 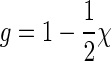 , where v, e, r are the number of discs, ribbons, and boundary components in
, where v, e, r are the number of discs, ribbons, and boundary components in 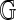 , respectively.
, respectively.
Without affecting topological type of the surface, one may collapse each backbone to a single vertex with the induced fattening called the polygonal model of the RNA (Fig. 10).
FIG. 10.

Inflation of a two-backbone diagram and collapse of its two backbones to two vertices.
This backbone collapse preserves orientation, Euler characteristic, and genus. It is reversible by inflating each vertex to form a backbone. Using the collapsed fat graph representation, we see that for a connected diagram over b backbones, the genus g of the surface is determined by the number n of arcs and the number r of boundary components, namely, 2 − 2g − r = v − e = b − n.
Boundary components are in the following, oftentimes referred to as loops. We distinguish the following loop-types:
• hairpin loops, which are boundary components of length one,
• interior loops, which are boundary components of length two,
• multi-loops, which are boundary components of length 2 ≥ 3.
We furthermore distinguish within multiloops pseudoknot loops, which are multiloops containing some crossing arcs in the diagram representation. In interaction structures, we shall distinguish α-loops and β-loops, and α stacks and β stacks, depending on whether or not they contain only arcs whose endpoints are on one backbone.
3. Shapes
A diagram is called a preshape if it contains neither 1-arcs [the arcs have the form (i, i + 1)] nor stacks (parallel arcs), and isolated vertices (the vertices not paired). A preshape without a rainbow is called pure. A shape is then obtained from a pure preshape by adding a rainbow for every backbone (Fig. 11). We can obtain the shape of a planted diagram by iterating the following two steps: First collapse each stack into an arc; secondly remove all the 1-arcs and isolated vertices. Iteration generates an unique diagram without stacks, 1-arcs, and isolated vertices (Fig. 12).
FIG. 11.

(A) The four shapes of genus 1 over one backbone. (B) The two shapes of genus 0 over two backbones.
FIG. 12.

From a diagram to a shape by removing all 1-arc and parallel arcs. The dashed arc is a rainbow, displayed together with a nested preshape.
For fixed genus g, there exist only finitely many shapes over one backbone (two backbones) (Andersen et al., 2012; Reidys et al., 2011).
Lemma 3.1.
Given a one-backbone shape of genus g with n edges, we have 2g + 1 ≤ n ≤ 6g − 1. Therefore, for fixed genus g, there exist only finitely many shapes.
Proof. First note that if there is more than one boundary component, then there must be an arc with different boundary components on its two sides, and removing this arc decreases r by exactly one while preserving g since the number of arcs is given by n = 2g + r − 1. Furthermore, if there are vl boundary components of length l in the polygonal model, then 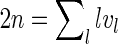 since each side of each arc is traversed once by the boundary (including the plant). For a shape, v1 = 1, because the plant gives the only boundary component of length 1; v2 = 0 by the definition of shapes. It therefore follows that
since each side of each arc is traversed once by the boundary (including the plant). For a shape, v1 = 1, because the plant gives the only boundary component of length 1; v2 = 0 by the definition of shapes. It therefore follows that 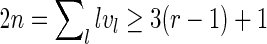 , so 2n = 4g + 2r − 2 ≥ 3r − 2, that is, 4g ≥ r. Thus, we have n = (2g + 4g − 1) = 6g − 1, that is, any shape can contain at most 6g − 1 arcs. The lower bound 2g + 1 follows directly from n = 2g + r − 1 since r ≥ 2.
, so 2n = 4g + 2r − 2 ≥ 3r − 2, that is, 4g ≥ r. Thus, we have n = (2g + 4g − 1) = 6g − 1, that is, any shape can contain at most 6g − 1 arcs. The lower bound 2g + 1 follows directly from n = 2g + r − 1 since r ≥ 2.
For fixed genus g, the number of arcs in the shape is at most 6g − 1, and the second assertion follows. ■
Lemma 3.1 implies that the generating function for one-backbone shapes of genus g is a polynomial. For example, for the shapes over one backbone with genus 1 to 3, we have
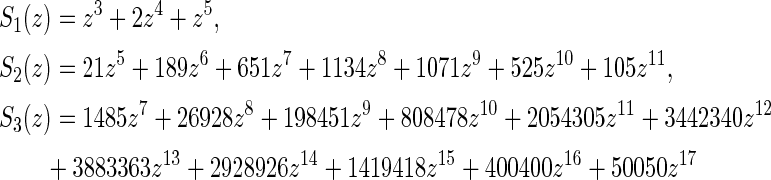 |
Explicit formulas for the coefficients of the shape polynomial of arbitrary fixed genus have been given in Huang and Reidys (2014). There the Poincaré dual of shapes, a unicellular map, was constructed, and a construction of Chapuy (2011) is refined to slice such a map into a tree with certain labeled vertices. The latter represent the blueprint to rebuild the original unicellular map and the shape, respectively.
Theorem 3.2.
(Huang and Reidys, 2014) The shape polynomial of genus g is given by
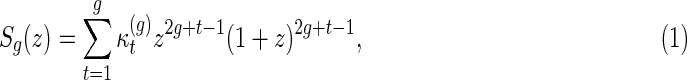 |
where
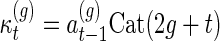 and
and
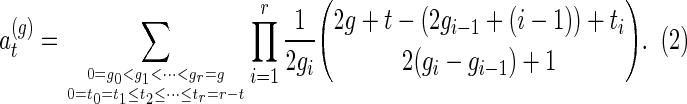 |
Huang and Reidys (2014) furthermore derives from the underlying bijections a uniform generation algorithm, UniformShape, for shapes of a fixed genus g, which has linear time complexity.
Li and Reidys (personal communication, 2014) study the sequence 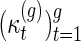 (Table 1), which emerged originally in the computation of the virtual Euler characteristic of a curve (Harer and Zagier, 1986). Li and Reidys (personal communication, 2014) shows that
(Table 1), which emerged originally in the computation of the virtual Euler characteristic of a curve (Harer and Zagier, 1986). Li and Reidys (personal communication, 2014) shows that 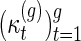 is log-concave and hence unimodal and derives
is log-concave and hence unimodal and derives
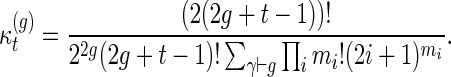 |
Table 1.
The Coefficients 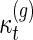
| g = 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| t = 0 | 1 | 21 | 1485 | 225225 | 59520825 |
| 1 | 105 | 18018 | 4660227 | 1804142340 | |
| 2 | 50050 | 29099070 | 18472089636 | ||
| 3 | 56581525 | 78082504500 | |||
| 4 | 117123756750 |
Furthermore,
Proposition 3.3.
(Li and Reidys, personal communication, 2014)
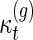 satisfies
satisfies
 |
where
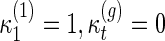 , if t < 1 or t > g.
, if t < 1 or t > g.
The above recursion has also been derived by Chekhov (1997) using matrix models.
4. Shapes Over Two Backbones
In this section, we study shapes over two backbones. Our main observation is that shapes over two backbones correspond to particular shapes over one backbone with topological genus increased by one.
We denote a shape over one backbone by (B, α), where
 |
is the sequence of vertices along the backbone and α is a fixed-point free involution, which contains (R1, S1) as one cycle (rainbow); α-cycles represent edges, and (R1, S1) is the plant.
We shall now distinguish two types of shapes. A shape is an A-shape if the vertex following α(1) is paired with the last vertex before S1 and a B-shape otherwise (Fig. 13). Let the set of A- and B-shapes having n edges and genus g be denoted by 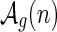 and
and 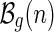 , respectively. Furthermore, let
, respectively. Furthermore, let 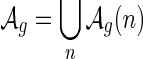 and
and 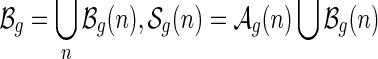 .
.
FIG. 13.

A-shapes [α(1) + 1 = 4 is paired with 6] and B-shapes [α(1) + 1 = 5 is not paired with 6].
Lemma 4.1.
We have a bijection:
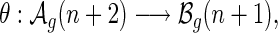 |
that is, there exists a pairing (x, θ(x)) associated to each A-shape and its unique B-shape. In particular,
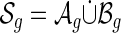 |
and
 .
.
Proof. Let 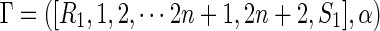 be an A-shape having n + 2 arcs, containing the arc (α(1) + 1, 2n + 2). Since Γ is a shape, there are no nested arcs or 1-arcs, whence removal of (α(1) + 1, 2n + 2) maps an A-shape into a B-shape.
be an A-shape having n + 2 arcs, containing the arc (α(1) + 1, 2n + 2). Since Γ is a shape, there are no nested arcs or 1-arcs, whence removal of (α(1) + 1, 2n + 2) maps an A-shape into a B-shape.
Furthermore, as an A-shape, Γ has a boundary component of size three, γ3, traversing the sides of the rainbow, (1, α(1)) and (α(1) + 1, 2n + 2). Let θ be the mapping defined by removing the arc (α(1) + 1, 2n + 2) together with its incident vertices and subsequent relabeling of the remaining vertices. Then θ decreases both: the number of boundary components, r, as well as the number of arcs n + 2 by 1. To see this, we note that (α(1) + 1, 2n + 2) is traversed by two distinct boundary components, γ, γ3. Removing (α(1) + 1, 2n + 2) consequently merges γ and γ3, whence the number of boundary components decreases by one. Euler's characteristic equation, 2 − 2g − r = 1 − (n + 2), shows that θ preserves g (Fig. 14).
FIG. 14.

θ: removal of (α(1) + 1, 2n + 2) creates a B-shape.
We next specify θ−1. Given a B-shape having n + 1 edges and genus g, we insert an arc with endpoints between [α(1), α(1) + 1] and [2n, S1] and subsequently relabel the diagram. This insertion maps any B-shape into an A-shape. Namely, by construction, it creates neither nested arcs nor 1-arcs (the latter would imply that the rainbow has a nested arc). After relabeling, the inserted arc is incident to (α(1) + 1, 2n + 2) and creates a new boundary component, γ3, as specified above. Euler's characteristic equation then shows that θ−1 does preserve genus (Fig. 14). ■
Let 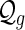 denote the set of shapes over two backbones of genus g, and
denote the set of shapes over two backbones of genus g, and 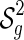 denote the set of pairs of disconnected one-backbone shapes whose sum of genera equals g. Let
denote the set of pairs of disconnected one-backbone shapes whose sum of genera equals g. Let 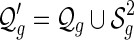 .
.
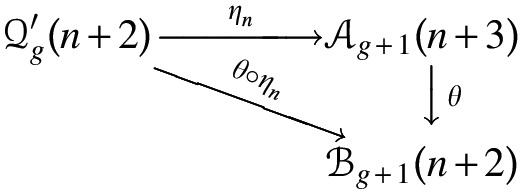
Theorem 4.2.
We have the following commutative diagram of bijections:

Proof. Since any 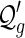 -diagram has a unique number of arcs, it suffices to specify the bijections ηn.
-diagram has a unique number of arcs, it suffices to specify the bijections ηn.
An 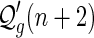 -element can be denoted by
-element can be denoted by
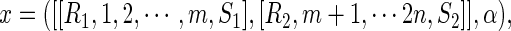 |
having the rainbows (R1, S1), (R2, S2).
We define the mapping ηn as follows:
• first we glue the two backbones into
 |
• secondly we add a new rainbow,
• thirdly we relabel the vertices.
This produces a unique backbone
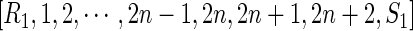 |
and transforms the two rainbows into the new arcs
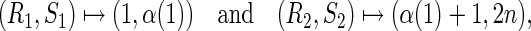 |
respectively. Accordingly, ηn(x) is an A-shape having (n + 3) edges (Fig. 15).
FIG. 15.

The mapping η.
The mapping ηn eliminates one backbone, that is, b′ = b − 1; generates a γ3-boundary component merging the two original rainbow-boundaries and adds a new rainbow boundary, that is, r′ = r; and adds one edge, that is, n′ = n + 3. In view of 2 − 2g − r = 2 − (n + 2) we obtain
 |
which proves that 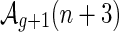 .
.
We next construct 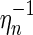 as follows: Consider an A-shape
as follows: Consider an A-shape 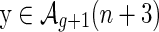 , then
, then
• remove the rainbow,
• cut the backbone between α(1) and α(1) + 1, and
• relabel the two respective backbones.
By construction, the edges (1, α(1)), (α(1) + 1, 2n) become the rainbows of the new backbones. The mapping 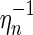 reverses ηn, and our above accounting of backbones, boundary components, and edges applies here. Thus
reverses ηn, and our above accounting of backbones, boundary components, and edges applies here. Thus 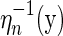 is a two-backbone diagram of genus g having n + 2 edges (Fig. 15). ■
is a two-backbone diagram of genus g having n + 2 edges (Fig. 15). ■
Corollary 4.3.
Let
 be a shape over two backbones containing ℓ-multiloops, then
be a shape over two backbones containing ℓ-multiloops, then
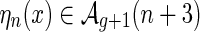 is an A-shape over one backbone having ℓ + 1 multiloops.
is an A-shape over one backbone having ℓ + 1 multiloops.
Proof. The map ηn merges two rainbow-boundary components of x and the new rainbow into a multiloop of length 3 (Fig. 15). ■
A first application of Theorem 4.2 is a uniform generation algorithm for shapes over two backbones of fixed topological genus g. We show the pseudocode in Algorithm 1.
Algorithm 1:
Uniform generation of shapes over two backbones
| 1: | UniformBi-shape (TargetGenus) |
| 2: | while 1 do |
| 3: | 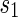 ← UnifromShape(TargetGenus + 1) ← UnifromShape(TargetGenus + 1) |
| 4: | if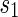 is type Athen is type Athen
|
| 5: | 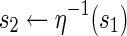
|
| 6: | else |
| 7: | 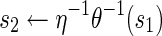
|
| 8: | end if |
| 9: | ifConnection (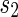 ) then ) then
|
| 10: | return
|
| 11: | end if |
| 12: | end while |
Corollary 4.4.
Algorithm 1 generates two-backbone shapes of genus g uniformly.
Proof. UniformShape (Huang and Reidys, 2014) generates one-backbone shape uniformly and any two-backbone shape corresponds to either an A-shape via η or a B-shape via 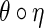 . Since A- and B-shapes are generated uniformly, any two-backbone shape is generated uniformly with multiplicity two. ■
. Since A- and B-shapes are generated uniformly, any two-backbone shape is generated uniformly with multiplicity two. ■
Let 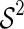 denote the set of pairs of disconnected shapes whose sum of genera equals g and let
denote the set of pairs of disconnected shapes whose sum of genera equals g and let 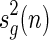 denote the number of these shapes having n arcs. Then
denote the number of these shapes having n arcs. Then 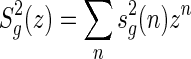 satisfies
satisfies 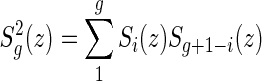 .
.
Theorem 4.5.
The polynomial of shapes of genus g over two backbones,
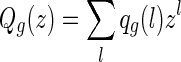 |
, is given by
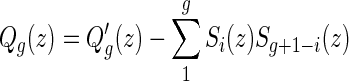 , where
, where
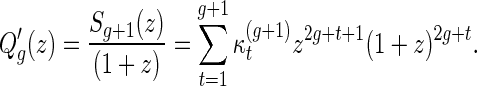 |
Proof. Each 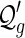 -diagram is a
-diagram is a 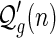 -diagram for a unique n. As such we have
-diagram for a unique n. As such we have
Suppose the generating function of A- and B-shapes is 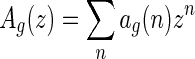 and
and 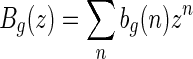 , respectively. From the bijection
, respectively. From the bijection 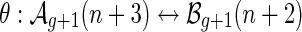 , we obtain bg+1(n + 2) = ag+1(n + 3). Then Sg+1(z) = Ag+1(z) + Bg+1(z) implies Sg+1(z) = (1 + 1/z)Ag+1(z), or equivalently,
, we obtain bg+1(n + 2) = ag+1(n + 3). Then Sg+1(z) = Ag+1(z) + Bg+1(z) implies Sg+1(z) = (1 + 1/z)Ag+1(z), or equivalently,  . By the bijection η, the generalized two-backbone shape
. By the bijection η, the generalized two-backbone shape 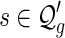 has one arc less than
has one arc less than 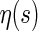 , which implies
, which implies
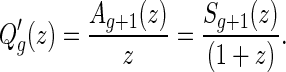 |
Subtracting the set of disconnected two-backbone shapes, 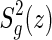 , the result follows. ■
, the result follows. ■
For genus g = 0, 1, 2, we accordingly have
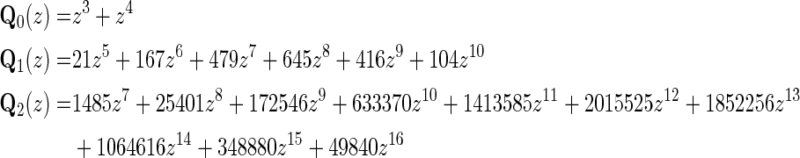 |
5. Fibers
In the previous section, we computed the shape polynomials of shapes over two backbones of fixed topological genus. Their coefficients can be recursively determined and are directly related to the coefficients of polynomials of shapes over one backbone.
Furthermore, Theorem 4.2 implies a linear time sampling algorithm for such two-backbone shapes of genus g. By means of their preimages, shapes induce a natural partition of RNA complexes, and here we shall study the sets of RNA complexes having a fixed shape, 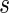 , to which we refer to as the fiber of
, to which we refer to as the fiber of 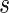 .
.
Given a two-backbone shape having l arcs and genus g, 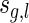 , let
, let 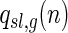 be the number of two-backbone matchings of genus g having the shape
be the number of two-backbone matchings of genus g having the shape 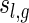 .
.
Theorem 5.1.
The generating function of matchings of genus g having shape
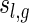 is given by
is given by
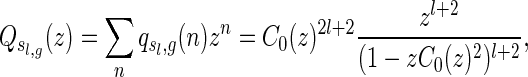 |
where
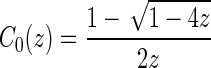 . In particular, the number of two-backbone structures of length n having genus g and shape
. In particular, the number of two-backbone structures of length n having genus g and shape
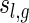 depends only on l and
depends only on l and
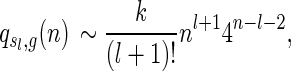 |
where k is some positive constant.
Proof. By the following steps, we can inflate an RNA-complex from a shape (Fig. 16).
FIG. 16.
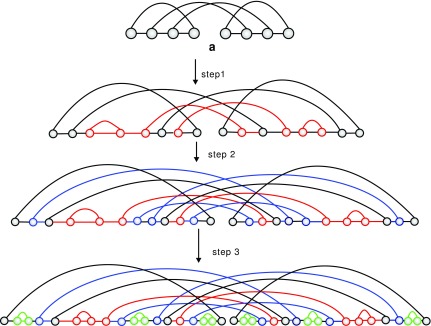
(a) A shape of genus 1 with 4 arcs; step 1: inflate each arc to a sequence of induced arcs (red); step 2: inflate each exterior arc to a stack (blue); step 3: insert a 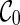 -matching into the σ-intervals (green).
-matching into the σ-intervals (green).
Step 1: We inflate each arc in 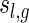 into a sequence of induced arcs; an induced arc
into a sequence of induced arcs; an induced arc  is an exterior arc together with at least one nontrivial genus 0 matching in either one or both P-intervals. Clearly, we have N(z) = z(2(C0(z) − 1) + (C0(z) − 1)2) = z(C0(z)2 − 1). Furthermore, we inflate the arc into a sequence
is an exterior arc together with at least one nontrivial genus 0 matching in either one or both P-intervals. Clearly, we have N(z) = z(2(C0(z) − 1) + (C0(z) − 1)2) = z(C0(z)2 − 1). Furthermore, we inflate the arc into a sequence  of induced arcs
of induced arcs 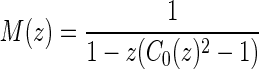 . Inflating all l + 2 arcs (including the two rainbows) into a sequence of induced arcs leads to
. Inflating all l + 2 arcs (including the two rainbows) into a sequence of induced arcs leads to
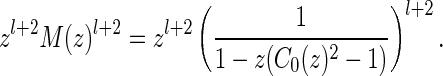 |
Denote the matching after this step by x1.
Step 2: We inflate each arc in x1 into a stack. The corresponding generating function is
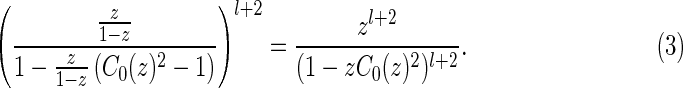 |
Step 3: We insert a  matching into the respective (2l + 2) σ-intervals of
matching into the respective (2l + 2) σ-intervals of 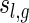 . The corresponding generating function is C0(z)2l+2.
. The corresponding generating function is C0(z)2l+2.
Combining the above three steps, we derive
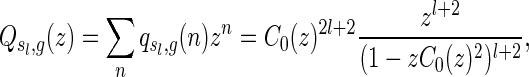 |
where 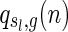 denotes the number of genus g matchings generated from
denotes the number of genus g matchings generated from 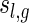 .
.
The generating function has a unique, dominant singularity ρ = 1/4 with multiplicity l + 2. Standard singularity analysis (Flajolet and Sedgewick, 2009) implies
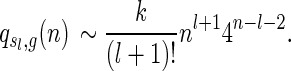 |
■
Corollary 5.2.
The generating function Wg(z) of two-backbone matchings of genus g is given by
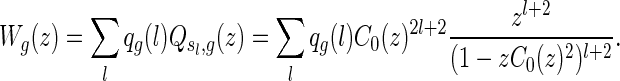 |
In particular, we have 
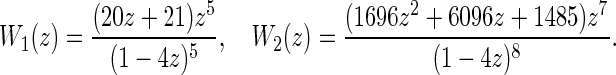 |
We conclude this section by discussing loops in shape-fibers. By construction, there are only multiloops and pseudoknot-loops in a shape. We observe that the lengths of the original shape-loops increase in structures of the shape-fiber. Structures of the shape-fiber exhibit, in addition, hairpin loops, interior loops, and two types of multiloops (Fig. 17).
FIG. 17.
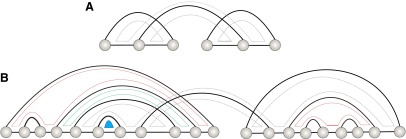
A shape with a distinguished loop (A). Inflation generates hairpin loops (blue), interior loops (green), and two types of nonshape multiloops (red) (B). The length of the distinguished shape-loop increased by two.
6. Discussion
In this article we study shapes of RNA complexes. We show that these shapes are directly related to shapes of RNA structures of increased topological genus. More precisely, we show in Lemma 4.1 that there is a bipartition of RNA-shapes into A-shapes and B-shapes. Furthermore, A- and B-shapes are in one-to-one correspondence. We establish in Theorem 4.2 that each respective type is in one-to-one correspondence to shapes of RNA complexes. These relations have various implications.
First, Lemma 3.1 guarantees that there are only finitely many such shapes. This leads to the shape polynomials for shapes of fixed topological genus g. The above correspondences reduce the computation of the coefficients of these polynomials for shapes of RNA complexes to those of shapes of RNA structures. For the latter, Proposition 3.3 gives a simple two-term recursion, which allows us to obtain any such polynomials for shapes of structures and complexes of fixed topological genus in constant time.
Secondly we obtain a sampling algorithm, Algorithm 1, for shapes of RNA complexes that have linear time complexity. Algorithm 1 and the sampling algorithm of RNA shapes are freely available online. This algorithm provides us with a plethora of statistics for shapes of RNA complexes of fixed topological genus. To illustrate local and global uniformity, we display in Figure 18 the multiplicities of shapes of genus 1. Here by local uniformity we mean that we can uniformly sample shapes of RNA complexes with a fixed number of arcs.
FIG. 18.
Global and local sampling of shapes of RNA complexes of fixed topological genus: N = 5 × 105 shapes of genus 1 were generated, and we display their multiplicities (dots) together with the binomial coefficients that are observed from uniform sampling (A). Local sampling: we generate N = 5 × 105 shapes of genus 1 with Seven arcs (B).
Lemma 3.1 shows that there are only finitely many shapes of RNA complexes. Hence the shape polynomial determines their numbers filtered by the number of arcs. This means that we can extract a finite observable from interaction structures that captures their topological core.
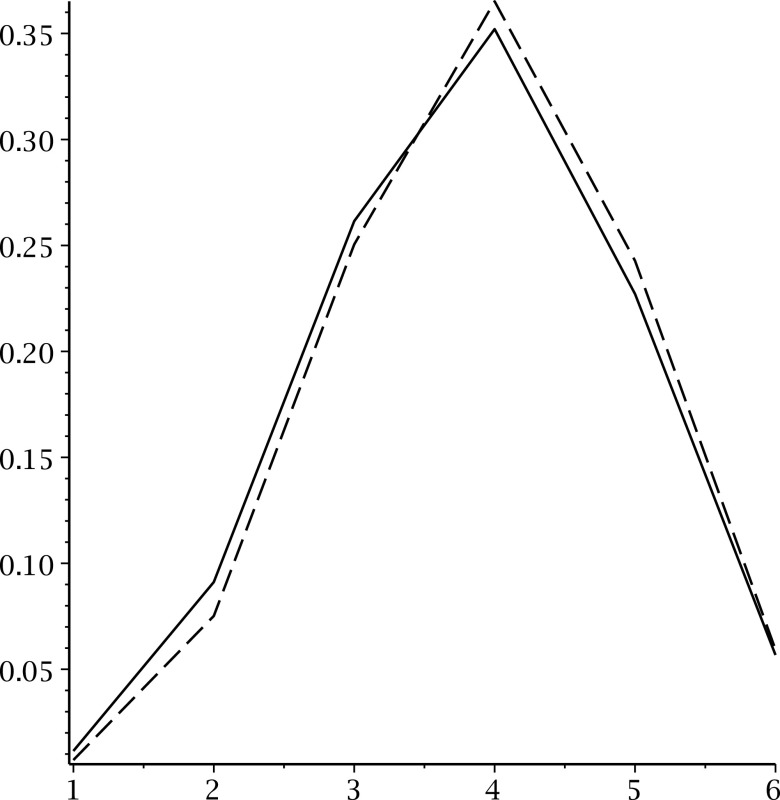
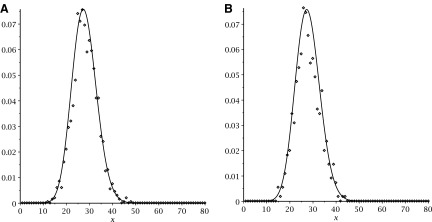
Let us calibrate this information by inspecting what happens when we sample uniformly RNA complexes of fixed topological genus (Fu et al., 2013). We uniformly sample RNA complexes having genus 1 and record the frequencies of their associated shapes. We observe that the distribution of shapes of different lengths equals the distribution obtained by normalizing the coefficients of the shape polynomial (Fig. 19).
FIG. 19.
Uniform sampling of RNA complexes of genus 1 with length 40, 80, 100, 150, 200, and (5 × 105). The solid curve displays the distribution induced by the coefficients of the shape polynomial, while the dashed curve displays distribution obtained from the sampling. Displayed is the average of the coefficients obtained from sampling the above different lengths.
Accordingly, the shape polynomial represents precisely the uniform case. As a result we can now compute the shapes of databases of RNA complexes and derive empirical coefficients (distributions) and hence extract finite information from databases reflecting the topological properties of the biological complexes.
Along these lines we study the shapes of biological RNA complexes obtained from (Richter and Backofen, 2012). Because the data set contained only exterior arcs, we derived only one shape of genus zero (Fig. 20).
FIG. 20.
The shape extracted from the biological RNA complexes (Richter and Backofen, 2012).
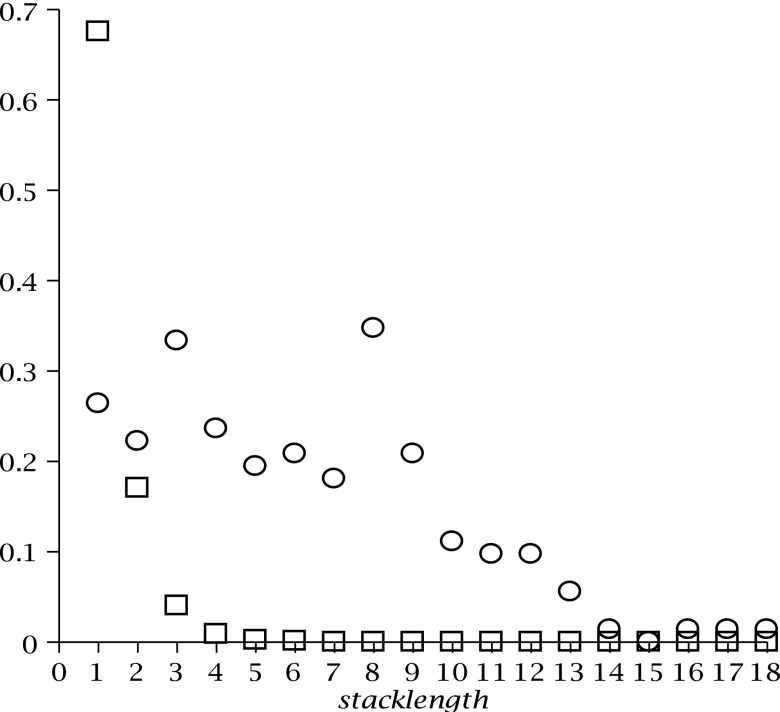
We accordingly compare the distribution of the exterior stack lengths of biological with that of uniformly sampled RNA complexes (Fig. 21).
FIG. 21.
The distribution of the lengths of exterior stacks in uniformly sampled structures having the shape in Figure 20 (box); the distribution of the length of exterior stacks in the biological RNA complexes obtained from Richter and Backofen (2012) (circle).
We finally study loops in shapes of RNA complexes. By construction, such loops are multiloops, except for the two rainbow loops. We uniformly generate 5 × 105 shapes of RNA complexes from genus 0 to 5 and display the average number of loops (Fig. 22). The data suggest a central limit theorem for the average number of loops since their mean scales linearly with topological genus.
FIG. 22.

The distribution of the average number of loops in the shapes of different genus: (A) the distribution of the α-loops (loops contained in one backbone) and (B) the distribution of the β-loops (loops over two backbones).
Acknowledgments
We wish to thank Fenix W.D. Huang and Thomas J.X. Li for discussions. This work is funded by the Future and Emerging Technologies (FET) programme of the European Commission within the Seventh Framework Programme (FP7), under the FET-Proactive grant agreement TOPDRIM, FP7-ICT-318121.
Author Disclosure Statement
No competing financial interests exist.
References
- Andersen J.E., Huang F.W.D., Penner R.C., and Reidys C.M.2012. Topology of RNA-RNA interaction structures. J. Comp. Biol. 19, 928–943 [DOI] [PubMed] [Google Scholar]
- Andersen J.E., Penner R.C., Reidys C.M., and Waterman M.S.2011. Topological classification and enumeration of RNA structures by genus. J. Math. Biol. 1–18 [DOI] [PubMed] [Google Scholar]
- Bachellerie J.-P., Cavaillé J., and Hüttenhofer A.2002. The expanding snoRNA world. Biochimie 84, 775–790 [DOI] [PubMed] [Google Scholar]
- Banerjee D., and Slack F.2002. Control of developmental timing by small temporal RNAs: a paradigm for RNA–mediated regulation of gene expression. Bioessays 24, 119–129 [DOI] [PubMed] [Google Scholar]
- Benne R.1989. RNA–editing in trypanosome mitochondria. Biochimica et Biophysica Acta (BBA)-Gene Structure and Expression 1007, 131–139 [DOI] [PubMed] [Google Scholar]
- Bon M., Vernizzi G., Orland H., and Zee A.2008. Topological classification of RNA structures. J. Mol. Biol. 379, 900–911 [DOI] [PubMed] [Google Scholar]
- Chapuy G.2011. A new combinatorial identity for unicellular maps, via a direct bijective approach. Adv. Appl. Math. 47, 874–893 [Google Scholar]
- Chekhov L.1997. Matrix model tools and geometry of moduli spaces. Acta Applicandae Mathematica 48, 33–90 [Google Scholar]
- Flajolet P., and Sedgewick R.2009. Analytic Combinatorics. Cambridge University Press, Cambridge, MA [Google Scholar]
- Fu B.M.M., Han H.S.W., and Reidys C.M.2013. On the RNA-RNA interaction structures of fixed topological genus. arXiv:1311.0684v2 [DOI] [PubMed]
- Harer J., and Zagier D.1986. The euler characteristic of the moduli space of curves. Invent. Math. 85, 457–486 [Google Scholar]
- Heffter L.1891. Über das Problem der Nachbagebiete. Math. Ann. 38, 477–508 [Google Scholar]
- Huang F.W.D., and Reidys C.M.2014. Shapes of topological RNA structures. arXiv:1403.2908 [DOI] [PubMed]
- Kleitman D.1970. Proportions of irreducible diagrams. Studies in Appl. Math. 49, 297–299 [Google Scholar]
- Kugel J.F., and Goodrich J.A.2007. An RNA transcriptional regulator templates its own regulatory RNA. Nature Chemical Biology 3, 89–90 [DOI] [PubMed] [Google Scholar]
- Lyngsø R.B., and Pedersen C.N.2000. Pseudoknots in RNA secondary structures. InProceedings of the fourth annual international conference on Computational Molecular Biology ACM, pp. 201–209 [Google Scholar]
- Massey W.S.1967. Algebraic Topology: An Introduction. Springer-Verlag, New York [Google Scholar]
- McManus M.T., and Sharp PA.2002. Gene silencing in mammals by small interfering RNAs. Nature Reviews Genetics 3, 737–747 [DOI] [PubMed] [Google Scholar]
- Narberhaus F., and Vogel J.2007. Sensory and regulatory RNAs in prokaryotes: A new german research focus. RNA Biology 4, 160–164 [DOI] [PubMed] [Google Scholar]
- Nussinov R., Pieczenik G., Griggs J.R., and Kleitman D.J.1978. Algorithms for loop matchings. SIAM Journal on Applied Mathematics 35, 68–82 [Google Scholar]
- Orland H., and Zee A.2002. RNA folding and large N matrix theory. Nuclear Physics B 620, 456–476 [Google Scholar]
- Penner R.C.2004. Cell decomposition and compactification of Riemann's moduli space in decorated Teichmüller theory, 263–301. InTongring N., and Penner R.C., ed. Woods Hole Mathematics-Perspectives in Math and Physics. World Scientific, Singapore [Google Scholar]
- Penner R.C., Knudsen M., Wiuf C., and Andersen J.E.2010. Fatgraph models of proteins. Comm. Pure Appl. Math. 63, 1249–1297 [Google Scholar]
- Penner R.C., and Waterman M.S.1993. Spaces of RNA secondary structures. Advances in Mathematics 101, 31–49 [Google Scholar]
- Reidys C.M., Huang F., Andersen J.E., et al. 2011. Topology and prediction of RNA pseudoknots. Bioinformatics 27, 1076–1085 [DOI] [PubMed] [Google Scholar]
- Reidys C.M., Wang R.R., and Zhao A.Y.Y.2010. Modular, k-noncrossing diagrams. The Electronic Journal of Combinatorics 17, 1 [Google Scholar]
- Richter A.S., and Backofen R.2012. Accessibility and conservation: General features of bacterial small RNA–mRNA interactions? RNA Biology 9, 954–965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivas E., and Eddy S.R.1999. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J. Mol. Biol. 285, 2053–2068 [DOI] [PubMed] [Google Scholar]
- Vernizzi G., and Orland H.2005. Large–N random matrices for RNA folding. Acta PhysicA PolonicA Series B 36, 2821 [Google Scholar]
- Vernizzi G., Orland H., and Zee A.2005. Enumeration of RNA structures by matrix models. Physical Review Letters 94, 168103. [DOI] [PubMed] [Google Scholar]
- Waterman M.S.1978a. Combinatorics of RNA hairpins and cloverleaves. Studies Appl. Math 60, 91–96 [Google Scholar]
- Waterman M.S.1978b. Secondary structure of single–stranded nucleic acids. Adv. Math. Suppl. Studies 1, 167–212 [Google Scholar]