FRACTAL ANALYSIS OF BLOOD-TISSUE EXCHANGE KINETICS

INTRODUCTION

Having a “fractal nature” implies that one or more features of a system or phenomenon appear to have similar characteristics when examined over a range scale. Mathematical fractals are generated by recursive expressions wherein each generation is derived from the preceding in a specific way, a precise deterministic fashion or a looser probabilistic fashion.

Several elements of the processes of delivery by flow and transmembrane transport of substrates in an organ have been observed to follow fractal kinetics. The anatomy of the vascular tree, at least the length, diameters and pressures, can be roughly described as fractals (Suwa et al, 1963, 1971). Regional flow heterogeneity in the myocardium is distinctly fractal having the same shape of distribution at increasingly fine sample volumes, and spreading with a fractal dimension of 1.2 to 1.3 (Bassingthwaighte, 1987). The flow heterogeneity may be mainly stochastic, and anatomic geometry more deterministic.

A specific application of the fractal approach is in the interpretation of indicator dilution curves for estimating membrane transport. This is done by projecting the heterogeneity of local flows to the size of the exchange unit, and using this degree of heterogeneity in the analysis of multi-capillary organ models. The fractal approach removes substantial bias in the estimates of the permeability-surface area products for the capillary and cell membranes, leaving relatively small random error.

Perhaps even more important in microcirculatory events is the fluctuating nature of the intravascular velocities and diameters. These are not strongly influenced by the pulsatile arterial pressure, but operate on a more local basis. The physiological basis for the fractal behavior needs to be worked out.

SPATIAL HETEROGENEITY OF REGIONAL MYOCARDIAL BLOOD FLOWS

Microsphere deposition has long been the method of choice for estimating regional flows, both at the organ level and regionally within organs. In the heart, the flow heterogeneity has been found to be large (Bassingthwaighte et al, 1972, Yipintsoi et al, 1973; Archie et al, 1974, King et al, 1985), but there was a nagging suspicion amongst some critics that this was due in a major way to the technique itself. King et al (1985) demonstrated that the regional flow profiles in awake baboons remained essentially constant for many hours. The stability of the distributions of microsphere depositions could not have occurred if the variance was due simply to methodologic scatter. Indeed the stability was such that any region that had a local flow greater than 150% of the mean flow for the heart at one moment, did not, on any of five other occasions over 6 to 21 hours, have an observed flow as low as the mean flow. Likewise, any region having a flow of 50% or less of the average for the heart, did not increase its flow to the average on any of five other observations times. Thus, even if microspheres were giving erroneous values, they certainly gave reproducible values.

In these hearts the total variance divided by the square of the mean flow was about 0.11. The microsphere variance was observed to be 0.005 in 200 mg pieces of about 40 g baboon hearts. King and Bassingthwaighte (unpublished) found that the temporal fluctuation was slightly more, 0.01 of the 0.11. Together methodologic noise and temporal fluctuations accounted for 0.015 of the 0.11. The major fraction of the remaining variance, 0.085 of 0.11 or 77%, was due to a stable pattern of regional flows.

Interestingly, there is no consistency in the spatial patterns from one heart to another. It appears that the high and low flow regions are disordered, but as we shall see, using fractals, they are not random.

Is the stable pattern due to reproducible bias in the microsphere technique

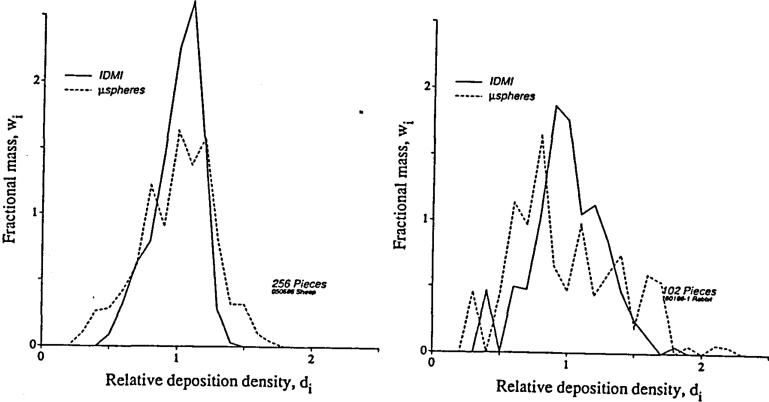
This could not be tested prior to the development of a new reference technique for the estimation of local flows, a “molecular microsphere” which travels dissolved in plasma and is not subject to rheologic biases at branch points in the arterial tree. The substance is iodinated desmethylimipramine (IDMI) (Little et al, 1983, 1986) which is over 99% extracted during single passage through the hearts of rabbits and sheep, and so is delivered and deposited in tissue (by binding) in proportion to local flow. Direct comparisons between microspheres and IDMI injected simultaneously were made in rabbits (Bassingthwaighte, Malone et al, 1987) and in sheep (unpublished). The distributions were very similar; in Figure 1 are shown two of the comparisons where the greatest differences were observed. There was a small systematic bias: microspheres were deposited preferentially in high flow regions and therefore were in lower concentrations than IDMI in low flow regions. This bias broadens their distributions a bit compared to IDMI, as the figure shows.

Figure 1.

Probability density functions of regional left ventricular blood flows relative to the mean flow in the left ventricles of hearts of open chested rabbits and sheep. Microspheres and IDMI were injected simultaneously into the left atrium. Rabbit (right): the relative dispersions (SD/mean) were 41.1% and 24.9% for microspheres and IDMI. Sheep (left): the relative dispersions (SD/mean) were 27.6% and 17.0% for micro-spheres and IDMI.

Despite the scatter and distinct bias in the microsphere-IDMI relationship, the probability density functions of microsphere depositions are not much broader than those of the IDMI distributions. The conclusion is that, although there are systematic deviations from strict accordance with local flows, these are not so marked as to cause gross overestimation of the heterogeneity of flows normally present in moderately large regions. Nevertheless, the errors are systematic and in the low flow regions are large enough that caution (and maybe corrections) should be used in interpretation. Our evidence in rabbit and sheep hearts (Bassingthwaighte, Malone et al, 1987, for rabbits) affirms what would be predicted from the theory of Fung (1973), Yen and Fung (1978), and the hydraulics experiments of Chien et al (1985), namely that one would expect a preferential deposition of 15 micron diameter microspheres into regions of higher than average flow and less deposition in low flow regions. This reinforces and explains better the results of Yipintsoi et al (1973) that suggested biasing effects of branching flow and microsphere distributions affected endo/epi gradients. The effect would be greater in larger hearts due to the larger transmural pressure gradients during systole.

Systematic Biases Due to Heterogeneity

One of the effects of flow heterogeneity is to cause dispersion of tracer that passes through the organ. The organ acts as a low pass filter, reducing the amplitude of any fluctuations in concentrations at the inflow so that they are slurred before reaching the output. The sharpness of the peak in the outflow dilution curve is reduced compared to the inflow peak. The heterogeneity, a combination of a heterogeneity of vascular velocities and a heterogeneity of vascular path lengths, can be modeled in an infinite number of fashions. None can be explicitly proven to be the correct representation unless the model represents a known, precisely described portion of a vascular network. Several simple networks were described by Bassingthwaighte and Goresky (1984), for substances of low permeability and of low intratissue diffusibility; many models will give fairly similar results because the transfer function of the organ will be dominated by the intravascular transport. There is quite likely a fractal basis for the dispersion of the intravascular indicator (Bassingthwaighte, 1987). [For highly diffusible indicators the story is different because whenever there is diffusional exchange between pathways, the transport function has a shape governed by both flow and diffusion; substances of differing diffusibility will have differing proportions of the entering material traverse different pathways. Diffusional shunting between entering and draining vessels is one mechanism producing distortion of the transport functions (Bassingthwaighte, Yipintsoi and Knopp, 1984).]

Systematic underestimates of capillary PS with heterogeneity

The traditional Crone-Renkin expression, PS = F ln(1-E), where PS is capillary permeability-surface area product, F is flow and E is maximum extraction of tracer during transorgan passage, is a good expression when flows are everywhere uniform and there is no tracer reflux from tissue. But is there is intraorgan heterogeneity of flows, the mean extraction E is underestimated because the reflux from the high flow regions masks the higher extractions in the low flow regions, and PS is underestimated systematically. The error is large, 35 to 60% when the relative dispersion of flows is 30 to 50%. A method for avoiding the error is to use multicapillary models and a fractal-based estimate of the heterogeneity.

A Fractal Analysis of Spatial Heterogeneity

In estimating regional flows from the local concentration of a deposited tracer, if one chops the organ into large pieces, one gets a low estimate of the relative dispersion of flows. Cutting the tissue more finely reveals broader heterogeneity. For the heart the relationship reveals similarity of a fractal type, namely the relative dispersion is a fractal function of pieces size:

$$\mathrm{RD}\left(\mathrm{w}\right)=\mathrm{RD}(\mathrm{w}=1\mathrm{g}){\mathrm{w}}^{1-\mathrm{D}}$$ (1)

where RD(w) is the relative dispersion (the standard deviation of the distribution divided by the mean) for a particular piece size, w, RD(w=1g) is the RD at an arbitrary reference point for 1 g pieces, and D is the fractal dimension. For baboon and sheep hearts RD(w=1g) is about 18% and the fractal D is about 1.2 to 1.3. The value of D would be 2.0 if the heterogeneity were random as it is for Brownian motion or molecular diffusion. The value of 1.2 suggests an ordered arrangement with continuity in flows in adjacent regions.

Using the fractal D to estimate capillary PS

The estimation of RD at the level of the functional microvascular unit size involves an extrapolation to a smaller size of tissue piece than one in which flow can be measured by standard techniques even using the molecular microsphere. If the fractal relationship holds down to 1 mg pieces, the unit size estimated by Bassingthwaighte, Yipintsoi and Harvey (1974), then RD(0.001g) = 18%(0.001)⁻² = 72%. This large degree of heterogeneity of flows would then be used in a multicapillary model, fitting the tracer dilution curves to provide the correct overall transorgan extraction, the E in the Crone-Renkin expression.

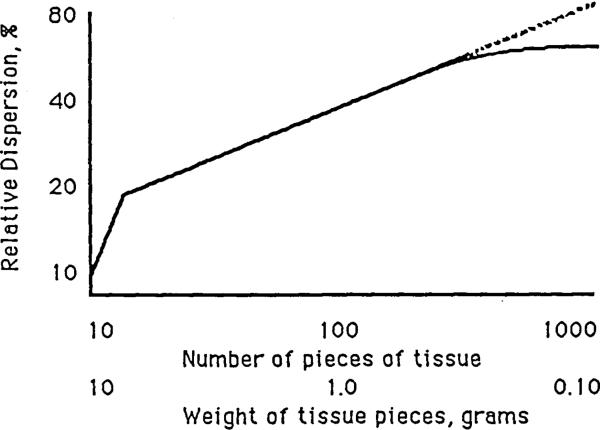
There is some chance that this approach would overestimate the heterogeneity: it is likely that flows in neighboring microvascular units are similar and that the degree of association falls off with distance. This means that instead of the infinitely fractal relationship defined by Equation 1, the relationship flattens or curves toward a plateau at small pieces as suggested by Figure 2. Rigaut (1983) in looking at the lengths of contours of pulmonary alveolar boundaries observed a convex upward curvature toward a plateau on the plot of the logarithm of total length versus the “stride length”, the length of the measuring calipers. The relationship was fractal, that is, linear on the log-log plot, at large caliper lengths, but fell below the fractal relationship at short caliper lengths, giving a concave downward curvature. This is natural, since the maximum radius of curvature of a lipid bilayer is about 30 nm, and irregularity in the contour must diminish to that of a smooth contour at caliper lengths, ε, of this order. Rigaut's empirical equation for the boundary length L, at each ε, is:

$$\mathrm{L}\left(\epsilon \right)=\frac{{\mathrm{L}}_{\text{max}}}{1+{\alpha }^{\mathrm{c}}{\epsilon }^{\mathrm{c}}}$$ (2)

Figure 2.

Deviation from a fractal relationship occurs when there is a tendency for small regions to have uniform flow.

This expression gives curvature, plateauing at L_max at small ε, and curving asymptotically toward a downward sloping straight line at large ε. The scalar α and the exponent c are not readily interpretable except in the extreme case where L_max → ∞, α^c → ∞, and c → D–1, which is a normal fractal relationship. However, Rigaut's equation is an excellent provocation to develop expressions which express directly the fractal D and the rate of convergence to the non fractal plateau. At this point, how to handle such pseudofractal relationships in a physically or physiologically meaningful mathematical fashion is not clear.

TEMPORAL FLUCTUATIONS IN INTRAVASCULAR VELOCITIES AND FLOWS

Microscopic observations of intracapillary and intra-arteriolar velocities can now be made using modern techniques of image acquisition and analysis, as by Slaaf et al (1986, 1987), and Kislyakov et al (1987). If the vessels were rigid pipes, then the velocities would be proportional to aortic pressure, but all of such velocity observations show fluctuations which are different in form from aortic pressure. If local arteriolar flows were totally unrelated to the aortic driving pressure this would be surprising, especially for oscillations at cardiac frequency, but autoregulatory phenomena certainly inhibit flow changes at lower frequencies (Baer et al, 1984).

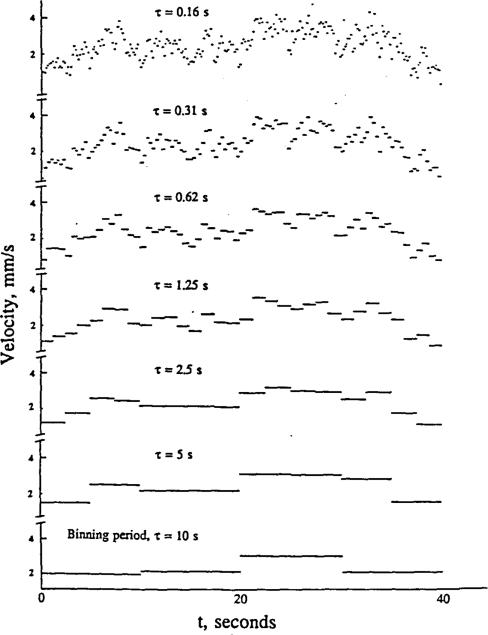
How to characterize fluctuations has been a problem. Autocorrelation techniques show a dependence on binning duration, i.e. on the length of intervals over which flow is averaged. Frequency transforms such as finite Fourier series representation have an appropriate general form, except that they inevitably alias the high frequency information and do not provide a good description allowing comparison of one situation to another. A fractal approach has the virtue of encompassing a wide range of frequencies, unfettered by the artifact of frequency foldover (aliasing). The key is to examine the data, not with a single sampling frequency, but with a number of binning durations, τ, extending over a wide range. The idea is expressed in Figure 3; the measurement of velocity is the average over an interval, τ. The topmost “curve” represents data binned at 0.16 second intervals. Binning over larger τ's reduces the excursions. Taking the relative dispersions at each τ is a simple way of summarizing such data. We observe, on data taken from the published figures of Kislyakov et al (1987) that a

$$\mathrm{RD}\left(\tau \right)=\mathrm{RD}(\tau =1){\tau }^{1-{\mathrm{D}}_{\tau }}$$

Figure 3.

Diagrammatic representation of data showing temporal fluctuations. The raw “data” of the top panel are then binned over successively longer times τ for the panels below. Lower resolution detection, e.g. a filtered signal or a long time constant in the transduction system, results in underestimation of the excursions. As with the spatial fractals, projection to higher frequencies may be justified.

where D_τ is the fractal dimension for the temporal fluctuations. The data were velocities in pial vessels of 6 or 7 microns diameter with τ in seconds. The function RD(τ) = 11.2 τ^-0.37 fitted well, the correlation coefficient being r = -0.995, over the range of τ's from 0.14 to 2.8 seconds.

Velocities cannot be infinitely fractal. High frequency fluctuations require high forces (energy, work) to produce the accelerations required to change velocity. In other words, the inertia of a moving column of blood is such that velocity changes cannot be instantaneous. The corollary is that the fractal relationship must at some small values of τ show a “concave downward” pattern. This is completely analogous to the plateauing in the spatial domain.

DISCUSSION

Mandelbrot's writings have fostered much development in the applications of fractals to describing physical features. Many interesting ideas are presented in his books (e.g. 1983). Peitgen and Richter (1986) give a nice introduction to the mathematics and some wonderful pictures. Applications to dynamic phenomena are anticipated by the efforts to describe chaos, on which Holden has edited a very useful book (Holden, 1986). Transitions from laminar to disturbed or turbulent flow may be described as mathematical predictions of instability or non-predictable behavior (Devaney, 1987).

At the membrane level, time-dependent ionic channel fluctuations have been described by Liebovitch et al (1987), in terms of a single fractal dimension replacing more cumbersome traditional descriptions. At a multicellular level, Glass et al (in Holden's book, 1986) describe chaotic cardiac rhythms, a natural evolution from the old clinical description of atrial fibrillation as an irregularly irregular rhythm.

Our approach to describing heterogeneity of regional blood flows by fractals in space and time may be novel in away. The simplified description of “heterogeneity” by the relative dispersion or coefficient of variation is not, but the 2-parameter description of heterogeneity (RD[w=1] and D_w or RD[τ=1] and Dτ) is apparently new. It is clearly useful since such a descriptor allows comparisons of data between different laboratories to be made in a meaningful way. In the past a description of RD in regional flow might have differed from that in another lab only because the sample size, w, or the binning times, τ, differed. Now we can use two parameter descriptors, which should be comparable from lab to lab and independent of the particular w's to τ's chosen by an investigator.

CONCLUSION

Fractal approaches provide another analytical tool for examining biological phenomena. In some instances they will go beyond description to allow new insight. This transition has not yet been made very often in circulatory studies. The first applications have been to structure. Now the attempt is to examine dynamic situations as well.