Abstract
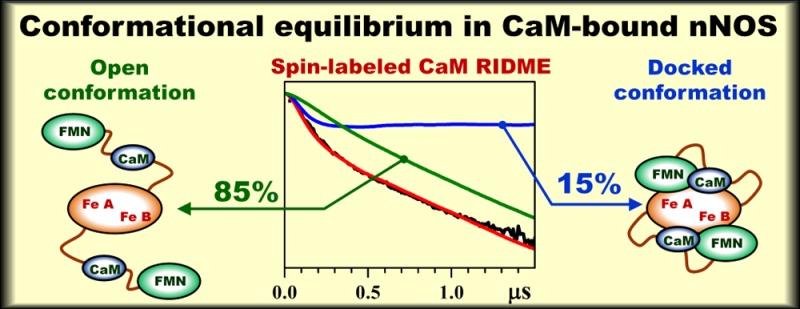
The binding of calmodulin (CaM) to neuronal nitric oxide synthase (nNOS) enables formation of the output state of nNOS for nitric oxide production. Essential to NOS function is the geometry and dynamics of CaM docking to the NOS oxygenase domain, but little is known about these details. In the present work, the domain docking in a CaM-bound oxygenase/FMN (oxyFMN) construct of nNOS was investigated using the relaxation-induced dipolar modulation enhancement (RIDME) technique, which is a pulsed electron paramagnetic resonance technique sensitive to the magnetic dipole interaction between the electron spins. A cysteine was introduced at position 110 of CaM, after which a nitroxide spin label was attached at the position. The RIDME study of the magnetic dipole interaction between the spin label and the ferric heme centers in the oxygenase domain of nNOS revealed that, with increasing [Ca2+], the concentration of nNOS·CaM complexes increases and reaches a maximum at [Ca2+]/[CaM] ≥ 4. The RIDME kinetics of CaM-bound nNOS represented monotonous decays without well-defined oscillations. The analysis of these kinetics based on the structural models for the open and docked states has shown that only about 15 ± 3% of the CaM-bound nNOS is in the docked state at any given time, while the remaining 85 ± 3% of the protein is in the open conformations characterized by a wide distribution of distances between the bound CaM and the oxygenase domain. The results of this investigation are consistent with a model that the Ca2+–CaM interaction causes CaM docking with the oxygenase domain. The low population of the docked state indicates that the CaM-controlled docking between the FMN and heme domains is highly dynamic.
Introduction
Mammalian nitric oxide synthase (NOS) is a homodimeric flavo-hemoprotein that catalyzes the oxidation of l-arginine to NO, with NADPH and O2 acting as cosubstrates.1 There are three NOS isoforms: endothelial, neuronal, and inducible (eNOS, nNOS, and iNOS, respectively). Each NOS subunit contains a C-terminal electron-supplying reductase domain with binding sites for NADPH (the electron source), FAD, and FMN and an N-terminal catalytic heme-containing oxygenase domain. The oxygenase and FMN domains are connected by a calmodulin (CaM) binding linker, which is tightly bound to CaM in iNOS at a basal calcium level, while CaM binding to nNOS and eNOS requires a significantly higher Ca2+ concentration.2
CaM is an indispensable control element in NOS function.2 The binding of CaM activates NO synthesis in eNOS and nNOS by (i) enabling the FMN domain transitions between its electron-accepting position (input state) and an electron-donating position (output state)3−10 and (ii) facilitating the proper docking of the FMN domain on to the oxygenase domain, which enables efficient FMN–heme interdomain electron transfer (IET).10−12 CaM is also important for proper alignment of the FMN and heme domains in iNOS.12,13
The CaM-dependent FMN–heme IET is essential for the delivery of electrons required for O2 activation in the heme domain and the subsequent NO synthesis by NOS. However, the mechanism of CaM activation is not well understood.14 The crystal structures are only available for truncated NOS domains, including the oxygenase domains of each of the NOS isoforms,15−17 rat nNOS reductase constructs,18,19 and CaM-bound human iNOS FMN domain,20 along with CaM bound to peptides corresponding to the CaM-binding region in eNOS,21 nNOS (PDB ID 2O60), and iNOS (PDB ID 3GOF). Although high-resolution X-ray crystallographic structures have been obtained for certain segments of nNOS and other NOS isoforms, the details of how the various tethered NOS domains interact with CaM and how CaM binding influences functionally important interactions among the domains are not known.
Herein we employed the pulsed electron paramagnetic resonance (EPR) relaxation-induced dipolar modulation enhancement (RIDME) technique22,23 to monitor the binding of spin-labeled CaM (SL CaM) to nNOS and to determine the position of the nitroxide spin label (SL) with respect to the heme centers of the dimeric oxygenase domain. Wild-type CaM does not contain cysteine amino acid residues, but a cysteine can be readily introduced at a selected CaM site by site-directed mutagenesis. In this work, to enable the spin-labeling, a cysteine was introduced at position 110. Recent work showed that this mutation has little effect on nNOS enzyme activation.24 In order to simplify the system, we used the bidomain nNOS oxyFMN construct, which contains the oxygenase and FMN domains, as well as the CaM binding region, but lacks the NADPH and FAD binding domains.25,26 This NOS construct is a valid model of the electron-donating (output) state of the FMN domain.25,27−29
Materials and Methods
Preparation of Spin-Labeled Calmodulin
Construction, purification, and spin-labeling of T110C mutant CaM are described in the Supporting Information. The spin-labeling efficiency and selectivity have been confirmed by tryptic digestion and mass spectrometry (Figure S1 in the Supporting Information).
Expression and Purification of Rat nNOS oxyFMN
The rat nNOS oxyFMN plasmid26 was cotransformed with CaM expression vector (p209) into Escherichia coli BL21(DE3) cells by electroporation. The transformed cells were grown at 37 °C in terrific broth in the presence of 100 μg/mL ampicillin and 34 μg/mL chloramphenicol. Protein expression was induced by adding induction cocktail (0.5 mM isopropyl β-d-thiogalactopyranoside, 0.4 mM δ-aminolevulinic acid, and a pinch of riboflavin) when the cell culture reached an optical density of 1.0 at 600 nm. After incubation at 25 °C for 40 h, the cells were harvested at 4 °C.
Cells were resuspended in the lysis buffer (pH 7.5) containing 50 mM Tris-HCl, 10% glycerol, 200 mM NaCl, 0.5 mM CaCl2, 5 mM β-mercaptoethanol, three complete protease inhibitor tablets (Roche), 10 μM H4B, and 0.5 mg/mL lysozyme. The cells were lysed using a digital sonicator. The lysate was centrifuged at 30 000 rpm for 40 min at 4 °C. The supernatant was then loaded onto a Co2+-chelating column (Talon metal affinity resin, Clontech) pre-equilibrated with five bed-volumes of equilibration buffer (50 mM Tris-HCl, 10% glycerol, 200 mM NaCl, 0.5 mM CaCl2, pH 7.5). The column was washed with ten bed-volumes of equilibration buffer containing 15 mM imidazole, and the contents were then eluted with a 15–150 mM imidazole gradient in the elution buffer (50 mM Tris-HCl, 10% glycerol, 200 mM NaCl, 0.5 mM CaCl2, pH 7.5). The eluted protein was pooled, concentrated, and dialyzed into the storage buffer (50 mM Tris-HCl, 10% glycerol, 200 mM NaCl, 1 mM DTT, 10 μM H4B, pH 7.5).
For preparation of the SL CaM-bound nNOS EPR samples, the coexpressed CaM was removed by dialysis against the storage buffer containing 2 mM EGTA. The molar concentration of the nNOS protein was determined on the basis of the heme content via difference spectra of the ferrous–CO adduct.30 The purified protein was aliquoted and stored at −80 °C.
Preparation of the EPR Samples
Chelex 100 iron form resin (Bio-Rad) was used to remove the background Ca2+ from the nanopure water for preparation of the calcium-free EPR buffer (50 mM Bis-Tris propane, 200 mM NaCl, 3 mM imidazole, 42% ethylene glycol, pH 7.4). Imidazole was added to convert the heme centers of the nNOS oxyFMN construct to the low-spin Fe(III) state. The spin-labeled T110C CaM and nNOS oxyFMN were concentrated and dialyzed into the EPR buffer and the EPR buffer containing 20 μM H4B, respectively. Solutions containing SL CaM and nNOS oxyFMN were gently mixed (final concentration 110 μM and 55 μM, respectively), and CaCl2 was then added to prepare solutions with final total Ca2+ concentrations of 0.22, 0.5, 1, 2, and 5 mM. About 40 μL of each solution was transferred into EPR tubes and rapidly frozen in a pentane and liquid nitrogen slurry.
EPR Measurements
The experiments have been performed on the homemade broad-band pulsed EPR spectrometer at the University of Arizona.31 The detailed experimental conditions are given in the figure captions.
Results and Discussion
General Structural Model
The overall structural model of this work is shown in Figure 1. According to this model, without Ca2+ present in solution, CaM does not form a complex with nNOS (panel A of Figure 1). As the Ca2+ concentration increases, CaM binds Ca2+ (up to four Ca2+ ions per CaM molecule), and Ca2+·CaM can now bind to the CaM binding region spanning residues 725–745 of the flexible tether connecting the oxygenase and FMN domains of nNOS (panels B and C in Figure 1).
Figure 1.
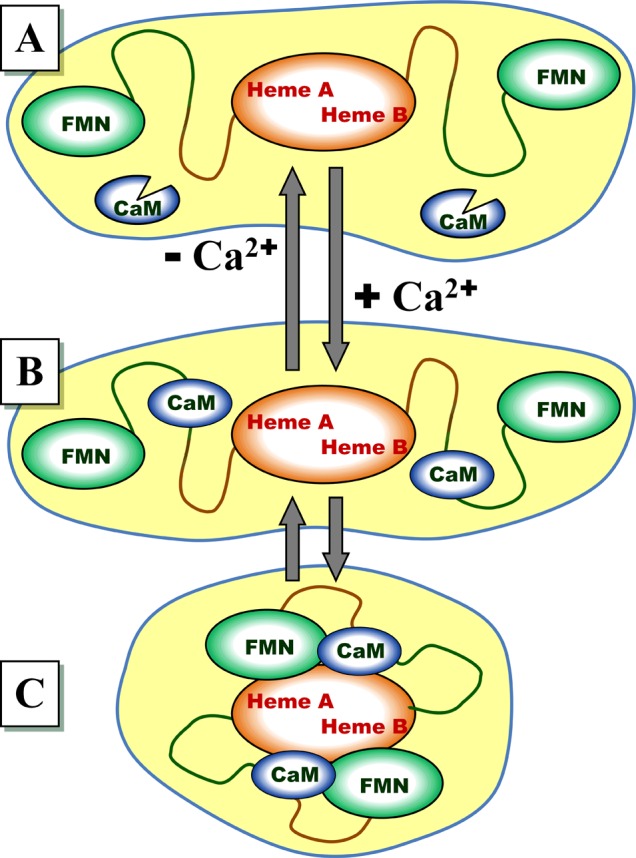
Model describing the effect of Ca2+ on the structural rearrangements in nNOS. (A) Without Ca2+ in solution, no CaM binding to nNOS occurs, and the docking complex between the FMN domain and the heme domain does not form. (B and C) When Ca2+ ions are present in solution (up to four Ca2+ ions per CaM molecule), CaM binds to the nNOS CaM-binding motif, which facilitates the formation of the IET-competent docking complex between the FMN and heme domains. The CaM-bound nNOS is in equilibrium between the structurally disordered open state (B) and the IET-capable docked state (C).
For the purposes of this work, we will distinguish two qualitatively different structural states of the CaM-bound nNOS: the open (undocked) state, where the bound CaM can move freely within the range of positions permitted by the flexibility and length of the tether (panel B in Figure 1), and the docked state (panel C), where the docking of the bound CaM to the oxygenase domain facilitates and strengthens the docking of the FMN domain.32 The specific structural models for the docked and undocked states used in the interpretation of the experimental results of this work will be presented below.
RIDME Measurements
The structural arrangements described in the previous section can be distinguished by using RIDME, one of the pulsed EPR techniques sensitive to the magnetic dipole interaction between the SL and the Fe(III) ions of the heme centers. The meaningful use of the alternative pulsed EPR technique sensitive to the magnetic dipole interaction between the paramagnetic centers, the electron–electron double resonance (ELDOR), is hampered for this system by the unfavorable EPR properties of the ferric heme centers (strong 14N electron spin-echo envelope modulation (ESEEM) and significant g-anisotropy). This has been discussed in our previous work, where the distance of 18.8 Å between the heme center and the FMN semiquinone radical of the docked FMN domain was determined by RIDME.33
The RIDME measurements were performed using the refocused stimulated electron spin-echo (ESE) pulse sequence (Figure S2 in the Supporting Information). The refocused stimulated ESE signal from the SL was measured as a function of the interval between the first and second mw pulses, τ, at a fixed time interval between the second and third pulses, T. These measurements were performed at two temperatures, Tlow and Thigh, selected in such a way that the longitudinal relaxation time of the heme center, T1Fe, was very long at Tlow (T1Fe ≫ T) but relatively short at Thigh [τ < T1Fe ≪ T, so that the time interval T effectively corresponded to a complete relaxation of the Fe(III) spins]. The specific temperatures used in our experiments were Tlow = 8 K and Thigh = 25 K. These temperatures are determined by the relaxation properties of the ferric heme center(s) of NOS established in our previous work.33 The quotient of the ESE traces, VQ(τ) = V(τ,Thigh)/V(τ,Tlow), represents the RIDME trace whose amplitude dependence on τ is caused by the magnetic dipole interaction of the SL with the Fe(III) spins. An example of the original experimental RIDME traces obtained in this work is shown in Figure S3 of the Supporting Information.
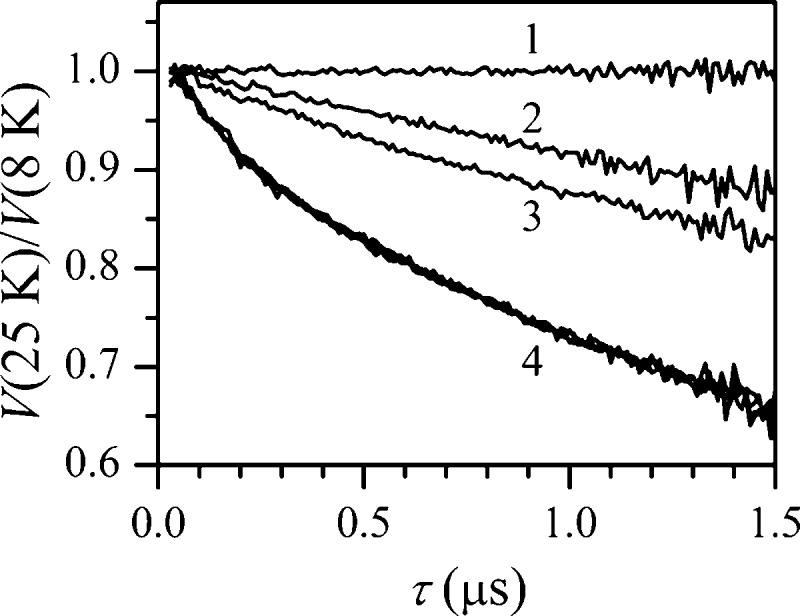
Figure 2 shows the quotient RIDME traces for the samples containing nNOS oxyFMN and SL CaM obtained at different concentrations of Ca2+ and also the trace for SL CaM without nNOS. One can see that while the latter trace (trace 1) is approximately constant (understandably so, since no fast-relaxing species is present in solution), those of the samples with nNOS represent monotonously decaying functions. The slowest decay observed for the sample with [Ca2+] = 0 (trace 2) is caused by the magnetic dipole interaction of the SL with the uniformly distributed Fe(III) spins. The trace for the sample with [Ca2+] = 0.22 mM shows somewhat faster decay (trace 3), indicating the onset of CaM binding to nNOS. Starting from [Ca2+] = 0.5 mM the decay does not increase further (overlaid traces labeled as 4 in Figure 2), which indicates the maximum concentration of nNOS·CaM complex achievable at [Ca2+] ≥ 0.5 mM.
Figure 2.
RIDME traces obtained by division of the refocused stimulated ESE decays of the SL recorded at the temperature of 25 K by those recorded at 8 K. Trace 1 is obtained for the sample of 110 μM SL CaM without nNOS, containing 1 mM Ca2+. Traces 2–4 are obtained for the samples of 110 μM SL CaM with 55 μM nNOS oxyFMN construct, containing various concentrations of Ca2+. For traces 2 and 3, [Ca2+] = 0 and 0.22 mM, respectively. Trace 4 represents an overlay of the traces obtained for [Ca2+] = 0.5, 1, 2, and 5 mM. Experimental conditions: mw frequency, 30.276 GHz; B0 = 1077.2 mT (maximum of the SL signal); mw pulses, 20, 20, 20, and 30 ns; time interval between the second and third mw pulses, T = 20 μs.
Figure 3 shows the [Ca2+] dependence of the RIDME effect in the samples containing nNOS relative to the effect observed in the sample with [Ca2+] = 0. This effect was calculated by (i) dividing the RIDME traces of Figure 2 obtained for all of nNOS-containing samples by trace 2 (to eliminate the effect of the uniformly distributed spins), (ii) subtracting 1, (iii) dividing the resulting traces by the average of those obtained from traces in group 4 of Figure 2, and (iv) averaging the amplitude of the obtained traces (which are approximately horizontal lines) over the time interval τ. The horizontal axis is calibrated in the [Ca2+]/[CaM] units. One can see that the RIDME effect saturates at [Ca2+]/[CaM] ≥ 4, which is expected because one CaM molecule can only bind up to four Ca2+ ions in its EF-hands. Since the calcium concentrations are much higher than the physiological concentrations (nanomolar level),34 additional discussion of EC50(Ca2+) for CaM binding would be susceptible to overinterpretation.
Figure 3.
[Ca2+] dependence of the RIDME effect in the samples of nNOS oxyFMN containing SL CaM. The RIDME effect was calculated by (i) dividing traces 2–4 of Figure 2 by trace 2 (to eliminate the effect of dipole interaction of the SL with uniformly distributed Fe(III) spins), (ii) normalizing the resulting quotient traces by the average of the traces obtained from group 4 in Figure 2 (i.e., those corresponding to [Ca2+] ≥ 0.5 mM), and (iii) taking the average value over the resulting normalized traces.
RIDME Analysis and Simulations
The analysis (using numerical simulations) of the experimental RIDME traces of Figure 2 can ideally provide information about the structure and relative statistical weights of the docked and open states of the CaM-bound nNOS (Figure 1C,B, respectively). As a preparation for this analysis, one must divide the traces obtained at [Ca2+] > 0.5 mM by the trace obtained at [Ca2+] = 0. This is the first operation of those used to obtain the data shown in Figure 3 above, which eliminates the effect from uniformly distributed matrix nNOS. The resulting traces represent a sum of two contributions: (i) the generally nonconstant (decaying or oscillating) contribution from the CaM·nNOS complexes and (ii) the constant contribution from the free CaM molecules (if any).
The black solid trace 1 in each panel of Figure 4 shows the result of the division of the average of the RIDME traces corresponding to [Ca2+] ≥ 0.5 mM (since these traces were similar, the average was taken to increase the signal-to-noise ratio) by the trace corresponding to [Ca2+] = 0. In order to analyze this trace, one has to take into account that the oxygenase domain contains two heme Fe(III) centers that simultaneously interact with the SL. The longitudinal relaxation of these heme centers during the time interval T (between the second and third mw pulses of the refocused stimulated ESE sequence) at 25 K results in the spin flip probability of 0.5 for each of these centers. The resulting distribution of the relaxation outcomes is as follows: 25% of the Fe(III) pairs do not flip; in 50% of the Fe(III) pairs, one of the spins flips (25% each); and in 25% of the Fe(III) pairs, both spins flip. In the last group, one-half of the population undergoes a flip between |αβ⟩ and |βα⟩ states, while the other half flips between |αα⟩ and |ββ⟩ states. The statistics of the Fe(III) spin flips is used to evaluate the resulting change in the local magnetic field at the position of the SL and to calculate the RIDME effect.
Figure 4.
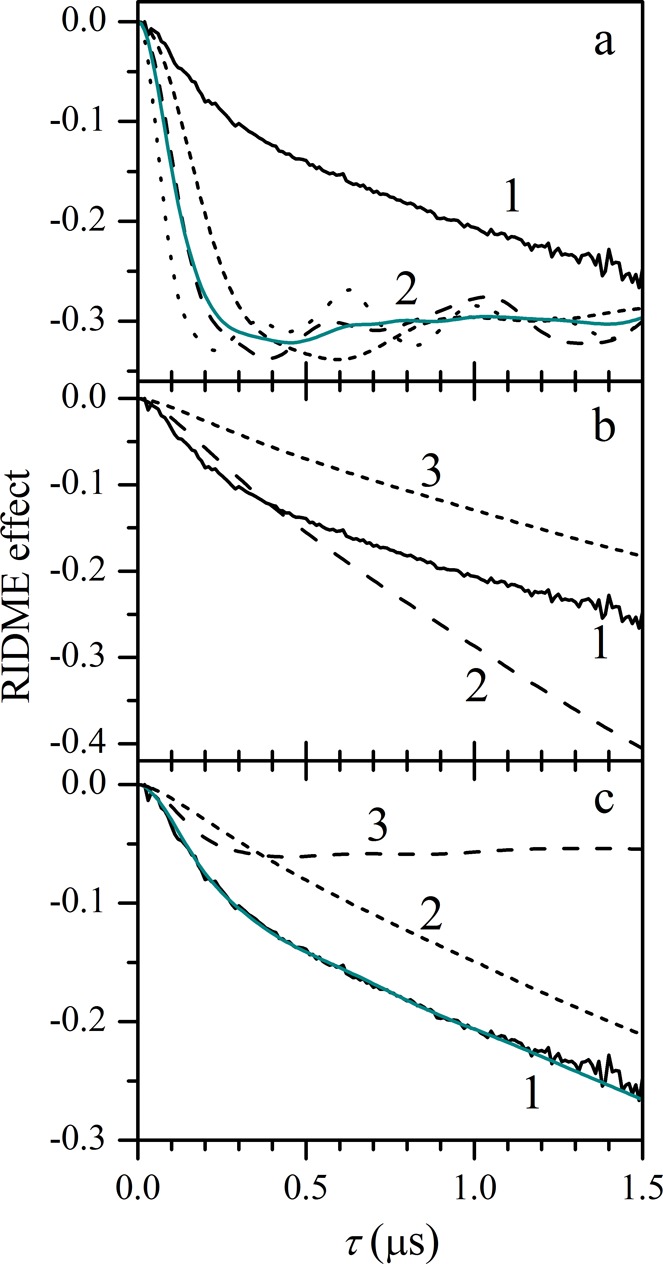
Numerical simulations of the RIDME effect for various structural models of nNOS. Solid black trace 1 in each panel is the experimental RIDME effect in the samples of CaM-bound nNOS oxyFMN. (a) Traces in group 2 are examples of simulations based on the docking model in Figure 5. The various traces are simulated for the distances between the SL and the two Fe(III) centers of (36, 31) Å (long dashes), (40, 36) Å (short dashes), and (31, 26) Å (dots). The solid cyan trace is an average over several SL positions within the uncertainty range, including the above three, (38, 27) Å, and (34, 33) Å. The simulated traces were multiplied by 0.4 to provide for convenient scaling of the figure. (b) Long-dashed trace 2 is simulated using the open state model in Figure 6. Short-dashed trace 3 is obtained from trace 2 by multiplication by 0.45 to approximately equalize its slope with that of the experimental trace. (c) An example of simulation (solid cyan trace) with a superposition model corresponding to 12% of the docked state and 88% of the open state. Traces 2 and 3 show the contributions of the open and docked states, respectively, into the cyan trace. See the text for details.
The experimental RIDME trace of Figure 4 cannot be explained by a single structure with a fixed distance between the SL and the heme centers because in this case oscillations rather than a monotonous decay would be observed (relevant examples are shown by the dashed and dotted traces in Figure 4a and discussed below). This indicates that the majority of the CaM-bound nNOS is in the open state (Figure 1B) that is characterized by a broad distribution of the SL positions relative to the oxygenase domain. The lack of well-defined oscillations also prevents one from obtaining accurate information on the CaM position in the docked state directly from the RIDME trace using the standard approach, which consists of estimating the characteristic distance from the oscillation frequency. In this situation, we have to rely on the structure of the docked state obtained from docking calculations for validating the results of numerical simulations of the RIDME kinetics.
Next we will describe the structural information pertaining to our analysis of the experimental RIDME trace of Figure 4 in terms of relative populations of the docked and open states. The crystal structures of nNOS oxygenase domain and of the CaM unit bound to the CaM-binding region are available (PDB ID 2G6K and 2O60, respectively), and the solution structures will be assumed to be the same. Although the crystal structure of the docked state has not yet been determined, the computer modeling allows one to predict the relative arrangement of the oxygenase and FMN domains and the bound CaM unit in the docked state. We constructed a docking model of nNOS FMN domain along with CaM on to the oxygenase domain (Figure 5). This was accomplished by closely referencing to the docking model reported recently for the system of murine iNOS based on hydrogen–deuterium exchange mass spectrometry results.32 According to our model, the SL in the docked state is located at the distances of about 36 and 31 Å (as measured to the Oγ atom of Thr110, which corresponds in the mutant CaM to Sγ of Cys110, to which the SL is attached) from the iron ions of the two heme centers of the oxygenase domain, the distance between which is 34 Å.
Figure 5.
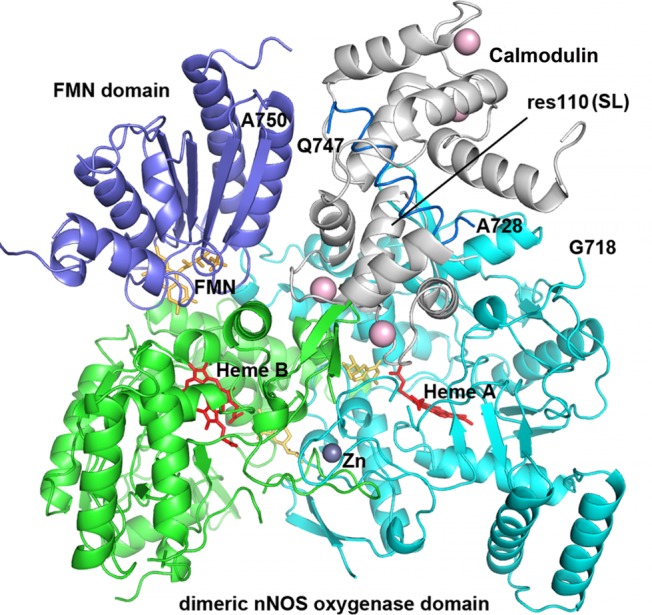
Docking model of nNOS FMN domain (purple, PDB ID 1TLL) onto the dimeric oxygenase domain (cyan and green, PDB ID 4JSH) in the presence of CaM (gray, PDB ID 2O60). For clarity, the second FMN domain and CaM molecule are not displayed. The SL site (res110) in CaM is labeled, so are the terminal residues in oxygenase and FMN domains that connect with the CaM-binding peptide. The docking model was constructed by carefully cross-checking against the iNOS model reported recently32 in terms of which residues are involved in the docking surface among the proteins.
In the open state, the SL position is assumed to be uniformly distributed within a sphere of the radius corresponding to the full extension of the flexible tether joining the oxygenase domain with the bound CaM, with the exclusion of inaccessible regions, in particular, the part of space occupied by the oxygenase domain (also see below). The structural model for the open state is schematically shown in Figure 6. The quantitative information pertaining to this model is as follows. The flexible tether joining the oxygenase domain with the bound CaM is a random coil spanning residues 706–731. With 3.5–3.6 Å per residue, this corresponds to the maximum backbone extension of 89 ± 1 Å. The SL is located at about 15 Å from Phe731, which makes the total maximum possible distance between the oxygenase domain and the SL equal to ∼104 Å.
Figure 6.
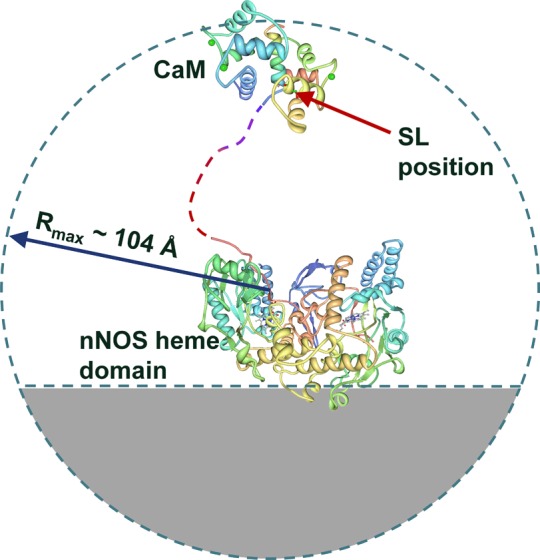
Structural model of the open state used in RIDME simulations. The SL position is averaged over the sphere centered at the peptide nitrogen of Tyr706, with the radius of 104 Å. The regions occupied by the oxygenase domain and the gray part of the sphere on the far side of the oxygenase domain (40 Å from the center to the cutoff plane) are excluded from the calculation as inaccessible. See the text for further details.
The size of the dimeric oxygenase domain has characteristic dimensions of ∼90 × 50 × 50 Å3 and is comparable with the tether length. Therefore, the bound CaM cannot reach the parts of the spherical region on the far side of oxygenase domain. Predicting the exact shape of this inaccessible region requires calculating all possible configurations of the tether wrapping around the oxygenase domain surface. Since the oxygenase domain shape is not accurately described by any analytical function (e.g., a sphere or an ellipsoid), such a calculation is prohibitively time-consuming and practically unrealistic. An approximate exclusion region, however, can be predicted on the basis of comparison of the characteristic size of the oxygenase domain with the tether length. In this particular case it represents a part of the sphere on the far side of the oxygenase domain shown by the gray area in Figure 6.
An important comment about the SL position should be made. Since the specific conformation of the SL or distribution thereof in CaM is unknown (which is a common situation in site-directed spin-labeling), one has to consider the uncertainty in the position of the >N–O• radical fragment arising from the rotational degrees of freedom of single bonds between the >N–O• fragment and the S–S bridge, which is approximately 6 Å in every direction (see Figure S4 of the Supporting Information). This uncertainty is not important for the open state of NOS because the distances there are distributed within very large limits (∼100 Å in every direction). For the docked state, however, this uncertainty has to be considered explicitly (see below).
Using the structural models presented above, we performed numerical simulations of the RIDME effect for the docked and open states of nNOS. In these simulations, the heme centers were assumed to have isotropic g = 2.2. Such an approximation is unavoidable because the orientations of the heme g-frames with respect to the oxygenase domain of nNOS are not known. Neglecting the actual g-anisotropy [(g1, g2, g3) = (1.85, 2.30, 2.52)], however, does not result in the loss of potentially obtainable structural information because (i) the anisotropy is fairly small, (ii) in the open state the heme–SL radius vectors are orientationally disordered with respect to the g-frames, and (iii) in the docked state the potential changes in the RIDME frequencies resulting from taking the g-anisotropy into account are smaller than the changes from the uncertainty in the SL position.
The results of the calculations for the docked state are shown by group 2 of dashed and dotted traces in Figure 4a. These traces were calculated for three different SL positions within the ±6 Å range of uncertainty mentioned above. Note that they exhibit well-defined oscillations with the frequencies equal to the dipole interactions (expressed in frequency units) between the SL and the heme centers and are very different from the experimental trace 1. A distribution of the SL position within the uncertainty range does not create a better agreement: while the oscillations are suppressed, the trace practically flattens out starting from 250 to 300 ns (solid trace of cyan color in Figure 4a).
The long-dashed trace 2 in Figure 4b shows the calculation result for the open state. This trace exhibits significantly smaller curvature and greater slope than the experimental one (trace 1). Although the slope of the calculated trace can be reduced by assuming less than 100% formation of the low-spin ferric state of the heme centers or the presence of some unbound CaM (short-dashed trace 3 in Figure 4b), this does not help with improving the agreement because the curvature then becomes even smaller.
While the docked or open state models by themselves result in simulated RIDME traces significantly different from the experimental one, the agreement can be reached for a combination of the two states. To estimate the relative contributions of the docked and open states, the calculated RIDME trace for the open state (long-dashed trace in Figure 4b) was multiplied by the scaling factor Copen < 1 (as exemplified by the short-dashed trace in Figure 4b) to approximate the asymptotic slope of the experimental trace and subtracted from the latter. The resulting difference trace corresponds to the docked state. Numerical simulations of the difference trace were then performed for various SL positions. The SL position in these simulations was characterized by the distance RSL from the midpoint between the Fe(III) ions of the heme centers (that are 34 Å apart) and by the angle θSL that the radius-vector RSL makes with the line joining the heme centers (the definitions are shown in the graphical form in Figure S6 of the Supporting Information). In order to fit the amplitude of the difference RIDME trace, the simulated traces were multiplied by the scaling factor Cdock < 1.
The simulations have shown that there is only a relatively narrow range of the scaling factors Copen (0.45–0.52) that result in the difference traces that could be reproduced by numerical simulations. Using the smaller Copen of 0.45 allows one to obtain the approximate fit of the difference trace with θSL ∼ 60°, RSL uniformly distributed between 31 and 46 Å, and Cdock ≈ 0.1. The larger Copen of 0.52 results in θSL ∼ 75°, RSL uniformly distributed between 30 and 36 Å, and Cdock ≈ 0.075 (see Figures S7 and S8 in the Supporting Information for simulation examples). For comparison, the docking model (Figure 5) places Sγ of Cys110 (to which the SL is attached) of mutant CaM at θSL ∼ 80° and RSL = 29 Å. Thus, the SL position at θSL ∼ 75° used in the simulation is in good agreement with the docking model: the 5° angular difference at the distance of ∼30 Å translates into the difference in position of <3 Å, within the uncertainty range related to the SL conformational flexibility (±6 Å; see Figure S4 of the Supporting Information). The solutions corresponding to the smaller θSL are progressively less likely (e.g., at θSL = 60° and RSL = 30 Å the distance between the SL >N–O• fragment and the predicted anchoring position at Sγ is about 10 Å).
Using the obtained values of scaling factors Copen and Cdock, the population of the docked state can be estimated as Pdock = Cdock/(Cdock + Copen). The population of the open state is Popen = 1 – Pdock. On the basis of the range of Copen (0.45–0.52) and the corresponding range of Cdock (0.1–0.075), one can estimate Pdock = 15 ± 3%, with the smaller values corresponding to the more probable solution with θSL ∼ 75°. The simulation for θSL = 75° that is in reasonable agreement with the experimental RIDME trace and with the docking model is shown in Figure 4c.
Interpretation of the Results
The results of the present RIDME work indicate that the SL···Fe(III) distance is highly distributed and dynamic, even in the CaM-bound nNOS. This is consistent with the FMN domain tethered shuttle model:27,35 CaM activates nNOS by enabling transitions between conformational states, and the FMN domain moves back and forth to contact the ferredoxin–NADP+-reductase module and the NOS heme domain. This model is similar to that of NADPH–cytochrome P450 reductase and P450 BM3 (e.g., a hinge movement of the FMN domain toward the heme domain in P450 BM3 was proposed36), which derives from P450 reductase37,38 and P450 BM3 structures, including the crystal structure of the BM3 heme–FMN complex.39 The FMN–heme IET occurs in the docked state, but the interdomain FMN–heme interactions in NOS enzymes are rather weak, and the docking complexes are short-lived.29,40 The FMN–heme IET rate in the bidomain oxyFMN construct is therefore limited by the relatively infrequent formation of the docked IET-competent complexes. We have recently shown that the retarded IET in the E546N mutant of human iNOS oxyFMN is not caused by an altered conformation of the docked FMN–heme complex but by a lower population of the IET-active conformation.41 On the other hand, in the nNOS holoenzyme, the electron transfer to the heme center is more likely limited by passage through a conformational bottleneck (that does not exist in the oxyFMN construct).4,10
It is interesting to compare the findings of our RIDME study with the results of FMN fluorescence lifetime investigations performed in solutions at room temperature.4,42 The populations of the docked and open conformations of CaM-bound nNOS oxyFMN in frozen solution estimated from our RIDME measurements are about 15% and 85%, respectively. The corresponding populations estimated for iNOS oxyFMN from room temperature FMN fluorescence measurements are about 25–30% and 75–70%.42 Fluorescence lifetime data for nNOS oxyFMN construct have not been reported yet, but the population breakdown obtained for the full-length nNOS enzyme4 suggests that the nNOS oxyFMN construct in terms of the docked and open state populations should be similar to that of iNOS oxyFMN. One has to note that the docked state population estimates in the literature4,42 depend on the assignment of the fluorescence component with ∼1 ns lifetime. While there is little doubt that this component is caused by the FMN–heme interaction, it is not clear if the relative arrangement of the oxygenase and heme domains enabling this interaction is unique and corresponds to the docking complex only. Therefore, we believe that the 25–30% population of the docked state derived from the fluorescence investigations4,42 represents an upper limit estimate.
Another factor that makes the comparison of the RIDME and fluorescence lifetime results not entirely straightforward is that the former pertain to the NOS-bound CaM, while the latter pertain to FMN. The comparison is justified by the fact that FMN and CaM are located in close proximity (they are separated by a linker that is only 7 residues long, compared to 25 residues between CaM and the oxygenase domain) and can be approximately considered as a single structural unit. Therefore, we conclude that the RIDME and fluorescence data are at least in a semiquantitative agreement.
On a more general level, the above comparison tests a commonly used paradigm that the structural distribution in a frozen solution represents a “snapshot” of the dynamic equilibrium in fluid solution. While this paradigm is obviously convenient, it has to be used with caution. The relevant literature appears to be rather scarce, but examples of both small43 and large44 temperature- and phase-dependent conformational distribution changes are available. The joint results of this RIDME investigation and the FMN fluorescence studies indicate that for the NOS oxyFMN constructs the “snapshot” approximation is at least semiquantitative.
The broad structural distribution of CaM-bound nNOS detected by RIDME is in agreement with a low-resolution cryo-electron microscopy (EM) study of eNOS holoenzyme,45 which indicated that a large (although unquantified) fraction of NOS is in distributed conformations even when CaM is bound. The overall conformational equilibrium in CaM-bound nNOS was estimated in another cryo-EM study,46 which showed that the CaM-bound nNOS holoenzyme adopts an ensemble of open and closed conformational states, with only about 15% in the closed conformation. The closed state as used in the EM work46 represents a structural category that corresponds to the nNOS protein folded on itself, as opposed to the extended and intermediate (V-shaped) states where the oxygenase–FMN–reductase domain “arms” are spread wide apart. This classification of the conformational states categorizes the perceived overall shapes of the entire nNOS dimer, but not the relative arrangement of the specific structural parts of the protein.
It is important to note that although the docking complex studied in our work obviously corresponds to a subset of the closed conformations in the EM work,46 the specific closed conformation stabilized by cross-linking and characterized in detail46 is very different and is far from optimal for the FMN–heme IET since the FMN domain there is still too far (∼100 Å) from the hemes. In addition, the FMN domain in the three-dimensional reconstruction model46 is proximal to the side of substrate-access channel of the heme domain (but kinetics and mutational studies47,48 have consistently shown that the FMN domain docks to the back face of the heme domain where the heme is closest to the protein surface). Further FMN domain motions (swing and rotation) are clearly required prior to the IET. Therefore, the 15% population of the closed state found in the cryo-EM work does not translate directly to the population of the FMN–heme IET-competent conformation and represents, at best, the upper limit estimate for the docked FMN/heme state. To improve the docked state geometry and statistics estimates, a high-resolution structure of the functional full-length NOS state should be obtained.
Although the docked fraction of about 15% estimated by RIDME measurements is relatively small, it is not negligible: its presence indicates that the free energies of the docked and open states are comparable. The presence of the measurable population of the docked state is also important from the mechanistic viewpoint because it implies a possibility of minor local structural adjustments in the docked state itself to reach the FMN–heme docking geometry most suitable for the IET. Finally, our results are agreeable with the notion that CaM docking with the oxygenase domain is necessary to facilitate the rather weak interdomain FMN–heme interactions required for efficient IET, which was first experimentally established in an isotope exchange mass spectrometry study of murine iNOS oxyFMN protein.32
The system investigated in this work is characterized by a wide distribution of distances between the paramagnetic centers, and the RIDME trace represents a relatively featureless monotonous decay. In a recent pulsed ELDOR study49 of the magnetic dipole interaction between flavin semiquinone radicals in FAD and FMN domains of nNOS (a system qualitatively similar to ours, with two domains connected by a flexible tether), clear oscillations in the ELDOR trace were observed, indicating that a significant fraction of the protein was in well-defined structural states. Unfortunately, no analysis of the distributed fraction was performed in their work, and the percentages allotted to each fraction were not determined.
Conclusions
In this work, we have studied the binding of SL CaM to nNOS oxyFMN bidomain construct using pulsed EPR (the RIDME technique) to detect the specific magnetic dipole interaction between the SL and the ferric heme centers of nNOS. It was found that the binding saturates at [Ca2+]/[CaM] ≥ 4, which is expected from the number of the calcium binding sites in CaM. The analysis of the RIDME traces has shown that only about 15 ± 3% of the CaM-bound nNOS is in the IET-competent docked state at any given time, while the remaining 85 ± 3% of the protein is in the open conformations characterized by a wide distribution of the distances between the bound CaM and the oxygenase domain. The low population of the docked state found in this RIDME study indicates that the CaM-controlled docking between the primary functional FMN and heme domains is highly dynamic. The overall approach of this work to the analysis of the RIDME data can be used for obtaining information about the structural state(s) of other protein systems consisting of domains connected by a flexible tether.
Acknowledgments
We thank Dr. Daniel Southworth for helpful discussions. This work was supported by grants to C.F. from the National Institutes of Health (GM081811), the National Science Foundation (CHE-1150644), AHA Grant-in-Aid (12GRNT11780019), and GM57353 (T.L.P). This project was also supported by grants from the National Center for Research Resources (5P20RR016480-12) and the National Institute of General Medical Sciences (8 P20 GM103451-12).
Glossary
Abbreviations
- NO
nitric oxide
- NOS
nitric oxide synthase
- nNOS
neuronal NOS
- CaM
calmodulin
- CaM-T110C
CaM where threonine 110 is mutated to a cysteine
- oxyFMN
bidomain NOS construct in which only oxygenase and FMN domains along with CaM-binding region are present
- FMN
flavin mononucleotide
- IET
interdomain electron transfer
- EPR
electron paramagnetic resonance
- ESE
electron spin-echo
- RIDME
relaxation-induced dipolar modulation enhancement
- mw
microwave.
Supporting Information Available
Details of construction, purification, and spin-labeling of T110C mutant CaM, mass spectrometry of tryptic digestion of SL CaM, refocused stimulated ESE pulse sequence used for RIDME measurements, example of original RIDME traces, a sketch explaining the uncertainty of the SL position, and simulations of the RIDME trace corresponding to the docked conformation. This material is available free of charge via the Internet at http://pubs.acs.org
Author Contributions
⊥ These authors contributed equally.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Alderton W. K.; Cooper C. E.; Knowles R. G. Nitric Oxide Synthases: Structure, Function and Inhibition. Biochem. J. 2001, 357, 593–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roman L. J.; Martasek P.; Masters B. S. S. Intrinsic and Extrinsic Modulation of Nitric Oxide Synthase Activity. Chem. Rev. 2002, 10241179–1189. [DOI] [PubMed] [Google Scholar]
- Feng C.; Chen L.; Li W.; Elmore B. O.; Fan W.; Sun X. Dissecting Regulation Mechanism of the FMN to Heme Interdomain Electron Transfer in Nitric Oxide Synthases. J. Inorg. Biochem. 2014, 1300130–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salerno J. C.; Ray K.; Poulos T.; Li H.; Ghosh D. K. Calmodulin Activates Neuronal Nitric Oxide Synthase by Enabling Transitions between Conformational States. FEBS Lett. 2013, 587144–47. [DOI] [PubMed] [Google Scholar]
- Feng C. Mechanism of Nitric Oxide Synthase Regulation: Electron Transfer and Interdomain Interactions. Coord. Chem. Rev. 2012, 2563–4393–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan Z.-W.; Haque M. M.; Wei C.-C.; Garcin E. D.; Getzoff E. D.; Stuehr D. J. Lys842 in Neuronal Nitric-Oxide Synthase Enables the Autoinhibitory Insert To Antagonize Calmodulin Binding, Increase FMN Shielding, and Suppress Interflavin Electron Transfer. J. Biol. Chem. 2010, 28553064–3075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haque M. M.; Panda K.; Tejero J.; Aulak K. S.; Fadlalla M. A.; Mustovich A. T.; Stuehr D. J. A Connecting Hinge Represses the Activity of Endothelial Nitric Oxide Synthase. Proc. Natl. Acad. Sci. U. S. A. 2007, 104229254–9259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuehr D. J.; Tejero J.; Haque M. M. Structural and Mechanistic Aspects of Flavoproteins: Electron Transfer through the Nitric Oxide Synthase Flavoprotein Domain. FEBS J. 2009, 276153959–3974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welland A.; Garnaud P. E.; Kitamura M.; Miles C. S.; Daff S. Importance of the Domain–Domain Interface to the Catalytic Action of the NO Synthase Reductase Domain. Biochemistry 2008, 47379771–9780. [DOI] [PubMed] [Google Scholar]
- Feng C. J.; Tollin G.; Hazzard J. T.; Nahm N. J.; Guillemette J. G.; Salerno J. C.; Ghosh D. K. Direct Measurement by Laser Flash Photolysis of Intraprotein Electron Transfer in a Rat Neuronal Nitric Oxide Synthase. J. Am. Chem. Soc. 2007, 129175621–5629. [DOI] [PubMed] [Google Scholar]
- Feng C. J.; Tollin G. Regulation of Interdomain Electron Transfer in the NOS Output State for NO Production. Dalton Trans. 2009, 34, 6692–6700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng C. J.; Dupont A.; Nahm N.; Spratt D.; Hazzard J. T.; Weinberg J.; Guillemette J.; Tollin G.; Ghosh D. K. Intraprotein Electron Transfer in Inducible Nitric Oxide Synthase Holoenzyme. J. Biol. Inorg. Chem. 2009, 141133–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman E.; Spratt D. E.; Mosher J.; Cheyne B.; Montgomery H. J.; Wilson D. L.; Weinberg J. B.; Smith S. M. E.; Salerno J. C.; Ghosh D. K.; Guillemette J. G. Differential Activation of Nitric-Oxide Synthase Isozymes by Calmodulin–Troponin C Chimeras. J. Biol. Chem. 2004, 2793233547–33557. [DOI] [PubMed] [Google Scholar]
- Spratt D. E.; Taiakina V.; Palmer M.; Guillemette J. G. Fret Conformational Analysis of Calmodulin Binding to Nitric Oxide Synthase Peptides and Enzymes. Biochemistry 2008, 474612006–12017. [DOI] [PubMed] [Google Scholar]
- Crane B. R.; Arvai A. S.; Ghosh D. K.; Wu C. Q.; Getzoff E. D.; Stuehr D. J.; Tainer J. A. Structure of Nitric Oxide Synthase Oxygenase Dimer with Pterin and Substrate. Science 1998, 27953592121–2126. [DOI] [PubMed] [Google Scholar]
- Raman C. S.; Li H. Y.; Martasek P.; Kral V.; Masters B. S. S.; Poulos T. L. Crystal Structure of Constitutive Endothelial Nitric Oxide Synthase: A Paradigm for Pterin Function Involving a Novel Metal Center. Cell 1998, 957939–950. [DOI] [PubMed] [Google Scholar]
- Li H. Y.; Shimizu H.; Flinspach M.; Jamal J.; Yang W. P.; Xian M.; Cai T. W.; Wen E. Z.; Jia Q. A.; Wang P. G.; Poulos T. L. The Novel Binding Mode of N-Alkyl-N′-hydroxyguanidine to Neuronal Nitric Oxide Synthase Provides Mechanistic Insights into NO Biosynthesis. Biochemistry 2002, 414713868–13875. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Martasek P.; Paschke R.; Shea T.; Masters B. S. S.; Kim J. J. P. Crystal Structure of the FAD/NADPH-Binding Domain of Rat Neuronal Nitric-Oxide Synthase—Comparisons with NADPH-Cytochrome P450 Oxidoreductase. J. Biol. Chem. 2001, 2764037506–37513. [DOI] [PubMed] [Google Scholar]
- Garcin E. D.; Bruns C. M.; Lloyd S. J.; Hosfield D. J.; Tiso M.; Gachhui R.; Stuehr D. J.; Tainer J. A.; Getzoff E. D. Structural Basis for Isozyme-Specific Regulation of Electron Transfer in Nitric-Oxide Synthase. J. Biol. Chem. 2004, 2793637918–37927. [DOI] [PubMed] [Google Scholar]
- Xia C.; Misra I.; Iyanagi T.; Kim J.-J. P. Regulation of Interdomain Interactions by Calmodulin in Inducible Nitric Oxide Synthase. J. Biol. Chem. 2009, 2844430708–30717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aoyagi M.; Arvai A. S.; Tainer J. A.; Getzoff E. D. Structural Basis for Endothelial Nitric Oxide Synthase Binding to Calmodulin. EMBO J. 2003, 224766–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulik L. V.; Dzuba S. A.; Grigoryev I. A.; Tsvetkov Y. D. Electron Dipole–Dipole Interaction in ESEEM of Nitroxide Biradicals. Chem. Phys. Lett. 2001, 3433–4315–324. [Google Scholar]
- Kulik L. V.; Grishin Y. A.; Dzuba S. A.; Grigoryev I. A.; Klyatskaya S. V.; Vasilevsky S. F.; Tsvetkov Y. D. Electron Dipole–Dipole ESEEM in Field-Step ELDOR of Nitroxide Biradicals. J. Magn. Reson. 2002, 157161–68. [DOI] [PubMed] [Google Scholar]
- Spratt D. E.; Taiakina V.; Palmer M.; Guillemette J. G. Differential Binding of Calmodulin Domains to Constitutive and Inducible Nitric Oxide Synthase Enzymes. Biochemistry 2007, 46288288–8300. [DOI] [PubMed] [Google Scholar]
- Ghosh D. K.; Holliday M. A.; Thomas C.; Weinberg J. B.; Smith S. M. E.; Salerno J. C. Nitric-Oxide Synthase Output State—Design and Properties of Nitric-Oxide Synthase Oxygenase/FMN Domain Constructs. J. Biol. Chem. 2006, 2812014173–14183. [DOI] [PubMed] [Google Scholar]
- Li H. Y.; Igarashi J.; Jamal J.; Yang W. P.; Poulos T. L. Structural Studies of Constitutive Nitric Oxide Synthases with Diatomic Ligands Bound. J. Biol. Inorg. Chem. 2006, 116753–768. [DOI] [PubMed] [Google Scholar]
- Feng C. J.; Tollin G.; Holliday M. A.; Thomas C.; Salerno J. C.; Enemark J. H.; Ghosh D. K. Intraprotein Electron Transfer in a Two-Domain Construct of Neuronal Nitric Oxide Synthase: The Output State in Nitric Oxide Formation. Biochemistry 2006, 45206354–6362. [DOI] [PubMed] [Google Scholar]
- Feng C. J.; Thomas C.; Holliday M. A.; Tollin G.; Salerno J. C.; Ghosh D. K.; Enemark J. H. Direct Measurement by Laser Flash Photolysis of Intramolecular Electron Transfer in a Two-Domain Construct of Murine Inducible Nitric Oxide Synthase. J. Am. Chem. Soc. 2006, 128113808–3811. [DOI] [PubMed] [Google Scholar]
- Ilagan R. P.; Tejero J. S.; Aulak K. S.; Ray S. S.; Hemann C.; Wang Z.-Q.; Gangoda M.; Zweier J. L.; Stuehr D. J. Regulation of FMN Subdomain Interactions and Function in Neuronal Nitric Oxide Synthase. Biochemistry 2009, 48183864–3876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillan K.; Masters B. S. S. Optical-Difference Spectrophotometry as a Probe of Rat-Brain Nitric-Oxide Synthase Heme–Substrate Interaction. Biochemistry 1993, 32389875–9880. [DOI] [PubMed] [Google Scholar]
- Astashkin A. V.; Enemark J. H.; Raitsimring A. 26.5–40 GHz Ka-Band Pulsed EPR Spectrometer. Concepts Magn. Reson., Part B 2006, 29B3125–136. [Google Scholar]
- Smith B. C.; Underbakke E. S.; Kulp D. W.; Schief W. R.; Marletta M. A. Nitric Oxide Synthase Domain Interfaces Regulate Electron Transfer and Calmodulin Activation. Proc. Natl. Acad. Sci. U. S. A. 2013, 11038E3577–E3586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astashkin A. V.; Elmore B. O.; Fan W.; Guillemette J. G.; Feng C. Pulsed EPR Determination of the Distance between Heme Iron and FMN Centers in a Human Inducible Nitric Oxide Synthase. J. Am. Chem. Soc. 2010, 1323412059–12067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran Q.-K.; Leonard J.; Black D. J.; Persechini A. Phosphorylation within an Autoinhibitory Domain in Endothelial Nitric Oxide Synthase Reduces the Ca2+ Concentrations Required for Calmodulin to Bind and Activate the Enzyme. Biochemistry 2008, 47287557–7566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh D. K.; Salerno J. C. Nitric Oxide Synthases: Domain Structure and Alignment in Enzyme Function and Control. Front. Biosci. 2003, 8, D193–D209. [DOI] [PubMed] [Google Scholar]
- Munro A. W.; Leys D. G.; McLean K. J.; Marshall K. R.; Ost T. W. B.; Daff S.; Miles C. S.; Chapman S. K.; Lysek D. A.; Moser C. C.; Page C. C.; Dutton P. L. P450 BM3: The Very Model of a Modern Flavocytochrome. Trends Biochem. Sci. 2002, 275250–257. [DOI] [PubMed] [Google Scholar]
- Hubbard P. A.; Shen A. L.; Paschke R.; Kasper C. B.; Kim J.-J. P. NADPH-Cytochrome P450 Oxidoreductase. J. Biol. Chem. 2001, 2763129163–29170. [DOI] [PubMed] [Google Scholar]
- Wang M.; Roberts D. L.; Paschke R.; Shea T. M.; Masters B. S. S.; Kim J. J. P. Three-Dimensional Structure of NADPH-Cytochrome P450 Reductase: Prototype for FMN- and FAD-Containing Enzymes. Proc. Natl. Acad. Sci. U. S. A. 1997, 94168411–8416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sevrioukova I. F.; Li H.; Zhang H.; Peterson J. A.; Poulos T. L. Structure of a Cytochrome P450–Redox Partner Electron-Transfer Complex. Proc. Natl. Acad. Sci. U. S. A. 1999, 9651863–1868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W.; Fan W.; Elmore B. O.; Feng C. Effect of Solution Viscosity on Intraprotein Electron Transfer between the FMN and Heme Domains in Inducible Nitric Oxide Synthase. FEBS Lett. 2011, 585162622–2626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W.; Chen L.; Lu C.; Elmore B. O.; Astashkin A. V.; Rousseau D. L.; Yeh S.-R.; Feng C. Regulatory Role of Glu546 in Flavin Mononucleotide–Heme Electron Transfer in Human Inducible Nitric Oxide Synthase. Inorg. Chem. 2013, 5294795–4801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh D. K.; Ray K.; Rogers A. J.; Nahm N. J.; Salerno J. C. FMN Fluorescence in Inducible Nos Constructs Reveals a Series of Conformational States Involved in the Reductase Catalytic Cycle. FEBS J. 2012, 27971306–1317. [DOI] [PubMed] [Google Scholar]
- Georgieva E. R.; Roy A. S.; Grigoryants V. M.; Borbat P. P.; Earle K. A.; Scholes C. P.; Freed J. H. Effect of Freezing Conditions on Distances and Their Distributions Derived from Double Electron Electron Resonance (Deer): A Study of Doubly-Spin-Labeled T4 Lysozyme. J. Magn. Reson. 2012, 216069–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kensch O.; Restle T.; Wöhrl B. M.; Goody R. S.; Steinhoff H.-J. Temperature-Dependent Equilibrium between the Open and Closed Conformation of the P66 Subunit of HIV-1 Reverse Transcriptase Revealed by Site-Directed Spin Labelling. J. Mol. Biol. 2000, 30141029–1039. [DOI] [PubMed] [Google Scholar]
- Persechini A.; Tran Q. K.; Black D. J.; Gogol E. P. Calmodulin-Induced Structural Changes in Endothelial Nitric Oxide Synthase. FEBS Lett. 2013, 5873297–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yokom A. L.; Morishima Y.; Lau M.; Su M.; Glukhova A.; Osawa Y.; Southworth D. R. Architecture of the Nitric Oxide Synthase Holoenzyme Reveals Large Conformational Changes and a Calmodulin-Driven Release of the FMN Domain. J. Biol. Chem. 2014, 289, 16855–16865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tejero J.; Hannibal L.; Mustovich A.; Stuehr D. J. Surface Charges and Regulation of FMN to Heme Electron Transfer in Nitric-Oxide Synthase. J. Biol. Chem. 2010, 2853527232–27240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimanuki T.; Sato H.; Daff S.; Sagami I.; Shimizu T. Crucial Role of Lys(423) in the Electron Transfer of Neuronal Nitric-Oxide Synthase. J. Biol. Chem. 1999, 2743826956–26961. [DOI] [PubMed] [Google Scholar]
- Sobolewska-Stawiarz A.; Leferink N. G. H.; Fisher K.; Heyes D. J.; Hay S.; Rigby S. E. J.; Scrutton N. S. Energy Landscapes and Catalysis in Nitric-Oxide Synthase. J. Biol. Chem. 2014, 2891711725–11738. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.