Abstract
Purpose
The purpose of this work was to improve the robustness of existing chemical shift encoded water-fat separation methods by incorporating object-based information of the B0 field inhomogeneity.
Theory
The primary challenge in water-fat separation is the estimation of phase shifts that arise from B0 field inhomogeneity, which is composed of the background field and susceptibility-induced field. The susceptibility-induced field can be estimated if the susceptibility distribution is known or can be approximated. In this work, the susceptibility distribution is approximated from the source images using the known susceptibility values of water, fat, and air. The field estimate is then demodulated from the source images prior to water-fat separation.
Methods
Chemical shift encoded source images were acquired in anatomical regions that are prone to water-fat swaps. The images were processed using algorithms from the ISMRM Fat-Water Toolbox, with and without the object-based field map information. The estimates were compared to examine the benefit of using the object-based field map information.
Results
Multiple cases are shown in which water-fat swaps were avoided by using the object-based information of the B0 field map.
Conclusion
Object-based information of the B0 field may improve the robustness of existing chemical shift encoded water-fat separation methods.
Keywords: magnetic resonance imaging, chemical shift encoded water-fat separation, Dixon imaging, susceptibility
INTRODUCTION
Chemical shift encoded techniques for water-fat separation have experienced considerable development and application in recent decades. Originally proposed by Dixon (1) and subsequently expanded by Glover et al. (2), these techniques have been adopted by applications that require improved visualization of water-based tissues as well as those that demand robust fat suppression in areas of severe B0 field inhomogeneity. In addition, the use of chemical shift encoding in T1-weighted contrast enhanced imaging is particularly important since alternatives such as short-tau inversion recovery (STIR) techniques (3) should be avoided with post-contrast T1-weighted imaging. A variety of water-fat separation techniques have been proposed, including a single-echo method (4), dual-echo methods (1,5–8), as well as numerous 3+-echo methods (2,9–11)
The primary challenge in water-fat separation is the estimation of the time-dependent phase shifts that arise from B0 field inhomogeneity. If the B0 field map can be estimated accurately, then the water and fat signals can be uniquely separated using a straightforward linear inversion. However, inaccurate estimation of the B0 field map can lead to swaps of the water and fat signals. This is commonly recognized as the main challenge for chemical shift encoded water-fat separation methods.
Robust estimation of the B0 field map has been a major focus of technical development in water-fat separation. To overcome the ambiguity when estimating the B0 field map, many techniques assume that the field is slowly varying (11–19). However, this assumption is empirically based and does not fully represent the underlying physics of the B0 field perturbations. Nevertheless, it is sufficiently valid in many cases, which explains the effectiveness of these techniques. Recent work from Yu et al. has exploited the material properties of tissue by using the spectral complexity of fat to reduce water-fat swaps (20). However, none of the previously developed methods use any anatomical or other geometrically based information to aid in the determination of the B0 field map. The use of such information may further improve the robustness of existing water-fat separation methods.
Past work in electromagnetic theory has shown that the component of the B0 magnetic field that is caused by susceptibility variations can be estimated efficiently and with high accuracy if the susceptibility distribution of the object being imaged is known (21–24). Further, this susceptibility-induced field represents a significant portion of the field inhomogeneity that must be resolved for accurate separation of the chemical species. Interestingly, previous techniques for chemical shift encoded water-fat separation do not exploit this information.
Therefore, the purpose of this work was to develop a framework for incorporating object-based information of the B0 field map into chemical shift encoded water-fat separation. The proposed method is intended to augment, rather than to replace, existing techniques for water-fat separation. This method may be used with any complex-based water-fat separation algorithm to improve the robustness of the algorithm.
THEORY
The signal from a voxel containing water (ρw) and fat (ρf) experiencing a local B0 field inhomogeneity (ψ, in Hz), measured at echo time tn can be written as
| [1] |
where represents a known multi-peak fat spectrum (25,26), αp is the relative amplitude of the pth fat peak (such that ), Δfp is the frequency shift (in Hz) of the pth fat peak relative to the water peak, and N denotes complex additive white Gaussian noise (AWGN). The effects of T2* have been ignored since they do not generally affect the quality of water-fat separation, however the approach described in this paper could also be applied to methods using T2* correction (27).
Separating water and fat requires the estimation of the unknown parameters from the multi-echo measurements. In the presence of AWGN, the maximum likelihood estimate is typically found by minimizing the least-squares cost. However, the least-squares cost contains multiple local minima as a function of ψ(12). Converging to a local minimum may result in a swap of the water and fat signals. Past works have proposed to overcome the challenge of multiple local minima by constraining the estimate of the B0 field map to be slowly varying (5,7–9,11–19). However, the assumption of a slowly varying B0 field breaks down in regions where the susceptibility distribution changes rapidly (e.g. air-tissue interfaces), in anatomical regions with irregular geometry (e.g. brachial plexus and ankle), and in isolated regions of anatomy (e.g. liver dome or two legs imaged axially). Further, assumptions regarding the degree of field map smoothness generally have no physical basis and are chosen empirically.
The B0 field inhomogeneity can be written as ψ = ψb +ψs, where ψb represents the background field, which is caused by the shim fields and imperfections in the magnet system, and ψs represents the susceptibility-induced field, which results from the interaction of the object being imaged with the applied magnetic field. Because of the low order shim fields on MR systems, rapidly varying B0 fields can be attributed to the susceptibility-induced field. The susceptibility-induced field (ψs) can be estimated if the susceptibility distribution of the object (χ) is known (24), i.e.
| [2] |
In Eq. 2, * denotes convolution, γ/2π is the gyromagnetic ratio (i.e. 42.58 MHz/T for 1H), B0 is the main magnetic field strength (in T), and represents the dipole response kernel, where θ is the angle with respect to the main magnetic field axis and r is the position vector. Eq. 2 can be equivalently represented in Fourier-space (21–23) as:
| [3] |
where k = [kx, ky, kz] denotes the location in Fourier-space, and kH represents the conjugate transpose of k. By convention, the z-axis is oriented along the superior-inferior direction (i.e. direction of the main magnetic field) and the x-y plane is the plane orthogonal to this axis. In a Cartesian acquisition, the points along the z-axis can be calculated as [-Nz/2:Nz/2-1]/FOVz, where Nz (assumed to be an even value) and FOVz are the number of acquired points and the field-of-view in the z-direction, respectively (similar for the x- and y- directions). The value of ψs is undefined at k = 0. Since this point defines the DC offset of the B0 field in image space, it may be reasonable to set it to zero (23), although other offsets based on the center frequency of the magnet could be chosen. The calculation of ψs is typically performed in Fourier-space, rather than in image-space, because it is more computationally efficient. The image domain representation, ψs(r), can then be determined using the inverse Fourier transform of Eq. 3. Note that d(r) and χ(r) must be appropriately zero-padded before Fourier transform to avoid the effects of circular convolution when evaluating Eq. 3 (28).
The susceptibility-induced field that is calculated using Eq. 3 serves as the object-based field map estimate. This object-based field map estimate is demodulated from the multi-echo sources images, as shown in Eq. 4, where N̂ represents complex AWGN.
| [4] |
The resultant multi-echo source images, ŝ(tn), are expected to have a majority of the B0 field demodulated by this object-based field map estimate. The demodulation step is expected to simplify the task of the subsequent water-fat separation algorithm, which must now only correct for the slowly varying background field (ψb) and any remaining susceptibility-induced field component (ψs − ψ̂s).
Due to the nonlocal response of the dipole kernel in Eq. 2 (24), calculation of ψ̂s requires 3D information about the susceptibility distribution. However, approximating the susceptibility distribution in regions outside of the imaging field-of-view (FOV) is not possible without additional assumptions, and therefore an incomplete estimation of the susceptibility-induced field may occur near the edges of the imaging FOV. These effects were analyzed via the point-spread function (PSF) of the dipole kernel d(r). In particular, we focused on the PSF along the slice-encoding direction because many water-fat separation algorithms impose field map constraints only in 2D, and thus may be least robust to these artifacts along the slice-encoding direction.
METHODS
Experiments were conducted after obtaining informed consent and IRB approval using a clinical 1.5T scanner (HDxt, v16.0, GE Healthcare, Waukesha, WI) and a clinical 3T scanner (MR750 v22.0, GE Healthcare, Waukesha, WI). Cardiac datasets were acquired in 28 subjects using a 3D free-breathing, navigated, cardiac-gated four-echo SPGR sequence (29). Data were also acquired in the ankle from six volunteers and in the brachial plexus from five volunteers (one volunteer was scanned twice, on different days) using a 3D three-echo SPGR sequence. Lastly, data were acquired in the abdomen from ten volunteers using a 3D breath-held six-echo (six monopolar echoes per TR) SPGR sequence. We were unable to acquire the abdominal datasets using a true dual-echo acquisition because of the unavailability of the product reconstruction pipeline, which was needed to obtain the source images from the acquired data. To serve as a surrogate, a six-echo acquisition was used, from which the source images at two echoes could be extracted. The source images at echoes 4 and 5 were selected because they maximized the effective number of signal averages (NSA) over all possible echo combinations for this particular six-echo acquisition (8). Table 1 lists the acquisition parameters for each of the datasets that are presented in this work.
Table 1.
Acquisition parameters for each of the datasets presented in this work. Each dataset was acquired using a 3D SPGR sequence. nTE denotes the number of echo times and ΔTE represents the echo time spacing.
| Anatomy | Matrix Size | Imaging Plane |
B0 Field (T) |
nTE | TE1 (ms) |
ΔTE (ms) |
|---|---|---|---|---|---|---|
| Cardiac | 256×256×50 | Axial | 3 | 4 | 1.22 | 0.98 |
| Ankle | 256×256×48 | Sagittal | 1.5 | 3 | 1.984 | 1.588 |
| Brachial Plexus | 256×256×30 | Coronal | 1.5 | 3 | 1.984 | 1.588 |
| Abdomen | 256×256×28 | Axial | 1.5 | 2* | 7.42* | 2.06 |
The abdominal datasets were acquired using a six-echo acquisition, however only echoes 4 and 5 were used for the dual-echo, voxel-independent reconstruction.
Prior to any further processing, the raw source images were corrected for the effects of gradient nonlinearity and were coil-combined using an adaptive phase preserving algorithm (30). Because the proposed method uses object-based information, it was important to correct for the gradient nonlinearity effects, which introduce image distortions, before generating the estimate of the B0 field. All further processing was then done in Matlab (The Mathworks Inc., Natick, MA) (64-bit Linux, 4 Octo Core AMD 6134, 128 GB RAM).
The coil-combined multi-echo source images were first processed using algorithms from the ISMRM Fat-Water Toolbox (31). To demonstrate the general applicability of the proposed method, the cardiac datasets were processed using a graphcut algorithm (15), the brachial plexus datasets were processed using hierarchical IDEAL (19), the ankle datasets were processed using a region-merging algorithm (12), and the abdominal datasets were processed using a dual-echo method with flexible choice of echo times (8). Note that the dual-echo algorithm that appears in the Fat-Water Toolbox is a voxel-independent method, which does not incorporate neighborhood information when estimating the phase shifts that are caused by B0 inhomogeneity.
For the dual-echo algorithm, the weighted smoothing of the phasors was found to increase the occurrence of incomplete water-fat separation. Therefore, the smoothing was removed from the reconstruction. Other than this modification, no changes were made to the default settings of each algorithm in the Fat-Water Toolbox. For those algorithms that implemented water-fat separation in 2D, the 3D datasets were processed on a slice-by-slice basis.
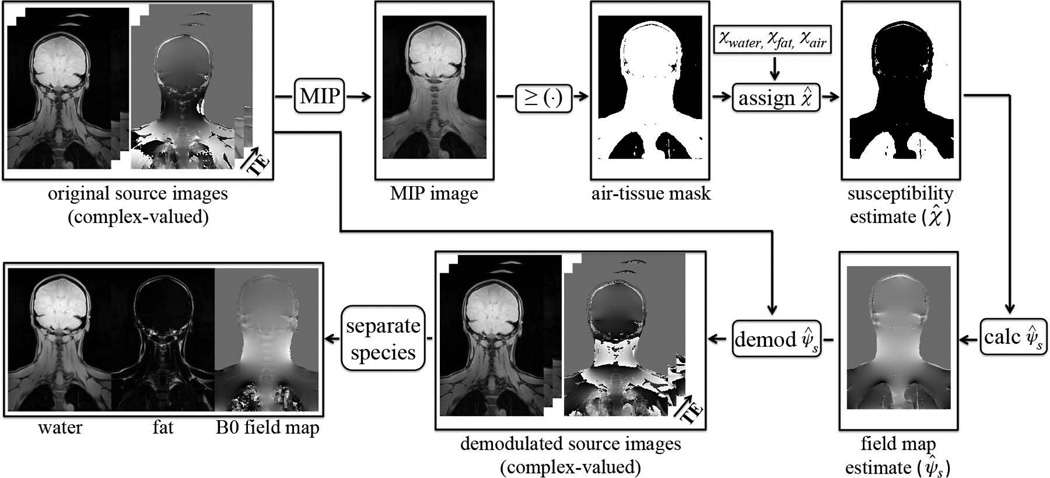
Each dataset was then processed a second time using the identical algorithm as described above, but after the object-based field map estimate had been first demodulated from the multi-echo source images. The object-based field map was estimated using the source images that were acquired at multiple echo times. Figure 1 shows a flowchart of the proposed approach. A maximum intensity projection (MIP) image was calculated from the multi-echo source images by projecting along the echo time dimension. A binary mask consisting of regions that contain either air or tissue was then created from the MIP image. To create the binary mask, an air-tissue threshold was set at 5% of the maximum value in the MIP image. Those voxels in the MIP that were below the threshold were considered to contain air while those above the threshold were considered to contain tissue. An estimated susceptibility distribution (χ̂) was generated from the binary mask, using the known susceptibility values of water, fat, and air (32,33). Because water-fat separation had not yet occurred, an equal distribution of water and fat was assumed, to minimize the maximum error of the susceptibility estimate over all possible water-fat ratios. A susceptibility value of −8.42ppm was assumed, which is the average of the susceptibility of water (−9.05ppm) and fat (−7.79ppm) (32,33). For the voxels containing air, a susceptibility value of 0.36ppm was used (32). The estimated susceptibility-induced field (ψ̂s) was then calculated via Eq. 3. To compensate for center frequency shifts during pre-scan, a constant shift was applied to ψ̂s such that its mean value over the regions of tissue was zero. Finally, the susceptibility-induced field was demodulated from the original multi-echo source images.
Figure 1.
Flowchart of the proposed approach. A maximum intensity projection (MIP) image is calculated from the multi-echo source images by projecting along the echo time dimension. An air-tissue mask is then created from the MIP image. The estimated susceptibility distribution is generated from the air-tissue mask, using the known susceptibility value of air and the mean of the values of water and fat. The estimated susceptibility-induced field is calculated and is then demodulated from the original source images. Finally, the demodulated source images serve as the input into any water-fat separation algorithm.
The demodulated multi-echo source images were processed with the same algorithm that was used to process the original source images. The two results (i.e. with and without demodulation of the object-based field map estimate) were visually compared to determine whether using the object-based field map information improved the quality of the water-fat separation. In addition, the total reconstruction time for each approach was computed using the Matlab profile function.
RESULTS
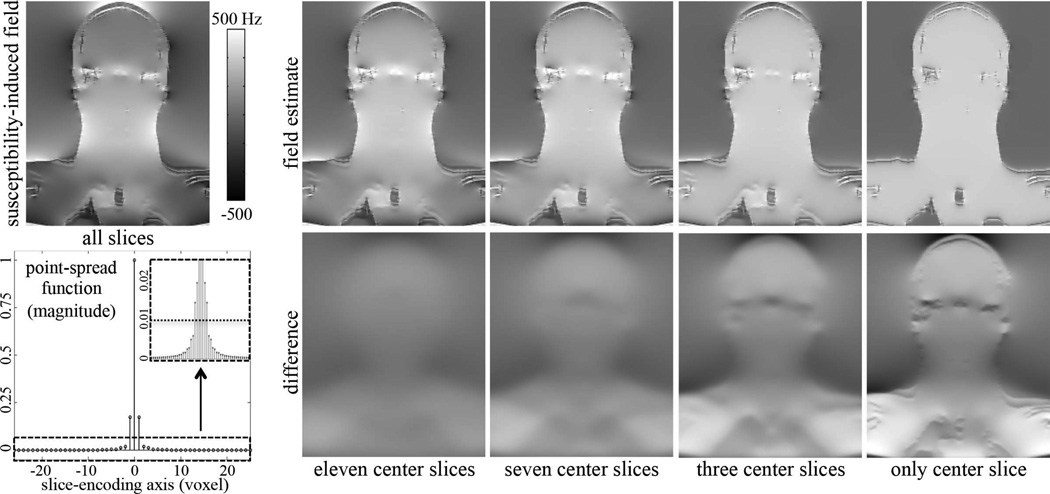
Figure 2 shows the susceptibility-induced field for the center slice of a 3D acquisition that was estimated using all slices of the volume. The PSF of the dipole kernel along the slice-encoding axis is also shown. The PSF was normalized such that its maximum value equals one. It is important to note that the energy of the PSF is concentrated near the origin, which suggests that only a small subset of the neighboring slices, rather than the full 3D volume, may be used to sufficiently represent the susceptibility-induced field at the center slice. To determine the number of neighboring slices, a threshold on the magnitude of the normalized PSF was established. From the inset of the PSF in Figure 2, a sharp transition is observed as the coefficient magnitudes cross a value of 0.01. Using this threshold of 0.01, a total of only seven slices (i.e. three slices on each side of the center slice) would be required to represent the susceptibility-induced field at the center slice. Figure 2 shows the susceptibility-induced fields that were estimated using only a subset of the total slices, as well as their corresponding differences. It is seen that the field estimate using only the seven center slices captures much of the susceptibility-induced variations. The PSF was computed assuming that the 3D acquisition was done in the coronal plane. Similar results (not shown) were found for both sagittal and axial acquisitions.
Figure 2.
(top left): The susceptibility-induced field that was calculated using all slices of a 3D acquisition. (bottom left): The point-spread function (PSF) of the dipole kernel along the slice-encoding axis. Notice that the energy of the PSF is concentrated near the origin, which suggests that only a subset of the neighboring slices may be used to calculate the susceptibility-induced field at the center slice. A threshold of 0.01 was established (dotted line), which corresponded to a total of seven slices (i.e. three slices on each side of the center slice). (right): The susceptibility-induced fields that were estimated using only a subset of the total slices, as well as the corresponding difference images. Using only the seven center slices captures much of the susceptibility-induced variations.
Water-fat swaps were visually observed in six of the 28 cardiac datasets that were processed using graphcut. All observed swaps occurred near the dome of the liver. The proposed method resolved the swaps in all six cases and did not introduce any new swaps. Figure 3 shows the water and fat estimates from one cardiac dataset, with and without the object-based field map information. A swap was observed in the dome of the liver when using graphcut alone. By first demodulating the object-based field map estimate from the original multi-echo source images, the graphcut method was able to correctly separate water and fat. For reference, both the object-based field map estimate and the final field map estimate are shown. It is seen that the object-based field map estimate provided an accurate estimate of the B0 field. The calculation and demodulation of the object-based field map estimate took 3.3s for the entire 3D dataset. For comparison, the average reconstruction time for each 2D slice using graphcut (with or without demodulation of the object-based field map estimate) was 18s, or approximately 15 minutes for the 50 slices.
Figure 3.
Water, fat, and B0 field estimates using a graphcut algorithm, without and with the object-based field map information. The B0 field estimate in the bottom row is shown as a sum of the object-based field estimate and the remaining field that was estimated by graphcut. A swap is observed in the dome of the liver when using graphcut alone (white arrow). When the object-based field map estimate is first demodulated from the original source images, the graphcut method correctly separates the water and fat signals. Further, notice that the object-based field map estimate provides an accurate estimate of the B0 field map. In the liver dome, the mean / minimum / maximum differences between the object-based estimate and the final estimate were 16.7 / −64.1 / 77.5Hz, respectively.
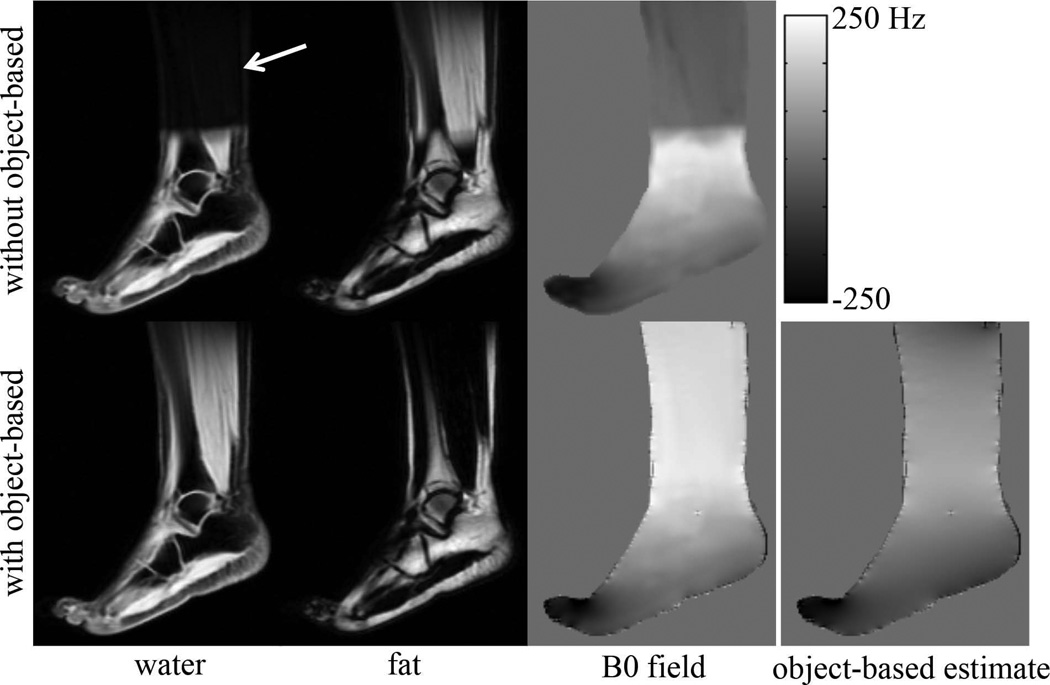
Water-fat swaps were observed in three of the six ankle datasets that were processed using region-merging. The proposed method resolved the swaps in all three cases and did not introduce any new swaps. Figure 4 shows the water and fat estimates from one of the ankle datasets using region-merging, with and without the object-based field map information. The severe B0 field inhomogeneity in this anatomy caused a swap of the water and fat signals when using region-merging alone. By first demodulating the object-based field map estimate from the original source images, region-merging successfully separated the water and fat signals. Calculation and demodulation of the 3D object-based field map estimate required 1.9s of computation time for the entire 3D dataset. The average reconstruction time for each 2D slice using region-merging (with or without demodulation of the object-based field map estimate) was 31s, or approximately 25 minutes for the 48 slices.
Figure 4.
Water, fat, and B0 field estimates in the ankle using a region-merging algorithm, without and with the object-based field map information. The B0 field estimate in the bottom row is shown as a sum of the object-based field estimate and the remaining field that was estimated by region-merging. The rapidly varying B0 field in this anatomy caused a swap when the source images were processed using only region-merging (white arrow). By first demodulating the object-based field map estimate from the source images, region-merging was able to correctly separate the water and fat signals. The object-based field map estimate provided an accurate estimate of the field inhomogeneity, especially in the region of the toe.
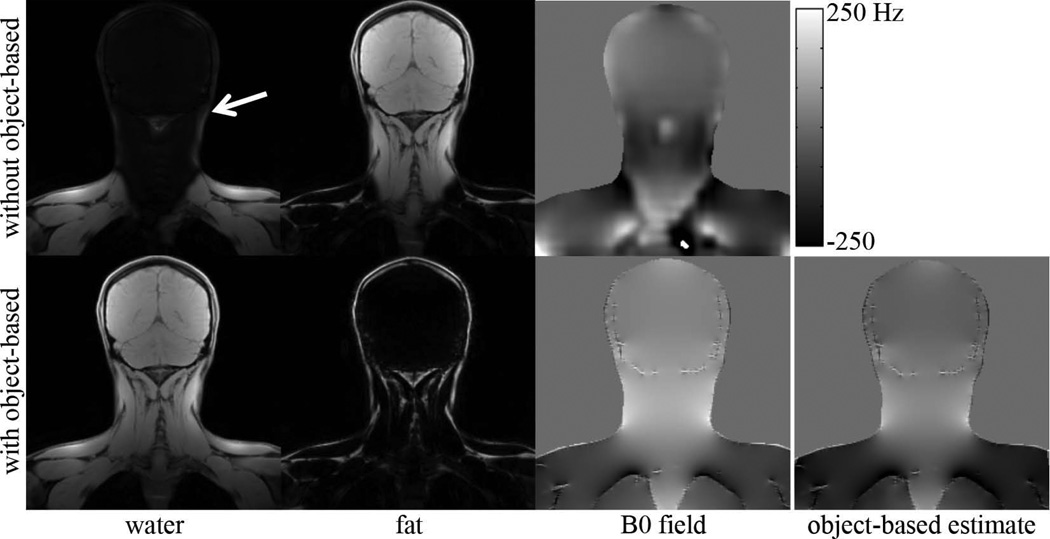
Water-fat swaps were observed in four of the six brachial plexus datasets that were processed using hierarchical IDEAL. The proposed method resolved the swaps in all four cases and it did not introduce any new swaps. Figure 5 shows the water and fat estimates of the brachial plexus using hierarchical IDEAL, with and without the object-based field map estimate. The water and fat estimates using only hierarchical IDEAL exhibited swaps of the water and fat signals. In contrast, by first demodulating the object-based field map estimate from the original source images, hierarchical IDEAL was able to correctly separate the water and fat signals. Calculation and demodulation of the object-based field map estimate took 2.1s for the entire 3D dataset. The reconstruction time for the 3D volume using hierarchical IDEAL (with or without demodulation of the object-based field map estimate) was approximately 55s.
Figure 5.
Water, fat, and B0 field estimates in the brachial plexus using hierarchical IDEAL, without and with the object-based field map information. The B0 field estimate in the bottom row is shown as a sum of the object-based field estimate and the remaining field that was estimated by hierarchical IDEAL. Water-fat swaps in the head and neck (white arrow) are properly resolved by hierarchical IDEAL only when the object-based field map estimate is first demodulated from the source images.
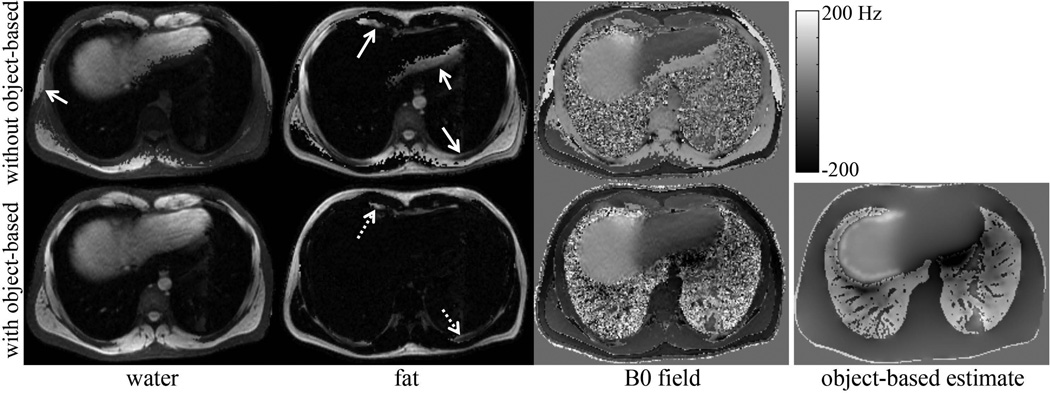
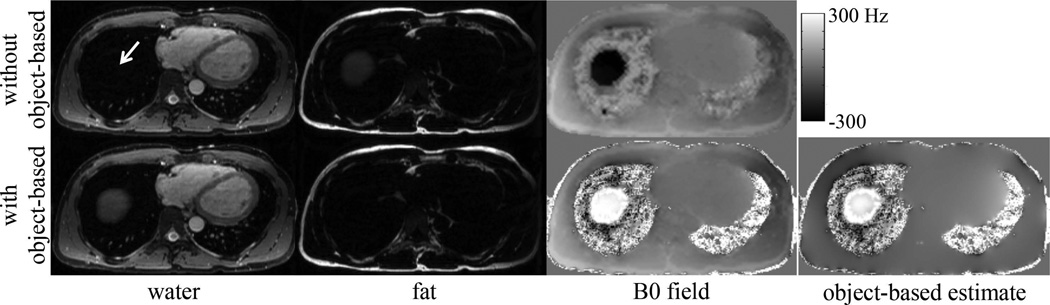
Water-fat swaps were observed in all of the abdominal datasets that were reconstructed using the dual-echo, voxel-independent method. This was expected due to the known limitation of voxel-independent methods to robustly estimate the B0 field map in regions of severe field inhomogeneity. The proposed method was unable to resolve all of the swaps, however a marked improvement in the water-fat separation was observed especially at the air-tissue interfaces. Figure 6 shows the water, fat, and B0 field map estimates from one subject using the dual-echo, voxel-independent method and the proposed method. Water-fat swaps were largely resolved when the object-based field map estimate was first demodulated, however swaps are still visible. The calculation and demodulation of the object-based field map estimate took 1.9s for the entire 3D dataset. The reconstruction time for the 3D volume using the dual-echo, voxel-independent method (with or without demodulation of the object-based field map estimate) was approximately 1.2s.
Figure 6.
Water, fat, and B0 field map estimates in the abdomen using a voxel-independent algorithm, without and with the object-based field map information. Numerous swaps are seen throughout the abdomen, some of which are highlighted (solid arrows). By first demodulating the object-based field map estimate, the voxel-independent method demonstrates an improvement in the water-fat separation. However, some swaps are still visible in the reconstructed images (dashed arrows).
DISCUSSION
In this work we have described a novel technique that augments existing chemical shift encoded water-fat separation methods by incorporating object-based information of the B0 field map into the reconstruction. We have demonstrated that using this information can improve the robustness of existing water-fat separation methods. We propose that this approach may be effective as a preprocessing of the multi-echo source images, and therefore should be applicable to any complex-based chemical shift encoded water-fat separation method. The primary advantage of this approach is that it exploits a physical property of the imaging volume (i.e. susceptibility distribution based on the anatomy) rather than relying solely on assumptions of field map smoothness. It is particularly applicable when imaging regions in which the B0 field map varies rapidly, either due to abrupt changes in the susceptibility distribution or in anatomy with irregular geometry.
The calculation of the object-based field map estimate was implemented efficiently using a point-wise multiplication in Fourier-space. In all examples, the calculation and demodulation of the 3D object-based field map took less than 3.5s seconds, representing a minimal increase to the overall reconstruction time while consistently improving the robustness of water-fat separation. No significant difference in the reconstruction time of the water-fat separation algorithm was observed after using the object-based field map estimate. However, because this estimate is a fairly accurate representation of the true B0 field, it may be possible to reduce the reconstruction time, particularly for iterative gradient-based methods with carefully chosen convergence criteria. In this work, the default criterion for each algorithm was used.
The main limitation of this approach is related to the assumption of the magnetic susceptibility distribution. The assumptions used in this work should be valid for most situations unless there is a foreign body with high susceptibility (e.g. metallic prosthesis). Further, iron is the only naturally occurring substance with high susceptibility that can occur in high concentration within tissue. In the case of tissue iron overload, it may be possible to approximate the R2* from the multi-echo source images, and use that value to estimate the susceptibility of those tissues (34). In addition, the air-tissue mask was determined by using a 5% threshold on the MIP image. The accuracy of the object-based field map estimate will be affected by the accuracy of the air-tissue mask, however we have found that setting a threshold value within a range of 3-9% does not significantly affect the final water-fat separation. When using thresholds above 9%, the bone, which has a susceptibility value close to that of tissue (32), may be masked as air. This error in the air-tissue masking may introduce error in the object-based field map estimate. It should be noted that the air-tissue masking algorithm that we have used was sufficient for the cases that were tested in this work, and that the modular nature of our proposed framework would allow the use of more sophisticated air-tissue masking algorithms.
The forward calculation of the field inhomogeneity requires 3D information of the susceptibility distribution. Thus, the proposed method may not be suitable for 2D imaging unless multiple closely spaced slices are acquired, providing an accurate 3D representation of the tissue. Further, incomplete estimation of the susceptibility-induced field in 3D acquisitions may occur at the edges of the imaging FOV. For the slices at either edge of the imaging volume, one may be able to synthetically extend the imaging volume by replicating or extrapolating the edge slices. This would only serve as an approximation of the actual slices, but it may be adequate for improving the accuracy of the field map estimate for the edge slices. Based on our analysis of the point-spread function of the dipole kernel, we estimate that errors in the estimate of the susceptibility-induced field map may occur for the three slices at each end of a 3D volume. Further work is required to determine the performance of the proposed algorithm at the edges of volumetric acquisitions.
Finally, the proposed method was not tested using data from a true dual-echo acquisition. This was not possible due to the unavailability at our site of the product reconstruction pipeline that was needed to obtain the complex-valued, gradient nonlinearity-corrected source images from the acquired data. Indeed, the proposed method may provide greatest benefit to two-point water-fat separation algorithms, which are widely used for 3D volumetric imaging and are known to be especially vulnerable to swaps because of the limited number of measurements.
In conclusion, we have described a novel approach to improve the robustness of existing water-fat separation algorithms by incorporating object-based information of the B0 field inhomogeneity. This approach can be applied to any complex-based chemical shift encoded water-fat separation technique. Initial results are highly promising for improving the robustness of water-fat separation.
ACKNOWLEDGEMENTS
The authors thank the developers of and contributors to the ISMRM Fat-Water Toolbox. They also thank Valentina Taviani, PhD for the cardiac datasets used in this study. They acknowledge the support of the NIH (RC1 EB010384, R01 DK083380, R01 DK088925, and R01 DK096169), and the Wisconsin Alumni Research Foundation (WARF) Accelerator Program. They also wish to thank GE Healthcare for their support.
REFERENCES
- 1.Dixon WT. Simple proton spectroscopic imaging. Radiology. 1984;153:189–194. doi: 10.1148/radiology.153.1.6089263. [DOI] [PubMed] [Google Scholar]
- 2.Glover GH, Schneider E. Three-point Dixon technique for true water/fat decomposition with B0 inhomogeneity correction. Magn Reson Med. 1991;18:371–383. doi: 10.1002/mrm.1910180211. [DOI] [PubMed] [Google Scholar]
- 3.Bydder G, Steiner R, Blumgart L, Khenia S, Young I. MR imaging of the liver using short TI inversion recovery sequences. J Computer Assisted Tomography. 1985;9:1084–1089. doi: 10.1097/00004728-198511000-00015. [DOI] [PubMed] [Google Scholar]
- 4.Yu H, Reeder SB, McKenzie CA, Brau AC, Shimakawa A, Brittain JH, Pelc NJ. Single acquisition water-fat separation: feasibility study for dynamic imaging. Magn Reson Med. 2006;55:413–422. doi: 10.1002/mrm.20771. [DOI] [PubMed] [Google Scholar]
- 5.Ma J. Breath-hold water and fat imaging using a dual-echo two-point Dixon technique with an efficient and robust phase-correction algorithm. Magn Reson Med. 2004;52:415–419. doi: 10.1002/mrm.20146. [DOI] [PubMed] [Google Scholar]
- 6.Xiang QS. Two-point water-fat imaging with partially-opposed-phase (POP) acquisition: an asymmetric Dixon method. Magn Reson Med. 2006;56:572–584. doi: 10.1002/mrm.20984. [DOI] [PubMed] [Google Scholar]
- 7.Eggers H, Brendel B, Duijndam A, Herigault G. Dual-echo Dixon imaging with flexible choice of echo times. Magn Reson Med. 2011;65:96–107. doi: 10.1002/mrm.22578. [DOI] [PubMed] [Google Scholar]
- 8.Berglund J, Ahlstrom H, Johansson L, Kullberg J. Two-point Dixon method with flexible echo times. Magn Reson Med. 2011;65:994–1004. doi: 10.1002/mrm.22679. [DOI] [PubMed] [Google Scholar]
- 9.Xiang QS, An L. Water-fat imaging with direct phase encoding. J Magn Reson Imaging. 1997;7(6):1002–1015. doi: 10.1002/jmri.1880070612. [DOI] [PubMed] [Google Scholar]
- 10.Reeder SB, Wen Z, Yu H, Pineda AR, Gold GE, Markl M, Pelc NJ. Multicoil Dixon chemical species separation with an iterative least-squares estimation method. Magn Reson Med. 2004;51:35–45. doi: 10.1002/mrm.10675. [DOI] [PubMed] [Google Scholar]
- 11.Yu H, Reeder SB, Shimakawa A, Brittain JH, Pelc NJ. Field map estimation with a region growing scheme for iterative 3-point water-fat decomposition. Magn Reson Med. 2005;54:1032–1039. doi: 10.1002/mrm.20654. [DOI] [PubMed] [Google Scholar]
- 12.Lu W, Hargreaves BA. Multiresolution field map estimation using golden section search for water-fat separation. Magn Reson Med. 2008;60:236–244. doi: 10.1002/mrm.21544. [DOI] [PubMed] [Google Scholar]
- 13.Hernando D, Haldar JP, Sutton BP, Ma J, Kellman P, Liang ZP. Joint estimation of water/fat images and field inhomogeneity map. Magn Reson Med. 2008;59:571–580. doi: 10.1002/mrm.21522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jacob M, Sutton BP. Algebraic decomposition of fat and water in MRI. IEEE Trans Med Imaging. 2009;28:173–184. doi: 10.1109/TMI.2008.927344. [DOI] [PubMed] [Google Scholar]
- 15.Hernando D, Kellman P, Haldar J, Liang ZP. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magn Reson Med. 2010;63:79–90. doi: 10.1002/mrm.22177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Doneva M, Bornert P, Eggers H, Mertins A, Pauly J, Lustig M. Compressed sensing for chemical shift-based water-fat separation. Magn Reson Med. 2010;64:1749–1759. doi: 10.1002/mrm.22563. [DOI] [PubMed] [Google Scholar]
- 17.Berglund J, Johansson L, Ahlstrom H, Kullberg J. Three-point Dixon method enables whole-body water and fat imaging of obese subjects. Magn Reson Med. 2010;63:1659–1668. doi: 10.1002/mrm.22385. [DOI] [PubMed] [Google Scholar]
- 18.Sharma SD, Hu HH, Nayak KS. Accelerated water–fat imaging using restricted subspace field map estimation and compressed sensing. Magn Reson Med. 2012;67:650–659. doi: 10.1002/mrm.23052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tsao J, Jiang Y. Hierarchical IDEAL: fast, robust, and multiresolution separation of multiple chemical species from multiple echo times. Magn Reson Med. 2013;70:155–159. doi: 10.1002/mrm.24441. [DOI] [PubMed] [Google Scholar]
- 20.Yu H, Reeder SB, Shimakawa A, McKenzie CA, Brittain JH. Robust multipoint water-fat separation using fat likelihood analysis. Magn Reson Med. 2012;67:1065–1076. doi: 10.1002/mrm.23087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Salomir R, de Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering. 2003;19B:26–34. [Google Scholar]
- 22.Marques JP, Bowtell R. Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering. 2005;25B:65–78. [Google Scholar]
- 23.Koch KM, Papademetris X, Rothman DL, de Graaf RA. Rapid calculations of susceptibility-induced magnetostatic field perturbations for in vivo magnetic resonance. Phys Med Biol. 2006;51:6381–6402. doi: 10.1088/0031-9155/51/24/007. [DOI] [PubMed] [Google Scholar]
- 24.de Rochefort L, Brown R, Prince MR, Wang Y. Quantitative MR susceptibility mapping using piece-wise constant regularized inversion of the magnetic field. Magn Reson Med. 2008;60:1003–1009. doi: 10.1002/mrm.21710. [DOI] [PubMed] [Google Scholar]
- 25.Yu H, Shimakawa A, McKenzie CA, Brodsky E, Brittain JH, Reeder SB. Multiecho water-fat separation and simultaneous R2* estimation with multifrequency fat spectrum modeling. Magn Reson Med. 2008;60:1122–1134. doi: 10.1002/mrm.21737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hamilton G, Yokoo T, Bydder M, Cruite I, Schroeder ME, Sirlin CB, Middleton MS. In vivo characterization of the liver fat 1H MR spectrum. NMR Biomed. 2011;24:784–790. doi: 10.1002/nbm.1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yu H, McKenzie CA, Shimakawa A, Vu AT, Brau AC, Beatty PJ, Pineda AR, Brittain JH, Reeder SB. Multiecho reconstruction for simultaneous water-fat decomposition and T2* estimation. J Magn Reson Imaging. 2007;26:1153–1161. doi: 10.1002/jmri.21090. [DOI] [PubMed] [Google Scholar]
- 28.Porat B. A course in digital signal processing. New York: Wiley; 1997. [Google Scholar]
- 29.Taviani V, Hernando D, Francois CJ, Shimakawa A, Vigen KK, Nagle SK, Schiebler ML, Grist TM, Reeder SB. Whole-heart chemical shift encoded water-fat MRI. Magn Reson Med. doi: 10.1002/mrm.24982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med. 2000;43:682–690. doi: 10.1002/(sici)1522-2594(200005)43:5<682::aid-mrm10>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 31.Hu HH, Bornert P, Hernando D, Kellman P, Ma J, Reeder S, Sirlin C. ISMRM workshop on fat-water separation: insights, applications and progress in MRI. Magn Reson Med. 2012;68:378–388. doi: 10.1002/mrm.24369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996;23:815–850. doi: 10.1118/1.597854. [DOI] [PubMed] [Google Scholar]
- 33.Hopkins JA, Wehrli FW. Magnetic susceptibility measurement of insoluble solids by NMR: magnetic susceptibility of bone. Magn Reson Med. 1997;37:494–500. doi: 10.1002/mrm.1910370404. [DOI] [PubMed] [Google Scholar]
- 34.Hernando D, Cook RJ, Diamond C, Reeder SB. Magnetic susceptibility as a B0 field strength independent MRI biomarker of liver iron overload. Magn Reson Med. 2013;70:648–656. doi: 10.1002/mrm.24848. [DOI] [PMC free article] [PubMed] [Google Scholar]