A Systems Approach to Integrative Biology: An Overview of Statistical Methods to Elucidate Association and Architecture

Abstract

An organism’s ability to maintain a desired physiological response relies extensively on how cellular and molecular signaling networks interpret and react to environmental cues. The capacity to quantitatively predict how networks respond to a changing environment by modifying signaling regulation and phenotypic responses will help inform and predict the impact of a changing global enivronment on organisms and ecosystems. Many computational strategies have been developed to resolve cue–signal–response networks. However, selecting a strategy that answers a specific biological question requires knowledge both of the type of data being collected, and of the strengths and weaknesses of different computational regimes. We broadly explore several computational approaches, and we evaluate their accuracy in predicting a given response. Specifically, we describe how statistical algorithms can be used in the context of integrative and comparative biology to elucidate the genomic, proteomic, and/or cellular networks responsible for robust physiological response. As a case study, we apply this strategy to a dataset of quantitative levels of protein abundance from the mussel, Mytilus galloprovincialis, to uncover the temperature-dependent signaling network.

Introduction

Regulatory systems are ubiquitous in biology and span all physical levels from genomic regulation to signal transduction and ecological networks. Emergent phenomena are a property of biological systems and are, by definition, responses that cannot be deduced from the sum of all parts; emergent behavior is fundamentally non-intuitive (Funtowicz and Ravetz 1994). Integration of experimental data with systems-level computational models enables greater understanding of emergent properties. For example, inference of a directed regulatory protein network can reveal emergent properties by uncovering dynamics through feedback and crosstalk (Bhalla and Iyengar 1999). Systems approaches have been rapidly embraced by many cellular and molecular biologists and have become commonplace in understanding high-volume datasets across a variety of experiments (Janes et al. 2004; Tong et al. 2004; Purvis et al. 2012). Similarly, the field of integrative and comparative biology is primed for the integration of computation with quantitative experimental data for the purpose of understanding regulation within and among organisms subject to different environmental perturbations. (Many systems approaches require understanding linear algebra; we encourage readers to familiarize themselves with the works of Gilbert Strang (2003) and Carl Meyer (2000)). In this study, we take a stepwise approach to observe emergent phenomenon by deriving a directed protein network in the organism, Mytilus galloprovincialis.

Cue–Signal–Response

Computational models can be used to resolve/elucidate complex relationships among observed system components, or state variables, and predict responses to unknown conditions. Such predictive models require quantitative data that sample a specified number of variables (p) under a specific number of conditions (n). Any condition that stimulates or perturbs a system is defined as a cue. Conditions vary in nature and include external stimuli or perturbations (e.g., different temperature conditions or the addition of a small molecule). Other conditions can reflect the number of replicate experiments or observed time points. Biological and technical replicates are necessary to quantify confidence and account for biological variance as well as instrument error. Additionally, sampling the p variables in time provides unmatched insight into dynamic regulation. Hence, the number of conditions, n, encompasses the number of perturbations, replicates, and time points for a given experiment.

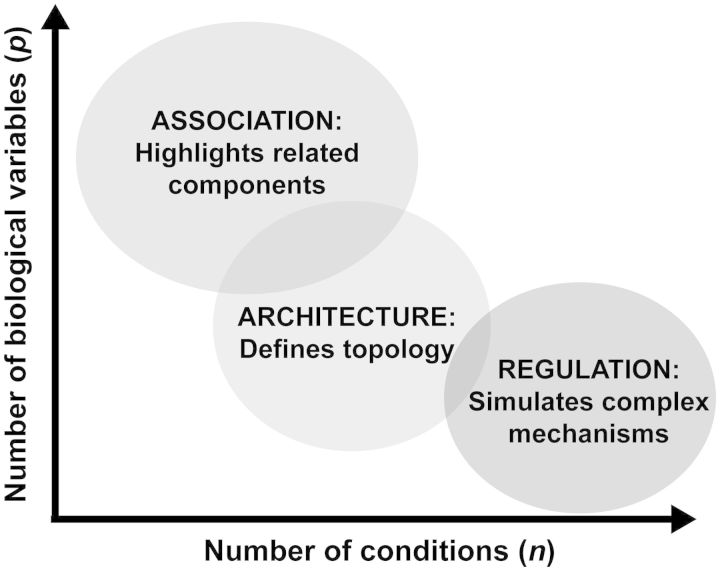
The final outcome of the experiment, often phenotypic, is defined as the response. The intermediate variables that aim to explain a specific response are signals. From these experimental data, we can define a cue–signal matrix, X, of n × p dimensions and a response vector, y, of n × 1 dimensions. While there is no hard rule for how many variables and conditions are necessary to produce a computational model, the general relationship between explanatory variables, conditions, and type of model is shown in Fig. 1. In general, increasing p can expand the likelihood of finding relevant variables that can accurately describe a given response. However, when p >> n, it is challenging to infer regulation, and algorithms often are limited to ascribing association. Increasing n by sampling diverse conditions can increase the variance of the data facilitating the identification of first-order regulation, or architecture, in systems such as cell signaling or ecological networks. Increasing n by the inclusion of replicates can add confidence to a given hypothesis (e.g., determining whether two proteins have significantly different abundance between conditions). Depending on the research question, it can be desirable to sample multiple replicates under a given condition, increase the search space by including diverse conditions, or a combination of both. If the signals are sampled at many unique time points, it is possible to gain insight into higher-order, dynamic regulation such as feedback and crosstalk (Zheng et al. 2013). Therefore, the size and structure of the experimental data can significantly impact the utility and application of computational strategies.

Fig. 1.

Relating data type and dimension to modeling strategies. Association, architecture, and regulation are three broad paradigms for mathematical modeling of biological systems. When the number of observed variables is significantly greater than the number of experimental conditions, computational strategies that inform association and correlation are most applicable. As the number of experimental conditions increases, one can begin to infer network topology and architecture. Regulation is best understood in the context of time, when system dynamics are appropriately evaluated.

All models are based on assumptions and therefore flawed; they provide an imperfect representation of the complexity inherent in biological systems. However, computational methods can be useful in guiding our understanding of the underlying complexity and predicting unknown responses. Selecting an informative model to answer a specific biological question requires balancing the strengths and limitation of each technique. Here, we discuss two broad categories of predictive modeling: association and network-architecture. Depending on the nature of the dataset, one or more of these methods can be useful. For each category, we discuss and apply representative algorithms that have been successfully implemented for other biological datasets (Jong 2002).

Temperature-mediated protein abundance and regulation in mussels

As filter-feeders, mussels are a keystone of the coastal ecosystem (Gosling et al. 1992). Mytilus galloprovincialis is a mussel of Mediterranean origin that over the past century has replaced the native Mytilus trossulus from southern California to the San Francisco bay (Braby and Somero 2006, 1). While M. galloprovincialis has been shown to be the more heat-resistant species (Braby and Somero 2006, 2), the effects of increased temperature and climatic change on this invasive species are still unknown. Modeling how protein abundance (signals) within this species respond to temperature (cue) can aid our understanding of how the coastal ecosystem can continue to change within a dynamic environment.

Through computational modeling, we seek to identify proteins that are most affected by changes in temperature. We use M. galloprovincialis as a model organism in a case study to demonstrate how the integration of experimental and computational techniques allows understanding of an organism’s responses to environmental cues. It is important to note that despite the focus of our study, the following methods are highly extensible and can be applied at different physical scales across cellular, organismal, and ecological levels.

Results

Mytilus galloprovincialis was subtidally collected. The animals were acclimatized to 13°C for 4 weeks and gradually exposed to 13°C, 24°C, 28°C, and 32°C (at a rate of 6°C/h). After a 1-h incubation at these temperatures, mussels were given time to synthesize proteins for 24 h at 13°C before gill tissue was dissected and analyzed for changes in protein abundance (Tomanek and Zuzow 2010). The gill tissue was solubilized and quantified by 2D electrophoresis. Each spot on the gel was identified using mass spectrometry. These data, outlined in Table 1, were previously published (Tomanek and Zuzow 2010). The study included 47 proteins (p) and 3 non-reference conditions (n). The cue in this example is temperature at 24°C, 28°C, and 32°C; proteins were normalized to measurements at 13°C.

Table 1.

Protein identifications (using MS/MS) of spots changing with temperature treatment in Mytilus galloprovincialis

ID	Protein name	Average protein levels (relative to 13°C)
		24	28	32
P1A	Hsp70	1.23	3.45	2.25
P2	Hsc70	3.41	1.69	1.67
P1B	Hsp70	2.06	2.44	13.25
P1C	Hsp70	0.95	2.97	5.80
P1D	Hsp70	1.64	0.74	2.30
P3	Hsp90	2.40	2.29	1.22
P4A	Alpha-crystalline-Hsp23	1.35	1.70	2.77
P4B	Alpha-crystalline-Hsp23	1.02	1.54	2.62
P4C	Alpha-crystalline-Hsp23	2.17	2.16	1.94
P5	Hsp27	0.73	3.17	3.74
P6	Proteasome-alpha-type_1	1.18	0.84	0.43
P7	Proteasome-alpha-type_6	0.64	0.74	0.73
P8	Proteasome-beta-type_3	0.65	0.53	0.46
P9	Proteasome-beta-type_2	0.81	0.49	0.49
P10	Proteasome-beta-type_6	0.80	1.27	2.38
P11	Arginine_kinase	0.79	0.40	0.32
P12	Pyrophosphatase	0.71	0.60	0.67
P13	Nucleoside_diphosphate_kinase	0.86	0.65	0.49
P14	Aspartate_amino_transferase	0.90	0.60	0.43
P15	Phosphoenol_pyruvate_carboxykinase	0.21	0.36	0.44
P16	Cytosolic_malate_dehydrogenase	0.99	0.96	0.72
P17A	Isocitrate_dehydrogenase_(NADP)	0.72	0.75	0.76
P17B	Isocitrate_dehydrogenase_(NADP)	2.11	2.43	3.41
P17C	Isocitrate_dehydrogenase_(NADP)	0.56	0.49	0.52
P18A	Cu-Zn_Superoxide_dismutase	1.02	0.19	0.24
P18B	Cu-Zn_Superoxide_dismutase	1.24	5.88	9.66
P19	Thiamine_pyrophosphate_transketolase	1.56	1.04	1.20
P20	6-Phospho-glucono_lactonase	0.80	1.96	3.56
P21A	Alpha-tubulin	1.29	1.56	1.00
P21B	Alpha-tubulin	1.23	1.50	0.84
P21C	Alpha-tubulin	1.25	0.64	0.25
P21D	Alpha-tubulin	0.58	0.48	1.10
P22A	Beta-tubulin	1.20	2.32	1.79
P22B	Beta-tubulin	1.37	1.36	1.08
P22C	Beta-tubulin	1.28	0.54	0.62
P22D	Beta-tubulin	1.01	1.32	0.65
P22E	Beta-tubulin	1.52	1.93	0.79
P23	Gelsolin	1.20	0.95	0.73
P24A	Actin	0.64	0.89	1.08
P24B	Actin	0.42	0.48	1.20
P25A	G-protein_beta-subunit	1.36	1.13	0.35
P25B	G-protein_beta-subunit	1.14	0.87	0.70
P26	Ras-like_GTP-binding_protein_RhoA	0.54	2.05	2.42
P27A	Major_vault_protein	1.17	0.68	0.45
P27B	Major_vault_protein	1.15	0.75	0.65
P27C	Major_vault_protein	0.37	1.13	2.16
P28	Ribosomal_protein_2S	2.09	1.87	3.03

Source: Table reproduced from data in Tomanek 2010.

Association

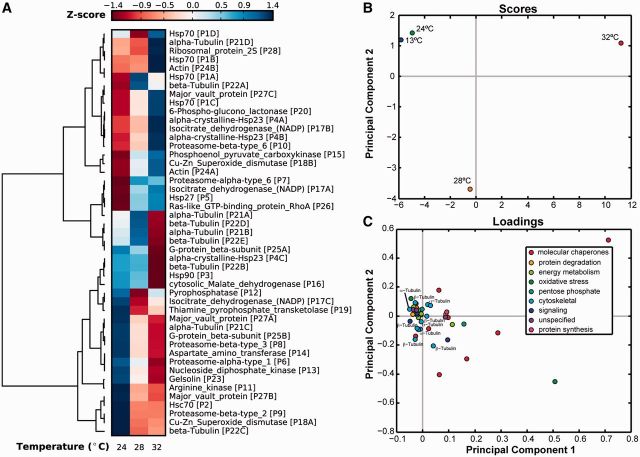
Associations can inform the type of relationship or interaction among input variables and output variables. Variables with similar functions, upstream regulators, or stimuli can respond similarly and cluster together in a dataset. Clustering techniques are used to identify variables that exhibit similar characteristics within the scope of the data. Figure 2A displays the z-scored data on protein abundance in a clustered heat map. Hierarchical clustering, on the left of the heat map, identifies proteins that are statistically similar. Clustering was performed by mean-centering and scaling each variable (protein abundance) to unit variance and identifying pairwise linkages using Ward’s method of minimum variance (Ward 1963). There are various methods of preprocessing data that can affect the corresponding results and interpretation. We z-scored the data in order to identify qualitatively similar clusters across conditions instead of identification of quantitatively similar clusters based on the magnitude of the variance. The Ward method was chosen among other possible multiple-linkage methods because studies have shown that it reflects the highest accuracy in separating randomly generated bivariate data when the number of members in each group are relatively equal (Ferreira and Hitchcock 2009).

Fig. 2.

(A) Heatmap of protein abundances in M. galloprovincialis. Protein abundances are normalized by taking the z-score of each predictor variable across conditions. Columns represent protein abundances at the given temperature in °C relative to those at 13°C. This figure was produced from data in Tomanek and Zuzow (2010). Protein names are followed by the ID number to differentiate similar proteins. Ward hierarchical clustering reveals that proteins in similar functional groups exhibit similar protein expression data. Tight clustering of the tubulin family shows that the experimental design and clustering method capture most of the variance in the data. PCA of relative protein abundances in M. galloprovincialis at 13°C, 24°C, 28°C and 32°C. The scores (B) and loadings (C) from PC decomposition are shown with the inclusion of the first two PCs. The scores show that the data at 13°C and 24°C have the most similarity. The loadings are colored according to their putative functional group. Both α-tubulin and β-tubulin proteins are labeled and cluster tightly together.

Treating replicates as separate conditions can validate the computational analysis. If replicates do not have a close linkage, it is possible that the algorithm is inappropriate for the structure of the data or that there are extrinsic sources of variance. These sources can include technical error, biological variance, or other factors outside of the scope of experimental design and control. In addition, comparison of analysis results with prior biological knowledge further validates the results. Since our data are without biological replicates, we can only validate the clustering method on prior knowledge.

We observed the clustering of closely related proteins in the tubulin family supporting validity of the computational method. In addition, many of the proteins cluster into canonical cytoskeletal, energy metabolism, and molecular chaperone functional groups.

Principal component analysis

Principal component analysis (PCA) transforms a high-dimensional dataset, through linear projection, into a lower dimensional space (Smith 2002). The first principal component (PC) is the latent or hidden variable, a linear combination of measured variables, that captures the most variance in the data. The second PC explains the most variance remaining after the first PC has been removed from the dataset, and so forth. Each PC exposes an underlying source of variance within the data, which can correspond to a condition such as a biological process or molecular function. While the actual meaning of each PC cannot be validated, it can be inferred from information outside of the numerical model.

The scores show the relationship between conditions (in this case, temperature) and the loadings show the relationship among variables (in this case, specific proteins). Variables with similar scores and loadings tend to cluster more tightly than less similar variables. Figure 2B shows the scores of the dataset. Figure 2C shows the loadings of the mussel dataset projected onto the first two PCs.

Each column of the cue-signal matrix, X, as well as the response vector, y, can be scaled to reflect unit-variance before PC decomposition. This is useful if the quantified experimental variables reflect significantly different scales or meanings. In this analysis, we did not normalize the data to unit-variance as each column measured a similar property, protein abundance, within the same organism and tissue. Examination of the scores plot can be used to determine appropriateness of the pre-processing of the data as well as the employed algorithm. For example, if replicates are treated as separate conditions, their projections on the scores plot should cluster closer in space than that of non-replicated conditions (see Tomanek and Zuzow 2010, fig. 12, for an example). If the replicates do not cluster closely relative to other perturbations, it may be indicative of sources of variance outside of the control of the experimental design. In the absence of published replicates, we examine the average abundance at the four (temperature) conditions. Data corresponding to the 13°C and the 24°C temperatures cluster closely together, suggesting that they contain similar data and possibly similar predictive capacity.

Examination of the loadings plot shows that many proteins within the same functional group cluster together, as expected. From inspection, energy metabolism and cytoskeletal proteins pack along the PC1 axis. This suggests that the first PC may capture the variance associated with changes in temperature. We anticipated this outcome as many of these proteins are known to change abundance in response to temperature. Conversely, molecular chaperone proteins are not tightly clustered, reflecting the diversity of their roles within the organism. In addition, small heat shock proteins might not cluster tightly due to the fact that they are modified through post-translational modifications, specifically, acetylation and phosphorylation (Tomanek and Zuzow 2010). (Many unsupervised clustering methods are available to quantify specific clusters of variables in principal component space as well as without transformation; for more information, we refer the reader to James et al. (2013) and Murphy (2012).)

Regression

Regression is the mathematical formalization of an association relationship (James et al. 2013). Linear regression is the simplest form of regression where an output vector, y, of dimension n × 1 is represented as a linear combination of the columns of an input matrix, X, of dimension n × p. If the input variables are mean-centered with unit-variance, the equation is given by the following, where β is the vector of weights with dimension p × 1:

(1)

The resulting coefficients in β provide information on the contribution of each explanatory variable to the response. For example, a negative 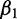suggests the first variable, 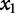, negatively contributes to the response. If 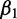is positive, it suggests that 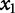positively contributes to the response. If 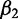has a greater magnitude than 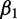(i.e., 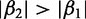), then the second protein is believed to have greater impact than the first on the overall response of the system when the input data are standard normal. Choosing informative predictors from prior knowledge can increase the probability of developing a useful model.

Assessing fit

A common metric for assessing the fit of data to a model is the coefficient of determination, 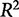(Hawkins et al. 2003), defined as:

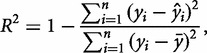(2)

where n is the number of observations, 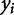is an observed output response, 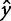is the model-predicted response, and 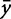is the expected value, or mean, of the output based on experimental observation. The numerator represents the sum of squared error, while the denominator quantifies the biological variance as the total sum of error.

A perfect fit is denoted by an 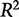of 1, where 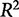ranges between −∞ and 1. This definition accounts for variance in the biological observations, as shown in the denominator; when the variance is high, the sum of squared error is weighted less than if the variance is low. By definition, the denominator would tend to 0 as the variance of the data tends to 0. This means we cannot develop an informative model when the data have little variance, i.e., the different experimental conditions have no effect on the system.

The problem is that the 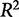value does not account for whether a model is overfit, that is, having more parameters than are necessary to be useful in predicting unknown responses from the input data. 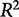increases with the addition of explanatory variables so a matrix with a sufficiently large number of explanatory variables can almost always produce an 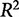near 1. The inclusion of these unnecessary variables in the model, though, often reduces the predictive power of the model—the ability of the model to predict the output from new conditions. For this reason, overfit models often predict the training data perfectly, but fail to accurately predict test or validation data. A method called cross-validation is better suited to assessing the predictive utility of a model.

Cross-validation

Cross-validation involves separating the data into a training and a test set. The data can be separated in various ways; for simplicity we use leave-one-out cross-validation. This method omits one condition (now the test set) and fits a model to the remaining data (the training set); the resulting model is then used to predict the test set. The utility of the model can be assessed by observing how far the prediction varies from the experimentally observed data point. This is performed by sequentially omitting one condition at a time, in this case, each of the three temperatures. Then, we quantitatively assess the predictive capacity of the model. One method of doing this is using the predicted residual sum of squares (PRESS) statistic (Holiday et al. 1995), defined as:

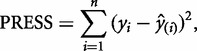(3)

where 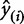is the predicted y from a model that is not trained on that particular condition. When choosing among multiple potential models, one should select a model that minimizes the PRESS function. Another statistic, the cross-validated goodness of fit, 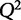(Hawkins et al. 2003), is often used because of its interpretability and similar structure to 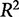. 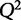is defined as:

(4)

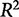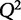A model with perfect predictive capacity has a of 1, and similarly to , can range between −∞ and 1. When selecting between two potential models, the one with the higher value of 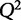may be indicative of a model with higher predictive power.

Multiple linear regression

Multiple linear regression is a type of regression that uses multiple signals to describe a response. To solve for the weights of explanatory variables we can use ordinary least squares (OLS) regression, defined as:

(5)

This equation solves for the set of parameters, β_fit, that minimizes the value of the contained function. Values in the calculated β_fit vector represent the predicted weights of variables in X on explaining y. It is impossible to know the true values of β, therefore β_fit represents the estimated values, of the weights. As an example, we defined the protein P20, 6-phosphogluconolactonase, from Table 1 as the response variable and the other proteins as the signal, X. To model the contribution of explanatory variables on multiple outputs, each variable can be iteratively defined as the response, y, and regression performed in a similar manner. Cross-validating the β-values with P20 as the output generated a 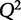of −10.8. As the 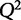is far from the ideal value of 1, we can safely assume that the model is overfit. We therefore need a method to select only relevant variables needed to create a useful model to explain the abundance of 6-phosphogluconolactonase.

Variable selection

One method to reduce the number of parameters in OLS is to provide a penalty for β-values that are non zero, thus reducing overfitting. This strategy can be performed with backward selection, forward selection, or the least absolute shrinkage and selection operator (LASSO) (Tibshirani 1997). LASSO provides the constraint that most β-values are zero, resulting in a sparse solution. This particular addition to the OLS optimization is known as the 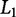penalty (Zou and Hastie 2003), which penalizes according to the 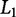norm, also known as the Manhattan distance, and is the sum of absolute differences:

(6)

LASSO contains one tuning parameter, λ, that determines the strength of the penalty and therefore sparsity of the β-vector. To determine the best predictive model, λ can be varied to give the maximal 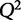. A similar approach, Ridge regression, employs the Euclidean, or 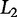norm (Zou and Hastie 2003) to penalize β-values with a large absolute value and is useful for regression with few perturbations relative to the number of variables being sampled (i.e., p ≫ n) (Hoerl and Kennard 1970). Elastic net is an additional regression technique that combines both the 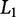and 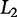penalties (Zou and Hastie 2003) and has been useful in large datasets such as those common in genomic studies (Cho et al. 2010).

We start by solving for the optimal λ that predicts 6-phosphogluconolactonase from the other 46 proteins. We utilized lasso() with cross-validation in Matlab R2013a (Mathworks) yielding an optimal cross-validated parameter of λ = 0.01. We input this value again into lasso() to provide a sparse set of predictors that explain the protein abundance of 6-phosphono-gluconolactonase. In this case, the relevant predictors are Hsp70 and Cu-Zn superoxide dismutase. Using this 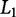penalty, the 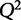has increased from −10.8 to 0.23, indicating that the model has more predictive power than simple OLS regression.

We find these results compelling; Cu-Zn superoxide dismutase might be indicative of oxidative stress, while 6-phosphogluconolactonase, a member of the pentose-phosphate pathway, provides NADPH and thereby reducing equivalents for glutathione. This reduction is subsequently used to scavenge reactive oxygen species. Furthermore, reactive oxygen species damage proteins and therefore require molecular chaperones such as Hsp70 (Tomanek and Zuzow 2010).

Architecture

Associations are useful in integrative and comparative biology for predicting certain desired variables from a series of predictors. However, another level of understanding can be derived by observing how each of the test variables interacts with each other within a specified system topology, or network architecture. The process of reverse engineering these networks from variable data under a set of conditions is known as network inference. Network inference is one method of finding relationships (edges) between variables (nodes) in complex biological systems. Nodes can represent diverse biological components such as genes, proteins, or organisms as well as a related pertinent variable such as a drug intervention, environmental stimulus, or cell phenotype. Edges can represent relationships such as physical interactions between nodes, which are represented as lines between nodes. Networks can also show dependence of one variable on another represented as a directed arrow between the explanatory (parent) node and the dependent (daughter) node. By assaying the value of measured variables under diverse conditions, the functional connections between the variables can be inferred using various computational algorithms. Network inference has shown significant impact in analyzing biological systems as it is able to identify novel connections among variables as well as offering predictive insight into how a system will respond under new conditions (Hecker et al. 2009).

Types of networks

Networks fall into two general categories: undirected and directed. Undirected networks indicate whether two variables interact in some manner and are often represented by lines connecting different nodes. These can be useful in understanding the underlying structure of life systems such as protein–protein interactions or cooperation in ecological networks. Directed networks describe how information flows from one node to another and is often represented with arrows connecting the nodes. Directed networks are able to elucidate the sequence of signaling events that govern a defined response. Elucidating interactions and upstream regulators can help identify novel control inputs and inform perturbation strategies to enforce a desired response. In the context of cell signaling, potential control inputs or perturbations can reflect novel drugs aimed to prevent proliferation of cancer; in organismal biology, the perturbation can be an environmental condition that contains an invasive species or pathogenic organism. Directed networks have been used to gain insight into intracellular signaling cascades (Sachs et al. 2005), as well as predator–prey models in ecosystems (Winemiller 1990).

Correlation networks

A correlation network is a simple means of identifying undirected connections among variables. Here, we use pairwise Pearson correlation coefficients (r) of all 47 proteins and 1 variable for the cue, temperature. The equation for r is given by the following:

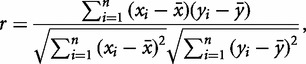(7)

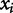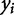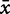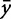where and represent the two observed variables at observation i, and and represent the expected values for x and y, respectively. Since the Pearson correlation coefficient normalizes each variable intrinsically, the value of r is invariant to scaling of the data, making it a consistent metric for comparison.

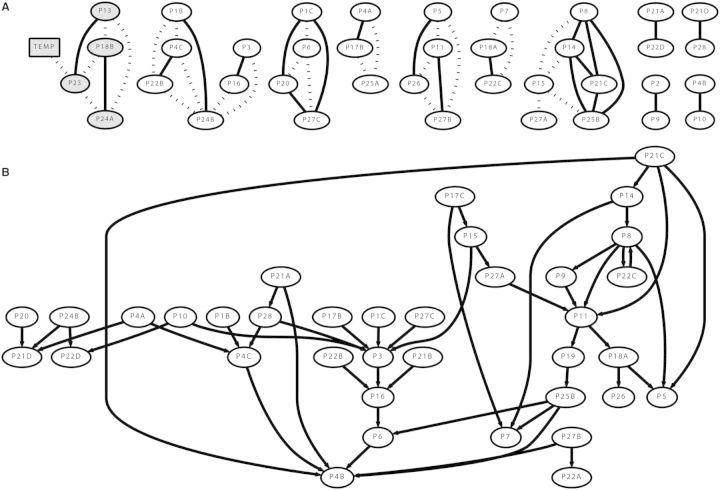
In order to display the data, we arbitrarily retained 48 edges, the same number as nodes. The analysis of determining the optimal threshold of edges is outside the scope of this study. The resulting undirected network is shown in Fig. 3A. Positive correlations are displayed with a solid line and negative correlations with a dashed line. This type of analysis provides informed hypotheses of proteins that can lie within the same pathway or can be coregulated.

Fig. 3.

(A) Undirected protein regulatory network in M. galloprovincialis. Pearson correlation coefficients are used to identify nodes, or proteins, that are similarly regulated and subsequently clustered. Temperature, highlighted in the shaded subnetwork, is shown to interact with P23 (gelsolin), which interacts with P13 (nucleoside diphosphate kinase), P18B (Cu-Zn superoxide dismutase), and P24A (actin). Positive correlations are shown with a solid line and negative correlations with a dashed line. The disconnected networks suggest that most proteins interact with a close neighborhood of proteins, rather than more globally across the network. (B) Directed protein regulatory network inferred using the GENIE3 algorithm. Directed networks illustrate information flow as described by the arrows among nodes. This network suggests that P21A (α-tubulin) and P6 (proteasome-α-type-1) are upstream regulators of P4B (α-crystalline-Hsp23).

The resulting network architecture suggests that the cue variable, temperature, may have an interaction with P23 (gelsolin), which then may interact with P13 (nucleoside diphosphate kinase), P18B (Cu-Zn superoxide dismutase), and P24A (actin). We find it compelling that gelsolin, an actin severing protein, may interact with actin and superoxide dismutase, since it is established that oxidative stress leads to modifications of the actin cytoskeleton (Dalle-Donne et al. 2001).

Regression-based networks

Regression networks offer another level of analysis by iteratively treating each variable as the response, allowing all other signaling variables to serve as the predictors or explanatory variables (Myers 1990). To infer the structure of the network between variables we also applied the GENIE3 (for GEne Network Inference with Ensemble of trees) algorithm, which employs a network inference technique called Random Forests (Irrthum et al. 2010). GENIE3 was chosen because of its top performance in inferring network structure with high accuracy using benchmark in silico and in vivo datasets. The high quality of this algorithm in comparison to others is described in the DREAM5 (Dialogue for Reverse Engineering Assessments and Methods: Challenge 5) network inference challenge (Marbach et al. 2012). We therefore chose this algorithm to examine the protein abundance network in mussels after perturbation with several temperatures.

GENIE3 was performed using the same 48 variables (47 protein abundances + temperature) and we specified two parameters as previously described (Irrthum et al. 2010), the number of trees (500), and the number of randomly selected variables for each node of a tree (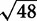). The edge confidences were ordered by the importance metric assigned to each potential edge as defined in the GENIE3 algorithm (Irrthum et al. 2010). For comparison, we applied an arbitrary threshold to retain 48 edges, as shown in Fig. 3B.

This type of analysis shows a tractable flow of information within the mussel protein network under various temperatures. While the Pearson correlation network shows proteins that may share a functional relationship through an undirected network, the GENIE3-derived network shows how information about the abundance of one protein may affect the abundance of another protein.

While inferring the directionality of a system’s information flow in the absence of time-resolved data might seem counterintuitive, directionality can be inferred by comparing the amount of variance that is explained in one variable by another. Knowledge of the state of variable A may give information on the state of variable B, whereas knowing the state of variable B may give very little information on the state of variable A. In a classic example, knowing that it is raining informs whether grass (outside) is wet. However, knowing that the grass is wet offers less information on the state of the weather, since wet grass can result from a variety of sources. In this way, we can hypothesize the directionality that rain causes the grass to be wet and not vice-versa.

Both inferred networks in this study offer useful insight into the network architecture and address distinct biological questions. The GENIE3 network differs from the correlation network because different inference methods resolve different types of interactions. Integrating multiple networks usually increases accuracy of network inference (Marbach et al. 2012).

Additional inference methods

Several types of network inference methods are available, and fall into four broad categories: regression (Haury et al. 2012), mutual information (Margolin et al. 2006), correlation (Stuart et al. 2003), and Bayesian (Yu et al. 2004; Ciaccio et al. 2010). Each type of inference method has its own strengths, and selecting the appropriate one is context specific and depends both on the available data and on the question being posed (Marbach et al. 2012).

Conclusions

Network inference is a particularly powerful strategy that quantitatively defines network structure and the impact of environmental perturbations to specific signaling variables. Understanding the systems-level properties that emerge from complex networks can elucidate associations among network variables, as well as between these variables and their environment.

We highlighted methods that identify similarities, find associations, and determine interactions between different proteins in mussels’ gill tissue. Our results imply novel regulatory mechanisms, highlight the effect of temperature on proteins, and provide hypotheses suggesting potential proteins responsible for temperature resistance in the invasive mussel, M. galloprovincialis, in the southern Californian coastal region.

The methods and principles described in this study are applicable across a diverse range of experiments and datasets. Studies of association and network architecture can be applied to identify hidden relationships among observed variables. We seek to uncover the complex regulatory mechanisms to predict biological responses under various unknown environmental conditions. Ultimately, predicting responses closes the gap between understanding regulation and controlling complex biological systems (Bagheri et al. 2007; Cowan et al. 2014). Further insight into the complexity inherent in biological regulation can be derived by sampling the system at different times post-stimuli. The resulting dynamic data support the development of more sophisticated mechanistic models, such as series of differential equations (Bagheri et al. 2011). Integrating such computational strategies with quantitative data will allow the biological community to gain greater insight into the regulatory structure of complex systems at different temporal and physical scales.

Funding

The National Cancer Institute of the National Institutes of Health under Award Number U54CA143869. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This collaboration was facilitated by NSF IOS 1243801 to D.K. Padilla. J.D. Finkle was supported in part by NIH PHS GRANT, number 5 T32 GM 008449, through the Biotechnology Training Program directed by Dr. Lonnie Shea. A.Y.Xue was supported in part by the Biotechnology Cluster through the Graduate School at Northwestern University.