A Structural-informatics Approach for Tracing β-Sheets: Building Pseudo-C^α Traces for β-Strands in Intermediate-resolution Density Maps

Abstract

We report the development of two computational methods to assist density map interpretation at intermediate resolutions: sheettracer for building pseudo-C^α models of β-sheets, and a deconvolution method for enhancing features attributed to major secondary structural elements. Sheettracer is tightly coupled with sheetminer, which was developed to locate sheet densities in intermediate-resolution density maps. The results from sheetminer are used as inputs to sheettracer, which employs a multistep ad hoc morphological analysis of sheet densities to trace individual strands of β-sheets. The methods were tested on simulated density maps from 12 protein crystal structures that represent a reasonably complete sampling of sheet morphology. The sheet-tracing results were quantitatively assessed in terms of sensitivity, specificity and rms deviations. Furthermore, sheettracer and the deconvolution method were rigorously tested on experimental maps of the λ2 protein of reovirus at resolutions of 7.6 Å and 11.8 Å. Our results clearly demonstrate the capability of sheettracer in building pseudo-C^α models of β-sheets in intermediate-resolution density maps and the power of the deconvolution method in enhancing the performance of sheettracer. These computational methods, along with other related ones, should facilitate recognition and analysis of folding motifs from experimental data at intermediate resolutions.

Introduction

In this post-genomics era,¹ structural biologists are faced with the challenges of analyzing increasingly complex biological systems, many of which only yield density maps at low to intermediate-resolution.² This is particularly true for single-particle electron cryomicroscopy (cryo-EM) of supermolecular complexes.^3–11 In X-ray crystallographic structure determinations, crystals of large complexes often fail to diffract beyond 4 Å. Moreover, even for some well-diffracting crystals, the structures have to be solved in a stepwise process at progressively enhanced resolutions before atomic resolution is achieved. This was certainly true for the 50 S ribosomal subunit, which was solved first at 9 Å, and then at 5 Å, and finally at 2.4 Å.^12–14 In all such studies involving intermediate-resolution density maps, it is nearly impossible to build reasonably accurate atomic models with conventional methods. However, it would be enormously helpful if the locations of major secondary structural elements could be reliably defined, and this in turn would enable the construction of accurate pseudo-atomic models. Such models can facilitate structure determination to higher resolutions and also assist further biochemical studies and functional interpretation. In fact, significant insights into the architecture and organization of structures are often obtained once major secondary structural elements are located.

α-Helices and β-sheets constitute the major secondary structural elements in proteins. It has recently been shown that α-helices, which have an approximately cylindrical shape, can be located in intermediate-resolution density maps via a five-dimensional cross-correlation search.¹⁵ However, β-sheets are much more difficult to identify in intermediate-resolution density maps because they usually do not adopt a single, characteristic shape. Moreover, variations in the number of strands and the length of each strand result in β-sheets of various sizes and shapes.

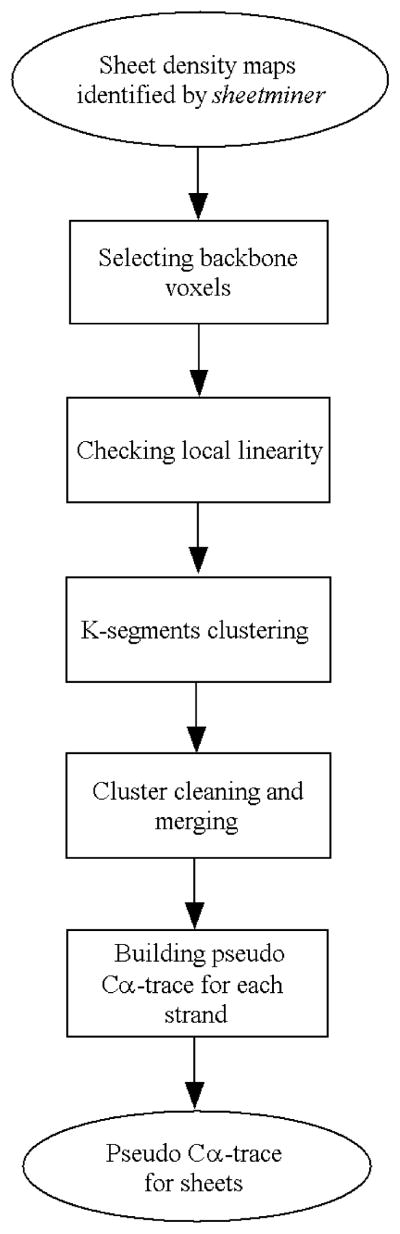
Despite such challenges, we have identified a set of unique morphological features that can be used to assist the location of β-sheets at intermediate resolutions. This process is carried out in two steps using the programs sheetminer and sheet-tracer. We have recently shown that sheetminer is able to locate reliably the regions belonging to β-sheets in intermediate-resolution density maps.¹⁶ Here, we describe the development of another tool, sheettracer, that traces pseudo-C^α atoms in the β-sheet density maps output by sheetminer.¹⁶ A flowchart that depicts the overall procedure of sheettracer is presented in Figure 1.

Figure 1.

Flowchart for the computational procedure of sheettracer in intermediate-resolution density maps.

The integration of sheetminer¹⁶ and sheettracer with other methods such as helixhunter¹⁵ will enable the building of pseudo-C^α traces in intermediate-resolution density maps obtained from any experimental measurements. This in turn will enhance the interpretation of structural data at intermediate resolutions. These methods offer a distinct advantage in that they significantly enhance model building experiments by narrowing the volume of a density map that must be searched and eliminating the need for global, brute-force fitting procedures.

Results

Step-wise discerning of β-strands

The sheetminer¹⁶ program outputs clusters of voxels, with each cluster delineating a thin, but continuous volume of density presumed to represent a single β-sheet. sheettracer then employs a multi-step process to build pseudo-C^α traces in each identified sheet. These steps are first illustrated using as an example one β-sheet of the apical domain of the molecular chaperonin GroEL, also known as the minichaperone¹⁷ (PDB code 1fy9).

In the first step, a local peak filter was applied to each cluster of voxels (Figure 2(a)) output by sheet-miner to identify voxels that are most likely involved in forming the backbones of individual strands (Figure 2(b)). The local peak-filtering algorithm emphasizes high local density values and thereby adjusts to variations in the magnitude of densities throughout the map, which permits, for example, effective selection of backbone voxels even in regions of relatively weak density. The next step involved condensing the selected voxels using local first principal component axis projection, which acts to enforce the voxel distribution along the longest axis and one meant to coincide with a strand backbone (Figure 2(c)). This process results in a significantly narrowed distribution of voxels and makes subsequent local linearity filtering more efficient. Surviving voxels were then subjected to a local linearity filter that picks backbone voxels exhibiting properties of good local linearity (Figure 2(d)). This filtering method acts to remove inter-strand voxels and results in a significantly narrowed distribution of backbone voxels. k-Segments clustering¹⁸ was employed in the next step to group voxels into smaller subsets, each of which is expected to represent one part of a β-strand (Figure 2(e)), and subsequently all subsets belonging to the same strand were merged. At this point, each cluster of voxels represents an independent β-strand and a pseudo-C^α trace was then built for each strand.

Figure 2.

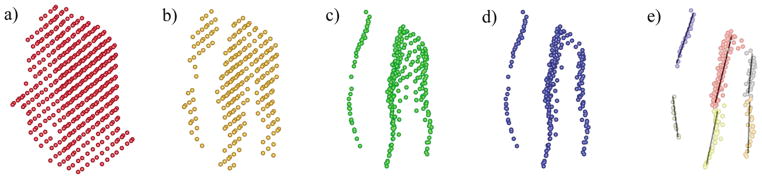
Step-wise processing of sheet density maps to discern individual β-strands, using the sheet in the GroEL minichaperone as an example. (a) Sheet density identified by sheetminer shown in voxels. (b) Selected voxels by local peak filter. (c) Surviving voxels after local first principal component axis projection using the voxels in (b) as input. (d) Surviving voxels after local linearity filtering using the voxels in (c) as input. (e) Clustered backbone voxels after k-segments processing. The lines are the fitted segments (the first principal component axes).

Discerning β-strands and building pseudo-C^α traces in p21^H-ras

The p21^H-ras molecule, which contains a single, six-stranded β-sheet, was used to test sheettracer. Analysis was performed on a relatively thin, but continuous, sheet density map produced by sheet-miner from a map of the protein simulated at 6 Å resolution (Figure 3(a)). A simulated density map was obtained from the crystal structure using the EMAN program ¹⁹. Several steps of pre-processing, as described in Methods, led to a set of points that represent the topological features of the sheet (Figure 3(b)). The k-segments algorithm¹⁸ was then used to separate these points into groups. Cluster cleaning and merging were then applied to each group of points to ensure that each group represents an independent strand (Figure 3(c), groups are separately colored). Such groupings of points permitted us to then make pseudo-C^α traces for all six strands (Figure 4(b)).

Figure 3.

Sheet-tracing results based on a 6 Å simulated density map of p21^H-ras. (a) Isolated thin, but continuous, sheet density map output from sheetminer. (b) Backbone voxels for delineating the strands. (c) Clusters of voxels after k-segments processing. Each cluster represents one strand (in a different color).

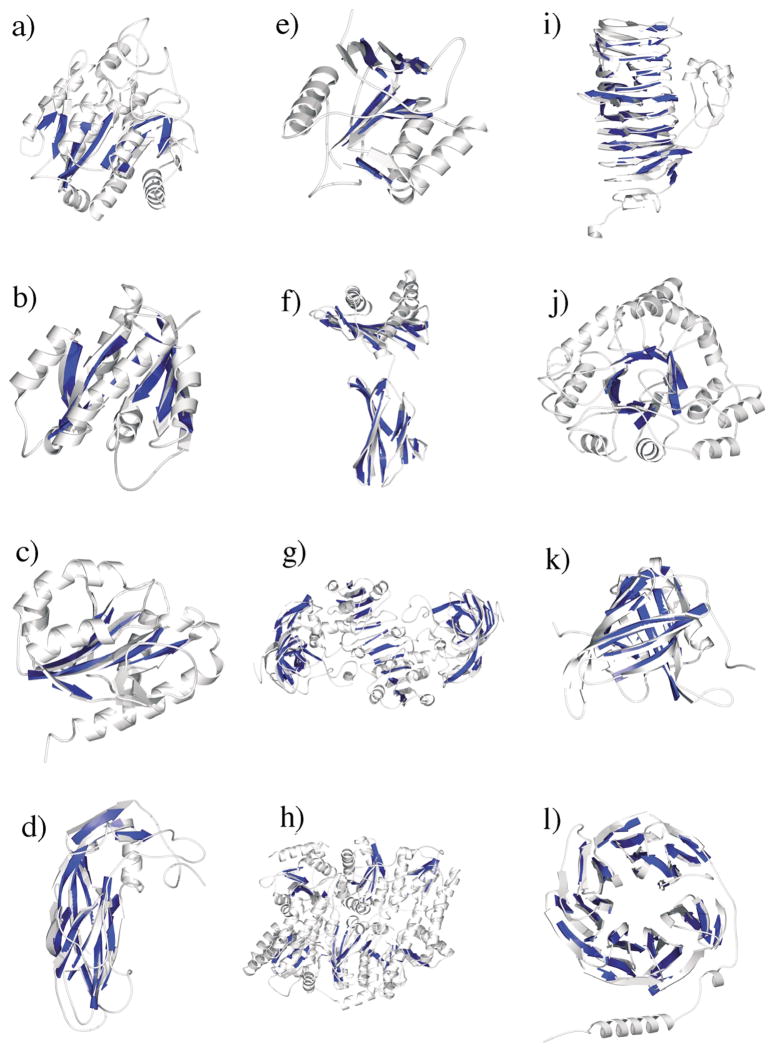
Figure 4.

Sheet-tracing results for all 12 proteins based on 6 Å simulated density maps. The pseudo-C^α traces depicted in darker color are superimposed on the X-ray structures of the proteins shown in lighter color using MOLSCRIPT software.⁵¹ The proteins are: (a) carboxypeptidase A; (b) p21^H-ras; (c) flavodoxin; (d) VP1 protein of human rhinovirus 14; (e) the GroEL minichaperone; (f) human class I major histocompatibility antigen; (g) horse liver alcohol dehydrogenase; (h) MoFe protein of nitrogenase; (i) bacteriophage P22 tailspike protein; (j) aldose reductase; (k) retinol-binding protein; and (l) phosducin. The arrows in the pseudo-C^α traces are artificially assigned based on the crystal structures.

Discerning β-strands and building pseudo-C^α traces in 12 proteins

As a further test of the ability of sheettracer to discern individual β-strands in sheet densities of different morphology, we examined simulated density maps of 12 structurally unrelated proteins whose high-resolution crystal structures are available from the Protein Data Bank (PDB). This set of protein structures was chosen because the number, size, and shape of β-sheets vary widely among them and therefore they should provide a reasonably complete sampling of known β-sheet morphologies. Four of the structures contain a single β-sheet with varying size and number of strands: carboxypeptidase A²⁰ (PDB code 5cpa), p21^H-ras21 (PDB code 121p), flavodoxin²² (PDB code 1ag9), and VP1 protein of human rhinovirus 14²³ (PDB code 4rhv). Four contain multiple independent β-sheets: the GroEL minichaperone¹⁷ (two sheets, PDB code 1fy9), human class I major histocompatibility antigen²⁴ (three sheets, PDB code 1duz), horse liver alcohol dehydrogenase²⁵ (five sheets, PDB code 6adh), and MoFe protein of nitrogenase²⁶ (six sheets, PDB code 1h1l). The last four contain rich β-motifs such as the β-barrel and β-propeller: bacteriophage P22 tailspike protein²⁷ (PDB code 1tsp), aldose reductase²⁸ (PDB code 1ads), retinol-binding protein²⁹ (PDB code 1aqb), and phosducin³⁰ (PDB code 1b9x).

The sheet-tracing results on the 12 proteins are shown in Figure 4 with the built pseudo-C^α traces superimposed on the crystal structures. The results were statistically analysed in terms of three separate measures: sensitivity, specificity, and root-mean-square (rms) deviations. As had similarly been used in quantitative analysis of sheet-mining results,¹⁶ sensitivity refers to the probability of correctly identifying true sheet C^α-atoms, whereas specificity defines the probability of correctly identifying non-sheet C^α-atoms. The rms deviation is calculated by computing the average distance of each built pseudo-C^α-atom from its closest sheet C^α-atom in the superimposed crystal structure. The average sensitivity and specificity for all 12 proteins are 79.5% and 96.3%, respectively (Table 1). Moreover, regardless of which β-sheet morphology is tested, the rms deviations always remain smaller than 2.0 Å, with an average of 1.54 Å (see footnote to Table 1 for more details concerning the calculation of rms deviation). Given the limited resolution upon which our analysis was based, such statistical results of trace building seem quite promising. Note that sheettracer is unable to specify strand directions, consequently these have been assigned according to the known X-ray structures (Figure 4).

Table 1.

Quantitative analysis of the sheet-tracing results at 6 Å

PDB code	No. total Cα	No. sheet Cα found by STRIDE	No. true sheet Cα found by sheettracer	No. true sheet Cα missed by sheettracer	No. false sheet Cα found by sheettracer	Specificity (%)	Sensitivity (%)	rms deviations (Å)
5cpa	308	53	32	21	2	99.2	60.4	1.48
121p	167	47	42	5	2	98.3	89.4	1.51
1ag9	176	33	26	7	5	96.5	78.8	1.35
4rhv	209	85	82	3	2	98.4	96.4	1.54
1fy9	214	54	33	21	1	99.4	61.1	1.35
1duz	276	119	88	31	14	91.1	73.9	1.62
6adh	749	174	152	22	56	90.3	87.4	1.75
1h1l	998	140	113	27	14	98.4	80.7	1.65
1tsp	391	189	149	40	3	98.5	78.8	1.57
1ads	316	39	33	6	0	100.0	84.6	1.40
1aqb	176	82	58	24	5	94.7	70.7	1.49
1b9x	341	180	165	15	15	90.7	91.7	1.81
Average						96.3	79.5	1.54

The number of C^α-atoms of β-sheets in the crystal structures (third column) was determined by the method STRIDE.⁵⁰ The sheet-tracing results were based on 6 Å simulated density maps. The crystal structures were first superimposed on the simulated density maps. The number of true sheet C^α-atoms found by sheettracer (fourth column) was then defined as the number of sheet C^α-atoms in the atomic coordinates that spatially fall inside the sheet regions defined by sheettracer. The number of true sheet C^α-atoms missed by sheettracer (fifth column) was defined as the number of sheet C^α-atoms in the atomic coordinates that spatially fall outside the sheet regions defined by sheettracer. The number of false sheet C^α-atoms (sixth column) was defined as the number of non-sheet C^α-atoms in the atomic coordinates that spatially fall inside the sheet regions defined by sheettracer. The specificity value (seventh column) was calculated by the formula: 1 – (sixth column/(second column – third column)) and the sensitivity value (eighth column) was calculated by the formula: fourth column/third column. The rms deviations of built pseudo-C^α traces were derived from the distance of each pseudo-C^α-atom to its nearest C^α-atom on β-strands in the superimposed crystal structures. This calculation was only performed for found pseudo-C^α-atoms. Please note, for all the calculations, no sequence identity of C^α-atoms was concerned. As a result, the rms deviation calculated here is not the same as the conventional rms deviation based on atomic structures. The nearly perfect specificity values are the results of the multi-step denoising process implemented in sheettracer.

A new method for deconvolution of density maps

As demonstrated in the previous sections, we can usually build the pseudo-C^α traces with reasonable confidence, but mistakes do occur, especially when maps at lower resolutions are analysed. Therefore, to help enhance our ability to build the pseudo-C^α traces in intermediate-resolution density maps, we developed a new computational method for deconvoluting the density maps. The net result of deconvolution is to enhance the features of secondary structural elements in density maps. A simple example of this is illustrated in Figure 5(a). The left panel shows a synthetic two-dimensional (2D) geometrical object and the middle panel shows the same object contaminated with a level of noise that nearly renders features in the original object indistinguishable. The right panel shows the results of a dramatic recovery of object features after deconvolution is performed.

Figure 5.

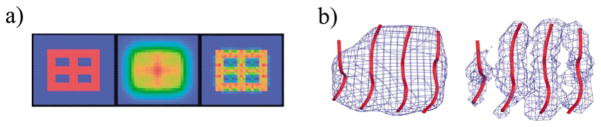
A new deconvolution method. (a) A simple 2D example of deconvolution. The left is the original image, the middle is the image rendered with noises and the right is deconvoluted image. (b) A 3D example for deconvolution (right) on a piece of β-sheet density blurred to 8 Å (left). The C^α traces of the sheet (red) are superimposed on the density.

We then tested the method on a simulated 3D density map (Figure 5(b)). A single β-sheet structure was blurred to 8 Å (Figure 5(b), left), at which point a straightforward building of pseudo-C^α traces became difficult. After deconvolution, strands are more clearly resolved in the density map (Figure 5(b), right). The subsequent building of pseudo-C^α traces on the deconvoluted map was a trivial process.

Experimental density maps of the λ2 protein of reovirus were then used to further test the deconvolution method. To perform the test in a more systematic and self-consistent way, the cryo-EM structures of reovirus have been reconstructed to 7.6 Å resolution from 7939 single-particle images (100%-particle structure) and to 11.8 Å resolution from a subset (12.5%) of the same particle images (12.5%-particle structure). Two helices in the λ2 protein that are distinct in the 100%-particle structure (Figure 6(a)) are bridged by density that appears to interconnect the helices in the 12.5%-particle structure (presumably owing to the higher noise level) (Figure 6(b)). Deconvolution of the lower resolution density map clearly yields a map with distinct densities for the helices (Figure 6(c)).

Figure 6.

The improved appearance of secondary structural elements in the experimental density map of the λ2 protein of reovirus by the deconvolution. (a) The cryo-EM structure generated using 100% particle images (100%-particle structure) highlighting the two well-separated helices. (b) The structure generated using 12.5% particle images (12.5%-particle structure) in which the two distinct helices are wrongfully connected. (c) The deconvolution procedure recovered the separation of these two helices in the 12.5%-particle structure.

Deconvolution and trace building in simulated density maps of 12 proteins

As has been demonstrated in previous sections, sheettracer is capable of building pseudo-C^α traces in simulated maps limited to 6 Å resolution. Attempts to trace C^α-paths in lower resolution maps generally failed. To test its effectiveness in assisting sheet-tracing, we explored the utility of combining our deconvolution method with sheet-tracer to enable sheets to be traced at lower resolutions. The results of tracing with simulated maps of p21^ras at 8 Å and 9 Å are shown in Figure 7. The sensitivity, specificity and rms deviations are 76.6%, 98.3%, 1.65 Å and 70.2%, 96.7%, 1.73 Å for the 8 Å and 9 Å data, respectively. We then applied the same procedure to simulated density maps of the other 11 proteins at 8 Å, and obtained average sensitivity, specificity and rms deviations of 71.3%, 93.8% and 1.77 Å, respectively (Table 2). These results clearly demonstrate that the deconvolution method does enhance density interpretation in sheettracer.

Figure 7.

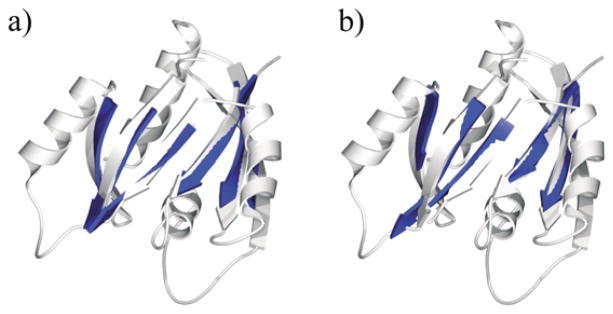
Sheet-tracing results for p21^ras at resolutions of (a) 8 Å and (b) 9 Å after deconvolution. The built pseudo-C^α traces of the sheets (blue) are shown on top of the ribbon diagrams of the crystal structure (lighter color).

Table 2.

Quantitative analysis of the sheet-tracing results at 8 Å

PDB codes	No. total Cα	No. sheet Cα found by STRIDE	No. true sheet Cα found by sheettracer	No. true sheet Cα missed by sheettracer	No. false sheet Cα found by sheettracer	Specificity (%)	Sensitivity (%)	rms deviations (Å)
5cpa	308	53	34	19	6	97.6	64.1	1.59
121p	167	47	33	14	4	98.3	76.6	1.65
1ag9	176	33	24	9	6	95.8	72.7	2.37
4rhv	209	85	80	5	10	91.9	94.1	1.55
1fy9	214	54	36	18	3	98.1	66.7	1.56
1duz	276	119	77	42	12	92.4	64.7	1.86
6adh	749	174	129	45	43	92.5	74.1	1.84
1h1l	998	140	100	40	21	97.6	71.4	1.83
1tsp	391	189	127	62	24	88.1	67.2	1.61
1ads	316	39	23	16	8	97.1	59.0	1.80
1aqb	176	82	63	19	6	93.6	76.8	1.73
1b9x	341	180	122	58	28	82.6	67.8	1.84
Average						93.8	71.3	1.77

The sheet-tracing results were based on 8 Å simulated density maps using the combination of sheettracer and the deconvolution method. The detailed calculation of sensitivity and specificity and the explanation of rms deviations can be found in the footnote to Table 1.

Deconvolution and trace building in experimental maps of the λ2 protein of reovirus

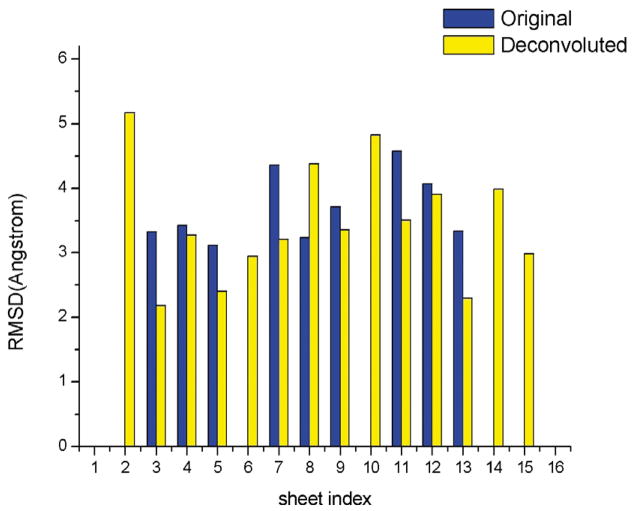
To test their applicability to real experimental data, sheettracer and the deconvolution method were employed to build pseudo-C^α traces in the 7.6 Å cryo-EM structure of the λ2 protein of reovirus,³¹ whose crystal structure has been solved independently³² (PDB code 1ej6) and could be used to validate the sheet-tracing results. The λ2 protein has 16 β-sheets, 12 of which contain three or more strands. The results of building pseudo-C^α traces by sheettracer on the 7.6 Å map of λ2 protein with and without deconvolution are shown in Figure 8. With the exception of sheet 8, the rms deviations of pseudo-C^α traces obtained from the deconvolved maps are much better than those obtained from the original map. Moreover, deconvolution enhanced five additional sheets (sheets 2, 6, 10, 14, and 15) for which pseudo-C^α traces could not be built from the original maps prior to deconvolution. The results of our tests with simulated and real experimental data clearly suggest that sheettracer and deconvolution together provide a powerful approach to analyze maps with unavoidable phase errors.

Figure 8.

Comparison of sheet-tracing results in the 7.6 Å density maps of the λ2 protein of reovirus with (yellow bar) and without (blue bar) deconvolution. There are a total of 16 β-sheets, 12 of which are large (three-stranded or more) and four are small (short two-stranded). In all but one (sheet 8) case, the deconvolution resulted in smaller rms deviations relative to the crystal structure than without. Moreover, the deconvolution brought up five additional β-sheets (sheets 2, 6, 10, 14, and 15) for which no pseudo-C^α traces could be built on the original maps without deconvolution.

Discussion

Here, we report the development of two computational methods that can be used to assist density interpretation at intermediate resolutions. These include sheettracer for building pseudo-C^α models of β-sheets, and a deconvolution method for enhancing the features of secondary structural elements. sheettracer is tightly coupled to sheetminer,¹⁶ which was developed to locate sheet densities in intermediate-resolution density maps. Simulated 6 Å density maps from 12 representative protein crystal structures, encompassing a wide range of sheet morphologies, were used to test both programs. sheettracer successfully built pseudo-C^α models in the sheet densities output by sheetminer, with average values of 79.5%, 96.3% and 1.54 Å for sensitivity, specificity and rms deviations, respectively. With even lower-resolution (8 Å ) simulated data, the deconvolution method permitted sheettracer to build pseudo-C^α models with average values of 71.3%, 93.8% and 1.77 Å for sensitivity, specificity and rms deviations, respectively. Furthermore, sheettracer and the deconvolution method were rigorously tested on experimental maps of the λ2 protein of reovirus at 7.6 Å and 11.8 Å resolutions. The results of all tests consistently demonstrated the capabilities of the sheettracer program and deconvolution method to construct accurate pseudo-C^α models of β-sheets in intermediate-resolution density maps.

sheettracer employs an ad hoc morphological analysis of density maps based on two observations: that protein main-chain density is relatively higher in magnitude than that in side-chains and that all neighboring β-strands are parallel or nearly parallel. The former property stimulates the use of local peak-filtering as a means to select backbone voxels, whose geometrical distribution helps define sheet morphology. The latter property permits local first principal component axis projection to condense the density without losing intra-strand connectivity. In contrast to other thinning schemes that only consider the contacting neighbors, this local projection scheme reinforces the linear distribution of voxels but simultaneously increases the distance between voxels of different strands. The net result of this condensation is a significantly increased efficiency in k-segments clustering. It needs to be pointed out that, although the lattice grid of the density map may become broken by translocating voxels in condensation, the major topological features of the voxel distribution are maintained and the pseudo-C^α tracing can still be successfully performed on clustered voxels.

At intermediate resolutions, it is impossible to differentiate C^α-atoms from other backbone atoms. Hence, it is reasonable to only use C^α-atoms to model strand traces. For trace building, it is required to define the end-point voxels that correspond to the C^α-atoms at the N and C termini of a β-strand. Based on the fact that the N and C-terminal C^α-atoms of a β-strand are the most distant from each other within a β-strand, we define the two voxels of the largest distance within a cluster as the end-point C^α-atoms. The trace is built starting from one of the end-point C^α-atoms and is extended toward the second by an interval of 3.8 Å. Such a scheme can potentially introduce systematic errors ranging between 0 Å and 1.9 Å along the strand axis. Along with these longitudinal errors, strand curvature could introduce lateral errors, since the k-segments clustering algorithm uses a set of sequential straight lines to approximate a curved structure. For those β-sheets with highly twisted or curved strands, the traced pseudo-C^α-atoms would exhibit larger rms deviations relative to the real structures. In our tests, the rms deviations between modeled pseudo-C^α-atoms and the known sheet C^α-atoms in the 12 control protein structures averaged 1.54 Å and 1.77 Å for the 6 Å and 8 Å simulated density maps, respectively. The magnitude of these deviations clearly indicates that the strands and pseudo-C^α-atoms have been reasonably accurately located.

The input to sheettracer consists of sheet density maps identified by sheetminer from raw density maps. Hence, the tracing generated by sheettracer depends, at least in part, on the reliability of sheetminer. In general, the sensitivity of tracing results is closely linked to the performance of sheetminer, but the specificity of tracing results is always quite good, which we attribute to the multi-step denoising implemented in sheettracer. Moreover, as is true for sheetminer, the performance of sheet-tracer is also related to the size of β-sheets. sheet-tracer generally performs better at tracing strands in sheets when the strands are long and their number is large. This reflects, in part, the fact that the identification errors tend to concentrate at the edges of β-sheets. Similar constraints also occur in helix-hunting algorithms where it is difficult to precisely define helix length.¹⁵ However, this may not be too problematic because the exact length of secondary structural elements in high-resolution structures can vary depending on which assignment method is employed. Furthermore, identification of folding motifs tends not to be critically sensitive to the exact length of secondary structural elements. Folding motifs are instead defined by the overall spatial arrangement of secondary structural elements. Indeed, within a given fold a particular secondary structural element can vary considerably in length for all the structures with the same fold in the Structure Classification of Proteins database.^33,34

Our results have additionally clearly demonstrated that the deconvolution method significantly enhances one’s ability to build pseudo-C^α traces for β-strands at relatively low resolutions. We currently have no objective, quantitative measure of how much the deconvolution method improves the effective resolution. Rather, it is important to emphasize that the criteria used to signify success of the new methods are the improved effectiveness and accuracy of building structural models into density maps. For example, the deconvolution method is effective because it extended our ability to trace pseudo-C^α positions in simulated maps at resolutions as low as 8–9 Å. Finally, it is noteworthy that the deconvolution method is able to enhance all secondary structural elements in both simulated and experimental maps.

At this stage in our development of structural-information tools, the sequence identity of amino acid residues cannot be discerned purely based on ad hoc morphological analysis of intermediate-resolution density maps. Furthermore, the relative orientations of the strands (parallel or anti-parallel) cannot be discriminated. These represent the largest obstacles in building a complete set of atomic coordinates for any protein structure. However, some of these obstacles might be overcome or circumvented by linking our methods with other computational structure prediction methods.^{15,35 –38} Once all the pseudo C^α-atom positions are determined or predicted, energy calculations can be performed to verify the validity of the pseudo-model or to refine it to produce a more reasonable one.

Computational tools designed to help identify and trace secondary structural elements in intermediate-resolution density maps will likely prove valuable for several reasons. First, the building of pseudo-C^α traces will stimulate more targeted biochemical and functional studies of biological systems and will facilitate structure refinement at higher resolutions. Second, the ability to build pseudo-C^α traces in intermediate-resolution maps has the potential to help identify novel protein folds especially in instances where fast, automated, screening procedures fail to yield crystals suitable for high-resolution crystallographic studies. The combination of our methods with related ones^15,35–38 will eventually make it feasible to reveal folding motifs from diffraction data at intermediate or lower resolutions. Third, the secondary structural elements revealed by our and related methods¹⁵ will generate reliable landmarks for docking atomic models of sub-components or homology-derived models into intermediate-resolution density maps of supermolecular complexes. Docking accuracy is known to be significantly improved if even just a few points inside a density map can be reliably identified.³⁹ Finally, our sheet-searching methods offer a potential to assist the deciphering of folding motifs in amyloid fibrils,^40,41 which are rich in β-sheets⁴² and for which high-resolution crystal structures are not available. Although current experimental data on these fibrils are limited to 20–30 Å,^40,41 a combination of improvements in the resolutions achieved in experimental measurements along with an enhanced ability to analyze lower-resolution data with methods like ours will eventually help provide new structural insights.

Methods

sheettracer traces individual β-sheets using the relatively thin, but continuous, sheet density maps output from sheetminer.¹⁶ The overall procedure of sheettracer is shown in the flowchart in Figure 1.

Pre-processing of sheet density maps

The products from sheetminer¹⁶ are relatively thin sheet densities containing clusters of voxels that are continuously distributed in space. Each cluster is presumed to represent a single sheet. In order to discern the positions of individual strands in the sheet density, a set of pre-processing steps is applied to each individual cluster.

Local peak filtering for selecting backbone voxels

Here, voxels are selected from each voxel cluster that likely form the backbones of individual strands. Since voxels close to strand backbones usually have higher density values, the voxels assigned to the main chains are selected based on their density values contained in the original maps. However, because densities are unevenly distributed across sheets, simply selecting a desired number of voxels with the highest density values would fail to represent the 3D structure of the sheet. Hence, we developed a special local peak filtering method that emphasizes high local density values and identifies backbone voxels by comparing neighboring voxels (Figure 9(a)).

Figure 9.

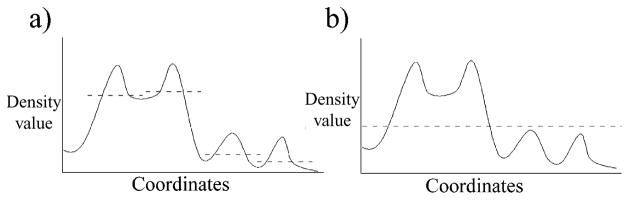
(a) A 1D example of a local peak filter. (b) A 1D example of a traditional biliteral filter. Both in 1D and 3D examples, the local peak filter has better performance in identifying local peaks that is critical to finding main-chain densities in weaker regions.

Application of the local peak filter begins with assigning a local-peak-count number to each voxel (initially set to zero). For each voxel, the average density of all voxels contained within a sphere of 3 Å in radius is calculated and those voxels in the sphere with a density value greater than the average have their local-peak-count number increased by 1. The peak counting operation loops over all voxels and assigns each voxel a local-peak-count number. Upon completion of this process, all voxels are sorted according to their local-peak-count numbers. The top 50% of voxels with highest local-peak-count numbers are categorized as backbone voxels, whereas the lowest 50% are discarded. This method reduces the effects of bias that might occur owing to variations in density throughout the map and permits selection of backbone voxels even in regions where the density is relatively weak (Figure 9(a)). Indeed, this method provides more robust results than can be obtained using traditional bilateral filters (Figure 9(b)).

Local first principal component axis projection

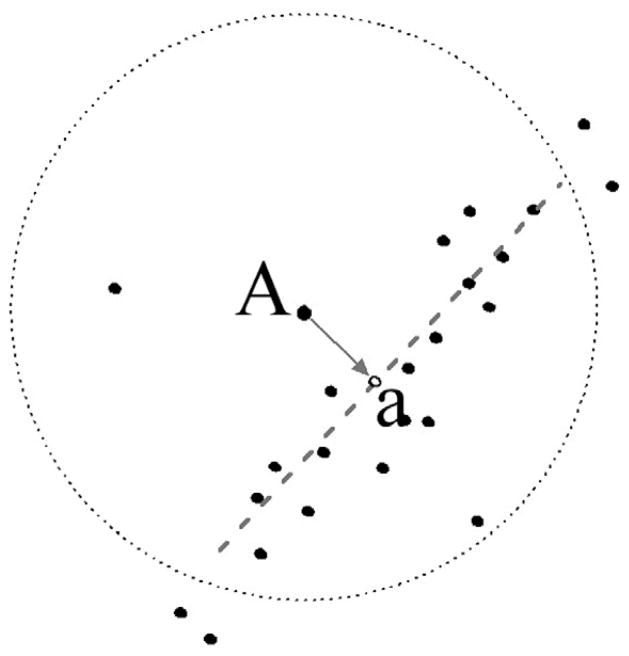
Backbone voxels selected through use of the local peak filter are then subjected to a local first principal component axis projection, which increases contrast and thereby facilitates subsequent selection operations. The advantage of this projection procedure is that voxels are not shuffled along the first principal component axis. Instead, the voxel distribution along the longest axis, coincident with the strand backbone, is emphasized. In this procedure, each voxel is vertically projected to its local first principal component axis, which is calculated for voxels within a sphere of radius of 3 Å (Figure 10). All subsequent analyses are performed with the translocated voxels. In doing so, the distribution of voxels is significantly narrowed, which will make the subsequent local linearity filtering more efficient.

Figure 10.

Scheme for local first principal component axis projection. The position of “a” is the projection of voxel “A” on the axis (dotted line).

Local linearity filtering

Based on the notion that genuine backbone voxels in sheets ought to exhibit good linearity with other voxels belonging to the same strand, this pre-processing step is designed to further select backbone voxels based on their local linearity.

For each selected backbone voxel, the local linearity is examined to detect if the distribution is linear as would be expected for real strands, or if the voxels are just randomly distributed in a cloud due to noise in the data. To analyze voxels in this way, we create a cylinder (0.75 Å in radius and 8 Å in length), centered on each voxel and large enough to encompass about two amino acid residues, and a concord sphere with diameter equal to the length of the cylinder. All possible cylinder orientations are tested within the sphere to find the orientation where the largest number of voxels are included in the cylinder (Figure 11). The ratio of the number of voxels in the cylinder to that in the sphere is then calculated. A ratio approaching 1.0 suggests that voxels are linearly distributed around the central voxel, whereas smaller values indicate a more dispersed distribution in this region. Any voxel with a ratio smaller than 0.4 is discarded in our scheme.

Figure 11.

Scheme for local linearity filtering. The linearity is defined as the ratio of the number of voxels in the cylinder to that in the sphere. In this example the linearity is 10/13 = 0.77.

k-Segments clustering

The k-segments algorithm¹⁸ is designed to separate backbone voxels from different β-strands into different groups so a pseudo-C^α trace can later be modeled into each group. The algorithm employs an incremental procedure to find principal curves by fitting line segments into the data space, which in this study is spanned by the voxels. Principal curves are the non-linear generalization of principal components that give a summarization of the data in terms of a 1D space non-linearly embedded in the data space.¹⁸ Intuitively, a principal curve “passes through the middle of the (curved) data cloud”¹⁸ (Figure 12).

Figure 12.

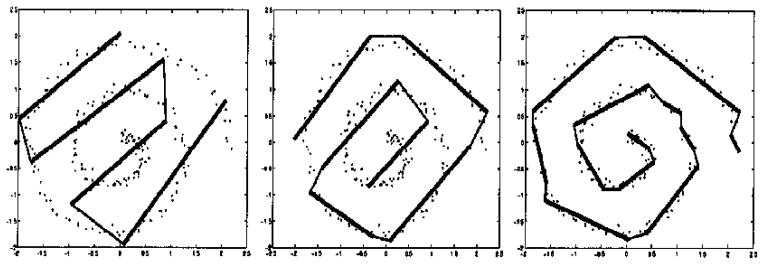
Demonstration of k-segments algorithm on a noisy spiral data set. Results using four, six, and 12 segments (from left to right) are shown. The dots are the data, and the thicker lines are the fitted segments. The Figure is adapted from the original literature.¹⁸

In k-segments clustering, a threshold cluster number is set to stop the algorithm from inserting new clusters once this number is exceeded. In our implementation of k-segments clustering, we set this number equal to the number of backbone voxels, which is directly correlated with the number of amino acid residues in β-sheets. A voxel to cluster ratio of 40:1 is empirically chosen to produce about two amino acid residues per cluster. It is notable that this ratio is only used to establish a stop point for the algorithm, and the actual size of clusters can vary greatly. We have also learned that good performance is generally obtained if the length of the first principal component is set to 2σ centered at the centroid of the cluster, where σ² is the variance of the distance between voxel projections to the centroid along the first principal component axis.

Cluster cleaning and evaluation

The k-segments clustering yields several voxel clusters along with their first principal component axes. Ideally, each cluster will represent a single strand or part of one strand. However, clusters sometimes will contain voxels from separate strands and also voxels that do not belong to a strand and may have arisen from noise in the data. Hence, additional filtering operations are performed to remove or reduce these artifacts.

Breaking up mixed clusters

Density maps that contain very curved local structures can prove problematic because they may lead the k-segments algorithm to generate clusters with a mixture of voxels from different strands. To help identify problematic clusters, the program OPTICS⁴³ is used to analyze each cluster and check the reachability between voxels within the same cluster. If the reachability gap exceeds 2 Å in any cluster and a voxel from another cluster is within 2 Å of the two voxels separated by this gap, the cluster is subdivided into two clusters at the interface of the gap. The effect of this procedure is to break up all mixed clusters into smaller, independent clusters that can subsequently be merged with other clusters that belong to the same strand.

Detection and removal of spurious voxels

Typically, spurious voxel clusters, which we attribute to noise in the data, appear to be neither parallel nor semi-parallel with any other clusters, whereas the backbones of two neighboring strands in genuine β-sheets are parallel or semi-parallel and separated by about 4.5 Å. Therefore, spurious clusters are identified by means of an exhaustive search that checks the crossing angles between each pair of neighboring first principal component axes. The crossing angle is defined as the acute angle formed by the pair of neighboring axes. The first principal component axes of neighboring clusters representing real strands should have characteristic small crossing angles. If the angle between two neighboring clusters exceeds 40°, the angle sum for each of the two clusters will be calculated. The angle sum is defined as the sum of crossing angles between the first principal component axis of the current cluster and those of the six closest clusters. This value indicates how well the first principal component axis of a particular cluster fits in the context of other local clusters. If there are less than six neighboring clusters, all crossing angles are summed. The cluster with the largest angle sum value is no longer treated as a cluster, and its voxels are redistributed among neighboring clusters based on identifying the cluster whose first principal component axis is closest.

Cluster merging

Since the ratio of the number of amino acid residues to segments is 2 in k-segments clustering, it is very likely that several independent clusters of voxels may combine forming one single strand. This is particularly true for strands with highly curved structures. However, to successfully trace consecutive C^α atoms on each strand, clusters belonging to the same strand need to be merged together.

The merge operation is initiated by pairing the ends of first principal component axes of different clusters. The first principal component axis of each cluster has two ends, hence, for N clusters there exist 2N(N – 1) pairs. Two ends are considered for merging if the angle penalty is smaller than 120° and the isolation distance is larger than 2 Å. The angle penalty is defined as the sum of the angles formed by the first principal component axes of the two clusters and the line connecting the two closest ends (Figure 13). The isolation distance is the shortest distance between this line and the first principal component axes of any other cluster.

Figure 13.

Illustration of angle penalty for cluster merging scheme. Angle penalty is determined by the two neighboring first principal component axes and equals the sum of α and β.

Obviously, the angle penalty will be small for two neighboring clusters belonging to the same strand. In the merging algorithm, all eligible end pairs are sorted according to their angle penalty, and the merging operation starts with the pair having the smallest angle penalty. Although one end could be paired with different partners, the nature of β-strands dictates that each end can only be paired once. Therefore, after one end is merged with its partner, any other pairs that include this end are no longer considered. As the merging operation proceeds through all eligible pairs, clusters assigned to the same strand are merged. The final product is a set of voxel groups, each of which is presumed to delineate a single strand.

Building pseudo-C^α traces for strands

The next step involves building a pseudo-C^α trace in each of the voxel clusters. Since voxels are grouped by strands, each pseudo-C^α trace delineates one strand. However, the connectivity between strands and the directionality of each strand must be ignored because such information cannot be discerned from density maps at low to intermediate resolutions.

Strand walking

The first step in defining the trace of pseudo-C^α-atoms in a single group of voxels requires that the two endpoint voxels, corresponding to the N and C-terminal C^α-atoms of a particular strand be identified. The end-point voxels are chosen as belonging to the pair of voxels that are most distant from each other within a group, as would be expected for a β-strand. One end-point voxel defines the first pseudo-C^α position. Based on an average 3.8 Å separation between adjacent C^α-atoms along a β-strand, a sphere of radius 3.8 Å (centered at the first pseudo-C^α position) is drawn and the voxel with the largest neighboring voxel number within 2 Å is defined as the next pseudo-C^α position. If two points have the same number of neighboring voxels, the one with the smallest distance to the mass center of all neighbors is chosen to be the next pseudo-C^α position. The procedure is designed to extend the pseudo-C^α trace along the line of maximum density in the cluster, which would coincide with the backbone of the strand. To avoid backward extension, all voxels within 3.8 Å to an already-built pseudo-C^α will not be counted in the search for the next C^α-atom. Note that it is possible while searching the density in regions of discontinuity to fail to find a point with any neighbor voxel within 2 Å. In this circumstance, the next C^α is chosen to lie at a position along the line connecting the current C^α and the second end-point voxel at a distance of 3.8 Å from the current C^α. This strategy assures that the C^α trace is continuous until the second end-point voxel falls within 3.8 Å of a built C^α-atom.

Strand seeding

It is important to emphasize that, in our strategy, the overall trajectories of the strands are provided by the voxel groups from ad hoc morphological analysis of density maps and no information is derived from 3D structural prediction methods. Once a trajectory is known, a pseudo-C^α trace can be built in a variety of ways. Sometimes, especially with experimental density maps, the noise level may be high and this may lead to only a portion of the sheet being located by the procedure described above. In such instances, a complementary procedure can be employed to complete the building of the missing strands. The procedure is based on the knowledge that the distance between two adjacent β-strands is always 4.5 Å and the distance between consecutive C^α-atoms along a strand is 3.8 Å. With this intrinsic logic, it is then possible to “grow” missing strands from the identified ones (i.e. using defined strands as seeds for other strands). To accomplish this, strands are added at both sides of the existing strands until the edges of sheet density map are reached. Finally, because of the inherent curvature of β-sheets, the extended strands need to be adjusted to best fit the density map.

A method for blind deconvolution of density maps

Building C^α traces into low-resolution density maps is inherently problematic. In an attempt to at least partially overcome this obstacle, we implemented a deconvolution method derived from the image restoration method.⁴⁴ Deconvolution can be used to enhance the appearance of major secondary structural elements and this in turn permits better tracing of β-strands. Other methods such as the watershed transform for segmentation of density maps also provide objective means to interpret features in maps.⁴⁵

Image restoration generally refers to processes designed to recover an image from a degraded observation. Restoration methods have enjoyed widespread application in a number of fields such as artificial satellite imaging, remote sensing, and medical imaging. Improvement of image quality often enhances the ability to extract “hidden” information from observations that would otherwise be difficult to interpret or would be misleading. The same holds true for the interpretation of features contained in density maps. Hence, proper deconvolution of density maps has the potential to improve the accuracy with which pseudo-C^α traces can be built.

The general principle of our blind deconvolution of 3D maps involves the iterative minimization of a convex cost function. This cost function, also known as nonnegativity and support constraints recursive inverse filtering (NAS-RIF) technique, belongs to the class of non-parametric finite support blind image restoration methods.^44,46–48 The basic assumptions are that a biological molecule of finite extent is imaged against a uniform, gray background, and the edges of the molecule are completely or almost completely contained in the observed frame. Neither statistical knowledge nor a parametric model of the point-spread-function (PSF) is needed for the original image. The only requirement for restoration is the non-negativity of the original image and support size of the molecule. The support size is defined as the smallest rectangle containing the entire molecule. The image is restored in a process that filters the degraded image to generate an image estimate and this process involves the simultaneous identification of the original image and the PSF from the degraded image.

The following linear model is assumed to represent the degradation of the original image:

$$g(x,y,z)=f(x,y,z)\ast h(x,y,z)+n(x,y,z)$$

where (x, y, z) are the 3D discrete pixel coordinates, g(x, y, z) is the experimental, degraded image, f (x, y, z) is the undegraded, original image that we wish to restore, h(x, y, z) is the PSF, n(x, y, z) is the additive noise, and * represents the 3D linear convolution operation.

The NAS-RIF technique applies a variable filter u(x, y, z) to the degraded image g(x, y, z) and generates as output an estimate of the original image f̂ (x, y, z). This estimate is then projected through a non-linear (NL) filter that employs a non-expansive mapping into the space that the known characteristics of the original image is represented. The difference between the projected image f̂_NL(x, y, z) and the image estimate f̂(x, y, z) is treated as the error function to update the variable filter u(x, y, z). The cost function used is:

$$J(u)=\sum _{\forall (x,y,z)}{e}^2(x,y,z)+\gamma {\left[\sum _{\forall (x,y,z)}u(x,y,z)-1\right]}^2$$

where γ in the second term is non-zero only when the background color is black. This term is used to constrain the parameters away from the trivial all-zero global minimum. The first term e²(x, y, z) has the form of:

$$\sum _{(x,y,z)\in D_{sup}}{\widehat{f}}^2(x,y,z)\left[\frac{1-sgn(\widehat{f}(x,y,z))}{2}\right]+\sum _{(x,y,z)\in {\overline{D}}_{sup}}{[\widehat{f}(x,y,z)-L_{\mathrm{B}}]}^2$$

where f̂(x, y, z) = g(x, y, z) * u(x, y, z), D_sup is the set of all pixels inside the support, and D̄_sup is the set of all pixels outside the support. The constant L_B is zero for black background. It can be shown that the cost function J(u) is convex so that a convergence to a global minimum and the uniqueness of the solution are possible.⁴⁹ Note, the filter u(x, y, z) has a dimension N_xu × N_yu × N_zu, here N_xu is the number of pixels in the x direction. All the elements in the filter are the variables for optimizing the restoration. In practice, with a voxel volume of 1 ų, a filter of size of N_xu = N_yu = N_zu = 5 produced optimal restoration.

Computer source codes

The computer source codes for sheettracer and deconvolution will be soon released as a part of a comprehensive software package OPUS for modeling protein structures and dynamics at low to intermediate resolutions. They are currently available directly from the authors upon request prior to the final release.

Abbreviations used

cryo-EM

electron cryomicroscopy

D

dimensional

PDB

Protein Data Bank

rms

root-mean-square