Dynamic mechanical finite element model of biological cells for studying cellular pattern formation

Abstract

Understanding the geometric, topologic, and mechanical properties of cells and their interactions is critical for studying tissue pattern formation and organ development. Computational model and tools for simulating cell pattern formation have broad implications in studying embryogenesis, blood-vessel development, tissue regeneration, and tumor growth. Although a number of cell modeling methods exist, they do not simultaneously account for detailed cellular shapes as well as dynamic changes in cell geometry and topology. Here we describe a dynamic finite element cell model (dFEMC) for studying populations of cells and tissue development. By incorporating details of cell shape, cell growth and shrinkage, cell birth and death, cell division and fusion, our method can model realistically a variety problems of cell pattern formation. We give two examples of applying our method to the study of cell fusion and cell apoptosis. The dFEMC model developed here provides a general computational framework for studying dynamics pattern formation of tissue.

I. INTRODUCTION

Cells are the building blocks of an organism, Properties and interactions of cells largely determines the behavior of an organism [1]. Understanding how properties of individual cells and cell-cell interactions affect cellular pattern formation is critical to the studies of important problems such as embryogenesis, blood-vessel development, organ regeneration, tumor growth, and tumor angiogenesis.

Computational modeling of cells has become increasingly important to gain insight into understanding of cellular pattern formation and to aid in design of further experimental investigations. A number of computational methods have been developed to study embryogenesis, blood-vessel development, organ regeneration, tumor growth [2]–[14]. One widely used method is the cellular Potts model, in which each cell is modeled as a collection of about 25–50 lattice sites [9], [13]. However, cell shape and topology are not modeled explicitly and extensive postprocessing is required if realistic cell shape is desired [15].

Another class of methods are center-based models [8], [14], which approximate cells as spheres. Cells can interact with each other and respond to environmental stimuli. Cell growth, cell division, and cell migration can all be modeled as well. However, no details of cell shapes are described and any shape deformation from sphere is not modeled.

Vertex models are another group of widely used models [10]–[12], [16]. They are based on the postulation that cell shape is determined by minimizing the energy due to forces acting on cell junctions. They can incorporate properties of cell shape, size and elasticity to model cell birth, and growth. However, cell shapes in vertex models are usually not modeled in sufficient details and initial conditions are highly restrictive.

Finite element models [4]–[7] incorporating physical and mechanical details of cells can provide very realistic descriptions of cell shapes. However, existed methods cannot be used to study dynamic changes in population of cells.

Here we describe a novel dynamic finite element based cell model (dFEMC) by incorporating algorithms from computational geometry, including triangular mesh generation, bounding volume construction, Delaunay triangulation, with the goal to simulate dynamic changes in cellular patterns with accurate description of cell shapes. Our method enables a broad range of cellular events such as cell death and tissue fusion to be studied computationally in details.

II. Models and Methods

A. Linear elastic model

We assume that each cell has linear elastic properties [17]. We denote one cell with certain shape in two dimensional space as the connected points set {Ω : x = [x₁, x₂]^T}, where x₁, x₂ are world coordinates of x. The displacement of one point x in Ω is defined as u (x) = [u₁(x), u₂(x)]^T. The strain energy Ω of is defined as: $\epsilon (\underset{\_}{\mathrm{u}})=\frac{1}{2}{\int }_{\mathrm{\Omega }}{\underset{\_}{\epsilon }}^{T}d\underset{\_}{\mathrm{x}}$, where ε is the strain vector: ε = [ε_x1, ε_x2, ε_x2x1]^T, where ε_x1 = ∂u₁/∂x₁, ε_x2 = ∂u₂/∂x₂, ε_x2x1 = ∂u₁/∂x₂ + ∂u₂/∂x₁. We can rewrite this as ε = Bu, where

$$B=\left|\begin{array}{ll}\frac{\partial }{\partial x_1}\hfill & 0\hfill \\ 0\hfill & \frac{\partial }{\partial x_2}\hfill \\ \frac{\partial }{\partial x_2}\hfill & \frac{\partial }{\partial x_1}\hfill \end{array}\right|.$$

The stress, namely, the average internal force on unit area due to shape deformation, can be expressed as vector σ related to the strain vector through Hooke’s law by σ = Dε, where D is a symmetric material stiffness matrix defined by two lamé material constants λ and μ:

$$D=\left|\begin{array}{lll}\lambda +2\mu \hfill & \lambda \hfill & 0\hfill \\ \lambda \hfill & \lambda +2\mu \hfill & 0\hfill \\ 0\hfill & 0\hfill & \mu \hfill \end{array}\right|$$

Assuming external forces f(x) are applied to the boundary Γ of a cell Ω. We can express the strain energy and the work done by external forces through the potential energy function using the relation below:

$$\epsilon (\underset{\_}{\mathrm{u}})=\frac{1}{2}{\int }_{\mathrm{\Omega }}{\underset{\_}{\mathrm{u}}}^T{B}^{T}DB\underset{\_}{\mathrm{u}}d\underset{\_}{\mathrm{x}}-{\int }_{\mathrm{\Gamma }}{f}^T\underset{\_}{\mathrm{u}}da.$$

B. Finite Element Discretization

For each cell, we use 20~30 nodes to represent its boundary. Triangular mesh tilling the cell is then generated using the farthest point sampling method [18], which partitions the cell domain into individual sub-domains of triangles (Figure 1 a, b).

Fig. 1.

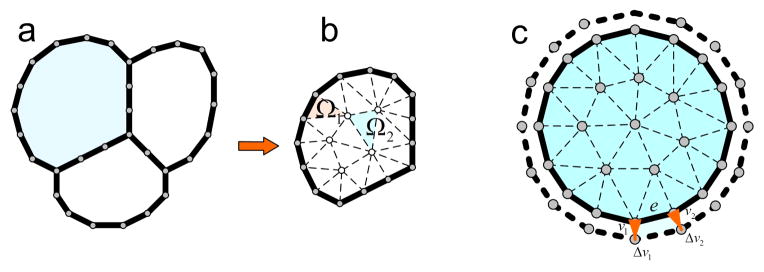
Geometric discretization for cells: (a). An example of a toy model of a tissue consisting of 3 cells. The boundary of each cell is represented by a number of nodes. (b). For each cell, triangular mesh is generated using the farthest point sampling method [18]. (c). Cell grows from time step t to t+1: volume change can be attributed to individual boundary element, with their total sum to ΔV

Each triangle element Ω_e is defined by three nodes $P_i^e$, i = 1, 2, 3. A node has a position in the natural coordinates L = [L₁, L₂, L₃]^T within the triangle and world coordinates x = [1, x₁, x₂]^T, subject to

$$\begin{array}{l}\left|\begin{array}{l}1\\ x_1\\ x_2\end{array}\right|=\left|\begin{array}{lll}1& 1& 1\\ x_{11}^e& x_{21}^e& x_{31}^e\\ x_{12}^e& x_{22}^e& x_{32}^e\end{array}\right|\left|\begin{array}{c}{L}_1\\ L_2\\ L_3\end{array}\right|,\\ \left|\begin{array}{c}{L}_1\\ L_2\\ L_3\end{array}\right|=\frac{1}{2A^e}\left|\begin{array}{ccc}{a}_1^e& a_2^e& a_3^e\\ b_1^e& b_2^e& b_3^e\\ c_1^e& c_2^e& c_3^e\end{array}\right|\left|\begin{array}{l}1\\ x_1\\ x_2\end{array}\right|,\end{array}$$

where A^e is the area of Ω_e and $x_{i1}^e,x_{i2}^e$ are the world coordinates of $P_i^e$. We use barycentric coordinates for points within an element. The displacement field representing strain interrelationship between nodes of Ω_e can be written in terms of linear correlation between natural coordinates and world coordinates :

$${\underset{\_}{\mathrm{u}}}^e(\underset{\_}{\mathrm{x}})=\sum _{i=1}^3{N}_i^e(\underset{\_}{\mathrm{x}}){\underset{\_}{\mathrm{u}}}_i^e,$$

where

$$N_i^e=L_i=\frac{1}{2A^e}(a_i^e+b_i^e{x}_1+c_i^e{x}_2).$$

We can find the solution to the deformation problem under external force by assuming the potential energy of an element reaches its minimum, which happens when ∂ε(u) = 0. We also notice that:

$$\begin{array}{l}\frac{\partial {\underset{\_}{\mathrm{u}}}^e}{\partial x_1}=\sum _{i=1}^3\frac{\partial N_i^e(\underset{\_}{\mathrm{x}})}{\partial x_1}{\underset{\_}{\mathrm{u}}}_i^e=\sum _{i=1}^3\frac{b_i^e}{2A^e}{\underset{\_}{\mathrm{u}}}_i^e\\ \frac{\partial {\underset{\_}{\mathrm{u}}}^e}{\partial x_2}=\sum _{i=1}^3\frac{\partial N_i^e(\underset{\_}{\mathrm{x}})}{\partial x_2}{\underset{\_}{\mathrm{u}}}_i^e=\sum _{i=1}^3\frac{c_i^e}{2A^e}{\underset{\_}{\mathrm{u}}}_i^e.\end{array}$$

We can then rewrite the equilibrium equation for element Ω_e as:

$$0={\int }_{{\mathrm{\Omega }}_e}{B}^{eT}D{B}^e{u}^{e}dx-f^e,$$

where f^e is the discretized force vector for the element, and

$$B^e=\frac{1}{2A^e}\left|\begin{array}{llllll}{b}_1^e& 0& b_2^e& 0& b_3^e& 0\\ 0& c_1^e& 0& c_2^e& 0& c_3^e\\ c_1^e& b_1^e& c_2^e& b_2^e& c_3^e& b_3^e\end{array}\right|,$$

which leads to the equation K^eu^e = f^e, where K^e = B^eTDB^eA^e is the element stiffness matrix of the triangle element. Assemble each element stiffness matrix into one global stiffness matrix resulting in a large sparse linear system Ku = f. The behavior of the whole system at a specific time then can be simulated by solving this linear equation.

C. Cell growth model

At the initial state, each cell maintains a sphere-like shape. The intersection between two cells, if exists, is expressed as the intersection line segment. During the cell growth process, the shape of each cell deforms in response to external forces exerted by adjacent cells. To model cell growth, we assume that the growth is induced by the cell internal pressure forces. For a cell C growing from time step t to t+1, we distribute the cell volume change ΔV onto each cell boundary node v_i as ΔV_i (Figure 1 c). ΔV_i can be written as:

$$\mathrm{\Delta }{V}_i=\frac{1}{2}\mid \mathrm{\Delta }{\underset{\_}{\mathrm{v}}}_i\times \underset{\_}{\mathrm{e}}\mid ,$$

where v_i is the displacement vector of node v_i and e is the edge vector associated with node v_i, and “×” is vector cross product. We then have:

$$\mathrm{\Delta }{V}_i=\frac{1}{2}\mid \mathrm{\Delta }{\underset{\_}{\mathrm{v}}}_i\times \underset{\_}{\mathrm{e}}\mid =\frac{1}{2}\mid \frac{1}{2}{\underset{\_}{\mathrm{a}}}_{v_i}{(\mathrm{\Delta }t)}^2\times \underset{\_}{\mathrm{e}}\mid ,$$

where a_vi is the acceleration rate of node v_i. Using Newton’s Law, we have:

$$\mathrm{\Delta }{V}_i=\frac{1}{2}\mid \frac{1}{2}\frac{F_{v_i}}{m}{(\mathrm{\Delta }t)}^2\times \underset{\_}{\mathrm{e}}\mid =\frac{1}{2}\rho \mid {\underset{\_}{\mathrm{F}}}_{v_i}\times \underset{\_}{\mathrm{e}}\mid ,$$

where m is the mass of the node v_i, ρ = (Δt)²/2m, and F_vi is the internal pressure forces exerted on node v_i.

We can derive the internal pressure forces F_vi necessary for the cell growth by solving the above equation for a given ΔV_i. These pressure forces depend on cell growth rate and the elastic properties of the cell wall, and can be equivalently treated as the boundary conditions to trigger the growth process which will impact on the whole tissue.

D. Detecting cell contacts

Collision or cell contacts occur when neighboring cells grow into each other. Collision detection and correction are critical to model the dynamics of cell growth and cell death. At the initial state, we use Delaunay triangulation to detect potential colliding pairs of cells. For each pair, axis-aligned bounding boxes [19] are then used to detect the collision nodes on both cells. As cells grow into certain shapes that deviate from sphere or if one cell is dead and erased from the system, we use the BD-Tree [20] to locate bounding spheres wrapping around the cells. These bounding spheres are then used for another round of Delaunay triangulation to detect potential colliding cell pairs.

E. Topologic and geometric changes

There are three types of topologic and geometric changes when cell grow or shrink. A change is required when cell size change significantly:

• Node merging: When collision is detected between two cells, we align the colliding nodes and merge them to the same position by moving them onto the aligned boundary line segment (Figure 2).

• Edge division: When one edge is longer than a predefined threshold, we divide this edge by adding one new node at the midpoint of the edge of its corresponding cell.

• Edge removal: When one edge is shorter than a predefined threshold, we remove this edge by erasing one node from the corresponding cell.

Fig. 2.

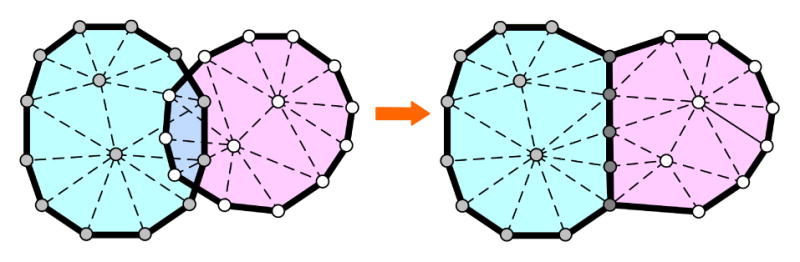
Node merging: collision detected between cells and collided nodes are aligned and then corrected

Our model is implemented in C++.

III. Results

A. Cell fusion

We now describe applications of our model. We assume cell growth occurs in a constant environment. The first application we study is cell fusion, which occurs when two or more groups of cells separated spatially come into contact and fused into one single larger tissue. Cell fusion is important for many biological processes including cancer metastasis [21] and wound healing [22]. The etiology of these defects are complex and involve many processes, including adhesion, apoptosis, and cell migration.

We use a simple example to demonstrate the geometric and topologic changes of modeled fusion events (Figure 3a, b). With our method, we can monitor the incremental steps of cell growth, and track the occurrence of cell fusion events.

Fig. 3.

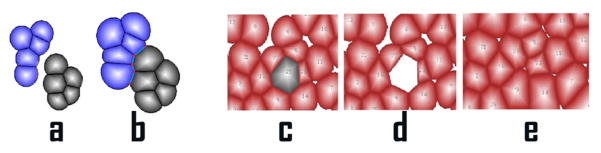
Fusion of tissues and cell death: (a). Two separate tissues. (b). Fusion of these two tissues after cell growth. (c). A picture of one tissue where the gray cell is about to die. (d). The gray cell died and removed from the system. (e). The adjacent cells continue to grow and occupy the space of the dead cell.

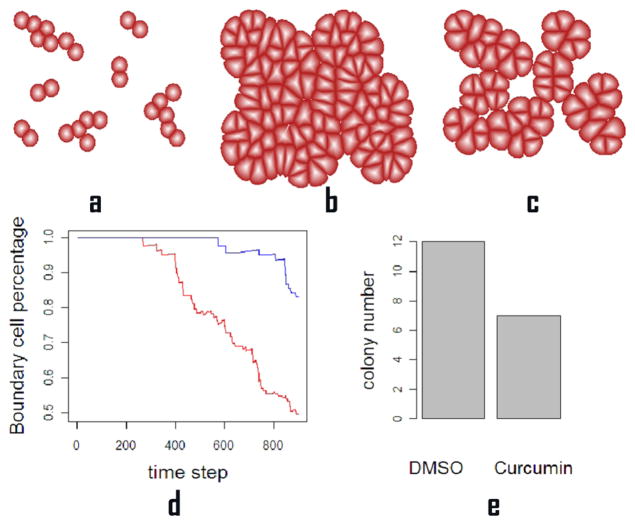
We then apply our method to study cancer cell growth. Curcumin, an antitumor agent derived from the perennial herb, exhibits cancer preventive and therapeutic properties by suppressing tumor growth [23]. We simulate cancer cells growth under suppressions from curcumin. For comparison, we also study cancer cell growth under DMSO, another antitumor agent [24].

We setup the initial state as a set of cancer cells and begin their growth process under different conditions of growth rate σ = αC, where C is the colony number of the tissue obtained from the experiments and α is constant to adjust the growth rate to match the biological time to simulation time. We run both simulations for 800 times and compare the computational results with experimental data [25]. The curcumin agent exhibited stronger suppression effect on cancer cells than DMSO agent, which is shown in Figure 4.

Fig. 4.

Cancer cell growth under suppression induced by antitumor agents. (a). The initial state of cell growth. (b). Tumor tissue after 800 time steps using growth parameter modeling the effects of suppression from DMSO. (c). Tumor tissue after 800 time steps using growth parameter modeling the effects of suppression from curcumin. (d). The percentage of boundary cells, namely, the number of cell on boundary of the tissue over the total cell number, at each time step for DMSO treatment (red) and for curcumin treatment (blue). The higher boundary cells percentage indicates a more scattered cell population. (e). The colony number for DMSO and curcumin treatments. We count every 9 cells as one colony. The colony number ratio between the two treatments, 12 against 7, is consistent with the colony number ratio between the two treatments found in experiment studies [25].

B. Cell apoptosis

We also study cell apoptosis, namely, programmed cell death, which is essential for many important biological processes including homeostatic tissue size control [26]. We first illustrate with a simple example. A cell is dead and erased from the system with its space occupied by its adjacent cells [27] (Figure 3c, d, e).

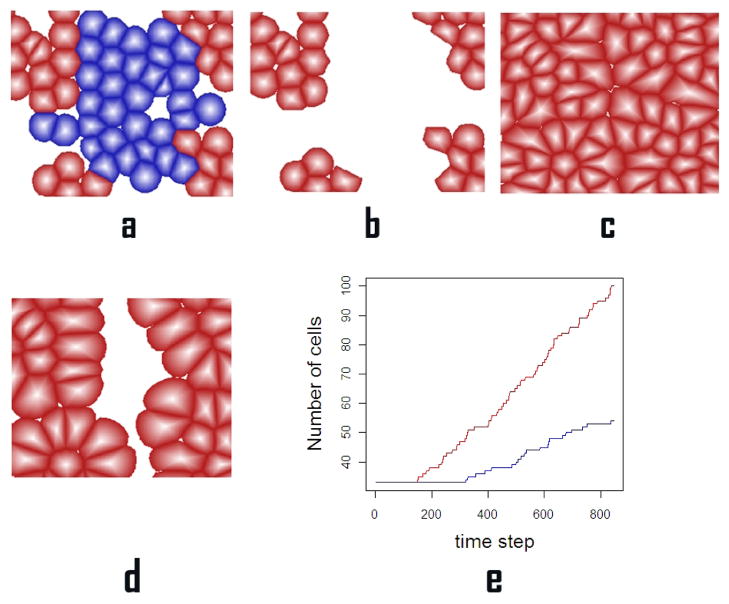
We then apply our model to simulate wound healing. Bisphosphonates(BPs) are known to be effective in the treatment and prevention of osteoporosis, hypercalcemia and other solid tumors. It is reported that BPs may inhibit normal epithelial wound healing thus contributing to persistent exposure of underlying bone and development of osteonecrosis of the jaws [28]. Here we simulate the wound healing process of oral epithelial cells with and without suppress from pamidronate, a second-generation BP. For the initial state, we have a tissue consisting of oral keratinocytes cells. Wound is then inflicted to the tissue by erasing a subset of 33 cells out of total 66 cells from the system. Wound healing is modeled using different growth rates when treated with and without pamidronate. We run simulations for 800 time steps and compare the computational results with the experimental data [28]. The effects of pamidronate delaying wound healing is shown in Figure 5.

Fig. 5.

Wound healing under growth suppression induced by pamidronate: (a). A wound of an oral tissue where the set of blue cells are subject to infliction of wound. (b). The tissue suffers injury where blue cells are erased from the system. (c). Wound healing is completed after 800 time steps without suppression from pamindronate. (d). Wound healing after 800 time steps with suppression from pamindronate. There are gaps remaining between tissues (e). The total number of cells within the tissue: wound healing without suppression from pamindronate (red) and wound healing under suppression from pamindronate (blue).

IV. Conclusion

Here we present a novel method called dFEMC to realistically model cell growth, death, division, migration, and fusion, along with accurate description of cell shapes, which is based on a dynamic finite element model combined with algorithms from computational geometry based on physical and mechanical properties of cells. Our method allows simulation of many cellular events, and results in preliminary studies are consistent with experimental data.