Reconstructing protein remodeled membranes in molecular detail from mesoscopic models

Abstract

We present a method for “inverse coarse graining,” rebuilding a higher resolution model from a lower resolution one, in order to rebuild protein coats for remodeled membranes of complex topology. The specific case of membrane remodeling by N-BAR domain containing proteins is considered here, although the overall method is general and thus applicable to other membrane remodeling phenomena. Our approach begins with a previously developed, discretized mesoscopic continuum membrane model (EM2) which has been shown to capture the reticulated membrane topologies often observed for N-BAR/liposome systems by electron microscopy (EM). The information in the EM2 model — directions of the local curvatures and a low resolution sample of the membrane surface — is then used to construct a coarse-grained (CG) system with one site per lipid and 26 sites per protein. We demonstrate the approach on pieces of EM2 structures with three different topologies that have been observed by EM: A tubule, a “Y” junction, and a torus. We show that the approach leads to structures that are stable under subsequent constant temperature CG simulation, and end by considering the future application of the methodology as a hybrid approach that combines experimental information with computer modeling.

Introduction

In biology, Ångstrom scale changes in a single protein can have dramatic effects at the level of an entire organism. The profoundly multiscale nature of biological problems makes their study by simulation and theory interesting but at the same time exceptionally challenging. In this paper we continue the development of a multiscale modeling approach to the problem of membrane remodeling by proteins, with the specific example being the members of the Bin/Amphiphysin/Rvs (BAR) domain family. The new development in the present work is a method for “inverse coarse graining” a mesoscopic continuum membrane model, with the result that continuum remodeled membranes with complex topologies are used to build models in which individual proteins are resolved at a coarse-grained (CG) level.

N-BAR domain biology

The members of the BAR domain protein family are essential factors in several crucial cellular pathways, such as clathrin mediated endocytosis^{1, 2} and T-tubule morphogenesis.^{3, 4} These pathways generally require dramatic remodeling of the cell membrane; in the cases just mentioned BAR domain family proteins are involved in forming tubular membrane invaginations with diameters on the order of 10 nm. When studied in vitro, purified BAR proteins are observed to remodel liposomes into a variety of morphologies, including tubules, vesicles, and reticulated structures, depending on protein concentration as well as liposome composition and size. High resolution crystal structures have been solved for several BAR domains,^5-12 and all share the common structural topology of a crescent shaped coiled-coil homodimer.^{13, 14} Here we focus on a subset of the family known as N-BARs, where the N indicates that each homodimer includes an N-terminal amphipathic helix of about 5 turns, which is likely both important to sense membrane curvature^{15, 16} and to induce membrane curvature by folding and inserting into one leaflet of the bilayer.^{7, 17-20} In particular, we focus on the N-BAR domain of endophilin, one of two N-BARs involved in forming very highly curved tubules at the necks of budding clathrin coated vesicles. Endophilin is unique among BARs in that it contains an extra amphipathic “insert helix” under the arch of the BAR.^{7, 9}

EM2 model for membrane remodeling

In this paper, we describe an approach that begins with a mesoscopic continuum description of a biological membrane, previously developed to understand the process of membrane remodeling by N-BAR domain containing proteins on liposome scales.^{21, 22} Ultimately, our goal is to study membrane remodeling on liposome scales, for which an atomistic description would comprise on the order of 10⁹ atoms and demand simulation timescales on the order of minutes — clearly beyond the reach of atomically detailed simulation for any foreseeable future. This motivated the development of the mesoscopic continuum description, which is based not on the familiar Helfrich Hamiltonian²³ for membrane deformations, but rather a Hamiltonian first introduced by Fischer²⁴ which admits the study of symmetry breaking membrane inclusions²⁵ such as the amphipathic helices of N-BAR domains. The mesoscopic continuum model is studied computationally by discretizing the Fischer Hamiltonian onto “smooth particles,”^26-28 essentially a computational grid that evolves naturally as the shape of the membrane deforms. The resulting continuum model, referred to in our earlier group papers and in the following as “elastic membrane, version 2” (EM2),^{21, 22, 29-32} parallelizes efficiently over thousands of processors, making tractable the simulation of membrane remodeling phenomena on the lengthscale of 500 nm diameter liposomes. EM2 has demonstrated the ability to predict the topology of complex, reticulated membrane structures that were in turn observed by electron microscopy (EM) at high N-BAR domain concentrations.²²

Coarse-grained model of N-BAR remodeling

A single EM2 mesoscopic “particle” represents a patch of membrane roughly 5-10 nm in diameter, and represents the local density of protein as a continuous field that controls the amplitude and direction of the two local spontaneous curvatures. The EM2 level of modeling therefore cannot divulge molecular level details of the coat of protein that generates the curvature, though very recently cryo-EM has revealed the existence of such a coat,³³ and high-resolution cryo-EM of F-BARs has revealed a highly ordered helical coat or “lattice” of protein for the remodeled tubular structures.³⁴ In order to address this limitation, we have developed a CG membrane³⁵ and N-BAR³⁶ model that we have used to study the initial phase of membrane remodeling at the scale of small liposomes.³⁷ The N-BAR model contains the essential features of the domain — the overall arched shape, sites to model the amphipathic moieties, and interactions between the underside of the arch and the membrane to capture the electrostatics. The goal is that eventually this approach will allow a truly multiscale bridge between the atomistic and the scale of the remodeled membrane structures, so that, for example, the effect of point mutations of the N-BAR proteins can be propagated systematically to the lengthscales that describe clathrin mediated endocytosis. Even at the CG level, however, global remodeling is not tractable, though local remodeling has been observed with CG models in liposome scale simulations³⁷ and on small patches of membrane.^38-40

In this paper we develop a new approach to this multiscale problem that combines the success of the EM2 level of modeling with the quasi-molecular detail of the CG description, which resolves individual proteins and lipids (at a CG level). We describe a method to map the surface of a complex, reticulated membrane as calculated by the mesoscopic EM2 level model — approximately one EM2 site per 150 lipids — back into a CG representation in which every lipid is represented by one (elliptical) interaction site, with an additional headgroup site for membrane-protein interactions, and each protein is represented by 26 interaction sites. This is a significant accomplishment, as the surfaces of these membranes are highly convoluted, and simply rebuilding a consistent structure that resolves the lipids and proteins is a very challenging problem. We then show that CG models so obtained are amenable to molecular dynamics simulation, allowing us to test whether the coats reconstructed in this manner are able to stabilize the curvatures observed in the EM2 model, and opening the possibility to study the local dynamics and structure of the protein coats responsible for membrane remodeling. The method we develop here is also an important first step toward a hybrid approach, in which EM data, mesoscopic EM2 level modeling, and the CG membrane protein model are combined in a multiscale fashion to rebuild the protein coats of reticulated membranes, such as are observed in the T-tubule network and the Golgi apparatus. Here, we apply the approach to membrane remodeling by the N-BAR domain of endophilin.^{7, 9, 20, 41}

Results

In the following we reconstruct the endophilin N-BAR coat for three different pieces of a mesoscopic EM2 simulation structure (Figure 1), chosen to represent structural motifs in N-BAR remodeled liposomes that are experimentally observed by EM. The three examples are characterized at the EM2 level by very different local curvature fields, which translates into N-BAR coats distinguished by quite different degrees of local order, as measured by the extent to which a local neighborhood of N-BAR domains are parallel to each other.

Figure 1.

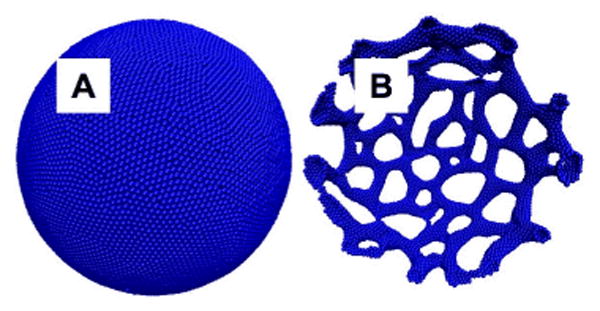
Initial configuration (Panel A) and final configuration (Panel B) of a 500 nm diameter EM2 liposome after 2(10⁷) timesteps of mesoscopic simulation. The critical control parameter is the maximum local spontaneous curvature induced by the N-BAR domain density, as previously reported²² a value of 0.09 nm^-1 is both consistent with atomistic simulations of N-BAR remodeling⁴⁸ and predicts reticulated morphologies that are experimentally observed by EM. Each EM2 particle is rendered as a sphere.

N-BAR coated tubules

Figure 3 illustrates the process of rebuilding the protein coat for a cylindrical piece of an EM2 membrane. The centers of the EM2 particles define a surface and their orientations define the local direction of the largest principal curvature.^{22, 32} The membrane is rebuilt by tiling the EM2 surface with triangular patches of pre-relaxed CG membrane, while the initial configuration of the protein coat is defined by assuming that the individual N-BAR domains lie with their long axis along the direction of maximum local curvature, which orients the arch of the N-BAR and the amphipathic helices for maximum curvature induction. (More details of this methodology are given in the Model and Methods section at the end of the paper.) The initial configuration in Panel E, consisting of 117 proteins and 12,662 lipids (15,704 CG particles) was next subjected to an extensive minimization and heating protocol, after which it is evolved under constant volume and temperature, allowing the membrane-protein system to relax locally from bias introduced during the reconstruction process. During this time (2 million CG integration timesteps) the diameter of the tubule relaxes by a few percent from an initial value of about 34 nm, measured including the protein coat. The protein coat stabilizes the tubular membrane — in its absence the membrane contracts and reforms into micellar like structures. Figure 4 shows the extent to which the local neighborhood of an N-BAR domain is ordered. The direction of the long axis of each BAR domain is calculated, and then the (unsigned) dot product between pairs of BAR domains is averaged over the local neighborhood (defined by a 15 nm cutoff) of each. The analysis readily picks out defects — places where a single BAR domain is disordered relative to the rest of the coat. While such defects likely exist in real BAR domain coats, they would be very difficult to observe by cryo-EM reconstruction, since such defects are either averaged over or else discarded during the classification step. Identifying the morphological signature of such defects is one potentially powerful application of the present approach, as eliminating such defects would improve the resolution of reconstructions.

Figure 3.

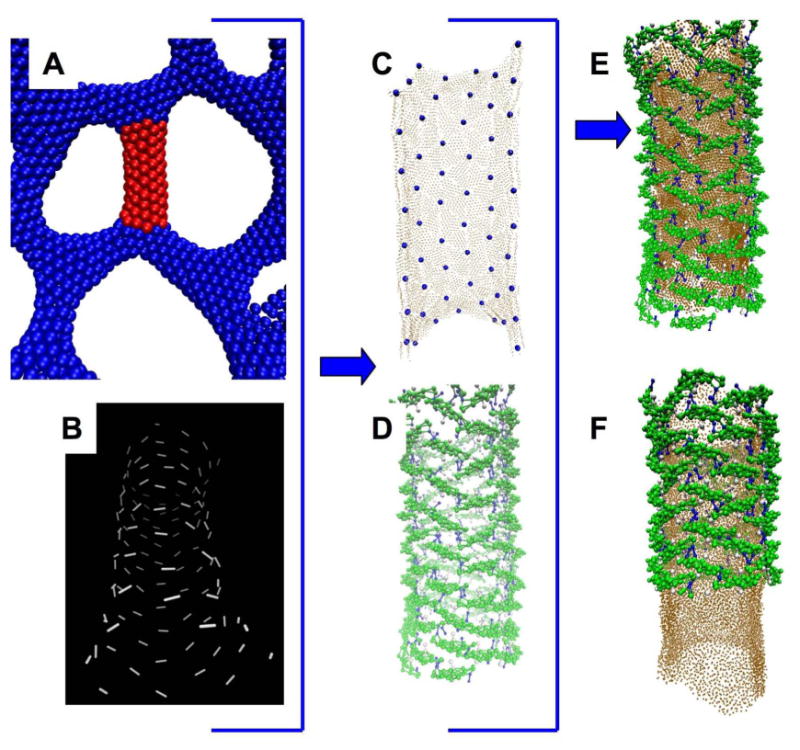
Reconstructing the N-BAR coat in molecular detail from a mesoscopic EM2 simulation configuration at much longer lengthscales. Panel A shows a close-up of the region of the EM2 structure in red that is the starting point for the reconstruction. Panel B shows the direction of the larger of the two local principal curvatures carried by each EM2 particle for the tubular section shown in red in panel A, the configuration is tilted to make clear the fact the largest principal curvature wraps on average around the tubule. Panel C shows the coarse-grained membrane (brown) reconstructed from the EM2 surface, with the positions of the centers of the EM2 particles that define the surface indicated by small blue spheres. Panel D shows the coarse-grained endophilin reconstructed from the positions and directions of the largest principle curvatures of the EM2 particles. Panel E shows the merged initial configuration of the protein and membrane. Panel F shows the configuration after 2(10⁶) CG simulation timesteps, thermostatted by the Nosé-Hoover method at 300 K. The protein is cutaway in the bottom portion so that the membrane is visible.

Figure 4.

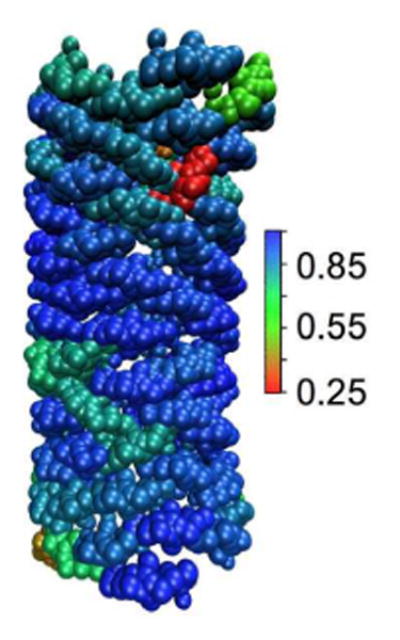
Local orientational order of a tubular reverse mapped EM2 N-BAR domain coat. The configuration in Panel F of Figure 2 is colored to show the orientational order in the neighborhood of each N-BAR domain. The color scale reflects the average of the unsigned dot product between the direction of the long axis of each N-BAR domain and its immediate neighbors.

Three tubule “Y” junction

The reticulated structures observed by low resolution EM contain cylindrical membrane regions, but also contain regions that are much more complex, which when abstracted as surfaces would possess curvatures which vary over the surface in direction and magnitude. As these regions are better characterized by their variability rather than their similarity, they do not admit averaging and high resolution reconstruction by ordinary methods. However, it would be interesting to resolve the molecular detail of such structures, because such surfaces exist in nature and are likely formed by curvature generating proteins.¹⁷ Figure 5 shows a “Y” junction observed in the EM2 model (Panel A), the EM2 curvature field at each particle (Panel A), the initial (Panel C) and final configuration (Panel D) after the relaxation protocol and 2 million CG MD timesteps at 300 K. The system consists of 173 proteins and 19,335 CG lipids (23,843 total CG sites). Figure 6 shows the local orientational order of the BAR domains for the Y junction. It is clear that protein coat is disordered in the region where the three tubules intersect, which results in turn in a more isotropic local curvature.

Figure 5.

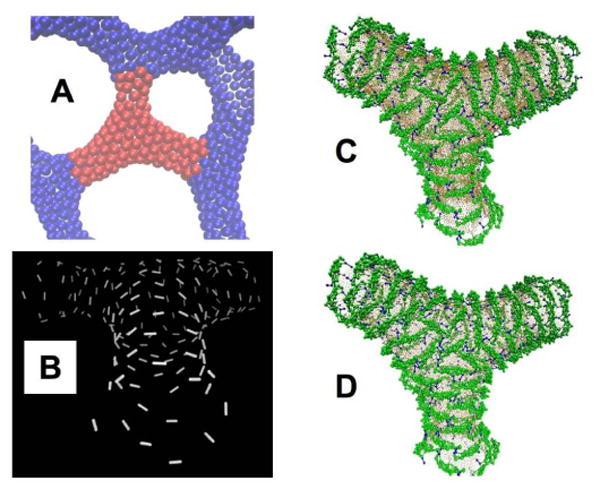
Reconstructing the N-BAR coat in regions “Y” junctions where three tubules intersect. Panel A shows in red the region of the mesoscopic EM2 simulation structure that is reverse mapped. Panel B shows the direction of the largest principal curvature at each EM2 quasiparticle particle, the configuration is tilted to make clearer the local order. Panel C shows the initial configuration of the CG protein and membrane, panel D shows the final configuration after 2 million CG MD integration steps.

Figure 6.

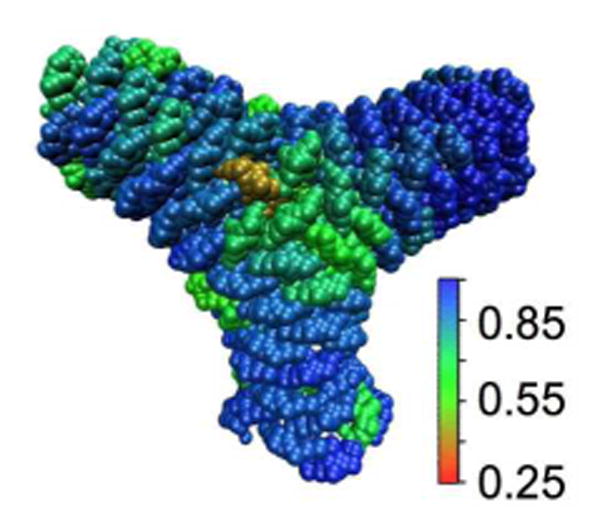
Local orientational order of the Y junction, measured as described in the caption to Figure 3. Note that there is considerably more disorder in the junction region than in the typical tubular region.The color scale reflects the average of the unsigned dot product between the direction of the long axis of each N-BAR domain and its immediate neighbors.

N-BAR coated torus junction

A common feature that is evident in low resolution EM images of N-BAR remodeled liposomes is the appearance of circular features of a diameter of roughly 40-50 nm, which appear to have BAR domain density which is oriented along the radius of the circular feature. (See arrows in Panel B in Figure 2.) As such features are also predicted in EM2 models of remodeled liposomes, we decided to use our reverse mapping method to study the protein coat around such features. As in the case of the “Y” junction, such features are passed over when selecting regions for averaging and high resolution reconstruction, and so the information contained in the EM images is not sufficient alone to reconstruct the protein density.

Figure 2.

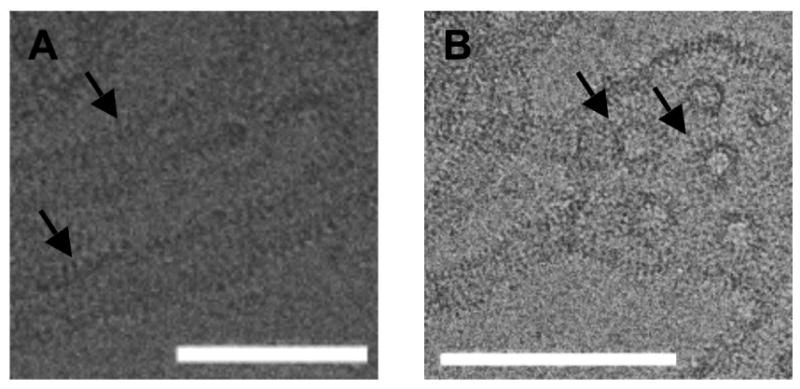
Experimental EM images of endohilin N-BAR remodeled liposomes (provided courtesy of Carsten Mim and Vinzenz Unger, Northwestern University). Panel A shows two tubules with striations indicated by black arrows. The scale bar is 70 nm. Panel B shows a remodeled membrane that contains both tubules and striated holes, the latter indicated by the arrows. The white scale bar in each figure is 140 nm.

Figure 7 shows the reconstruction process for a complicated junction, the central feature of which is a circular hole of approximately the diameter observed in Figure 2. The EM2 field lines in Panel B already suggest protein density that wraps around the cylindrical portions of the torus, perhaps forming striations as observed in the EM image. This is indeed confirmed by the initial reconstruction, shown in Panel E. The protein coat ringing the inside of the torus feature is very suggestive of the striations or hash marks ringing similar features in the experimental images (see arrows in Panel B, Figure 2, and Figure 3 in Ref.²²). While rebuilding the structure in molecular detail is a far from a trivial task, it must be at a minimum demonstrated that the system is stable under constant temperature simulation. After all, the membrane is under significant stress, while the protein coat must accommodate a spatially varying curvature even more complex that that observed in Figures 4 and 5. To this end, the system consisting of 431 proteins and 51,621 lipids (62,827 CG sites total) was subjected to an extensive relaxation and heating protocol, after which it was integrated at 300 K for 10 million CG MD timesteps. In the absence of the protein coat, the system begins to show signs of instability already at 2 million timesteps, suggesting that the protein coat is essential to stabilize this topologically complex structure.

Figure 7.

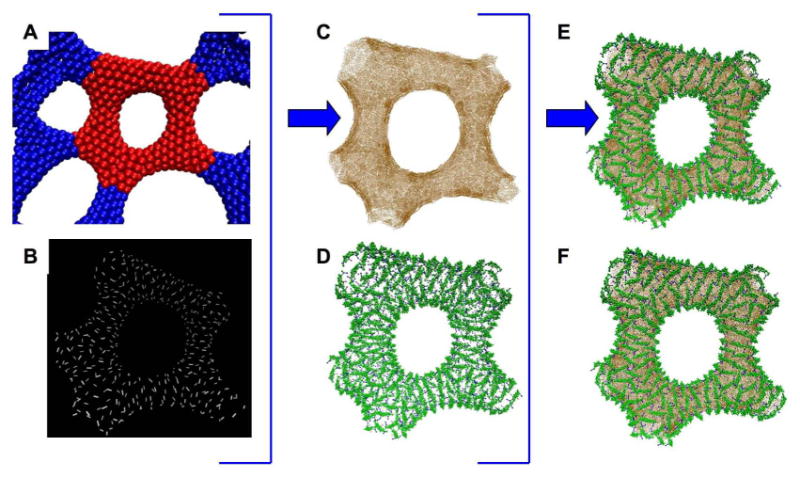
Reconstructing a more complex remodeled membrane topology. The original mesoscopic EM2 simulation structure is shown in panel A, with the reconstructed area highlighted in red. Panel B shows the direction of the larger of the two principal curvatures associated with each EM2 quasiparticle. Panels C and D show the initial CG membrane and protein configurations, panel E shows the merged configuration before relaxation, heating, and simulation. Panel F shows that configuration after 10 million CG MD timesteps at 300 K. Note the striations around the torus, reminiscent of those observed in the experimental EM image, Figure 2 panel B.

Figure 8 shows the local orientational order in the protein coat around the torus junction, calculated as described earlier. It is interesting that the coat is able to maintain significant orientational order over relatively short stretches of the torus, between where other junctions must be accommodated. In fact, the protein coat shows fairly high orientational order all the way around the inside of the torus, even where it is adjacent to disordered, junction regions. This perhaps accounts for the fact that hash marks suggestive of protein density are often visible around these features in the experimental images.

Figure 8.

Local orientational order of the CG N-BAR domains in the torus reconstruction. Shown is an analysis of the local orientational order for the final simulation configuration depicted in Panel F of figure 7, calculated as described in the main text. In light of the striations indicated in panel B of Figure 2, it is noteworthy that the N-BAR coat appears to maintain significant orientational order along the inner portion of the torus. The color scale reflects the average of the unsigned dot product between the direction of the long axis of each N-BAR domain and its immediate neighbors.

Discussion

We have presented an approach to transform a long length scale, mesoscopic model of a membrane remodeled by proteins into a higher resolution CG model in which the protein and membrane are resolved in semi-molecular detail. This is a nontrivial feat, as each quasiparticle in the mesoscopic model is an abstract entity, representing a patch of membrane on the order of ∼5-10 nm, with the protein and local curvature represented by smooth spatially varying fields. The reconstruction method uses the surface defined by the centers of the EM2 quasiparticles to rebuild the membrane from pre-relaxed patches of CG membrane, and the surface and local direction of the curvature field at each point to rebuild the protein coat. We have demonstrated that the method successfully rebuilds topologically complex protein membrane surfaces that are produced in vitro by endophilin N-BAR domains and experimentally observed by EM. Importantly, we have also demonstrated that the structures so generated are amenable to constant temperature CG molecular dynamics, in the process demonstrating that the CG membrane-protein model stabilizes these highly curved, complex structures for the initial CG MD runs. It is therefore feasible to use the present combined multiscale mesoscopic-CG approach to define complex initial conditions (structures) that can in turn be used as starting points for much longer CG MD simulations designed to refine the remodeled membrane structures based on higher resolution CG-scale interactions not contained in the mesoscopic EM2 model (e.g., specific protein-membrane interactions arising from the amphipathic helices of the N-BAR domains).

The work presented here is therefore just the first step in a much more ambitious goal, in which we aim to develop a hybrid approach that combines the strengths of high-resolution cryo-EM reconstructions, low resolution EM of reticulated membranes, EM2 mesoscopic modeling, and the quasi-molecular scale CG model. High resolution cryo-EM reconstructions of highly ordered tubules provide detailed observations of important structural features, such as amphipathic helix pairing, helical coat structure, and BAR-BAR interactions, but cannot resolve less ordered, topologically complex regions of reticulated membranes. However, such information can be incorporated into the EM2 to CG reconstruction algorithm presented here. On the other hand, the EM2 model resolves how the membrane curvature accommodates regions that are not well ordered cylinders, and which are not amenable to high resolution reconstruction. The role of the low resolution EM observations is to steer the EM2 model into a physiologically realistic region of the parameter space, as described in a previous publication.²² Ultimately, we intend to use this hybrid approach to develop molecular resolution models of cellular structures, possibly involving multiple proteins, that are characterized by complex curvature and reticulated topologies, and then perform dynamical simulations of such models on micron lengthscales. Neither purely “bottom up” nor “top down” coarse graining, and neither purely computational nor experimental in methodology, this approach will offer a promising route to capture the true multiscale character of cellular biology.

Model and Methods

EM2 model

The EM2 model was previously described, we recount the main points here for completeness. EM2 begins with an anisotropic continuum model of membrane deformations,²⁴ which is then discretized by the smooth particle method.^26-28 The EM2 particles are immersed in a “bath” of solvent particles which can exchange N-BAR domain density with the membrane. The interaction between EM2 particles is parameterized to reproduce the bending modulus of the membrane. The local N-BAR domain density on an EM2 particle also contributes to the local deformation by controlling the local spontaneous curvature, with the local N-BAR domain density in turn depending on the local curvature via a curvature coupling term. The parameters for the EM2 model were taken from previous work,²² and correspond to an intermediate value of the spontaneous curvature. At these parameters, an EM2 configuration that is initially a 500 nm diameter liposome is remodeled into reticulated configurations (Figure 1) that are frequently observed in EM of N-BAR remodeled liposomes (Figure 2).

Coarse-grained membrane model

The CG lipid model has been previously described,³⁵ but is briefly recounted here for completeness. Each lipid is mapped into a single Gay-Berne ellipsoid⁴² with an aspect ratio of three to one. In order to capture the basic structure of a lipid within the Gay-Berne framework, the symmetry of the interaction along the long axis of the ellipsoid is broken, so that each ellipsoid has a “head” and a “tail.” The in-plane component of the interaction is determined directly from atomistic simulations of 50/50 mixtures of dioleoyl-phosphatidylserine/phosphatidylcholine via multiscale coarse-graining,^43-45 which was found to be essential to develop a liquid CG bilayer with reasonable diffusion constant. Despite the substantial simplifications inherent in this model, it captures many of the important long-wavelength features of the bilayer, such as self assembly and the correct bending modulus.

Coarse-grained endophilin N-BAR model

A 26 site CG model of the N-BAR domain of endophilin was developed. The atomistic to CG mapping was determined from a 75 nsec atomistic simulation of the N-BAR⁴⁶ bound to a membrane by the essential dynamics coarse-graining method,⁴⁷ so that the CG sites are sufficient to represent the slow dynamics of the protein. The interactions among the CG sites within one protein are harmonic springs, determined by the heteroENM method,³⁶ so that they reproduce the inter-site distance fluctuations observed in the atomistic simulation. The atomistic and CG protein are shown in Figure 9. All membrane-protein protein-protein interactions are of the Gay-Berne type. The interactions between the membrane and the sites under the arch of the protein have a well-depth of 5 kcal/mol, the diameter of the protein sites is 1 in reduced units. The amphipathic helix sites have an additional interaction with the tip of the Gay-Berne lipids to parameterize the amphipathic “wedge” insertion mechanism, as previously described.³⁷

Figure 9.

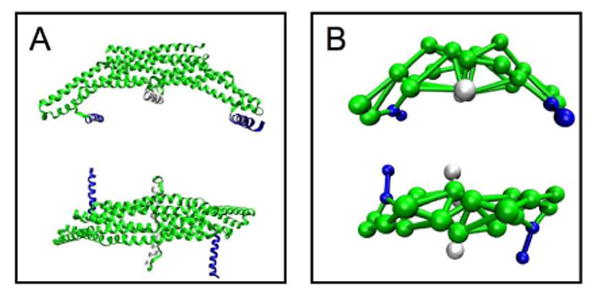
All atom structure of endophilin N-BAR (panel A) and the 26 site CG endophilin model (Panel B). The four N-terminal amphipathic helix sites are shown in blue, the amphipathic insert helix sites are shown in white, the rest of the domain is in green.

Reverse mapping EM2 configurations into coarse-grained models

An EM2 configuration is a set of points (approximately 15,000 in this case) that define the midplane of a membrane (a two dimensional surface). The EM2 surface can be quite complicated, with regions that are locally deformed like saddles, cylinders, or cups. The challenge is to fill in the spaces between the EM2 points with CG lipids, in this case represented by Gay-Berne ellipsoids (more details on the CG lipids follow below), with the coordinates of the CG lipids close enough to a “good” configuration that they can be used as the starting configuration for an MD simulation. This was accomplished in several steps. First, the surface defined by the EM2 points was tiled with non-overlapping triangles whose vertices are EM2 points and whose edges are nearest neighbor EM2 points. Each such triangle defines a local coordinate frame, the orientation of which is defined by the normal to the triangle. The next task is to fill each triangular patch of membrane with CG lipids. In order to reduce simulation time spent equilibrating the configuration, each triangular patch of membrane was filled with CG lipids selected from a pre-equilibrated patch of membrane, by transforming a small patch of pre-equilibrated membrane to the local frame of the triangle, and selected those lipids which lie inside the triangle. Inevitably, steric clashes between lipids arise at the edges of the triangular patches; these are identified by an orientation dependent overlap search among lipids in neighboring triangular patches. (A neighbor list is built during the reconstruction process by tracking which lipids belong to which triangle, saving considerable time during the search.)

Finally, the protein coat must be rebuilt from the EM2 information. Each EM2 particle carries a local coordinate frame that defines the membrane normal and the direction of the largest spontaneous curvature. We assume that the BAR domain's long axis along the direction of maximum spontaneous curvature and the arch of the BAR points along the membrane normal; this orients the positive charges under the arch to interact with the negative charges and the N-terminal and insert helices to effect maximum local spontaneous curvature. This assumption is supported by low resolution EM images which shown a parallel striping of protein that is roughly aligned as described, so that the protein coat wraps around the protein coated tubule. (See for example arrows in panel A in Figure 2). In the future a hybrid approach which combines the EM2 level information with high resolution cryo-EM reconstruction data will be pursued to determine the structure of the coat, but even the present approach already generates quite reasonable structures, as far as can be determined by comparing to the low resolution EM data that is available.

Coarse-grained MD simulation protocol

The orientation dependent overlap search eliminates steric clashes with potentials on the order of 10⁴ kcal/mol, but many significant overlaps remain. These are relaxed over a series of constant temperature simulation segments during which the temperature is increased from 20 K and the integration timestep is increased from 10^-7 psec. After 8 simulation segments totaling 8,000 timesteps, the simulation is usually stable at 300 K and a timestep of 0.0005 psec. The simulation is coupled to a thermal bath by the Nosé-Hoover method and is integrated by the velocity Verlet algorithm using a code developed in our group. The edges of the CG structure are not periodic across the simulation cell boundary, since the structures themselves are not periodic. Between the CG structure and the boundary of the simulation cell there is a buffer of 5-10 nm, by the time the simulations presented here are terminated the exposed edges of the membrane have healed into half micelle like structures. In the future the effect of the rest of the reticulated structure will be modeled by applying soft restraints on the positions of all boundary CG sites.