Predicting proton titration in cationic micelle and bilayer environments

Abstract

Knowledge of the protonation behavior of pH-sensitive molecules in micelles and bilayers has significant implications in consumer product development and biomedical applications. However, the calculation of pK_a’s in such environments proves challenging using traditional structure-based calculations. Here we apply all-atom constant pH molecular dynamics with explicit ions and titratable water to calculate the pK_a of a fatty acid molecule in a micelle of dodecyl trimethylammonium chloride and liquid as well as gel-phase bilayers of diethyl ester dimethylammonium chloride. Interestingly, the pK_a of the fatty acid in the gel bilayer is 5.4, 0.4 units lower than that in the analogous liquid bilayer or micelle, despite the fact that the protonated carboxylic group is significantly more desolvated in the gel bilayer. This work illustrates the capability of all-atom constant pH molecular dynamics in capturing the delicate balance in the free energies of desolvation and Coulombic interactions. It also shows the importance of the explicit treatment of ions in sampling the protonation states. The ability to model dynamics of pH-responsive substrates in a bilayer environment is useful for improving fabric care products as well as our understanding of the side effects of anti-inflammatory drugs.

I. INTRODUCTION

Understanding the titration behavior of molecules in surfactant or lipid assemblies is important in consumer product development and biomedical applications.

For example, fabric softeners containing ester quaternary ammonium compounds are sensitive to variation in the pH condition due to the titration of hydrolysis product fatty acids, which leads to marked change in vesicle dispersion stability.¹ Size distributions and aggregation behavior of liposomes are also affected by the protonation state of fatty acids.²

In biomedical applications, one active area of research is the design of pH-responsive vesicles or liposomes that can release cargo upon reaching a target site that has a local pH which is different from the blood stream, e.g., tumor.^3–5 Since the release of cargo in response to a pH change of less than 1 unit is desired, precise tuning of the protonation equilibria of the constituent molecules in the nanocarrier is required. In another example, knowledge of the protonation state of anti-inflammatory drugs is highly desirable, as it affects the partitioning within and transport through the cell membranes, potentially hindering efficacy or causing unwanted side effects.⁶

Molecular dynamics (MD) simulations have been applied in the past to examine the effect of protonation state on the structure and dynamics of surfactant or lipid bilayers,^6–9 micelles,⁹ and vesicles.¹⁰ However, these simulations were performed with fixed protonation states, and as such they cannot give pK_a’s or model pH-dependent conformational changes or phase transitions. For calculating the pK_a’s of molecules in micelles or bilayers, traditional structure-based methods such as Poisson-Boltzmann calculations are not suitable, as the aggregate undergoes large structure fluctuation and it is unclear as to the position of the titratable group within the micelle/bilayer and the effective dielectric constant in the hydrophobic interior. Continuous constant pH molecular dynamics (CpHMD)^11,12 utilizes a set of titration coordinates that are coupled to the atomic coordinates and propagated simultaneously. Thus, the protonation states of all titratable sites can be monitored over the course of the MD simulation, taking into account changes in the local environment while avoiding the need to specify the dielectric constant. Combined with advanced sampling protocols such as temperature- or pH-based replica exchange (REX),^13,14 CpHMD affords robust and accurate prediction of protein pK_a values.¹⁵ The original CpHMD, which is solely based on the generalized-Born (GB) implicit-solvent model,^11,12 was recently revised to incorporate a hybrid-solvent scheme, which makes use of the explicit-solvent model for more accurate conformational sampling and retains the GB model for generating solvation forces on the titration coordinates to ensure rapid convergence.¹⁴ After demonstrating the higher accuracy for protein pK_a calculations relative to the GB-based CpHMD,^14,16 the hybrid-solvent CpHMD was applied to simulate the titration of the 12-carbon fatty acid (lauric acid, Figure 1, top) in three ionic and non-ionic micelles.¹⁷ In comparison to the pK_a’s calculated from the GB-based CpHMD simulations, a dramatic difference is seen for the cationic micelle of dodecyl trimethylammonium chloride (DTA, Figure 1, middle). The hybrid-solvent CpHMD resulted in a positive pK_a shift of 1.5 (relative to the model value), much closer to the experimental shift of 0.1 compared to the negative shift of −3.0 from the GB-based CpHMD.¹⁷ The analysis suggested that the improvement is due to the more accurate representation of the conformational dynamics of the micelle, which is too rigid and compact in the GB solvent, while the remaining error, i.e., overestimation of the pK_a shift, is due to the neglect of the effect of explicit ions, which is significant for the DTA micelle but cannot be captured by the Debye-Hückel screening term in the hybrid-solvent CpHMD.¹⁷

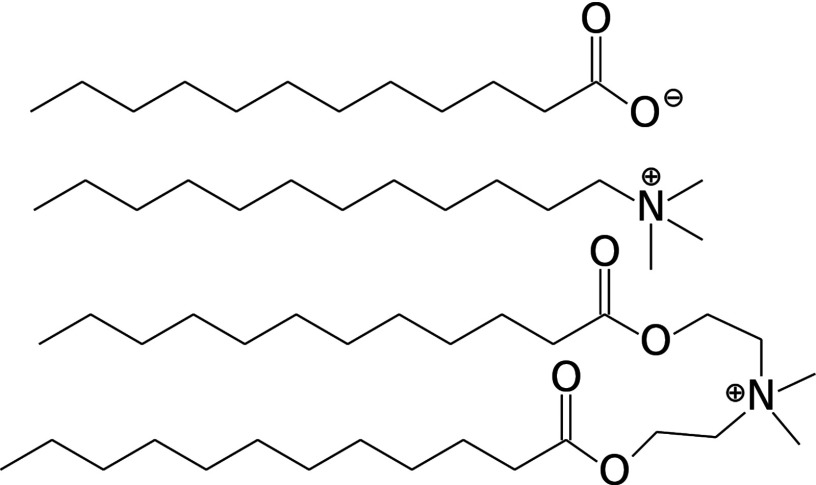
FIG. 1.

Chemical structures of the unprotonated 12-carbon fatty acid (top), DTA (middle), and the 12-carbon DEEDMAC (DM12, bottom).

Most recently, an all-atom CpHMD method was developed, which uses explicit solvent to drive the dynamics in both conformational and protonation states, thus enabling the effects of ions to be explicitly taken into account.¹⁸ Furthermore, titratable co-ions¹⁸ or water molecules¹⁹ are included in the simulation system to ensure charge neutrality under all pH conditions and at all time. Here we apply the all-atom CpHMD with titratable water to reexamine the titration of lauric acid in the DTA micelle. Additionally, we simulate the titration and predict the pK_a of a fatty acid in bilayers of diethyl ester dimethylammonium chloride (DEEDMAC, Figure 1, bottom), which is a cationic surfactant used in fabric softeners.²⁰ Similar quaternary ammonium surfactants have been used in gene delivery liposomes.²¹ To contrast the behavior of liquid- and gel-phase bilayers, we use DEEDMAC with 12- and 18-carbon tails, which will be referred to as DM12 and DM18, respectively. A single fatty acid matching the tail length of the surfactants is embedded in each system. These simulations allow us to test the ability of all-atom CpHMD in predicting the pK_a and modeling protonation-coupled conformational dynamics in micelle and bilayer environments. While only one titrating molecule was used in these simulations, there is little computational overhead involved in titrating multiple groups. We have previously used the hybrid-solvent method to simulate the pH-dependent self-assembly of up to 40 lauric acids,^22,23 finding a bulk pK_a in excellent agreement with experiment, as well as reproducing the pH-dependent micelle-to-bilayer transition observed in experiment. Therefore, the technique can also be applied to more biologically or industrially relevant applications in which there are many titratable groups.

II. METHODS AND SIMULATION DETAILS

Simulations were performed using an in-house modified version of CHARMM (version 36b2),²⁴ in which the all-atom CpHMD¹⁸ with titratable water¹⁹ and pH-based REX protocol¹⁴ is implemented. The all-atom CpHMD is an extension of the original GB-based CpHMD method.^11–13 More details can be found in Ref. 18. The CHARMM36 lipid force field²⁵ was used to represent the hydrocarbon tails, while the CHARMM22 force field was used to represent the protonated and unprotonated carboxylic acid headgroup.²⁶ The CHARMM-modified TIP3P was used to represent water.

The DTA micelle consisting of 59 DTA and 1 lauric acid was built following our previous work.^17,27 This size was chosen as it is approximately the aggregation number of DTA micelles,²⁸ and the surfactant to fatty acid ratio was about 60–1 in the experiment that determined the pK_a shift of lauric acid in DTA micelles.²⁹ The system was solvated in an octahedral box, with at least 10 Å between surfactant atoms and the box edge. Fifty-nine chlorides were added as counterions with additional 9 sodium and 9 chlorides giving an ionic strength of 150 mM, consistent with our previous simulations.¹⁷ The bilayer systems were built using scripts from CHARMM-GUI^30,31 modified to accommodate DEEDMAC (DM12 and DM18). The upper leaflet consisted of 35 DM12/DM18 and 1 fatty acid, and the lower leaflet contained 36 DM12/DM18. The number of lipids was chosen as that used in the development of the CHARMM36 lipid force field.²⁵

To match the tail length, the 12-carbon lauric acid and 18-carbon stearic acid were used as the fatty acids in the DM12 and DM18 systems, respectively. Seventy-one chloride counterions were added to neutralize the DEEDMAC molecules. The DM12 and DM18 systems were solvated with 4840 and 5306 waters molecules, respectively. In all three systems a titratable water was coupled to the fatty acid to ensure constant charge¹⁹ along with a sodium counterion for neutrality.

For each system, 7 pH replicas, spanning pH 4–7 in 0.5 unit increments, were run simultaneously, with exchanges between the adjacent replicas attempted every 500 steps (1 ps) according to the Metropolis criterion. Each replica was subject to molecular dynamics under NPT conditions at 300 K and 1 atm via the Hoover thermostat³² and the Langevin piston pressure coupling algorithm,³³ respectively. A 2 fs time step was used as bonds involving hydrogen were constrained using the SHAKE algorithm. Non-bonded interactions were truncated at 14 Å, and the generalized reaction field method was used to compute long-range electrostatics.³⁴ The simulation length for each replica was 20 ns, resulting in an aggregate sampling time of 140 ns per system.

III. RESULTS AND DISCUSSION

All-atom CpHMD simulations with the pH-REX protocol were performed for the cationic DTA micelle as well as the cationic DM12 and DM18 bilayers, each containing one fatty acid (see snapshots in Figure 2). Seven replicas were initiated at pH 4–7 with a spacing of 0.5 pH units. Sampling time was 20 ns per replica, for a total simulation time of 140 ns per system. Fatty acid unprotonated fractions were well converged after 10 ns (Figure S1 of the supplementary material³⁵). The resulting titration curves are given in Figure 3.

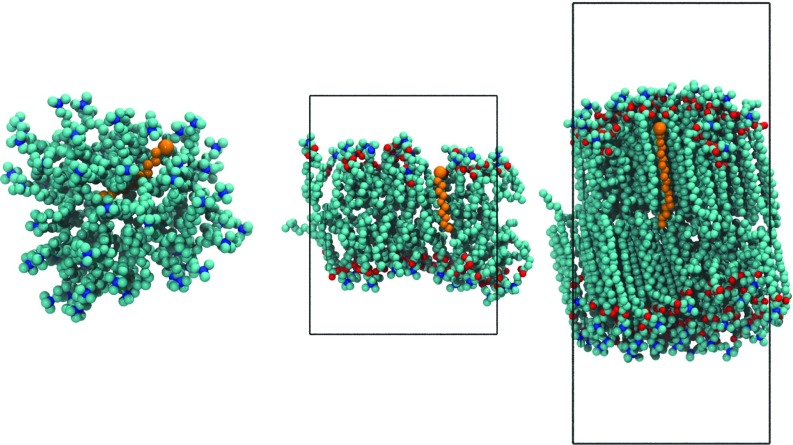
FIG. 2.

Snapshots of a fatty acid in a DTA micelle (left), liquid-phase DM12 (middle), and gel-phase DM18 bilayer (right). Fatty acids are shown in orange, with the larger bead representing the carboxylic acid headgroup. Red, blue, and cyan beads represent the surfactant oxygen, nitrogen, and carbon atoms, respectively. Hydrogens, ions, waters, and some surfactant molecules are hidden for clarity.

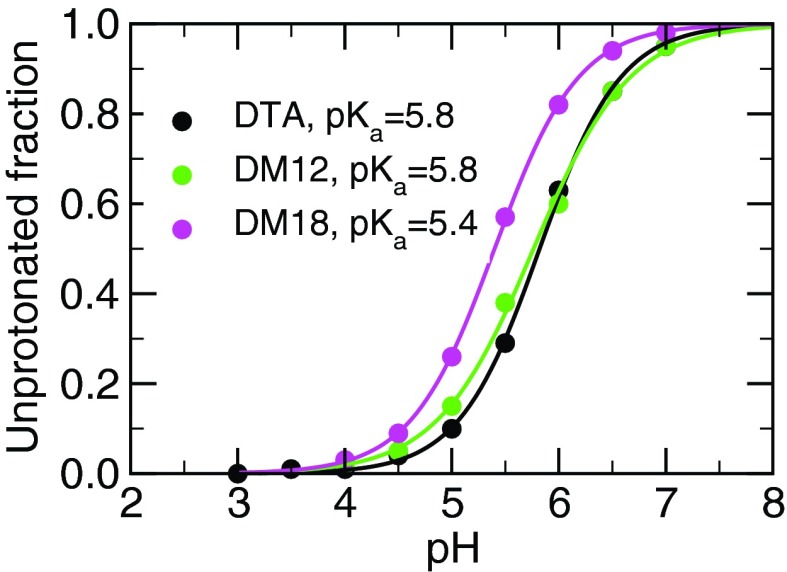
FIG. 3.

Titration curves for fatty acid in the micelle and bilayers. Unprotonated fractions were averaged over the final 10 ns of the 20 ns per replica simulations. Solid lines are best fits to the Hill equation. The standard deviations of the calculated pK_a values for the DTA, DM12, and DM18 systems are 0.2, 0.3, and 0.2, respectively.

The fatty acid in the DTA micelle has a pK_a of 5.8±0.2, a shift of 0.8 relative to the model value, which is 0.7 units lower, and closer to the experimental value (0.1), than the previous hybrid-solvent result.¹⁷ The pK_a shifts obtained using CpHMD with different solvent methods are summarized in Table S1 in the supplementary material.³⁵ To understand the difference, we compare the position of the fatty acid carboxylate group within the micelle, its exposure to water, and its interaction with DTA headgroups. Interestingly, the local environment and degree of solvent exposure of the fatty acid headgroup in the all-atom simulation are nearly identical to those in the hybrid-solvent CpHMD (Figures S2– S4 of the supplementary material³⁵). Thus, the reduction in the pK_a overestimation is due to the inclusion of the explicit interactions with the chloride counter-ions. In fact, the hybrid-solvent simulations gave a pK_a shift of 0.6 in the absence of salt.¹⁷ Thus, the explicit ions reduce the electrostatic stabilization due to the attractive interaction with DTA but with a magnitude smaller than that predicted by the Debye-Hückel screening term.

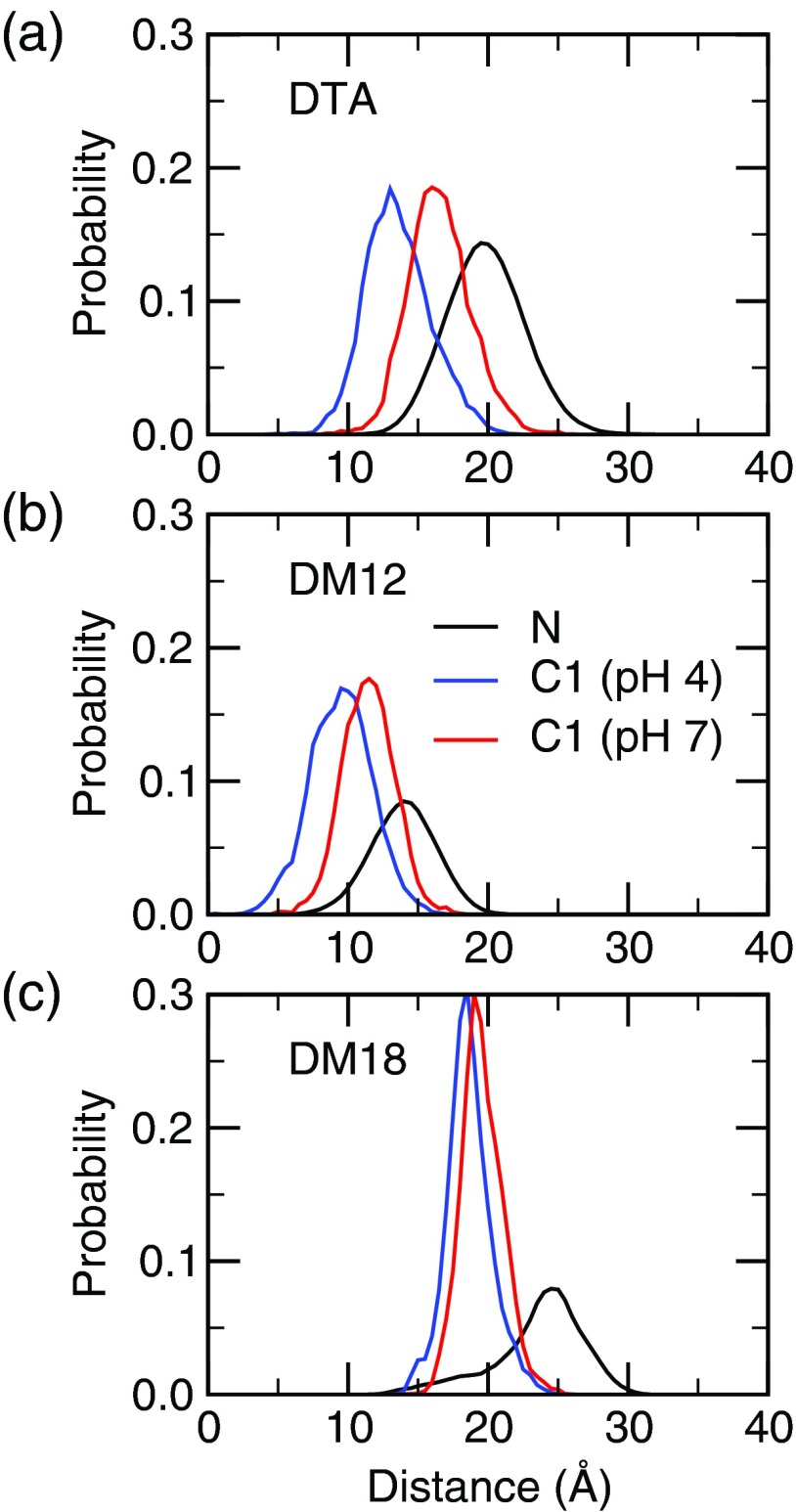
For the fatty acid in the cationic DM12 and DM18 bilayers, our calculations gave a pK_a of 5.8±0.3 and 5.4±0.2, representing a shift of 0.8 and 0.4 relative to the model, respectively. Thus, the pK_a shift in the liquid bilayer is the same as that in the micelle of the same charge, whereas the pK_a shift in the analogous gel-phase bilayer is 0.4 pH units lower. To rationalize the trend in the pK_a shift, we first examine the position of the fatty acid headgroup relative to the bilayer/micelle center of mass (Figure 4). The fatty acid position relative to the surfactant-water interface in the liquid bilayer and micelle is similar. Upon deprotonation, the fatty acid headgroup moves about 3 Å towards the water interface in both the micelle and the DM12 bilayer. By contrast, in the gel bilayer, which has restricted mobility, the vertical movement of the fatty acid is only about 0.5 Å.

FIG. 4.

Distance of the indicated atom types from the center of mass for the DTA micelle (a), DM12 bilayer (b), and DM18 bilayer (c). In the latter two the distance is measured along the bilayer normal.

We examine the factors that result in the pK_a shift of fatty acid in the cationic micelle or bilayer environments. According to our previous work, the desolvation term, defined as the difference in the desolvation energy between the charged and neutral forms, favors the protonated state and contributes a positive pK_a shift.¹⁷ The Coulombic term, defined as the electrostatic stabilization of the charged vs. the neutral form in the cationic environment contributes a negative pK_a shift. The magnitude of the latter is somewhat reduced by the destabilization of the charged carboxylate by the chloride counterions.

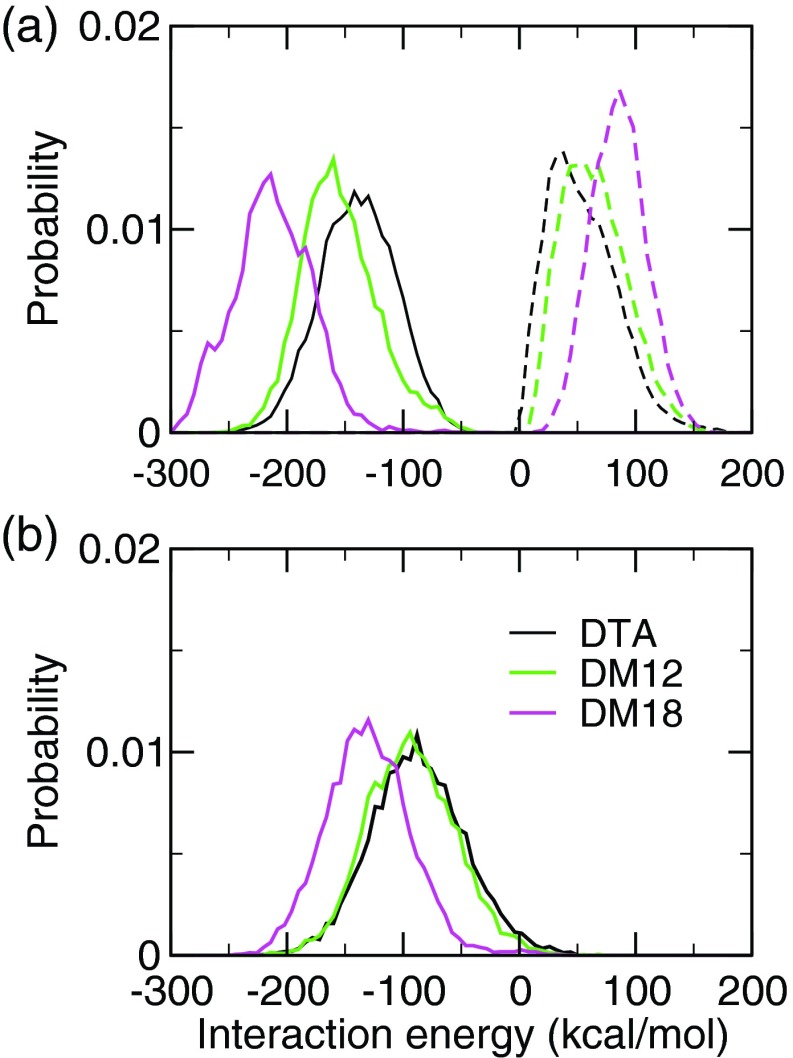
To compare the pK_a downshift due to stabilization by the cationic environment, we calculated the interaction energies between the carboxylate group and cationic surfactant headgroups in the three environments, while taking into account the explicit interactions of the former with the chloride counterions. In the gel bilayer, as compared to the liquid micelle and bilayer, both the attractive and repulsive energies are greater (Figure 5(a)). The latter is due to the increased number of chloride ions at the bilayer-water interface (Figure S6 of the supplementary material³⁵). However, the increase in attractive energy is not completely offset by the increase in repulsion, resulting in a greater net stabilization of the carboxylate in the gel bilayer as compared to the liquid micelle and bilayer (Figure 5(b)). Thus, the pK_a downshift due to the Coulombic stabilization by the cationic environment is similar in the liquid micelle and bilayer, and greater in the gel bilayer. It also demonstrates the need for the inclusion of explicit ions in the calculation of the titration coordinates, as in all three systems the pK_a would be predicted to be too low if the ion interactions were neglected.

FIG. 5.

(a) Interaction energy between the fatty acid headgroup and the surfactant headgroups (solid) as well as chloride ions (dashed) in the micelle and bilayer environments at pH 7. (b) Sum of the interactions shown in the top panel.

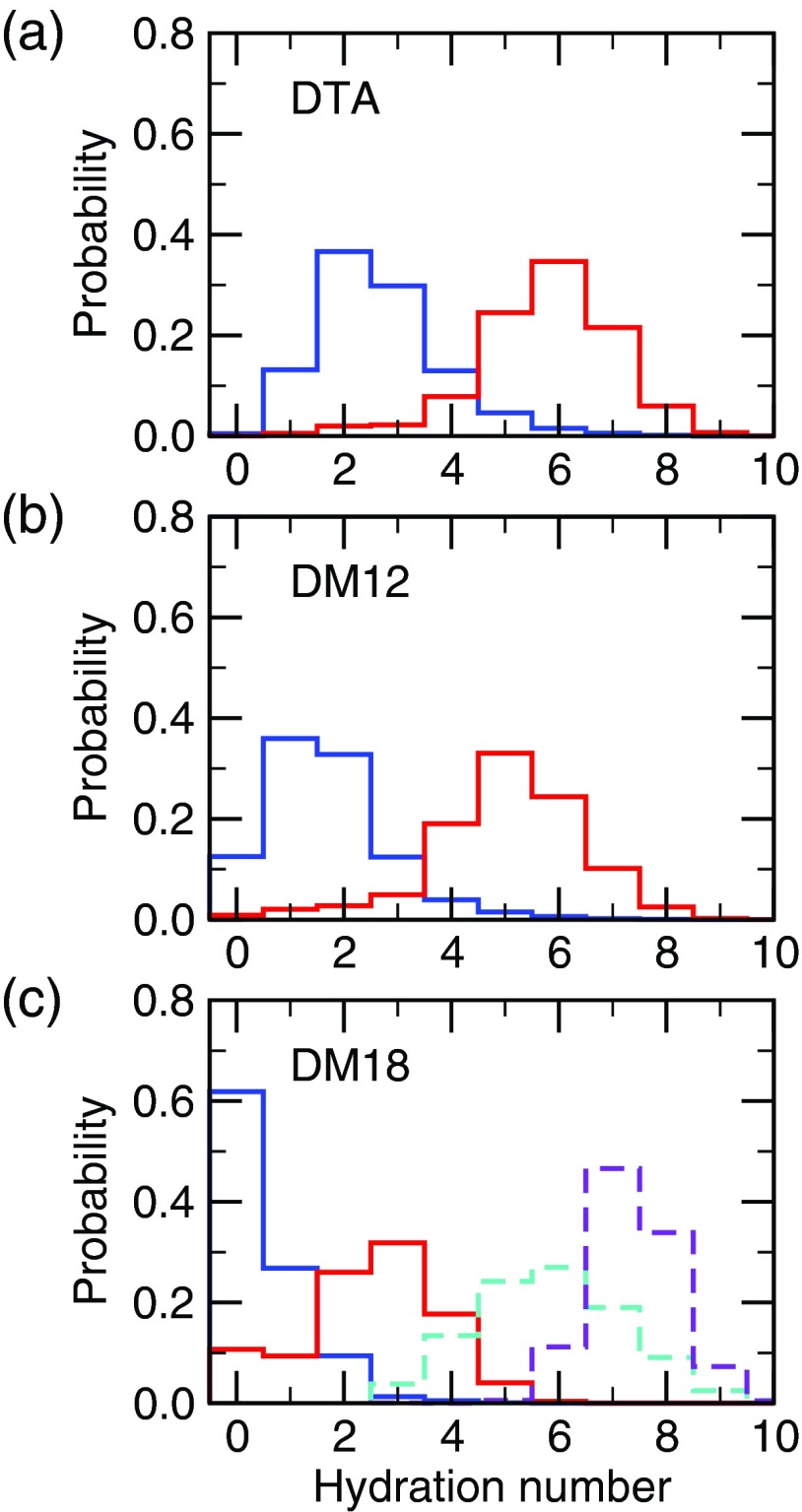
To assess the desolvation term, we calculated the probability distributions of the hydration number, defined as the number of water molecules within a 3.5 Å radius of the fatty acid headgroup. In the micelle, the average hydration number is 5.8 for the charged state and 2.7 for the neutral state (Figure 6(a)), consistent with the movement of the fatty acid towards the micelle center upon protonation (see Figure 4). In the liquid DM12 bilayer, the probability distributions shift lower by about one unit, with an average hydration number of 5.0 and 1.7 for the charged and neutral states, respectively (Figure 6(b)). Although the fatty acid is not farther from the surfactant-water interface in the DM12 bilayer as compared to the micelle (Figure 4), the DM12 headgroups are more closely packed in the bilayer as compared to DTA in the micelle, which reduces the number of water molecules that can reach the carboxyl group (see radial distribution functions between surfactant headgroups in Figure S5 of the supplementary material³⁵). In the DM18 gel bilayer, the distributions further shift lower, with an average hydration number of 2.5 and 0.5 for the charged and neutral states, respectively (Figure 6(c)). In the neutral state, about 60% of the time the fatty acid is fully buried in the hydrophobic core (no water within 3.5 Å). This behavior is expected as a result of the impeded mobility of fatty acid in the rigid gel phase, and the tight packing of the DM18 headgroups.

FIG. 6.

Probability distribution of the hydration number of the fatty acid in (a) DTA micelle, (b) DM12 bilayer, and (c) DM18 bilayer. Charged (pH 7) and neutral (pH 4) states are indicated in red and blue, respectively. Hydration number is defined as the number of water oxygens within 3.5 Å of a carboxyl oxygen. The distribution for a fatty acid in water is shown on the bottom plot in dashed lines for the charged (pH 7, purple) and neutral state (pH 4, cyan).

It is instructive to compare the distributions of the hydration number of the charged and neutral fatty acid in the micelle and bilayer environments to those in water (Figure 6(c), dashed lines). For the liquid micelle and bilayer, a large difference is seen for the neutral state, i.e., the desolvation of a neutral fatty acid, which is the main contributor for the positive pK_a shift. The average solvation number of the neutral fatty acid is decreased by 3.1 and 4.1 in DTA and DM12, respectively, compared to solution. In contrast, the charged fatty acid hydration number only decreases by 1.6 and 2.4 in the micelle and liquid bilayer, respectively. For the gel bilayer, however, the magnitude of desolvation for both charged and neutral states is large, with the average hydration number decreasing by 4.9 and 5.3, respectively, compared to the fatty acids in solution. This indicates that even though the neutral form is more stabilized as compared to that in the liquid micelle and bilayer, the desolvation term may not be larger because it is offset by the unfavorable desolvation of the charged form. In fact, the difference in the average hydration number between the charged and neutral state for the gel bilayer is 2.0, while it is 3.1 and 3.3 for the liquid micelle and bilayer, respectively. Thus, based on this analysis, the positive pK_a shift due to the desolvation term is similar for the liquid micelle and bilayer and likely smaller for the gel bilayer.

IV. CONCLUSION

We have applied all-atom CpHMD with the pH-REX protocol to simulate the titration of a fatty acid in cationic micelle, liquid, and gel bilayers. The calculated shifts relative to the model pK_a are 0.8, 0.8, and 0.4, respectively. The former value represents an improvement of 0.7 units over the previous hybrid-solvent CpHMD simulation and is attributed to the explicit calculation of the interactions with ions. Analysis reveals that the lower pK_a shift in the gel bilayer is mainly due to the increased electrostatic stabilization by the cationic environment as compared to the analogous liquid micelle and bilayer, despite the fact that protonated lauric acid is significantly more desolvated in the gel bilayer. These results demonstrate the utility of the all-atom CpHMD method in predicting protonation states and pH-dependent conformational dynamics in surfactant/lipid environments. This technique can be used, for example, to study the partitioning of pH-sensitive pharmaceuticals such as anti-inflammatory drugs in lipid membranes, which can give insight into the mechanism of their unwanted side effects.⁶