Communication: Charge, diffusion, and mobility of proteins through nanopores

Abstract

Implementation of Einstein's law connecting charge, diffusion coefficient, and mobility to interpret experimental data on proteins from single molecule electrophoresis through nanopores faces serious difficulties. The protein charge and diffusion coefficient, inferred with the Einstein law, can be orders of magnitude smaller than their bare values depending on the electrolyte concentration, pore diameter, chemical nature of the pore wall, and the externally applied voltage. The main contributors to the discrepancies are the coupled dynamics of the protein and its counterion cloud, confinement effects inside the pore, and the protein-pore-surface interaction. We have addressed these ingredients by harking on classical theories of electrophoresis of macroions and hydrodynamics inside pores, and deriving new results for pore-protein interactions. Putting together various components, we present approximate analytical formulas for the effective charge, diffusion coefficient, and mobility of a protein in the context of single molecule electrophoresis experiments. For the omnipresent pore-protein interactions, nonlinear dependence of the velocity of protein on voltage sets in readily and analytical formulas for this effect are presented. The derived formulas enable the determination of the bare charge and size of a protein from the experimentally measured apparent values.

I. INTRODUCTION

The fundamental law relating the charge Q, diffusion coefficient D, and electrophoretic mobility μ of an ion in a solution is the Einstein equation

$$\mu =\frac{QD}{k_{B}T},$$ (1)

where k_BT is the Boltzmann constant times the absolute temperature, and μ = U/E is the ratio of the velocity U of the ion to the externally applied electric field E. Although this law is derived from equilibrium considerations and in the linear response regime, it is routinely used to characterize proteins in single molecule electrophoresis experiments with nanopores,^1–14 where non-equilibrium effects are omnipresent. By fitting the experimentally determined histograms of the transit times of the protein molecule in a nanopore with a one-dimensional diffusion-drift model, D and U of the protein molecule are obtained. These values of D and U are then used to get the protein charge Q by using Eq. (1) and the protein radius R_g by additionally using the Stokes-Einstein relation for a sphere D = k_BT/(6πηR_g) (η is viscosity of the electrolyte solution). It turns out that Eq. (1) is dramatically inadequate in inferring the fundamental characteristics of the protein molecules from the single-molecule electrophoresis through nanopores.^13,14

The failure of Eq. (1) arises from many factors working together. As the charged molecule moves down the electric potential gradient along the pore, it faces an opposing drag from its counterion cloud. The drags of the protein and the counterion cloud are mediated by hydrodynamic and electrostatic forces inside the pore. The finite size of the pore restricts the translational degree of freedom in directions orthogonal to the pore axis. In addition, the protein molecules can adsorb at the pore wall resulting in a reduced mobility. Although a complete resolution of all of these issues is an insurmountable task, we present here an approximate generalization of Eq. (1) by allowing for protein-counterion-cloud dynamics, confinement effects from the pore, and protein-pore-wall interaction as

$$\mu =\frac{Q_{eff}{D}_{eff}}{k_{B}T},$$ (2)

where Q_eff and D_eff are the effective charge and effective diffusion coefficient depending on the electrolyte concentration, pore radius, and pore-protein interaction energy. In addition, we give analytical formulas for the nonlinear dependence of μ on E and the mean translocation time. Equation (2) may be taken as a generalization of Q_eff and D_eff in bulk electrophoresis^16–18 to the presence of the pore.

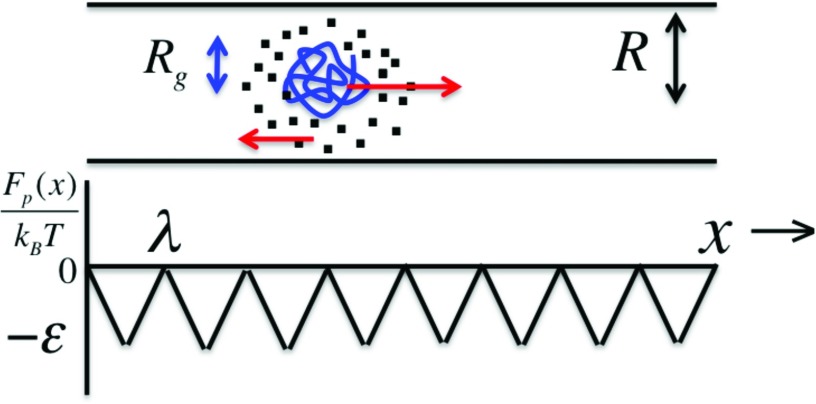
We consider the mobility of a protein molecule of radius of gyration R_g and net surface charge Q inside a cylindrical pore of uniform radius R and length L containing an electrolyte solution (with monovalent salt concentration c_s and viscosity η) under a constant electric field E along the pore axis (Figure 1). The potential interaction F_p between the protein and the pore wall is modeled as a saw-tooth periodic potential of period λ (comparable to 2R_g) and depth εk_BT. Each barrier is associated with the protein migration by a distance of 2R_g. Ignoring the inertial force, the Langevin equation for the instantaneous velocity of the macromolecule along the pore (x-direction) is

$$-\zeta \frac{dx}{dt}+f+f_{random}=0,$$ (3)

where −ζdx/dt is the frictional force (with ζ = k_BT/D being the friction coefficient), f_random is the random force arising from the collisions of solvent molecules with the protein, and f is the net force on the protein from the external electric field f_E, counterion cloud f_cloud, confinement inside the pore f_conf, and pore-protein interaction f_p,

$$f=f_E+f_{cloud}+f_{conf}+f_p.$$ (4)

We address below successively the three major components of the problem, viz., collective dynamics of the protein and its counterion cloud, confined hydrodynamic transport inside the pore, and the effect of potential interaction between the protein and the pore wall.

FIG. 1.

Counterion cloud drags the protein in the opposite direction and gives an apparent charge different from protein's bare charge. The pore-protein interaction, modeled as a periodic potential, dramatically changes the diffusion coefficient and the voltage dependence of velocity of the protein.

II. PROTEIN-COUNTERION DYNAMICS

Without any confinement effects, the velocity v(r) of the fluid at location r outside the protein is given by the linearized Navier-Stokes equation in the steady state limit

$$-\eta {\nabla }^2\mathbf{v}\left(\mathbf{r}\right)+\nabla p\left(\mathbf{r}\right)=\rho \left(\mathbf{r}\right)\mathbf{E}\left(\mathbf{r}\right),$$ (5)

where ρ(r) is the local charge density from all small ions surrounding the protein and E(r) is the local electric field and p is the pressure. By combining Eqs. (3)–(5) for a spherical particle and taking E(r) as $E\widehat{x}$, and using the Debye-Hückel theory and no-slip boundary condition at the particle surface, Hückel derived the velocity U = ⟨dx/dt⟩ as¹⁵

$$\zeta U=QE-\frac{\kappa R_g}{(1+\kappa R_g)}QE,$$ (6)

where the two terms on the right-hand side are from f_E and f_cloud, respectively. κ is the inverse Debye length, and for an aqueous solution at 25°C of monovalent salt at concentration c_s in molarity, $\kappa =3.28\sqrt{c_s}$ nm⁻¹.

Combining the two terms on the right-hand side of Eq. (6),

$$\zeta U=\frac{Q}{(1+\kappa R_g)}E\equiv Q_{eff}E;Q_{eff}=\frac{Q}{(1+\kappa R_g)},$$ (7)

where the macromolecule and its counterion cloud are taken as a collective entity (quasiparticle) with an effective charge Q_eff which is much less than the bare charge Q. Several attempts to improve Hückel's theory are found in the literature.^19–22 The most notable is from Henry (by accounting for local electric field near the particle arising from the continuity of current at the particle surface) with the result¹⁹

$$Q_{eff}=\frac{Q}{(1+\kappa R_g)}g\left(\kappa R_g\right),$$ (8)

where the Henry correction g(κR_g) varies between 1 and 3/2 for nonconducting macroions, given by

$$\begin{array}{ccc}\hfill g\left(\alpha \right)& =& 1+\frac{{\alpha }^2}{16}-\frac{5{\alpha }^3}{48}-\frac{{\alpha }^4}{96}+\frac{{\alpha }^5}{96}\hfill \\ & & +\frac{{\alpha }^4}{8}\left(1-\frac{{\alpha }^2}{12}\right)e^{\alpha }{E}_1\left(\alpha \right),\hfill \end{array}$$ (9)

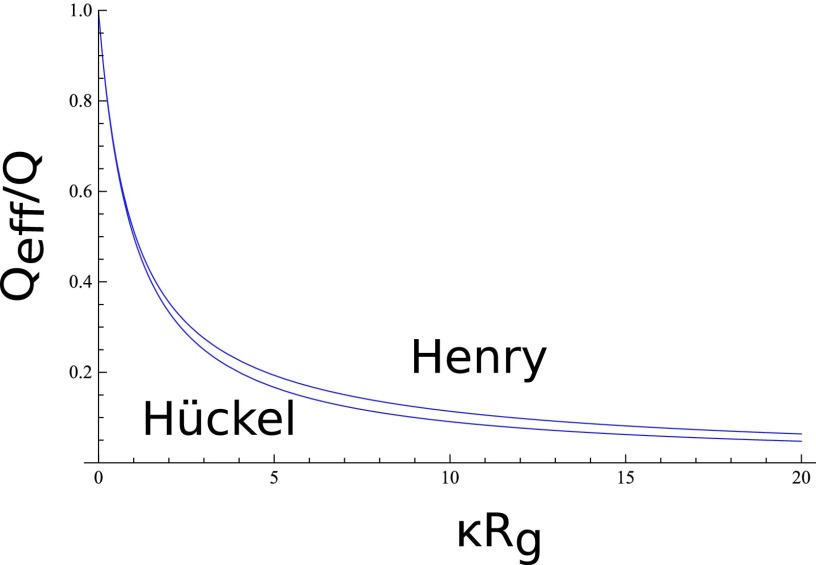
with E₁(α) being the exponential integral ${\int }_{\alpha }^{\infty }{e}^{-x}dx/x$. The ratio Q_eff/Q is plotted in Figure 2 as a function of κR_g for the Hückel (Eq. (7)) and Henry (Eq. (8)) expressions. The drag force from the counterion cloud significantly affects the inference of the protein charge in electrophoresis measurements. For example, for a protein of radius 1.5 nm in 1 M KCl, κR_g = 5 and the effective charge is seen from Figure 2 to be reduced to about 20% of the bare charge.

FIG. 2.

The apparent charge Q_eff is much smaller than Q depending on κR_g.

III. CONFINEMENT EFFECTS

The diffusion and convection of a macromolecule are hindered by the physical boundary of the pore. Considering an uncharged spherical particle confined inside a cylindrical pore, the hard excluded volume effect and hydrodynamic interaction among the particle along the pore axis and the pore wall were addressed by Ferry²³ and Faxén,²⁴ respectively. As a result, the diffusion coefficient D_p of the particle inside the pore is substantially reduced, given by (known as the Renkin equation²⁵)

$$\begin{array}{ccc}\hfill \frac{D_p}{D}& =& {\left(1-\frac{R_g}{R}\right)}^2[1-2.104\left(\frac{R_g}{R}\right)\hfill \\ & & +2.09{\left(\frac{R_g}{R}\right)}^3-0.95{\left(\frac{R_g}{R}\right)}^5].\hfill \end{array}$$ (10)

More recently, Dechadilok and Deen²⁶ have provided a better formula for D_p given by

$$\begin{array}{ccc}\hfill \frac{D_p}{D}& =& 1+\frac{9}{8}\left(\frac{R_g}{R}\right)\ln \left(\frac{R_g}{R}\right)-1.56034\left(\frac{R_g}{R}\right)\hfill \\ & & +0.528155{\left(\frac{R_g}{R}\right)}^2+1.91521{\left(\frac{R_g}{R}\right)}^3\hfill \\ & & -2.81903{\left(\frac{R_g}{R}\right)}^4+0.270788{\left(\frac{R_g}{R}\right)}^5\hfill \\ & & +1.10115{\left(\frac{R_g}{R}\right)}^6-0.435933{\left(\frac{R_g}{R}\right)}^7.\hfill \end{array}$$ (11)

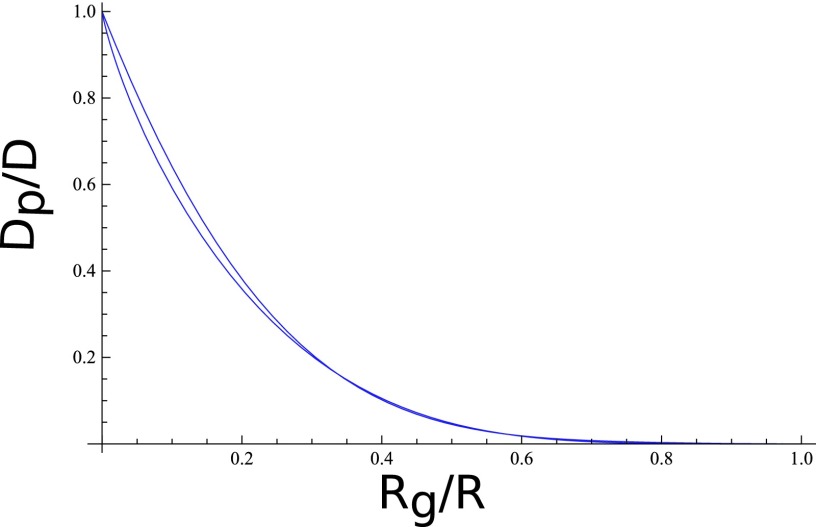
A plot of D_p/D versus R_g/R is given in Figure 3 for both Ferry-Faxén-Renkin and Dechadilok-Deen equations. Clearly, D_p is substantially smaller than D. A generalization of Faxén's result for restricted hydrodynamics involving macroions and counterion clouds in an electrolyte solution is nontrivial and entails numerical work. As we expect the dominant effect from the finite pore volume to arise from the excluded volume effect and as the hydrodynamic and electrostatic interactions are to be screened to some extent, we are here content with the above formulas for D_p and Q_eff.

FIG. 3.

Effect of pore confinement on diffusion coefficient according to Ferry-Faxén-Renkin (top curve) and Dechadilok-Deen (bottom curve).

IV. PORE-PROTEIN INTERACTION

We now consider the effect of the periodic potential energy profile along the pore on the diffusion and drift of the protein molecule. The Langevin equation from Eqs. (3) and (4) is

$$\frac{dx}{dt}=\frac{D_p}{k_{B}T}(f_E+f_{cloud}+f_p)+{\sqrt{D}}_p\Gamma \left(t\right),$$ (12)

where the confinement effect is subsumed into D_p and the fluctuation-dissipation theorem for the random noise Γ(t) is satisfied. The force f_p due to pore-protein interaction is −∂F_p(x)/∂x, where F_p is taken as the saw-tooth periodic potential,

$$\frac{F_p\left(x\right)}{k_{B}T}\equiv {\tilde{F}}_p\left(x\right)=\left\{\begin{array}{cc}\hfill -\frac{2\epsilon x}{\lambda }& \hfill 0<x<\frac{\lambda }{2},\\ \hfill -2\epsilon +\frac{2\epsilon x}{\lambda }& \hfill \frac{\lambda }{2}<x<\lambda ,\end{array}\right.$$ (13)

ε is the strength of the attractive energy in units of k_BT as sketched in Figure 1. Since the net effect of f_E and f_cloud is to yield the apparent charge Q_eff, we write f_E + f_cloud = Q_eff E as −∂(−Q_eff Ex)/∂x. Therefore, Eq. (12) becomes

$$\frac{dx}{dt}=-D_p\frac{\partial \tilde{F}\left(x\right)}{\partial x}+{\sqrt{D}}_p\Gamma \left(t\right),$$ (14)

with

$$\tilde{F}\left(x\right)=-{\tilde{Q}}_{eff}Ex+{\tilde{F}}_p\left(x\right),$$ (15)

where ${\tilde{Q}}_{eff}\equiv Q_{eff}/\left(k_{B}T\right)$. The Fokker-Planck equation for the probability of finding the protein at x and time t, and the flux J, follows from Eq. (12) as^10,28

$$\begin{array}{c}\hfill \frac{\partial P(x,t)}{\partial t}=-\frac{\partial }{\partial x}J=D_p\frac{\partial }{\partial x}\left\{\left[\frac{\partial \tilde{F}\left(x\right)}{\partial x}P(x,t)\right]+\frac{\partial P(x,t)}{\partial x}\right\}.\end{array}$$ (16)

A. Effective diffusion coefficient

The presence of the potential well (or a potential barrier) inside every period of the potential energy profile modifies the diffusion coefficient. For E = 0, the law of diffusion for each period λ obeys

$${\lambda }^2=2D_{eff}{\tau }_0,$$ (17)

where τ₀ is the mean first passage time for one period (with reflecting boundary condition at x = 0 and absorbing boundary condition at x = λ, and E = 0),

$${\tau }_0=\frac{1}{D_p}{\int }_0^{\lambda }dy{e}^{{\tilde{F}}_p\left(y\right)}{\int }_0^{y}dx{e}^{-{\tilde{F}}_p\left(x\right)}.$$ (18)

Substituting Eq. (13) into Eq. (18), we get from Eq. (17)

$$D_{eff}=D_p\frac{{\epsilon }^2}{(1-e^{-\epsilon })(e^{\epsilon }-1)}.$$ (19)

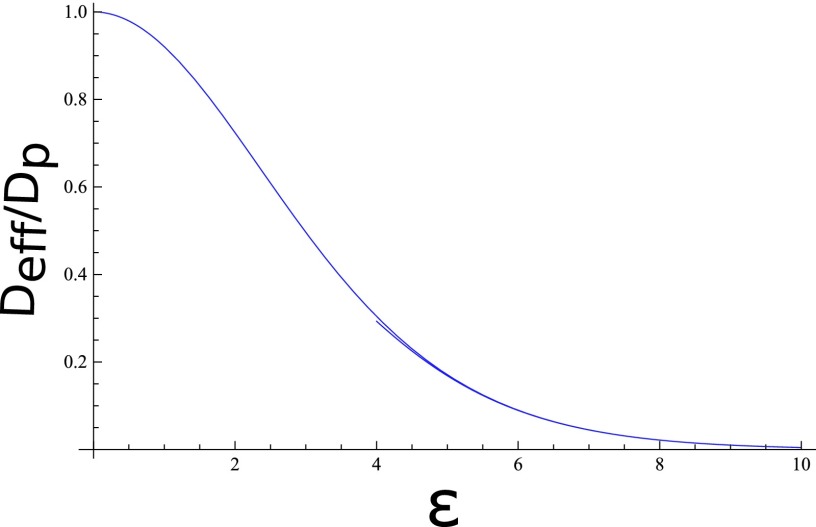
This exact result is plotted in Figure 4 as a function of ε (interaction energy in units of k_BT). The diffusion coefficient is seen to decrease significantly as the barrier height increases. The asymptotic limits of Eq. (19) are

$$\frac{D_{eff}}{D_p}=\left\{\begin{array}{cc}\hfill 1-\frac{{\epsilon }^2}{12}+\cdots & \hfill \epsilon \ll 1,\\ \hfill {\epsilon }^2{e}^{-\epsilon }& \hfill \epsilon \gg 1.\end{array}\right.$$ (20)

The large barrier result is reminiscent of the Kramer's formula for barrier crossing, but with a different prefactor ε². This limit is also included in Figure 4. By measuring D_eff and using Eq. (19), the pore-protein interaction energy can be determined.

FIG. 4.

Dependence of diffusion coefficient on pore-protein interaction energy. Bottom curve is from Eq. (20).

B. Electrophoretic mobility

The probability to find the macromolecule at x in the steady state (J = constant) follows from an integration of Eq. (16) as

$$P\left(x\right)=e^{-\tilde{F}\left(x\right)}\left[P(x=0)-\frac{J}{D_p}{\int }_0^{x}d{x}^{\prime }{e}^{\tilde{F}\left(x^{\prime }\right)}\right].$$ (21)

For the periodic potential ${\tilde{F}}_p\left(x\right)$, the standard analysis gives (for m = integer)^27–29

$$P(m\lambda +x)=P\left(x\right);P(x=0)=\frac{J}{D_p}\frac{I_{+}}{(1-e^{-{\tilde{Q}}_{eff}E\lambda })},$$ (22)

with

$$I_{\pm }={\int }_0^{\lambda }dx{e}^{\pm \tilde{F}\left(x\right)}.$$ (23)

Averaging Eq. (14) over the normalized P(x) in each period, and with ⟨Γ(t)⟩ = 0, the average velocity of the protein is

$$U=\lambda D_p\frac{(1-e^{-2\theta })}{[I_{+}{I}_{-}-(1-e^{-2\theta })Y]},$$ (24)

where

$$\theta ={\tilde{Q}}_{eff}E\lambda /2;Y={\int }_0^{\lambda }dx{e}^{-\tilde{F}\left(x\right)}{\int }_0^{x}dy{e}^{\tilde{F}\left(y\right)}.$$ (25)

Substituting Eq. (15) into Eqs. (23) and (25), we get

$$\begin{array}{c}\hfill I_{\pm }=\frac{\lambda }{2}\left[\pm \frac{1}{(\theta +\epsilon )}(1-e^{\mp (\theta +\epsilon )})\pm \frac{e^{\mp (\theta +\epsilon )}}{(\theta -\epsilon )}(1-e^{\pm (\epsilon -\theta )})\right],\end{array}$$ (26)

and

$$\begin{array}{ccc}\hfill Y& =& {\left(\frac{\lambda }{2}\right)}^2\{\frac{(e^{\theta +\epsilon }-1)}{{(\theta +\epsilon )}^2}+\frac{(e^{\theta -\epsilon }-1)}{{(\theta -\epsilon )}^2}\hfill \\ & & +\frac{1}{({\theta }^2-{\epsilon }^2)}[-2\theta +e^{\theta }(e^{\theta }-e^{\epsilon })(1-e^{-\theta -\epsilon })]\}.\hfill \end{array}$$ (27)

The exact analytical expression for the velocity is given by Eqs. (24), (26), and (27) as a function of the effective charge Q_eff, pore diffusion coefficient D_p, pore-protein interaction energy ε, period of the potential λ, and the strength of the electric field E.

In the linear response regime (θ ≪ 1), Eq. (24)) reduces to

$$U={\tilde{Q}}_{eff}{D}_p\frac{{\epsilon }^2}{(1-e^{-\epsilon })(e^{\epsilon }-1)}E={\tilde{Q}}_{eff}{D}_{eff}E,$$ (28)

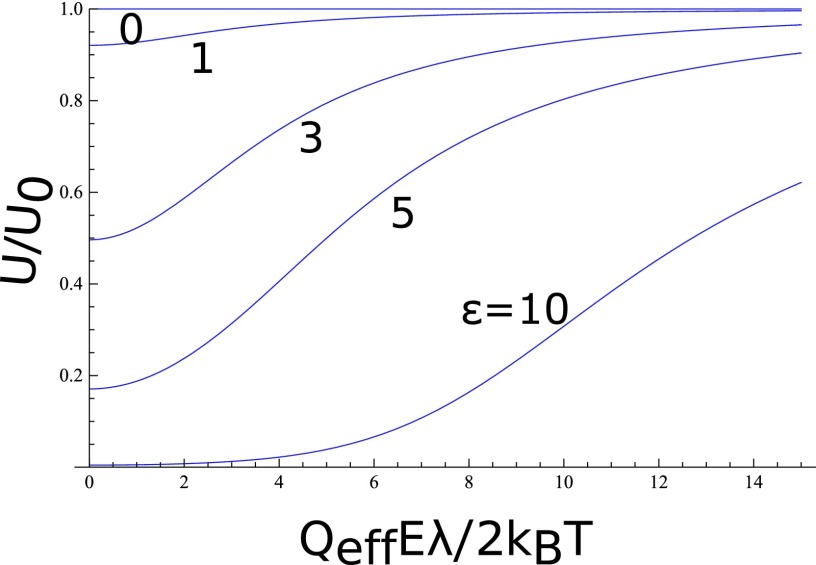
in view of Eq. (19). However, the linear response regime is valid only for very small values of θ for ε ≠ 0, as can be seen in Figure 5, where $U/{\tilde{Q}}_{eff}{D}_{eff}E$ from Eq. (24) is plotted against $\theta ={\tilde{Q}}_{eff}E\lambda /2$ for different values of ε.

FIG. 5.

Velocity reduction by pore-protein interaction energy ε and the onset of nonlinear dependence on the electric field. U₀ is the velocity in the linear response regime $D_p{\tilde{Q}}_{eff}E$.

C. Average translocation time

The average translocation time for the protein through the nanopore of length L with N periods (L = Nλ) is given by the mean first passage time

$$\tau =\frac{1}{D_p}{\int }_0^{L}dy{e}^{\tilde{F}\left(y\right)}{\int }_0^{y}dx{e}^{-\tilde{F}\left(x\right)},$$ (29)

where the reflecting boundary condition at x = 0 and absorbing boundary condition at x = L are used with the initial position of the protein being at x = 0. Using Eqs. (13), (15), and (22),

$$\tau =N{\tau }_1+\frac{1}{D_p}\sum _{m=1}^{N-1}{\int }_{m\lambda }^{(m+1)\lambda }dy{e}^{\tilde{F}\left(y\right)}{\int }_0^{m\lambda }dx{e}^{-\tilde{F}\left(x\right)},$$ (30)

where τ₁ is the mean first passage time over one period (with $\tilde{F}$ replacing ${\tilde{F}}_p$ in Eq. (18), as a generalization to E ≠ 0). Combination of Eqs. (13), (15), (25), and (30) gives

$$\begin{array}{ccc}\hfill {\tau }_1& =& \frac{1}{D_p}{\left(\frac{\lambda }{2}\right)}^2\{\frac{(e^{-\theta -\epsilon }-1)}{{(\theta +\epsilon )}^2}+\frac{(e^{-\theta +\epsilon }-1)}{{(\theta -\epsilon )}^2}\hfill \\ & & +\frac{1}{({\theta }^2-{\epsilon }^2)}[1+2\theta -e^{-\theta }(e^{\epsilon }+e^{-\epsilon })+e^{-2\theta }]\}\hfill \end{array}$$ (31)

and

$$D_p\tau =D_{p}N{\tau }_1+\frac{I_{+}{I}_{-}}{(1-e^{2\theta })}\left[-N+\frac{(1-e^{-2N\theta })}{(1-e^{-2\theta })}\right]$$ (32)

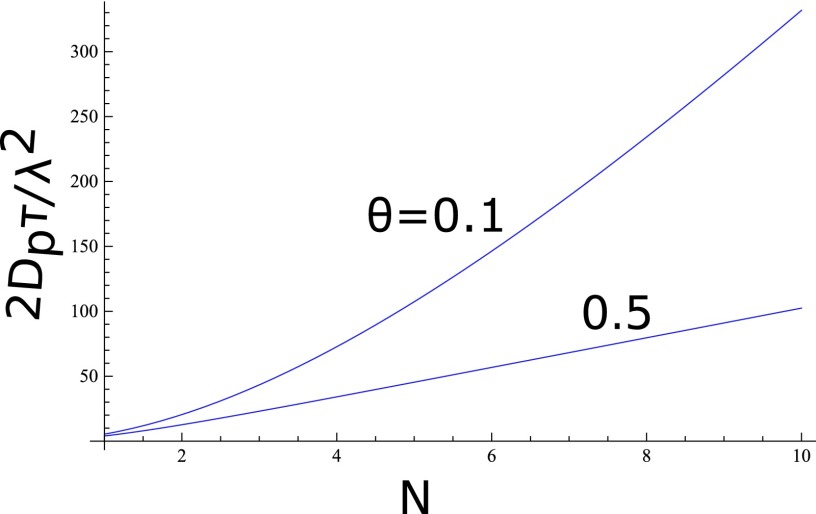
with I_± given in Eq. (26). The above equation provides the complete dependence of the average translocation time on the pore length (L = Nλ) in terms of ε and E. As an illustration, a plot of Eq. (32) as 2D_pτ/λ² vs. N is given in Figure 6. The above formula reduces to the expected limits. For E → 0, it becomes the law of diffusion,

$$L^2=2D_{eff}\tau ,$$ (33)

and for ε = 0, it becomes the familiar drift-diffusion formula,^10,30

$$D_p\tau =\frac{1}{{\tilde{Q}}_{eff}E}\left[L+\frac{1}{{\tilde{Q}}_{eff}E}(e^{-{\tilde{Q}}_{eff}EL}-1)\right].$$ (34)

In its own right, Eq. (34) is a crossover between the diffusive law τ = L²/(2D_p) for ${\tilde{Q}}_{eff}EL\ll 1$ and the drift law $\tau =L/\left(D_p{\tilde{Q}}_{eff}E\right)=L/U$ for ${\tilde{Q}}_{eff}EL\gg 1$.

FIG. 6.

Dependence of mean translocation time on pore length for ε = 5 and $\theta ={\tilde{Q}}_{eff}E\lambda /2=0.1$ (top) and 0.5 (bottom).

Combination of Eqs. (8), (11), (19), (24)–(27), and (32) gives the full set of equations for the effective charge, effective diffusion coefficient, velocity, and mean translocation time in terms of Q, D, pore radius R, inverse Debye length κ, protein radius R_g, period λ and strength ε of the pore-protein interaction potential, and the electric field. The effective values of diffusion coefficient and velocity obtained from fitting experimental translocation time histograms are shrouded by the various contributing factors in these equations. The derived formulas constitute a good starting point in sorting out Q, D, and μ from nanopore electrophoresis experiments.