An image-guidance system for dynamic dose calculation in prostate brachytherapy using ultrasound and fluoroscopy

Abstract

Purpose:

Brachytherapy is a standard option of care for prostate cancer patients but may be improved by dynamic dose calculation based on localized seed positions. The American Brachytherapy Society states that the major current limitation of intraoperative treatment planning is the inability to localize the seeds in relation to the prostate. An image-guidance system was therefore developed to localize seeds for dynamic dose calculation.

Methods:

The proposed system is based on transrectal ultrasound (TRUS) and mobile C-arm fluoroscopy, while using a simple fiducial with seed-like markers to compute pose from the nonencoded C-arm. Three or more fluoroscopic images and an ultrasound volume are acquired and processed by a pipeline of algorithms: (1) seed segmentation, (2) fiducial detection with pose estimation, (3) seed matching with reconstruction, and (4) fluoroscopy-to-TRUS registration.

Results:

The system was evaluated on ten phantom cases, resulting in an overall mean error of 1.3 mm. The system was also tested on 37 patients and each algorithm was evaluated. Seed segmentation resulted in a 1% false negative rate and 2% false positive rate. Fiducial detection with pose estimation resulted in a 98% detection rate. Seed matching with reconstruction had a mean error of 0.4 mm. Fluoroscopy-to-TRUS registration had a mean error of 1.3 mm. Moreover, a comparison of dose calculations between the authors’ intraoperative method and an independent postoperative method shows a small difference of 7% and 2% forD₉₀ and V₁₀₀, respectively. Finally, the system demonstrated the ability to detect cold spots and required a total processing time of approximately 1 min.

Conclusions:

The proposed image-guidance system is the first practical approach to dynamic dose calculation, outperforming earlier solutions in terms of robustness, ease of use, and functional completeness.

I. INTRODUCTION

Prostate cancer is the most common cancer among men in the United States (US), accounting for nearly 235 000 new diagnoses and 30 000 deaths per year.¹ Permanent prostate brachytherapy (PPB) is considered a standard option of care, and it has been estimated that up to 250 000 patients in the US have been treated with PPB during the past decade.² PPB is a procedure that involves the permanent implantation of approximately 50–120 radioactive seeds into the prostate via transperineal needles. The goal is to optimally position the seeds in order to achieve adequate dose to prostatic tissue while minimizing dose to normal tissue. The vast majority of PPB procedures are performed using transrectal ultrasound (TRUS) as the imaging modality for guiding the planning and implantation stages. Following implantation, the patient is imaged most commonly by computed tomography (CT) within 30 days of the procedure to verify the final dosimetry.

Although it can be used successfully, contemporary PPB procedures may not achieve optimal results because the dynamic changes in prostate shape and seed positions that occur during seed implantation are not yet quantifiable with current technology. While an initial treatment plan to optimally position the seeds in the prostate is created prior to implantation, the seeds may move in relation to the prostate during the operation due to prostate edema or seed migration. As a result, for truly optimal results the treatment plan should be modified intraoperatively, a technique known as intraoperative treatment planning (ITP). However, as noted in a report by the American Brachytherapy Society in 2001, the major limitation of ITP is the inability to localize the seeds in relation to the prostate.³ Even today, localization of seeds in relation to the prostate has not been practically realizable. If this ability to localize seeds existed, PPB could be improved by a process called dynamic dose calculation, i.e., continuous updating of the dose distribution calculated from the localized deposited seed positions. This dosimetric feedback would inform the physician performing brachytherapy how to modify the plan for ITP and, if required, additional seeds may be implanted immediately in the operating room (OR). Without dynamic dose calculation, suboptimal treatment would only be detected after dosimetry by CT in which case it must be decided whether to accept the treatment as is or to return for additional therapy.

Dynamic dose calculation is a bold step forward in optimizing patient-specific care through PPB, but has been limited primarily by the weaknesses of TRUS. While TRUS is a valuable intraoperative tool for contouring the prostate during planning and for visualizing needles during implantation, it is difficult to use TRUS alone to localize seeds for dosimetry. False positives occur due to calcifications, bleeding, and air bubbles, while false negatives occur due to shadowing effects and poor image quality. In fact, it has become widely accepted that TRUS alone is insufficient to localize seeds in relation to the prostate.⁴ Alternative technologies have been suggested to supplement or entirely replace TRUS to localize seeds.⁵ One approach is based on cone-beam CT using a motorized encoded C-arm.⁶ Although effective in localizing seeds, such C-arms are uncommon in the OR and require a large orbit around the patient which is impractical to accomplish in the typically confined brachytherapy setup. Another approach is based on magnetic resonance imaging (MRI).⁷ MRI is excellent for imaging prostate tissue and is capable of imaging implanted seeds; however, intraoperative MRI is cumbersome, expensive, and slow, while typically requiring robotics to operate within the confined bore of the scanner. There are other approaches, such as those based on vibro-acoustography^8,9 and photoacoustic imaging,^10–12 but such technologies are still in early developmental stages.

On the other hand, a promising method for localizing seeds is based on the fusion of ultrasound and fluoroscopy. Fluoroscopy can visualize the metallic seeds well, but alone it cannot visualize the prostate. It therefore makes a perfect complement to ultrasound, which is sufficient in visualizing the prostate, but insufficient in visualizing the seeds. Several groups have successfully combined the two imaging modalities for PPB, most commonly using radiation therapy simulators or encoded isocentric C-arms.^13–17 The most common fluoroscopic imaging device currently found in ORs across the world, however, is the mobile nonisocentric C-arm, and it is used by many brachytherapists (in addition to TRUS) to visually verify needle or seed placement. Although more challenging, fusion of TRUS with such ubiquitous C-arms for seed localization would have a much wider impact than the specialized equipment proposed in many research papers.

Recently, Jain et al.¹⁸ has proposed a prototype image-guidance system based on TRUS and mobile nonisocentric C-arm fluoroscopy. A central component to their system is the fluoroscope tracking fiducial (FTRAC),¹⁹ a tube compactly composed of several radio-opaque features that innovatively serves the dual purpose of recovering poses from the nonencoded C-arm needed for seed reconstruction and providing the necessary link between the fluoroscopy and ultrasound coordinate systems that is needed for mechanical registration. However, the FTRAC has several drawbacks. First, the FTRAC restricts fluoroscopic acquisition because the technician must position the C-arm in at least three distinct poses where the FTRAC and seeds are in the same field of view yet do not overlap. This is a challenging task since the C-arm already has little room to maneuver as the C-arm detector is typically confined to a small space between the raised legs of the patient in the lithotomy position. Second, the FTRAC complicates segmentation because its many features (i.e., nine points, three lines, and two ellipses) must all be segmented. Although automatic segmentation algorithms exist,^20,21 these algorithms frequently fail, and manual correction is both tedious and time-consuming. Finally, the mechanical registration that comes with the FTRAC is unsatisfactory. While a rough registration may be achieved, it is reported that an FTRAC-based system has an undesirable mean absolute system error of 4 mm in a training phantom, due to mechanical precalibration errors or biases that may be present during seed reconstruction.¹⁸ The error is likely to be greater in patients as a result of prostate deformation, since the TRUS probe must be inserted to capture TRUS images but removed to capture fluoroscopic images. Other components of the FTRAC system are also problematic. The seed segmentation algorithm²² requires user intervention via a manually selected region of interest (ROI), which precludes the possibility of an automatic pipeline for image processing. As well, the reconstruction algorithm known as MARSHAL (Ref. 23) is sensitive to pose errors, which means that inaccurate measurement of pose causes large seed position estimation errors.

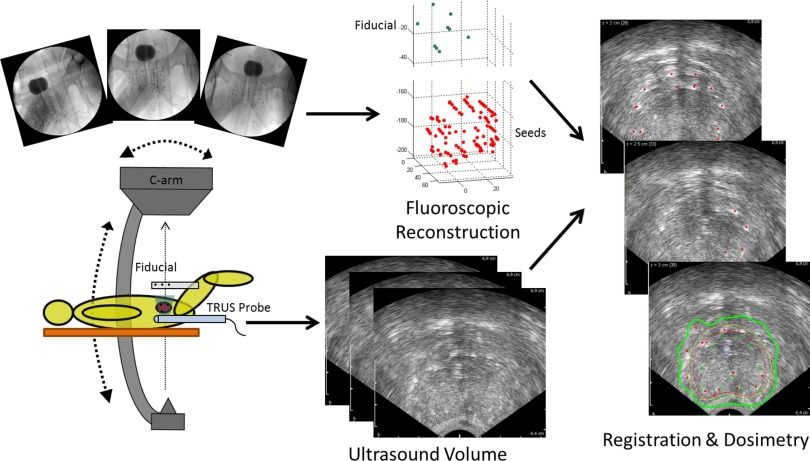
In this paper, we present an image-guidance system for PPB dynamic dose calculation which outperforms earlier solutions in terms of robustness, ease of use, and functional completeness. Our proposed system follows a simple workflow (see Fig. 1). Three or more distinct 2D fluoroscopic images of the seeds and a simple fiducial with seed-like markers are taken generally within a 20° cone of the anterior–posterior axis of the patient lying on the table. TRUS images are taken to acquire the prostate volume. These images are processed in the following steps: (1) seed segmentation, (2) fiducial detection with pose estimation, (3) seed matching with reconstruction, and (4) fluoroscopy-to-TRUS registration. While some of these individual steps have been previously published, none of the papers presenting them has addressed the system workflow as a whole. We present all the pieces integrated together to form the first practical system for dynamic dose calculation validated on 10 phantom cases and 37 patients.

FIG. 1.

Workflow of our image-guidance system for dynamic dose calculation. At least three fluoroscopic images are taken of the implanted seeds and the fiducial above the patient's abdomen (the dark round object in the images is a Foley catheter balloon optionally filled with contrast to identify the bladder). An ultrasound volume of the seed-filled prostate is acquired. Both image sets are processed to calculate dose.

II. METHODS

II.A. Equipment and protocol

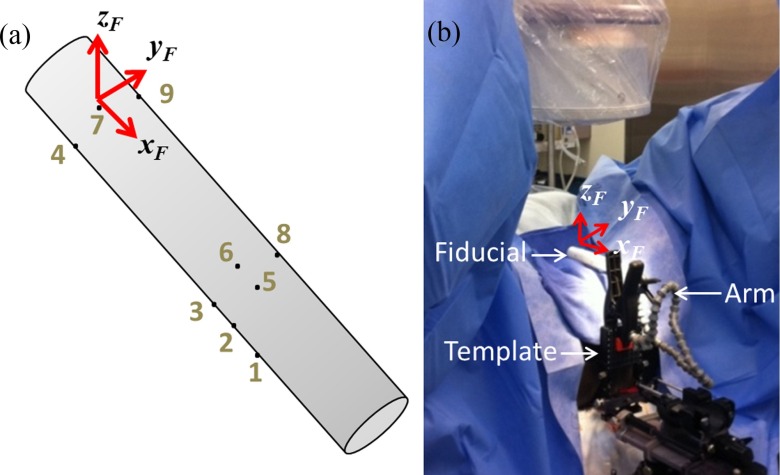
A few pieces of equipment are required for our system. The first two are the imaging devices, which are the ultrasound scanner with a TRUS probe and the mobile C-arm. The C-arm must be calibrated, and is generally done by capturing an image of a two-plane calibration phantom to compute intrinsic camera parameters (i.e., focal length and image center) and image distortion parameters.²⁴ The last piece of equipment is a fiducial that is used to track the C-arm pose. Our fiducial is a cylindrical radiolucent tube with nine radio-opaque seed-like markers (see Fig. 2). In contrast to fiducials with beads or other geometric markers (like the FTRAC) that degrade automatic seed segmentation when their x-ray projection overlaps the implanted seeds,^18,19 the x-ray projection of our fiducial can overlap the implanted seeds with no ill effects because its markers are automatically segmented just like implanted seeds. This gives the technician freedom to maneuver the C-arm by large angles in order to obtain the distinguishable poses required for reconstruction. Moreover, while other fiducials require separate image processing steps for seeds and fiducial, our process only requires one (marker and seed) segmentation and reconstruction algorithm. This represents a shift from the conventional paradigm and is a key advantage of our overall approach. By treating the fiducial markers as if they were seeds, the workflow is significantly streamlined, and this simplicity helps to reduce the opportunities for errors.

FIG. 2.

Simple marker-based fiducial. (a) Illustration of fiducial with markers and coordinate system identified. (b) Photograph of fiducial clipped to needle-guiding template with a flexible arm in the OR.

The configuration of the nine markers in our fiducial is arbitrary. In fact, the only requirement in our experience is that at least four markers should be placed in a 3D configuration for more accurate pose tracking. Such liberty in configuration also makes the fiducial inexpensive to manufacture, especially when compared to the FTRAC and other alternative tracking systems. A potential limitation of this fiducial is that it does not provide poses as accurate as the FTRAC. In particular, point-based fiducials like ours are reported to have an accuracy of about 1 mm for translation and 1° for rotation as opposed to the FTRAC's mean accuracies of 0.56 mm and 0.33°.¹⁹ However, it is sufficiently accurate for our seed reconstruction algorithm (described below). Another advantage of our overall approach is that we use a computational algorithm to register the fluoroscopy and ultrasound images; therefore, the fiducial may be positioned in the field of view using a simple flexible arm rather than a rigid mechanical support. This further reduces manufacturing costs and increases adaptability to varying body habitus.

The protocol for our system begins with the patient placed on the surgical table and anesthetized in the dorsal lithotomy position. Prostate contouring and dosimetric planning under TRUS guidance is completed during the intraoperative planning stage using commercial brachytherapy planning software. Whenever dosimetry is needed, a TRUS volume is acquired by recording transverse ultrasound slices at 1 mm intervals while the TRUS probe is continuously retracted from a few millimeters cranial to the base of the prostate to a few millimeters caudal to the apex. Fluoroscopic images are then acquired using a frame grabber by capturing at least three distinct images within a 20° cone around the patient's anterior–posterior axis with the TRUS probe fully retracted and the fiducial attached to the needle-guiding template, with any deformation caused by this retraction accounted for later in our computational registration algorithm. All images are processed by the four algorithms. During processing, the user may interact with the graphical user interfaces (GUIs) that have been set up for validation and for any required manual adjustments. As additional seeds are implanted, the imaging protocol may be repeated as many times as desired to calculate intraoperative dosimetry. We now describe each algorithm in detail.

II.B. Seed segmentation

The first step in the image processing pipeline is to segment seeds in three or more acquired 2D fluoroscopic images in preparation for seed matching with reconstruction. The algorithm takes a distortion-corrected image as input and outputs the 2D coordinates of every seed in the image (see Fig. 3). Since our fiducial is composed of seed-like point markers, the marker coordinates are also output without differentiating markers from seeds; this distinction is left for the next step of fiducial detection with pose estimation. The algorithm is also designed to segment the seeds without a user-defined ROI, but it may use a selected ROI when one is needed, such as when a patient has metallic implants that would generate many false positives otherwise. Moreover, the algorithm attempts to separate overlapping seeds, but even if all the seeds are not perfectly recovered by this step, the remaining “hidden” seeds are recovered in our later step of seed matching with reconstruction.

FIG. 3.

Seed segmentation and fiducial detection. (a) Before seed segmentation. (b) After seed segmentation and before fiducial detection, with single seeds (dots) and overlapping seeds (circles) identified. (c) After fiducial detection with markers identified (bright dots).

Our seed segmentation algorithm is based on our previously published method on simultaneous fiducial and seed segmentation²¹ with some modification to only involve seed segmentation and to more accurately separate overlapping seeds. Briefly stated, the algorithm performs a morphological image processing algorithm known as top-hat by reconstruction to improve contrast between the seeds and the background of the inputted image. After applying Otsu's threshold, the result is a binary image with the seeds displaying as white regions. Next, to separate overlapping seeds, we conservatively set the maximum possible number of seeds in each region to five, although it is rare to have a region with more than three seeds in actual patient images. We then perform a k-means clustering on the coordinates in each region (e.g., if the region contains coordinate [50 100] with an intensity of 128 gray-values, there would 128 instances of the data point [50 100] in the input to k-means), setting the number of clusters to this maximum number of overlapping seeds. If the resulting cluster coordinates are unreasonable by being too close in Euclidean distance (i.e., within 1.5 mm) or too different in pixel intensity (i.e., greater than 15 gray-values), we assume the wrong number of clusters was input into the k-means algorithm and reduce it by one. This is iterated until the result from the k-means clustering algorithm satisfies our conditions of pixel distance and intensity. Note that at least one seed will be identified per region through this process.

II.C. Fiducial detection with pose estimation

The second step is fiducial detection with pose estimation, which aims to distinguish the fiducial marker coordinates from among the segmented coordinates and calculate the respective pose from the marker coordinates for the later step of seed matching with reconstruction. This step takes as input the segmented coordinates from the previous step and outputs the ones belonging to the fiducial as well as the corresponding pose (see Fig. 3). We also assume the 3D model of the fiducial is known and there is some general knowledge of the pose (in our case, the length of the fiducial is oriented approximately foot-to-head and pose is roughly along the anterior–posterior axis), both of which are reasonable to know in a clinical setting. The fact that the fiducial model is one of the inputs also allows this algorithm to work for fiducials of arbitrary configuration.

Overall, this step is performed by iterating between two subfunctions we call projection matching and pose estimation. Given a 3D pose, the projection matching subfunction finds the best fit of the corresponding 2D fiducial model projection among the segmented coordinates. Given proposed 2D fiducial coordinates, the pose estimation subfunction calculates the optimal 3D pose corresponding to those coordinates. The algorithm is initialized with our assumed general knowledge of the pose (i.e., along the anterior–posterior axis of the patient). However, since this initial pose is not perfect, iteration between the two subfunctions improves the results, with the outputs of each subfunction serving as the inputs to the other. This continues until convergence, which is generally within three iterations.

The details of the projection matching subfunction are as follows (see Fig. 4). First, the two furthest points are identified in the projection of the fiducial model [see Fig. 4(a)]. Next, these furthest points are registered in 2D with scale to a pair of segmented coordinates [see Fig. 4(b)]. Then, the registered projection is overlaid on all the segmented coordinates to find the closest corresponding matches [see Fig. 4(c)]. Afterward, a mean Euclidean distance weighted by scale between the registered projection and its closest matches [see Fig. 4(d)] is computed as

$$\frac{1}{s}\frac{1}{N_M}\sum _{i=1}^{N_M}{e}_i,$$

where s is the scale as determined by the 2D registration, N_M is the number of fiducial markers, and e_i is the distance between the ith registered point and its closest match (two of which will be zero due to the registration). In principle, this would be repeated over all pairs of segmented coordinates, and the closest points corresponding to the registration with the least error would be output as the best projection match. However, to speed up computation time, we also use two constraints that come from the assumption that the actual pose is within certain limits of the initial pose, thus reducing search time. The first constraint is to consider only the pairs of segmented points that have a distance within a certain fraction of that of the furthest two points in the projection, in our case 25%, since we assume that magnification will not differ greatly. The second constraint is that the pairs of segmented coordinates must result in registrations within 15° of in-plane rotation, since we do not expect to capture images with the fiducial oriented at a greater angle. With this approach, we would theoretically produce a match with an error metric of zero if the fiducial is moved in 3D via four of the six degrees of freedom with respect to the initial pose. This is accomplished through the 2D registration with scale, which accounts for parallel movement (two translational degrees of freedom and one rotational degree of freedom, specifically yaw) and perpendicular movement (the third translational degree of freedom resulting in magnification) with respect to the imaging plane. Because of these assumptions, we observe experimentally that most errors in projection matching are caused by the unaccounted differences about the other two rotational degrees of freedom (pitch and roll).

FIG. 4.

Steps in projection matching. (a) Find the two furthest points in the projection (connected by line). (b) Register the projection (crosses) to a pair of segmented coordinates (dots). (c) Find the closest segmented coordinates (circles) to the registered projection (there are fewer circles than crosses because some registered projection coordinates match to the same segmented coordinates). (d) Calculate error, which in this case is high because it is not the correct match. After repeating these steps for all pairs of segmented coordinates, the match with least error is outputted.

The other subfunction, pose estimation, is essentially an optimization problem with “projection error” as the cost function. To compute projection error, we consider that the image homogeneous coordinates, ${\mathit{p}}_{\mathit{i}}^{\mathit{I}}={[p_{ix}^I,p_{iy}^I,1]}^T$, of the ith fiducial marker with world homogeneous coordinates, ${\mathit{p}}_{\mathit{i}}^{\mathit{W}}={[p_{ix}^W,p_{iy}^W,p_{iz}^W,1]}^T$, is calculated as

$${\mathit{p}}_{\mathit{i}}^{\mathit{I}}=\left[\begin{array}{cccc}\hfill f/s_x& \hfill 0& \hfill u_0& 0\\ \hfill 0& \hfill f/s_y& \hfill v_0& 0\\ \hfill 0& \hfill 0& \hfill 0& 1\end{array}\right]\left[\begin{array}{cc}\hfill \mathit{R}\left(\mathit{\Phi }\right)& \hfill \mathit{t}\\ \hfill \underline{0}& \hfill 1\end{array}\right]{\mathit{p}}_{\mathit{i}}^{\mathit{W}},$$

where f is the focal length of the C-arm, (s_x,s_y) is the pixel sampling interval, and (u₀, v₀) is the image center, assumed to be known through calibration, and $\mathit{R}\left(\mathit{\Phi }\right)$ and t are the pose rotation in rotation matrix form and the pose translation vector, respectively. If the homogeneous segmented coordinates of the fiducial marker is notated as ${\widehat{\mathit{p}}}_{\mathit{i}}^{\mathit{I}}={\left[{\widehat{p}}_{ix}^I,{\widehat{p}}_{iy}^I,1\right]}^T$, projection error is therefore computed as $E_i=\Vert {\mathit{p}}_{\mathit{i}}^{\mathit{I}}-{\widehat{\mathit{p}}}_{\mathit{i}}^{\mathit{I}}\Vert$. Therefore, the pose estimation problem becomes

$$\underset{\mathit{\Phi },\mathit{t}}{\arg \min }\sum _{i=1}^{N_M}{E}_i,$$

where N_M is the number of fiducial markers. This problem is solved by Newton's method.²⁵

II.D. Seed matching with reconstruction

The pipeline continues with the third step of seed matching with reconstruction, which computes a 3D seed cloud from the three or more distinct fluoroscopic images. This algorithm takes as input the total number of implanted seeds and the previously computed results of 2D seed/marker coordinates and C-arm poses from all the images, and outputs the 3D coordinates with respect to the fiducial coordinate system [see Fig. 5]. The algorithm we use is known as APC-REDMAPS published by Lee et al.^26,27 It is a robust reconstruction algorithm that resolves hidden seeds while being insensitive to pose errors.

FIG. 5.

Seed reconstruction from fluoroscopy and registration to TRUS. (a) Three fluoroscopic images with segmented seeds and fiducial. At least three fluoroscopic images are needed for the reconstruction. (b) Reconstructed seeds (dots below) and fiducial (dots above). Note that the fiducial is properly separated from implanted seed cloud. (c) Before registration. The reconstructed seed cloud (dots) is centered on the ultrasound volume with the prostate contour. (d) After registration. Note that the registered seeds are positioned on the hyperechoic regions.

To describe APC-REDMAPS briefly, the crux of the reconstruction problem is to determine the unique correspondences of all the seeds among the images. However, since seeds may be hidden, this assignment problem should be modified so that each segmented coordinate may be assigned multiple times across images. In the case of the minimum of three images, it may be formulated as the following large combinatorial optimization problem:²⁶

$$\begin{array}{c}\underset{x_{ijk}}{\min }{\sum }_{i=1}^{N_1}{\sum }_{j=1}^{N_2}{\sum }_{k=1}^{N_3}{c}_{ijk}(\mathit{\Phi },\mathbf{t})x_{ijk}\hfill \\ \mathrm{s}.\mathrm{t}.{\sum }_{j=1}^{N_2}{\sum }_{k=1}^{N_3}{x}_{ijk}\ge 1,\forall i\hfill \\ {\sum }_{i=1}^{N_1}{\sum }_{k=1}^{N_3}{x}_{ijk}\ge 1,\forall j\hfill \\ {\sum }_{i=1}^{N_1}{\sum }_{j=1}^{N_2}{x}_{ijk}\ge 1,\forall k\hfill \\ {\sum }_{i=1}^{N_1}{\sum }_{j=1}^{N_2}{\sum }_{k=1}^{N_3}{x}_{ijk}=N\hfill \\ x_{ijk}\in \{0,1\},\forall i,j,k\hfill \end{array},$$

where N is the total number of implanted seeds; N₁, N₂, N₃ are the numbers of segmented seeds in images 1, 2, and 3, respectively; c_ijk is the cost of matching seeds i, j, and k from images 1, 2, and 3, respectively, and is a function of pose rotation $\mathit{\Phi }=({\varphi }_1,{\varphi }_2,{\varphi }_3)$ and translation t = (t₁, t₂, t₃); and x_ijk is a binary variable equal to 1 if seeds i, j, and k from images 1, 2, and 3, respectively, are matched or 0 otherwise. In other words, the algorithm finds the matching that minimizes an overall cost such that the following constraints are satisfied: (1) every segmented seed in each image is matched at least once, and (2) the total number of matches is equal to the total number of implanted seeds. The particular cost metric that is used is known as “reconstruction accuracy,” which is defined as the root mean squared distance between the backprojected lines and their symbolic intersection. While it would normally be expensive to solve this huge optimization problem, the algorithm greatly reduces computation time by exploiting the nature of this cost metric to prune numerous impossible solutions, and by converting this NP-hard binary integer program into a polynomial-time linear program.²⁶ Once this matching optimization problem is solved, reconstruction naturally follows by computing the symbolic intersection of the matched backprojected lines.

At this stage, although the optimization problem is solved, there may still be inaccurate seed matches due to pose errors. We further refine the reconstruction through automatic pose correction. The inspiration for this method comes from the fact that the 3D reconstructed seed cloud itself may serve as a model for refining the initial poses which were computed using only the fiducial markers. Automatic pose correction is similar to the previous pose estimation subfunction, but the projection error is now minimized over the reconstructed points rather than over the fiducial markers alone, as we have correspondences of each 3D coordinate ${\mathit{p}}_{\mathit{i}}^{\mathit{W}}$ to their respective 2D segmented coordinates ${\widehat{\mathit{p}}}_{\mathit{ij}}^{\mathit{I}}$ in each jth image. The ensuing poses may then be reused for reconstruction, resulting in iterations between seed matching and automatic pose correction. This makes APC-REDMAPS robust to pose errors, which is critical for our marker-based fiducial. We refer readers to Lee et al.²⁷ for more details of the algorithm.

II.E. Fluoroscopy-to-TRUS registration

The last step of the imaging pipeline is fluoroscopy-to-TRUS registration. The idea is to take the 3D seed coordinates computed from the fluoroscopic images and to position them properly in the TRUS volume for dosimetry. The algorithm thus inputs the 3D reconstructed seed coordinates and the acquired TRUS volume, and outputs a registered set of seed coordinates with respect to the TRUS coordinate system (see Fig. 5). The prostate contour outlined during planning is used as a volume of interest (VOI), but if it is unavailable, a VOI may be manually selected. We use an image-based point-to-volume registration method published by Dehghan et al.²⁸ that affinely registers the reconstructed seeds to the bright hyperechoic regions of the TRUS volume.

The algorithm completes the following steps. It begins by thresholding the TRUS volume to isolate the outlier hyperechoic regions of the TRUS volume which are likely to be seeds. Next, a morphological distance transform followed by a Gaussian blurring function is applied to provide an intensity gradient to guide optimization. Imposing realistic constraints on the parameters, the registration is then formulated as the following constrained optimization:

$$\begin{array}{c}\arg \underset{\mathit{\Phi },\mathbf{t},\lambda }{\max }S(\mathit{\Phi },\mathbf{t},\lambda )\hfill \\ \mathrm{s}.\mathrm{t}.{\mathit{\Phi }}_{\min }<\mathit{\Phi }<{\mathit{\Phi }}_{\max }\hfill \\ {\mathbf{t}}_{\min }<\mathbf{t}<{\mathbf{t}}_{\max }\hfill \\ {\lambda }_{\min }<\lambda <{\lambda }_{\max }\hfill \end{array},$$

where $\mathit{\Phi }=({\varphi }_1,{\varphi }_2,{\varphi }_3)$ and t = (t₁, t₂, t₃) are the registration rotation and translation, respectively, and λ is a registration scaling factor in the anterior–posterior direction (hence, an affine registration) to account for the prostate deformation caused by the TRUS probe pressure which is present in the TRUS volume but not in the fluoroscopy seed reconstruction. The cost metric, $S(\mathit{\Phi },\mathbf{t},\lambda )$, is defined as the summation of image intensity over cuboids of size Δx × Δy × Δz around each reconstructed seed after registration, and is computed as

$$\begin{array}{ccc}\hfill S(\mathit{\Phi },\mathbf{t},\lambda )& =& \sum _{i=1}^N\underset{-\frac{\Delta z}{2}}{\overset{\frac{\Delta z}{2}}{\int }}\underset{-\frac{\Delta y}{2}}{\overset{\frac{\Delta y}{2}}{\int }}\underset{-\frac{\Delta x}{2}}{\overset{\frac{\Delta x}{2}}{\int }}{I}_G\left(T(\mathit{\Phi },\mathbf{t},\lambda ;{\mathit{s}}_i)\right.\hfill \\ & & \left.+\left[\begin{array}{c}x\hfill \\ y\hfill \\ z\hfill \end{array}\right]\right)dxdydz,\hfill \end{array}$$

where I_G(x, y, z) is the processed and Gaussian-blurred TRUS volume, $T(\mathit{\Phi },\mathbf{t},\lambda ;{\mathit{s}}_i)$ is the affine transform of s_i which is the coordinate of seed i in the fluoroscopy coordinate system. The particular optimization used is a robust and efficient stochastic optimization method known as the covariance matrix adaptation-evolution strategy (CMA-ES).²⁹ The optimization is initialized by centering the reconstruction within the provided prostate contour or manual VOI. We refer readers to Dehghan et al.²⁸ for more details.

Combining these algorithms, we have an image-guidance system which localizes implanted seeds for dynamic dose calculation. A straightforward computation based on seed activity information and these registered seed coordinates results in our final desired dosimetry.

III. EXPERIMENTS AND RESULTS

III.A. Phantom study

The system was evaluated on ten phantom cases using an OEC 9800 C-arm (GE Healthcare, Milwaukee, WI) and a BK Pro Focus ultrasound scanner (BK Medical, Peabody, MA). Each phantom was composed of gelatin and implanted with inert Palladium-103 seeds (Theragenics, Buford, GA) using surgical needles. Transverse TRUS images and three fluoroscopic images were taken of the implanted seeds. The slice intervals and pixel sizes for the TRUS images are reported in Table I and each fluoroscopic image had a pixel size of 0.44 × 0.44 mm². The C-arm was calibrated for each phantom case, and the images were processed by our pipeline.

TABLE I.

Phantom overall results.

		TRUS volume		Overall error (mm), mean ± Std
Phantom	Number of seeds	Slice interval (mm)	Pixel size (mm2)	x	y	z	Overall
1	65	0.5	0.2000 × 0.2062	0.2 ± 0.2	0.7 ± 0.5	0.7 ± 0.6	0.7 ± 0.8
2	65	0.5	0.2000 × 0.2062	0.2 ± 0.2	0.5 ± 0.3	0.7 ± 0.6	0.7 ± 0.9
3	64	0.5	0.1948 × 0.1984	0.5 ± 0.3	0.5 ± 0.4	0.7 ± 0.5	0.7 ± 1.0
4	64	0.5	0.1948 × 0.1984	0.5 ± 0.3	0.5 ± 0.4	0.6 ± 0.5	0.6 ± 0.6
5	64	2.0	0.1948 × 0.1984	0.6 ± 0.4	0.7 ± 0.5	1.1 ± 0.8	1.1 ± 0.4
6	64	2.0	0.1948 × 0.1984	0.6 ± 0.4	0.7 ± 0.4	1.1 ± 0.8	1.1 ± 0.9
7	16	1.0	0.1834 × 0.1796	0.3 ± 0.3	0.7 ± 0.3	1.0 ± 0.5	1.0 ± 0.7
8	16	1.0	0.1834 × 0.1796	0.3 ± 0.2	0.9 ± 0.4	1.1 ± 0.5	1.1 ± 0.4
9	24	1.0	0.1834 × 0.1796	0.2 ± 0.2	1.0 ± 0.5	0.9 ± 0.7	0.9 ± 0.4
10	24	1.0	0.1834 × 0.1796	0.4 ± 0.2	0.5 ± 0.3	0.6 ± 0.5	0.6 ± 0.7
Overall				0.4 ± 0.3	0.6 ± 0.4	0.8 ± 0.7	1.3 ± 0.6

The overall results of the phantom cases are shown in Table I. To calculate overall error, we manually segmented seeds in the TRUS images. The seed locations computed by the proposed system using all three fluoroscopic images were compared to these manual segmentations. This resulted in an overall error of 1.3 mm with 0.4, 0.6, and 0.8 mm errors along the x, y, and z axes, respectively, where x is oriented right (left with respect to patient), y is oriented up (anterior with respect to patient), and z is oriented out of the image in this ultrasound coordinate system (inferior with respect to patient). The error along the y axis is generally larger than that in the x axis, which may be explained by the fact that the seeds in the TRUS volume often appear as hyperechoic streaks rather than spots, especially in phantom cases. These streaks point away from the TRUS probe and consequently tend to be more difficult to localize along the y axis than along the x axis. The error in the z axes is the greatest of the errors among all axes; this is explained by the fact that it is the dimension of poorest pixel resolution. Finally, an overall error of 1.3 mm is considered well within clinically acceptable limits, as it is reported that seed localization uncertainty of 2 mm results in less than 5% deviation of prostate D₉₀, i.e., the minimum dose received by 90% of the prostate.³⁰

III.B. Clinical study

The system was also evaluated on 37 patients with signed informed consent and under approval of the Institutional Review Board at the Johns Hopkins Hospital (Baltimore, MD) using an OEC 9800 C-arm (GE Healthcare, Milwaukee, WI) and a BK Pro Focus ultrasound scanner (BK Medical, Peabody, MA). Treatment planning was completed by the software known as VariSeed 8.0 (Varian, Palo Alto, CA), and Palladium-103 seeds (Theragenics, Buford, GA) were delivered into the prostate via needles and a Mick applicator (Mick Radio-Nuclear Instruments, Mount Vernon, NY). For this study, images were acquired after all seeds were implanted. Transverse TRUS images were acquired at 1 mm intervals except for two cases (patients 25 and 33) which had 2.5 mm intervals. For the first 24 patients, the TRUS images had pixel size of 0.1793 × 0.1793 mm², while those of the last 13 patients had pixel size of 0.1652 × 0.1652 mm². Although only three fluoroscopic images are required to run our system, a total of six images were systematically acquired at different poses for research purposes. Each fluoroscopic image had a pixel size of 0.44 × 0.44 mm². The total time for TRUS and fluoroscopy image acquisition was approximately 2 min. The C-arm was calibrated for each patient. Each step in the pipeline was tested producing the following results.

The results for seed segmentation are shown in Table II. Among 21 912 seeds and markers present in 222 images, the overall false negative rate was 1% and false positive rate was 5%. False negatives were defined as actual seeds or markers that were in the field of view but were either completely missed in the automatic segmentation or resulted in an incorrect reconstruction due to failed separation of slightly overlapping seeds, while false positives were defined as segmented coordinates that were not actually seeds or markers. All rates were averaged over all six images per patient and calculated with the actual number of seeds and markers as the denominator. The detected number of seeds and markers was also averaged over the six fluoroscopic images taken per patient. Note that it is possible to detect a fewer number of seeds and markers than are actually present but still have 0% false negative and false positive rates (e.g., patient 34) due to overlapping seeds. Also, ten of these cases, identified in Table II, had implants or other radio-opaque objects (e.g., TRUS probe or radio-opaque cloth) in the field of view and therefore generated a large number of false positives. If these ten patients were excluded, the overall false positive rate would reduce to 2%.

TABLE II.

Seed segmentation and fiducial detection results. Bolded patients had other radio-opaque objects in the field of view; overall rates in parentheses were calculated with grayed patients excluded.

	Actual Number	Average detected	False	False	Fiducial
	of seeds	number of seeds	negative	positive	detection
Patient	and markers	and markers	rate (%)	rate (%)	rate (%)
1	112	108	1	1	100
2	87	85	1	3	83
3	70	70	0	4	100
4	86	83	2	2	100
5	84	88	2	10	100
6	66	64	2	4	100
7	87	81	2	1	96
8	75	73	1	2	100
9	110	103	5	2	100
10	91	88	1	1	100
11	102	97	1	2	100
12	87	98	0	16	100
13	121	116	1	2	100
14	101	105	0	6	100
15	119	129	1	13	100
16	114	116	1	8	91
17	98	114	1	22	100
18	123	119	0	1	100
19	101	103	1	6	100
20	115	120	2	13	100
21	83	90	1	17	96
22	106	100	2	3	96
23	106	103	0	1	100
24	101	95	1	1	100
25	89	86	1	1	96
26	92	94	2	9	100
27	110	108	0	4	100
28	81	78	3	3	96
29	113	113	0	6	93
30	89	86	1	1	83
31	107	102	1	3	100
32	103	99	1	1	100
33	102	103	1	4	100
34	108	104	0	0	100
35	104	100	1	3	100
36	112	107	1	4	96
37	97	97	1	4	100
Overall rate			1 (1)	5 (2)	98 (98)

The results for fiducial detection with pose estimation are also found in Table II. While overall fiducial detection rate is 98%, it is 100% for most cases. This rate was averaged over all six images per patient after correcting any errors in seed segmentation and calculated with the total number of markers as the denominator. Thus, if a partial detection occurred with eight of the nine markers detected, the fiducial detection rate would be 89%.

The results for seed matching with reconstruction are shown in Table III. The six fluoroscopic images captured per patient were partitioned by pose into two sets of three images each, thus forming two reconstructions per patient. There are no ground truth seed positions for these clinical cases, so instead we used reconstructions from five or all six images as our ground truth. This resulted in an overall mean reconstruction error of 0.4 mm, close to the 0.5 mm mean reconstruction error reported by Lee et al.²⁷ Moreover, automatic pose correction generally resulted in less than 2° rotational correction and 5 mm translational correction. It therefore shows that the marker-based fiducial does not alter the reconstruction accuracy of APC-REDMAPS.

TABLE III.

Reconstruction, registration, and dose calculation results. D₉₀ is the minimum dose received by 90% of the prostate volume given in percentage of the prescribed dose, and V₁₀₀ is the percentage of the prostate volume that received at least 100% of the prescribed dose.

						Prostate dose
	Reconstruction error (mm),	Registration error (mm),				metrics
	mean ± Std	mean ± Std				D90		V100
Patient	Overall	x	y	z	Overall	US/FL (%)	MR/CT (%)	US/FL (%)	MR/CT (%)
1	0.8 ± 0.3	0.4 ± 0.5	0.4 ± 0.4	1.2 ± 0.9	1.6 ± 0.8	129	123	99.0	99.5
2	0.4 ± 0.4	0.3 ± 0.2	0.2 ± 0.3	0.7 ± 1.0	0.9 ± 0.9	125	115	94.8	95.1
3	0.3 ± 0.2	0.4 ± 0.4	0.9 ± 0.8	0.9 ± 0.9	1.6 ± 1.0	114	115	93.0	95.1
4	0.4 ± 0.2	0.3 ± 0.3	0.7 ± 0.3	0.8 ± 0.7	1.2 ± 0.6	153	130	98.9	98.0
5	0.6 ± 0.4	0.3 ± 0.3	0.5 ± 0.4	0.5 ± 0.3	0.9 ± 0.4	131	126	97.1	98.6
6	0.6 ± 0.5	0.6 ± 0.9	0.8 ± 0.7	0.7 ± 0.3	1.4 ± 0.9
7	0.6 ± 0.3	0.3 ± 0.4	0.4 ± 0.3	0.9 ± 0.7	1.1 ± 0.7	132	100	98.3	90.1
8	0.5 ± 0.3	0.5 ± 0.4	0.5 ± 0.4	0.6 ± 0.3	1.1 ± 0.4	136	134	99.8	99.0
9	1.2 ± 1.3	0.4 ± 0.3	0.5 ± 0.4	0.9 ± 0.6	1.2 ± 0.4	125	118	97.4	97.6
10	0.5 ± 0.5	0.2 ± 0.2	0.5 ± 0.5	0.9 ± 0.7	1.2 ± 0.7	115	115	97.0	99.0
11	0.4 ± 0.3	0.4 ± 0.3	0.5 ± 0.5	1.1 ± 0.7	1.4 ± 0.6	123	125	94.3	98.5
12	0.4 ± 0.2	0.4 ± 0.4	0.5 ± 0.4	0.8 ± 0.6	1.2 ± 0.5	154	146	99.4	99.8
13	0.3 ± 0.2	0.4 ± 0.5	0.7 ± 0.6	0.8 ± 0.7	1.4 ± 0.5	131	118	99.3	97.3
14	0.3 ± 0.2	0.3 ± 0.3	0.5 ± 0.2	0.8 ± 0.7	1.1 ± 0.6	113	109	95.2	93.2
15	0.9 ± 0.6	0.2 ± 0.2	0.6 ± 0.5	1.0 ± 0.7	1.3 ± 0.6	108	106	93.2	93.8
16	0.3 ± 0.4	0.2 ± 0.2	0.4 ± 0.3	0.8 ± 0.7	1.1 ± 0.6	143	146	99.5	98.6
17	0.4 ± 0.4	0.2 ± 0.1	0.4 ± 0.3	0.9 ± 0.8	1.2 ± 0.7	140	151	98.9	99.6
18	0.5 ± 0.5	0.4 ± 0.5	0.7 ± 0.6	0.8 ± 0.5	1.4 ± 0.5	169	146	98.6	99.2
19	0.4 ± 0.3	0.2 ± 0.1	0.4 ± 0.3	0.5 ± 0.3	0.8 ± 0.3	130	132	97.8	98.7
20	0.4 ± 0.3	0.5 ± 0.5	0.2 ± 0.2	0.9 ± 0.5	1.2 ± 0.5	117	124	93.6	98.5
21	0.4 ± 0.3	0.3 ± 0.2	0.8 ± 0.6	1.0 ± 0.6	1.4 ± 0.6	137	124	99.3	97.6
22	0.2 ± 0.2	0.1 ± 0.1	0.7 ± 0.8	1.0 ± 0.5	1.3 ± 0.8	132	139	97.0	99.5
23	0.5 ± 0.7	0.3 ± 0.2	0.9 ± 0.5	0.8 ± 0.6	1.3 ± 0.7	165	144	96.8	99.3
24	0.4 ± 0.3	0.4 ± 0.4	0.5 ± 0.6	1.3 ± 1.0	1.7 ± 0.8	115	113	95.3	96.1
25	0.3 ± 0.7	0.4 ± 0.4	0.5 ± 0.4	1.4 ± 1.3	1.7 ± 1.2
26	0.3 ± 0.2	0.2 ± 0.2	0.6 ± 0.6	0.9 ± 0.6	1.2 ± 0.5	114	110	96.8	96.9
27	0.3 ± 0.4	0.5 ± 0.4	0.6 ± 0.4	0.7 ± 0.5	1.1 ± 0.5	125	107	95.4	92.0
28	0.3 ± 0.2	0.1 ± 0.0	0.4 ± 0.3	0.9 ± 0.6	1.0 ± 0.6	127	118	98.5	95.3
29	0.5 ± 0.4	0.4 ± 0.4	0.5 ± 0.6	0.9 ± 0.8	1.2 ± 0.9	136	129	99.6	98.5
30	0.3 ± 0.2	0.5 ± 0.3	0.6 ± 0.6	1.0 ± 0.7	1.4 ± 0.6	124	106	96.1	93.9
31	0.5 ± 0.3	0.3 ± 0.4	0.4 ± 0.4	1.0 ± 1.1	1.3 ± 1.0
32	0.3 ± 0.2	0.5 ± 0.6	0.4 ± 0.3	0.8 ± 0.7	1.2 ± 0.7	119	130	94.1	98.4
33	0.2 ± 0.2	0.6 ± 0.6	0.6 ± 0.4	1.2 ± 0.7	1.7 ± 0.7
34	0.2 ± 0.2	0.4 ± 0.4	0.4 ± 0.4	0.5 ± 0.3	0.9 ± 0.3	125	123	96.4	94.9
35	0.3 ± 0.2	0.3 ± 0.2	0.4 ± 0.4	1.0 ± 0.7	1.3 ± 0.6	116	119	93.9	96.4
36	0.3 ± 0.2	0.3 ± 0.3	0.4 ± 0.3	0.5 ± 0.6	0.9 ± 0.5
37	0.2 ± 0.2	0.6 ± 0.3	0.7 ± 0.6	0.8 ± 0.6	1.4 ± 0.5	120	124	94.6	96.9
Overall	0.4 ± 0.5	0.4 ± 0.4	0.5 ± 0.5	0.9 ± 0.7	1.3 ± 0.7

The results for fluoroscopy-to-TRUS registration are also found in Table III. While reconstructions with three images would be used in a typical workflow, these results show registration errors from reconstructions with five or six images so the registration algorithm may be evaluated separately from any errors made in previous steps, as has been done for all the other clinical results presented thus far. However, since the difference between these reconstructions is small (0.4 mm on average as shown in Table III), we expect registration errors would not be much greater in a typical workflow. Like reconstruction, there are no ground truth seed positions for these clinical cases, so instead we manually selected seed-like hyperechoic spots throughout the entire prostate, carefully examined and compared to the implantation plan to confirm they were true seeds. Unlike phantom images, manual segmentation of all implanted seeds in patient TRUS images was challenging. Therefore, we selected ten seeds per patient in this way. This resulted in an overall mean registration error of 1.3 mm with 0.4, 0.5, and 0.9 mm errors along the x, y, and z axes, respectively. This agrees closely to the overall mean registration error of 1.5 mm reported by Dehghan et al.²⁸ with 0.5, 0.5, and 1.1 mm errors along the x, y, and z axes, respectively. Overall, this demonstrates that the seed reconstruction using the marker-based fiducial does not affect the performance of the registration algorithm.

Finally, a comparison of prostate dose metrics is also included in Table III to validate our results. Two commonly used dose metrics, D₉₀ (the minimum dose received by 90% of the prostate volume, given in percentage of the prescribed dose) and V₁₀₀ (the percentage of the prostate volume that received at least 100% of the prescribed dose) were calculated using our intraoperative ultrasound-fluoroscopy method (US/FL) and an independent postoperative MRI-CT method (MR/CT). The MRI and CT image sets were acquired a day after seed implantation, and the two volumes were rigidly registered. Prostate contours were delineated on the CT images with the aid of fused MRI for the MRI-CT method because the outline of the prostate is more visible in MRI than in CT alone. For our US/FL method, although it would be preferable to use contours from postoperative ultrasound, the contours were taken instead from preoperative ultrasound because (1) the outline of the prostate is more visible and easily delineated without implanted seeds, and (2) it is more realistic to use in the clinical setting since it is unlikely to be practical for the physician to recontour after every ultrasound image acquisition. Some patients were excluded from this comparison (patients 6, 25, 31, 33, and 36) due to missing MRI data or because their ultrasound images were taken too coarsely at greater than 1 mm intervals. While there are imperfections in this comparison due to prostate edema and deformation, the prostate dose metrics from both methods are in general agreement with each other, with an average percent difference of 7% for D₉₀ and 2% for V₁₀₀. We therefore see that intraoperative dosimetry calculated with our US/FL method produces similar results to postoperative dosimetry using MR/CT.

IV. DISCUSSION

Our fiducial in some ways is similar to an idea proposed by Todor et al.,¹⁴ who use a modified TRUS probe unit embedded with a set of five noncoplanar radio-opaque markers that can be identified in both fluoroscopic and ultrasound coordinate systems. The known positions of the markers may then be used to reconstruct the 3D positions of the seeds and to register fluoroscopy to ultrasound. However, there are several key differences that should be noted. First, there is a difference for the purpose of the markers, as Todor et al. intend to resolve both reconstruction and registration problems with the markers while our fiducial focuses solely on pose estimation. With such modularization, we allow ourselves the flexibility to use the best methods to address each specific problem rather than deal with potential tradeoffs in attempting to solve multiple problems simultaneously. Second, Todor et al. embed their markers to a modified TRUS probe while we attach our markers to a separate radiolucent cylinder. This is an important difference as the setup proposed by Todor et al. is unfriendly both from the standpoint of workflow and from that of automatic seed segmentation, since the probe would need to be tampered with and its radio-opaqueness would interfere with segmentation algorithms. Finally, the main difference between our fiducial and theirs is the fact that our markers appear like seeds under fluoroscopy. This is an essential feature that allows the rest of our system to work since we may then treat markers and seeds alike under segmentation and reconstruction.

All four individual steps in our pipeline perform similarly or better to recent competing algorithms. For seed segmentation, the 1% false negative rate and 2% false positive rate is a slight improvement to the 1% false negative rate and 3% false positive rate resulting from our own previously published method.²¹ For fiducial detection, although there are no other known algorithms addressing the same fiducial detection problem we encounter, an imperfect comparison may be made between our 98% detection rate and the reported 88% clinical detection rate of an FTRAC detection algorithm.²¹ For reconstruction, the 0.4 mm mean error of APC-REDMAPS outperforms the 0.6 mm error reported for MARSHAL (Ref. 23) that is utilized in the system presented by Jain et al.¹⁸ Finally, for registration, our mean error of 1.3 mm is much better than the 2.9 mm reported for another recent fluoroscopy-to-TRUS registration algorithm.³¹

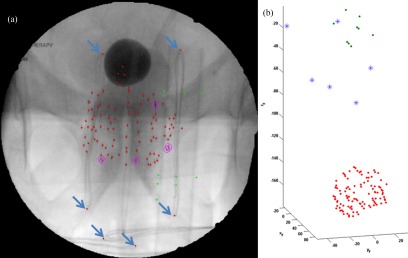
As mentioned previously, there are ten cases when our seed segmentation algorithm performs poorly due to radio-opaque implants or objects in the field of view. In these cases, it is necessary to rerun the segmentation on a user-selected ROI and manually correct the segmentation result. However, it is interesting to note that if we manually segment these undesired radio-opaque objects, we may use our system in an unconventional way to determine the location of these objects. Figure 6 shows an example where a surgical cloth with embedded radio-opaque loops was incidentally included in the fluoroscopy field of view. We manually segmented the ends of the individual loops (see arrows) and reconstructed them. Reconstruction confirmed that the loops were located far from the implanted seed cloud, indicating that they were indeed not part of an object implanted in the patient but actually within the cloth lying on the patient's abdomen. Although not part of the original intent of our system, this suggests that our system may be applied to localize objects besides seeds in applications beyond the scope of PPB.

FIG. 6.

Reconstruction of extraneous objects. (a) Fluoroscopic image with ends of radio-opaque loops segmented (see arrows). (b) Reconstruction showing loops (stars) between seeds (dots below) and fiducial (dots above).

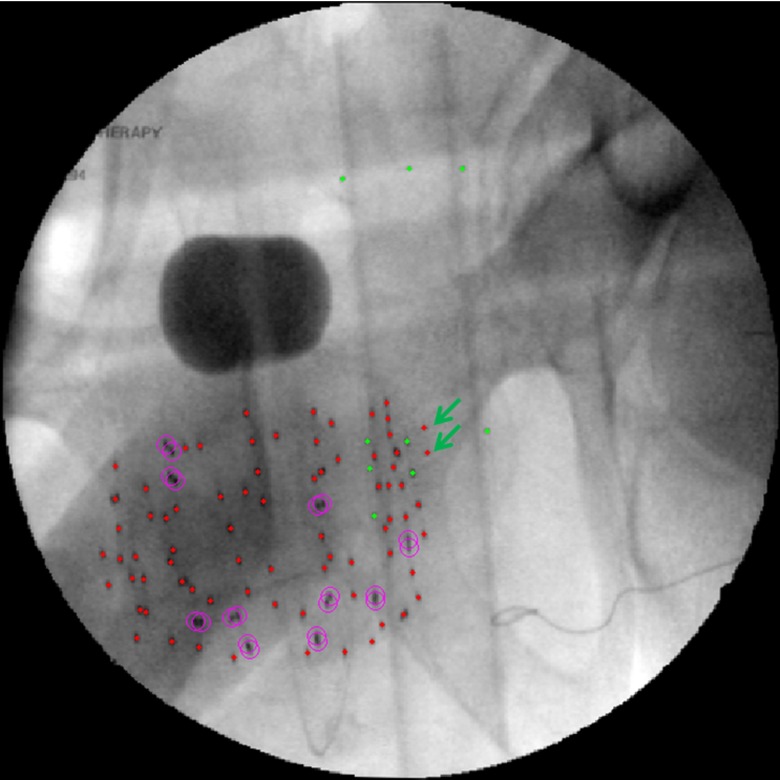
While our fiducial detection algorithm detects the fiducial perfectly most of the time, in the instances when it is imperfect, the algorithm at least detects some of the markers in all our patient cases. The most common partial detection occurs when the lower portion of the fiducial overlaps with the seed cloud, resulting in the misdetection of two fiducial markers (see Fig. 7). This suggests that a fiducial configuration with the markers more separated may result in higher detection rates, although the current configuration is sufficient for our purposes.

FIG. 7.

Misdetection of two fiducial markers (see arrows).

The system as a whole also has the capability of detecting cold spots as shown in Fig. 8. This highlights the utility of the system, as cold spots may then be addressed immediately in the OR rather than requiring the patient to return for additional therapy after being discharged. Note, however, that the treatment plans for these 37 patients were not modified dynamically using our system since our goal was to first obtain the data to validate our algorithms. A clinical trial is pending to use the system intraoperatively to modify the treatment plan for dynamic dose calculation.

FIG. 8.

Intraoperative dosimetry result showing a cold spot. (a) TRUS image is overlaid with the prostate contour and the 100% isodose level (bright line) computed from the registered seed reconstruction (dots). (b) 3D rendering of the same prostate and 100% isodose level; cold spot is evident at the anterior base of the prostate.

Finally, the total computation time for all image processing steps was approximately 1 min. On a computer with a 2.33 GHz dual-core processor, both seed segmentation and fiducial detection with pose estimation on average took approximately 2 s. APC-REDMAPS reconstruction with three fluoroscopic images and registration of the reconstructed seeds to ultrasound on average required 6 and 30 s, respectively. While this total computation time is already clinically acceptable, additional time may be saved by beginning the pipeline immediately after the first fluoroscopic image is taken so some processing could occur while additional images are acquired.

V. CONCLUSION

In this paper, we presented the full workflow of the first practical image-guidance system for prostate brachytherapy dynamic dose calculation. With the help of a marker-based fiducial and four robust image processing algorithms, implanted seed locations in the prostate are accurately and quickly computed with unprecedented convenience. While there are alternative systems for dynamic dose calculation under development, none has been practically realizable for general clinical use. On the other hand, our system is cost-effective, simple to use, and is expected to ultimately lead to improved treatment outcomes for prostate cancer patients.