Abstract
Gaining a deeper understanding of enzyme catalysis is of great practical and fundamental importance. Over the years it has become clear that despite advances made in experimental mutational studies, a quantitative understanding of enzyme catalysis will not be possible without the use of computer modeling approaches. While we believe that electrostatic preorganization is by far the most important catalytic factor, convincing the wider scientific community of this may require the demonstration of effective rational enzyme design. Here we make the point that the main current advances in enzyme design are basically advances in directed evolution and that computer aided enzyme design must involve approaches that can reproduce catalysis in well-defined test cases. Such an approach is provided by the empirical valence bond method.
I. Introduction
Many life processes are controlled by the action of enzymes and thus a deeper understanding of enzyme catalysis is of great practical and fundamental importance. Such an understanding is also important for refining various biotechnological processes. Overall, the nature of enzyme catalysis has been the subject of intensive studies for more than a century (e.g., [1]) and the emergence of X-ray structural determination of enzymes [2] has offered the chance to explore a structure/catalysis relationship. Over the years it has become clear that despite advances in experimental mutational studies (e.g., [3,4]), a quantitative understanding will not be possible without computer modeling approaches. In fact, quantitative computational approaches have emerged (e.g., [5,6]) and the idea that the catalysis is mainly due to electrostatic preorganization [7] has been illustrated in many cases (see [8]). Nevertheless, many workers still overlook what was found in computational studies of the origin of catalysis and some tend to accept ideas like dynamics (see below) and other exotic factors as key contributions. This is problematic since none of these ideas has been shown to contribute to catalysis by consistent computational studies or by any direct experiment. Perhaps one of the best ways to establish the importance of quantifying different catalytic factors is to be able to guide rational design and refinement of enzymes. The challenges and the advances on this front will be among the main subjects of our review.
We will start with what has been learnt from consistent computational studies about the origin of enzyme catalysis. We will then consider the current state of computer aided enzyme design and the fact that most of the advances are still done by directed evolution. Finally, we will point out that rational design should be based on the ability to predict the actual catalytic power of different design constructs.
II. Modeling Enzymatic Reactions in Well-Defined Active Sites
Before moving to the subject of enzyme design it is important to review the current state of modeling enzymatic reactions. The first attempt to model an enzymatic reaction consistently [9] introduced the QM/MM method and explored the electrostatic contribution in the catalytic reaction of lysozyme. Subsequently, it became clear that molecular orbital (MO) QM/MM methods could not give reliable results with the computational resources available in the 80s and 90s, due to the difficulty of obtaining any reasonable sampling. This led to the development of the empirical valence bond (EVB) method, with its focus on the difference between the enzyme and solution reactions that allowed for reliable free energy calculations. The main subsequent advances on the “technical” front have involved the use of ab initio [10] QM/MM (QM(ai)/MM) with reliable sampling. The slow progress in this direction reflected the insufficient realization of the fact that QM(ai)/MM calculations without sampling and with only energy minimization are likely to lead to arbitrary results. A further problem has been the assumption that reliable free energy calculations with semiempirical models or low level DFT can be used to obtain reliable results. This problem could have been minimized significantly by calibrating the semiempirical calculations on reference solution reactions as is done in the EVB. Fortunately, the ability to obtain reliable QM(ai)/MM results (at least in solution) has been greatly advanced by the use of the EVB as a reference potential for the QM(ai)/MM calculations. This reference potential idea has been advanced by us since 1992 (see discussion in [10]) and is now called the paradynamics (PD) approach [11]. However, although the PD philosophy is now adopted by several groups (see [10]) and is more effective than the alternative (elegant and seemingly automatic) metadynamics (MTD) approach [12], it has not found widespread use. The problem here is not so much in the use of the MTD but in the fact that some of the users seem to believe that invoking the name MTD is equal to obtaining reliable results in solution and enzymes. The situation is particularly challenging when one tries to use the MTD or even the PD in enzymes. Here, even now, it is still not clear that fully converging QM(ai)/MM free energies can be obtained in highly charged active sites. The best current solution seems to be to perform the most careful QM(ai)/MM calculations both with PMF and PD on the reference solution reaction, to calibrate the EVB surface on the solution surface and then to move to the protein with the EVB surface (see [13], for example).
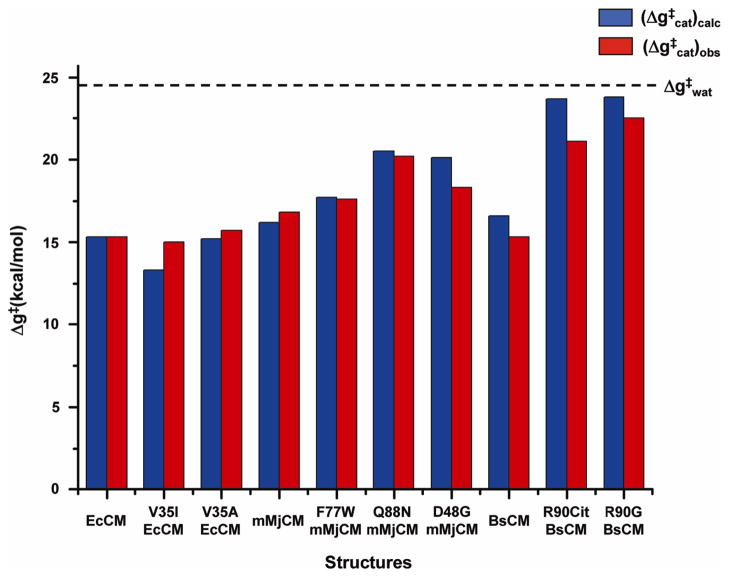
Since this work deals mainly with calculations of mutational effects, we present in Fig. 1 the results of an EVB study of the catalytic contributions of various residues in chorismate mutase CM [14,15]. The figure demonstrates that the EVB model can serve as an effective and accurate tool in the final stages of computer aided enzyme design. Other approaches for fast screening were found to be less accurate and mainly useful for the qualitative screening of ionized residues [15,16].
Figure 1.
Comparing the calculated (in blue) and observed (in red) activation free energies for the indicated systems. The dashed line designates the activation free energy of the reaction in aqueous solution (taken from [15]).
III. Key Catalytic Concepts
Extensive computer simulations of different enzymatic reactions have repeatedly indicated that the main catalytic factor is associated with electrostatic stabilization of the transition state [8]. It was concluded [7,8] that the source of the TS stabilization is the reduction in the reorganization energy upon moving from solution to the protein (with its polar preorganization [7]). This idea has been also supported by studies of other research groups (e.g., [6]).
Although the preorganization idea has been accepted by some, other catalytic options continue to be propagated. These include the idea of ground state destabilization (e.g., [17,18]) and the idea that enzymes work by dynamical effects, tunneling and compression (e.g., [19]). Unfortunately, the corresponding catalytic effects have been found to be very small or non-existent by studies that actually examined each of them in a quantitative way (e.g., see [20] and below). Here, we do not have the space to repeat the details of the systematic studies that also included major efforts and insistence on defining the relevant issues. However, it may be very instructive to comment on the currently most popular proposal, namely the dynamical proposal. This proposal implies that somehow special conformational motions of the protein help to reduce the chemical barrier by dynamical effects (effects that do not reflect the Boltzmann probability, e.g. see [21–26] and the discussion in [27]). However, we established repeatedly that dynamical contributions to catalysis are small [20,28] and that the inertial effect of the conformational motion is dissipated before it can be transferred to the chemical direction [8]. Significantly, we were able to explore the millisecond time range [29] and to show that dynamical effects do not contribute to catalysis in one of the popular model systems (namely adenylate kinase (ADK)).
A high profile work [30] that was written after our analysis of ADK tried to establish the dynamical proposal by freezing conformational motions in dihydrofolate reductase (DHFR), and argued that the reduced catalysis cannot reflect reduction in preorganization, but rather dynamical effects. However our subsequent EVB work [31] has clearly established that none of the structural observations of ref. [30] could assess the reorganization effects (this can only be done by computation), and has shown that all the observed barrier increases can be reproduced quantitatively by the increase in activation free energy. Interestingly, subsequent theoretical works [32,33] reached the same conclusions as those established in our study.
A similar problem has been associated with the idea of quantum tunneling and other nuclear quantum mechanical (NQM) effects in enzyme catalysis (e.g., [34]). Here it is useful to point out that using our quantized classical path (QCP) approach [35,36], we demonstrated that the corresponding NQM contributions are similar in the protein and in solution [28,37]. Furthermore, the original tunneling idea postulated that compression makes the barrier narrower, increases tunneling and accelerates reactions. However (see [38]), we have demonstrated that in all the proton and hydrogen transfer reactions the compression leads to a reduction and disappearance of the barrier and that the tunneling actually increases upon increase in donor –acceptor distance. Strangely, none of the supporters of the tunneling/compression idea has dealt with our clear analysis and argument.
The difficulty in focusing on or accepting the electrostatic preorganization idea can be demonstrated by studies of the binding of a series of phenolate transition states (TSAs) to ketosteroid isomerase (KSI), which found a small change in the binding energy upon significant change in charge delocalization of the TSAs [39]. This finding was taken as a proof that electrostatic effects do not contribute to the catalytic power of KSI in a major way. However, our systematic analysis [40] of the relationship between the binding of the TSAs and the chemical catalysis by KSI, reproduced both the very small electrostatic contribution to the binding of the TSAs and the very large contribution to the binding of the actual TS. It was found that the electrostatic preorganization contributions to the binding of the enolate intermediate of KSI (and the TS) are much larger than the corresponding effect on the binding of the TSAs. Subsequent challenges (e.g., [41]) to our findings were resolved in [42]. It is encouraging to note that some of those who challenged the preorganization idea in KSI are now confirming it [43].
Overall we believe that only computer simulations can resolve the above controversies and that any proposal must come with a qualitative estimate of the magnitude of the given effect.
IV. Computer Aided Enzyme Design
In view of the above discussion one can argue that enzyme design should be based on the ability to predict the expected catalytic effect. As a start we point out that the attempts to use enzyme engineering to explore enzyme catalysis date back to the early eighties (e.g., [3,44]). These studies were followed by early computational studies with reasonable reliability [45,46] and with subsequent studies of mutational effects (e.g., [46]). Recent years witnessed major new advances in enzyme design, both in attempts to change the activity of existing enzymes and to create new enzymes (e.g., [4,47–60]). However, most of the recent attempts at using computational approaches in enzyme design have not involved approaches that can reproduce the relevant activation barriers, even in cases where the structure of the enzyme substrate complex is known. However, it is instructive to consider the current state of the field.
IV.1 Attempts at designing Kemp eliminases as a general example
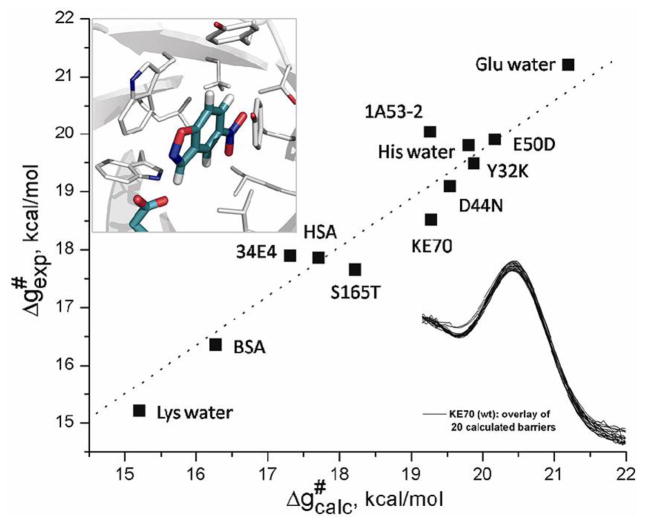
One of the most visible attempts at enzyme design has been the design of Kemp eliminases (e.g., [61]). Here we started by noting that the actual catalytic effect relative to the correct reference reaction (namely the reaction in a solvent cage) is actually very small [16,62]. We then reproduced the observed catalytic effect [16,62], while realizing that this system is not the best candidate for demonstrating effective catalysis, since the change in the residual charges upon moving from the RS to the TS is relatively small, thus making it hard to exploit preorganization effects. Nevertheless, we explored the origin of the small but meaningful catalytic improvement obtained by directed evolution experiments (e.g., [55,63]). It was found that the directed evolution used the simple and not sophisticated trick of destabilizing the charges of the reactant state (ground state destabilization) that is not used by any of the enzymes studied by us that have been refined by real evolution. We also examined the catalytic effect of changing the proton acceptor in Kemp eliminase and reproduced the corresponding observed LFER [16] (see Fig. 2).
Figure 2.
Calculated and observed activation barriers for the different Kemp eliminases studied in our works [16,62].
It is useful to point out that other attempts to explore and refine the Kemp eliminase by computational approaches have not reached a quantitative level. This point is obvious when one considers the gas phase models that were used for the initial screening in some cases (e.g., [61]). Similarly, MM simulations [64] can tell us about the optimal donor/acceptor geometries but are unlikely to be able to predict the catalytic trends in properly oriented systems. Furthermore, even semiempirical MO-QM/MM studies with a fixed main chain [65] that perform nicely in exploring the effect of changing the distance between the donor and acceptor (i.e. the Glu to Asp mutation [66]), could not reproduce the effect of changing the environment (which occurs in directed evolution experiments and is usually responsible for the catalytic activity). Alternatively, ref. [64] attempted to use the ONIOM truncated protein model but obtained relatively poor agreement (with a spread of about 12 kcal mol−1 for experimental deviations of 2 kcal mol−1). This work implies that a predictive power requires a very high level QM method. However, predictive approaches like the EVB are not interested in predicting the absolute QM energy of the substrate since what counts is the change in this energy upon moving from water to the protein active site.
IV.2 Phosphate triester and lactone as an example of promiscuity
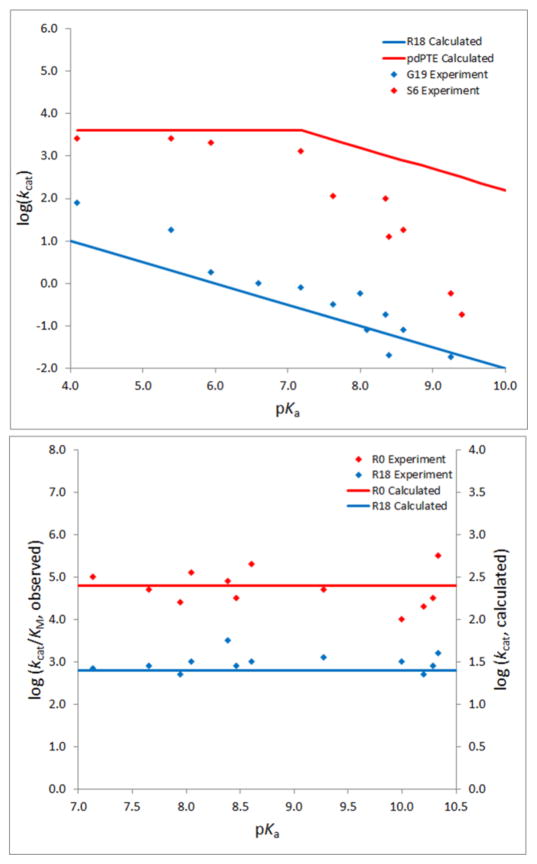
Considering the fact that Kemp eliminase is not the enzyme where one can best demonstrate the advantage of quantitative enzyme design, it is useful to explore systems with large catalytic effects, where we have large changes in charges during the formation of the TS. A promising direction is provided by considering the evolution from phosphotriesterase (with a paraoxon substrate) to arylesterase (with a 2-naphthylhexanoate substrate [67]). The observed trend presents a functional tradeoff, which seems to be a general phenomenon [68–71]. In exploring the above trend we examined a strategy of evaluating the catalytic effect for a whole set of different mutants for three possible mechanisms (MJL Mills et al., unpublished), where the first involves an attack from a −OH nucleophile that is situated between the two Zn ions, the second involves an attack by a −OH nucleophile that is bound to one Zn ion, and the third involves a proton transfer from the attacking −OH to an Asp residue that ligates one of the Zn ions. It was found that the second mechanism produced by far the best results and thus should allow us to make useful predictions.
An important “hint” that emerged from our study was the finding that we can reproduce the observed LFER by using a three state EVB model where the rate determining barrier differs between the phosphotriesterases and arylesterases. This finding indicates that the combination of experimental LFER studies with computational modeling can be a very useful guide in enzyme design.
IV.3 Enantioselectivity
Another important aspect of the design front is the issue of controlling the enantioselectivity of enzyme active sites (e.g., see [49,72–74]). Our studies in this direction focused on the ability to use the EVB in an analysis that considers the protein relaxation consistently. The first benchmark focused on the reproduction of the experimentally observed enantioselectivity (E) of Candida antarctica lipase A (CALA) [54] and succeeded to obtain reasonable results for both the overall E and the contribution to E from kcat. In particular, we have been successful in direct mutations from R to S [75]. More recently [76] we succeeded to reproduce the effect of large steric effects on the selectivity of CALB [77], a challenge that has not been met by other approaches. Furthermore, the combination of the EVB with our restraint release approach [78] reproduced the entropic contribution to selectivity.
Efforts in studies of enantioselectivity by others (e.g., [79,80]) are also instructive.
V. Other Systems
Recent advances in design, including directed evolution studies [52] of carbonic anhydrase II (CA II), succeeded to generate a modest increase in the esterase activity. Another advance has been reported by Pecoraro and coworkers [81], who constructed an artificial metalloprotein on the skeleton of three helix bundles with two metal binding sites where one has a similar first coordination sphere to that of CA II. This system provides an excellent opportunity to compare CA to a designer enzyme and to determine what the crucial differences are. A recent study [54] redesigned a mononuclear zinc enzyme in adenosine deaminase as a template for the catalysis of organophosphate. Subsequent directed evolution steps led to a very large increase of kcat (relative to the original design).
Finally, it might be useful to comment on the long ongoing attempt to design non-biological artificial catalysts (e.g., [82,83]). A part of this effort has suffered from the fact that the synthetic community has not been familiar with the true catalytic effects such as the preorganization effect (see discussion in [84]). Here, as in the case of enzyme catalysis, we do not see a substitute to serious computer modeling of the origin of the catalytic effect. Among the very few examples we like to mention a study of cyclodextrin catalysis [85] and a recent study [84] that have elucidated the electrostatic origin of the catalytic action of the supramolecular host of ref. [86].
VI. Concluding Remarks
This work discussed the current state of modeling enzyme catalysis and computer aided enzyme design. Overall, we believe that the main effect is polar preorganization and that the difficulties in appreciating this issue are based on insufficient familiarity with physical chemistry concepts and the slow realization of the fact that consistent computational results are the only way to identify the origin of enzyme catalysis. As much as enzyme design is concerned, it seems to us that many people do not see the difference between approaches that can be used as predictive tools and approaches that cannot even reproduce the catalytic effects in well-defined active sites. Here it is important to emphasize that in contrast to statements [63] such as “More effective designs should also consider the computation of substrate floppiness, of pKa values of key residues, and of water molecules”, we and others have used such approaches for many years and of course have also used them in enzyme design studies (e.g., [62]). Of course, it remains to be seen whether consistent calculations can guide the design of effective new enzymes. On the other hand, we believe that we can exploit our ability to predict reliably long range electrostatic contributions to catalysis and stability and to systematically and iteratively refine the catalytic activity of designer enzymes [62]. In this case, however, we cannot obtain enormous effect from distant residues.
At present, most (if not all) of the successful advances in enzyme design have been due to directed evolution rather than by computational guidance. Thus, in addition to the obvious need to improve the computational strategies, it would be interesting to use computational approaches to reproduce, analyze and guide the sequence “moves” of directed evolution experiments.
In concluding this review we would like to point out that despite the non-impressive current state of computer aided enzyme design, there is no doubt that the future must be quite promising. That is, in view of the rapid increase in computer power and the gradual realization that enzyme design must involve reliable modeling of the chemical step, it is very likely that designer enzymes will eventually reach very significant catalytic effects.
Figure 3.
The calculated and observed LFERs for phosphotriesters and arylesters.
Highlights.
The origin of enzyme catalysis can only be determined by computational approaches.
Enzyme catalysis is due to preorganization, and not to other exotic factors.
Computer aided enzyme design must be able to produce known catalytic effects.
The EVB model allows one to produce the trend of directed evolution.
At present the main advances in enzyme design are due to directed evolution.
Acknowledgments
This work was supported by grants from the National Institutes of Health (GM24491), National Science Foundation (MCB- 243719) and the National Cancer Institute (1U19CA105010).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Maria P. Frushicheva, Email: mpfrush@mit.edu.
Matthew J. L. Mills, Email: millsmj@usc.edu.
Patrick Schopf, Email: pschopf@usc.edu.
Manoj K. Singh, Email: manojsin@usc.edu.
Bibliography
- 1.Buchner E. Nobelprize.org, editor. Nobel Lecture: Cell-Free Fermentation. Nobel Media AB 2013; 1907. [Google Scholar]
- 2.Phillips DC. Hen Egg-White Lysozyme Molecule. Proc Natl Acad Sci U S A. 1967;57:484. doi: 10.1098/rspb.1967.0034. [DOI] [PubMed] [Google Scholar]
- 3.Fersht A. Structure and mechanism in protein science : a guide to enzyme catalysis and protein folding. New York: W.H. Freeman; 1999. [Google Scholar]
- 4.Hilvert D. Critical Analysis of Antibody Catalysis. Annual Review of Biochemistry. 2000;69:751–793. doi: 10.1146/annurev.biochem.69.1.751. [DOI] [PubMed] [Google Scholar]
- 5.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. New York: John Wiley & Sons; 1991. [Google Scholar]
- 6.Mulholland AJ. Computational enzymology: modelling the mechanisms of biological catalysts. Biochemical Society Transactions. 2008;36:22–26. doi: 10.1042/BST0360022. [DOI] [PubMed] [Google Scholar]
- 7.Warshel A. Energetics of Enzyme Catalysis. Proceedings of the National Academy of Sciences of the United States of America. 1978;75:5250–5254. doi: 10.1073/pnas.75.11.5250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Warshel A, Sharma PK, Kato M, Xiang Y, Liu H, Olsson MHM. Electrostatic basis for enzyme catalysis. Chemical Reviews. 2006;106:3210–3235. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 9.Warshel A, Levitt M. Theoretical Studies of Enzymic Reactions - Dielectric, Electrostatic and Steric Stabilization of Carbonium-Ion in Reaction of Lysozyme. Journal of Molecular Biology. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 10.Kamerlin SCL, Haranczyk M, Warshel A. Progress in ab Initio QM/MM free-energy simulations of electrostatic energies in proteins: Accelerated QM/MM studies of pKa, redox reactions, and solvation free energies. The Journal of Physical Chemistry B. 2009;113:1253–1272. doi: 10.1021/jp8071712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Plotnikov NV, Warshel A. Exploring, Refining, and Validating the Paradynamics QM/MM Sampling. The Journal of Physical Chemistry B. 2012;116:10342–10356. doi: 10.1021/jp304678d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Laio A, Parrinello M. Escaping free-energy minima. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Prasad BR, Plotnikov NV, Lameira J, Warshel A. Quantitative exploration of the molecular origin of the activation of GTPase. Proc Natl Acad Sci U S A. 2013;110:20509–20514. doi: 10.1073/pnas.1319854110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vardi-Kilshtai A, Roca M, Warshel A. The empirical valence bond as an effective strategy for computer-aided enzyme design. Biotechnology Journal. 2009;4:495–500. doi: 10.1002/biot.200800299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Roca M, Vardi-Kilshtai A, Warshel A. Toward accurate screening in computer aided enzyme design. Biochemistry. 2009;48:3046–3056. doi: 10.1021/bi802191b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Frushicheva MP, Cao J, Warshel A. Challenges and Advances in Validating Enzyme Design Proposals: The Case of Kemp Eliminase Catalysis. Biochemistry. 2011;50:3849–3858. doi: 10.1021/bi200063a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gao JL. Catalysis by enzyme conformational change as illustrated by orotidine 5′-monophosphate decarboxylase. Current Opinion in Structural Biology. 2003;13:184–192. doi: 10.1016/s0959-440x(03)00041-1. [DOI] [PubMed] [Google Scholar]
- 18.Richard JP, Amyes TL. On the importance of being zwitterionic: enzymatic catalysis of decarboxylation and deprotonation of cationic carbon. Bioorganic Chemistry. 2004;32:354–366. doi: 10.1016/j.bioorg.2004.05.002. [DOI] [PubMed] [Google Scholar]
- 19.Klinman JP. Enzyme Dynamics Control of Active-Site Compression. Nature Chemistry. 2010;2:907–909. doi: 10.1038/nchem.886. [DOI] [PubMed] [Google Scholar]
- 20.Kamerlin SCL, Warshel A. At the dawn of the 21st century: Is dynamics the missing link for understanding enzyme catalysis? Proteins: Structure, Function, and Bioinformatics. 2010;78:1339–1375. doi: 10.1002/prot.22654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE. Intrinsic dynamcs of an enzyme underlies catalysis. Nature Letters. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 22.Henzler-Wildman KA, Thai V, Lei M, Ott M, Wolf-Watz M, Fenn T, Pozharski E, Wilson MA, Petsko GA, Karplus M, et al. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 23.Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- 24.Benkovic SJ, Hammes GG, Hammes-Schiffer S. Free-energy landscape of enzyme catalysis. Biochemistry. 2008;47:3317–3321. doi: 10.1021/bi800049z. [DOI] [PubMed] [Google Scholar]
- 25.Bhabha G, Lee J, Ekiert DC, Gam J, Wilson IA, Dyson HJ, Benkovic SJ, Wright PE. A dynamic knockout reveals that conformational fluctuations influence the chemical step of enzyme catalysis. Science. 2011;332:234–238. doi: 10.1126/science.1198542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nagel ZD, Klinman JP. A 21st century revisionist’s view at a turning point in enzymology. Nature Chemical Biology. 2009;5:543–550. doi: 10.1038/nchembio.204. [DOI] [PubMed] [Google Scholar]
- 27.Warshel A, Sharma PK, Kato M, Xiang Y, Liu H, Olsson MH. Electrostatic basis for enzyme catalysis. Chem Rev. 2006;106:3210–3235. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 28.Olsson MHM, Parson WW, Warshel A. Dynamical contributions to enzyme catalysis: Critical tests of a popular hypothesis. Chemical Reviews. 2006;106:1737–1756. doi: 10.1021/cr040427e. [DOI] [PubMed] [Google Scholar]
- 29.Pisliakov AV, Cao J, Kamerlin SC, Warshel A. Enzyme millisecond conformational dynamics do not catalyze the chemical step. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:17359–17364. doi: 10.1073/pnas.0909150106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bhabha G, Lee J, Ekiert DC, Gam J, Wilson IA, Dyson HJ, Benkovic SJ, Wright PE. A Dynamic Knockout Reveals That Conformational Fluctuations Influence the Chemical Step of Enzyme Catalysis. Science. 2011;332:234–238. doi: 10.1126/science.1198542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31••.Adamczyk AJ, Cao J, Kamerlin SC, Warshel A. Catalysis by dihydrofolate reductase and other enzymes arises from electrostatic preorganization, not conformational motions. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:14115–14120. doi: 10.1073/pnas.1111252108. This paper further established our argument that the dynamical proposal is invalid by analyzing the actual meaning of the study of ref. [30]. It is shown that in a contrast to the assertions of ref. [30], mutations of DHFR that are supposed to reduce catalysis by reducing the dynamics are changing the catalysis by increasing the activation free energy. It is also clarified that the reorganization energy cannot be assesed by the reported structural studies and instead should be evaluated by computer simulations. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Boekelheide N, Salomon-Ferrer R, Miller TF. Dynamics and dissipation in enzyme catalysis. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:16159–16163. doi: 10.1073/pnas.1106397108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fan Y, Cembran A, Ma SH, Gao JL. Connecting Protein Conformational Dynamics with Catalytic Function As Illustrated in Dihydrofolate Reductase. Biochemistry. 2013;52:2036–2049. doi: 10.1021/bi301559q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Knapp MJ, Klinman JP. Environmentally coupled hydrogen tunneling - Linking catalysis to dynamics. European Journal of Biochemistry. 2002;269:3113–3121. doi: 10.1046/j.1432-1033.2002.03022.x. [DOI] [PubMed] [Google Scholar]
- 35.Hwang J-K, Warshel A. A Quantized Classical Path Approach for Calculations of Quantum Mechanical Rate Constants. The Journal of Physical Chemistry. 1993;97:10053–10058. [Google Scholar]
- 36.Hwang J-K, Warshel A. How Important are Quantum Mechanical Nuclear Motions in Enzyme Catalysis? Journal of the American Chemical Society. 1996;118:11745–11751. [Google Scholar]
- 37.Olsson MHM, Siegbahn PEM, Warshel A. Simulations of the large kinetic isotope effect and the temperature dependence of the hydrogen atom transfer in lipoxygenase. Journal of the American Chemical Society. 2004;126:2820–2828. doi: 10.1021/ja037233l. [DOI] [PubMed] [Google Scholar]
- 38.Kamerlin SCL, Warshel A. An analysis of all the relevant facts and arguments indicates that enzyme catalysis does not involve large contributions from nuclear tunneling. Journal of Physical Organic Chemistry. 2010;23:677–684. doi: 10.1002/poc.1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kraut DA, Sigala PA, Pybus B, Liu CW, Ringe D, Petsko GA, Herschlag D. Testing Electrostatic Complementarity in Enzyme Catalysis: Hydrogen Bonding in the Ketosteroid Isomerase Oxyanion Hole. PLoS Biology. 2006;4:0501–0519. doi: 10.1371/journal.pbio.0040099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Warshel A, Sharma PK, Chu ZT, Aqvist J. Electrostatic Contributions to Binding of Transition State Analogues Can Be Very Different from the Corresponding Contributions to Catalysis: Phenolates Binding to the Oxyanion Hole of Ketosteroid Isomerase. Biochemistry. 2007;46:1466–1476. doi: 10.1021/bi061752u. [DOI] [PubMed] [Google Scholar]
- 41.Schwans JP, Kraut DA, Herschlag D. Determining the catalytic role of remote substrate binding interactions in ketosteroid isomerase. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:14271–14275. doi: 10.1073/pnas.0901032106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kamerlin SCL, Sharma PK, Chu ZT, Warshel A. Ketosteroid isomerase provides further support for the idea that enzymes work by electrostatic preorganization. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:4075–4080. doi: 10.1073/pnas.0914579107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fafarman AT, Sigala PA, Schwans JP, Fenn TD, Herschlag D, Boxer SG. Quantitative, directional measurement of electric field heterogeneity in the active site of ketosteroid isomerase. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:E299–E308. doi: 10.1073/pnas.1111566109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wells JA, Cunningham BC, Graycar TP, Estell DA. Importance of Hydrogen-Bond Formation in Stabilizing the Transition-State of Subtilisin. Philosophical Transactions of the Royal Society a-Mathematical Physical and Engineering Sciences. 1986;317:415–423. [Google Scholar]
- 45.Hwang JK, Warshel A. Semiquantitative Calculations of Catalytic Free-Energies in Genetically Modified Enzymes. Biochemistry. 1987;26:2669–2673. doi: 10.1021/bi00384a003. [DOI] [PubMed] [Google Scholar]
- 46.Rao SN, Singh UC, Bash PA, Kollman PA. Free-Energy Perturbation Calculations on Binding and Catalysis after Mutating Asn-155 in Subtilisin. Nature. 1987;328:551–554. doi: 10.1038/328551a0. [DOI] [PubMed] [Google Scholar]
- 47.Kiss G, Celebi-Olcum N, Moretti R, Baker D, Houk KN. Computational Enzyme Design. Angewandte Chemie-International Edition. 2013;52:5700–5725. doi: 10.1002/anie.201204077. [DOI] [PubMed] [Google Scholar]
- 48•.Hilvert D. Design of Protein Catalysts. Annual Review of Biochemistry. 2013;82:447–470. doi: 10.1146/annurev-biochem-072611-101825. An instructive review of the current state of the field. [DOI] [PubMed] [Google Scholar]
- 49•.Barrozo A, Borstnar R, Marloie G, Kamerlin SC. Computational Protein Engineering: Bridging the Gap between Rational Design and Laboratory Evolution. International Journal of Molecular Sciences. 2012;13:12428–12460. doi: 10.3390/ijms131012428. An instructive review with emphasis on the issue of promiscuity. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wijma HJ, Janssen DB. Computational design gains momentum in enzyme catalysis engineering. Febs Journal. 2013;280:2948–2960. doi: 10.1111/febs.12324. [DOI] [PubMed] [Google Scholar]
- 51.Copley SD. Enzymes with extra talents: moonlighting functions and catalytic promiscuity. Current Opinion In Chemical Biology. 2003;7:265–272. doi: 10.1016/s1367-5931(03)00032-2. [DOI] [PubMed] [Google Scholar]
- 52.Gould SM, Tawfik DS. Directed evolution of the promiscuous esterase activity of carbonic anhydrase II. Biochemistry. 2005;44:5444–5452. doi: 10.1021/bi0475471. [DOI] [PubMed] [Google Scholar]
- 53.Marti S, Andres J, Moliner V, Silla E, Tunon I, Bertran J. Predicting an improvement of secondary catalytic activity of promiscuous isochorismate pyruvate lyase by computational design. Journal of the American Chemical Society. 2008;130:2894–2895. doi: 10.1021/ja078334c. [DOI] [PubMed] [Google Scholar]
- 54.Magnusson AO, Takwa M, Hamberg A, Hult K. An S-Selective Lipase Was Created by Rational Redesign and the Enantioselectivity Increased with Temperature. Angewandte Chemie International Edition. 2005;44:4582–4585. doi: 10.1002/anie.200500971. [DOI] [PubMed] [Google Scholar]
- 55.Khersonsky O, Rothlisberger D, Dym O, Albeck S, Jackson CJ, Baker D, Tawfik DS. Evolutionary optimization of computationally designed enzymes: Kemp eliminases of the KE07 series. Journal of Molecular Biology. 2010;396:1025–1042. doi: 10.1016/j.jmb.2009.12.031. [DOI] [PubMed] [Google Scholar]
- 56.Babtie AC, Bandyopadhyay S, Olguin LF, Hollfelder F. Efficient catalytic promiscuity for chemically distinct reactions. Angewandte Chemie, International Edition in English. 2009;48:3692–3694. doi: 10.1002/anie.200805843. [DOI] [PubMed] [Google Scholar]
- 57.Garcia-Seisdedos H, Ibarra-Molero B, Sanchez-Ruiz JM. Probing the mutational interplay between primary and promiscuous protein functions: a computational-experimental approach. PLoS Computational Biology. 2012;8:e1002558. doi: 10.1371/journal.pcbi.1002558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Khersonsky O, Tawfik DS. Enzyme promiscuity: a mechanistic and evolutionary perspective. Annual Review of Biochemistry. 2010;79:471–505. doi: 10.1146/annurev-biochem-030409-143718. [DOI] [PubMed] [Google Scholar]
- 59.Althoff EA, Wang L, Jiang L, Giger L, Lassila JK, Wang Z, Smith M, Hari S, Kast P, Herschlag D, et al. Robust design and optimization of retroaldol enzymes. Protein Science. 2012;21:717–726. doi: 10.1002/pro.2059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Siegel JB, Zanghellini A, Lovick HM, Kiss G, Lambert AR, St Clair JL, Gallaher JL, Hilvert D, Gelb MH, Stoddard BL, et al. Computational design of an enzyme catalyst for a stereoselective bimolecular Diels-Alder reaction. Science. 2010;329:309–313. doi: 10.1126/science.1190239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Rothlisberger D, Khersonsky O, Wollacott AM, Jiang L, DeChancie J, Betker J, Gallaher JL, Althoff EA, Zanghellini A, Dym O, et al. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453:190–U194. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- 62.Frushicheva MP, Cao J, Chu ZT, Warshel A. Exploring challenges in rational enzyme design by simulating the catalysis in artificial kemp eliminase. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:16869–16874. doi: 10.1073/pnas.1010381107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63•.Khersonsky O, Kiss G, Rothlisberger D, Dym O, Albeck S, Houk KN, Baker D, Tawfik DS. Bridging the gaps in design methodologies by evolutionary optimization of the stability and proficiency of designed Kemp eliminase KE59. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:10358–10363. doi: 10.1073/pnas.1121063109. An interesting refinement of Kemp eliminase which demonstrates on the one hand the power of directed evolution, but on the other hand involves computational attempts that are simply unable to reproduce or rationalize the experimental trend. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kiss G, Rothlisberger D, Baker D, Houk KN. Evaluation and ranking of enzyme designs. Protein Science. 2010;19:1760–1773. doi: 10.1002/pro.462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Alexandrova AN, Rothlisberger D, Baker D, Jorgensen WL. Catalytic mechanism and performance of computationally designed enzymes for Kemp elimination. J Am Chem Soc. 2008;130:15907–15915. doi: 10.1021/ja804040s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Alexandrova AN, Jorgensen WL. Origin of the activity drop with the E50D variant of catalytic antibody 34E4 for Kemp elimination. Journal of Physical Chemistry B. 2009;113:497–504. doi: 10.1021/jp8076084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67••.Tokuriki N, Jackson CJ, Afriat-Jurnou L, Wyganowski KT, Tang R, Tawfik DS. Diminishing returns and tradeoffs constrain the laboratory optimization of an enzyme. Nature Communications. 2012:3. doi: 10.1038/ncomms2246. An instructive study of the tradeoffs in catalytic activity upon conversion from phosphotriesterase to arylesterase. [DOI] [PubMed] [Google Scholar]
- 68.Aharoni A, Gaidukov L, Khersonsky O, Gould SM, Roodveldt C, Tawfik D. The ‘evolvability’ of promiscuous protein functions. Nature Genetics. 2005;37:73–76. doi: 10.1038/ng1482. [DOI] [PubMed] [Google Scholar]
- 69.Khersonsky O, Roodveldt C, Tawfik D. Enzyme promiscuity: evolutionary and mechanistic aspects. Current Opinion in Chemical Biology. 2006;10:498–508. doi: 10.1016/j.cbpa.2006.08.011. [DOI] [PubMed] [Google Scholar]
- 70.Poelwijk FJ, de Vos MG, Tans SJ. Tradeoffs and optimality in the evolution of gene regulation. Cell. 2011;146:462–470. doi: 10.1016/j.cell.2011.06.035. [DOI] [PubMed] [Google Scholar]
- 71.Amar D, Berger I, Amara N, Tafa G, Meijler MM, Aharoni A. The Transition of Human Estrogen Sulfotransferase from Generalist to Specialist Using Directed Enzyme Evolution. Journal of Molecular Biology. 2012;416:21–32. doi: 10.1016/j.jmb.2011.12.013. [DOI] [PubMed] [Google Scholar]
- 72.Reetz MT. Controlling the enantioselectivity of enzymes by directed evolution: practical and theoretical ramifications. Proceedings of the National Academy of Sciences of the United States of America. 2004;101:5716–5722. doi: 10.1073/pnas.0306866101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Reetz MT. Laboratory evolution of stereoselective enzymes: a prolific source of catalysts for asymmetric reactions. Angewandte Chemie, International Edition in English. 2011;50:138–174. doi: 10.1002/anie.201000826. [DOI] [PubMed] [Google Scholar]
- 74.Sandstrom AG, Wikmark Y, Engstrom K, Nyhlen J, Backvall JE. Combinatorial reshaping of the Candida antarctica lipase A substrate pocket for enantioselectivity using an extremely condensed library. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:78–83. doi: 10.1073/pnas.1111537108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Frushicheva MP, Warshel A. Towards Quantitative Computer-Aided Studies of Enzymatic Enantioselectivity: The Case of Candida antarctica Lipase A. ChemBioChem. 2012;13:215–223. doi: 10.1002/cbic.201100600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Schopf P, Warshel A. Validating computer simulations of enantioselective catalysis; reproducing the large steric and entropic contributions in Candida Antarctica lipase B. Proteins: Structure, Function, and Bioinformatics. 2014 doi: 10.1002/prot.24506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Magnusson AO, Takwa M, Harnberg A, Hult K. An S-selective lipase was created by rational redesign and the enantioselectivity increased with temperature. Angewandte Chemie-International Edition. 2005;44:4582–4585. doi: 10.1002/anie.200500971. [DOI] [PubMed] [Google Scholar]
- 78.Singh N, Warshel A. A comprehensive examination of the contributions to the binding entropy of protein-ligand complexes. Proteins-Structure Function and Bioinformatics. 2010;78:1724–1735. doi: 10.1002/prot.22689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Siegbahn PEM, Himo F. The quantum chemical cluster approach for modeling enzyme reactions. Wiley Interdisciplinary Reviews-Computational Molecular Science. 2011;1:323–336. [Google Scholar]
- 80.Hopmann KH, Hallberg BM, Himo F. Catalytic mechanism of limonene epoxide hydrolase, a theoretical study. Journal of the American Chemical Society. 2005;127:14339–14347. doi: 10.1021/ja050940p. [DOI] [PubMed] [Google Scholar]
- 81.Zastrow ML, Peacock AFA, Stuckey JA, Pecoraro VL. Hydrolytic catalysis and structural stabilization in a designed metalloprotein. Nature Chemistry. 2012;4:118–123. doi: 10.1038/nchem.1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Breslow R. Biomimetic Chemistry and Artificial Enzymes - Catalysis by Design. Accounts of Chemical Research. 1995;28:146–153. [Google Scholar]
- 83.Cram DJ. The Design of Molecular Hosts, Guests, and Their Complexes. Science. 1988;240:760–767. [PubMed] [Google Scholar]
- 84.Frushicheva MP, Mukherjee S, Warshel A. Electrostatic Origin of the Catalytic Effect of a Supramolecular Host Catalyst. The Journal of Physical Chemistry B. 2012;116:13353–13360. doi: 10.1021/jp3084327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Luzhkov V, Aqvist J. Free-energy perturbation calculations of binding and transition-state energies: hydrolysis of phenyl esters by beta-cyclodextrin. Chemical Physics Letters. 1999;302:267–272. [Google Scholar]
- 86.Pluth MD, Bergman RG, Raymond KN. Proton-Mediated Chemistry and Catalysis in a Self-Assembled Supramolecular Host. Accounts of Chemical Research. 2009;42:1650–1659. doi: 10.1021/ar900118t. [DOI] [PubMed] [Google Scholar]