Probing Hydrophilic Interface of Solid/Liquid-Water by Nanoultrasonics

Abstract

Despite the numerous devoted studies, water at solid interfaces remains puzzling. An ongoing debate concerns the nature of interfacial water at a hydrophilic surface, whether it is more solid-like, ice-like, or liquid-like. To answer this question, a complete picture of the distribution of the water molecule structure and molecular interactions has to be obtained in a non-invasive way and on an ultrafast time scale. We developed a new experimental technique that extends the classical acoustic technique to the molecular level. Using nanoacoustic waves with a femtosecond pulsewidth and an ångström resolution to noninvasively diagnose the hydration structure distribution at ambient solid/water interface, we performed a complete mapping of the viscoelastic properties and of the density in the whole interfacial water region at hydrophilic surfaces. Our results suggest that water in the interfacial region possesses mixed properties and that the different pictures obtained up to now can be unified. Moreover, we discuss the effect of the interfacial water structure on the abnormal thermal transport properties of solid/liquid interfaces.

Solid/liquid-water interface is of fundamental importance in various natural phenomena ranging from surface wetting¹, electrolysis², to protein folding³, wherein the first few water molecular layers govern interface-mediated properties and energy transfer. A variety of techniques, including scanning probe microscopy⁴,⁵, surface forces apparatus⁶, diffraction techniques⁷,⁸, nonlinear optical spectroscopy¹,⁹, and infrared and THz spectroscopy¹⁰ have been employed to investigate the physical properties of interfacial water. Numerous studies have been devoted to the investigation of the interaction of water with substrate under different conditions, such as the influence of the length of the charge dipoles on a solid surface¹¹,¹², the humidity¹³ and various other parameters¹⁴. However, the ångström-scale feature and the picosecond relaxation dynamics of water have made it challenging to experimentally understand how the water molecules interact with the substrate and with each other.

Ultrasound has not only the potential to get access to the structure of materials, but also to its viscoelastic properties. It is therefore used in many fields from medical¹⁵ to underwater imaging¹⁶. When the frequency of acoustic waves reach over the THz range, their wavelength in water can be down to few angstroms, which means that information on the molecular structure and the binding strength can be retrieved. To generate such frequencies, the nano-ultrasonics technique¹⁷, based on the femtosecond laser excitation of a piezoelectric nanolayer¹⁸,¹⁹, has revealed itself very useful to characterize material properties, ranging from ångström-level interface roughness²⁰ to THz frequency acoustic-phonon attenuation²¹,²². With an ultrahigh spatial resolution and picometer-level displacement as perturbations in the measurement, nano-ultrasonics technique could provide the first ever noninvasive measurement of mass density and visco-elastic properties of interfacial water at an ambient solid surface with both high temporal and spatial resolutions.

Here we apply femtosecond acoustic pulse with a subnanometer pulsewidth to noninvasively diagnose the hydration structure at an ambient solid/water interface. The ultrafast acoustic impulse response of the interfacial water, unlike that of the solid/ice interface which can be well explained by mechanical properties of bulk ice²², indicates that the liquid water next to our studied specific solid surface can be 5 times denser and 2 times more rigid than bulk water. The observed high mass density and high elastic modulus, combined to the low acoustic losses close to the surface, reveal an almost solid like structure of water and strong interactions between water molecules and the studied hydrophilic surface. Meanwhile, further from the surface, the high acoustic dissipation shows that this interfacial water layer is more viscous than bulk water. Our study indicates that the femtosecond nanoultrasonics can directly access the mass density and elastic/inelastic properties of interfacial water layers with a 3Å spatial resolution, providing key information for energy transfer at solid-water interface as well as the structure and the bonding strength of the interfacial hydration water.

Results

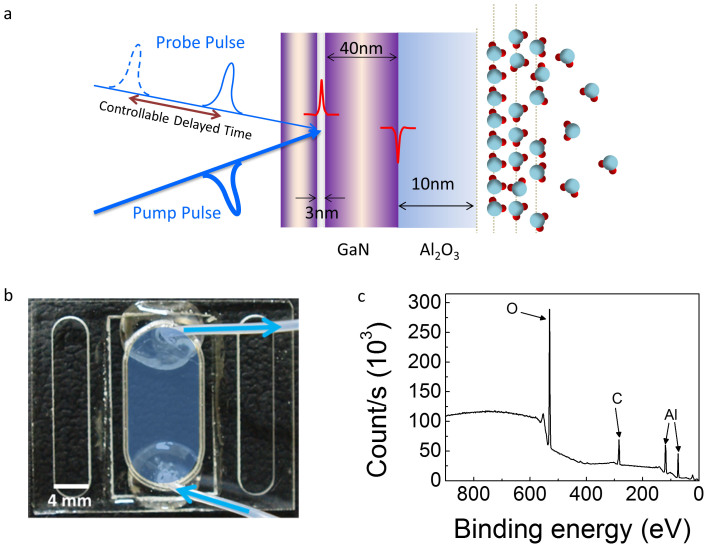
Nanoultrasonic experiments are based on the optical excitation of a piezoelectric semiconductor single quantum well (SQW) that launches a broadband nanoacoustic pulse. This pulse then travels within the sample, gets reflected by the multiple interfaces and finally is detected when it reaches the SQW again, as depicted in figure 1(a)¹⁸,¹⁹. The spectrum of thus excited acoustic pulse range from few GHz to above THz, which has made this technique a powerful tool to image or characterize nanoscale materials. Indeed, in recent years, this method has not only been successfully applied to characterize the surface roughness of materials²⁰, but also the acoustic attenuation up to 650 GHz in SiO₂²¹ and more recently we showed the possibility to measure the attenuation up to 1 THz.²² The nanoultrasonic technique allows generating nanoacoustic waves (NAW) with a pulsewidth of 3 nm and a ~10⁻⁴ peak intensity of strain, corresponding to a ~0.3-pm displacement, allowing the non-invasive characterization of the interface. In this pulse-and-echo scheme, the measured sub-picosecond temporal shape of acoustic echoes and thus transformed complex acoustic reflection spectrum of the solid-water interface, with an acoustic frequency bandwidth up to 1 THz, can unravel the interfacial structure of the water with a spatial resolution around half of the acoustic pulsewidth, which can be as fine as 3Å in liquid water due to its much reduced sound velocity (see supplementary information). Moreover, the penetration depth of the THz acoustic pulse in liquid water is only a few intermolecular distances (~2 nm), thus the acoustic reflection measurement has interface specificity and can be applied to diagnose solid/ambient water interface.

Figure 1.

(a) Schematic representation of the experimental configuration. (b) Photograph of the microfluidic channel. (c) X-ray photoelectron spectrum of the sample.

The sample we used in our experiment consist of a 3 nm InGaN SQW embedded in GaN, covered with a layer of Al₂O₃, as shown in figure 1(a) (see methods). We chose to grow Al₂O₃ because of the important role the interface between water and metal oxide plays in nature²³,²⁴. On top of the Al₂O₃ layer, we deposited a microfluidic channel, which can be seen in figure 1(b), which allows a better control of the water thickness and stability during the experiments. With a sub-nanometer resolution, the surface characterization is critical. We therefore performed AFM measurements of the surface roughness, in order to estimate the frequency dependent losses induced by scattering²⁰. We obtained a rms roughness σ = 0.5 nm. We then characterized the pollution of the surface using X-ray photoelectron spectroscopy. As shown in figure 1(c), spectral signature of Ga, N and O can be observed. The line of C is not related to our sample pollution but to the X-ray source. By comparing the amplitude of each peak, and taking into account the sensitivity of the system to each element, we can estimate the composition of the surface²⁵. We find a concentration of 38% for Al and 62% for O, really close to a 2/3 ratio. This ratio means that Al and O are in stoichiometric quantity, and so, the adsorption of oxygen at the bare Al₂O₃ surface is relatively small.

We performed the nanoultrasonics experiments, first on the bare Al₂O₃ surface. Then, without moving the sample, we inject water and perform a second experiment. This technique allows to get rid of uncertainty due to the change of position²². Once the SQW absorbs the laser pulse, it launches an acoustic wave. This wave, then, propagates towards the surface, gets partially reflected or transmitted at the different interfaces, and is detected when it arrives back in the SQW. Figure 2(a) shows the transient transmission changes recorded with and without water at the Al₂O₃ surface.

Figure 2.

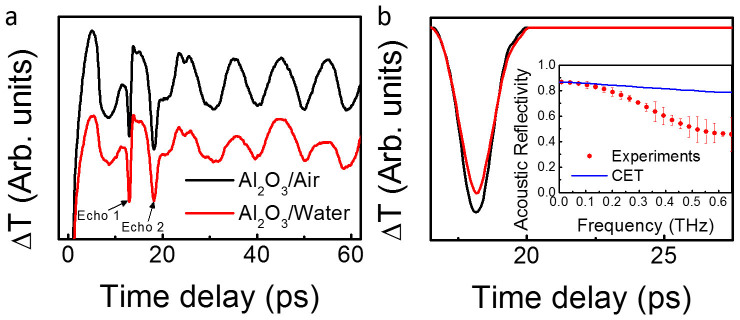
(a) Transient transmission changes (ΔT) obtained at a pump and probe wavelength of 400 nm with and without water. (b) Transient transmission changes induced by the acoustic waves reflected by the Al₂O₃/air or Al₂O₃/water after subtraction of the other contributions. Inset: Frequency dependent acoustic reflectivity obtained experimentally or using continuum elastic theory (CET).

On these traces, one observes multiple contributions. First, we observe oscillations all along the trace. These oscillations, the so-called Brillouin oscillations, are due to the interference between probe light reflected by interfaces and the probe light reflected by the travelling acoustic wave²⁶. On top of these oscillations, some dips appear, noted echo 1 and 2 in Fig. 2(a). The first echo is observed at 12.5 ps, in good agreement with the expected round trip time for the acoustic waves reflected by the GaN/Al₂O₃ interface. The second echo corresponds to the acoustic waves that travel from the SQW to the Al₂O₃/air or Al₂O₃/water interface and back to SQW.

As we mentioned previously, we are performing the experiment in-situ to limit the experimental uncertainty. However, in order to determine the effect of the introduction of water on the acoustic reflection, we need to separate this effect from the optical contribution of the water layer. To do so, we normalize the signals by the echo of the GaN/Al₂O₃ interface. Indeed, if this echo is similar in both cases, it means that the acoustic energy transmitted to the alumina is the same. Therefore the differences we observe are due to the acoustic modifications induced by the introduction of water. In Fig. 2(b), we reproduce the echoes reflected from the Al₂O₃/air or Al₂O₃/water interface after removal of the Brillouin oscillations and normalization by echo 1. When we compare these two echoes, we observe that the echo reflected at the interface with water is slightly delayed and broader due to the complex structure of water at the interface. By performing the Fourier transform of both signals and from the ratio, thus further normalizing the effect of surface roughness and limited pulsewidth, we obtain the frequency dependent acoustic reflectivity of the Al₂O₃/water interface. In the inset of Fig. 2(b), we reproduce the thus calculated acoustic reflectivity, as well as the expected acoustic reflectivity using continuum elastic theory (CET)²². One remarks a good agreement at low frequency (<0.2 THz), however, at higher frequencies, the reflection is weaker than calculated with CET. In other words, short wavelength acoustic waves are sensitive to the microscopic structure of water at the interface, and water cannot be considered as a homogeneous medium anymore.

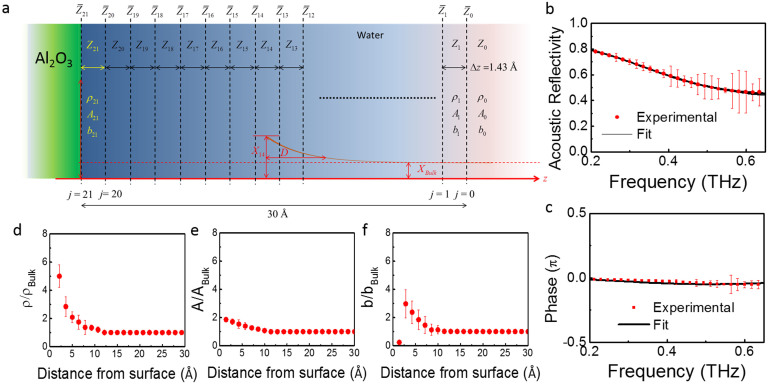
It is known that the intermolecular interaction between substrate and liquid will generally make the properties of the interfacial liquid different from those of bulk¹,²,³,⁴,⁵,⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴. Our observed acoustic reflection spectra can thus help to discover the viscoelastic properties of interfacial water and unravel the intermolecular interactions inside. In order to be able to describe our experimental results we use a discrete model to represent interfacial water. Since the acoustic pulse is a quasi-plane wave and the studied system is laterally homogeneous, the experimental system can be considered as a 1-dimensional problem. Here, a typical ultrasonic analysis algorithm is adopted to determine the acoustic properties of water as a function of distance from the solid surface. In this algorithm, water at the interface is divided into thin layers with variable density, ρ, elastic modulus, A, and viscosity, b as can be seen in Fig. 3a. Then, the effective acoustic impedance can be calculated in a similar way to the electromagnetic transmission line theory²⁷:

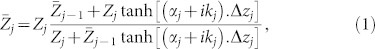with:

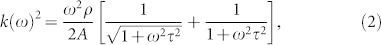and

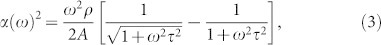where Δz_j is the thickness of the j-th segment, Z_j is its acoustic impedance and τ = b/A is the viscous relaxation time. In our study, the term viscosity refers to the phenomena responsible for the loss of the acoustic signal. The possible mechanisms responsible for sound attenuation are thermal conduction and molecular motion²⁸. At j = 0, the input acoustic impedance, 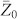, is trivially equal to the acoustic impedance of bulk water, Z₀ = Z_Bulk. We assume that the fast sound phenomenon²⁹ is still invalid in water at our studied frequency and simply take the values of acoustic properties of bulk water from Ref. 24. Here the thickness of every segment, Δz_j, is set to half of the spatial resolution of the acoustic pulse, which also corresponds to the half water molecule size. Since the penetration depth of our acoustic wave pulse is less than 2 nm, considering a 3nm-thick water layer in the calculation is sufficient. In the fitting process, ρ, A, and b of each segment within 10 Å from the solid surface can vary freely under a converging constraint and the properties of water behind 10 Å from the solid surface asymptotically transform to the bulk-state values in an exponential way (see supplementary information). Under this setup, the totally 27 parameters can be uniquely determined by finding the best fit of the full complex reflection spectra, shown in Fig. 3b and c, with a number of data points much over 27. Using this method, we can have access to the density, elastic modulus and viscosity profile of water. The profiles obtained for the Al₂O₃/water interface are shown in Fig. 3(d), (e) and (f). In this profile the x-axis corresponds to the distance from the surface, and the origin is defined as the center of the atomic plane that is terminating the Al₂O₃ surface.

Figure 3.

(a) The laterally-homogenous experimental system can be considered as an ultrasonic A-scan system. (b) Amplitude of the acoustic reflectivity of the GaN/air interface, simulation of the reflectivity using continuum elasticity theory and best fitted result using our algorithm. (c) Phase of the acoustic reflectivity of the GaN/air interface, simulation of the reflectivity using continuum elasticity theory and best fitted result using our algorithm. (d–f) The spatial distribution of the density, elastic modulus and viscosity for water at the interface with amorphous Al₂O₃ obtained by fitting the complex reflection spectrum. All data are normalized to the values of bulk water. The origin of the x-axis corresponds to the center of the atomic plane terminating the Al₂O₃ surface.

In a zone extending from the surface to 1 nm from it, we observe that the density, as well as the bulk modulus and the damping of water are different from bulk water. If we now look in details each parameter, we observe that the local density is up to five times higher than bulk water, revealing a solid-like layer, and thus a good ordering close to the surface. A consequence of this structure can be seen by observing the profile of the bulk modulus. Indeed, due to this high density the average bonding between water molecules become stronger and thus the bulk modulus higher. Contrarily to the density and the bulk modulus, the viscosity is not monotonically varying towards the value in bulk water, but experiences some fluctuations. Close to the surface, the value is really close to zero, which means that the acoustic energy is not easily dissipated, similarly to solids. Low acoustic losses at the surface of Al₂O₃ is a clear consequence of the organized structure, and reveals that water is behaving as a solid since it has a high density, strong bonding and dissipate acoustic energy as a solid. Further from the surface, the damping term becomes much higher, about three times the value of bulk water. In liquid, the attenuation of ultrasound is mostly due to molecular motion, so that the expression of viscosity is given by:

where η is the dynamic viscosity and η_b is the bulk viscosity. In this region, the high viscosity therefore means that water molecules have a longer relaxation time than bulk water. Indeed, the high density means that the molecules are more closely packed and therefore that their degrees of freedom are restrained. It suggests that the structural relaxation of water molecules takes longer time.

It is important to note that different from numerous reports, we do not observe some clear layering in the density³⁰,³¹. However a layering effect is suggested from the damping term profile of Fig. 3(f). Close to the surface, we have a solid like layer with a low viscosity and then the viscosity becomes higher than water similar to a viscous liquid. The observation of this solid-like viscosity behavior closer to the surface is in good agreement with literature³². The absence of layering effect in the density or bulk modulus can be explained by the relatively high roughness of the Al₂O₃ surface, σ = 5 Å, which is larger than the distance between the expected layers, thus smoothing out the layering information. Even though we calibrate the surface roughness effect by dividing the Al₂O₃/water interface spectrum by the Al₂O₃/air interface spectrum, this normalization procedure improve the resolution but is not able to recover the layering effect information. For further discussion on the effect of surface roughness, please refer to supplementary information. One should also note that the density profiles obtained by molecular dynamics simulation usually exhibits an area of few angstrom thicknesses, in which no water molecules can be found³³. This area corresponds to the length of the bond between the substrate and water. In our case, we describe water as a succession of thin continuous media. Acoustic waves do not propagate in vacuum but propagate through bonds. A vacuum area without water molecule would mean that acoustic waves cannot propagate and this is against our ultrasonic observation. In ultrasound, the boundary between the solid and water is located in the middle of the bond between water and Al₂O₃. In order to follow the tradition of molecular dynamics simulation for easier comparison, in Fig. 3(d–f), we have shifted the observed ultrasonic profiles, so that the origin is located at the center of the atomic plane terminating the solid. A more detailed discussion to compare our acoustic results with the conventional view provided by molecular dynamics simulation is given in the supplementary information.

Discussion

In addition to disclosing the properties of interfacial water, our dynamic study also provides substantial implications for the fundamental nature laws. The observed decay of the acoustic reflectivity at higher frequencies (Inset of Fig. 2(b)) reveals that such phonons are more likely to be transferred into water, compared to the prediction of the continuum elastic theory which neglects the interfacial water structure. It means that when the frequency of phonons becomes high, or in other words when they become sensitive to the interfacial structure, they can more easily transmit to water. In the field of cryogenics, this abnormal heat transport phenomenon has been intensively studied and was found to substantially decrease thermal boundary resistances across a solid/liquid interface, the so-called Kapitza anomaly²⁷,³⁴. Transition from normal-to-anomalous Kapitza resistance typically occurs near 1 K up to 10 K, where the dominant acoustic phonons for heat transport have corresponding frequencies between 90 GHz to 900 GHz, similar to the frequency range of this study as shown in Fig. 1. However, in our study, we only consider longitudinal phonons arriving at the solid/water interface with a normal incidence, which represent only a small part of all phonons participating to the heat conduction (see supplementary information), nevertheless the modified behavior we observed compared to the acoustic mismatch model can also be applied to other phonons. Several mechanisms³⁴ responsible for Kapitza anomaly have been proposed and examined, including liquid boundary layer, conduction electron, phonon attenuation, surface roughness, localized states at the interface, and mode conversion. However, conventional phonon spectroscopy cannot perform quantitative studies for specular/diffusive scatterings due to the lack of phase information for the observed acoustic phonons. Recently, we confirmed the dominant role of surface roughness in diffuse phonon scatterings at solid/air and solid/solid interfaces by using nanoultrasonics to measure the frequency-dependent specular scattering probabilities of coherent acoustic phonons at crystal boundaries with well characterized surface conditions²⁰. The surface roughness scattering induces a decrease of the resistance but cannot fully explain the experimental observations. The study reported here clearly indicates that the interfacial liquid structure which acts as an impedance-matching layer is the other dominant mechanism, besides the surface roughness, that gives rise to Kapitza anomaly. Taking advantage of the room-temperature-operated THz-bandwidth coherent phonon source which is capable of distinguishing between specular scatterings and diffuse scatterings²⁰, we thus not only for the first time observed the Kapitza anomaly happening at the solid/water interface, but also further clarify the long-standing puzzles on the origins of Kapitza anomaly. It is also important to know that this Kapitza anomaly phenomenon at the solid/water interface can never be performed at cryogenic temperatures, because at such a low temperature water will not be in the liquid form. This breakthrough should inspire a refreshing way to inspect the problem of energy transports across aqueous solid boundaries, such as the efficient coupling of sub-THz coherent acoustic vibrations from nanoparticles to the surrounding water³⁵. Similar phenomenon has recently been reported by using time-domain thermoreflectance³⁶, showing the thermal conductance of hydrophilic surfaces is 2–3 times higher than that of hydrophobic surfaces. Our result shows that the efficient energy transport across the hydrophilic surface is not merely resulted from the strong bonding but also due to the high mass density and the ordered structure of interfacial water. On the other hand, for hydrophobic surfaces, the high mass density and ice like properties of interfacial water are not expected³⁷. The absence of this feature would make the roughness-scattering the dominant effect to determine the frequency-dependent thermal boundary resistance, while the influence of the interfacial water will be diminished.

Extension from classical to molecular-level ultrasonics is potentially useful for resolving the ongoing debates regarding water due to its unique capability to directly resolve the intermolecular force interactions. The ability of noninvasive probing with picometer perturbations could also enable in situ monitoring of solvation interactions during molecular manipulations for hydrogen energy and biomedical applications. Moreover, this technique will have wide applicability to investigating various solid/liquid interfaces and lead to new insights into the fields of molecular hydrodynamics and condensed matter physics. Indeed, we have demonstrated that interfacial water on a hydrophilic surface can exhibit both liquid- and solid-like features and that the current observations can be unified thanks to the high resolution picture of interfacial water we are giving. Our results also bring a new point of view on the anomalous heat transfer at solid-liquid interface by bringing a microscopic description of the molecular structure at the interface. Those findings may give important insights into thermodynamic studies, such as wetting properties¹ and adhesion energy³⁸, on solid/water interfaces.

Methods

Nanoultrasonics

The nanoultrasonic experiment is based on the femtosecond acoustic pulse and echo technique. The mode-locked Ti:Sapphire laser pulse with a 76-MHz repetition rate and a 100-fs pulsewidth was first frequency-doubled by a beta barium borate (BBO) crystal to a wavelength of 400 nm in order to selectively excite the 3 nm In_0.1Ga_0.9N single quantum well. After second harmonic generation, the laser beam, passed through a blue colour filter and a half-wave plate, was divided into a pump and a probe beams by a polarizing beam splitter. The pump beam was focused on to the InGaN SQW to generate a 400 femtosecond longitudinal acoustic pulse through screening of the piezoelectric field inside the SQW²¹,²². When the acoustic pulse echo returned and passed through the InGaN SQW again, the strain-pattern-induced optical transient transmissivity change due to the quantum confined Franz-Keldish effect was subsequently measured by the probe beam with an optical delay time controlled by a mechanical translational stage. To enhance the signal to noise ratio, pump beam was chopped by an acousto-optic modulator and the signal of probe beam detected by a photodiode was demodulated by a lock-in amplifier. Typical pump fluence and focused spot diameter were 80 µJ/cm² and ~30 µm, exciting one-dimensional acoustic pulses with ~10⁻⁴ strain in the solid. In order to ensure in situ measurements with and without water loading, the pump and probe beams were incident from the sapphire side of the sample.

Sample preparation

The opto-acoustic transducer is a 3 nm-thick In_0.1Ga_0.9N single quantum well grown by Metal Organic Chemical Vapor Deposition (MOCVD) on a 2 μm-thick GaN buffer layer with a 300 µm-thick sapphire substrate. On top of the opto-acoustic transducer is an 40 nm-thick p-GaN cap layer with a root-mean-square roughness around 1.2Å on the Ga-terminated GaN(0001) surface. A 10 nm layer of amorphous Al₂O₃ was deposited by Atomic Layer Deposition (ALD). The water used in this work is liquid chromatography (L. C.) grade. To prevent water evaporation and enable precise positioning, a microfluidic channel was fabricated to facilitate water loading. The microfluidic channel is formed by bonding the sample surface and a BK7 glass by ultraviolet curing of an optical adhesive (NOA81). The BK7 glass surface was laser patterned to define the channel of water flow.

Sample characterization

The surface condition was carefully characterized by AFM, (Veeco innova) before the nanoultrasonic experiments. Topographical images were obtained with a silicon tip in tapping mode. The surface topographical images of the Al₂O₃ surfaces were then treated by using image processing software to obtain the root-mean-square roughness. 1 × 1, 5 × 5 and 10 × 10 µm² images on various locations of the sample surfaces were obtained to verify the homogeneity of the roughness. Moreover, the pollution at the sample surfaces was characterized by X-ray photoelectron spectroscopy (VG Scientific ESCALAB 250). The experiments were performed at a pressure of 1.10⁻¹⁰ Torr with a monochromatic X-Ray source at 1486.6 eV. The spot size was 650 µm and the pass energy was 20 eV.

Author Contributions

C.-K.S. designed the experiments, P.-A.M., C.-C.C., Y.-C.W., H.-Y.C., S.-C.Y., Y.-R.H. and I.-J.C. performed the experiments. P.-A.M., C.-C.C. and C.-K.S. analyzed the data and wrote the manuscript. P.-A.M., C.-C.C., Y.-C.W., V.G. and C.-K.S. developed the genetic algorithm. M.-J.C. and J.-K.S. provided the sample. Y.-W.C. and J.-L.K. performed molecular dynamic simulation.

Supplementary Material

Supplementary Information

Supplementary Information