Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Sep 1;4:6239. doi: 10.1038/srep06239

Statistical Signs of Social Influence on Suicides

Hygor Piaget M Melo 1,a, André A Moreira 1, Élcio Batista 2, Hernán A Makse 3, José S Andrade 1
PMCID: PMC4150102  PMID: 25174706

Abstract

By treating the suicide as a social fact, Durkheim envisaged that suicide rates should be determined by the connections between people and society. Under the same framework, he considered that crime is bound up with the fundamental conditions of all social life. The social effect on the occurrence of homicides has been previously substantiated, and confirmed here, in terms of a superlinear scaling relation: by doubling the population of a Brazilian city results in an average increment of 135% in the number of homicides, rather than the expected isometric increase of 100%, as found, for example, for the mortality due to car crashes. Here we present statistical signs of the social influence on the suicide occurrence in cities. Differently from homicides (superlinear) and fatal events in car crashes (isometric), we find sublinear scaling behavior between the number of suicides and city population, with allometric power-law exponents, β = 0.84 ± 0.02 and 0.87 ± 0.01, for all cities in Brazil and US counties, respectively. Also for suicides in US, but using the Metropolitan Statistical Areas (MSAs), we obtain β = 0.88 ± 0.01.

It is not uncommon in nature to observe properties that present non-trivial forms of scale dependence. This is the case, for instance, of critical phenomena, where scaling invariance, universal properties and renormalization concepts constitute the theoretical framework of a well-established field in physics4. In biology, the so-called allometric relations certainly represent outstanding examples of natural scaling laws. Precisely, allometry implies the use of power-laws, Y ∝ Mβ, to describe the dependence of a wide range of anatomical, physiological and behavioral properties, denoted here as Y, on the size or the body mass of different animal species, M. If the scaling exponent is β = 1, the variables Y and M are trivially proportional, and the relation between them is said to be isometric, while β ≠ 1 indicates an allometric type of relationship. The so-called “three-quarters law” or Kleiber's law, as originally proposed by the agricultural biologist Max Kleiber in 19475, is surely one of the most prominent allometric relations found in natural sciences. Based on an extensive set of experimental data, this fundamental law states that the metabolic rate of all animals should scale to the 3/4 power of their corresponding masses6,7.

In analogy with biological scaling laws, Bettencourt et al.2 showed that, regardless the enormous complexity and diversity of human behavior and the extraordinary geographic variability of urban settlements, cities belonging to the same urban system obey pervasive allometric relations with population size, therefore exhibiting nonextensive rates of innovation, wealth creation, patterns of consumption, human social behavior, and several other properties related to the urban infrastructure. The authors then conclude that all data can be grouped into three categories, namely, material infrastructure, individual human needs, and patterns of social activity. Despite the unambiguous presence of power-laws, the urban indicators do not necessarily follow a universal behavior. Instead the results can be divided in three different classes. The isometric (linear) case (β = 1) typically reflects the scaling of individual human needs, like the number of jobs, houses, and water consumption. As in biology, the allometric sublinear behavior (β < 1) implies an economy of scale in the quantity of interest, because its per capita measurement decreases with population size. In the case of cities, this is materialized, for example, in the number of gasoline stations, the total length of electrical cables, and the road surface (material and infrastructure). The case of superlinear allometry (β > 1) in urban indicators emerges whenever the complex patterns of social activity have significant influence. Wages, income, growth domestic product, bank deposits, as well as rates of invention, measured by new patents and employment in creative sectors, all display a superlinear increase with population size2. While these results indicate that larger cities are associated with higher levels of human productivity and quality of life, superlinear scaling can also characterize negative urban scenarios, such as the prospect of living costs, crime rates, pollution and disease incidence2,3,8,9,10.

Methods

Brazilian Data

We analyzed data available for all Brazilian cities from 1992 to 2009, made freely available by the Brazil's public healthcare system DATASUS11. Here we consider that cities are the smallest administrative units with local government. The data consist of the number of homicides, suicides, and deaths in traffic accidents as well as the population for each city.

US Data

We used data from the National Cancer Institute SEER, Surveillance Epidemiology and End Results downloaded from http://seer.cancer.gov/data/. The Institute provides mortality data aggregated for three or five years. To compare with Brazil, we use suicide mortality data for each American county and MSA (Metropolitan Statistical Area) accumulated through the five years of 2003 to 2007. Since the population is almost constant for a five years period, we adopted the average population as a measurement for the population on the allometry relation.

Exponent Determination

In order to reduce fluctuations, we first apply a non-parametric fitting method to the data, namely, the Nadaraya-Watson kernel regression17,18. We also compute the 95% (α = 0.05) confidence interval (CI) by the so-called α/2 quantile function over 300 random bootstrapping samples. The power-law exponent is calculated by performing an ordinary least square (OLS) fitting19 over the results of the Nadaraya-Watson kernel regression in the population interval [104, 106] for Brazilian cities, and [105, 107] for American MSAs.

Results

Allometry in Urban Indicators

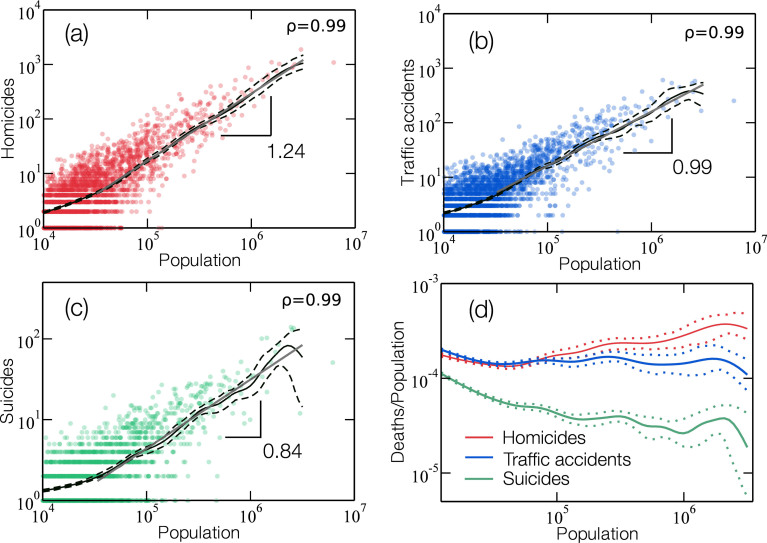
The main goal here is to investigate the scaling behavior with city population of three urban indicators, namely the number of homicides, deaths in traffic accidents and suicides. For this, we analyzed data available for all Brazilian cities as well as suicide for US counties and MSAs, as presented previously on Materials and Methods. For 2009 in Brazil, as shown in Fig. 1, the increase in the number of casualties D with city population P for the three death causes can be properly described in terms of power-laws, D = D0Pβ, where D0 is a costant pre-factor, and the exponent β reflects a global property at play across the urban system. Interestingly, while the number of deaths by traffic accidents display isometric scaling, β ≈ 1, homicides and suicides are both allometric, but obeying superlinear and sublinear scaling with population, respectively. These results suggest that the decision to commit a crime or to suicide, instead of being purely a consequence of individual choices, might have strong correlations with the underlying complex social organization and interactions. This does not seem to be the case of traffic accidents, since the strong evidence for isometric scaling, β = 0.99 ± 0.02, indicates that such events should result from random processes, i.e., no social relations need to be implied among the involved people.

Figure 1. Scaling relations for homicides, traffic accidents, and suicides for the year of 2009 in Brazil.

Figure 1

Open in a new tab

The small circles show the total number of deaths by (a) homicides (red), (b) traffic accidents (blue), and (c) suicides (green) vs the population of each city. Each graph represents only one urban indicator, and the solid gray line indicate the best fit for a power-law relation, using OLS regression, between the average total number of deaths and the city size (population). To reduce the fluctuations we also performed a Nadaraya-Watson kernel regression17,18. The dashed lines show the 95% confidence band for the Nadaraya-Watson kernel regression. The ordinary least-squares (OLS)19 fit to the Nadaraya-Watson kernel regression applied to the data on homicides in (a) reveals an allometric exponent β = 1.24 ± 0.01, with a 95% confidence interval estimated by bootstrap. This is compatible with previous results obtained for U.S.2 that also indicate a super-linear scaling relation with population and an exponent β = 1.16. Using the same procedure, we find β = 0.99 ± 0.02 and 0.84 ± 0.02 for the numbers of deaths in traffic accidents (b) and suicides (c), respectively. The values of the Pearson correlation coefficients ρ associated with these scaling relations are shown in each plot. This non-linear behavior observed for homicides and suicides certainly reflects the complexity of human social relations and strongly suggests that the the topology of the social network plays an important role on the rate of these events. (d) The solid lines show the Nadaraya-Watson kernel regression rate of deaths (total number of deaths divided by the population of a city) for each urban indicator, namely, homicides (red), traffic accidents (blue), and suicides (green). The dashed lines represent the 95% confidence bands. While the rate of fatal traffic accidents remains approximately invariant, the rate of homicides systematically increases, and the rate of suicides decreases with population.

From the superlinear scaling exponent found for the number of homicides in Brazil at the year 2009, β = 1.24 ± 0.01, one should expect that, by doubling the population of a city, the number of homicides would grow approximately by a factor of 135% in average, instead of just growing 100%, as if we had an isometric scaling. This super-linear behavior is consistent with that found for serious crimes in USA2. The result obtained for suicide scaling seems quite surprising. As depicted in Fig. 1c, the number of suicides scales with the population size as a power law with exponent β = 0.84 ± 0.02, which implies an “economy of scale” of 22% in comparison with isometric scaling, similar to Kleiber's law for metabolic rates and animal masses. This sublinear behaviour is reminiscent of the seminal study by Émile Durheim1, one of the fathers of modern sociology. In his book Suicide, Durkheim explored the differences in average suicide rates among Protestants and Catholics, arguing that stronger social control among Catholics leads to lower suicide rates. The crucial contribution from Durkheim was certainly to treat the suicide as a social fact, by explaining variations in its rate at a macro level as a direct consequence of society-scale phenomena, such as lack of connections between people (group attachment) and lack of regulations of behavior, rather than individuals' feelings and motivations.

The discrepancies observed in the scaling behaviors of homicides, deaths in traffic accidents and suicides become even more evident if we plot the average number of deaths per capita against city population, as shown in Fig. 1d. Under this framework, the systematic decrease in suicide rate with population indicates that a large supply of potential social contacts and interactions might work as an “antidote” for this tragic event. This result is consistent with the idea that human happiness is more a collective phenomenon than a consequence of individual well-being conditions. In analogy with health, it is then possible to consider a “happiness epidemy” spreading in a social network12. In Fig. 2 we show the dependence on time of the exponent β for a period of 18 years, from 1992 to 2009. We see a robust behavior for β, in such a way that, for different years, we still observe β > 1.0 for homicides, β < 1.0 for suicides, and β slightly above 1.0 for deaths by traffic accidents.

Figure 2. Temporal evolution of allometric exponent β for homicides (red squares), deaths in traffic accidents (blue circles), and suicides (green diamonds).

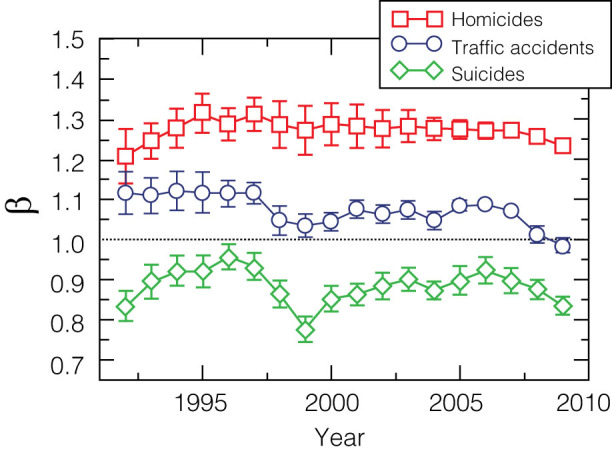
Figure 2

Open in a new tab

Time evolution of the power-law exponent β for each behavioral urban indicator in Brazil from 1992 to 2009. We can see that the non-linear behavior for homicides and suicides are robust for this 19 years period, and for the traffic accidents the exponent remain close to 1.0.

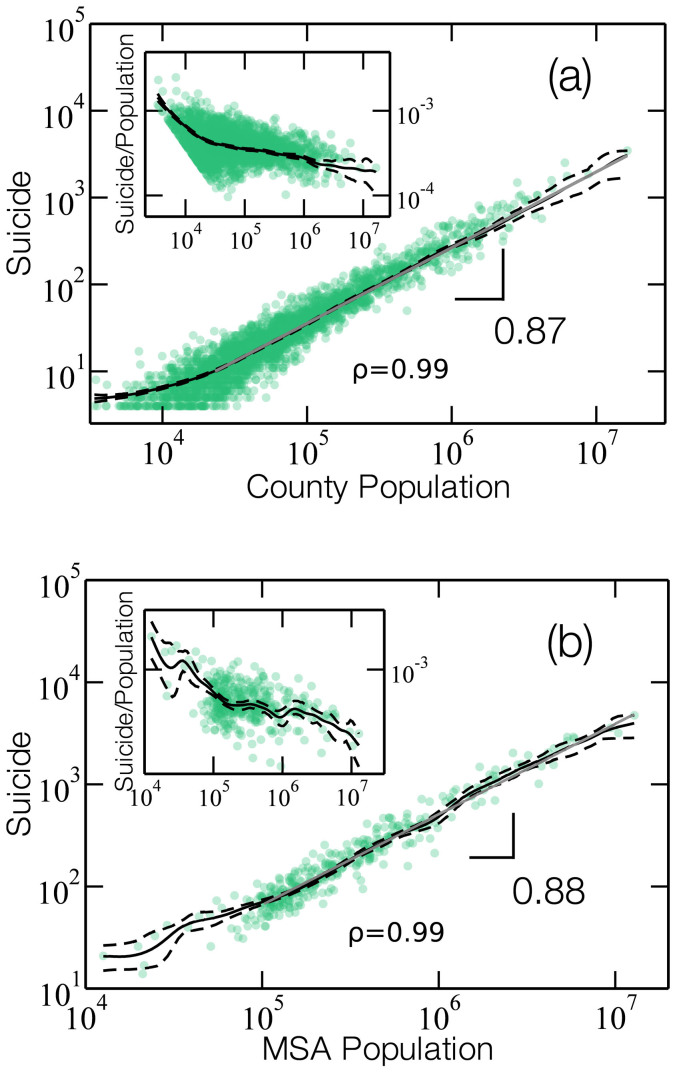
We also analyzed data available for suicides in all US counties and MSAs. The data is an accumulation of the total number of suicides during a period of five years, from 2003 to 2007. In Figs. 3a and 3b we show the dependence of the total number of suicides during these five years on the average population for each county and MSA, respectively. As depicted, the number of suicides also scales with a sub-linear power law with exponent β = 0.87 ± 0.01 for counties, and β = 0.88 ± 0.01 for MSAs, which are in agreement with our previous results for Brazil.

Figure 3. Scaling relationship between suicides and population for US counties and MSAs.

Figure 3

Open in a new tab

The small circles show the total number of suicides over five years (2003 to 2007) vs the average population for counties (a) and MSAs (b). The solid gray line indicate the best fit of a power law, using OLS regression, between the average total number of suicides and population. The dashed black lines delimit the 95% confidence band given by the Nadaraya-Watson kernel regression (solid black line)17,18. The allometric exponents are obtained through an ordinary least-squares (OLS) fit19 over the Nadaraya-Watson kernel regression applied to the suicides data. The values of the Pearson correlation coefficients ρ associated with these scaling relations are shown in each plot. We find β = 0.87 ± 0.01 for counties and β = 0.88 ± 0.01 for MSAs with a 95% confidence interval estimated by bootstrap. The insets in each graph show the systematic decreases of suicide rates with population in both cases.

In Fig. 4 we show the countour plot for the conditional probability of the rate of fatality, given a population size. In order to obtain the approximate density, we perform a kernel-density estimation over the sample of all Brazilian cities in 2009. The lines in Fig. 4 indicate the limits below which 10%, 50% and 90% of the data points are located. Besides confirming the superlinear, linear, and sublinear behaviors, these results also show how the probability distribution of rates of fatality varies with the population size. Also, the 10% and 90% lines are representative of expected extreme cases of low and high fatalities, respectively.

Figure 4. Fatality per capita versus population for homicides, traffic accidents, and suicides.

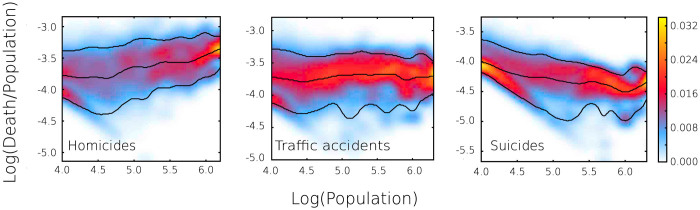
Figure 4

Open in a new tab

The color map represents the conditional probability density obtained by kernel density estimation. The bottom and top lines correspond to the 10% and 90% bounds of the distribution for each population size, that is 80% of the sampled points are between these lines. The middle line is the 50% level or “median” expected for each population size. The diagonal shape observed in the left side of density maps are cases of low number of fatal events, one or two fatalities. After this region we observe that the three level lines wiggle around an average power-law behavior. In the case of homicides the three level lines indicate an increase in the expected density of fatality with the population size. Similarly, for traffic accidents the lines are close to horizontal, that is, the probability distribution for the rate of fatality is near independent of the population. For suicides, the median shows a slight decrease with population size, while the 90% level, that is associated with cases of extreme rates of suicide, shows a pronounced decrease. The sublinear growth observed for suicides, as depicted in Fig. 1c, is likely due to the suppression of these extremely high rates in large urban areas.

Discussion

Allometric relations are ubiquitous in Nature, appearing in a wide variety of biological, sociological, chemical and physical systems2,4,13. Even the arrangement of Lego pieces has been recently reported to obey a sublinear scaling between the number of pieces types vs. the total number of pieces for many Lego sets14. As originally proposed in biology by Kleiber5 and extended later by others13, a single power law comprising 27 orders of magnitude can associate the metabolisms of a microscopical bacteria and a blue whale, weighting a few picograms and more than 100 t, respectively. Unlike allometric relations in Biology, few attempts have been made to explain the origin of universal scaling laws describing urban indicators. In a recent study15, a quantitative framework has been developed to consider the interactions between people over a social network that is capable to predict the allometric scaling for urban systems.

Here we studied the scaling relation with population of three behavioral urban indicators, namely, number of homicides, victims of vehicle crashes, and suicide events. We show that, unlike the incidence of vehicle crashes with fatal victims, which exhibits isometric (linear) scaling, homicides and suicides are characterized by allometric behaviors, superlinear and sublinear, respectively.

Precisely, we found that the superlinear scaling relation for the number of homicides has an allometric exponent that lies between 1.21 and 1.31 along the years, between 1992 and 2009. Despite all their positive attributes8,9 (e.g., higher incomes and levels of creative activities), these results show that larger and urbanized cities also have a dark side, namely, higher levels of violence. Interestingly, the effect is exactly the opposite in the number of suicide events, which typically follow a sublinear scaling with population, with an allometric exponent value that varies in the range between 0.78 and 0.95. Such a result led us to conjecture that a suicide event should not be taken as an isolated individual decision. Many other hypothesis could be proposed to explain the observed higher rate of suicides of small cities. In any case, our idea is consistent with the conceptual framework put forward by Durkheim1, under which suicides need to be treated as social facts, actually affected by complex human relations. Our hypothesis is also in agreement with the recent finding by Schlapfer et al.20 that both the number of social contacts and the total communication intensity grow superlinearly with city population. The sublinear behavior found can be even considered as a counter-intuitive result. The more common and straightforward view would be to associate the suicide causes uniquely to a health condition of psychological or mental illness that could nevertheless be strongly linked to external urban factors. For instance, traffic jams, pollution, and stressful jobs all create a harmful environment for the population. However, the fact that we found sublinearity, namely, that the number of suicides is disproportionately small for larger cities, discloses an entirely different perspective. We conjecture that this property can be intimately related with an “emotional epidemy” as previously hypothesized12,16. This phenomenon can explain the systematic attenuation through the social network of contagious emotions states of potentially suicidal individuals.

Author Contributions

H.P.M.M., A.A.M., E.B., H.A.M. and J.S.A. designed research, performed research, and wrote the manuscripts.

Acknowledgments

We also thank the Brazilian Agencies CNPq, CAPES, FUNCAP and FINEP, the FUNCAP/CNPq Pronex grant, and the National Institute of Science and Technology for Complex Systems in Brazil for financial support. Hernan Makse thanks NIH and ARL for financial support. We thank Prof. César Barreira for valuable discussions during the development of this work.

References

  1. Durkheim, Émile. Le suicide: étude de sociologie (Flix Alcan, Paris, 1897). [Google Scholar]
  2. Bettencourt L. M., Lobo J., Helbing D., Khnert C. & West G. B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. of Sci. USA 104, 7301–7306 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Alves L. G., Ribeiro H. V., Lenzi E. K. & Mendes R. S. Distance to the scaling law: a useful approach for unveiling relationships between crime and urban metrics. PLoS One 8, e69580 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Stanley H. Eugene. Introduction to phase transitions and critical phenomena (Oxford University Press, New York, 1987). [Google Scholar]
  5. Kleiber M. Body size and metabolic rate. Physiol. Rev. 27, 511–541 (1947). [DOI] [PubMed] [Google Scholar]
  6. Kleiber M. The fire of life: an introduction to animal energetics (John Wiley, New York, 1961). [Google Scholar]
  7. Schmidt–Nielsen K. Scaling: why is animal size so important? (Cambridge University Press, Cambridge, 1984). [Google Scholar]
  8. Bettencourt L. M., Lobo J., Strumsky D. & West G. B. Urban scaling and its deviations: Revealing the structure of wealth, innovation and crime across cities. PloS One 5, e13541 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bettencourt L. M. & West G. A unified theory of urban living. Nature 467, 912–913 (2010). [DOI] [PubMed] [Google Scholar]
  10. Oliveira E. A., Andrade Jr J. S. & Makse H. A. Large cities are less green. Sci. Rep. 4, 4235 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Brazils Public healthcare System (SUS), Department of Data Processing (DATASUS). Available: http://www.datasus.gov.br/ Accessed 2012 Jun 1.
  12. Fowler J. H. & Christakis N. A. Dynamic spread of happiness in a large social network: longitudinal analysis over 20 years in the framingham heart study. Br. Med. J. 337, 23–27 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. West G. B., Brown J. H. & Enquist B. J. A general model for the origin of allometric scaling laws in biology. Science 276, 122–126 (1997). [DOI] [PubMed] [Google Scholar]
  14. Changizi M. A., McDannald M. A. & Widders D. Scaling of differentiation in networks: Nervous systems, organisms, ant colonies, ecosystems, businesses, universities, cities, electronic circuits, and Legos. J. Theor. Biol. 218, 215–237 (2002). [DOI] [PubMed] [Google Scholar]
  15. Bettencourt L. M. The origins of scaling in cities. Science 340, 1438–1441 (2013). [DOI] [PubMed] [Google Scholar]
  16. Alison L. et al. Emotions as infectious diseases in a large social network: the SISa model. Proc. R. Soc. B 277, 3827–3835 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Nadaraya E. A. On Estimating Regression. Theor. Probab. Appl. 9, 141–142 (1964). [Google Scholar]
  18. Watson G. S. Smooth regression analysis. Sankhya Ser. A 26, 359–372 (1964). [Google Scholar]
  19. Montgomery D. C. & Peck E. A. Introduction to Linear Regression Analysis (Wiley, New York, 1992). [Google Scholar]
  20. Schlpäfer M. et al. The scaling of human interactions with city size. arXiv:1210.5215v2 (2013). [DOI] [PMC free article] [PubMed]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES