Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Sep 1;4:6257. doi: 10.1038/srep06257

Manipulation of acoustic focusing with an active and configurable planar metasurface transducer

Jiajun Zhao 1,2, Huapeng Ye 1, Kun Huang 1, Zhi Ning Chen 1, Baowen Li 2,3, Cheng-Wei Qiu 1,a
PMCID: PMC4150112  PMID: 25174409

Abstract

It has a pivotal role in medical science and in industry to concentrate the acoustic energy created with piezoelectric transducers (PTs) into a specific area. However, previous researches seldom consider the focal resolution, whose focal size is much larger than one wavelength. Furthermore, there is to date no such design method of PTs that allows a large degree of freedom to achieve designed focal patterns. Here, an active and configurable planar metasurface PT prototype is proposed to manipulate the acoustic focal pattern and the focal resolution freely. By suitably optimized ring configurations of the active metasurface PT, we demonstrate the manipulation of focal patterns in acoustic far fields, such as the designed focal needle and multi foci. Our method is also able to manipulate and improve the cross-sectional focal resolution from subwavelength to the extreme case: the deep sub-diffraction-limit resolution. Via the acoustic Rayleigh-Sommerfeld diffraction integral (RSI) cum the binary particle swarm optimization (BPSO), the free manipulation of focusing properties is achieved in acoustics for the first time. Our approach may offer more initiatives where the strict control of acoustic high-energy areas is demanding.

Research on acoustic focusing has led to various applications such as nondestructive testing techniques that inspect materials for hidden flaws1,2,3. Usually PTs are the most commonplace devices serving as the actuators of acoustic focusing. As the mechanism, when an electric field is applied across piezoelectric materials, the polarized molecules will align with the electric field, causing the materials to change dimensions4,5. Apart from the industrial applications, acoustic focusing utilized in medical science contributes significantly to therapeutic techniques as well. Ultrasound waves excited by PTs are capable of transmitting energy inside a body for medical purposes such as diagnostic sonography6. Other examples include focused ultrasound surgery that generates localized heating to treat tumors7,8, and lithotripsy that breaks up kidney stones9.

To avoid the bulky size of a curved PT, the flat annular Fresnel PT has been invented over decades, reducing the volume of piezoelectric portions into a flat layer10. However as the sacrifice, Fresnel PT intrinsically cannot concentrate the excited acoustic energy completely, as it is always accompanied with higher-order diffraction. In detail, a planar PT using a Fresnel equal-spaced array will inevitably generate the parasitic multiple divergent beams and higher-order convergent beams, making the focal spots less applicable. Actually, there has been to date no such acoustic design technique that allows us to achieve arbitrarily designed focal pattern along the axis. For example, one expected focal pattern for ultrasonic surgery is a specific segment of high acoustic energy along the axis (both its distance away from the PT and its focal depth are designable), i.e., an acoustic far-field focal needle, which was never obtained by PTs. A finite-length focal-needle pattern is also quite promising for particle operation and acceleration, which was developed in optics11,12.

Additionally, the focal resolution created with traditional PTs is usually low, whose focal size is much larger than one wavelength λ. Since the focal resolution can be improved with the wave frequency increased, previous researches usually ignore the consideration of improving the resultant focal resolution. However, it is noteworthy that an excitation of a higher frequency demands more energy consumption and suffers stronger attenuation. Besides, acoustic aberration could also severely blur the focal resolution. Thus, the rational improvement is to increase the relative focal resolution with the same excited frequency remaining.

In this paper, we establish the acoustic PT prototype, whose piezoelectric elements are squeezed into a flat thin layer compared to the scale of the entire device. The active planar interface also extends the knowledge of acoustic metasurface engineering for the deflection of sound beams using passive elements13,14. Through the optimized ring configurations of the active metasurface PT, we are able to manipulate the focal pattern and the focal resolution in acoustic far fields. Firstly, we design the far-field finite-length focal needle with the manipulated distance and depth. Its focal resolution is subwavelength for the full width at half maximum (FWHM), and it propagates without divergence for a distance of ~5.9λ as designed, longer than the depth ~ 4λ of the reported optical needle15. These two designed focusing properties created with PTs were never achieved in acoustics, to the best of our knowledge. To further verify the robustness of our manipulation of the focal pattern, via another optimized ring configuration, we obtain the designed far-field multi foci, whose FWHM (~0.45λ) beats the Rayleigh diffraction limit of conventional acoustic instruments (0.5λ). Besides, to demonstrate the manipulation of the focal resolution, we design the extreme case of the super-oscillatory super resolution, whose size is ~0.3λ in acoustic far fields, much smaller than the diffraction limit.

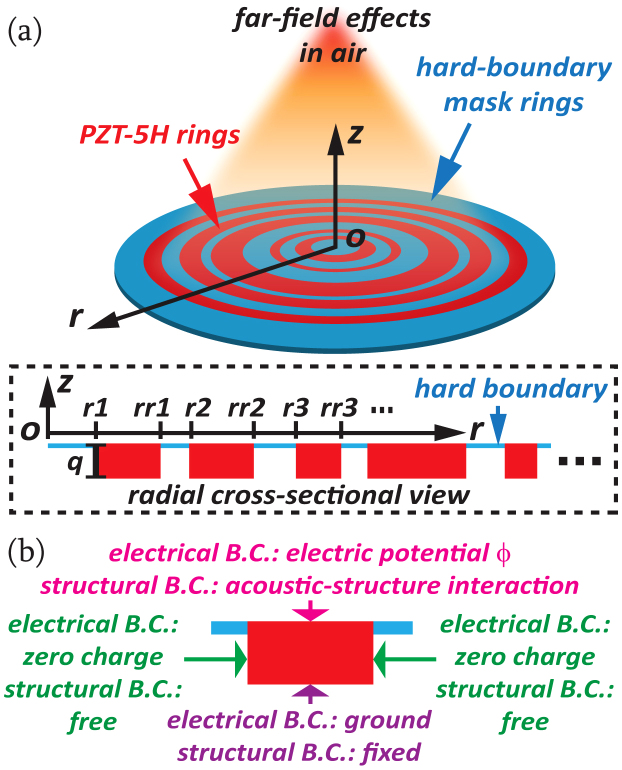
In the three-dimensional view of the configurable planar metasurface PT prototype in Fig. 1(a), piezoelectric rings (red) are unevenly spaced with hard-boundary mask rings (blue) in between. A type of common artificial ceramic is employed as the piezoelectric material: lead zirconate titanate PZT-5H16. In the radial view, the thickness q is set identical for all PZT-5H rings, and the ring configuration (r1, rr1, r2, rr2 …) will be optimized according to different focusing manipulation. The thin hard-boundary mask rings in between, through which no sound can pass, are the complements of the spaced gaps between PZT-5H rings, co-planar with z = 0. The entire PT is axisymmetric with respect to +z, and the upper surface of the structure at z = 0 can be regarded as a flat active metasurface according to the radial cross-sectional view. In our following demonstrations in air (density: ρ0 = 1.21 kg/m3; speed of sound: c0 = 343 m/s), we will show the designed focal pattern and the focal resolution created with the PT prototype in acoustic far fields, the simulation of which is carried out by the finite element method (FEM). In detail, COMSOL Multiphysics is the platform we use, and the simulation is facilitated by the coupling of the embedded acoustic module and the acoustic-piezoelectric interaction module concurrently.

Figure 1.

Figure 1

Open in a new tab

(a) Schematics of the configurable planar metasurface PT prototype. Inside the dashed box is the radial cross-sectional view of the ring configuration, showing the unevenly-distributed piezoelectric elements and the hard boundaries. (b) The B.C.s of each piezoelectric ring observed from the radial cross-sectional view.

The design method and the related physics are elaborated in this part. The electromechanical constitutive equations governing the piezoelectric effect of PZT-5H are written in the stress-charge form17:

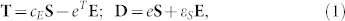graphic file with name srep06257-m1.jpg

where T and S are the vectors of stress and strain; E = −∇φ is the electric field, which is rephrased with the electric potential φ exerted on the PZT-5H rings; cE the elasticity matrix evaluated at a constant electric field; e the coupling matrix; D the electric displacement; εS the electric permittivity matrix evaluated at a constant mechanical strain. Usually, cE is straightforwardly given as an anisotropic symmetric matrix; εS = ε0εrS includes the relative permittivity matrix εrS. These parameters of PZT-5H are listed in Supplementary Information. For each PZT-5H ring whose poling direction is aligned toward +z, the boundary conditions (B.C.s) are indicated in Fig. 1(b). The structural B.C.s for the inner and the outer sides are free of constraint, while the bottom is fixed with the structural displacement u = 0. The top undergoes the interaction between sounds and structures17:

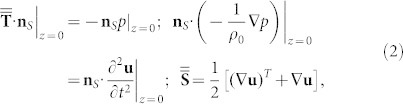graphic file with name srep06257-m2.jpg

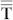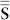where Inline graphic and Inline graphic are the tensors of stress and strain; nS is the outward-pointing unit normal vector seen from inside PZT-5H. Briefly, the first equality indicates the acoustic pressure load p; the second makes the normal acceleration of p on the boundary z = 0 equal to that of the structural displacement; the third is the intrinsic constitutive equation of 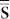Inline graphic and u inside solids. Meanwhile, the electrical B.C.s for the inner and the outer sides are free of charge nS · D = 0, whilst the bottom touches ground φ = 0. The top is assigned with monochromatic φ = V0cos(2πft). One common technique to impose the voltage bias is a sandwiched structure with PTH-5H elements between two Au electrode layers.

Next, in order to manipulate the far-field focal pattern or the focal resolution created with the planar metasurface PT prototype, we propose the acoustic RSI in conjunction with BPSO18,19,20. The derivation starts from the Kirchhoff-Helmholtz integral22:

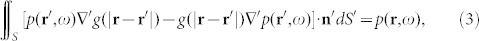graphic file with name srep06257-m3.jpg

where r∈Ω, g(x) = exp(ik0x)/(4πx) and k0 = 2πf/c0. p(·) and g(·) are monochromatic wave functions defined throughout the domain Ω bounded by a closed surface S, while n′·∇′ denotes the differentiation along the inward normal to S. Provided that Ω is the half space z ≥ 0, S thus consists of the plane z = 0 and a hemisphere of infinite radius, centered at the origin. After adopting the Sommerfeld radiation condition 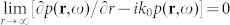Inline graphic to Eq. (3), we obtain:

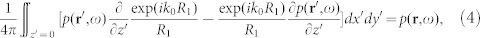graphic file with name srep06257-m4.jpg

where 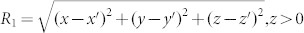Inline graphic. On the other hand, if r situates in the lower half space z < 0, we will obtain23:

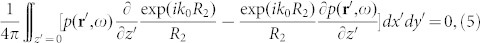graphic file with name srep06257-m5.jpg

where 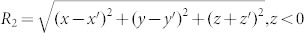Inline graphic. Subsequently, making use of the connection between R1 and R2 at z = 0, we incorporate Eq. (4) and Eq. (5), bringing about the acoustic RSI:

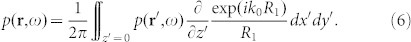graphic file with name srep06257-m6.jpg

Applying the first-order Born approximation24 to Eq. (6), which simplifies the vibration at the fluid-solid interfaces at z = 0 to be uniform and binary, we finalize the equation as the acoustic RSI cum BPSO:

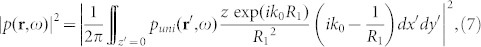graphic file with name srep06257-m7.jpg

where puni(·) is a binary function describing the ring configuration at z = 0, optimized for the designed focal pattern or focal resolution |p(r,ω)|2. Other than the requirement of acoustic pressure as well as its normal derivative in Eq. (3), Eq. (7) only requires the acoustic pressure on the surface, suitably for BPSO.

In general, BPSO is a nature-inspired evolutionary algorithm for stochastic optimization20. At first, the designed energy distribution |p(r,ω)|2 will be preset to benchmark acoustic focal patterns or resolutions in respective scenarios. Simultaneously, by means of Eq. (7), BPSO will be implemented to optimize the parameter r = [r1,r2,r3,…,rN] in order to fulfill the benchmark |p(r,ω)|2. For simplicity, the ring width Δr of the planar metasurface PT is fixed in our design. Once r is given, one can obtain another parameter rr = [rr1,rr2,rr3,…,rrN] by rr = r + Δr. Then, the parameters r and rr determine the ring configuration in Fig. 1(a). Although the fixed Δr sets a constraint in designing the active metasurface PT, this low-cost approach always works well in many applications21, as we will show later.

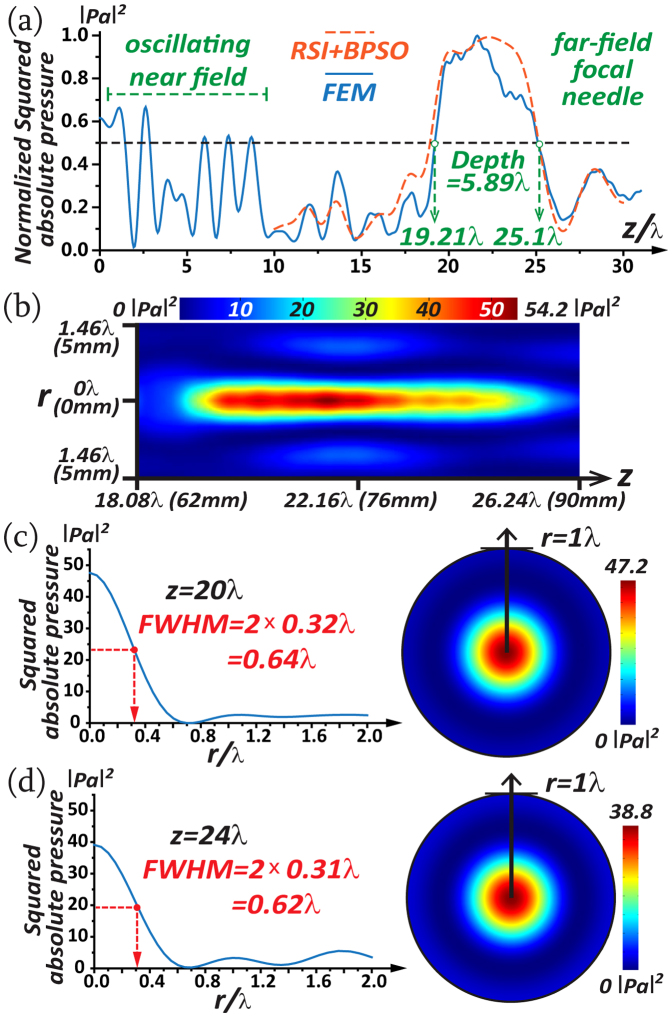
To vindicate the proposed method, i.e. the acoustic RSI cum BPSO, in the manipulation of acoustic focusing, we first demonstrate the manipulation of the acoustic focal patterns such as the designed focal needle and the designed multi foci. The arbitrary design of a focal pattern is impossible if we simply resort to acoustic wavefront construction by the method of effective medium25,26. In our case for the pattern of a finite-length focal needle on axis, we conveniently select V0 = 5V and f = 100 kHz that generates acoustic waves of λ = 3.43 mm in the space z > 0. Note that for the purpose of a finite-length focal-needle pattern in the far field, we require a depth of continuous acoustic focal energy along the axis with the low energy level at the rest, whilst the location, i.e., both the depth of the needle and the specific positions of the two ends away from the transducer, could be subtly designed as well. In Fig. 2(a), the on-axis focal-needle pattern, whose position is preset to extend from 19.2λ to 25.1λ, is designed as the orange dashed curve |p(r,ω)|2, while simultaneously the optimized ring configuration is calculated by the acoustic RSI cum BPSO as described above. The optimized ring configuration listed in Supplementary Information includes 30 PZT-5H rings with the maximum radius ~180 mm, while q is adjusted optimally to be 4 mm.

Figure 2.

Figure 2

Open in a new tab

(a) The normalized squared absolute pressure, displaying the pattern of the designed finite-length far-field focal needle. (b) The field distribution of the squared absolute pressure around the focal needle. (c,d) The radial distributions of the squared absolute pressure at the cross sections z = 20λ and z = 24λ, with their respective field distributions.

In the same plot, the full-wave acoustic field generated by the planar and active metasurface PT as the real case is simulated by the FEM as the blue curve, using Eqs. (1,2), and the result coincides with the designed finite-length focal-needle pattern (orange dashed curve). It is noteworthy that the standing-wave-like oscillation from 0λ to ~10λ along z agrees with the classic characteristic of acoustic near fields22. Besides, we notice that most energy is focused into the designed far-field focal region from 19.21λ to 25.1λ, implying the focal needle of the depth 5.89λ as designed, longer than the depth ~ 4λ of the reported optical needle15. In Fig. 2(b), the field pattern of |p(r,ω)|2 simulated by FEM around the focal needle is displayed. The contrast between the intense needle and the ambient quiet field is apparent, which meets the requirement of the focal-needle shape.

It is necessary to mention the subwavelength focal resolution of the focal-needle pattern in Fig. 2(c,d). The radial distributions of the squared absolute pressure are plotted on the left while their field distributions are on the right. The FWHM of the focal size in the far field is measured to be ~0.64λ at z = 20λ and z = 24λ, smaller than one wavelength but larger than the diffraction limit. We may also conclude from Fig. 2(c,d) that the acoustic needle pattern is formed of a nearly constant subwavelength width throughout. Moreover, the intensity of the sidelobes in Fig. 2(c,d) is drastically smaller than the central intensity, crucially for potential imaging applications. Note that such subwavelength acoustic focusing is generated in the true far field without resorting to evanescent acoustic waves limited to the near field only. We believe this is the first time that the pattern of an acoustic finite-length focal needle is actualized.

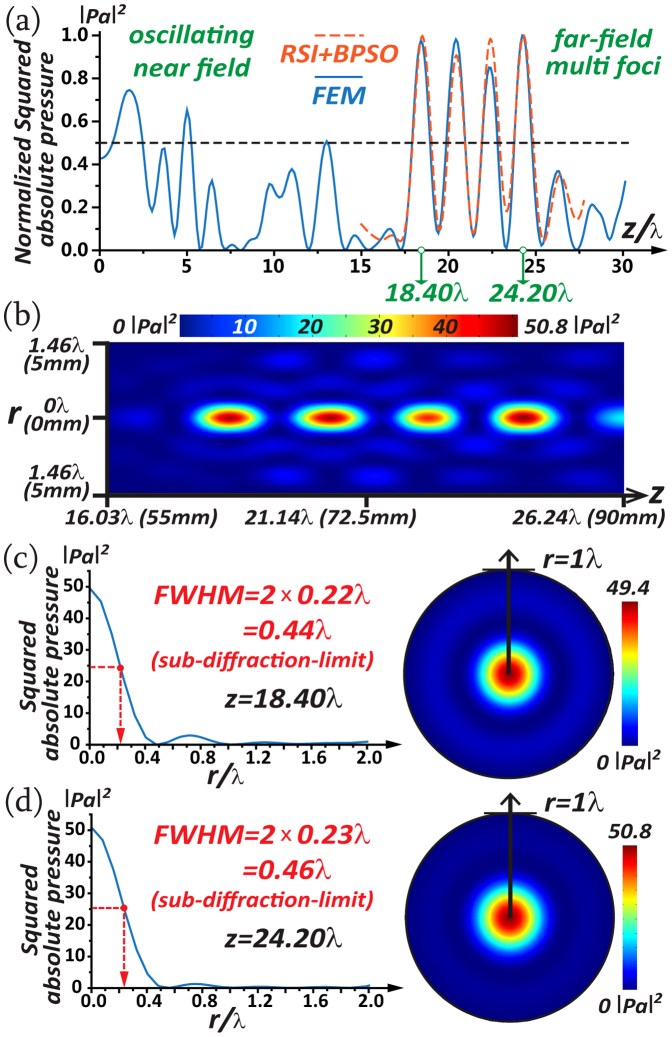
To further show the robustness of the acoustic-focusing manipulation, we take the example of the acoustic far-field multi foci as another designed focal pattern. Here, the multi foci are designed as the four discrete foci along the axis in the far field. The corresponding normalized energy pattern |p(r,ω)|2 designed by the acoustic RSI cum BPSO is the orange dashed curve in Fig. 3(a), using the ring configuration which is simultaneously optimized in this case. Note that the ring configuration here is designed and optimized in the same way except for a different focal pattern (benchmark). It includes 28 PZT-5H rings, whose parameters are listed in Supplementary Information. q = 3 mm is optimized here while V0 and f remain the same. The blue curve indicates the full-wave simulation by FEM using Eqs. (1,2). Again, the satisfactory agreement between these two outcomes confirms our pattern design. The corresponding field distribution in Fig. 3(b) is simulated with respect to |p(r,ω)|2 around the multi foci. Also, we notice that the focal resolution (FWHM ~0.45λ) of the multi foci in Fig. 3(c,d) is subwavelength and even beats the Rayleigh diffraction limit of 0.5λ, which was never realized in terms of PT technology.

Figure 3.

Figure 3

Open in a new tab

(a) The normalized squared absolute pressure, displaying the pattern of the designed far-field multi foci. (b) The field distribution of the squared absolute pressure around the multi foci. (c,d) The radial distributions of the squared absolute pressure at the cross sections z = 18.4λ and z = 24.2λ, and their respective field distributions.

As mentioned in the above two cases, by means of the properly-optimized ring configurations, we are able to achieve the designed acoustic focal patterns with a subwavelength resolution as well as a sub-diffraction-limit resolution. The underlying physics of achieving the focal resolution beyond the restriction of diffraction limit by means of the multi-ring active metasurface transducer is the interference and the diffraction of excited sound beams, which has been thoroughly elaborated as a wave phenomenon in the scenario of optics21. In essence, the superposition of the excited zero-order Bessel patterns at the focal plane breaches the traditional Rayleigh diffraction limit, while the algorithm BPSO simultaneously optimizes the ring configuration to further improve the acoustic focal resolution21. If we intend to further enhance the focal resolution to the deep sub-diffraction-limit focal size substantially smaller than 0.38λ, the situation will turn into the extreme case of the super-oscillatory super resolution18,19.

Our design method, the acoustic RSI cum BPSO in terms of PT technology, is able to manipulate the acoustic focal resolution as well and to increase it to the acoustic super-oscillatory super resolution. In this case, we choose V0 = 100V and f = 40 kHz for the electric potential exerted on all PZT-5H rings, which produce acoustic waves of λ = 8.575 mm in air. After setting the acoustic super-oscillatory super resolution (FWHM = 0.3λ at z = 20.06λ) as the designed focal resolution, we simultaneously optimize the ring configuration of the active metasurface PT in the same say, which includes 19 PZT-5H rings as shown in Supplementary Information, while q = 2 mm is adopted here optimally. The optimized result is the orange dashed curve in Fig. 4, showing the designed radial distribution of the normalized |p(r,ω)|2 at z = 20.06λ. The blue curve shows the corresponding full-wave simulation. The field distribution of the squared absolute pressure at the same cross section is plotted on the right in Fig. 4 to exhibit the result of the focal-resolution manipulation.

Figure 4. The radial distribution of the normalized squared absolute pressure at the cross section z = 20.06λ on the left, showing the focal size of the far-field acoustic super-oscillatory super resolution.

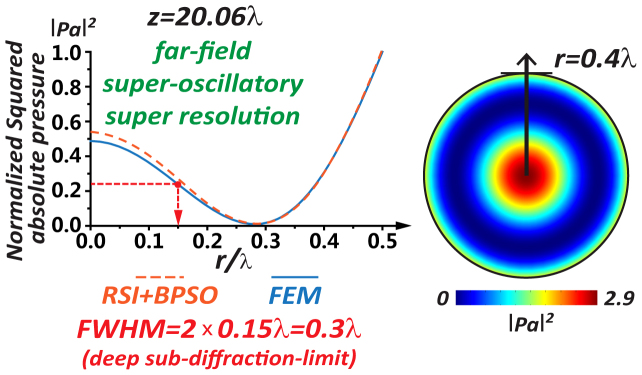
Figure 4

Open in a new tab

On the right is the corresponding field distribution of the squared absolute pressure.

We manage to control the focal size of the super-oscillatory super resolution to be 0.3λ in acoustic far fields, substantially smaller than 0.5λ. Nevertheless, if the FWHM of the focal spot is smaller than 0.38λ, there is an inevitable tradeoff uniquely in terms of the super-oscillatory case, which does not exist for a larger FWHM. Namely, the cost of the super-oscillatory super resolution is that most on-axis focal energy would be unavoidably squeezed away into the sidelobes as shown in Fig. 419,21. In principle, the deep sub-diffraction-limit super resolution can be manipulated to be infinitesimal, but the sacrifice is the increasingly-outsized sidelobes that make the super-oscillatory super resolution less efficient. However in spite of the naturally-inevitable tradeoff in the super-oscillatory case, people also try applying it in biological imaging18.

Physically, the proposed active and configurable planar metasurface PT used for the manipulation of acoustic focusing is a sort of binary-amplitude exciter for directly focusing the excited sounds into a certain pattern or a designed resolution in the post-evanescent fields, by optimally modifying the constructive interference of a large amount of acoustic beams. The acoustic RSI cum BPSO is applied to optimize the ring configuration on the active metasurface after certain focusing targets such as focal patterns or focal resolutions are chosen. Additionally, the manipulation of acoustic focusing is not the translation from optics, whose binary mask is passive without energy feeding27. Here, we fundamentally change the passive binary-amplitude baffle in optics into the active binary-amplitude exciter in acoustics that transforms itself into the feeding. Furthermore, we demonstrate the versatility of our design method, such as the realization of the focal-needle pattern, the multi-foci pattern and the manipulated super-oscillatory super resolution in acoustic far fields. Consequently, this approach to manipulate focusing properties is unique in acoustics.

In summary, we propose the method to manipulate the acoustic far-field focusing created with the active and configurable planar metasurface PT. The designed focal patterns and focal resolutions are demonstrated respectively. By means of the acoustic RSI cum BPSO, a large degree of freedom is obtained to manipulate various far-field focusing phenomena via optimized ring configurations. Here for the first time, the pattern of a finite-length focal needle of a subwavelength resolution is designed and realized; another example is the creation of the multi-foci pattern of a sub-diffraction-limit resolution; for the focal-resolution manipulation, the extremely-high resolution, i.e., the acoustic super-oscillatory super resolution, is demonstrated as well using the active and configurable planar metasurface PT prototype. Due to these significant advantages and versatility, the manipulation of acoustic focusing may offer a reformative framework in medical and industrial technology where the strict control of acoustic high-energy areas is demanding (biomedical actuator, focused ultrasound surgery, lithotripsy, nondestructive testing, etc.).

Author Contributions

J.Z., H.Y. and K.H. developed the theory and performed the numerical experiments. J.Z. and C.W.Q. conceived the idea and prepared the manuscript. Z.N.C. and B.L. contributed in the analysis. All authors edited the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep06257-s1.pdf (30.9KB, pdf)

References

  1. Song S. J., Shin H. J. & Jang Y. H. Development of an ultrasonic phased array system for nondestructive tests of nuclear power plant components. Nucl. Eng. Des. 214, 151 (2002). [Google Scholar]
  2. Chatillon S., Cattiaux G., Serre M. & Roy O. Ultrasonic non-destructive testing of pieces of complex geometry with a flexible phased array transducer. Ultrasonics 38, 131 (2000). [DOI] [PubMed] [Google Scholar]
  3. Shin S. W., Qureshi A. R., Lee J. Y. & Yun C. B. Piezoelectric sensor based nondestructive active monitoring of strength gain in concrete. Smart Mater. Struct. 17, 055002 (2008). [Google Scholar]
  4. Jaffe B., Cook W. R. & Jaffe H. Piezoelectric Ceramics (Academic, New York, 1971). [Google Scholar]
  5. Liu W. & Ren X. Large piezoelectric effect in Pb-free ceramics. Phys. Rev. Lett. 103, 257602 (2009). [DOI] [PubMed] [Google Scholar]
  6. Kim E. K. et al. New sonographic criteria for recommending fine-needle aspiration biopsy of nonpalpable solid nodules of the thyroid. AJR Am. J. Roentgenol. 178, 687 (2002). [DOI] [PubMed] [Google Scholar]
  7. Kennedy J. E. High-intensity focused ultrasound in the treatment of solid tumors. Nat. Rev. Cancer 5, 321 (2005). [DOI] [PubMed] [Google Scholar]
  8. Stewart E. A. et al. Focused ultrasound treatment of uterine fibroid tumors: Safety and feasibility of a non-invasive technique. Am. J. Obstet. Gynecol. 189, 48 (2003). [DOI] [PubMed] [Google Scholar]
  9. Averkiou M. A. & Cleveland R. O. Modeling of an electrohydraulic lithotripter with the KZK equation. J. Acoust. Soc. Am. 106, 102 (1999). [DOI] [PubMed] [Google Scholar]
  10. Drinkwater B. W. & Wilcox P. D. Ultrasonic arrays for non-destructive evaluation: A review. NDT & E Int. 39, 525 (2006). [Google Scholar]
  11. Wang J., Chen W. & Zhan Q. Engineering of high purity ultra-long optical needle field through reversing the electric dipole array radiation. Opt. Express 18, 21965 (2010). [DOI] [PubMed] [Google Scholar]
  12. Friese M. E. J., Nieminen T. A., Heckenberg N. R. & Rubinsztein-Dunlop H. Optical alignment and spinning of laser-trapped microscopic particles. Nature 394, 348 (1998). [Google Scholar]
  13. Zhao J., Li B., Chen Z. & Qiu C. W. Manipulating acoustic wavefront by inhomogeneous impedance and steerable extraordinary reflection. Sci. Rep. 3, 2537 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Li Y. et al. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Sci. Rep. 3, 2546 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Wang H. et al. Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nat. Photonics 2, 501 (2008). [Google Scholar]
  16. Castellano R. N. & Feinstein L. G. Ion-beam deposition of thin films of ferroelectric lead zirconate titanate (PZT). J. Appl. Phys. 50, 4406 (1979). [Google Scholar]
  17. Auld B. A. Acoustic Fields and Waves in Solids (Wiley, New York, 1973). [Google Scholar]
  18. Rogers E. T. F. et al. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 11, 432 (2012). [DOI] [PubMed] [Google Scholar]
  19. Ye H. et al. Creation of longitudinally polarized subwavelength hotspot with ultra-thin planar lens: Vectorial Rayleigh-Sommerfeld method. Laser Phys. Lett. 10, 065004 (2013). [Google Scholar]
  20. Jin N. & Rahmat-Samii Y. Advances in particle swarm optimization for antenna designs: real-number, binary, single-objective and multiobjective implementations. IEEE Trans. Antenna Propag. 55, 556 (2007). [Google Scholar]
  21. Huang K. et al. Optimization-free super-oscillatory lens using phase and amplitude masks. Laser Photon. Rev. 8, 152 (2014). [Google Scholar]
  22. Blackstock D. T. Fundamentals of Physical Acoustics (Wiley, New York, 2000). [Google Scholar]
  23. Born M. & Wolf E. Principles of Optics (Cambridge University Press, Cambridge, 1999). [Google Scholar]
  24. Sakurai J. J. Modern Quantum Mechanics (Addison Wesley, New York, 1994). [Google Scholar]
  25. Zhao J., Li B., Chen Z. & Qiu C. W. Redirection of sound waves using acoustic metasurface. Appl. Phys. Lett. 103, 151604 (2013). [Google Scholar]
  26. Li Y. et al. Acoustic focusing by coiling up space. Appl. Phys. Lett. 101, 233508 (2012). [Google Scholar]
  27. Rogers E. T. F. et al. Super-oscillatory optical needle. Appl. Phys. Lett. 102, 031108 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep06257-s1.pdf (30.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES